Wytrzymałość materiałów

Dziedzina wytrzymałości materiałów (zwana także mechaniką materiałów ) zwykle odnosi się do różnych metod obliczania naprężeń i odkształceń w elementach konstrukcyjnych, takich jak belki, słupy i wały. Metody stosowane do przewidywania odpowiedzi konstrukcji pod obciążeniem i jej podatności na różne rodzaje uszkodzeń uwzględniają właściwości materiałów, takie jak granica plastyczności, wytrzymałość graniczna , moduł Younga i współczynnik Poissona . Ponadto uwzględniane są makroskopowe właściwości elementu mechanicznego (właściwości geometryczne), takie jak jego długość, szerokość, grubość, ograniczenia graniczne i nagłe zmiany geometrii, takie jak otwory.

Teorię rozpoczęto od rozważenia zachowania jedno- i dwuwymiarowych elementów konstrukcji, których stany naprężenia można przybliżyć jako dwuwymiarowe, a następnie uogólniono na trzy wymiary, aby opracować pełniejszą teorię sprężystego i plastycznego zachowania się materiałów . Ważnym pionierem mechaniki materiałów był Stephen Timoshenko .

Definicja

W mechanice materiałów wytrzymałość materiału to jego zdolność do wytrzymania przyłożonego obciążenia bez uszkodzenia lub odkształcenia plastycznego . Dziedzina wytrzymałości materiałów zajmuje się siłami i odkształceniami wynikającymi z ich działania na materiał. Obciążenie przyłożone do elementu mechanicznego wywoła siły wewnętrzne w elemencie zwane naprężeniami, gdy siły te są wyrażone w jednostkach. Naprężenia działające na materiał powodują odkształcenie materiału w różny sposób, włącznie z całkowitym jego złamaniem. Odkształcenie materiału nazywane jest odkształceniem, gdy te odkształcenia również są umieszczane na podstawie jednostek.

Aby ocenić nośność tego elementu, należy obliczyć naprężenia i odkształcenia powstające w elemencie mechanicznym. Wymaga to pełnego opisu geometrii pręta, jego ograniczeń, obciążeń przyłożonych do pręta oraz właściwości materiału, z którego jest zbudowany pręt. Przyłożone obciążenia mogą być osiowe (rozciąganie lub ściskanie) lub obrotowe (wytrzymałość na ścinanie). Dzięki pełnemu opisowi obciążenia i geometrii pręta można obliczyć stan naprężenia i stanu odkształcenia w dowolnym punkcie pręta. Znając stan naprężenia i odkształcenia w pręcie, można obliczyć wytrzymałość (nośność) tego pręta, jego odkształcenia (cechy sztywności) oraz jego stabilność (zdolność do zachowania pierwotnej konfiguracji).

Obliczone naprężenia można następnie porównać z pewną miarą wytrzymałości elementu, taką jak plastyczność materiału lub wytrzymałość ostateczna. Obliczone ugięcie pręta można porównać z kryteriami ugięcia opartymi na wykorzystaniu pręta. Obliczone obciążenie wyboczeniowe pręta można porównać z przyłożonym obciążeniem. Obliczoną sztywność i rozkład masy elementu można wykorzystać do obliczenia odpowiedzi dynamicznej elementu, a następnie porównać go ze środowiskiem akustycznym, w którym będzie on używany.

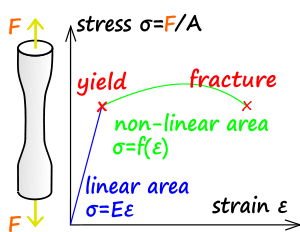
Wytrzymałość materiału odnosi się do punktu na inżynierskiej krzywej naprężenie-odkształcenie (granica plastyczności), powyżej którego materiał ulega odkształceniom, które nie zostaną całkowicie odwrócone po usunięciu obciążenia, w wyniku czego element będzie miał trwałe odkształcenie. Ostateczna wytrzymałość materiału odnosi się do maksymalnej osiągniętej wartości naprężenia. Wytrzymałość na pękanie to wartość naprężenia przy zerwaniu (ostatnia zarejestrowana wartość naprężenia).

Rodzaje obciążeń

• poprzeczne — siły przyłożone prostopadle do osi podłużnej pręta. Obciążenie poprzeczne powoduje zginanie i odchylanie elementu od jego pierwotnego położenia, przy czym wewnętrzne naprężenia rozciągające i ściskające towarzyszą zmianie krzywizny elementu. Obciążenie poprzeczne wywołuje również siły ścinające, które powodują odkształcenie ścinające materiału i zwiększają ugięcie poprzeczne pręta.
• Obciążenie osiowe — przyłożone siły są współliniowe z osią wzdłużną pręta. Siły powodują rozciąganie lub skracanie członka.
• skrętne — działanie skręcające spowodowane parą par sił przyłożonych zewnętrznie, jednakowych i skierowanych przeciwnie, działających na równoległych płaszczyznach lub przez pojedynczą parę zewnętrzną przyłożoną do pręta, którego jeden koniec jest unieruchomiony przed obrotem.

Warunki stresowe

Materiał jest obciążany a) ściskaniem, b) rozciąganiem, c) ścinaniem.

Naprężenie jednoosiowe wyraża się przez

${\ Displaystyle \ sigma = {\ Frac {F} {A}}}$

gdzie F jest siłą [N] działającą na powierzchnię A [m ² ]. Obszar może być obszarem niezdeformowanym lub obszarem zdeformowanym, w zależności od tego, czy przedmiotem zainteresowania jest naprężenie inżynierskie , czy naprężenie rzeczywiste.

• Naprężenie ściskające (lub ściskanie ) to stan naprężenia spowodowany przyłożonym obciążeniem, który działa w celu zmniejszenia długości materiału ( elementu ściskanego ) wzdłuż osi przyłożonego obciążenia, innymi słowy, jest to stan naprężenia, który powoduje ściśnięcie materiału. Prostym przypadkiem ściskania jest jednoosiowe ściskanie wywołane działaniem przeciwnych, pchających sił. Wytrzymałość na ściskanie materiałów jest na ogół wyższa niż ich wytrzymałość na rozciąganie. Jednak konstrukcje obciążone ściskaniem podlegają dodatkowym trybom uszkodzeń, takim jak wyboczenie , które są zależne od geometrii pręta.
• Naprężenie rozciągające to stan naprężenia wywołany przez przyłożone obciążenie, które ma tendencję do wydłużania materiału wzdłuż osi przyłożonego obciążenia, innymi słowy, naprężenie spowodowane ciągnięciem materiału . Wytrzymałość konstrukcji o równym polu przekroju obciążonych rozciąganiem jest niezależna od kształtu przekroju. Materiały obciążone rozciąganiem są podatne na koncentrację naprężeń , takich jak wady materiałowe lub nagłe zmiany geometrii. Jednak materiały wykazujące ciągliwość (na przykład większość metali) mogą tolerować pewne defekty, podczas gdy materiały kruche (takie jak ceramika) mogą zawieść znacznie poniżej ich ostatecznej wytrzymałości.
• Naprężenie ścinające jest stanem naprężenia wywołanym przez połączoną energię pary przeciwstawnych sił działających wzdłuż równoległych linii działania w materiale, innymi słowy naprężenie spowodowane przez powierzchnie materiału przesuwające się względem siebie . Przykładem jest cięcie papieru nożyczkami lub naprężenia spowodowane obciążeniem skrętnym.

Parametry naprężeń dla odporności

Odporność materiału można wyrazić kilkoma parametrami naprężeń mechanicznych . Termin wytrzymałość materiału jest używany w odniesieniu do parametrów naprężeń mechanicznych . Są to wielkości fizyczne o wymiarach jednorodnych względem ciśnienia i siły na jednostkę powierzchni . Tradycyjną jednostką miary siły są zatem MPa w Międzynarodowym Układzie Jednostek , a psi między zwyczajowymi jednostkami Stanów Zjednoczonych . Parametry wytrzymałościowe obejmują: granicę plastyczności, wytrzymałość na rozciąganie, wytrzymałość zmęczeniową, odporność na pękanie i inne parametry.

• Granica plastyczności to najmniejsze naprężenie, które powoduje trwałe odkształcenie materiału. W niektórych materiałach, takich jak stopy aluminium , punkt plastyczności jest trudny do zidentyfikowania, dlatego zwykle definiuje się go jako naprężenie wymagane do spowodowania odkształcenia plastycznego o wartości 0,2%. Nazywa się to stresem próbnym 0,2%.

• Wytrzymałość na ściskanie to stan graniczny naprężenia ściskającego , który prowadzi do zniszczenia materiału w postaci zniszczenia plastycznego (teoretyczna nieskończona plastyczność) lub zniszczenia kruchego (pęknięcie w wyniku propagacji pęknięć lub poślizgu wzdłuż słabej płaszczyzny - patrz wytrzymałość na ścinanie ) .
• Wytrzymałość na rozciąganie lub graniczna wytrzymałość na rozciąganie to stan graniczny naprężenia rozciągającego , który prowadzi do zniszczenia przy rozciąganiu na wzór zniszczenia ciągliwego (plastyczność jako pierwszy etap tego zniszczenia, pewne utwardzenie w drugim etapie i pęknięcie po ewentualnym „szyjce” formacja) lub kruche pęknięcie (nagłe pęknięcie na dwie lub więcej części w stanie niskiego naprężenia). Wytrzymałość na rozciąganie można podać jako naprężenie rzeczywiste lub naprężenie inżynierskie, ale najczęściej stosuje się naprężenie inżynierskie.
• Wytrzymałość zmęczeniowa jest bardziej złożoną miarą wytrzymałości materiału, która uwzględnia kilka epizodów obciążenia w okresie użytkowania obiektu i jest zwykle trudniejsza do oceny niż miary wytrzymałości statycznej. Wytrzymałość zmęczeniowa jest tu podawana jako prosty zakres ( ${\ Displaystyle \ Delta \ sigma = \ sigma _ {\ operatorname {max}} - \ sigma _ {\ operatorname {min} }}$ ). W przypadku obciążenia cyklicznego można to odpowiednio wyrazić jako amplitudę zwykle przy zerowym średnim naprężeniu, wraz z liczbą cykli do zniszczenia w tych warunkach naprężenia.

• Udarność to zdolność materiału do wytrzymania nagle przyłożonego obciążenia i jest wyrażana w kategoriach energii. Często mierzone za pomocą testu udarności Izoda lub testu udarności Charpy'ego , z których oba mierzą energię uderzenia wymaganą do pęknięcia próbki. Objętość, moduł sprężystości , rozkład sił i granica plastyczności wpływają na udarność materiału. Aby materiał lub przedmiot miał wysoką udarność, naprężenia muszą być równomiernie rozłożone w całym obiekcie. Musi również mieć dużą objętość przy niskim module sprężystości i wysokiej granicy plastyczności materiału.

Parametry odkształcenia dla rezystancji

• Odkształcenie materiału to zmiana geometrii powstająca pod wpływem naprężeń (w wyniku przyłożonych sił, pól grawitacyjnych, przyspieszeń, rozszerzalności cieplnej itp.). Odkształcenie wyraża się polem przemieszczenia materiału.
• Odkształcenie lub odkształcenie zredukowane to termin matematyczny, który wyraża trend zmiany odkształcenia w polu materialnym. Odkształcenie to odkształcenie na jednostkę długości. W przypadku obciążenia jednoosiowego przemieszczenie próbki (np. elementu prętowego) prowadzi do obliczenia odkształcenia wyrażonego jako iloraz przemieszczenia i pierwotnej długości próbki. Dla trójwymiarowych pól przemieszczeń wyraża się je jako pochodne funkcji przemieszczenia względem tensora drugiego rzędu (z 6 niezależnymi elementami).
• Ugięcie to termin opisujący wielkość, o jaką element konstrukcyjny jest przemieszczany pod wpływem przyłożonego obciążenia.

Relacje naprężenie-odkształcenie

Główny artykuł: Krzywa naprężenie-odkształcenie

Podstawowa odpowiedź statyczna próbki pod napięciem

• Elastyczność to zdolność materiału do powrotu do poprzedniego kształtu po uwolnieniu naprężeń. W wielu materiałach zależność między przyłożonym naprężeniem jest wprost proporcjonalna do wynikowego odkształcenia (do pewnej granicy), a wykres przedstawiający te dwie wielkości jest linią prostą.

Nachylenie tej linii jest znane jako moduł Younga lub „moduł sprężystości”. Moduł sprężystości można wykorzystać do określenia zależności naprężenie-odkształcenie w liniowo-sprężystej części krzywej naprężenie-odkształcenie. Obszar liniowo-sprężysty znajduje się albo poniżej granicy plastyczności, albo jeśli granica plastyczności nie jest łatwa do zidentyfikowania na wykresie naprężenie-odkształcenie, definiuje się ją jako zawierającą się między 0 a 0,2% odkształcenia i jest definiowana jako obszar odkształcenia, w którym nie następuje uplastycznienie (trwałe odkształcenie).

• Plastyczność lub odkształcenie plastyczne jest przeciwieństwem odkształcenia sprężystego i jest określane jako odkształcenie nieodwracalne. Odkształcenie plastyczne zostaje zachowane po zwolnieniu przyłożonego naprężenia. Większość materiałów z kategorii liniowo-sprężystych jest zwykle podatna na odkształcenia plastyczne. Kruche materiały, takie jak ceramika, nie podlegają żadnym odkształceniom plastycznym i pękają przy stosunkowo niewielkich naprężeniach, podczas gdy materiały ciągliwe, takie jak metale, ołów lub polimery, odkształcą się plastycznie znacznie bardziej przed rozpoczęciem pękania.

Rozważ różnicę między marchewką a gumą do żucia. Marchewka będzie się bardzo mało rozciągać przed pęknięciem. Z drugiej strony guma balonowa do żucia ulegnie ogromnej deformacji plastycznej, zanim ostatecznie pęknie.

Warunki projektowe

Wytrzymałość graniczna jest atrybutem związanym z materiałem, a nie tylko z konkretną próbką wykonaną z materiału, i jako taka jest podawana jako siła na jednostkę powierzchni przekroju poprzecznego (N/m 2 ⁾ . Ostateczna wytrzymałość to maksymalne naprężenie, jakie materiał może wytrzymać, zanim pęknie lub osłabnie. Na przykład maksymalna wytrzymałość na rozciąganie (UTS) stali AISI 1018 wynosi 440 MPa. W jednostkach imperialnych jednostką naprężenia jest lbf/in² lub funt-siła na cal kwadratowy . Jednostka ta jest często określana skrótem psi . Tysiąc psi to skrót ksi .

Współczynnik bezpieczeństwa to kryterium projektowe, które musi spełniać zaprojektowany komponent lub konstrukcja. ${\ Displaystyle FS = UTS/R}$ , gdzie FS: współczynnik bezpieczeństwa, R: zastosowane naprężenie i UTS: maksymalne naprężenie (psi lub N/m ² )

Margines bezpieczeństwa jest również czasami używany jako kryterium projektowe. Jest zdefiniowany MS = Obciążenie niszczące/(Współczynnik bezpieczeństwa × Przewidywane obciążenie) − 1.

Na przykład, aby osiągnąć współczynnik bezpieczeństwa 4, dopuszczalne naprężenie elementu ze stali AISI 1018 można obliczyć jako ${\ Displaystyle R = UTS / FS}$ = 440/4 = 110 MPa lub ${\ Displaystyle R}$ = 110 × 10 ⁶ N/m ² . Takie dopuszczalne naprężenia są również znane jako „naprężenia projektowe” lub „naprężenia robocze”.

Naprężenia projektowe, które zostały określone na podstawie wartości granicznych lub granicy plastyczności materiałów, dają bezpieczne i wiarygodne wyniki tylko w przypadku obciążenia statycznego. Wiele części maszyn ulega uszkodzeniu, gdy jest poddawanych niestabilnym i stale zmieniającym się obciążeniom, nawet jeśli powstałe naprężenia są poniżej granicy plastyczności. Takie awarie nazywane są awariami zmęczeniowymi. Awaria polega na pęknięciu, które wydaje się być kruche z niewielkimi lub żadnymi widocznymi oznakami ustępowania. Jednakże, gdy naprężenie jest utrzymywane poniżej „stresu zmęczeniowego” lub „stresu granicznego wytrzymałości”, część będzie trwać w nieskończoność. Czysto odwracalne lub cykliczne naprężenie to takie, które zmienia się między równymi dodatnimi i ujemnymi szczytowymi naprężeniami podczas każdego cyklu działania. W czysto cyklicznym stresie średni stres wynosi zero. Kiedy część jest poddawana cyklicznemu naprężeniu, znanemu również jako zakres naprężeń (Sr), zaobserwowano, że uszkodzenie części następuje po pewnej liczbie zmian naprężeń (N), nawet jeśli wielkość zakresu naprężeń jest poniżej granica plastyczności materiału. Ogólnie rzecz biorąc, im wyższy zakres naprężeń, tym mniejsza liczba odwróceń potrzebnych do awarii.

Teorie awarii

Główny artykuł: Teoria uszkodzeń materiałów

Istnieją cztery teorie zniszczenia: teoria maksymalnego naprężenia ścinającego, teoria maksymalnego naprężenia normalnego, teoria maksymalnej energii odkształcenia i teoria maksymalnej energii odkształcenia. Z tych czterech teorii zniszczenia teoria maksymalnego naprężenia normalnego ma zastosowanie tylko do materiałów kruchych, a pozostałe trzy teorie mają zastosowanie do materiałów ciągliwych. Spośród trzech ostatnich teoria energii odkształcenia zapewnia najdokładniejsze wyniki w większości warunków stresowych. Teoria energii odkształcenia wymaga wartości współczynnika Poissona materiału części, który często nie jest łatwo dostępny. Teoria maksymalnego naprężenia ścinającego jest zachowawcza. Dla prostych jednokierunkowych naprężeń normalnych wszystkie teorie są równoważne, co oznacza, że ​​wszystkie teorie dadzą ten sam wynik.

• Teoria maksymalnego naprężenia ścinającego - Teoria ta postuluje, że uszkodzenie nastąpi, jeśli wielkość maksymalnego naprężenia ścinającego w części przekroczy wytrzymałość materiału na ścinanie określoną na podstawie testów jednoosiowych.
• Teoria maksymalnego naprężenia normalnego – ta teoria zakłada, że ​​uszkodzenie nastąpi, jeśli maksymalne naprężenie normalne w części przekroczy ostateczne naprężenie rozciągające materiału określone na podstawie testów jednoosiowych. Teoria ta dotyczy tylko materiałów kruchych. Maksymalne naprężenie rozciągające powinno być mniejsze lub równe ostatecznemu naprężeniu rozciągającemu podzielonemu przez współczynnik bezpieczeństwa. Wielkość maksymalnego naprężenia ściskającego powinna być mniejsza niż ostateczne naprężenie ściskające podzielone przez współczynnik bezpieczeństwa.
• Teoria maksymalnej energii odkształcenia - Teoria ta postuluje, że uszkodzenie nastąpi, gdy energia odkształcenia na jednostkę objętości spowodowana przyłożonymi naprężeniami w części jest równa energii odkształcenia na jednostkę objętości w granicy plastyczności w teście jednoosiowym.
• Teoria maksymalnej energii odkształcenia – Teoria ta jest również znana jako teoria energii ścinania lub teoria von Misesa-Hencky'ego . Teoria ta postuluje, że uszkodzenie nastąpi, gdy energia odkształcenia na jednostkę objętości spowodowana przyłożonymi naprężeniami w części będzie równa energii odkształcenia na jednostkę objętości na granicy plastyczności w teście jednoosiowym. Całkowitą energię sprężystości spowodowaną odkształceniem można podzielić na dwie części: jedna część powoduje zmianę objętości, a druga część powoduje zmianę kształtu. Energia odkształcenia to ilość energii potrzebna do zmiany kształtu.
• Mechanika pękania została założona przez Alana Arnolda Griffitha i George'a Rankine'a Irwina . Ta ważna teoria jest również znana jako numeryczne przeliczanie twardości materiału w przypadku istnienia pęknięć.

Wytrzymałość materiału zależy od jego mikrostruktury . Procesy inżynieryjne, którym poddawany jest materiał, mogą zmienić tę mikrostrukturę. Różnorodne mechanizmy wzmacniające , które zmieniają wytrzymałość materiału, obejmują utwardzanie przez zgniot , wzmacnianie roztworem stałym , utwardzanie wydzieleniowe i wzmacnianie granic ziaren i może być wyjaśnione ilościowo i jakościowo. Mechanizmom wzmacniającym towarzyszy zastrzeżenie, że niektóre inne właściwości mechaniczne materiału mogą ulec degeneracji, próbując wzmocnić materiał. Na przykład we wzmacnianiu granic ziaren, chociaż granica plastyczności jest maksymalizowana wraz ze zmniejszaniem się wielkości ziaren, ostatecznie bardzo małe rozmiary ziaren powodują, że materiał jest kruchy. Ogólnie rzecz biorąc, granica plastyczności materiału jest odpowiednim wskaźnikiem wytrzymałości mechanicznej materiału. Rozważane w połączeniu z faktem, że granica plastyczności jest parametrem, który przewiduje odkształcenie plastyczne w materiale można podejmować świadome decyzje, jak zwiększyć wytrzymałość materiału w zależności od jego właściwości mikrostrukturalnych i pożądanego efektu końcowego. Wytrzymałość jest wyrażana w postaci granicznych wartości naprężenia ściskającego , rozciągającego i ścinającego , które spowodowałyby uszkodzenie. Efekty obciążenia dynamicznego są prawdopodobnie najważniejszym praktycznym zagadnieniem wytrzymałości materiałów, zwłaszcza problemem zmęczenia materiału . Powtarzające się obciążenia często inicjują kruche pęknięcia, które rosną aż do wystąpienia awarii. Pęknięcia zaczynają się zawsze o godz koncentracji naprężeń , zwłaszcza zmian przekroju poprzecznego produktu, w pobliżu otworów i narożników, przy nominalnych poziomach naprężeń znacznie niższych niż podane dla wytrzymałości materiału.

Zobacz też

• Pełzanie (odkształcenie) — Tendencja materiału stałego do powolnego przemieszczania się lub trwałego odkształcania pod wpływem naprężeń mechanicznych
• Mapa mechanizmu deformacji – Mikroskopowe procesy odpowiedzialne za zmiany struktury, kształtu i objętości materiału Strony wyświetlające krótkie opisy celów przekierowania
• Dynamika – dział fizyki badający siły i ich wpływ na ruch
• Zmęczenie (materiał) - Inicjacja i propagacja pęknięć w materiale w wyniku obciążenia cyklicznego
• Inżynieria kryminalistyczna - Badanie awarii związanych z interwencją prawną
• Mechanika pękania - Dziedzina mechaniki badająca propagację pęknięć w materiałach
• Odporność na pękanie – współczynnik intensywności naprężeń, przy którym propagacja pęknięcia drastycznie wzrasta
• Wykaz właściwości materiałów § Właściwości mechaniczne
• Wybór materiału – proces wyboru materiału do konkretnej aplikacji Strony wyświetlające opisy wikidanych jako rozwiązanie awaryjne
• Dyfuzja molekularna - Ruch termiczny cząstek cieczy lub gazu w temperaturach powyżej zera absolutnego
• Wytrzymałość właściwa – Stosunek wytrzymałości do masy materiału
• Statyka – Dział mechaniki zajmujący się równowagą sił w układach nieruchomych
• Uniwersalna maszyna wytrzymałościowa – Rodzaj urządzenia do określania wytrzymałości materiału na rozciąganie lub ściskanie

Dalsza lektura

• Fa-Hwa Cheng, inicjały. (1997). Wytrzymałość materiału. Ohio: McGraw-Hill
• Mechanika materiałów, EJ Hearn
•   Alfirević, Ivo. Wytrzymałość materiałów I. Tehnička knjiga, 1995. ISBN 953-172-010-X .
•   Alfirević, Ivo. Wytrzymałość materiałów II . Tehnička knjiga, 1999. ISBN 953-6168-85-5 .
• Ashby, MF Wybór materiałów w projektowaniu . Pergamon, 1992.
•   Piwo, FP, ER Johnston i in. Mechanika materiałów , wydanie 3. McGraw-Hill, 2001. ISBN 0-07-248673-2
• Cottrell, AH Mechaniczne właściwości materii . Wiley, Nowy Jork, 1964.
•   Den Hartog, Jacob P. Wytrzymałość materiałów . Dover Publications, Inc., 1961, ISBN 0-486-60755-0 .
• Drucker, DC Wprowadzenie do mechaniki ciał stałych odkształcalnych . McGraw-Hill, 1967.
• Gordon, JE Nowa nauka o mocnych materiałach . Princeton, 1984.
•   Groover, Mikell P. Podstawy nowoczesnej produkcji , wydanie 2. John Wiley & Sons, Inc., 2002. ISBN 0-471-40051-3 .
•   Hashemi, Javad i William F. Smith. Podstawy inżynierii materiałowej i inżynierii materiałowej , wydanie 4. McGraw-Hill, 2006. ISBN 0-07-125690-3 .
•   Hibbeler, Statyka RC i Mechanika Materiałów , wydanie SI. Prentice-Hall, 2004. ISBN 0-13-129011-8 .
•   Lebiediew, Leonid P. i Michael J. Cloud. Przybliżanie doskonałości: podróż matematyka do świata mechaniki . Princeton University Press, 2004. ISBN 0-691-11726-8 .
•   Rozdział 10 – Wytrzymałość elastomerów , AN Gent, WV Mars, w: James E. Mark, Burak Erman i Mike Roland, redaktor(e), The Science and Technology of Rubber (wydanie czwarte), Academic Press, Boston, 2013, strony 473–516, ISBN 9780123945846 , 10.1016/B978-0-12-394584-6.00010-8
•   Mott, Robert L. Stosowana wytrzymałość materiałów , wydanie 4. Prentice-Hall, 2002. ISBN 0-13-088578-9 .
•   Popov, Egor P. Mechanika inżynierska ciał stałych . Prentice Hall, Englewood Cliffs, NJ, 1990. ISBN 0-13-279258-3 .
• Ramamrutham, S. Wytrzymałość materiałów .
•   Shames, IH i FA Cozzarelli. Analiza naprężeń sprężystych i niesprężystych . Prentice-Hall, 1991. ISBN 1-56032-686-7 .
•   Timoshenko S. Wytrzymałość materiałów , wydanie 3. Wydawnictwo Krieger, 1976, ISBN 0-88275-420-3 .
• Tymoszenko, SP i DH Young. Elementy wytrzymałości materiałów , wydanie 5. (System MKS)
• Davidge, RW, Mechaniczne zachowanie ceramiki, Cambridge Solid State Science Series, (1979)
• Trawnik, BR, Pęknięcie kruchych ciał stałych, Cambridge Solid State Science Series, wyd. 2. (1993)
• Green, D., Wprowadzenie do właściwości mechanicznych ceramiki, Cambridge Solid State Science Series, wyd. Clarke, DR, Suresh, S., Ward, IMBabu Tom.K (1998)

Linki zewnętrzne

• Teorie awarii
• Studia przypadków w przypadku awarii strukturalnych