Stres (mechanika)

Ten artykuł dotyczy naprężeń w mechanice klasycznej (continuum). Aby zapoznać się z naprężeniami w materiałoznawstwie, zobacz Wytrzymałość materiałów .

W przypadku innych zastosowań zobacz Stres .

Naprężenia Naprężenia
szczątkowe wewnątrz plastikowego kątomierza są widoczne w świetle spolaryzowanym .
Wspólne symbole	σ
jednostka SI	pascal
Inne jednostki	psi , bar
W jednostkach podstawowych SI	Pa = kg ⋅ m −1 ⋅ s −2
Wymiar	${\ Displaystyle {\ mathsf {L}} ^ {- 1} {\ mathsf {M}} {\ mathsf {T}} ^ {- 2}}$

W mechanice kontinuum naprężenie jest wielkością fizyczną opisującą wielkość sił powodujących deformację. Naprężenie definiuje się jako siłę na jednostkę powierzchni . Kiedy obiekt jest rozrywany przez siłę, powoduje to wydłużenie, które jest również znane jako odkształcenie, podobnie jak rozciąganie elastycznej taśmy, nazywane jest naprężeniem rozciągającym. Ale kiedy siły powodują ściskanie obiektu, nazywa się to naprężeniem ściskającym. Powstaje, gdy działają siły takie jak rozciąganie lub ściskanie działać na ciało. Im większa jest ta siła i im mniejszy jest przekrój poprzeczny ciała, na które działa, tym większe jest naprężenie. Dlatego naprężenie jest mierzone w niutonach na metr kwadratowy (N/m ² ) lub paskalach (Pa).

Naprężenie wyraża siły wewnętrzne , które sąsiednie cząstki ciągłego materiału wywierają na siebie nawzajem, podczas gdy odkształcenie jest miarą odkształcenia materiału. Na przykład, gdy solidny pionowy pręt podtrzymuje ciężar znajdujący się nad głową , każda cząsteczka w pręcie naciska na cząstki znajdujące się bezpośrednio pod nim. Gdy ciecz znajduje się w zamkniętym pojemniku pod ciśnieniem , każda cząsteczka jest popychana przez wszystkie otaczające ją cząsteczki. Ścianki pojemnika a ciśnienie -powierzchnia indukująca (taka jak tłok) naciska na nie w reakcji (newtonowskiej) . Te siły makroskopowe są w rzeczywistości wypadkową bardzo dużej liczby sił międzycząsteczkowych i zderzeń między cząstkami w tych cząsteczkach . Akcent jest często reprezentowany przez małą grecką literę sigma ( σ ).

Odkształcenie wewnątrz materiału może powstać w wyniku różnych mechanizmów, takich jak naprężenie wywierane przez siły zewnętrzne na materiał sypki (np. grawitacja ) lub na jego powierzchnię (np. siły kontaktowe , ciśnienie zewnętrzne lub tarcie ). Każde odkształcenie (odkształcenie) materiału stałego generuje wewnętrzne naprężenie sprężyste , analogiczne do siły reakcji sprężyny , które ma tendencję do przywracania materiału do pierwotnego, nieodkształconego stanu. W cieczach i gazach , tylko odkształcenia zmieniające objętość generują trwałe naprężenia sprężyste. Jednakże, jeśli odkształcenie zmienia się stopniowo w czasie, nawet w płynach zwykle występuje pewne naprężenie lepkie , przeciwstawiające się tej zmianie. Naprężenia sprężyste i lepkie są zwykle łączone pod nazwą naprężenia mechaniczne .

Naprężenia mechaniczne

Znaczące naprężenia mogą występować nawet wtedy, gdy odkształcenie jest znikome lub nie występuje (powszechne założenie przy modelowaniu przepływu wody). Stres może istnieć przy braku sił zewnętrznych; takie wbudowane naprężenia są ważne na przykład w betonie sprężonym i szkle hartowanym . Naprężenia mogą być również wywierane na materiał bez zastosowania sił wypadkowych , na przykład przez zmiany temperatury lub składu chemicznego lub przez zewnętrzne pola elektromagnetyczne (jak w piezoelektrycznych i magnetostrykcyjne ).

Zależność między naprężeniem mechanicznym, odkształceniem i szybkością zmian odkształcenia może być dość skomplikowana, chociaż przybliżenie liniowe może być w praktyce odpowiednie, jeśli wielkości są wystarczająco małe. Naprężenia przekraczające pewne granice wytrzymałości materiału powodują trwałe odkształcenia (takie jak płynięcie plastyczne , pękanie , kawitacja ) lub nawet zmianę jego struktury krystalicznej i składu chemicznego .

Historia

Most z czasów rzymskich w Szwajcarii . Kamienne łuki mostu podlegają ściskającym .

Inków na rzece Apurimac . Lina w moście podlega rozciągającym .

Ludzie wiedzieli o stresie wewnątrz materiałów od czasów starożytnych. Aż do XVII wieku zrozumienie to było w dużej mierze intuicyjne i empiryczne, choć nie przeszkodziło to w rozwoju stosunkowo zaawansowanych technologii, takich jak łuk kompozytowy i dmuchanie szkła .

W ciągu kilku tysiącleci zwłaszcza architekci i budowniczowie nauczyli się, jak łączyć starannie ukształtowane drewniane belki i kamienne bloki, aby wytrzymać, przenosić i rozprowadzać naprężenia w najbardziej efektywny sposób, za pomocą pomysłowych urządzeń, takich jak kapitele , łuki , kopuły , kratownice i latające przypory gotyckich katedr .

Starożytni i średniowieczni architekci opracowali pewne metody geometryczne i proste wzory do obliczania właściwych rozmiarów filarów i belek, ale naukowe zrozumienie naprężeń stało się możliwe dopiero po wynalezieniu niezbędnych narzędzi w XVII i XVIII wieku: rygorystyczny eksperymentalny eksperyment Galileo Galilei metoda , współrzędne i geometria analityczna Kartezjusza oraz prawa ruchu i równowagi Newtona oraz rachunek różniczkowy nieskończenie małych . Z tymi narzędziami, Augustin-Louis Cauchy był w stanie podać pierwszy rygorystyczny i ogólny model matematyczny zdeformowanego sprężystego ciała, wprowadzając pojęcia naprężenia i odkształcenia. Cauchy zauważył, że siła działająca na wyimaginowaną powierzchnię była funkcją liniową jej wektora normalnego; a ponadto musi to być funkcja symetryczna (o całkowitym pędzie zerowym). Zrozumienie naprężeń w cieczach rozpoczęło się od Newtona, który przedstawił wzór różniczkowy na siły tarcia (naprężenie ścinające) w równoległym przepływie laminarnym .

Przegląd

Definicja

Naprężenie definiuje się jako siłę działającą na „małą” granicę na jednostkę powierzchni tej granicy, dla wszystkich orientacji granicy. Wywodząc się z podstawowej wielkości fizycznej (siły) i czysto geometrycznej wielkości (obszaru), naprężenie jest również podstawową wielkością, taką jak prędkość, moment obrotowy lub energia , którą można określić ilościowo i przeanalizować bez wyraźnego uwzględnienia natury materiału lub jego fizyczne przyczyny.

Naprężenie w elemencie powierzchniowym (żółty krążek) to siła, jaką materiał po jednej stronie (kula górna) wywiera na materiał po drugiej stronie (kula dolna), podzielona przez pole powierzchni.

Zgodnie z podstawowymi założeniami mechaniki kontinuum stres jest pojęciem makroskopowym . Mianowicie cząstki brane pod uwagę w jej definicji i analizie powinny być na tyle małe, aby można je było traktować jako jednorodne pod względem składu i stanu, ale wciąż na tyle duże, aby można je było zignorować efekty i szczegółowe ruchy cząsteczek. Zatem siła między dwiema cząstkami jest w rzeczywistości średnią z bardzo dużej liczby sił atomowych między ich cząsteczkami; zakłada się, że wielkości fizyczne, takie jak masa, prędkość i siły, które działają przez masę ciał trójwymiarowych, takie jak grawitacja, są równomiernie rozłożone. W zależności od kontekstu można również założyć, że cząsteczki są wystarczająco duże, aby umożliwić uśrednienie innych cech mikroskopowych, takich jak ziarna metalowego pręta lub włókna kawałka drewna .

Ilościowo naprężenie jest wyrażone przez wektor trakcji Cauchy'ego T zdefiniowany jako siła rozciągająca F między sąsiednimi częściami materiału na wyimaginowanej powierzchni oddzielającej S , podzielona przez pole S . W płynie w spoczynku siła jest prostopadła do powierzchni i jest znanym ciśnieniem . W ciele stałym lub w przepływie lepkiej cieczy siła F może nie być prostopadła do S ; stąd naprężenie na powierzchni należy traktować jako wielkość wektorową, a nie skalarną. Ponadto kierunek i wielkość generalnie zależą od orientacji S . Zatem stan naprężenia materiału musi być opisany przez tensor , zwany tensorem naprężenia (Cauchy'ego) ; która jest funkcją liniową , która wiąże wektor normalny n powierzchni S z wektorem trakcji T w poprzek S . W odniesieniu do dowolnego wybranego układu współrzędnych , tensor naprężenia Cauchy'ego można przedstawić jako symetryczną macierz liczb rzeczywistych 3 × 3. Nawet w jednorodnym ciele tensor naprężenia może się różnić w zależności od miejsca i może zmieniać się w czasie; dlatego naprężenie w materiale jest na ogół zmiennym w czasie polem tensorowym .

Naprężenia normalne i ścinające

Dalsze informacje: ściskanie (fizyczne) i naprężenie ścinające

Ogólnie rzecz biorąc, naprężenie T , które cząstka P przykłada do innej cząstki Q na powierzchni S , może mieć dowolny kierunek względem S . Wektor T można traktować jako sumę dwóch składowych: naprężenia normalnego ( ściskania lub rozciągania ) prostopadłego do powierzchni oraz naprężenia ścinającego , które jest równoległe do powierzchni.

Jeśli przyjmuje się, że normalny wektor jednostkowy n powierzchni (wskazujący od Q w kierunku P ) jest stały, składową normalną można wyrazić za pomocą pojedynczej liczby, iloczynu skalarnego T · n . Ta liczba będzie dodatnia, jeśli P „ciągnie” Q (naprężenie rozciągające), a ujemna, jeśli P „pcha” Q (naprężenie ściskające). Składowa ścinająca jest wtedy wektorem T − ( T · n ) n .

Jednostki

Wymiarem naprężenia jest wymiar ciśnienia , dlatego jego współrzędne są mierzone w tych samych jednostkach co ciśnienie: mianowicie w paskalach (Pa, czyli niutonach na metr kwadratowy ) w systemie międzynarodowym lub funtach na cal kwadratowy (psi) w systemie imperialnym . Ponieważ naprężenia mechaniczne z łatwością przekraczają milion paskali, MPa, co oznacza megapaskal, jest powszechną jednostką naprężenia.

Przyczyny i skutki

Szklany wazon z efektem spękania . Pęknięcia są wynikiem krótkiego, ale intensywnego naprężenia powstałego, gdy częściowo stopiony kawałek jest zanurzany na krótko w wodzie.

Stres w ciele materialnym może być spowodowany wieloma przyczynami fizycznymi, w tym wpływami zewnętrznymi i wewnętrznymi procesami fizycznymi. Niektóre z tych czynników (takie jak grawitacja, zmiany temperatury i fazy oraz pola elektromagnetyczne) działają na masę materiału, zmieniając się w sposób ciągły wraz z pozycją i czasem. Inne czynniki (takie jak zewnętrzne obciążenia i tarcie, ciśnienie otoczenia i siły kontaktowe) mogą powodować naprężenia i siły, które koncentrują się na określonych powierzchniach, liniach lub punktach; i być może także w bardzo krótkich odstępach czasu (jak w impulsach spowodowanych kolizjami). W materii czynnej , samonapęd mikroskopijnych cząstek generuje makroskopowe profile naprężeń. Ogólnie rozkład naprężeń w ciele wyraża się jako odcinkowo ciągłą funkcję przestrzeni i czasu.

I odwrotnie, naprężenie jest zwykle skorelowane z różnymi efektami na materiał, w tym prawdopodobnie zmianami właściwości fizycznych, takich jak dwójłomność , polaryzacja i przepuszczalność . Naprężenie przez czynnik zewnętrzny zwykle powoduje pewne odkształcenie (odkształcenie) w materiale, nawet jeśli jest ono zbyt małe, aby je wykryć. W materiale stałym takie odkształcenie z kolei generuje wewnętrzne naprężenie sprężyste, analogiczne do siły reakcji rozciągniętej sprężyny , zmierzające do przywrócenia materiału do pierwotnego, nieodkształconego stanu. Materiały płynne (ciecze, gazy i plazmy ) z definicji mogą przeciwstawić się jedynie deformacjom, które zmieniłyby ich objętość. Jeśli jednak odkształcenie zmienia się w czasie, nawet w płynach zwykle będzie występować pewne naprężenie lepkie, przeciwstawiające się tej zmianie. Takie naprężenia mogą mieć charakter ścinający lub normalny. Molekularne pochodzenie naprężeń ścinających w płynach podano w artykule dotyczącym lepkości . To samo dla normalnych naprężeń lepkich można znaleźć w Sharma (2019).

Związek między naprężeniem a jego skutkami i przyczynami, w tym odkształceniem i szybkością zmian odkształcenia, może być dość skomplikowany (chociaż liniowe przybliżenie może być w praktyce odpowiednie, jeśli wielkości są wystarczająco małe). Naprężenia przekraczające pewne granice wytrzymałości materiału powodują trwałe odkształcenia (takie jak płynięcie plastyczne , pękanie , kawitacja ) lub nawet zmianę jego struktury krystalicznej i składu chemicznego .

Prosty stres

W niektórych sytuacjach naprężenia w ciele można odpowiednio opisać za pomocą pojedynczej liczby lub pojedynczego wektora (liczby i kierunku). Trzy takie proste sytuacje naprężeń, które często występują w projektowaniu inżynierskim, to jednoosiowe naprężenie normalne , proste naprężenie ścinające i izotropowe naprężenie normalne .

Jednoosiowe naprężenie normalne

Wyidealizowane naprężenie w pręcie prostym o jednolitym przekroju poprzecznym.

Typową sytuacją z prostym układem naprężeń jest sytuacja, w której prosty pręt o jednolitym materiale i przekroju poprzecznym jest poddawany rozciąganiu $przeciwne$ siły o wielkości wzdłuż jego osi. Jeśli układ jest w równowadze i nie zmienia się w czasie, a ciężar pręta można pominąć, to przez każdy przekrój poprzeczny pręta górna część musi ciągnąć dolną część z tą samą siłą, F z ciągłością przez cały pole przekroju , A . Dlatego naprężenie σ w całym pręcie, na dowolnej powierzchni poziomej, można wyrazić po prostu za pomocą pojedynczej liczby σ, obliczonej po prostu z wielkości tych sił F i pola przekroju poprzecznego A .

$${\ Displaystyle \ sigma = {\ Frac {F} {A}}}$$

Z drugiej strony, jeśli wyobrazimy sobie, że pręt jest cięty wzdłuż jego długości, równolegle do osi, nie będzie żadnej siły (a więc żadnego naprężenia) między dwiema połówkami w poprzek cięcia. Ten rodzaj naprężenia można nazwać (prostym) naprężeniem normalnym lub naprężeniem jednoosiowym; w szczególności (jednoosiowe, proste itp.) naprężenie rozciągające. Jeśli obciążenie jest ściskane na pręcie, a nie rozciągane, analiza jest taka sama, z wyjątkiem tego, że siła $F$ naprężenie zmieniają znak, a naprężenie nazywa się naprężeniem ściskającym.

Stosunek $_$ średnim Naprężenia mogą rozkładać się nierównomiernie na przekroju poprzecznym ( m – m ), zwłaszcza w pobliżu punktów mocowania ( n – n ).

Ta analiza zakłada, że ​​naprężenia rozkładają się równomiernie na całym przekroju. W praktyce, w zależności od tego, jak pręt jest zamocowany na końcach i jak został wyprodukowany, założenie to może się nie sprawdzić. W takim przypadku wartość będzie tylko średnim naprężeniem, zwanym naprężeniem $.$ lub naprężeniem nominalnym Jeśli jednak długość pręta L jest wielokrotnością jego średnicy D i nie ma poważnych defektów ani wbudowanych naprężeń, można założyć, że naprężenie jest równomiernie rozłożone na dowolnym przekroju poprzecznym, który jest większy niż kilka razy D od obu końców. (Ta obserwacja jest znana jako zasada Saint-Venanta ).

Normalne naprężenie występuje w wielu innych sytuacjach oprócz osiowego rozciągania i ściskania. Jeżeli sprężysty pręt o jednorodnym i symetrycznym przekroju zostanie zgięty w jednej z jego płaszczyzn symetrii, wynikowe naprężenie zginające nadal będzie normalne (prostopadłe do przekroju), ale będzie się zmieniać w przekroju: część zewnętrzna będzie być pod naprężeniem rozciągającym, podczas gdy wewnętrzna część zostanie ściśnięta. Innym wariantem naprężenia normalnego jest naprężenie obwodowe , które występuje na ściankach cylindrycznej rury lub naczynia wypełnionego płynem pod ciśnieniem.

Proste naprężenie ścinające

Naprężenie ścinające w poziomym pręcie obciążonym dwoma przesuniętymi blokami.

Inny prosty rodzaj naprężenia występuje, gdy równomiernie gruba warstwa elastycznego materiału, takiego jak klej lub guma, jest mocno przymocowana do dwóch sztywnych ciał, które są ciągnięte w przeciwnych kierunkach przez siły równoległe do warstwy; lub odcinek pręta z miękkiego metalu, który jest cięty przez szczęki narzędzia podobnego do nożyczek . Niech F będzie wielkością tych sił, a M będzie płaszczyzną środkową tej warstwy. Podobnie jak w normalnym przypadku naprężenia, część warstwy po jednej stronie M musi ciągnąć drugą część z taką samą siłą F . Zakładając, że kierunek sił jest znany, naprężenie w poprzek $M$ można wyrazić po prostu pojedynczą liczbą obliczoną po prostu na podstawie wielkości tych sił, F i pola przekroju poprzecznego, A .

$${\ Displaystyle \ tau = {\ Frac {F} {A}}}$$

Jednak w przeciwieństwie do normalnego naprężenia, to proste naprężenie ścinające jest skierowane równolegle do rozważanego przekroju, a nie prostopadle do niego. Dla dowolnej płaszczyzny S , która jest prostopadła do warstwy, wypadkowa siła wewnętrzna w poprzek S , a tym samym naprężenie, będzie wynosić zero.

Podobnie jak w przypadku pręta obciążonego osiowo, w praktyce naprężenie ścinające może nie rozkładać się równomiernie na warstwie; więc, jak poprzednio, stosunek F / A będzie tylko średnim („nominalnym”, „inżynierskim”) naprężeniem. Jednak ta średnia jest często wystarczająca do celów praktycznych. Naprężenie ścinające obserwuje się również w przypadku walcowego pręta, takiego jak wał jest poddawany przeciwstawnym momentom obrotowym na swoich końcach. W takim przypadku naprężenie ścinające na każdym przekroju poprzecznym jest równoległe do przekroju poprzecznego, ale zorientowane stycznie do osi i rośnie wraz z odległością od osi. Znaczące naprężenie ścinające występuje w środkowej płycie („środniku”) belek dwuteowych pod obciążeniem zginającym, z powodu środnika ograniczającego płyty końcowe („kołnierze”).

Stres izotropowy

Izotropowe naprężenie rozciągające. Lewy górny róg: Każda ściana sześcianu z jednorodnego materiału jest ciągnięta przez siłę o wartości F , przyłożoną równomiernie do całej ściany o polu A . Siła działająca na dowolny przekrój S sześcianu musi równoważyć siły przyłożone poniżej tego przekroju. W trzech pokazanych sekcjach siły są następujące : fa (prawy górny róg), $sqrt {3}}}$$\$ displaystyle { 2 (prawy dolny róg); a pole S wynosi ZA , ZA ${\ Displaystyle {\ sqrt {2}}}$ i odpowiednio ZA 3 $\ Displaystyle {\ sqrt {3}}/2} .$ Tak więc naprężenie w poprzek S wynosi F / A we wszystkich trzech przypadkach.

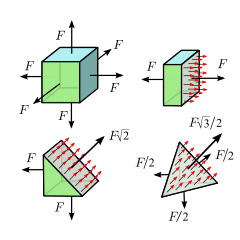
Inny prosty rodzaj naprężenia występuje, gdy ciało materialne jest pod jednakowym ściskaniem lub rozciąganiem we wszystkich kierunkach. Dzieje się tak na przykład w przypadku części cieczy lub gazu w stanie spoczynku, zamkniętej w jakimś pojemniku lub jako część większej masy płynu; lub wewnątrz sześcianu z elastycznego materiału, który jest ściskany lub ciągnięty ze wszystkich sześciu ścian przez równe prostopadłe siły – pod warunkiem, że w obu przypadkach materiał jest jednorodny, bez wbudowanych naprężeń oraz że wpływ grawitacji i innych sił zewnętrznych można zaniedbać.

W takich sytuacjach naprężenie na dowolnej wyimaginowanej powierzchni wewnętrznej okazuje się równe co do wielkości i zawsze skierowane prostopadle do powierzchni, niezależnie od jej orientacji. Ten rodzaj stresu można nazwać izotropowym normalnym lub po prostu izotropowym ; jeśli jest ściskający, nazywa się to ciśnieniem hydrostatycznym lub po prostu ciśnieniem . Gazy z definicji nie wytrzymują naprężeń rozciągających, ale niektóre ciecze mogą w pewnych okolicznościach wytrzymać bardzo duże ilości izotropowego naprężenia rozciągającego. zobacz rurkę Z.

Naprężenia cylindra

Części o symetrii obrotowej , takie jak koła, osie, rury i słupki, są bardzo powszechne w inżynierii. Często wzorce naprężeń występujące w takich częściach mają symetrię obrotową lub nawet cylindryczną . Analiza takich naprężeń walcowych może wykorzystać symetrię do zmniejszenia wymiaru domeny i/lub tensora naprężenia.

Ogólny stres

Często ciała mechaniczne doświadczają więcej niż jednego rodzaju naprężeń w tym samym czasie; nazywa się to stresem złożonym . W przypadku naprężenia normalnego i ścinającego wielkość naprężenia jest maksymalna dla powierzchni prostopadłych do określonego kierunku $zero$ na wszystkich powierzchniach równoległych do ${\ displaystyle d}$ . Kiedy naprężenie ścinające wynosi zero tylko na powierzchniach prostopadłych do jednego określonego kierunku, naprężenie nazywa się dwuosiowym i można je postrzegać jako sumę dwóch naprężeń normalnych lub ścinających. W najbardziej ogólnym przypadku, tzw naprężenie trójosiowe , naprężenie jest niezerowe na każdym elemencie powierzchni.

Tensor naprężenia Cauchy'ego

Główny artykuł: tensor naprężenia Cauchy'ego

Składowe naprężeń w trzech wymiarach

Ilustracja typowych naprężeń (strzałki) na różnych elementach powierzchniowych na granicy cząstki (kuli), w jednorodnym materiale pod równomiernym (ale nie izotropowym) naprężeniem trójosiowym. Normalne naprężenia na głównych osiach wynoszą +5, +2 i -3 jednostki.

Połączonych naprężeń nie można opisać za pomocą jednego wektora. Nawet jeśli materiał jest naprężony w ten sam sposób w całej objętości ciała, naprężenie na dowolnej wyimaginowanej powierzchni będzie zależeć od orientacji tej powierzchni w nietrywialny sposób.

Jednak Cauchy zauważył, że wektor naprężenia $.$ powierzchni zawsze będzie funkcją liniową $prostopadły$ normalnego powierzchni , wektora o długości jednostkowej, który jest do niego T ${\ Displaystyle T = {\ boldsymbol {\ sigma}} (n)}$ , gdzie funkcja spełnia ${\ displaystyle T = {\ boldsymbol {\ sigma}} (n)$

${\ Displaystyle {\ boldsymbol {\ sigma}} (\ alfa u + \ beta v) = \ alfa {\ pogrubiony symbol {\ sigma}} (u)+\beta {\boldsymbol {\sigma}}(v)}$

dla dowolnych wektorów i dowolnych liczb rzeczywistych ${\ displaystyle u, v}$${\ displaystyle \ alpha, \ beta}$ . Funkcja , nazywana obecnie $tensorem$ naprężenia (Cauchy'ego) , całkowicie opisuje stan naprężenia równomiernie obciążonego ciała (Obecnie każde liniowe połączenie między dwiema fizycznymi wielkościami wektorowymi nazywane jest tensorem , co odzwierciedla pierwotne użycie Cauchy'ego do opisania „napięć” (naprężeń) w materiale.) W rachunku tensorowym , $jest klasyfikowany$ tensor drugiego rzędu typu (0,2) .

Jak każda liniowa mapa między wektorami, tensor naprężenia można przedstawić w dowolnym wybranym kartezjańskim układzie współrzędnych za pomocą macierzy liczb rzeczywistych 3 × 3. W zależności od tego, czy współrzędne są ponumerowane, czy nazwane ${\ Displaystyle x_ {1}, x_ {2}, x_ {3}}$${\ Displaystyle x, y, z$ } macierz można zapisać jako

$${\ Displaystyle {\ rozpocząć {bmatrix} \ sigma _ {11} i \ sigma _ {12} i \ sigma _ {13} \ \\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}}$$

Lub

$${\ Displaystyle {\ rozpocząć {bmatrix} \ sigma _ {xx} i \ sigma _ {xy }&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{ zz}\\\koniec{bmacierzy}}}$$

Wektor naprężenia na powierzchni z $Displaystyle$ normalnym (który jest kowariantny - „wiersz; poziomy” - wektor $T = {\ boldsymbol {\ sigma}} (n)}$$n_ {1}, n_ {2}, n_ {3}}$ , jest więc iloczynem macierzowym ${\ Displaystyle T = n \ cdot {\ boldsymbol {\ sigma}}}$ (gdzie T w górnym indeksie to transpozycja , w wyniku czego otrzymujemy wektor kowariantny (wiersz)) (spójrz na tensor naprężenia Cauchy'ego ), czyli

${\ Displaystyle {\ rozpocząć {bmatrix} T_ {1} i T_ {2} i T_ {3} \ koniec {bmatrix}} = {\ rozpocząć {bmatrix} n_ {1} i n_ {2} i n_ { 3}\end{bmatrix}}\cdot {\begin{bmatrix}\sigma _{11}&\sigma _{21}&\sigma _{31}\\\sigma _{12}&\sigma _{22 }&\sigma _{32}\\\sigma _{13}&\sigma _{23}&\sigma _{33}\end{bmatrix}}}$

Liniowa zależność między i wynika z podstawowych praw zachowania $naprężeniowej$ liniowego i statycznej równowagi $.$ , a zatem jest matematycznie dokładna dla każdego materiału i dowolnej sytuacji Składowe tensora naprężenia Cauchy'ego w każdym punkcie materiału spełniają równania równowagi ( równania ruchu Cauchy'ego dla przyspieszenia zerowego). Ponadto zasada zachowania momentu pędu implikuje, że tensor naprężenia jest ${\ Displaystyle \ sigma _ {12} = \ sigma _ {21}}$ = $sigma _ {31}$ 13 \ } i ${\ Displaystyle \ sigma _ {23} = \ sigma _ {32}}$ . Dlatego stan naprężenia ośrodka w dowolnym momencie i chwili można określić tylko za pomocą sześciu niezależnych parametrów, a nie dziewięciu. Te mogą być napisane

${\ Displaystyle {\ rozpocząć {bmatrix} \ sigma _ {x} i \ tau _ {xy} i \ tau _{xz}\\\tau _{xy}&\sigma _{y}&\tau _{yz}\\\tau _{xz}&\tau _{yz}&\sigma _{z}\ koniec{bmacierz}}}$

gdzie elementy nazywane są prostopadłymi naprężeniami normalnymi (w stosunku do wybranego układu współrzędnych), ${\ Displaystyle \ sigma _ {x}, \ sigma _ {y}, \ sigma _ {z}}$ i ortogonalne naprężenia ścinające $\ tau _ {yz}}$ ,

Zmiana współrzędnych

Tensor naprężenia Cauchy'ego jest zgodny z prawem transformacji tensorowej przy zmianie układu współrzędnych. Graficzną reprezentacją tego prawa transformacji jest rozkładu naprężeń Mohra .

Jako symetryczna rzeczywista macierz 3 × 3, tensor naprężeń $trzy wzajemnie ortogonalne$ wektory własne o jednostkowej długości $}$${\ Displaystyle e_ {1}, e_$${3}$ i trzy wartości ${\ Displaystyle {\ boldsymbol {\ sigma}} e_ {i} = \ lambda _ {i} e_ {i}}$ . Dlatego $jest$ układzie współrzędnych z osiami trzy składowe normalne ${\ Displaystyle \ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3}}$ główne akcenty . Jeśli trzy wartości własne są równe, naprężenie jest izotropowe ściskanie lub rozciąganie, zawsze prostopadłe do dowolnej powierzchni, nie ma naprężenia ścinającego, a tensor jest macierzą diagonalną w dowolnym układzie współrzędnych.

Naprężenie jako pole tensorowe

Ogólnie rzecz biorąc, naprężenia nie rozkładają się równomiernie na ciało materialne i mogą zmieniać się w czasie. Dlatego tensor naprężenia należy zdefiniować dla każdego punktu i każdej chwili, biorąc pod uwagę nieskończenie małą cząstkę ośrodka otaczającego ten punkt i przyjmując średnie naprężenia w tej cząstce jako naprężenia w punkcie.

Stres w cienkich płytkach

Cysterna wykonana z giętych i spawanych blach stalowych.

Przedmioty stworzone przez człowieka są często wykonywane z płyt podstawowych z różnych materiałów poprzez operacje, które nie zmieniają ich zasadniczo dwuwymiarowego charakteru, takie jak cięcie, wiercenie, delikatne gięcie i spawanie wzdłuż krawędzi. Opis naprężeń w takich ciałach można uprościć, modelując te części jako dwuwymiarowe powierzchnie, a nie trójwymiarowe ciała.

W tym ujęciu redefiniuje się „cząstkę” jako nieskończenie mały fragment powierzchni płyty, tak że granica między sąsiednimi cząstkami staje się nieskończenie małym elementem liniowym; oba są niejawnie rozciągnięte w trzecim wymiarze, prostopadłym do (na wprost) płyty. „Naprężenie” jest następnie ponownie definiowane jako miara sił wewnętrznych między dwiema sąsiednimi „cząstkami” w poprzek ich wspólnego elementu liniowego, podzielona przez długość tej linii. Niektóre składowe tensora naprężeń można zignorować, ale ponieważ cząstki nie są nieskończenie małe w trzecim wymiarze, nie można już ignorować momentu obrotowego, jaki cząstka przykłada do swoich sąsiadów. Ten moment obrotowy jest modelowany jako a naprężenie zginające , które ma tendencję do zmiany krzywizny płyty. Jednak te uproszczenia mogą nie sprawdzać się przy spoinach, przy ostrych zagięciach i fałdach (gdzie promień krzywizny jest porównywalny z grubością blachy).

Naprężenia w cienkich belkach

W przypadku modelowania naprężeń wędkę można uznać za jednowymiarową.

Analizę naprężeń można znacznie uprościć również dla cienkich prętów, belek lub drutów o jednolitym (lub płynnie zmieniającym się) składzie i przekroju poprzecznym, które podlegają umiarkowanemu zginaniu i skręcaniu. W przypadku tych ciał można wziąć pod uwagę tylko przekroje prostopadłe do osi pręta i ponownie zdefiniować „cząstkę” jako kawałek drutu o nieskończenie małej długości między dwoma takimi przekrojami. Zwykłe naprężenie jest wtedy redukowane do wartości skalarnej (rozciąganie lub ściskanie pręta), ale należy wziąć pod uwagę również naprężenie zginające (które próbuje zmienić krzywiznę pręta w pewnym kierunku prostopadłym do osi) oraz naprężenie skrętne (które próbuje skręcić lub odkręcić go wokół własnej osi).

Inne opisy stresu

Szkło hartowane tylnej szyby samochodu. Zmiany naprężeń szkła są wyraźnie widoczne podczas fotografowania przez filtr polaryzacyjny (dolne zdjęcie).

Tensor naprężenia Cauchy'ego jest używany do analizy naprężeń ciał materialnych doświadczających niewielkich odkształceń , gdzie różnice w rozkładzie naprężeń w większości przypadków można pominąć. W przypadku dużych odkształceń, zwanych także odkształceniami skończonymi , wymagane są inne miary naprężeń, takie jak pierwszy i drugi tensor naprężenia Piola-Kirchhoffa , tensor naprężenia Biota i tensor naprężenia Kirchhoffa . Ciała stałe, ciecze i gazy mają pola naprężeń . Płyny statyczne podtrzymują normalne naprężenia, ale będą płynąć pod naprężeniami ścinającymi . Poruszający lepkie płyny mogą wytrzymywać naprężenia ścinające (ciśnienie dynamiczne). Ciała stałe mogą wytrzymać zarówno naprężenia ścinające, jak i normalne, przy czym ciągliwe zawodzą pod wpływem ścinania, a materiały kruche zawodzą pod wpływem naprężeń normalnych. Wszystkie materiały mają zależne od temperatury zmiany właściwości związanych z naprężeniami, a materiały nienewtonowskie mają zmiany zależne od szybkości.

Analiza naprężeń

Analiza naprężeń jest gałęzią fizyki stosowanej , która obejmuje określanie wewnętrznego rozkładu sił wewnętrznych w ciałach stałych. Jest to podstawowe narzędzie w inżynierii do badania i projektowania konstrukcji, takich jak tunele, tamy, części mechaniczne i ramy konstrukcyjne, pod określonymi lub oczekiwanymi obciążeniami. Jest to również ważne w wielu innych dyscyplinach; na przykład w geologii do badania zjawisk takich jak tektonika płyt , wulkanizm i lawiny ; oraz w biologii, aby zrozumieć anatomię żywych istot.

Cele i założenia

Analiza naprężeń dotyczy ogólnie obiektów i konstrukcji, co do których można założyć, że znajdują się w makroskopowej równowadze statycznej . Zgodnie z prawami dynamiki Newtona , wszelkie siły zewnętrzne przyłożone do takiego układu muszą być zrównoważone przez wewnętrzne siły reakcji, które prawie zawsze są siłami kontaktu powierzchniowego między sąsiednimi cząstkami - to znaczy jako naprężenie. Ponieważ każda cząsteczka musi być w równowadze, to naprężenie reakcji będzie generalnie rozprzestrzeniać się z cząstki na cząsteczkę, tworząc rozkład naprężeń w całym ciele. Typowym problemem w analizie naprężeń jest określenie tych naprężeń wewnętrznych, biorąc pod uwagę siły zewnętrzne działające na system. Te ostatnie mogą być siłami ciała (takie jak grawitacja lub przyciąganie magnetyczne), które działają w całej objętości materiału; lub skupione obciążenia (takie jak tarcie między osią a łożyskiem lub ciężar koła pociągu na szynie), które wyobraża się, że działają na dwuwymiarowym obszarze, wzdłuż linii lub w jednym punkcie.

W analizie naprężeń zwykle pomija się fizyczne przyczyny sił lub dokładny charakter materiałów. Zamiast tego zakłada się, że naprężenia są związane z odkształceniem (a w przypadku problemów niestatycznych z szybkością odkształcenia) materiału za pomocą znanych równań konstytutywnych .

Metody

Analizę naprężeń można przeprowadzić eksperymentalnie, przykładając obciążenia do rzeczywistego artefaktu lub modelu w skali i mierząc wynikające z nich naprężenia dowolną z kilku dostępnych metod. Takie podejście jest często stosowane do certyfikacji i monitorowania bezpieczeństwa. Jednak większość analiz naprężeń przeprowadza się metodami matematycznymi, zwłaszcza podczas projektowania. Podstawowy problem analizy naprężeń można sformułować za pomocą równań ruchu Eulera dla ciał ciągłych (które są konsekwencją praw Newtona dotyczących zachowania pędu liniowego i momentu pędu ) oraz Zasada naprężeń Eulera-Cauchy'ego wraz z odpowiednimi równaniami konstytutywnymi. Otrzymuje się w ten sposób układ równań różniczkowych cząstkowych obejmujących pole tensora naprężenia i pole tensora odkształcenia , jako nieznane funkcje do wyznaczenia. Zewnętrzne siły ciała pojawiają się jako niezależny („prawostronny”) składnik w równaniach różniczkowych, podczas gdy siły skupione pojawiają się jako warunki brzegowe. Podstawowym problemem analizy naprężeń jest zatem problem wartości brzegowych .

Analiza naprężeń w konstrukcjach sprężystych opiera się na teorii sprężystości i teorii nieskończenie małych odkształceń . Kiedy przyłożone obciążenia powodują trwałe odkształcenie, należy użyć bardziej skomplikowanych równań konstytutywnych, które mogą uwzględniać występujące procesy fizyczne ( płynięcie plastyczne , pękanie , zmiana fazy itp.). Jednak konstrukcje inżynierskie są zwykle projektowane w taki sposób, aby maksymalne oczekiwane naprężenia mieściły się w zakresie sprężystości liniowej (uogólnienie prawa Hooke'a dla nośników ciągłych); to znaczy odkształcenia spowodowane naprężeniami wewnętrznymi są z nimi związane liniowo. W tym przypadku równania różniczkowe definiujące tensor naprężenia są liniowe, a problem staje się znacznie prostszy. Po pierwsze, naprężenie w dowolnym punkcie będzie również funkcją liniową obciążeń. W przypadku wystarczająco małych naprężeń można zwykle założyć, że nawet układy nieliniowe są liniowe.

Uproszczony model kratownicy do analizy naprężeń, przy założeniu jednowymiarowych elementów poddanych równomiernemu rozciąganiu lub ściskaniu osiowemu.

Analiza naprężeń jest uproszczona, gdy wymiary fizyczne i rozkład obciążeń pozwalają na traktowanie konstrukcji jako jedno- lub dwuwymiarowej. Na przykład w analizie kratownic można założyć, że pole naprężeń jest jednolite i jednoosiowe na każdym elemencie. Następnie równania różniczkowe redukują się do skończonego zestawu równań (zwykle liniowych) ze skończoną liczbą niewiadomych. W innych kontekstach można zredukować trójwymiarowy problem do dwuwymiarowego i/lub zastąpić ogólne tensory naprężenia i odkształcenia prostszymi modelami, takimi jak jednoosiowe rozciąganie/ściskanie, proste ścinanie itp.

Mimo to w przypadkach dwu- lub trójwymiarowych należy rozwiązać problem z równaniem różniczkowym cząstkowym. Analityczne lub zamknięte rozwiązania równań różniczkowych można uzyskać, gdy geometria, relacje konstytutywne i warunki brzegowe są wystarczająco proste. W przeciwnym razie należy na ogół uciekać się do przybliżeń numerycznych, takich jak metoda elementów skończonych , metoda różnic skończonych i metoda elementów brzegowych .

Alternatywne miary stresu

Główny artykuł: Miary stresu

Inne przydatne miary naprężeń obejmują pierwszy i drugi tensor naprężenia Piola-Kirchhoffa , tensor naprężenia Biota i tensor naprężenia Kirchhoffa .

Tensor naprężenia Pioli-Kirchhoffa

W przypadku odkształceń skończonych tensory naprężeń Pioli-Kirchhoffa wyrażają naprężenie względem konfiguracji odniesienia. Kontrastuje to z tensorem naprężenia Cauchy'ego , który wyraża naprężenie względem obecnej konfiguracji. W przypadku nieskończenie małych odkształceń i obrotów tensory Cauchy'ego i Pioli – Kirchhoffa są identyczne. Podczas gdy tensor naprężenia Cauchy'ego odnosi się do naprężeń w bieżącej konfiguracji, gradient odkształcenia ${\ displaystyle {\ boldsymbol {\ sigma}}}$ a tensory odkształcenia są opisane przez odniesienie ruchu do konfiguracji odniesienia; zatem nie wszystkie tensory opisujące stan materiału są w konfiguracji odniesienia lub bieżącej. Opisanie naprężenia, odkształcenia i odkształcenia w konfiguracji odniesienia lub bieżącej ułatwiłoby zdefiniowanie modeli konstytutywnych (na przykład tensor naprężenia Cauchy'ego jest wariantem czystego obrotu, podczas gdy tensor odkształcenia odkształcenia jest niezmienny; stwarzając w ten sposób problemy w definiowaniu model konstytutywny, który wiąże zmienny tensor w kategoriach niezmienniczego podczas czystej rotacji; ponieważ z definicji modele konstytutywne muszą być niezmienne dla czystych rotacji). Pierwszy tensor naprężenia Pioli – Kirchhoffa, ${\ displaystyle {\ boldsymbol {P}}}$ jest jednym z możliwych rozwiązań tego problemu. Definiuje rodzinę tensorów, które opisują konfigurację ciała w stanie bieżącym lub referencyjnym. Pierwszy tensor naprężeń Pioli – Kirchhoffa wiąże siły w obecnej („przestrzennej”) konfiguracji z obszarami w $konfiguracji$ odniesienia („materiał”)

${\ Displaystyle {\ boldsymbol {P}} = J ~ {\ boldsymbol {\ sigma}} ~ {\ boldsymbol {F}} ^ {- T} ~}$

gdzie $jest$ gradientem deformacji i $_$ _ _ _ _

Jeśli chodzi o składowe w odniesieniu do bazy ortonormalnej , pierwsze naprężenie Pioli-Kirchhoffa jest określone wzorem

${\ Displaystyle P_ {iL} = J ~ \ sigma _ {ik} ~ F_ {Lk} ^ {- 1} =J~\sigma _{ik}~{\cfrac {\częściowe X_{L}}{\częściowe x_{k}}}~\,\!}$

Ponieważ odnosi się do różnych układów współrzędnych, pierwsze naprężenie Pioli-Kirchhoffa jest tensorem dwupunktowym . Ogólnie rzecz biorąc, nie jest symetryczny. Pierwsze naprężenie Pioli-Kirchhoffa jest trójwymiarowym uogólnieniem jednowymiarowej koncepcji naprężeń inżynierskich .

Jeśli materiał obraca się bez zmiany stanu naprężenia (rotacja sztywna), składowe pierwszego tensora naprężenia Pioli-Kirchhoffa będą się różnić w zależności od orientacji materiału.

Pierwsze naprężenie Pioli-Kirchhoffa jest energią sprzężoną z gradientem odkształcenia.

Drugi tensor naprężenia Pioli-Kirchhoffa

$konfiguracji z obszarami w konfiguracji odniesienia, 2. tensor naprężenia$ – Kirchhoffa wiąże siły w konfiguracji odniesienia z obszarami w odniesieniu konfiguracja. Siła w konfiguracji odniesienia jest uzyskiwana poprzez odwzorowanie, które zachowuje względną zależność między kierunkiem siły a normalną powierzchni w konfiguracji odniesienia.

${\ Displaystyle {\ boldsymbol {S}} = J ~ {\ boldsymbol {F}} ^ {-1} \ cdot {\ boldsymbol {\ sigma}} \ cdot {\ boldsymbol {F}} ^ {-T} ~ .}$

W notacji indeksowej w odniesieniu do bazy ortonormalnej,

$\ Displaystyle S_ {IL} = J ~ F_ {Ik} ^ {-1}~F_{Lm}^{-1}~\sigma _{km}=J~{\cfrac {\częściowe X_{I}}{\częściowe x_{k}}}~{\cfrac {\ częściowe X_{L}}{\częściowe x_{m}}}~\sigma _{km}\!\,\!}$

Ten tensor, tensor jednopunktowy, jest symetryczny. Jeśli materiał obraca się bez zmiany stanu naprężenia (rotacja sztywna), składowe drugiego tensora naprężenia Pioli-Kirchhoffa pozostają stałe, niezależnie od orientacji materiału.

Drugi tensor naprężenia Pioli – Kirchhoffa jest sprzężony z tensorem odkształcenia skończonego Greena – Lagrange'a .

Zobacz też

• Pochylenie się
• Wytrzymałość na ściskanie
• Analiza płaszczyzny krytycznej
• Mikroskop sił z sondą Kelvina
• Koło Mohra
• Elipsoida naprężeń Lamégo
• Stres resztkowy
• Wytrzymałość na ścinanie
• Śrutowanie
• Napięcie
• Tensor odkształcenia
• Tensor szybkości odkształcenia
• Tensor energii naprężenia
• Krzywa naprężenie-odkształcenie
• Koncentracja stresu
• Przejściowe obciążenie tarciem
• Wytrzymałość na rozciąganie
• Naprężenia termiczne
• Stres wirusowy
• Wydajność (inżynieria)
• Powierzchnia plonu
• Twierdzenie wirialne

Dalsza lektura

•   Chakrabarty, J. (2006). Teoria plastyczności (3 wyd.). Butterworth-Heinemann. s. 17–32. ISBN 0-7506-6638-2 .
•   Piwo, Ferdynand Pierre; Elwooda Russella Johnstona; Johna T. DeWolfa (1992). Mechanika materiałów . Profesjonalista McGraw-Hill. ISBN 0-07-112939-1 .
•   Brady, BHG; ET Brown (1993). Mechanika skał w górnictwie podziemnym (wyd. Trzecie). Wydawnictwo Naukowe Kluwer. s. 17–29. ISBN 0-412-47550-2 .
•   Chen, Wai-Fah; Baladi, GY (1985). Plastyczność gleby, teoria i realizacja . ISBN 0-444-42455-5 .
•   Chou, Pei Chi; Pagano, NJ (1992). Elastyczność: podejścia tensorowe, diadyczne i inżynierskie . Dover książki o inżynierii. Publikacje Dover. s. 1–33. ISBN 0-486-66958-0 .
•   Davis, RO; Selvadurai. APS (1996). Sprężystość i geomechanika . Wydawnictwo Uniwersytetu Cambridge. s. 16–26. ISBN 0-521-49827-9 .
•   Dieter, GE (3 wyd.). (1989). Metalurgia Mechaniczna . Nowy Jork: McGraw-Hill. ISBN 0-07-100406-8 .
•   Holtz, Robert D.; Kovacs, William D. (1981). Wprowadzenie do inżynierii geotechnicznej . Prentice-Hall seria inżynierii lądowej i mechaniki inżynierskiej. Prentice Hall. ISBN 0-13-484394-0 .
•   Jones, Robert Millard (2008). Teoria deformacji plastyczności . Korporacja Bull Ridge. s. 95–112. ISBN 978-0-9787223-1-9 .
•   Jumikis, Alfreds R. (1969). Teoretyczna mechanika gruntów: z praktycznymi zastosowaniami w mechanice gruntów i inżynierii fundamentów . Van Nostrand Reinhold Co. ISBN 0-442-04199-3 .
• Landau, LD i EMLifshitz. (1959). Teoria sprężystości .
•   Miłość, AEH (4 wyd.). (1944). Traktat o matematycznej teorii elastyczności . Nowy Jork: Dover Publications. ISBN 0-486-60174-9 .
•   Marsden, JE; Hughes, TJR (1994). Matematyczne podstawy elastyczności . Publikacje Dover. s. 132 –142. ISBN 0-486-67865-2 .
•   Parry, Richard Hawley Gray (2004). Kręgi Mohra, ścieżki naprężeń i geotechnika (wyd. 2). Taylora i Franciszka. s. 1–30. ISBN 0-415-27297-1 .
•   Rees, David (2006). Podstawowa plastyczność inżynierska - wprowadzenie do zastosowań inżynieryjnych i produkcyjnych . Butterworth-Heinemann. s. 1–32. ISBN 0-7506-8025-3 .
•   Tymoszenko, Stefan P .; Jamesa Normana Goodiera (1970). Teoria elastyczności (wyd. Trzecie). Wydania międzynarodowe McGraw-Hill. ISBN 0-07-085805-5 .
•   Tymoszenko, Stephen P. (1983). Historia wytrzymałości materiałów: z krótkim opisem historii teorii sprężystości i teorii struktur . Dover Książki o fizyce. Publikacje Dover. ISBN 0-486-61187-6 .