Lepkosprężystość

W materiałoznawstwie i mechanice kontinuum lepkosprężystość jest właściwością materiałów , które wykazują zarówno właściwości lepkie , jak i sprężyste podczas odkształcania . Lepkie materiały, takie jak woda, są odporne na przepływ ścinający i odkształcenia liniowe w czasie, gdy przyłożone jest naprężenie . Elastyczne materiały naprężają się podczas rozciągania i natychmiast wracają do swojego pierwotnego stanu po usunięciu naprężenia.

Materiały lepkosprężyste mają elementy obu tych właściwości i jako takie wykazują odkształcenie zależne od czasu. Podczas gdy elastyczność jest zwykle wynikiem wiązań wzdłuż płaszczyzn krystalograficznych w uporządkowanej bryle, lepkość jest wynikiem dyfuzji atomów lub cząsteczek wewnątrz materiału amorficznego .

Tło

W XIX wieku fizycy tacy jak Maxwell , Boltzmann i Kelvin badali i eksperymentowali z pełzaniem i regeneracją szkła , metali i gumy . Lepkosprężystość była dalej badana pod koniec XX wieku, kiedy polimery syntetyczne zostały opracowane i wykorzystane w różnych zastosowaniach. Obliczenia lepkosprężystości w dużym stopniu zależą od lepkości , η. Odwrotność η jest również znana jako płynność , φ. Wartość albo można wyprowadzić jako funkcję temperatury , albo jako daną wartość (np. dla dashpot ).

Różne typy odpowiedzi ( $)$ re na zmianę szybkości odkształcenia ( ${\ Displaystyle d \ varepsilon /$ }

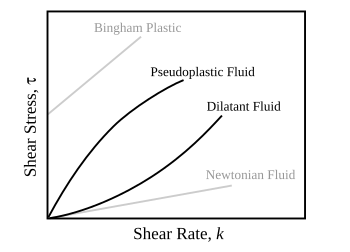
W zależności od zmiany szybkości odkształcenia w funkcji naprężenia wewnątrz materiału, lepkość można podzielić na liniową, nieliniową lub plastyczną. Kiedy materiał wykazuje odpowiedź liniową, jest klasyfikowany jako materiał newtonowski . W tym przypadku naprężenie jest liniowo proporcjonalne do szybkości odkształcania. Jeśli materiał wykazuje nieliniową odpowiedź na szybkość odkształcania, jest klasyfikowany jako płyn nienewtonowski . Istnieje również interesujący przypadek, w którym lepkość spada, gdy szybkość ścinania/odkształcania pozostaje stała. Materiał wykazujący tego typu zachowanie jest znany jako tiksotropowy . Ponadto, gdy naprężenie jest niezależne od tej szybkości odkształcenia, materiał wykazuje odkształcenie plastyczne. Wiele materiałów lepkosprężystych wykazuje gumy , które można wyjaśnić termodynamiczną teorią sprężystości polimerów.

Niektóre przykłady materiałów lepkosprężystych to polimery amorficzne, polimery półkrystaliczne, biopolimery, metale w bardzo wysokich temperaturach i materiały bitumiczne. Pękanie występuje, gdy naprężenie jest przykładane szybko i poza granicą sprężystości. Więzadła i ścięgna są lepkosprężyste, więc stopień potencjalnego ich uszkodzenia zależy zarówno od szybkości zmiany ich długości, jak i przyłożonej siły.

Materiał lepkosprężysty ma następujące właściwości:

• histereza jest widoczna na krzywej naprężenie-odkształcenie
• relaksacja naprężeń : stałe odkształcenie krokowe powoduje zmniejszenie naprężenia
• pełzanie : stałe naprężenie krokowe powoduje rosnące odkształcenie
• $}}}$ zależy od szybkości odkształcenia $varepsilon$ szybkości naprężenia

Zachowanie sprężyste a lepkosprężyste

Krzywe naprężenie-odkształcenie dla materiału czysto elastycznego (a) i materiału lepkosprężystego (b). Czerwony obszar to histerezy i pokazuje ilość energii traconej (w postaci ciepła) w cyklu ładowania i rozładowywania. Jest równa , $varepsilon$$}$ naprężenie i ${ \$ odkształceniem.

W przeciwieństwie do substancji czysto elastycznych, substancja lepkosprężysta ma składnik elastyczny i składnik lepki. Lepkość substancji lepkosprężystej nadaje substancji zależność szybkości odkształcania od czasu . Czysto elastyczne materiały nie rozpraszają energii (ciepła) po przyłożeniu obciążenia, a następnie jego usunięciu. Jednak substancja lepkosprężysta rozprasza energię po przyłożeniu obciążenia, a następnie usunięciu. Histereza obserwuje się na krzywej naprężenie-odkształcenie, przy czym powierzchnia pętli jest równa energii traconej podczas cyklu obciążenia. Ponieważ lepkość jest odpornością na aktywowane termicznie odkształcenie plastyczne, lepki materiał traci energię podczas cyklu ładowania. Odkształcenie plastyczne powoduje utratę energii, co nie jest charakterystyczne dla reakcji czysto elastycznego materiału na cykl obciążenia.

W szczególności lepkosprężystość jest przegrupowaniem molekularnym. Kiedy naprężenie jest przykładane do materiału lepkosprężystego, takiego jak polimer , części długiego łańcucha polimeru zmieniają położenie. Ten ruch lub przegrupowanie nazywa się pełzaniem . Polimery pozostają materiałem stałym, nawet jeśli te części ich łańcuchów przestawiają się, aby towarzyszyć naprężeniom, a gdy to nastąpi, powoduje to naprężenie wsteczne w materiale. Kiedy naprężenie wsteczne ma taką samą wielkość jak przyłożone naprężenie, materiał przestaje się pełzać. Kiedy pierwotne naprężenie zostanie usunięte, nagromadzone naprężenia wsteczne spowodują powrót polimeru do pierwotnej postaci. Materiał pełza, co daje przedrostek lepko-, a materiał w pełni się regeneruje, co daje przyrostek -elastyczność.

Lepkosprężystość liniowa i lepkosprężystość nieliniowa

Lepkosprężystość liniowa występuje wtedy, gdy funkcja jest rozdzielna zarówno pod względem odpowiedzi na pełzanie, jak i obciążenia. Wszystkie liniowe modele lepkosprężyste można przedstawić za pomocą równania Volterry łączącego naprężenie i odkształcenie :

$${\ Displaystyle \ varepsilon (t) = {\ Frac {\ sigma (t) }{E_{\text{inst,creep}}}}+\int _{0}^{t}K(tt'){\dot {\sigma}}(t')dt'}$$

Lub

$${\ Displaystyle \ sigma (t) = E _ {\ tekst {inst, zrelaksować} }\varepsilon (t)+\int _{0}^{t}F(tt'){\dot {\varepsilon}}(t')dt'}$$

Gdzie

• czas _
• ${\ Displaystyle \ sigma (t)}$ to stres
• jest napięciem. ${\ Displaystyle \ varepsilon (t)}$
• ${\ displaystyle E _ {\ tekst {inst, pełzanie}}}$ i ${\ displaystyle E _ {\ tekst {inst, relaks}}}$ to chwilowe moduły sprężystości dla pełzania i relaksacji
• K ( t ) jest funkcją pełzania
• F ( t ) jest funkcją relaksacyjną

Lepkosprężystość liniowa ma zwykle zastosowanie tylko do małych odkształceń .

Lepkosprężystość nieliniowa występuje, gdy funkcja nie jest rozdzielna. Zwykle dzieje się tak, gdy odkształcenia są duże lub gdy materiał zmienia swoje właściwości pod wpływem odkształceń. Nieliniowa lepkosprężystość wyjaśnia również obserwowane zjawiska, takie jak naprężenia normalne, rozrzedzanie przy ścinaniu i zagęszczanie rozciągające w płynach lepkosprężystych.

nieelastyczny jest szczególnym przypadkiem materiału lepkosprężystego: materiał nieelastyczny w pełni powróci do swojego pierwotnego stanu po usunięciu obciążenia .

Rozróżniając zachowania sprężyste, lepkie i lepkosprężyste, pomocne jest odniesienie się do skali czasowej pomiaru względem czasów relaksacji obserwowanego materiału, znanej jako liczba Deborah (De), gdzie:

$${\ Displaystyle De = \ lambda / t}$$

Gdzie

• ${\ displaystyle \ lambda}$ to czas relaksacji materiału
• ${\ displaystyle t}$ to czas

Moduł dynamiczny

Główny artykuł: Moduł dynamiczny

Lepkosprężystość jest badana za pomocą dynamicznej analizy mechanicznej , stosując niewielkie naprężenia oscylacyjne i mierząc wynikowe odkształcenie.

• Czysto elastyczne materiały mają naprężenia i odkształcenia w fazie, tak że reakcja jednego spowodowana przez drugi jest natychmiastowa.
• W czysto lepkich materiałach odkształcenie opóźnia naprężenie o fazę 90 stopni.
• Materiały lepkosprężyste wykazują zachowanie gdzieś pośrodku tych dwóch rodzajów materiałów, wykazując pewne opóźnienie w odkształceniu.

Złożony moduł dynamiczny G może być użyty do przedstawienia relacji między naprężeniem oscylacyjnym a odkształceniem:

$${\ Displaystyle G = G'+ iG''}$$

gdzie ${\ Displaystyle i ^ {2} = -1}$ ; ${\ displaystyle G'}$ to moduł składowania , a to moduł stratności : ${\ displaystyle G''}$

$${\ Displaystyle G' = {\ Frac {\ sigma _ {0}} {\ varepsilon _ {0}}} \ cos \ delta}$$

$${\ Displaystyle G'' = {\ Frac {\ sigma _ {0}} {\ varepsilon _ {0}}} \ sin \ delta}$$

gdzie i są odpowiednio amplitudami naprężenia i odkształcenia, $przesunięciem$$jest$$fazowym$ między

Modele konstytutywne liniowej lepkosprężystości

Porównanie pełzania i relaksacji naprężeń dla modeli trzy- i czteroelementowych

Materiały lepkosprężyste, takie jak polimery amorficzne, polimery półkrystaliczne, biopolimery, a nawet żywe tkanki i komórki, można modelować w celu określenia ich interakcji naprężenia i odkształcenia lub siły i przemieszczenia, a także ich zależności czasowych. Modele te, które obejmują model Maxwella , model Kelvina-Voigta , standardowy liniowy model bryłowy i model Burgersa , są wykorzystywane do przewidywania odpowiedzi materiału w różnych warunkach obciążenia.

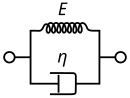
Zachowanie lepkosprężyste ma sprężyste i lepkie komponenty modelowane odpowiednio jako liniowe kombinacje sprężyn i dashpotów . Każdy model różni się rozmieszczeniem tych elementów, a wszystkie te modele lepkosprężyste można równoważnie modelować jako obwody elektryczne.

W równoważnym obwodzie elektrycznym naprężenie jest reprezentowane przez prąd, a szybkość odkształcenia przez napięcie. Moduł sprężystości sprężyny jest analogiczny do odwrotności indukcyjności obwodu (przechowuje energię), a lepkość deski do rezystancji obwodu (rozprasza energię).

Elementy sprężyste, jak wspomniano wcześniej, można modelować jako sprężyny o stałej sprężystości E, biorąc pod uwagę wzór:

$${\ Displaystyle \ sigma = E \ varepsilon}$$

gdzie σ to naprężenie, E to moduł sprężystości materiału, a ε to odkształcenie występujące pod danym naprężeniem, podobnie jak prawo Hooke'a .

Lepkie składniki można modelować jako dashpoty , tak że zależność naprężenie-szybkość odkształcenia można podać jako,

$${\ Displaystyle \ sigma = \ eta {\ Frac {d \ varepsilon} {dt}}}$$

gdzie σ to naprężenie, η to lepkość materiału, a dε/dt to pochodna odkształcenia po czasie.

Zależność między naprężeniem a odkształceniem można uprościć dla określonych szybkości naprężenia lub odkształcenia. W przypadku dużych naprężeń lub szybkości odkształcenia/krótkich okresów dominują składowe pochodne czasowe zależności naprężenie-odkształcenie. W tych warunkach można go przybliżyć jako sztywny pręt zdolny do przenoszenia dużych obciążeń bez deformacji. Stąd dashpot można uznać za „zwarcie”.

I odwrotnie, w stanach niskiego napięcia/dłuższych okresach czasu składowe pochodnej czasowej są pomijalne, a dashpot można skutecznie usunąć z systemu – obwód „otwarty”. W rezultacie tylko sprężyna podłączona równolegle do deski rozdzielczej przyczyni się do całkowitego obciążenia układu.

modelu Maxwella

Główny artykuł: materiał Maxwella

modelu Maxwella

Model Maxwella można przedstawić za pomocą czysto lepkiego tłumika i czysto elastycznej sprężyny połączonych szeregowo, jak pokazano na schemacie. Model można przedstawić za pomocą następującego równania:

$${\ Displaystyle \ sigma + {\ Frac {\ eta} {E}}} {\ kropka {\ sigma}} = \ eta {\ kropka {\ varepsilon}}}$$

W tym modelu, jeśli materiał jest poddawany stałemu naprężeniu, naprężenia stopniowo się zmniejszają . Kiedy materiał jest poddawany stałemu naprężeniu, odkształcenie składa się z dwóch składowych. Po pierwsze, element sprężysty pojawia się natychmiastowo, odpowiednio do sprężyny, i odpręża się natychmiast po zwolnieniu naprężenia. Drugi to składnik lepki, który zwiększa się wraz z upływem czasu pod wpływem obciążenia. Model Maxwella przewiduje, że naprężenie maleje wykładniczo w czasie, co jest dokładne dla większości polimerów. Jednym z ograniczeń tego modelu jest to, że nie przewiduje on dokładnie pełzania. Model Maxwella dla warunków pełzania lub stałego naprężenia zakłada, że ​​odkształcenie będzie rosło liniowo w czasie. Jednak polimery w większości wykazują spadek szybkości odkształcania w czasie.

Model ten można zastosować do miękkich ciał stałych: polimerów termoplastycznych w pobliżu ich temperatury topnienia, świeżego betonu (pomijając jego starzenie) oraz wielu metali w temperaturze zbliżonej do temperatury topnienia.

Model Kelvina-Voigta

Główny artykuł: materiał Kelvina-Voigta

Schematyczne przedstawienie modelu Kelvina – Voigta

Model Kelvina-Voigta, znany również jako model Voigta, składa się z tłumika Newtona i elastycznej sprężyny Hooke'a połączonych równolegle, jak pokazano na rysunku. Służy do wyjaśnienia pełzania polimerów.

Relacja konstytutywna jest wyrażona jako liniowe równanie różniczkowe pierwszego rzędu:

$${\ Displaystyle \ sigma = E \ varepsilon + \ eta {\ kropka {\ varepsilon}}}$$

Ten model przedstawia ciało stałe podlegające odwracalnemu, lepkosprężystemu odkształceniu. Po przyłożeniu stałego naprężenia materiał odkształca się z malejącą szybkością, asymptotycznie zbliżając się do odkształcenia w stanie ustalonym. Po zwolnieniu naprężenia materiał stopniowo rozluźnia się do stanu nieodkształconego. Przy stałym naprężeniu (pełzanie) model jest dość realistyczny, ponieważ przewiduje, że odkształcenie będzie dążyć do σ/E w miarę upływu czasu do nieskończoności. Podobnie jak model Maxwella, model Kelvina-Voigta ma również ograniczenia. Model bardzo dobrze radzi sobie z modelowaniem pełzania w materiałach, ale pod względem relaksacji model jest znacznie mniej dokładny.

Model ten można zastosować do polimerów organicznych, gumy i drewna, gdy obciążenie nie jest zbyt duże.

Standardowy liniowy model bryłowy

Główny artykuł: Standardowy liniowy model bryłowy

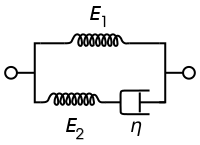
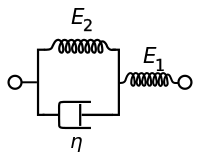
Standardowy liniowy model bryłowy, znany również jako model Zenera, składa się z dwóch sprężyn i dashpot. Jest to najprostszy model, który prawidłowo opisuje zachowanie pełzania i relaksacji naprężeń materiału lepkosprężystego. W przypadku tego modelu rządzącymi stosunkami konstytutywnymi są:

Reprezentacja Maxwella	Reprezentacja Kelvina
${\ Displaystyle \ sigma + {\ Frac {\ eta} {E_ {2}}} {\ kropka {\ sigma }}=E_{1}\varepsilon +{\frac {\eta (E_{1}+E_{2})}{E_{2}}}{\kropka {\varepsilon}}}$	${\ Displaystyle \ sigma + {\ Frac {\ eta} {E_ {1} +E_{2}}}{\dot {\sigma }}={\frac {E_{1}E_{2}}{E_{1}+E_{2}}}\varepsilon +{\frac {E_{ 1}\eta }{E_{1}+E_{2}}}{\kropka {\varepsilon}}}$

Pod stałym naprężeniem modelowany materiał natychmiast odkształci się do pewnego odkształcenia, które jest chwilową częścią sprężystą odkształcenia. Następnie będzie się nadal odkształcać i asymptotycznie zbliżać do odkształcenia w stanie ustalonym, które jest opóźnioną elastyczną częścią odkształcenia. Chociaż Standardowy liniowy model bryłowy jest dokładniejszy niż modele Maxwella i Kelvina-Voigta w przewidywaniu odpowiedzi materiału, matematycznie zwraca niedokładne wyniki dla odkształcenia w określonych warunkach obciążenia.

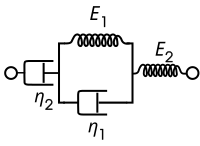
Wzór burgerów

Główny artykuł: materiał Burgery

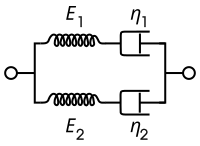
Model Burgersa składa się z dwóch elementów Maxwella połączonych równolegle lub elementu Kelvina-Voigta, sprężyny i deski rozdzielczej połączonych szeregowo. W przypadku tego modelu rządzącymi stosunkami konstytutywnymi są:

Reprezentacja Maxwella	Reprezentacja Kelvina
${\ Displaystyle \ sigma + \ lewo ({\ Frac {\ eta _ {1}} {E_ {1}}} + {\ Frac {\ eta _ {2}} {E_ {2}}} \ prawej) {\dot {\sigma }}+{\frac {\eta _{1}\eta _{2}}{E_{1}E_{2}}}{\ddot {\sigma }}=\left(\ eta _{1}+\eta _{2}\right){\dot {\varepsilon}}+{\frac {\eta _{1}\eta _{2}\left(E_{1}+E_{ 2}\right)}{E_{1}E_{2}}}{\ddot {\varepsilon}}}$	${\ Displaystyle \ sigma + \ lewo ({\ Frac {\ eta _ {1}} {E_ {1}}} + {\ Frac {\ eta _ {2}} {E_ {1}}} + {\ frac {\eta _{2}}{E_{2}}}\right){\dot {\sigma }}+{\frac {\eta _{1}\eta _{2}}{E_{1}E_ {2}}}{\ddot {\sigma }}=\eta _{2}{\dot {\varepsilon}}+{\frac {\eta _{1}\eta _{2}}{E_{1 }}}{\ddot {\varepsilon}}}$

Model ten uwzględnia przepływ lepki w standardowym liniowym modelu bryłowym, dając liniowo rosnącą asymptotę dla odkształcenia w ustalonych warunkach obciążenia.

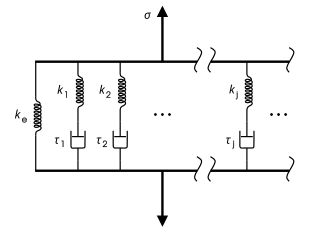
Uogólniony model Maxwella

Główny artykuł: Uogólniony model Maxwella

Schemat modelu Maxwella-Wiecherta

Uogólniony model Maxwella, znany również jako model Wiecherta, jest najbardziej ogólną postacią liniowego modelu lepkosprężystości. Bierze pod uwagę, że relaksacja nie występuje w jednym czasie, ale w rozkładzie czasów. Ze względu na segmenty molekularne o różnej długości, przy czym krótsze mają mniejszy udział niż dłuższe, występuje różny rozkład czasu. Model Wiecherta pokazuje to, mając tyle elementów Maxwella, ile potrzeba do dokładnego przedstawienia rozkładu. Rysunek po prawej stronie przedstawia uogólniony model Wiecherta. Zastosowania: metale i stopy w temperaturach niższych niż jedna czwarta ich bezwzględnej temperatury topnienia (wyrażonej w K).

Modele konstytutywne dla nieliniowej lepkosprężystości

Nieliniowe równania konstytutywne lepkosprężystości są potrzebne do ilościowego wyjaśnienia zjawisk zachodzących w płynach, takich jak różnice w naprężeniach normalnych, rozrzedzenie ścinające i pogrubienie rozciągające. Z konieczności historia doświadczana przez materiał jest potrzebna do uwzględnienia zachowania zależnego od czasu i jest zwykle uwzględniana w modelach jako jądro historii K .

Płyn drugiego rzędu

Główny artykuł: płyn drugiego rzędu

Płyn drugiego rzędu jest zwykle uważany za najprostszy nieliniowy model lepkosprężysty i zwykle występuje w wąskim obszarze zachowania materiałów występującym przy dużych amplitudach odkształcenia i liczbie Deborah między płynami newtonowskimi a innymi bardziej skomplikowanymi nieliniowymi płynami lepkosprężystymi. Równanie konstytutywne płynu drugiego rzędu jest określone wzorem:

$${\ Displaystyle \ mathbf {T} = - p \ mathbf {I} + 2 \ eta _ {0} \ mathbf {D} -\psi _{1}\mathbf {D} ^{\triangledown }+4\psi _{2}\mathbf {D} \bullet \mathbf {D} }$$

Gdzie:

• ${\ displaystyle \ mathbf {I}}$ jest tensorem tożsamości
• jest tensorem odkształcenia. ${\ displaystyle \ mathbf {D}}$
• ${\ Displaystyle \ eta _ {0}, \ psi _ {1}, \ psi _ {2}}$ oznaczają odpowiednio lepkość oraz pierwszy i drugi współczynnik naprężenia normalnego
• oznacza górną konwekcyjną pochodną tensora odkształcenia, gdzie ${\ Displaystyle \ mathbf {D} ^ {\ triangledown}}$
  $${\ Displaystyle \ mathbf {D} ^ {\ trójkąt w dół} \ równoważnik {\ kropka {\ mathbf {D}}} - (\ bigtriangledown \ mathbf {v} )^{\mathbf {T}}\bullet \mathbf {D} -\mathbf {D} \bullet \bigtriangledown \mathbf {v} }$$
  re ${\ Displaystyle {\ kropka {\ mathbf {D}}} \ równoważnik {\ Frac {\ częściowy} {\ częściowy t}} \ mathbf {D} + \$ jest materialną pochodną czasową tensora deformacji.

Model Maxwella z konwekcją górną

Główny artykuł: model Maxwella z górną konwekcją

Model Maxwella z górną konwekcją uwzględnia nieliniowe zachowanie w czasie w lepkosprężystym modelu Maxwella, podane przez:

$${\ Displaystyle \ mathbf {\ tau} + \ lambda \ mathbf {\ tau} ^ {\ trójkąt w dół} = 2 \ eta _ {0} \ mathbf {D}}$$

gdzie $oznacza$ tensor naprężenia

Model Oldroyda-B

Główny artykuł: model Oldroyd-B

Model Oldroyda-B jest rozszerzeniem modelu Upper Convected Maxwell i jest interpretowany jako rozpuszczalnik wypełniony elastycznym koralikiem i sprężynowymi hantlami. Model nosi imię jego twórcy, Jamesa G. Oldroyda .

Model można zapisać jako:

$${\ Displaystyle \ mathbf {T} + \ lambda _ {1} {\ stackrel {\ nabla} {\ mathbf {T}}} = 2 \ eta _{0}(\mathbf {D} +\lambda _{2}{\stackrel {\nabla}}{\mathbf {D}}})}$$

Gdzie:

• ${\ Displaystyle \ mathbf {T}}$ jest tensorem naprężenia ;
• ${\ Displaystyle \ lambda _ {1}}$ to czas relaksu;
• ${\ Displaystyle \ lambda _ {2}}$ to czas opóźnienia = ${\ Displaystyle {\ Frac {\ eta _ {s}}} {\ eta _ {0}}} \ lambda _ {1 }}$ ;
• ${\ Displaystyle {\ stackrel {\ nabla} {\ mathbf {T}}}}$ jest górną konwekcyjną pochodną czasową tensora naprężeń:
  $${\ Displaystyle {\ stackrel {\ nabla} {\ mathbf {T}}} = {\ Frac {\ częściowy} {\ częściowy t}} \ mathbf {T} + \ mathbf {v} \ cdot \ nabla \ mathbf { T} -((\nabla \mathbf {v} )^{T}\cdot \mathbf {T} +\mathbf {T} \cdot (\nabla \mathbf {v} ));}$$
• ${\ Displaystyle \ mathbf {v}}$ to prędkość płynu;
• ${\ Displaystyle \ eta _ {0}}$ to całkowita lepkość złożona z rozpuszczalnika i składników polimerowych, ${\ Displaystyle \ eta _ {0} = \ eta _ {s} + \ eta _ { p}}$ ;
• ${\ Displaystyle \ mathbf {D}}$ jest tensorem szybkości odkształcenia lub tensorem szybkości odkształcenia, ${\ Displaystyle \ mathbf {D} = {\ Frac {1} {2}}\left[{\boldsymbol {\nabla}}\mathbf {v} +({\boldsymbol {\nabla}}\mathbf {v})^{T}\right]}$ .

Chociaż model daje dobre przybliżenie płynów lepkosprężystych w przepływie ścinającym, ma niefizyczną osobliwość w przepływie rozciągającym, w którym hantle są rozciągane w nieskończoność. Jest to jednak specyficzne dla przepływu wyidealizowanego; w przypadku geometrii szczelin poprzecznych przepływ rozciągający nie jest idealny, więc naprężenie, chociaż pojedyncze, pozostaje całkowalne, chociaż naprężenie jest nieskończone w odpowiednio nieskończenie małym obszarze.

Jeśli lepkość rozpuszczalnika wynosi zero, model Oldroyda-B staje się modelem Upper Convected Maxwell .

modelu Wagnera

Główny artykuł: model Wagnera

Model Wagnera można uznać za uproszczoną praktyczną postać modelu Bernsteina-Kearsleya-Zapasa. Model został opracowany przez niemieckiego reologa Manfreda Wagnera .

Dla warunków izotermicznych model można zapisać jako:

$${\ Displaystyle \ mathbf {\ sigma} (t) = - p\mathbf {I} +\int _{-\infty}^{t}M(tt')h(I_{1},I_{2})\mathbf {B} (t')\,dt'}$$

Gdzie:

• ${\ Displaystyle \ mathbf {\ sigma} (t)}$ jest tensorem naprężenia Cauchy'ego w funkcji czasu t ,
• p to ciśnienie
• ${\ displaystyle \ mathbf {I}}$ jest tensorem jedności
• M to funkcja pamięci pokazująca, zwykle wyrażana jako suma wyrazów wykładniczych dla każdego trybu relaksacji :
  $${\ Displaystyle M (x) = \ suma _ {k = 1} ^ {m} {\ Frac {g_ {i }}{\theta _{i}}}\exp \left({\frac {-x}{\theta _{i}}}\right),}$$
  $gdzie dla$$;$ relaksacji jest relaksacji i jest czasem
• ${\ Displaystyle h (I_ {1}, I_ {2})}$ jest funkcją tłumienia odkształcenia , która zależy od pierwszego i drugiego niezmiennika tensora palca ${\ displaystyle \ mathbf {B}}$ .

Funkcja tłumienia odkształcenia jest zwykle zapisywana jako:

$${\ Displaystyle h (I_ {1}, I_{2})=m^{*}\exp(-n_{1}{\sqrt {I_{1}-3}})+(1-m^{*})\exp(-n_{2} {\ sqrt {I_ {2}-3}})}$$

Jeżeli wartość funkcji umocnienia odkształceniowego jest równa jeden, to odkształcenie jest małe; jeśli zbliża się do zera, wówczas deformacje są duże.

Prona seria

Główny artykuł: metoda Prony'ego

W jednowymiarowym teście relaksacji materiał jest poddawany nagłemu odkształceniu, które jest utrzymywane na stałym poziomie przez cały czas trwania testu, a naprężenie jest mierzone w czasie. Początkowe naprężenie jest spowodowane sprężystą reakcją materiału. Następnie naprężenie rozluźnia się w czasie z powodu efektów lepkości w materiale. Zazwyczaj stosuje się rozciąganie, ściskanie, ściskanie w masie lub ścinanie. Otrzymane dane dotyczące naprężenia w funkcji czasu można dopasować za pomocą szeregu równań, zwanych modelami. Zmienia się tylko notacja w zależności od rodzaju zastosowanego odkształcenia: oznacza się relaksację rozciągająco-ściskającą , oznacza się ${\ displaystyle E}$ mi ${\ Displaystyle G}$ , masa jest oznaczona ${\ Displaystyle K}$ . Szereg Prony'ego dla relaksacji ścinania to

$${\ Displaystyle G (t) = G _ {\ infty} + \ suma _ {i = 1} ^ {N} G_{i}\exp(-t/\tau _{i})}$$

gdzie $relaksacji$ długoterminowym modułem sprężystości po całkowitym rozluźnieniu materiału, $to$ mylić z ${\ displaystyle \tau _{i}}$ na diagramie); im wyższe są ich wartości, tym dłużej trwa relaksacja stresu. Dane są dopasowywane do równania za pomocą algorytmu minimalizacji, który dopasowuje parametry ( ${\ Displaystyle G_ {\ infty}, G_ {i}, \ tau _ {i}}),$ aby zminimalizować błąd między wartościami przewidywanymi a wartościami danych.

Otrzymuje się alternatywną postać, zauważając, że moduł sprężystości jest powiązany z modułem długookresowym przez

$${\ Displaystyle G (t = 0) = G_ {0} = G _ {\ infty} + \ suma _ {i = 1} ^ {N }Żołnierz amerykański}}$$

Dlatego,

$${\ Displaystyle G (t) = G_ {0} - \ suma _ {i = 1} ^ {N} G_ {i}\lewo[1-e^{-t/\tau _{i}}\prawo]}$$

Ta postać jest wygodna, gdy moduł sprężystości ścinającej jest uzyskiwany z danych niezależnych od danych relaksacyjnych i / lub do implementacji komputerowej, gdy pożądane jest określenie właściwości sprężystych oddzielnie od właściwości lepkich, sol {\ displaystyle G_ $}$ jak w Simulii (2010).

Eksperyment z pełzaniem jest zwykle łatwiejszy do przeprowadzenia niż eksperyment z relaksacją, więc większość danych jest dostępna jako podatność (pełzanie) w funkcji czasu. Niestety, nie jest znana zamknięta postać podatności (pełzania) pod względem współczynnika szeregu Prony'ego. Tak więc, jeśli ktoś ma dane dotyczące pełzania, nie jest łatwo uzyskać współczynniki szeregu (relaksacyjnego) Prony'ego, które są potrzebne na przykład w. Dogodny sposób uzyskania tych współczynników jest następujący. Najpierw dopasuj dane pełzania do modelu, który ma rozwiązania w formie zamkniętej zarówno pod względem zgodności, jak i relaksacji; na przykład model Maxwella-Kelvina (równ. 7.18-7.19) w Barbero (2007) lub Standardowy model bryłowy (równ. 7.20-7.21) w Barbero (2007) (sekcja 7.1.3). Gdy znane są parametry modelu pełzania, utwórz pseudodane relaksacji za pomocą sprzężonego modelu relaksacji dla tych samych czasów co oryginalne dane. Na koniec dopasuj pseudodane do szeregu Prony'ego.

Wpływ temperatury na zachowanie lepkosprężyste

Główny artykuł: Superpozycja czasu i temperatury

Wtórne wiązania polimeru stale pękają i odnawiają się w wyniku ruchu termicznego. Zastosowanie naprężenia faworyzuje niektóre konformacje kosztem innych, więc cząsteczki polimeru będą z czasem stopniowo „płynąć” do preferowanych konformacji. Ponieważ ruch termiczny jest jednym z czynników przyczyniających się do deformacji polimerów, właściwości lepkosprężyste zmieniają się wraz ze wzrostem lub spadkiem temperatury. W większości przypadków moduł pełzania, zdefiniowany jako stosunek przyłożonego naprężenia do odkształcenia zależnego od czasu, maleje wraz ze wzrostem temperatury. Ogólnie rzecz biorąc, wzrost temperatury koreluje z logarytmicznym spadkiem czasu potrzebnego do nadania równego odkształcenia pod stałym naprężeniem. Innymi słowy, rozciągnięcie materiału lepkosprężystego na taką samą odległość w wyższej temperaturze wymaga mniej pracy niż w niższej.

Bardziej szczegółowy wpływ temperatury na lepkosprężyste zachowanie polimeru można wykreślić, jak pokazano.

W typowych polimerach występuje głównie pięć regionów (niektóre oznaczone jako cztery, które łączą razem IV i V).

• Region I: W tym obszarze przedstawiony jest stan szklisty polimeru. Temperatura w tym obszarze dla danego polimeru jest zbyt niska, aby wywołać ruch molekularny. Stąd ruch cząsteczek jest zamrożony w tym obszarze. Właściwość mechaniczna jest twarda i krucha w tym regionie.
• Region II: Polimer przechodzi temperaturę zeszklenia w tym obszarze. Powyżej Tg energia cieplna dostarczana przez otoczenie wystarcza do odmrożenia ruchu cząsteczek. Molekuły mogą mieć lokalny ruch w tym regionie, co prowadzi do gwałtownego spadku sztywności w porównaniu z regionem I.
• Region III: region płaskowyżu gumowego. Materiały leżące w tym regionie miałyby elastyczność dalekiego zasięgu napędzaną przez entropię. Na przykład gumka jest nieuporządkowana w stanie początkowym tego regionu. Naciągając gumkę, wyrównujesz również strukturę, aby była bardziej uporządkowana. Dlatego po zwolnieniu gumki spontanicznie będzie szukać wyższego stanu entropii, a więc wraca do stanu początkowego. To właśnie nazywamy odzyskiwaniem kształtu elastyczności napędzanym entropią.
• Region IV: Zachowanie w obszarze gumowatego przepływu jest wysoce zależne od czasu. Polimery w tym regionie musiałyby zastosować superpozycję czasowo-temperaturową, aby uzyskać bardziej szczegółowe informacje, aby ostrożnie zdecydować, jak wykorzystać materiały. Na przykład, jeśli materiał jest używany do radzenia sobie z krótkim czasem interakcji, może przedstawiać się jako materiał „twardy”. Używając go do celów związanych z długim czasem interakcji, działałby jako „miękki” materiał.
• Region V: Lepki polimer łatwo przepływa w tym regionie. Kolejny znaczący spadek sztywności.

Zależność modułu od temperatury

Ekstremalnie niskie temperatury mogą spowodować, że materiały lepkosprężyste przejdą w fazę szklistą i staną się kruche . Na przykład wystawienie klejów wrażliwych na nacisk na ekstremalne zimno ( suchy lód , zamrażający spray itp.) powoduje utratę przyczepności, co prowadzi do rozwarstwienia.

Lepkosprężyste pełzanie

Główny artykuł: Pełzanie (deformacja)

a) Przyłożone naprężenie ib) Odkształcenie indukowane jako funkcje czasu w krótkim okresie dla materiału lepkosprężystego.

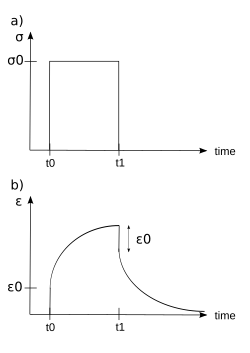
Materiały lepkosprężyste poddawane działaniu stałego naprężenia krokowego ulegają zależnemu od czasu wzrostowi odkształcenia. Zjawisko to znane jest jako pełzanie lepkosprężyste.

W $lepkosprężysty$ jest obciążany stałym naprężeniem, które utrzymuje się przez wystarczająco długi okres czasu. Materiał reaguje na naprężenie odkształceniem, które wzrasta, aż do ostatecznego zniszczenia materiału, jeśli jest to ciecz lepkosprężysta. Z drugiej strony, jeśli jest to lepkosprężyste ciało stałe, może ulec uszkodzeniu lub nie, w zależności od przyłożonego naprężenia w stosunku do ostatecznej wytrzymałości materiału. Gdy naprężenie jest utrzymywane przez krótszy okres czasu, materiał poddawany jest wstępnemu odkształceniu aż do czasu ${\ displaystyle t_ {1}}$$,$ a następnie stopniowo maleje do szczątkowego

Dane dotyczące pełzania lepkosprężystego można przedstawić, wykreślając moduł pełzania (stałe przyłożone naprężenie podzielone przez całkowite odkształcenie w określonym czasie) w funkcji czasu. Poniżej naprężenia krytycznego lepkosprężysty moduł pełzania jest niezależny od przyłożonego naprężenia. Rodzina krzywych opisujących odpowiedź odkształcenia w funkcji czasu na różne przyłożone naprężenia może być reprezentowana przez pojedynczą krzywą lepkosprężystego modułu pełzania w funkcji czasu, jeśli zastosowane naprężenia są poniżej krytycznej wartości naprężenia materiału.

Pełzanie lepkosprężyste jest ważne przy rozważaniu długoterminowego projektu konstrukcyjnego. Biorąc pod uwagę warunki obciążenia i temperatury, projektanci mogą wybrać materiały, które najlepiej odpowiadają żywotności komponentów.

Pomiar

Reometria ścinania

Reometry ścinające opierają się na idei umieszczania mierzonego materiału między dwiema płytami, z których jedna lub obie poruszają się w kierunku ścinania, aby wywołać naprężenia i odkształcenia w materiale. Badanie można przeprowadzić przy stałej szybkości odkształcania, naprężeniu lub w sposób oscylacyjny (forma dynamicznej analizy mechanicznej ). Reometry ścinające są zwykle ograniczone efektami krawędziowymi, w których materiał może wyciekać spomiędzy dwóch płyt i ślizgać się na granicy materiał/płyta.

Reometria ekstensyjna

Reometry ekstensjonalne, znane również jako ekstensjometry, mierzą właściwości lepkosprężyste, ciągnąc płyn lepkosprężysty, zwykle jednoosiowo. Ponieważ zazwyczaj wykorzystuje to siły kapilarne i ogranicza płyn do wąskiej geometrii, technika ta jest często ograniczona do płynów o stosunkowo niskiej lepkości, takich jak rozcieńczone roztwory polimerów lub niektóre stopione polimery. Reometry ekstensjonalne są również ograniczone efektami krawędziowymi na końcach ekstensjometru i różnicami ciśnień między wewnętrzną i zewnętrzną kapilarą.

Pomimo wspomnianych powyżej oczywistych ograniczeń, reometrię ekstensyjną można również przeprowadzić na płynach o dużej lepkości. Chociaż wymaga to użycia różnych instrumentów, te techniki i aparatura pozwalają na badanie rozciągających się właściwości lepkosprężystych materiałów, takich jak stopione polimery. Trzy najpowszechniejsze przyrządy do reometrii ekstensyjnej opracowane w ciągu ostatnich 50 lat to reometr typu Meissnera, reometr rozciągania włókien (FiSER) i reometr ekstensjonalny Sentmanat (SER).

Reometr typu Meissnera, opracowany przez Meissnera i Hostettlera w 1996 roku, wykorzystuje dwa zestawy przeciwbieżnych rolek do jednoosiowego naprężenia próbki. Ta metoda wykorzystuje stałą długość próbki podczas całego eksperymentu i podtrzymuje próbkę pomiędzy rolkami za pomocą poduszki powietrznej, aby wyeliminować efekt zwiotczenia próbki. Ma kilka problemów – po pierwsze, płyn może ślizgać się po paskach, co prowadzi do niższych prędkości odkształcania, niż można by się spodziewać. Ponadto sprzęt ten jest trudny w obsłudze i kosztowny w zakupie i utrzymaniu.

Reometr FiSER po prostu zawiera płyn pomiędzy dwiema płytkami. Podczas eksperymentu górna płyta jest utrzymywana nieruchomo, a do dolnej płytki przykładana jest siła, odsuwająca ją od górnej. Szybkość odkształcenia mierzy się szybkością zmiany promienia próbki w jej środku. Oblicza się go za pomocą następującego równania:

$${\ Displaystyle {\ kropka {\ epsilon}} = - {\ Frac {2} {R}} {dR \ ponad dt}}$$

gdzie $.$ wartością środkowego promienia $jest$ odkształcenia Lepkość próbki jest następnie obliczana przy użyciu następującego równania:

$${\ Displaystyle \ eta = {\ Frac {F} {\ pi R ^ {2} {\ kropka {\ epsilon}}}}}$$

gdzie $jest$$próbki$ , a siłą przyłożoną do próbki w celu jej rozerwania

Podobnie jak reometr typu Meissnera, reometr SER wykorzystuje zestaw dwóch rolek do naprężania próbki z określoną szybkością. Następnie oblicza lepkość próbki za pomocą dobrze znanego równania:

$${\ Displaystyle \ sigma = \ eta {\ kropka {\ epsilon}}}$$

gdzie $}$$,$$sigma$ to naprężenie to lepkość, a szybkość odkształcenia Naprężenie w tym przypadku jest określane za pomocą przetworników momentu obrotowego obecnych w przyrządzie. Niewielki rozmiar tego instrumentu sprawia, że ​​jest łatwy w użyciu i eliminuje zwisanie próbki między rolkami. Schemat przedstawiający szczegółowo działanie reometru ekstensyjnego SER można znaleźć po prawej stronie.

Schemat reometru ekstensjonalnego SER. Próbka (brązowa) jest trzymana w dwóch cylindrach (szarych), które są następnie obracane w przeciwnych kierunkach przy różnych prędkościach odkształcania. Moment obrotowy wymagany do odkształcenia próbki przy tych szybkościach jest obliczany za pomocą zestawu przetworników momentu obrotowego obecnych w przyrządzie. Te wartości momentu obrotowego są następnie konwertowane na wartości naprężeń, a naprężenia i szybkości odkształcania są następnie wykorzystywane do określenia lepkości próbki.

Inne metody

Chociaż istnieje wiele przyrządów do testowania odpowiedzi mechanicznej i lepkosprężystej materiałów, szerokopasmowa spektroskopia lepkosprężysta (BVS) i rezonansowa spektroskopia ultradźwiękowa (RUS) są częściej stosowane do testowania zachowania lepkosprężystego, ponieważ można je stosować powyżej i poniżej temperatury otoczenia i są bardziej specyficzne do badania lepkosprężystości. Te dwa instrumenty wykorzystują mechanizm tłumienia przy różnych częstotliwościach i przedziałach czasowych bez odwoływania się do superpozycji czasu i temperatury . Wykorzystanie BVS i RUS do badania właściwości mechanicznych materiałów jest ważne dla zrozumienia, jak zachowa się materiał wykazujący lepkosprężystość.

Zobacz też

• Plastik Binghama
• Biomateriał
• Biomechanika
• Lepkosprężystość krwi
• Płyny elastyczne o stałej lepkości
• Indeks deformacji
• Szklane przejście
• Klej wrażliwy na nacisk
• Reologia
• Elastyczność gumy
• Plastelina
• Lepkosprężystość kości
• Wiskoplastyczność
• Wiskoelastyczne dysze

• Silbey i Alberty (2001): Chemia fizyczna , 857. John Wiley & Sons, Inc.
• Alan S. Wineman i KR Rajagopal (2000): Odpowiedź mechaniczna polimerów: wprowadzenie
• Allen i Thomas (1999): Struktura materiałów , 51.
• Crandala i in. (1999): Wprowadzenie do mechaniki ciał stałych 348
• J. Lemaitre i JL Chaboche (1994) Mechanika materiałów stałych
• Yu. Dimitrienko (2011) Nieliniowa mechanika kontinuum i duże odkształcenia nieelastyczne , Springer, 772p