Proces izotermiczny

W termodynamice proces izotermiczny jest rodzajem procesu termodynamicznego , w którym temperatura T układu pozostaje stała: Δ T = 0. Zwykle ma to miejsce, gdy układ styka się z zewnętrznym zbiornikiem termicznym i następuje zmiana w układzie wystarczająco wolno, aby umożliwić ciągłe dostosowywanie systemu do temperatury zbiornika poprzez wymianę ciepła (patrz quasi-równowaga ). Dla kontrastu, an proces adiabatyczny to taki, w którym układ nie wymienia ciepła z otoczeniem ( Q = 0).

Po prostu możemy powiedzieć, że w procesie izotermicznym

${\ Displaystyle T = {\ tekst {stała}}}$
${\ Displaystyle \ Delta T = 0}$
${\ displaystyle dT = 0}$
Tylko w przypadku gazów doskonałych energia wewnętrzna ${\ Displaystyle \ Delta U = 0}$

podczas procesów adiabatycznych:

${\ displaystyle Q = 0.}$

Etymologia

Przymiotnik „izotermiczny” pochodzi od greckich słów „ἴσος” („isos”) oznaczających „równy” i „θέρμη” („terma”) oznaczającego „ciepło”.

Przykłady

Procesy izotermiczne mogą zachodzić w każdym systemie, który ma pewne sposoby regulacji temperatury, w tym w maszynach o wysokiej strukturze , a nawet w żywych komórkach. Niektóre części cykli niektórych silników cieplnych są przeprowadzane izotermicznie (na przykład w cyklu Carnota ). W analizie termodynamicznej reakcji chemicznych zwykle najpierw analizuje się, co dzieje się w warunkach izotermicznych, a następnie rozważa się wpływ temperatury. Zmiany fazowe , takie jak topnienie lub parowanie , są również procesami izotermicznymi, gdy, jak to zwykle bywa, zachodzą przy stałym ciśnieniu. Procesy izotermiczne są często wykorzystywane jako punkt wyjścia do analizy bardziej złożonych, nieizotermicznych procesów.

Procesy izotermiczne są szczególnie interesujące dla gazów doskonałych. Wynika to z drugiego prawa Joule'a , które mówi, że energia wewnętrzna ustalonej ilości gazu doskonałego zależy tylko od jego temperatury. Zatem w procesie izotermicznym energia wewnętrzna gazu doskonałego jest stała. Wynika to z faktu, że w gazie doskonałym nie występują siły międzycząsteczkowe . Należy zauważyć, że dotyczy to tylko gazów doskonałych; energia wewnętrzna zależy od ciśnienia, a także od temperatury dla cieczy, ciał stałych i gazów rzeczywistych.

Podczas izotermicznego sprężania gazu nad układem wykonywana jest praca polegająca na zmniejszeniu objętości i zwiększeniu ciśnienia. Praca nad gazem zwiększa energię wewnętrzną i powoduje wzrost temperatury. Aby utrzymać stałą temperaturę, energia musi opuścić układ w postaci ciepła i dostać się do otoczenia. Jeśli gaz jest doskonały, ilość energii wprowadzanej do środowiska jest równa pracy wykonanej nad gazem, ponieważ energia wewnętrzna się nie zmienia. W przypadku ekspansji izotermicznej energia dostarczana do układu działa na otoczenie. W obu przypadkach, za pomocą odpowiedniego połączenia, zmiana objętości gazu może wykonać użyteczną pracę mechaniczną. Aby uzyskać szczegółowe informacje na temat obliczeń, zob obliczenie pracy .

Dla procesu adiabatycznego , w którym ciepło nie przepływa do lub z gazu, ponieważ jego pojemnik jest dobrze izolowany, Q = 0. Jeśli nie ma również pracy, tj. swobodnego rozszerzania się , nie ma zmiany energii wewnętrznej. Dla gazu doskonałego oznacza to, że proces jest również izotermiczny. Zatem określenie, że proces jest izotermiczny, nie wystarcza do określenia unikalnego procesu.

Szczegóły dotyczące gazu doskonałego

Rysunek 1. Kilka izoterm gazu doskonałego na wykresie pV, gdzie p oznacza ciśnienie, a V objętość.

W szczególnym przypadku gazu, do którego ma zastosowanie prawo Boyle'a , iloczyn pV ( p dla ciśnienia gazu i V dla objętości gazu) jest stały, jeśli gaz jest utrzymywany w warunkach izotermicznych. Wartość stałej to nRT , gdzie n to liczba moli obecnego gazu, a R to stała gazu doskonałego . Innymi słowy, obowiązuje prawo gazu doskonałego pV = nRT . Dlatego:

{\ Displaystyle p = {nRT \ nad V} = {{\ tekst {stała}} \ ponad V}}

posiada. Rodzina krzywych generowanych przez to równanie jest pokazana na wykresie na rysunku 1. Każda krzywa nazywana jest izotermą, co oznacza krzywą w tej samej temperaturze T . Takie wykresy nazywane są diagramami wskaźników i zostały po raz pierwszy użyte przez Jamesa Watta i innych do monitorowania wydajności silników. Temperatura odpowiadająca każdej krzywej na rysunku wzrasta od lewego dolnego do prawego górnego rogu.

Obliczanie pracy

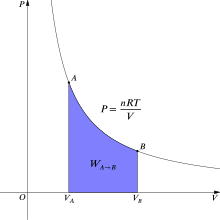
Rysunek 2. Fioletowy obszar przedstawia pracę dla tej zmiany izotermicznej.

W termodynamice odwracalna praca związana z przejściem gazu ze stanu A do stanu B wynosi

\ Displaystyle W_ {A \ do B} = - \ int _ {V_ {A}} ^ {V_ {B}} p \, dV}

gdzie p dla ciśnienia gazu i V dla objętości gazu. W przypadku odwracalnego procesu izotermicznego (stała temperatura T ) całka ta jest równa polu powierzchni pod odpowiednią izotermą PV (ciśnienie-objętość) i jest zaznaczona na fioletowo na rysunku 2 dla gazu doskonałego. Ponownie p = nRT / V i przy stałym T (ponieważ jest to proces izotermiczny), wyrażenie na pracę przyjmuje postać:

{\ Displaystyle W_ {A \ do B} = - \ int _ {V_ {A}} ^ {V_ {B}} p \, dV = - \ int _ {V_ {A}} ^ {V_ {B}} {\frac {nRT}{V}}dV=-nRT\int _{V_{A}}^{V_{B}}{\frac {1}{V}}dV=-nRT\ln {\frac { V_{B}}{V_{A}}}}

W konwencji IUPAC praca definiowana jest jako praca nad systemem przez jego otoczenie. Jeśli np. układ jest ściśnięty, to praca wykonywana jest nad układem przez otoczenie, więc praca jest dodatnia, a energia wewnętrzna układu wzrasta. I odwrotnie, jeśli system się rozszerza (tj. rozszerzanie się otaczającego systemu, więc swobodne rozszerzanie nie zachodzi), wtedy praca jest ujemna, ponieważ system działa na otoczenie, a energia wewnętrzna systemu maleje.

Warto również zauważyć, że dla gazów doskonałych, jeśli temperatura jest stała, energia wewnętrzna układu U również jest stała, a więc Δ U = 0. Ponieważ pierwsza zasada termodynamiki stwierdza, że Δ U = Q + W w Z konwencji IUPAC wynika, że Q = − W dla izotermicznej kompresji lub rozprężania gazów doskonałych.

Przykład procesu izotermicznego

Rysunek 3. Izotermiczna ekspansja gazu doskonałego. Czarna linia wskazuje ciągłe odwracalne rozszerzanie, podczas gdy czerwona linia wskazuje stopniowe i prawie odwracalne rozszerzanie przy każdym przyrostowym spadku ciśnienia gazu roboczego o 0,1 atm.

Odwracalna ekspansja gazu doskonałego może być wykorzystana jako przykład pracy wykonanej w procesie izotermicznym. Szczególnie interesujący jest stopień, w jakim ciepło jest przekształcane w użyteczną pracę, oraz związek między siłą ograniczającą a stopniem rozszerzalności.

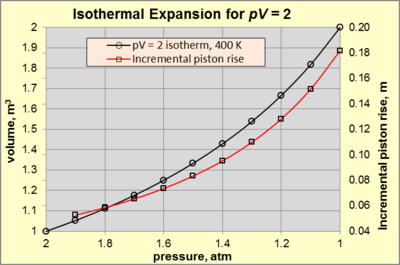
Podczas izotermicznej ekspansji gazu doskonałego zarówno $p$ , jak i $V$ zmieniają się wzdłuż izotermy ze stałym iloczynem $pV$ (tj. stałą T ). Rozważmy gaz roboczy w cylindrycznej komorze o wysokości 1 m i powierzchni 1 m ² (czyli 1 m ³ objętości) w temperaturze 400 K w równowadze statycznej . Otoczenie 1 atm (oznaczone jako $p surr$ ). Gaz roboczy jest zamknięty przez tłok połączony z urządzeniem mechanicznym, które wywiera siłę wystarczającą do wytworzenia ciśnienia roboczego gazu 2 atm (stan $A$ ). Przy każdej zmianie stanu $A$ , która powoduje spadek siły, gaz rozpręży się i wykona pracę nad otoczeniem. Rozszerzanie izotermiczne trwa tak długo, jak przyłożona siła maleje i dostarczana jest odpowiednia ilość ciepła, aby utrzymać $pV$ = 2 [atm·m ³ ] (= 2 atm × 1 m ³ ). Mówimy, że rozprężanie jest wewnętrznie odwracalne, jeśli ruch tłoka jest wystarczająco wolny, aby w każdej chwili podczas rozprężania temperatura i ciśnienie gazu były jednakowe i zgodne z prawem gazu doskonałego . Rysunek 3 przedstawia $p - V$ dla $pV$ = 2 [atm·m ³ ] dla rozszerzalności izotermicznej od 2 atm (stan $A$ ) do 1 atm (stan $B$ ).

Wykonana praca (oznaczona ) $się$ elementów Po pierwsze, praca rozprężania przeciw ciśnieniu otaczającej atmosfery (oznaczana jako $W p Δ V$ ), a po drugie, użyteczna praca mechaniczna (oznaczana jako $W mech$ ). Wyjściowym $mechem W$ mógłby tu być ruch tłoka, który obracałby korbą, która następnie obracałaby koło pasowe zdolne do podnoszenia wody z zalanych kopalni soli .

Displaystyle W_ {A \ do B} = - p \, V \ lewo (\ ln { \frac {V_{B}}{V_{A}}}\right)=-W_{p\Delta V}-W_{\rm {mech}}}

Układ osiąga stan $B$ ( $pV$ = 2 [atm·m ³ ] przy $p$ = 1 atm i $V$ = 2 m ³ ), gdy przyłożona siła osiąga zero. W tym momencie ${\ Displaystyle W_ {A \ do B}}$ równa się –140,5 kJ, a $W p Δ V$ wynosi –101,3 kJ. Przez różnicę, $W mech$ = –39,1 kJ, co stanowi 27,9% ciepła dostarczonego do procesu (-39,1 kJ / -140,5 kJ). Jest to maksymalna użyteczna ilość pracy mechanicznej, jaką można uzyskać z procesu w określonych warunkach. Procent $W mech$ jest funkcją $pV$ i $p surr$ i zbliża się do 100%, gdy $p surr$ zbliża się do zera.

Aby dokładniej zbadać naturę rozszerzalności izotermicznej, zwróć uwagę na czerwoną linię na rysunku 3. Stała wartość $pV$ powoduje wykładniczy wzrost wzrostu tłoka w stosunku do spadku ciśnienia. Na przykład spadek ciśnienia z 2 do 0,6969 atm powoduje podniesienie tłoka o 0,0526 m. Dla porównania spadek ciśnienia z 0,39 do 1 atm powoduje podniesienie tłoka o 0,418 m.

Zmiany entropii

Procesy izotermiczne są szczególnie wygodne do obliczania zmian entropii , ponieważ w tym przypadku wzór na zmianę entropii Δ S jest po prostu

{\ Displaystyle \ Delta S = {\ Frac {Q _ {\ tekst {rev}}} {T}}}

gdzie Q _rev to ciepło przekazywane (odwracalne wewnętrznie) do układu, a T to temperatura bezwzględna . Ta formuła jest ważna tylko dla hipotetycznego procesu odwracalnego ; to znaczy proces, w którym równowaga jest utrzymywana przez cały czas.

Prostym przykładem jest równowagowe przejście fazowe (takie jak topnienie lub parowanie) zachodzące w stałej temperaturze i ciśnieniu. Dla przemiany fazowej przy stałym ciśnieniu ciepło przekazywane do układu jest równe entalpii przemiany Δ H _tr , zatem Q = Δ H _tr . Przy dowolnym ciśnieniu będzie istniała temperatura przemiany T _tr , dla której dwie fazy są w równowadze (na przykład normalna temperatura wrzenia do odparowania cieczy pod ciśnieniem jednej atmosfery). Jeśli przejście odbywa się w takich warunkach równowagi, powyższy wzór może być użyty do bezpośredniego obliczenia zmiany entropii

{\ Displaystyle \ Delta S _ {\ tekst {tr}} = {\ Frac {\ Delta H _ {\ tekst {tr}}} {T_ {\ tekst {tr}}}}}

.

Innym przykładem jest odwracalna izotermiczna ekspansja (lub kompresja) gazu _doskonałego od początkowej objętości V _A i ciśnienia PA do końcowej objętości V _B i ciśnienia P _B . Jak pokazano w Obliczanie pracy , ciepło przekazywane do gazu wynosi

{\ Displaystyle Q = -W = nRT \ ln {\ Frac {V _ {\ tekst {B}}} {V _ {\ tekst {A}}}}}

.

Wynik ten dotyczy procesu odwracalnego, więc można go podstawić we wzorze na otrzymaną zmianę entropii

{\ Displaystyle \ Delta S = nR \ ln {\ Frac {V _ {\ tekst {B}}} {V _ {\ tekst {A}}}}}

.

Ponieważ gaz doskonały jest zgodny z prawem Boyle'a , można to przepisać, jeśli to pożądane, jako

{\ Displaystyle \ Delta S = nR \ ln {\ Frac {P _ {\ tekst {A}}} {P _ {\ tekst {B}}}}}

.

Po uzyskaniu tych wzorów można je zastosować do nieodwracalnego procesu , takiego jak swobodna ekspansja gazu doskonałego. Takie rozprężanie jest również izotermiczne i może mieć takie same stany początkowe i końcowe jak w rozprężaniu odwracalnym. Ponieważ entropia jest funkcją stanu (która zależy od stanu równowagi, a nie od ścieżki, którą układ podąża do tego stanu), zmiana entropii układu jest taka sama jak w procesie odwracalnym i jest dana wzorami powyżej. Zauważ, że wynik Q = 0 dla swobodnej ekspansji nie może być użyte we wzorze na zmianę entropii, ponieważ proces nie jest odwracalny.

Różnica między odwracalnym a nieodwracalnym polega na entropii otoczenia. W obu przypadkach otoczenie ma stałą temperaturę T , więc Δ S _sur = − Q / T ; znak minus jest używany, ponieważ ciepło przekazywane do otoczenia jest równe co do wielkości i ma przeciwny znak do ciepła Q przekazywanego do układu. W przypadku odwracalnym zmiana entropii otoczenia jest równa i przeciwna do zmiany w układzie, więc zmiana entropii wszechświata wynosi zero. W nieodwracalnym Q = 0, więc entropia otoczenia nie zmienia się, a zmiana entropii wszechświata jest równa ΔS dla układu.

Zobacz też

Efekt Joule'a-Thomsona
Ekspansja Joule'a (zwana także swobodną ekspansją )
Proces adiabatyczny
Proces cykliczny
Proces izobaryczny
Proces izochoryczny
Proces politropowy
Spontaniczny proces