Mechanika płynów

Mechanika płynów to dziedzina fizyki zajmująca się mechaniką płynów ( cieczy , gazów i plazmy ) oraz sił działających na nie. Ma zastosowanie w wielu dziedzinach, w tym w mechanice , lotnictwie , inżynierii lądowej , chemicznej i biomedycznej , geofizyce , oceanografii , meteorologii , astrofizyce i biologii .

Można ją podzielić na statykę płynów , badanie płynów w spoczynku; i dynamika płynów , badanie wpływu sił na ruch płynów. Jest to dział mechaniki kontinuum , przedmiotu modelującego materię bez korzystania z informacji, że składa się ona z atomów; to znaczy modeluje materię z makroskopowego punktu widzenia, a nie z mikroskopowego . Mechanika płynów, zwłaszcza dynamika płynów, jest aktywną dziedziną badań, zazwyczaj złożoną matematycznie. Wiele problemów jest częściowo lub całkowicie nierozwiązanych i najlepiej rozwiązywać je metodami numerycznymi , zwykle przy użyciu komputerów. Temu podejściu poświęcona jest współczesna dyscyplina, zwana obliczeniową dynamiką płynów (CFD). Prędkość obrazu cząstek , eksperymentalna metoda wizualizacji i analizy przepływu płynów, również wykorzystuje wysoce wizualny charakter przepływu płynów.

Krótka historia

Osobny artykuł: Historia mechaniki płynów

Badania mechaniki płynów sięgają co najmniej czasów starożytnej Grecji , kiedy Archimedes badał statykę płynów i pływalność oraz sformułował swoje słynne prawo, znane obecnie jako zasada Archimedesa , które zostało opublikowane w jego pracy O pływających ciałach — powszechnie uważanej za pierwsza poważna praca z mechaniki płynów. Szybki postęp w mechanice płynów rozpoczął się od Leonarda da Vinci (obserwacje i eksperymenty), Evangelista Torricelli (wynalazł barometr ), Izaaka Newtona (badanie lepkości ) i Blaise'a Pascala (badał hydrostatykę , sformułował prawo Pascala ), a był kontynuowany przez Daniela Bernoulliego z wprowadzenie matematycznej dynamiki płynów w Hydrodynamice (1739).

Przepływ nielepki był dalej analizowany przez różnych matematyków ( Jean le Rond d'Alembert , Joseph Louis Lagrange , Pierre-Simon Laplace , Siméon Denis Poisson ), a przepływ lepki był badany przez wielu inżynierów , w tym Jean Léonard Marie Poiseuille i Gotthilf Hagen . Dalszego uzasadnienia matematycznego dostarczyli Claude-Louis Navier i George Gabriel Stokes w równaniach Naviera-Stokesa i zbadano warstwy graniczne ( Ludwig Prandtl , Theodore von Kármán ), podczas gdy różni naukowcy, tacy jak Osborne Reynolds , Andrey Kolmogorov i Geoffrey Ingram Taylor pogłębił wiedzę na temat lepkości i turbulencji płynów .

Główne gałęzie

Statyka płynów

Główny artykuł: Statyka płynów

Statyka płynów lub hydrostatyka to gałąź mechaniki płynów, która bada płyny w stanie spoczynku. Obejmuje badanie warunków, w jakich płyny pozostają w spoczynku w stabilnej równowadze ; i kontrastuje z dynamiką płynów , badaniem płynów w ruchu. Hydrostatyka oferuje fizyczne wyjaśnienia wielu zjawisk życia codziennego, na przykład dlaczego ciśnienie atmosferyczne zmienia się wraz z wysokością , dlaczego drewno i olej unoszą się na wodzie i dlaczego powierzchnia wody jest zawsze równa niezależnie od kształtu pojemnika. Hydrostatyka ma fundamentalne znaczenie dla hydrauliki , inżynierii sprzętu do przechowywania, transportu i używania płynów . Dotyczy to również niektórych aspektów geofizyki i astrofizyki (na przykład zrozumienia tektoniki płyt i anomalii w polu grawitacyjnym Ziemi ), meteorologii , medycyny (w kontekście ciśnienia krwi ) i wielu innych dziedzin.

Dynamika płynów

Główny artykuł: Dynamika płynów

Dynamika płynów to subdyscyplina mechaniki płynów, która zajmuje się przepływem płynów — nauka o płynach i gazach w ruchu. Dynamika płynów oferuje systematyczną strukturę – która leży u podstaw tych praktycznych dyscyplin – obejmującą prawa empiryczne i półempiryczne wywodzące się z pomiaru przepływu i wykorzystywane do rozwiązywania praktycznych problemów. Rozwiązanie dynamiki płynów zwykle obejmuje obliczenie różnych właściwości płynu, takich jak prędkość , ciśnienie , gęstość i temperatura , w funkcji czasu i przestrzeni. Sama ma kilka subdyscyplin, w tym aerodynamikę (badanie powietrza i innych gazów w ruchu) oraz hydrodynamikę (badanie cieczy w ruchu). Dynamika płynów ma szeroki zakres zastosowań, w tym obliczanie sił i ruchów w samolotach , określanie masowego natężenia przepływu ropy naftowej przez rurociągi, przewidywanie zmieniających się wzorców pogodowych , zrozumienie mgławic w przestrzeni międzygwiezdnej i modelowanie eksplozji . Niektóre zasady dynamiki płynów są stosowane w inżynierii ruchu i dynamice tłumu.

Związek z mechaniką kontinuum

Mechanika płynów jest subdyscypliną mechaniki ośrodków ciągłych , jak pokazano w poniższej tabeli.

Mechanika ośrodków ciągłych Badanie fizyki materiałów ciągłych	Mechanika ciał stałych Badanie fizyki materiałów ciągłych o określonym kształcie spoczynku.	Elastyczność Opisuje materiały, które powracają do swojego kształtu spoczynkowego po usunięciu przyłożonych naprężeń .
		Plastyczność Opisuje materiały, które trwale odkształcają się po przyłożeniu wystarczającego naprężenia.	Reologia Badanie materiałów o właściwościach zarówno stałych, jak i płynnych.
	Mechanika płynów Badanie fizyki materiałów ciągłych, które odkształcają się pod wpływem siły.	Płyn nienewtonowski Nie podlegają szybkościom odkształcenia proporcjonalnym do przyłożonego naprężenia ścinającego.
		Płyny newtonowskie podlegają szybkościom odkształcenia proporcjonalnym do przyłożonego naprężenia ścinającego.

Z mechanicznego punktu widzenia płyn jest substancją, która nie wytrzymuje naprężeń ścinających ; dlatego płyn w spoczynku ma kształt naczynia, w którym się znajduje. Płyn w spoczynku nie ma naprężeń ścinających.

Założenia

Waga dla pewnej zintegrowanej ilości płynu w objętości kontrolnej otoczonej powierzchnią kontrolną .

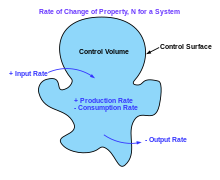
Założenia związane z mechaniczną obróbką płynów układu fizycznego można wyrazić za pomocą równań matematycznych. Zasadniczo zakłada się, że każdy system mechaniki płynów jest zgodny z:

• Ochrona masy
• Zachowanie energii
• Zachowanie pędu
• Założenie kontinuum

Na przykład założenie, że masa jest zachowana, oznacza, że ​​dla dowolnej ustalonej objętości kontrolnej (na przykład objętości kulistej) — otoczonej powierzchnią kontrolną — tempo zmian masy zawartej w tej objętości jest równe szybkości, z jaką masa przechodzi przez powierzchnię z zewnątrz do wewnątrz , pomniejszona o szybkość, z jaką masa przechodzi z wnętrza na zewnątrz . Można to wyrazić jako równanie w postaci całkowej po objętości kontrolnej.

Założenie kontinuum jest idealizacją mechaniki kontinuum , zgodnie z którą płyny można traktować jako ciągłe , mimo że w skali mikroskopowej składają się z cząsteczek . Przy założeniu kontinuum przyjmuje się, że makroskopowe (obserwowane / mierzalne) właściwości, takie jak gęstość, ciśnienie, temperatura i prędkość objętościowa, są dobrze zdefiniowane przy „nieskończenie małych” elementach objętościowych - małych w porównaniu z charakterystyczną skalą długości układu, ale duże w porównaniu do skali długości cząsteczek. Właściwości płynów mogą zmieniać się w sposób ciągły w zależności od elementu objętości i są to średnie wartości właściwości molekularnych. Hipoteza kontinuum może prowadzić do niedokładnych wyników w zastosowaniach takich jak przepływy z prędkością naddźwiękową lub przepływy molekularne w skali nano. Te problemy, dla których zawodzi hipoteza kontinuum, można rozwiązać za pomocą mechaniki statystycznej . Aby określić, czy hipoteza kontinuum ma zastosowanie, liczba Knudsena , zdefiniowana jako stosunek średniej molekularnej drogi swobodnej do charakterystycznej skali długości . Problemy z liczbami Knudsena poniżej 0,1 można ocenić za pomocą hipotezy continuum, ale można zastosować podejście molekularne (mechanika statystyczna) do znalezienia ruchu płynu dla większych liczb Knudsena.

Równania Naviera-Stokesa

Główny artykuł: równania Naviera-Stokesa

Równania Naviera-Stokesa (nazwane na cześć Claude-Louisa Naviera i George'a Gabriela Stokesa ) to równania różniczkowe opisujące równowagę sił w danym punkcie płynu. Dla nieściśliwego płynu z wektorowym polem prędkości równania Naviera-Stokesa są następujące: ${\ displaystyle \ mathbf {u}}$

${\ Displaystyle {\ Frac {\ częściowe \ mathbf {u}} {\ częściowe t}} + (\ mathbf {u} \cdot \nabla )\mathbf {u} =-{\frac {1}{\rho }}\nabla p+\nu \nabla ^{2}\mathbf {u} }$ .

Te równania różniczkowe są analogami dla materiałów odkształcalnych do równań ruchu Newtona dla cząstek - równania Naviera-Stokesa opisują zmiany pędu ${\ displaystyle p$ siły ) w odpowiedzi na ciśnienie i lepkość, sparametryzowane przez lepkość kinematyczną $} styl wyświetlania \nu }$ . Czasami do równań dodaje się siły ciała , takie jak siła grawitacji lub siła Lorentza.

Rozwiązań równań Naviera-Stokesa dla danego problemu fizycznego należy szukać za pomocą rachunku różniczkowego . W praktyce tylko najprostsze przypadki można rozwiązać dokładnie w ten sposób. Przypadki te na ogół dotyczą nieturbulentnego, stałego przepływu, w którym liczba Reynoldsa jest mała. W przypadku bardziej złożonych przypadków, zwłaszcza tych związanych z turbulencjami , takich jak globalne systemy pogodowe, aerodynamika, hydrodynamika i wiele innych, rozwiązania równań Naviera-Stokesa można obecnie znaleźć tylko za pomocą komputerów. Ta dziedzina nauki nazywa się obliczeniową dynamiką płynów .

Płyny nielepkie i lepkie

Nielepki płyn nie ma lepkości , ${\ displaystyle \ nu = 0}$ . W praktyce nielepki przepływ jest idealizacją , która ułatwia leczenie matematyczne. W rzeczywistości wiadomo, że czysto nielepkie przepływy są realizowane tylko w przypadku nadciekłości . W przeciwnym razie płyny są na ogół lepkie , właściwość, która jest często najważniejsza w warstwie granicznej w pobliżu powierzchni ciała stałego, gdzie przepływ musi odpowiadać warunkom braku poślizgu na ciele stałym. W niektórych przypadkach matematykę układu mechaniki płynów można potraktować, zakładając, że płyn na zewnątrz warstw granicznych jest nielepki, a następnie dopasowując jego rozwiązanie do rozwiązania dla cienkiej laminarnej warstwy granicznej.

W przypadku przepływu płynu przez porowatą granicę prędkość płynu może być nieciągła między płynem swobodnym a płynem w ośrodkach porowatych (jest to związane ze stanem Bobrów i Józefa). Ponadto przy niskich prędkościach poddźwiękowych warto założyć, że gaz jest nieściśliwy — to znaczy, że gęstość gazu nie zmienia się, mimo że zmienia się prędkość i ciśnienie statyczne .

Płyny newtonowskie i nienewtonowskie

Płyn newtonowski (nazwany na cześć Izaaka Newtona ) jest definiowany jako płyn , którego naprężenie ścinające jest liniowo proporcjonalne do gradientu prędkości w kierunku prostopadłym do płaszczyzny ścinania. Ta definicja oznacza, że ​​niezależnie od sił działających na płyn, płyn nadal płynie . Na przykład woda jest płynem newtonowskim, ponieważ nadal wykazuje właściwości płynne bez względu na to, jak bardzo jest mieszana lub mieszana. Nieco mniej rygorystyczna definicja mówi, że opór małego obiektu poruszającego się powoli w płynie jest proporcjonalny do siły przyłożonej do obiektu. (Porównaj tarcie ). Ważne płyny, takie jak woda, a także większość gazów, zachowują się — z dobrym przybliżeniem — jak płyn newtonowski w normalnych warunkach na Ziemi.

Z kolei mieszanie płynu nienewtonowskiego może pozostawić po sobie „dziurę”. Z czasem będzie się to stopniowo zapełniać — takie zachowanie obserwuje się w materiałach takich jak budyń, oobleck lub piasek (chociaż piasek nie jest płynem). Alternatywnie, mieszanie płynu nienewtonowskiego może spowodować zmniejszenie lepkości, dzięki czemu płyn wydaje się „cieńszy” (jest to widoczne w przypadku farb niekapiących ). Istnieje wiele rodzajów płynów nienewtonowskich, ponieważ definiuje się je jako coś, co nie spełnia określonej właściwości - na przykład większość płynów o długich łańcuchach molekularnych może reagować w sposób nienewtonowski.

Równania dla płynu newtonowskiego

Główny artykuł: płyn newtonowski

Stała proporcjonalności między tensorem naprężenia lepkiego a gradientem prędkości jest znana jako lepkość . Prostym równaniem opisującym zachowanie nieściśliwego płynu newtonowskiego jest:

${\ Displaystyle \ tau = - \ mu {\ Frac {\ operatorname {d} u} {\ operatorname {d} n}}}$

Gdzie

${\ Displaystyle \ tau}$ to naprężenie ścinające wywierane przez płyn („ przeciągnij ”), to lepkość płynu

$-$ stała proporcjonalności i

$\mathrm {d} u}{\mathrm {d} n}}}$ to gradient prędkości prostopadły do ​​kierunku ścinania.

${\ Displaystyle {\ frac$

W przypadku cieczy newtonowskiej lepkość z definicji zależy tylko od temperatury , a nie od działających na nią sił. Jeśli płyn jest nieściśliwy, równanie rządzące naprężeniem lepkim (we współrzędnych kartezjańskich ) ma postać

${\ Displaystyle \ tau _ {ij} = \ mu \ lewo ({\ Frac {\ częściowe v_ {i}} {\ częściowe x_ {j}}}+{\frac {\częściowy v_{j}}{\częściowy x_{i}}}\right)}$

Gdzie

${\ Displaystyle \ tau _ {ij}}$ to naprężenie ścinające na powierzchni elementu płynnego w ${\ Displaystyle i ^ {th}}$${\ Displaystyle j ^ {th}}$ kierunek

${\ displaystyle v_ {i}}$ to prędkość w ${\ displaystyle i ^ {th}}$ {

$\ displaystyle x_ {j}}$ to jot ${\ displaystyle j ^ { th}}$ współrzędna kierunku.

Jeśli płyn nie jest nieściśliwy, ogólna postać naprężenia lepkiego w płynie newtonowskim ma postać

$Displaystyle \ tau _ {ij} = \ mu \ left ({\frac {\częściowy v_{i}}{\częściowy x_{j}}}+{\frac {\częściowy v_{j}}{\częściowy x_{i}}}-{\frac {2} {3}}\delta _{ij}\nabla \cdot \mathbf {v} \right)+\kappa \delta _{ij}\nabla \cdot \mathbf {v} }$

gdzie jest $drugim współczynnikiem$ (lub lepkością objętościową). Jeśli płyn nie spełnia tej zależności, nazywa się go płynem nienewtonowskim , którego istnieje kilka rodzajów. Płyny nienewtonowskie mogą być plastyczne, plastyczne Binghama, pseudoplastyczne, dylatacyjne, tiksotropowe, reopektyczne, lepkosprężyste.

W niektórych zastosowaniach dokonuje się innego, z grubsza, szerokiego podziału na płyny: płyny idealne i nieidealne. Idealny płyn nie jest lepki i nie stawia żadnego oporu siłom ścinającym. Idealny płyn tak naprawdę nie istnieje, ale w niektórych obliczeniach założenie jest uzasadnione. Jednym z przykładów jest przepływ z dala od stałych powierzchni. W wielu przypadkach efekty lepkości koncentrują się w pobliżu granic ciał stałych (np. przepływ). Kiedy lepkość jest zaniedbana, człon zawierający tensor naprężeń lepkich $w$ Naviera-Stokesa znika. Równanie zredukowane w tej postaci nazywa się równaniem Eulera .

Zobacz też

• Zjawiska transportowe
• Aerodynamika
• Mechanika stosowana
• Zasada Bernoulliego
• Naczynia komunikacyjne
• Obliczeniowa dynamika płynów
• Mapa sprężarki
• Przepływ wtórny
• Różne typy warunków brzegowych w dynamice płynów

Dalsza lektura

•   Falkovich, Gregory (2011), Mechanika płynów (krótki kurs dla fizyków) , Cambridge University Press, doi : 10.1017/CBO9780511794353 , ISBN 978-1-107-00575-4
•   Kundu, Pijush K.; Cohen, Ira M. (2008), Mechanika płynów (wyd. 4 poprawione), Academic Press, ISBN 978-0-12-373735-9
•   Currie, IG (1974), Podstawy mechaniki płynów , McGraw-Hill, Inc. , ISBN 0-07-015000-1
•   Massey, B.; Ward-Smith, J. (2005), Mechanika płynów (wyd. 8), Taylor & Francis, ISBN 978-0-415-36206-1
•   Nazarenko, Sergey (2014), Fluid Dynamics via Examples and Solutions , CRC Press (grupa Taylora i Francisa), ISBN 978-1-43-988882-7

Linki zewnętrzne

• Darmowe książki Mechanika płynów
• Roczny przegląd mechaniki płynów zarchiwizowany 19.01.2009 w Wayback Machine
• CFDWiki – wiki referencyjne dotyczące obliczeniowej dynamiki płynów.
• Edukacyjna prędkość obrazu cząstek – zasoby i demonstracje