Równania Eulera (dynamika płynów)

Ten artykuł dotyczy równań Eulera w klasycznym przepływie płynów. W przypadku innych zastosowań zobacz Lista tematów nazwanych na cześć Leonharda Eulera .

Ta strona zakłada, że ​​obowiązuje mechanika klasyczna ; Aby zapoznać się z omówieniem przepływu płynu ściśliwego, gdy prędkości zbliżają się do prędkości światła, patrz relatywistyczne równania Eulera .

Przepływ wokół skrzydła. Ten nieściśliwy przepływ spełnia równania Eulera.

W dynamice płynów równania Eulera są zbiorem quasiliniowych równań różniczkowych cząstkowych rządzących przepływem adiabatycznym i nielepkim . Noszą one imię Leonharda Eulera . W szczególności odpowiadają one równaniom Naviera-Stokesa o zerowej lepkości i zerowej przewodności cieplnej .

Równania Eulera można zastosować do przepływu nieściśliwego lub ściśliwego . Nieściśliwe równania Eulera składają się z równań Cauchy'ego dotyczących zachowania masy i równowagi pędu, wraz z warunkiem nieściśliwości, że prędkość przepływu jest polem solenoidalnym . Ściśliwe równania Eulera składają się z równań zachowania masy, równowagi pędu i równowagi energii, wraz z odpowiednim równaniem konstytutywnym dla określonej gęstości energii płynu. Historycznie rzecz biorąc, Euler wyprowadził tylko równania zachowania masy i równowagi pędu. Jednak literatura dotycząca dynamiki płynów często odnosi się do pełnego zestawu ściśliwych równań Eulera - w tym równania energii - jako „ściśliwych równań Eulera”.

Charaktery matematyczne nieściśliwych i ściśliwych równań Eulera są raczej różne. Dla stałej gęstości płynu równania nieściśliwości można zapisać jako quasiliniowe adwekcji dla prędkości płynu wraz z eliptycznym równaniem Poissona dla ciśnienia. Z drugiej strony ściśliwe równania Eulera tworzą quasiliniowy hiperboliczny układ równań zachowania .

Równania Eulera można sformułować w „formie konwekcyjnej” (zwanej także „ formą Lagrange'a ”) lub „formie zachowania” (zwanej również „ formą Eulera ”). Forma konwekcyjna podkreśla zmiany stanu w układzie odniesienia poruszającym się z płynem. Forma zachowania kładzie nacisk na matematyczną interpretację równań jako równań zachowania dla objętości kontrolnej ustalonej w przestrzeni (co jest przydatne z numerycznego punktu widzenia).

Historia

Równania Eulera po raz pierwszy pojawiły się w opublikowanej formie w artykule Eulera „Principes généraux du mouvement des fluides”, opublikowanym w Mémoires de l'Académie des Sciences de Berlin w 1757 r. (Chociaż Euler wcześniej przedstawił swoją pracę Akademii Berlińskiej w 1752 r.). Równania Eulera były jednymi z pierwszych zapisanych równań różniczkowych cząstkowych , po równaniu falowym . W oryginalnej pracy Eulera układ równań składał się z równań pędu i ciągłości, a zatem był niedookreślony, z wyjątkiem przypadku przepływu nieściśliwego. Dodatkowe równanie, które nazwano warunkiem adiabatycznym , dostarczył Pierre-Simon Laplace w 1816 roku.

W drugiej połowie XIX wieku stwierdzono, że dla przepływów ściśliwych zawsze musi być zachowane równanie bilansu energii, a stan adiabatyczny jest konsekwencją podstawowych praw w przypadku rozwiązań gładkich. Wraz z odkryciem szczególnej teorii względności koncepcje gęstości energii, gęstości pędu i naprężenia zostały ujednolicone w koncepcji tensora naprężenia-energii , a energia i pęd zostały również ujednolicone w jedno pojęcie, wektor energii-pędu .

Nieściśliwe równania Eulera o stałej i jednorodnej gęstości

W postaci konwekcyjnej (tj. postaci z operatorem konwekcyjnym wyrażonym wprost w równaniu pędu ), nieściśliwe równania Eulera w przypadku gęstości stałej w czasie i jednolitej w przestrzeni to:

Nieściśliwe równania Eulera o stałej i jednorodnej gęstości ( postać konwekcyjna lub Lagrange'a )

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {D \ mathbf {u} \ ponad Dt} i = - \ nabla w + \ mathbf {g} \\\nabla \cdot \mathbf {u} &=0\end{aligned}}\right.}$

Gdzie:

• ${\ Displaystyle \ mathbf {u}}$ jest wektorem prędkości przepływu ze składnikami w N -wymiarowej przestrzeni ${\ Displaystyle u_ {1}, u_ {2}, \ kropki, u_{N}}$ ,
• ${\ Displaystyle {D \ mathbf {v} \ nad Dt} = {\ częściowe \ mathbf {v} \ ponad \ częściowe t} + \ mathbf {u} \ cdot \ nabla \ mathbf {v}}$ , dla funkcji ogólnej (lub pola) $jej$ materialną pochodną w czasie w odniesieniu do pola adwekcyjnego ${\ Displaystyle \ mathbf {u}}$ I
• ${\ Displaystyle \ nabla w}$ jest gradientem określonej (w sensie na jednostkę masy ) pracy termodynamicznej , wewnętrznym wyrazem źródłowym i
• ${\ Displaystyle \ nabla \ cdot \ mathbf {u}} jest$ rozbieżnością prędkości przepływu .
• reprezentuje przyspieszenia ciała (na jednostkę $masy$ ) działające na kontinuum, na przykład grawitację , przyspieszenia bezwładności, pola elektrycznego i tak dalej.

Pierwsze równanie to równanie pędu Eulera o jednolitej gęstości (dla tego równania również nie może być ono stałe w czasie). Rozszerzając pochodną materiałową , równania stają się:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {\ częściowe \ mathbf {u} \ ponad \ częściowe t} + (\mathbf {u} \cdot \nabla )\mathbf {u} &=-\nabla w+\mathbf {g} \\\nabla \cdot \mathbf {u} &=0\end{wyrównane}}\right. }$

W rzeczywistości dla przepływu o jednolitej gęstości obowiązuje następująca tożsamość: ${\ displaystyle \ rho _ {0}}$

${\ Displaystyle \ nabla w \ równoważnik \ nabla \ lewo ({\ Frac {p} {\ rho _ {0}}} \ prawej) = {\ Frac {1 }{\rho _{0}}}\na bla p}$

gdzie jest ciśnieniem mechanicznym ${\ displaystyle p}$ . Drugie równanie to więz nieściśliwy , stwierdzający, że prędkość przepływu jest polem solenoidalnym (kolejność równań nie jest przyczynowa, ale podkreśla fakt, że więz nieściśliwy nie jest zdegenerowaną postacią równania ciągłości , ale raczej równania energii , co stanie się jasne w dalszej części). Warto zauważyć, że równanie ciągłości byłoby wymagane również w tym nieściśliwym przypadku jako dodatkowe trzecie równanie w przypadku gęstości zmieniającej się w czasie lub zmieniającej się w przestrzeni. Na przykład, przy jednolitej gęstości, ale zmieniającej się w czasie, równanie ciągłości, które należy dodać do powyższego zestawu, odpowiadałoby:

${\ Displaystyle {\ Frac {\ częściowe \ rho} {\ częściowe t}} = 0}$

Tak więc przypadek stałej i jednorodnej gęstości jest jedynym, który nie wymaga równania ciągłości jako dodatkowego równania, niezależnie od obecności lub braku ograniczenia nieściśliwości. W rzeczywistości omawiany tutaj przypadek nieściśliwych równań Eulera o stałej i jednorodnej gęstości jest modelem zabawkowym zawierającym tylko dwa uproszczone równania, więc jest idealny do celów dydaktycznych, nawet jeśli ma ograniczoną przydatność fizyczną.

$Powyższe$ równania reprezentują zatem odpowiednio zachowanie masy 1 równanie skalarne) i pędu (1 równanie wektorowe zawierające składniki skalarne, gdzie $.$ fizycznym wymiarem interesującej nas przestrzeni) Prędkość przepływu i ciśnienie to tak zwane zmienne fizyczne .

W układzie współrzędnych określonym przez wektory prędkości i siły zewnętrznej ${\ Displaystyle \ lewo (x_ {1}, \ kropki, x_ {N} \ prawej$$} u} }$ i $}$ składniki ${\ Displaystyle (u_ {1}, \ kropki, u_ {N})$ i ${\ Displaystyle \ lewo (g_ {1}, \ kropki, g_ {N} \ prawej)}$ . Wówczas równania można zapisać w notacji z indeksem dolnym jako:

Osobliwości ${\ Displaystyle \ lewo \ { {\begin{wyrównane}{\częściowe u_{i} \ponad \częściowe t}+\sum _{j=1}^{N}{\częściowe \left(u_{i}u_{j}+w\delta _{ij}\right) \over \częściowe x_{j}}&=g_{i}\\\sum _{i=1}^{N}{\częściowe u_{i} \ponad \częściowe x_{i }}&=0\end{wyrównane}}\do prawej.}$

gdzie $indeksy dolne$$\$ j $}$ oznaczają N - wymiarowe komponenty przestrzeni, a to delta Kroeneckera stosowanie notacji Einsteina (gdzie suma jest implikowana przez powtarzające się indeksy zamiast notacji sigma ).

Nieruchomości

Chociaż Euler po raz pierwszy przedstawił te równania w 1755 r., wiele fundamentalnych pytań lub koncepcji na ich temat pozostaje bez odpowiedzi.

W trzech wymiarach przestrzennych, w pewnych uproszczonych scenariuszach, równania Eulera tworzą osobliwości.

Gładkie rozwiązania swobodnych (w sensie bez wyrazu źródłowego: g=0) równań spełniają zasadę zachowania właściwej energii kinetycznej:

${\ Displaystyle {\ częściowy \ nad \ częściowy t} \ lewo ({\ Frac {1} {2}} u ^ {2 }\right)+\nabla \cdot \left(u^{2}\mathbf {u} +w\mathbf {u} \right)=0}$

W przypadku jednowymiarowym bez członu źródłowego (zarówno gradientu ciśnienia, jak i siły zewnętrznej) równanie pędu staje się nielepkim równaniem Burgersa :

${\ Displaystyle {\ częściowe u \ ponad \ częściowe t} + u {\ częściowe u \ ponad \ częściowe x} = 0}$

To równanie modelu daje wiele informacji na temat równań Eulera.

Bezwymiarowość

Zobacz także: Równanie pędu Cauchy'ego § Bezwymiarowość

Aby równania były bezwymiarowe, $należy$ zdefiniować charakterystyczną $.$ i charakterystyczną Powinny one być tak dobrane, aby wszystkie zmienne bezwymiarowe były rzędu jednego. Otrzymuje się w ten sposób następujące zmienne bezwymiarowe:

${\ Displaystyle {\ rozpocząć {wyrównane} u ^ {*} i \ równoważnik {\ frac {u}{u_{0}}},\\[5pt]r^{*}&\equiv {\frac {r}{r_{0}}},\\[5pt]t^{*}& \equiv {\frac {u_{0}}{r_{0}}}t,\\[5pt]p^{*}&\equiv {\frac {w}{u_{0}^{2}}} ,\\[5pt]\nabla ^{*}&\equiv r_{0}\nabla \end{aligned}}}$

i wektora jednostkowego pola :

${\ Displaystyle {\ kapelusz {\ mathbf {g}}} \ równoważnik {\ Frac {\ mathbf {g}} {g}}}$

Podstawienie tych odwrotnych relacji w równaniach Eulera, określających liczbę Froude'a daje (pomijając * na wierzchołku):

Nieściśliwe równania Eulera o stałej i jednorodnej gęstości ( postać bezwymiarowa )

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {D \ mathbf {u} \ ponad Dt} i = - \ nabla w + { \frac {1}{\mathrm {Fr}}}{\hat {\mathbf {g}}}\\\nabla \cdot \mathbf {u} &=0\end{aligned}}\right.}$

Równania Eulera w granicy Froude'a (bez pola zewnętrznego) nazywane są równaniami swobodnymi i są konserwatywne. Granica wysokich liczb Froude'a (niskie pole zewnętrzne) jest zatem godna uwagi i można ją badać za pomocą teorii zaburzeń .

Formularz konserwacyjny

Zobacz też: Równanie zachowania

Postać zachowania podkreśla matematyczne właściwości równań Eulera, a zwłaszcza forma skrócona jest często najwygodniejsza dla symulacji obliczeniowej dynamiki płynów . Z obliczeniowego punktu widzenia korzystanie ze zmiennych konserwatywnych ma pewne zalety. Daje to początek dużej klasie metod numerycznych zwanych metodami konserwatywnymi.

Wolne równania Eulera są konserwatywne w tym sensie, że są równoważne równaniu zachowania:

${\ Displaystyle {\ Frac {\ częściowe \ mathbf {y}}} {\ częściowe t}} + \ nabla \ cdot \ mathbf {F} = {\ mathbf {0}}, }$

lub po prostu w notacji Einsteina:

${\ Displaystyle {\ Frac {\ częściowy y_ {j}} {\ częściowy t}} + {\ Frac {\ częściowy f_ {ij}}} {$

$gdzie$ wielkość zachowania $jest$ przypadku jest wektorem, a macierzą strumienia . Można to po prostu udowodnić.

Demonstracja formy konserwatorskiej

Po pierwsze, zachodzą następujące tożsamości:

${\ Displaystyle \ nabla \ cdot (w \ mathbf {I}) = \ mathbf {I} \ cdot \ nabla w + w \ nabla \ cdot \ mathbf {I} = \ nabla w}$

${\ Displaystyle \ mathbf {u} \ cdot \ nabla \ cdot \ mathbf {u} = \ nabla \ cdot (\ mathbf {u} \otimes \mathbf {u} )}$

gdzie ${\ displaystyle \ otimes}$ oznacza produkt zewnętrzny . Te same tożsamości wyrażone w notacji Einsteina to:

${\ Displaystyle \ częściowe _ {i} \ lewo (w \ delta _ { ij}\right)=\delta _{ij}\częściowa _{i}w+w\częściowa _{i}\delta _{ij}=\delta _{ij}\częściowa _{i}w=\częściowa _ {j} w}$

${j} \ częściowe _ {i} u_ {i} = \ częściowe _ {i} \ lewo (u_ { i}u_{j}\prawo)}$

gdzie I jest macierzą tożsamości o wymiarze N, a δ _ij jej elementem ogólnym, deltą Kroeneckera.

Dzięki tym tożsamościom wektorowym nieściśliwe równania Eulera o stałej i jednorodnej gęstości oraz bez pola zewnętrznego można zapisać w tzw .

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane}} {\ częściowe \ mathbf {u} \ nad \ częściowe t}+\nabla \cdot \left(\mathbf {u} \otimes \mathbf {u} +w\mathbf {I} \right)&=\mathbf {0} \\{\częściowe 0 \ponad \częściowe t}+\nabla \cdot \mathbf {u} &=0,\end{wyrównane}}\do prawej.}$

lub z notacją Einsteina:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ częściowe _ {t} u_ { j}+\częściowa _{i}\left(u_{i}u_{j}+w\delta _{ij}\right)&=0\\\częściowa _{t}0+\częściowa _{j} u_{j}&=0,\end{wyrównane}}\do prawej.}$

Wtedy nieściśliwe równania Eulera o jednolitej gęstości mają zmienne zachowania:

${\ Displaystyle {\ mathbf {y}} = {\ rozpocząć {pmatrix} \ mathbf {u} \\ 0 \ koniec {pmatrix}}; \ qquad {\ mathbf {F}} = {\ rozpocząć {pmatrix} \ mathbf {u} \otimes \mathbf {u} +w\mathbf {I} \\\mathbf {u} \end{pmatrix}}.}$

Zauważ, że w drugiej składowej u samo w sobie jest wektorem o długości N, więc y ma długość N+1, a F ma rozmiar N(N+1). Na przykład w 3D y ma długość 4, I ma rozmiar 3 × 3, a F ma rozmiar 4 × 3, więc wyraźne formy to:

${\ Displaystyle {\ mathbf {y}} = {\ rozpocząć {pmatrix} u_ {1} \\ u_ {2} \\ u_ {3} \\ 0 \ koniec {pmatrix}}; \ quad {\ mathbf {F } }={\begin{pmatrix}u_{1}^{2}+w&u_{1}u_{2}&u_{1}u_{3}\\u_{2}u_{1}&u_{2}^{ 2}+w&u_{2}u_{3}\\u_{3}u_{1}&u_{3}u_{2}&u_{3}^{2}+w\\u_{1}&u_{2}&u_ {3}\end{pmacierz}}.}$

W końcu równania Eulera można przekształcić w konkretne równanie:

Nieściśliwe równania Eulera o stałej i jednolitej gęstości ( zachowanie lub postać Eulera )

${\ Displaystyle {\ Frac {\ częściowy} {\ częściowy t}} {\ rozpocząć {pmatrix} \ mathbf {u} \ \0\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\mathbf {u} \otimes \mathbf {u} +w\mathbf {I} \\\mathbf {u} \end{pmatrix} }={\begin{pmacierz}\mathbf {g} \\0\end{pmacierz}}}$

Wymiary przestrzenne

W przypadku niektórych problemów, zwłaszcza gdy są używane do analizy przepływu ściśliwego w przewodzie lub w przypadku, gdy przepływ jest cylindrycznie lub sferycznie symetryczny, jednowymiarowe równania Eulera są użytecznym pierwszym przybliżeniem. Ogólnie równania Eulera rozwiązuje się metodą cech Riemanna . Obejmuje to znalezienie krzywych w płaszczyźnie zmiennych niezależnych (tj. $)$ , $wzdłuż$ których równania różniczkowe cząstkowe ( ) degenerują się do równań różniczkowych zwyczajnych (ODE). Numeryczne rozwiązania równań Eulera w dużej mierze opierają się na metodzie charakterystyk.

Nieściśliwe równania Eulera

W postaci konwekcyjnej nieściśliwe równania Eulera w przypadku zmiennej gęstości w przestrzeni to:

Nieściśliwe równania Eulera ( forma konwekcyjna lub Lagrange'a )

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {D \ rho \ nad Dt} i = 0 \\ {D \ mathbf {u} \over Dt}&=-{\frac {\nabla p}{\rho}}+\mathbf {g} \\\nabla \cdot \mathbf {u} &=0\end{wyrównane}} \Prawidłowy.}$

gdzie dodatkowymi zmiennymi są:

• ${\ Displaystyle \ rho} to$ gęstość masy płynu ,
• ${\ displaystyle p}$ to ciśnienie , ${\ displaystyle p = \ rho w}$ .

Pierwsze równanie, które jest nowe, to nieściśliwe równanie ciągłości . W rzeczywistości ogólne równanie ciągłości wyglądałoby następująco:

${\ Displaystyle {\ częściowe \ rho \ nad \ częściowe t} + \ mathbf {u} \ cdot \ nabla \ rho + \ rho \ nabla \ cdot \ mathbf {u} =0}$

ale tutaj ostatni składnik jest identycznie zerowy dla ograniczenia nieściśliwości.

Formularz konserwacyjny

Zobacz też: równanie zachowania

Nieściśliwe równania Eulera w granicy Froude'a są równoważne pojedynczemu równaniu zachowania z odpowiednio zachowaną wielkością i powiązanym strumieniem:

${\ Displaystyle {\ mathbf {y}} = {\ rozpocząć {pmatrix} \ rho \\\ rho \ mathbf {u} \\0 \ koniec {pmatrix}}; \ qquad {\ mathbf {F}} = {\ rozpocząć{pmatrix}\rho \mathbf {u} \\\rho \mathbf {u} \otimes \mathbf {u} +p\mathbf {I} \\\mathbf {u} \end{pmatrix}}.}$

Tutaj $}}$$N}$$Displaystyle$ ma długość i ma rozmiar $2$$(N + 2$ . Ogólnie (nie tylko w granicy Froude'a) równania Eulera można wyrazić jako:

${\ Displaystyle {\ Frac {\ częściowy} {\ częściowy t}} {\ rozpocząć {pmatrix} \rho \\\rho \mathbf {u} \\0\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\rho \mathbf {u} \\\rho \mathbf {u} \otimes \ mathbf {u} +p\mathbf {I} \\\mathbf {u} \end{pmatrix}}={\begin{pmatrix}0\\\rho \mathbf {g} \\0\end{pmatrix}} }$

Zmienne konserwatorskie

Zmienne dla równań w postaci zachowania nie są jeszcze zoptymalizowane. W rzeczywistości moglibyśmy zdefiniować:

${\ Displaystyle {\ mathbf {y}} = {\ rozpocząć {pmatrix} \ rho \\\ mathbf {j} \\ 0 \ koniec {pmatrix}}; \ qquad {\ mathbf {F}} = {\ rozpocząć { pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\,\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\{\frac {\mathbf { j} }{\rho }}\end{pmatrix}}.}$

Gdzie:

• ${\ Displaystyle \ mathbf {j} = \ rho \ mathbf {u}}$ to gęstość pędu , zmienna zachowania.

Nieściśliwe równania Eulera ( zachowanie lub forma Eulera )

${\ Displaystyle {\ Frac {\ częściowy}} {\ częściowy t}} {\ rozpocząć {pmatrix} \ rho \\\mathbf {j} \\0\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\,\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\{\frac {\mathbf {j} }{\rho }}\end{pmatrix}}={\begin{pmatrix}0\\ \mathbf {f} \\0\end{pmatrix}}}$

Gdzie:

• ${\ Displaystyle \ mathbf {f} = \ rho \ mathbf {g}}$ to gęstość siły , zmienna zachowania.

Równania Eulera

W różniczkowej postaci konwekcyjnej ściśliwe (i najbardziej ogólne) równania Eulera można krótko zapisać za pomocą notacji pochodnej materiałowej :

Równania Eulera ( forma konwekcyjna )

$Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {D \ rho \over Dt}&=-\rho \nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=-{\frac {\nabla p} {\rho }}+\mathbf {g} \\[1.2ex]{De \over Dt}&=-{\frac {p}{\rho }}\nabla \cdot \mathbf {u} \end{wyrównane }}\Prawidłowy.}$

gdzie dodatkowe zmienne to:

• ${\ displaystyle e}$ to określona energia wewnętrzna (energia wewnętrzna na jednostkę masy).

Powyższe równania przedstawiają zatem zachowanie masy , pędu i energii : równanie energii wyrażone w zmiennej energii wewnętrznej pozwala zrozumieć związek z przypadkiem nieściśliwym, ale nie w najprostszej postaci. Gęstość masy, prędkość przepływu i ciśnienie to tak zwane zmienne konwekcyjne (lub zmienne fizyczne lub zmienne lagrange'a), podczas gdy gęstość masy, gęstość pędu i całkowita gęstość energii to tak zwane zmienne konserwatywne (zwane także zmiennymi eulerowskimi lub matematycznymi) .

Jeśli rozszerzy się pochodną materiałową, powyższe równania to:

${\ Displaystyle \left\{{\begin{aligned}{\częściowy \rho \over \częściowy t}+\mathbf {u} \cdot \nabla \rho +\rho \nabla \cdot \mathbf {u} &=0\\ [1.2ex] {\frac {\częściowy \mathbf {u}}}{\częściowy t}}+\mathbf {u} \cdot \nabla \mathbf {u} +{\frac {\nabla p}{\rho} }&=\mathbf {g} \\[1.2ex]{\częściowe e \ponad \częściowe t}+\mathbf {u} \cdot \nabla e+{\frac {p}{\rho }}\nabla \cdot \mathbf {u} &=0\end{wyrównane}}\do prawej.}$

Wiązanie nieściśliwe (ponownie)

Wracając do przypadku nieściśliwego, staje się teraz jasne, że więz nieściśliwy typowy dla poprzednich przypadków jest w rzeczywistości szczególną postacią obowiązującą dla nieściśliwych przepływów równania energii , a nie równania masy. W szczególności ograniczenie nieściśliwości odpowiada następującemu bardzo prostemu równaniu energii:

${\ Displaystyle {De \ nad Dt} = 0}$

Zatem dla nieściśliwego, nielepkiego płynu właściwa energia wewnętrzna jest stała wzdłuż linii przepływu , również w przepływie zależnym od czasu. Ciśnienie w przepływie nieściśliwym działa jak mnożnik Lagrange'a , będący mnożnikiem więzu nieściśliwego w równaniu energetycznym, a co za tym idzie w przepływach nieściśliwych nie ma znaczenia termodynamicznego. W rzeczywistości termodynamika jest typowa dla przepływów ściśliwych i degeneruje się w przepływach nieściśliwych.

Na podstawie równania zachowania masy można zapisać to równanie w postaci zachowania:

${\ Displaystyle {\ częściowy \ rho mi \ nad \ częściowy t} + \ nabla \ cdot (\ rho e \ mathbf {u}) = 0}$

co oznacza, że ​​dla nieściśliwego, nieprzewodzącego, nieprzewodzącego przepływu równanie ciągłości zachodzi dla energii wewnętrznej.

Zachowanie entalpii

Ponieważ z definicji entalpia właściwa to:

${\ Displaystyle h = e + {\ Frac {p} {\ rho}}}$

Pochodną materialną określonej energii wewnętrznej można wyrazić jako:

${\ Displaystyle {De \ nad Dt} = {Dh \ nad Dt} - {\ Frac {1} {\ rho }}\left({Dp \nad Dt}-{\frac {p}{\rho}}{D\rho \nad Dt}\right)}$

Następnie podstawiając równanie pędu w tym wyrażeniu otrzymujemy:

${\ Displaystyle {De \ nad Dt} = {Dh \ nad Dt} - {\ Frac {1} {\ rho} }\left(p\nabla \cdot \mathbf {u} +{Dp \ponad Dt}\right)}$

A podstawiając to drugie w równaniu energii, otrzymujemy, że wyrażenie entalpii dla równania energii Eulera:

${\ Displaystyle {Dh \ nad Dt} = {\ Frac {1} {\ rho}} {Dp \ nad Dt}}$

W układzie odniesienia poruszającym się z nielepkim i nieprzewodzącym przepływem zmiana entalpii bezpośrednio odpowiada zmianie ciśnienia.

Termodynamika płynów doskonałych

W termodynamice zmiennymi niezależnymi są objętość właściwa i entropia właściwa , natomiast energia właściwa jest funkcją stanu tych dwóch zmiennych.

Wyprowadzenie postaci obowiązującej dla układów termodynamicznych

Biorąc pod uwagę pierwsze równanie, zmienną należy zmienić z gęstości na objętość właściwą. Zgodnie z definicją:

${\ Displaystyle v \ równoważnik {\ Frac {1} {\ rho}}}$

Zatem zachodzą następujące tożsamości:

${\ Displaystyle \ nabla \ rho = \ nabla \ lewo ({\ Frac {1} {v}} \ prawej) = - {\ Frac {1} v ^ {2}}} \ nabla v}$

${\ Displaystyle {\ Frac {\ częściowe \ rho} {\ częściowe t}} ={\frac {\częściowy }{\częściowy t}}\left({\frac {1}{v}}\right)=-{\frac {1}{v^{2}}}{\frac { \częściowy v}{\częściowy t}}}$

Następnie podstawiając te wyrażenia do równania zachowania masy:

${\ Displaystyle - {\ Frac {\ mathbf {u}} {v ^ {2}}} \ cdot \ nabla v- {\frac {1}{v^{2}}}{\frac {\częściowe v}{\częściowe t}}=-{\frac {1}{v}}\nabla \cdot \mathbf {u}}$

I mnożąc:

${\ Displaystyle {\ częściowe v \ nad \ częściowe t} + \ mathbf {u} \ cdot \ nabla v = v \ nabla \ cdot \ mathbf {u}}$

To równanie jest jedynym należącym do ogólnych równań continuum, więc tylko to równanie ma taką samą postać np. także w równaniach Naviera-Stokesa.

Z drugiej strony ciśnienie w termodynamice jest przeciwieństwem pochodnej cząstkowej właściwej energii wewnętrznej względem objętości właściwej:

${\ Displaystyle p (v, s) = - {\ częściowe e (v, s) \ ponad \ częściowe v}}$

ponieważ energia wewnętrzna w termodynamice jest funkcją dwóch wyżej wymienionych zmiennych, gradient ciśnienia zawarty w równaniu pędu należy wyrazić jako:

${\ Displaystyle - \ nabla p ( v, s) = - {\ frac {\ częściowe p} {\ częściowe v}} \ nabla v- {\ frac {\ częściowe p} {\ częściowe s}} \ nabla s = {\ frac {\ częściowe ^ { 2}e}{\częściowe v^{2}}}\nabla v+{\frac {\częściowe ^{2}e}{\częściowe v\częściowe s}}\nabla s}$

Dla zwięzłości wygodnie jest zmienić notację dla pochodnych drugiego rzędu:

${\ Displaystyle - \ nabla p (v, s) = e_ {vv} \ nabla v + e_ {vs} \ nabla s}$

Na koniec równanie energii:

${\ Displaystyle {De \ nad Dt} = - pv \ nabla \ cdot \ mathbf {u}}$

można dalej uprościć w postaci konwekcyjnej, zmieniając zmienną z energii właściwej na określoną entropię: w rzeczywistości pierwszą zasadę termodynamiki w postaci lokalnej można zapisać:

${\ Displaystyle {De \ nad Dt} = T {Ds \ nad Dt} -p {Dv \ nad Dt}}$

podstawiając materialną pochodną energii wewnętrznej, równanie energii przyjmuje postać:

${\ Displaystyle T {Ds \ nad Dt} + {\ Frac {p} {\ rho ^ {2}}} \ lewo ( {D\rho \over Dt}+\rho \nabla \cdot \mathbf {u} \right)=0}$

teraz termin w nawiasach jest identycznie zerowy zgodnie z zasadą zachowania masy, to równanie energii Eulera staje się proste:

${\ Displaystyle {Ds \ nad Dt} = 0}$

W przypadku płynu termodynamicznego ściśliwe równania Eulera najlepiej zapisać jako:

Równania Eulera ( forma konwekcyjna dla układu termodynamicznego )

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {Dv \over Dt}&=v\nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=ve_{vv}\nabla v+ve_{vs }\nabla s+\mathbf {g} \\[1.2ex]{Ds \na Dt}&=0\end{wyrównane}}\do prawej.}$

Gdzie:

• ${\ displaystyle v}$ to określona objętość
• ${\ Displaystyle \ mathbf {u}}$ jest wektorem prędkości przepływu
• ${\ displaystyle s}$ to specyficzna entropia

W ogólnym przypadku, a nie tylko w przypadku nieściśliwego, równanie energii oznacza, że ​​dla nielepkiego płynu termodynamicznego entropia właściwa wzdłuż linii przepływu jest stała , również w przepływie zależnym od czasu. Na podstawie równania zachowania masy można zapisać to równanie w postaci zachowania:

${\ Displaystyle {\ częściowy \ rho s \ nad \ częściowy t} + \ nabla \ cdot (\ rho s \ mathbf {u}) = 0}$

co oznacza, że ​​dla nielepkiego nieprzewodzącego przepływu równanie ciągłości zachodzi dla entropii.

Z drugiej strony dwie pochodne cząstkowe drugiego rzędu energii wewnętrznej właściwej w równaniu pędu wymagają określenia podstawowego równania stanu rozważanego materiału, tj. energii wewnętrznej właściwej w funkcji dwóch zmiennych objętości właściwej i specyficzna entropia:

${\ Displaystyle e = e (v, s)}$

Podstawowe równanie stanu zawiera wszystkie termodynamiczne informacje o układzie (Callen, 1985), dokładnie tak samo jak para termicznego równania stanu z kalorycznym równaniem stanu.

Formularz konserwacyjny

Zobacz też: Równanie zachowania

Równania Eulera w granicy Froude'a są równoważne pojedynczemu równaniu zachowania z odpowiednio zachowaną wielkością i powiązanym strumieniem:

${\ Displaystyle {\ mathbf {y}} = {\ rozpocząć {pmatrix} \ rho \\\ mathbf {j} \\ E ^ {t} \ koniec {pmatrix}}; \ qquad {\ mathbf {F}} = {\begin{pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\\left(E^ {t}+p\right){\frac {1}{\rho}}\mathbf {j} \end{pmatrix}}.}$

Gdzie:

• ${\ Displaystyle \ mathbf {j} = \ rho \ mathbf {u}}$ to gęstość pędu , zmienna zachowania.
• $_$ _ _ _ objętość jednostkowa).

Tutaj ma długość N + $.$ i ma rozmiar $N$ N + 2) Ogólnie (nie tylko w granicy Froude'a) równania Eulera można wyrazić jako:

Równanie(a) Eulera ( pierwotna konserwacja lub forma Eulera )

${\ Displaystyle {\ Frac {\ częściowe }{\częściowe t}}{\begin{pmatrix}\rho \\\mathbf {j} \\E^{t}\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\mathbf {j } \\{\frac {1}{\rho }}\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\\left(E^{t}+p\right){\ frac {1}{\rho}}\mathbf {j} \end{pmatrix}}={\begin{pmatrix}0\\\mathbf {f} \\{\frac {1}{\rho }}\mathbf {j} \cdot \mathbf {f} \end{pmatrix}}}$

Gdzie:

• ${\ Displaystyle \ mathbf {f} = \ rho \ mathbf {g}}$ to gęstość siły , zmienna zachowania.

Zauważmy, że również równanie Eulera, nawet gdy jest zachowawcze (brak pola zewnętrznego, granica Froude'a) nie ma niezmienników Riemanna . w ogóle Wymagane są dalsze założenia

Jednak wspomnieliśmy już, że dla płynu termodynamicznego równanie na całkowitą gęstość energii jest równoważne równaniu zachowania:

${\ Displaystyle {\ częściowe \ nad \ częściowe t} (\ rho s) + \ nabla \ cdot (\ rho s \ mathbf {u}) = 0 }$

Wówczas równania zachowania w przypadku płynu termodynamicznego wyraża się prościej jako:

Równanie(a) Eulera ( forma zachowania, dla płynów termodynamicznych )

${\ Displaystyle {\ Frac {\ częściowy}} {\ częściowy t}} {\ rozpocząć {pmatrix }\rho \\\mathbf {j} \\S\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\S{\frac {\mathbf {j} }{\rho }}\end{pmatrix}}={\begin{pmatrix}0\ \\mathbf {f} \\0\end{pmacierz}}}$

Gdzie:

• ${\ Displaystyle S = \ rho s}$ to gęstość entropii, termodynamiczna zmienna zachowania.

Inną możliwą postacią równania energii, szczególnie przydatną dla izobarii , jest:

${\ Displaystyle {\ Frac {\ częściowe H ^ {t}} {\ częściowe t}} + \ nabla \ cdot \ lewo (H^{t}\mathbf {u} \right)=\mathbf {u} \cdot \mathbf {f} -{\frac {\częściowe p}{\częściowe t}}}$

Gdzie:

• ${\ textstyle H ^ {t} = E ^ {t} + p = \ rho e + p + {\ Frac {1} {2}} \rho u^{2}}$ to całkowita gęstość entalpii .

Postać quasiliniowa i równania charakterystyczne

Rozszerzanie strumieni może być ważną częścią konstruowania solwerów numerycznych , na przykład poprzez wykorzystanie ( przybliżonych ) rozwiązań problemu Riemanna . W obszarach, w których wektor stanu y zmienia się płynnie, równania w postaci konserwatywnej można zapisać w postaci quasiliniowej:

${\ Displaystyle {\ Frac {\ częściowy \ mathbf {y}} {\ częściowy t}} + \ mathbf {A} _ {i} {\ Frac {\ częściowy \ mathbf {y}} {\ częściowy r_ {i} }}={\mathbf {0}}.}$

gdzie nazywane są jakobianami strumienia zdefiniowanymi jako macierze : ZA ${\ Displaystyle \ mathbf {A} _ {i}$

${\ Displaystyle \ mathbf {A} _ {i} (\ mathbf {y}) = {\ Frac {\ częściowe \ mathbf {f} _ {i} (\ mathbf {y})} {\ częściowe \ mathbf {y } }}.}$

Oczywiście ten jakobian nie występuje w obszarach nieciągłości (np. nieciągłości kontaktowe, fale uderzeniowe w nieprzewodzących przepływach nielepkich). Jeśli strumienie jakobianu $ujawniają$$są$ funkcjami wektora stanu równania .

Równania charakterystyczne

Ściśliwe równania Eulera można rozdzielić na zestaw równań falowych N + 2 opisujących dźwięk w kontinuum Eulera, jeśli są one wyrażone w charakterystycznych zmiennych zamiast w zmiennych konserwatywnych.

W rzeczywistości tensor A jest zawsze diagonalizowalny . Jeśli wartości własne (przypadek równań Eulera) są rzeczywiste, system jest zdefiniowany jako hiperboliczny , a fizyczne wartości własne reprezentują prędkości propagacji informacji. Jeśli wszystkie zostaną rozróżnione, układ jest zdefiniowany ściśle hiperbolicznie (zostanie to udowodnione w przypadku jednowymiarowych równań Eulera). Ponadto diagonalizacja ściśliwego równania Eulera jest łatwiejsza, gdy równanie energii jest wyrażone w zmiennej entropii (tj. równaniami dla płynów termodynamicznych) niż w innych zmiennych energetycznych. Stanie się to jasne po rozważeniu przypadku 1D.

Jeśli ${\ Displaystyle \ mathbf {p} _ {i}}$$jest$ prawym wektorem własnym macierzy odpowiadającym wartości własnej $i}}$ , budując macierz projekcji :

${\ Displaystyle \ mathbf {P} = \ lewo [\ mathbf {p} _ {1}, \ mathbf {p} _ {2}, ..., \ mathbf {p} _ {n}$

Ostatecznie można znaleźć charakterystyczne zmienne jako:

${\ Displaystyle \ mathbf {w} = \ mathbf {P} ^ {- 1} \ mathbf {y},}$

Ponieważ A jest stałe, pomnożenie pierwotnego równania 1-D w postaci strumienia-Jakoba przez P ^-1 daje charakterystyczne równania:

${\ Displaystyle {\ Frac {\ częściowe w_ {i}} {\ częściowe t}} + \ lambda _ {j} {\ Frac {\ częściowe w_ {i}}{\częściowe r_{j}}}=0_{i}}$

Oryginalne równania zostały rozdzielone na równania charakterystyczne N+2, z których każde opisuje prostą falę, a wartościami własnymi są prędkości fal. Zmienne wi nazywane są zmiennymi charakterystycznymi i stanowią podzbiór zmiennych konserwatywnych _. Rozwiązanie problemu wartości początkowej w odniesieniu do zmiennych charakterystycznych jest ostatecznie bardzo proste. W jednym wymiarze przestrzennym jest to:

${\ Displaystyle w_ {i} (x, t) = w_ {i} \ lewo (x- \ lambda _ {i} t, 0 \ Prawidłowy)}$

Następnie rozwiązanie pod względem pierwotnych zmiennych konserwatywnych uzyskuje się przez transformację wsteczną:

${\ Displaystyle \ mathbf {y} = \ mathbf {P} \ mathbf {w}}$

to obliczenie można wyrazić jako liniową kombinację wektorów własnych:

${\ Displaystyle \ mathbf {y} (x, t) = \ suma _ {i = 1} ^ {m }w_{i}\left(x-\lambda _{i}t,0\right)\mathbf {p} _{i},}$

Teraz staje się jasne, że zmienne charakterystyczne działają jak wagi w liniowej kombinacji jakobianowych wektorów własnych. Rozwiązanie można postrzegać jako superpozycję fal, z których każda jest przemieszczana niezależnie bez zmiany kształtu. Każda i -ta fala ma kształt w _i p _i oraz prędkość propagacji λ _i . Poniżej przedstawiamy bardzo prosty przykład tej procedury rozwiązania.

Fale w jednowymiarowym, nielepkim, nieprzewodzącym płynie termodynamicznym

Jeśli weźmie się pod uwagę równania Eulera dla płynu termodynamicznego z dwoma kolejnymi założeniami jednego wymiaru przestrzennego i swobodnego (brak pola zewnętrznego: g = 0):

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {\ częściowe v \ nad \ częściowe t} + u {\ częściowe v \ nad \ częściowe x} - v {\ częściowe u \ nad \częściowe x}&=0\\[1.2ex]{\częściowe u \nad \częściowe t}+u{\częściowe u \nad \częściowe x}-e_{vv}v{\częściowe v \nad \częściowe x}-e_{vs}v{\częściowe s \na \częściowe x}&=0\\[1.2ex]{\częściowe s \nad \częściowe t}+u{\częściowe s \na \częściowe x}& =0\koniec {wyrównany}}\do prawej.}$

Jeśli zdefiniujemy wektor zmiennych:

${\ Displaystyle \ mathbf {y} = {\ rozpocząć {pmatrix} v \\ u \\ s \ koniec {pmatrix}}}$

przypominając, że $}$ to określona objętość, $displaystyle$ przepływu, $v$ entropia, odpowiednia macierz Jakobian to: v {\

${\ Displaystyle {\ mathbf {A}} = {\ rozpocząć {pmatrix} u & -v & 0 \\ -e_ {vv} v & u i -e_ {vs} v \\ 0 i 0 i u \ koniec {pmatrix}}.}$

Najpierw należy znaleźć wartości własne tej macierzy, rozwiązując równanie charakterystyczne :

${\ Displaystyle \ det (\ mathbf {A} (\ mathbf {y}) - \ lambda (\ mathbf {y}) \ mathbf {ja}) = 0 }$

to jest wyraźnie:

${\ Displaystyle \ det {\ rozpocząć {bmatrix} u- \ lambda & -v & 0 \\ -e_ {vv} v&u-\lambda &-e_{vs}v\\0&0&u-\lambda \end{bmatrix}}=0}$

Ten wyznacznik jest bardzo prosty: najszybsze obliczenia rozpoczynają się od ostatniego wiersza, ponieważ ma on największą liczbę elementów zerowych.

${\ Displaystyle (u- \ lambda) \ det {\ rozpocząć {bmatrix} u- \ lambda & -v \\ -e_ {vv}v&u-\lambda \end{bmatrix}}=0}$

Teraz obliczając wyznacznik 2×2:

${\ Displaystyle (u- \ lambda) \ lewo ((u- \ lambda) ^ {2} -e_ {vv} v ^ { 2}\prawo)=0}$

definiując parametr:

${\ Displaystyle a (v, s) \ równoważnik v {\ sqrt {e_ {vv}}}}$

lub równoważnie w zmiennych mechanicznych, jak:

${\ Displaystyle a (\ rho, p) \ równoważnik {\ sqrt {\ częściowe p \ nad \ częściowe \ rho}}}$

Ten parametr jest zawsze rzeczywisty zgodnie z drugą zasadą termodynamiki . W rzeczywistości drugą zasadę termodynamiki można wyrazić kilkoma postulatami. Najbardziej elementarnym z nich pod względem matematycznym jest stwierdzenie wypukłości podstawowego równania stanu, czyli hessowskiej macierzy energii właściwej wyrażonej w funkcji objętości właściwej i entropii właściwej:

${\ Displaystyle {\ rozpocząć {pmatrix} e_ {vv} i e_ {vs} \\ e_ {vs} i e_ {ss} \ koniec {pmatrix}}}$

jest określony pozytywnie. To stwierdzenie odpowiada dwóm warunkom:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} e_ {vv} i> 0 \\ [1.2ex] e_ {vv} e_ {ss }-e_{vs}^{2}&>0\end{wyrównane}}\prawo.}$

Pierwszy warunek to ten, który gwarantuje, że parametr a jest zdefiniowany jako rzeczywisty.

Ostatecznie otrzymujemy charakterystyczne równanie:

${\ Displaystyle (u- \ lambda) \ lewo ((u- \ lambda) ^ {2} -a ^ {2} \ prawo) = 0 }$

To ma trzy rzeczywiste rozwiązania:

${\ Displaystyle \ lambda _ {1}(v,u,s)=ua(v,s)\quad \lambda _{2}(u)=u,\quad \lambda _{3}(v,u,s)=u+a (vs)}$

Wtedy macierz ma trzy rzeczywiste wartości własne, z których wszystkie są rozróżniane: równania Eulera 1D są układem ściśle hiperbolicznym .

W tym momencie należy wyznaczyć trzy wektory własne: każdy z nich uzyskuje się, podstawiając jedną wartość własną do równania wartości własnej, a następnie ją rozwiązując. Podstawiając pierwszą wartość własną λ ₁ otrzymujemy:

${\ Displaystyle {\ rozpocząć {pmatrix} a & - v & 0 \\ -e_ {vv} v & a & -e_ {vs }v\\0&0&a\end{pmatrix}}{\begin{pmatrix}v_{1}\\u_{1}\\s_{1}\end{pmatrix}}=0}$

Bazując na trzecim równaniu, które po prostu ma rozwiązanie s ₁ = 0, system redukuje się do:

${\ Displaystyle {\ rozpocząć {pmatrix} a&-v \\ -a ^ {2}/ v & a \ koniec {pmatrix}} {\ rozpocząć { pmatrix}v_{1}\\u_{1}\end{pmatrix}}=0}$

Dwa równania są jak zwykle zbędne, więc wektor własny jest definiowany za pomocą stałej mnożenia. Jako prawy wektor własny wybieramy:

${\ Displaystyle \ mathbf {p} _ {1} = {\ początek {pmatrix} v \\ a \\ 0 \ koniec {pmatrix}}}$

Pozostałe dwa wektory własne można znaleźć za pomocą analogicznej procedury, jak:

${\ Displaystyle \ mathbf {p} _ {2} = {\ rozpocząć {pmatrix} e_ {vs} \\ 0 \ \-\left({\frac {a}{v}}\right)^{2}\end{pmatrix}},\qquad \mathbf {p} _{3}={\begin{pmatrix}v\\ -a\\0\end{pmacierz}}}$

Następnie można zbudować macierz projekcji:

${\ Displaystyle \ mathbf {P} (v, u, s )=(\mathbf {p} _{1},\mathbf {p} _{2},\mathbf {p} _{3})={\begin{pmatrix}v&e_{vs}&v\\a&0&-a \\0&-\left({\frac {a}{v}}\right)^{2}&0\end{pmatrix}}}$

Wreszcie okazuje się, że zdefiniowanym wcześniej parametrem rzeczywistym a jest prędkość rozchodzenia się informacji charakterystyczna dla układu hiperbolicznego złożonego z równań Eulera, czyli jest to prędkość fali . Pozostaje do wykazania, że ​​prędkość dźwięku odpowiada szczególnemu przypadkowi transformacji izentropowej :

${\ Displaystyle a_ {s} \ równoważnik {\ sqrt {\ lewo ({\ częściowe p \ nad \ częściowe \ rho} \ prawej) _ {s}}}$

Kompresja i prędkość dźwięku

Prędkość dźwięku jest definiowana jako prędkość fali transformacji izentropowej:

${\ Displaystyle a_ {s} (\ rho, p) \ równoważnik {\ sqrt {\ lewo ({\ częściowe p \ nad \ częściowe \ rho} \ prawo )_{S}}}}$

z definicji ściśliwości izoentropowej:

${\ Displaystyle K_ {s} (\ rho, p) \ równoważnik {\ Frac {1} {\ rho}} \ lewo ({\ częściowe p \nad \częściowym \rho }\right)_{s}}$

prędkość dźwięku jest zawsze pierwiastkiem kwadratowym stosunku między ściśliwością izentropową a gęstością:

${\ Displaystyle a_ {s} \ równoważnik {\ sqrt {\ Frac {K_ {s}} {\ rho}}}}$

Gaz doskonały

Prędkość dźwięku w gazie doskonałym zależy tylko od jego temperatury:

${\ Displaystyle a_ {s} (T) = {\ sqrt {\ gamma {\ Frac {T} {m}}}}}$

Odliczenie formy obowiązującej dla gazów doskonałych

W gazie doskonałym przemianę izoentropową opisuje prawo Poissona:

${\ Displaystyle d \ lewo (p \ rho ^ {- \ gamma} \ prawej) _ {s} = 0}$

gdzie γ jest współczynnikiem pojemności cieplnej , stałą dla materiału. Wyjaśniając różnice:

${\ Displaystyle \ rho ^ {- \ gamma} (dp) _ {s} + \ gamma p \ rho ^ {- \ gamma -1}(d\rho )_{s}=0}$

i dzieląc dla ρ ^{- γ} d ρ :

${\ Displaystyle \ lewo ({\ częściowe p \ nad \ częściowe \ rho} \ prawo) _ {s} = \ gamma p \ rho}$

Następnie przez podstawienie w ogólnych definicjach gazu doskonałego ściśliwość izentropowa jest po prostu proporcjonalna do ciśnienia:

${\ Displaystyle K_ {s} (p) = \ gamma p}$

a wyniki prędkości dźwięku ( prawo Newtona-Laplace'a ):

${\ Displaystyle a_ {s} (\ rho, p) = {\ sqrt {\ gamma {\ Frac {p} {\ rho}}}}}$

Warto zauważyć, że dla gazu doskonałego obowiązuje prawo gazu doskonałego , które w formie matematycznej jest po prostu:

${\ displaystyle p = n T}$

gdzie n to gęstość liczbowa , a T to temperatura bezwzględna , pod warunkiem, że jest mierzona w jednostkach energetycznych (tj. w dżulach ) przez pomnożenie przez stałą Boltzmanna . Ponieważ gęstość masy jest proporcjonalna do gęstości liczbowej przez średnią masę cząsteczkową m materiału:

${\ Displaystyle \ rho = mn}$

Prawo gazu doskonałego można przekształcić do wzoru:

${\ Displaystyle {\ Frac {p} {\ rho}} = {\ Frac {T} {m}}}$

Podstawiając ten stosunek do prawa Newtona-Laplace'a, ostatecznie uzyskuje się wyrażenie prędkości dźwięku na gaz doskonały w funkcji temperatury.

Ponieważ entalpia właściwa gazu doskonałego jest proporcjonalna do jego temperatury:

${\ Displaystyle h = c_ {p} T = {\ Frac {\ gamma} {\ gamma -1}} {\ Frac {T} {m}}}$

prędkość dźwięku w gazie idealnym można również uzależnić tylko od jego określonej entalpii:

$\ Displaystyle a_ {s} (h) = {\ sqrt {(\ gamma -1) h}}}$

Twierdzenie Bernoulliego o ustalonym przepływie nielepkim

Twierdzenie Bernoulliego jest bezpośrednią konsekwencją równań Eulera.

Nieściśliwa obudowa i forma Baranka

Tożsamość rachunku wektorowego iloczynu krzyżowego zwijania zawiera:

${\ Displaystyle \ mathbf {v \ \ razy} \ lewo (\ mathbf {\ nabla \ razy F} \ prawej) = \ nabla _{F}\left(\mathbf {v\cdot F} \right)-\mathbf {v\cdot \nabla} \mathbf {F} \ ,}$

gdzie używana jest notacja Feynmana z indeksem dolnym , co oznacza $, że$ ​​​​gradient z indeksem dolnym działa tylko na współczynniku ${F}}$ .

Lamb w swojej słynnej klasycznej książce Hydrodynamics (1895), wciąż w druku, użył tej tożsamości do zmiany konwekcyjnego składnika prędkości przepływu w postaci obrotowej:

$​​{\ Displaystyle \ mathbf {u} \ cdot \ nabla \ mathbf {u} = {\ Frac {1} {2}} \ nabla \left(u^{2}\right)+(\nabla \times \mathbf {u} )\times \mathbf {u} }$

równanie pędu Eulera w postaci Lamba przyjmuje postać:

${\ Displaystyle {\ Frac {\ częściowe \ mathbf {u}} {\ częściowe t}} + {\ Frac {1} {2}} \ nabla \ lewo (u ^ {2} \ prawo) + (\ nabla \times \mathbf {u} )\times \mathbf {u} +{\frac {\nabla p}{\rho }}=\mathbf {g} ={\frac {\częściowo \mathbf {u} }{\ częściowe t}}+{\frac {1}{2}}\nabla \left(u^{2}\right)-\mathbf {u} \times (\nabla \times \mathbf {u} )+{\ frac {\nabla p}}{\rho}}}$

Zobacz także: Równanie pędu Cauchy'ego § Forma Baranka

Teraz, opierając się na innej tożsamości:

${\ Displaystyle \ nabla \ lewo ({\ Frac {p} {\ rho}} \ prawej) = {\ Frac {\ nabla p} {\ rho} }-{\frac {p}{\rho ^{2}}}\nabla \rho}$

równanie pędu Eulera przyjmuje postać optymalną do wykazania twierdzenia Bernoulliego dla przepływów ustalonych:

${\ Displaystyle \ nabla \ lewo ({\ Frac {1} {2}} u^{2}+{\frac {p}{\rho }}\right)-\mathbf {g} =-{\frac {p}{\rho ^{2}}}\nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u} )-{\frac {\częściowy \mathbf {u}}}{\częściowy t}}}$

W rzeczywistości, w przypadku zewnętrznego pola konserwatywnego , definiując jego potencjał φ:

${\ Displaystyle \ nabla \ lewo ({\ Frac {1} {2}} u^{2}+\phi +{\frac {p}{\rho }}\right)=-{\frac {p}{\rho ^{2}}}\nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u} )-{\frac {\częściowy \mathbf {u}}}{\częściowy t}}}$

W przypadku przepływu ustalonego pochodna prędkości przepływu po czasie zanika, więc równanie pędu przyjmuje postać:

${\ Displaystyle \ nabla \ lewo ({\ Frac {1} {2}} u ^ {2} +\phi +{\frac {p}{\rho }}\right)=-{\frac {p}{\rho ^{2}}}\nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u} )}$

A rzutując równanie pędu na kierunek przepływu, czyli wzdłuż linii prądu , iloczyn krzyżowy znika, ponieważ jego wynik jest zawsze prostopadły do ​​prędkości:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla \ lewo ({\ Frac {1} {2}} u ^ {2}+\phi +{\frac {p}{\rho}}\right)=-{\frac {p}{\rho ^{2}}}\mathbf {u} \cdot \nabla \rho}$

W ustalonym nieściśliwym przypadku równanie masy jest po prostu:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla \ rho = 0}$ ,

czyli zasada zachowania masy dla stałego przepływu nieściśliwego stwierdza, że ​​gęstość wzdłuż linii prądu jest stała . Wtedy równanie pędu Eulera w ustalonym nieściśliwym przypadku ma postać:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla \ lewo ({\ Frac {1} {2}} u ^ {2} + \ phi + { \frac {p}{\rho}}\right)=0}$

Wygoda definiowania całkowitej wysokości podnoszenia dla przepływu nielepkiej cieczy jest teraz oczywista:

${\ Displaystyle b_ {l} \ równoważnik {\ Frac {1} {2}} u ^ {2} + \ phi + {\ Frac {p} {\ rho }},}$

co można po prostu zapisać jako:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla b_ {l} = 0}$

Oznacza to, że równowaga pędu dla stałego, nielepkiego i nieściśliwego przepływu w zewnętrznym konserwatywnym polu wskazuje, że całkowita wysokość wzdłuż linii prądu jest stała .

Ściśliwe etui

W najbardziej ogólnym przypadku ustalonym (ściśliwym) równanie masy w postaci zachowania ma postać:

${\ Displaystyle \ nabla \ cdot \ mathbf {j} = \ rho \ nabla \ cdot \ mathbf {u} + \ mathbf {u} \ cdot \ nabla \ rho =0}$ .

Dlatego poprzednie wyrażenie brzmi raczej

${\ Displaystyle \ mathbf {u} \ cdot \ nabla \ lewo ({\ Frac {1} {2}} u ^ {2} +\phi +{\frac {p}{\rho}}\right)={\frac {p}{\rho}}\nabla \cdot \mathbf {u}}$

Prawa strona pojawia się na równaniu energii w postaci konwekcyjnej, która w stanie ustalonym brzmi:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla e = - {\ Frac {p} {\ rho}} \ nabla \ cdot \ mathbf {u}}$

Równanie energii przyjmuje zatem postać:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla \ lewo (e + {\ Frac {p} {\ rho}} + {\ Frac { 1}{2}}u^{2}+\phi \right)=0,}$

tak, że wewnętrzna energia właściwa pojawia się teraz w głowie.

Ponieważ potencjał pola zewnętrznego jest zwykle mały w porównaniu z innymi składnikami, wygodnie jest pogrupować te ostatnie w całkowitej entalpii :

${\ Displaystyle h ^ {t} \ równoważnik e + {\ Frac {p} {\ rho}} + {\ Frac {1} {2}} u ^ {2} }$

a niezmiennik Bernoulliego dla nielepkiego przepływu gazu to:

${\ Displaystyle b_ {g} \ równoważnik h ^ {t} + \ phi = b_ {l} + e,}$

co można zapisać jako:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla b_ {g} = 0}$

Oznacza to, że bilans energii dla stałego, nielepkiego przepływu w zewnętrznym polu konserwatywnym stwierdza, że ​​suma całkowitej entalpii i potencjału zewnętrznego jest stała wzdłuż linii prądu .

W zwykłym przypadku małego pola potencjalnego po prostu:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla h ^ {t} \ sim 0}$

Forma Friedmanna i forma Crocco

Zobacz też: Twierdzenie Crocco

Zastępując gradient ciśnienia gradientem entropii i entalpii, zgodnie z pierwszą zasadą termodynamiki w postaci entalpii:

${\ Displaystyle v \ nabla p = - T \ nabla s + \ nabla h}$

w konwekcyjnej postaci równania pędu Eulera dochodzi się do:

${\ Displaystyle {\ Frac {D \ mathbf {u}} {Dt}} = T \ nabla \, s-\ nabla \, h}$

Friedmann wydedukował to równanie dla konkretnego przypadku gazu doskonałego i opublikował je w 1922 r. Jednak równanie to jest ogólne dla nielepkiego nieprzewodzącego płynu i nie zawiera w sobie żadnego równania stanu.

Z drugiej strony, podstawiając formę entalpii pierwszej zasady termodynamiki w postać rotacyjną równania pędu Eulera, otrzymuje się:

${\ Displaystyle {\ Frac {\ częściowe \ mathbf {u}} {\ częściowe t}} + {\ frac {1}{2}}\nabla \left(u^{2}\right)+(\nabla \times \mathbf {u} )\times \mathbf {u} +{\frac {\nabla p}{ \rho }}=\mathbf {g}}$

oraz definiując określoną całkowitą entalpię:

${\ Displaystyle h ^ {t} = h + {\ Frac {1} {2}} u ^ {2}}$

dochodzi się do postaci Crocco – Vazsonyi (Crocco, 1937) równania pędu Eulera:

${\ Displaystyle {\ Frac {\ częściowe \ mathbf {u}} {\ częściowe t}} + (\ nabla \ razy \ mathbf {u} )\times \mathbf {u} -T\nabla s+\nabla h^{t}=\mathbf {g} }$

W przypadku ustalonym dwie zmienne, entropia i całkowita entalpia, są szczególnie przydatne, ponieważ równania Eulera można przekształcić w postać Crocco:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ mathbf {u} \ razy \ nabla \ razy \mathbf {u} +T\nabla s-\nabla h^{t}&=\mathbf {g} \\\mathbf {u} \cdot \nabla s&=0\\\mathbf {u} \cdot \ nabla h^{t}&=0\end{wyrównane}}\do prawej.}$

Wreszcie, jeśli przepływ jest również izotermiczny:

${\ Displaystyle T \ nabla s = \ nabla (Ts)}$

definiując określoną całkowitą energię swobodną Gibbsa :

${\ Displaystyle g ^ {t} \ równoważnik h ^ {t} + Ts}$

formę Crocco można zredukować do:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ mathbf {u} \ razy \ nabla \ razy \ mathbf {u} - \ nabla g^{t}&=\mathbf {g} \\\mathbf {u} \cdot \nabla g^{t}&=0\end{aligned}}\right.}$

Z tych zależności można wywnioskować, że specyficzna całkowita energia swobodna jest jednolita w stałym, bezrotacyjnym, izotermicznym, izoentropowym, nielepkim przepływie.

Nieciągłości

Zobacz też: Fale uderzeniowe i równanie Burgersa

Równania Eulera są quasiliniowymi równaniami hiperbolicznymi , a ich ogólnymi rozwiązaniami są fale . Przy pewnych założeniach można je uprościć, prowadząc do równania Burgersa . Podobnie jak znane fale oceaniczne , fale opisane równaniami Eulera „łamią się” i powstają tak zwane fale uderzeniowe ; jest to efekt nieliniowy i oznacza, że ​​rozwiązanie staje się wielowartościowe . Fizycznie oznacza to załamanie założeń, które doprowadziły do ​​sformułowania równań różniczkowych, i aby wydobyć dalsze informacje z równań, musimy wrócić do bardziej fundamentalnej postaci całkowej. Następnie słabe rozwiązania , pracując w „skokach” (nieciągłościach) do wielkości przepływu - gęstości, prędkości, ciśnienia, entropii - za pomocą równań Rankine'a-Hugoniota . Wielkości fizyczne rzadko są nieciągłe; w rzeczywistych przepływach te nieciągłości są wygładzane przez lepkość i wymianę ciepła . (Zobacz równania Naviera – Stokesa )

Propagacją wstrząsów zajmuje się – między innymi – aerodynamika i napęd rakietowy , gdzie występują dostatecznie szybkie przepływy.

Prawidłowe obliczenie wielkości continuum w strefach nieciągłych (np. fale uderzeniowe lub warstwy przyścienne) z form lokalnych (wszystkie powyższe formy są formami lokalnymi, gdyż opisywane zmienne są typowe dla jednego punktu w rozpatrywanej przestrzeni, tj. są lokalne zmiennych ) równań Eulera metodami różnic skończonych, na ogół zbyt wiele punktów przestrzennych i kroków czasowych byłoby potrzebnych dla pamięci komputerów teraz iw niedalekiej przyszłości. W takich przypadkach obowiązkowe jest unikanie lokalnych postaci równań zachowania, przechodzących przez niektóre formy słabe , takie jak postać o skończonej objętości .

Równania Rankine'a-Hugoniota

Zaczynając od najprostszego przypadku, należy rozważyć stałe równanie zachowania swobodnego w postaci zachowania w dziedzinie przestrzeni:

${\ Displaystyle \ nabla \ cdot \ mathbf {F} = \ mathbf {0}}$

gdzie ogólnie F jest macierzą strumienia. Całkując to lokalne równanie po ustalonej objętości Vm _otrzymujemy :

${\ Displaystyle \ int _ {V_ {m}} \ nabla \ cdot \ mathbf {F} \, dV = \ mathbf {0}.}$

Następnie na podstawie twierdzenia o dywergencji możemy tę całkę przekształcić w całkę brzegową strumienia:

${\ Displaystyle \ oint _ {\ częściowe V_ {m}} \ mathbf {F} \, ds = \ mathbf {0}.}$

Ta globalna forma po prostu stwierdza, że ​​​​nie ma strumienia netto zachowanej ilości przechodzącego przez region w przypadku stałego i bez źródła. W 1D objętość redukuje się do przedziału , którego granicą są ekstrema, wtedy twierdzenie o dywergencji sprowadza się do podstawowego twierdzenia rachunku różniczkowego :

${\ Displaystyle \ int _ {x_ {m}} ^ {x_ {m + 1}} \ mathbf {F} (x ') \ dx '=\mathbf {0} ,}$

to jest proste równanie różnic skończonych , znane jako relacja skoku :

${\ Displaystyle \ Delta \ mathbf {F} = \ mathbf {0}.}$

Można to wyrazić wyraźnie jako:

${\ Displaystyle \ mathbf {F} _ {m + 1} - \ mathbf {F} _ {m} = \ mathbf {0}}$

gdzie zastosowana notacja to:

${\ Displaystyle \ mathbf {F} _ {m} = \ mathbf {F} (x_ {m}).}$

Lub, jeśli wykonuje się całkę nieoznaczoną:

${\ Displaystyle \ mathbf {F} - \ mathbf {F} _ {0} = \ mathbf {0}.}$

Z drugiej strony przejściowe równanie zachowania:

${\ Displaystyle {\ częściowy y \ ponad \ częściowy t} + \ nabla \ cdot \ mathbf {F} = \ mathbf {0}}$

prowadzi do relacji skoku:

${\ Displaystyle {\ Frac {dx} {dt}} \, \ Delta u = \ Delta \ mathbf {F}.}$

W przypadku jednowymiarowych równań Eulera zmiennymi zachowania i strumieniem są wektory:

${\ Displaystyle \ mathbf {y} = {\ rozpocząć {pmatrix} {\ Frac {1} {v}} \\ j \\ E ^ {t} \ koniec {pmatrix} },}$

${\ Displaystyle \ mathbf {F} = {\ rozpocząć {pmatrix} j \\ vj ^ {2} + p \\ vj \left(E^{t}+p\right)\end{pmacierz}},}$

Gdzie:

• ${\ displaystyle v}$ to określona objętość,
• ${\ displaystyle j}$ to strumień masy.

W przypadku jednowymiarowym odpowiednie relacje skoków, zwane równaniami Rankine'a-Hugoniota , są następujące:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {\ Frac {dx} {dt}} \ Delta \ lewo ({\ Frac {1} {v}} \ prawej) & = \ Delta j \\ [1.2 ex] {\frac {dx}{dt}}\Delta j&=\Delta (vj^{2}+p)\\[1.2ex]{\frac {dx}{dt}}\Delta E^{t} &=\Delta (jv(E^{t}+p))\end{wyrównane}}\prawo..}$

W stałym jednowymiarowym przypadku staje się po prostu:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ Delta j & = 0 \\ [1.2ex] \ Delta \ lewo (vj ^ {2} + p \ prawo) & = 0 \\ [1.2ex] \ Delta \left(j\left({\frac {E^{t}}{\rho }}+{\frac {p}{\rho }}\right)\right)&=0\end{wyrównane}}\ Prawidłowy..}$

Dzięki równaniu różnicy mas równanie różnicy energii można uprościć bez żadnych ograniczeń:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ Delta j & = 0 \\ [1.2ex] \ Delta \ lewo (vj ^ { 2}+p\right)&=0\\[1.2ex]\Delta h^{t}&=0\end{aligned}}\right.,}$

gdzie $.$ całkowitą entalpią

Są to zwykle wyrażane w zmiennych konwekcyjnych:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ Delta j & = 0 \\ [1.2ex ]\Delta \left({\frac {u^{2}}{v}}+p\right)&=0\\[1.2ex]\Delta \left(e+{\frac {1}{2}} u^{2}+pv\right)&=0\end{aligned}}\right.,}$

Gdzie:

• ${\ displaystyle u}$ to prędkość przepływu
• ${\ displaystyle e}$ to specyficzna energia wewnętrzna.

Równanie energii jest integralną postacią równania Bernoulliego w przypadku ściśliwości. Poprzednie równania masy i pędu przez podstawienie prowadzą do równania Rayleigha:

${\ Displaystyle {\ Frac {\ Delta p} {\ Delta v}} = - {\ Frac {u_ {0} ^ {2}} {v_ {0}}}.}$

Ponieważ drugi człon jest stałą, równanie Rayleigha zawsze opisuje prostą prostą w płaszczyźnie ciśnienie-objętość niezależną od żadnego równania stanu, czyli linię Rayleigha. Przez podstawienie w równaniach Rankine'a-Hugoniota można to również wyrazić jako:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ rho u & = \ rho _ {0} u_ {0} \\ [1.2ex] \ rho u ^ {2} + p & = \ rho _ {0} u_ {0}^{2}+p_{0}\\[1.2ex]e+{\frac {1}{2}}u^{2}+{\frac {p}{\rho }}&=e_{ 0}+{\frac {1}{2}}u_{0}^{2}+{\frac {p_{0}}{\rho _{0}}}\end{aligned}}\right.. }$

Można również otrzymać równanie kinetyczne i równanie Hugoniota. Fragmenty analityczne nie są tutaj pokazane dla zwięzłości.

Zobacz też: równanie Rayleigha i równanie Hugoniota

Są to odpowiednio:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} u ^ {2} (v, p) & = u_ {0} ^ {2} + (pp_ {0}) (v_ {0} + v) \\[1.2ex]e(v,p)&=e_{0}+{\frac {1}{2}}(p+p_{0})(v_{0}-v)\end{wyrównane} }\Prawidłowy..}$

Równanie Hugoniota, sprzężone z podstawowym równaniem stanu materiału:

${\ Displaystyle e = e (v, p)}$

₀₀ opisuje ogólnie w płaszczyźnie ciśnienie-objętość krzywą przechodzącą przez warunki (v , p ), czyli krzywą Hugoniota, której kształt silnie zależy od rodzaju rozważanego materiału.

Zwyczajowo definiuje się również funkcję Hugoniota :

${\ Displaystyle {\ mathfrak {h}} (v, s) \ równoważnik e(v,s)-e_{0}+{\frac {1}{2}}(p(v,s)+p_{0})(v-v_{0})}$

pozwalającą na ilościowe określenie odchyleń od równania Hugoniota, podobnie jak poprzednia definicja wysokości podnoszenia , przydatna przy odchyleniach od równania Bernoulliego.

Forma o skończonej objętości

Z drugiej strony, całkując ogólne równanie zachowania:

${\ Displaystyle {\ Frac {\ częściowe \ mathbf {y}} {\ częściowe t}} + \ nabla \ cdot \ mathbf {F} = \ mathbf {s}}$

na ustalonej objętości V _m , a następnie na podstawie twierdzenia o dywergencji , staje się:

${\ Displaystyle {\ Frac {d} {dt}} \ int _ {V_ {m}} \ mathbf {y} dV + \ oint _ {\ częściowe V_ {m}} \ mathbf {F} \ cdot {\ kapelusz { n}}ds=\mathbf {S} .}$

Całkując to równanie również w przedziale czasu:

${\ Displaystyle \ int _ {V_ {m}} \ mathbf {y} (\ mathbf {r}, t_ {n + 1}) \, dV- \ int _ {V_ {m}} \ mathbf {y} ( \mathbf {r} ,t_{n})\,dV+\int _{t_{n}}^{t_{n+1}}\oint _{\częściowe V_{m}}\mathbf {F} \cdot {\ kapelusz {n}} \, ds \, dt = \ mathbf {0} .}$

Teraz definiując zachowaną ilość węzłów:

${\ Displaystyle \ mathbf {y} _ {m, n} \ równoważnik {\ Frac {1} {V_ {m}}} \int _{V_{m}}\mathbf {y} (\mathbf {r},t_{n})\,dV,}$

dedukujemy formę objętości skończonej:

${\ Displaystyle \ mathbf {y} _ {m, n + 1} = \ mathbf {y} _ {m, n} - {\ Frac {1} {V_ {m}}} \ int _ {t_ {n} }^{t_{n+1}}\oint _{\częściowe V_{m}}\mathbf {F} \cdot {\hat {n}}\,ds\,dt.}$

W szczególności w przypadku równań Eulera, po określeniu zachowanych wielkości, zmienne konwekcyjne są wyprowadzane przez podstawienie wsteczne:

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ mathbf {u} _ {m, n} & = {\ Frac {\ mathbf {j} _ {m, n}}} {\ rho _ {m, n }}}\\[1.2ex]e_{m,n}&={\frac {E_{m,n}^{t}}{\rho _{m,n}}}-{\frac {1} {2}}u_{m,n}^{2}\\[1.2ex]\end{aligned}}\right..}$

Wtedy wyraźne wyrażenia skończonej objętości oryginalnych zmiennych konwekcyjnych to:

Równania Eulera ( Forma objętości skończonej )

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} \ rho _ {m, n + 1} & = \ rho _ {m, n} - {\ Frac {1} {V_ {m}}} \ int _ {t_{n}}^{t_{n+1}}\oint _{\częściowe V_{m}}\rho \mathbf {u} \cdot {\hat {n}}\,ds\,dt\\ [1.2ex]\mathbf {u} _{m,n+1}&=\mathbf {u} _{m,n}-{\frac {1}{\rho _{m,n}V_{m} }}\int _{t_{n}}^{t_{n+1}}\oint _{\częściowe V_{m}}(\rho \mathbf {u} \otimes \mathbf {u} -p\mathbf {I} )\cdot {\hat {n}}\,ds\,dt\\[1.2ex]\mathbf {e} _{m,n+1}&=\mathbf {e} _{m,n }-{\frac {1}{2}}\left(u_{m,n+1}^{2}-u_{m,n}^{2}\right)-{\frac {1}{\ rho _{m,n}V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\częściowe V_{m}}\left(\rho e+{\ frac {1}{2}}\rho u^{2}+p\right)\mathbf {u} \cdot {\hat {n}}\,ds\,dt\\[1.2ex]\end{wyrównane }}\Prawidłowy..}$

Ograniczenia

Wykazano, że równania Eulera nie są kompletnym zbiorem równań, ale wymagają pewnych dodatkowych ograniczeń, aby dopuścić unikalne rozwiązanie: są to równania stanu rozważanego materiału. Aby zachować zgodność z termodynamiką , te równania stanu powinny spełniać dwie zasady termodynamiki. Z drugiej strony, z definicji systemy nierównowagowe opisywane są prawami leżącymi poza tymi prawami. Poniżej wymienimy kilka bardzo prostych równań stanu i odpowiadający im wpływ na równania Eulera.

Doskonały gaz politropowy

Zobacz też: gaz doskonały

Dla idealnego gazu politropowego podstawowe równanie stanu to:

${\ Displaystyle e (v, s) = e_ {0} e ^ {(\ gamma -1) m\left(s-s_{0}\right)}\left({v_{0} \over v}\right)^{\gamma -1}}$

gdzie $specyficzna$ energia, to $\ gamma }$ objętość, to $\$ entropia, $to$ masa cząsteczkowa, $m$ jest tutaj uważane za stałą ( proces politropowy ) i można wykazać, że odpowiada stosunkowi pojemności cieplnej . Można wykazać, że to równanie jest zgodne ze zwykłymi równaniami stanu stosowanymi w termodynamice.

Wykazanie zgodności z termodynamiką gazu doskonałego

Z termodynamicznej definicji temperatury:

${\ Displaystyle T (e) \ równoważnik {\ częściowe e \ nad \ częściowe s} = (\ gamma -1) ja}$

Gdzie temperatura jest mierzona w jednostkach energii. Na początku zauważ, że łącząc te dwa równania, można wydedukować prawo stanu gazu doskonałego :

${\ displaystyle pv = mT}$

lub w zwykłej formie:

${\ displaystyle p = nT}$

gdzie: ${\ Displaystyle n \ equiv {\ Frac {m} {v}}}$ jest liczbową gęstością materiału. Z drugiej strony prawo stanu gazu doskonałego jest mniej rygorystyczne niż rozważane pierwotne podstawowe równanie stanu.

Rozważmy teraz molową pojemność cieplną związaną z procesem x :

${\ Displaystyle c_ {x} = \ lewo (mT {\ częściowe s \ nad \ częściowe T} \ prawej) _ {x}}$

zgodnie z pierwszą zasadą termodynamiki:

${\ Displaystyle de (v, s) = - pdv + T \, ds}$

można to po prostu wyrazić jako:

${\ Displaystyle c_ {x} \ równoważnik m \ lewo ({\ częściowe e \ ponad \ częściowe T} \ prawo) _ {x }+mp\lewo({\częściowo v \nad \częściowo T}\prawo)_{x}}$

Teraz odwracając równanie na temperaturę T(e) wnioskujemy, że dla idealnego gazu politropowego izochoryczna pojemność cieplna jest stała:

${\ Displaystyle c_ {v} \ równoważnik m \ lewo ({\ częściowe e \ nad \ częściowe T} \ prawo) _{v}=m{de \ponad dT}={\frac {1}{(\gamma -1)}}}$

i podobnie dla idealnego gazu politropowego izobaryczna pojemność cieplna jest stała:

${\ Displaystyle c_ { p}\equiv m\left({\częściowe e \ponad \częściowe T}\right)_{p}+mp\left({\częściowe v \ponad \częściowe T}\right)_{p}=m{ de \over dT}+p\left({\częściowe v \ponad \częściowe T}\right)_{p}={\frac {1}{(\gamma -1)}}+1}$

Prowadzi to do dwóch ważnych zależności między pojemnościami cieplnymi : stała gamma faktycznie reprezentuje stosunek pojemności cieplnej w idealnym gazie politropowym:

$\ Displaystyle {\ Frac {c_ {p}} {c_ {v}}} = \ gamma}$

i dochodzimy również do relacji Meyera :

${\ Displaystyle c_ {p} = c_ {v} + 1}$

Energia właściwa wynosi zatem, odwracając zależność T(e):

${\ Displaystyle e (T) = {\ Frac {mT} {\ gamma -1}} = c_ {v} mT}$

Właściwa entalpia wynika z podstawienia tego ostatniego i idealnego prawa gazu:

${\ Displaystyle h (T) \ równoważnik e (T) + (pv) (T) =c_{v}mT+mT=c_{p}mT}$

Z tego równania można wyprowadzić równanie ciśnienia na podstawie jego termodynamicznej definicji:

${\ Displaystyle p (v, e) \ równoważnik - {\ częściowe e \ ponad \ częściowe v} = (\ gamma -1) { \frac {e}{v}}}$

Odwracając go, dochodzimy do mechanicznego równania stanu:

${\ Displaystyle e (v, p) = {\ Frac {pv} {\ gamma -1}}}$

Następnie dla gazu doskonałego równania Eulera ściśliwości można po prostu wyrazić w mechanicznych lub prymitywnych zmiennych objętości właściwej, prędkości przepływu i ciśnieniu, biorąc zestaw równań dla układu termodynamicznego i modyfikując równanie energii w równanie ciśnienia za pomocą tego mechanicznego równanie stanu. Ostatecznie w formie konwekcyjnej dają:

Równania Eulera dla idealnego gazu politropowego ( forma konwekcyjna )

${\ Displaystyle \ lewo \ {{\ rozpocząć {wyrównane} {Dv \ nad Dt} &=v\nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=v\nabla p+\mathbf {g} \\[1.2ex] {Dp \over Dt}&=-\gamma p\nabla \cdot \mathbf {u} \end{aligned}}\right.}$

aw jednowymiarowej postaci quasiliniowej dają:

${\ Displaystyle {\ Frac {\ częściowy \ mathbf {y}}} {\ częściowy t}} + \ mathbf {A} {\ Frac {\ częściowy \ mathbf {y}}} {\ częściowy x}} = {\ mathbf { 0} }.}$

gdzie zachowawcza zmienna wektora to:

${\ Displaystyle {\ mathbf {y}} = {\ rozpocząć {pmatrix} v \\ u \\ p \ koniec {pmatrix}}}$

a odpowiadająca jej macierz Jakobiana to:</ref>

${\ Displaystyle {\ mathbf {A}} = {\ rozpocząć {pmatrix} u&-v&0 \\0&u&v\\0&\ gamma p&u\ koniec {pmatrix}}.}$

Stały przepływ we współrzędnych materiałowych

W przypadku przepływu ustalonego wygodnie jest wybrać ramkę Freneta-Serreta wzdłuż linii prądu jako układ współrzędnych do opisu równania Eulera o ustalonym pędzie :

${\ Displaystyle {\ boldsymbol {u}} \ cdot \ nabla {\ boldsymbol {u}} = - {\ Frac {1} {\ rho}} \ nabla p,}$

gdzie $i$$oznaczają$ odpowiednio prędkość , $.$ gęstość _ _ _ _ _

Niech ${\ Displaystyle \ lewo \ {\ mathbf {e} _ {s} \ mathbf {e} _ {n} \ mathbf {e} _ {b} \ prawo \ }} będzie$ bazą ortonormalną Freneta-Serreta , która składa się odpowiednio ze stycznego wektora jednostkowego, normalnego wektora jednostkowego i binormalnego wektora jednostkowego do linii prądu. Ponieważ linia prądu jest krzywą styczną do wektora prędkości przepływu, lewą stronę powyższego równania, konwekcyjną pochodną prędkości, można opisać następująco:

${\ Displaystyle {\ rozpocząć {wyrównane} {\ boldsymbol {u}} \ cdot \ nabla {\ boldsymbol {u}} \\& = u {\ Frac {\ częściowe}} {\ częściowe s}}(u{\boldsymbol {e}}_{s})&({\boldsymbol {u}}=u{\boldsymbol {e}}_{s},~{\częściowe /\częściowe s} \equiv {\boldsymbol {e}}_{s}\cdot \nabla )\\&=u{\frac {\częściowe u}{\częściowe s}}{\boldsymbol {e}}_{s}+{ \frac {u^{2}}{R}}{\boldsymbol {e}}_{n}&(\ponieważ ~{\frac {\częściowy {\boldsymbol {e}}_{s}}{\częściowy s}}={\frac {1}{R}}{\boldsymbol {e}}_{n}),\end{wyrównane}}}$

gdzie jest promieniem krzywizny $linii$ prądu

Dlatego część pędu równań Eulera dla stałego przepływu ma prostą postać:

${\ Displaystyle {\ rozpocząć {przypadki} \ Displaystyle u {\ Frac {\ częściowe u} {\ częściowe s}} = - {\ Frac {1} {\ rho}}} {\ Frac {\ częściowe p} {\ częściowe s}}, \\\ Displaystyle {u ^ {2} \ ponad R} = - {\ Frac {1} {\ rho}} {\ Frac {\ częściowe p} {\ częściowe n}} & ({\ częściowe /\ częściowe n} \ równoważnik {\ boldsymbol {e}} _ {n} \ cdot \ nabla ), \\\ Displaystyle 0 = - {\ frac {1} {\ rho}}} {\ frac {\ częściowe p} {\częściowe b}}&({\częściowe /\częściowe b}\equiv {\boldsymbol {e}}_{b}\cdot \nabla).\end{przypadki}}}$

Dla przepływu barotropowego równanie Bernoulliego wyprowadza się z pierwszego równania: ${\ Displaystyle (\ rho = \ rho (p)$ }

${\ Displaystyle {\ Frac {\ częściowe} {\ częściowe s}} \ lewo ({\ Frac {u ^ {2}} {2}} + \int {\frac {\mathrm {d} p} {\rho}}\right)=0.}$

Drugie równanie wyraża, że ​​w przypadku, gdy linia prądu jest zakrzywiona, powinien istnieć gradient ciśnienia normalny do linii prądu, ponieważ przyspieszenie dośrodkowe paczki płynu jest generowane tylko przez normalny gradient ciśnienia.

Trzecie równanie wyraża, że ​​ciśnienie jest stałe wzdłuż osi binormalnej.

Twierdzenie o krzywiźnie usprawniającej

„Twierdzenie o krzywiźnie strumienia” stwierdza, że ​​​​ciśnienie na górnej powierzchni płata jest niższe niż ciśnienie daleko, a ciśnienie na dolnej powierzchni jest wyższe niż ciśnienie daleko; stąd różnica ciśnień między górną i dolną powierzchnią płata generuje siłę nośną.

Niech będzie odległością od środka krzywizny linii prądu, wtedy drugie równanie jest zapisane w następujący sposób: ${\ displaystyle r }$

${\ Displaystyle {\ Frac {\ częściowe p} {\ częściowe r}} = \ rho {\ Frac {u ^ {2}} {r}} ~ (> 0)}$

gdzie ${\ Displaystyle {\ częściowe / \ częściowe r} = - {\ częściowe / \ częściowe n}.}$

To równanie stwierdza:

W ustalonym przepływie nielepkiej cieczy bez sił zewnętrznych środek krzywizny linii prądu leży w kierunku malejącego ciśnienia promieniowego.

Chociaż ta zależność między polem ciśnienia a krzywizną przepływu jest bardzo użyteczna, nie ma nazwy w anglojęzycznej literaturze naukowej. Japońscy dynamika płynów nazywają tę zależność „twierdzeniem o krzywiźnie strumienia”.

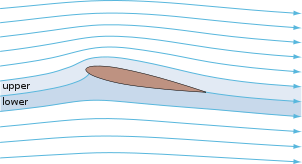
To „twierdzenie” jasno wyjaśnia, dlaczego w centrach wirów , które składają się z koncentrycznych kręgów linii prądu, występują tak niskie ciśnienia. Jest to również sposób na intuicyjne wyjaśnienie, dlaczego płaty generują siłę nośną .

Dokładne rozwiązania

Wszystkie potencjalne rozwiązania przepływu są również rozwiązaniami równań Eulera, aw szczególności nieściśliwych równań Eulera, gdy potencjał jest harmoniczny.

Dwuwymiarowy równoległy przepływ ścinający.

Rozwiązania równań Eulera z wirowością to:

• równoległe przepływy ścinające - gdzie przepływ jest jednokierunkowy, a prędkość przepływu zmienia się tylko w kierunkach przepływu krzyżowego, np. w kartezjańskim układzie współrzędnych $z)}$ , na przykład w $tylko$ - z jedyną niezerową składową prędkości zależną od ${\ Displaystyle u_ {x} (y, z)}$${\ displaystyle y} }$ i ${\ displaystyle z}$ a nie na ${\ displaystyle x.}$
• Przepływ Arnolda-Beltramiego-Childresa - dokładne rozwiązanie nieściśliwych równań Eulera.
• Dwa rozwiązania trójwymiarowych równań Eulera o symetrii cylindrycznej zostały przedstawione przez Gibbona, Moore'a i Stuarta w 2003 r. Te dwa rozwiązania mają nieskończoną energię; wybuchają wszędzie w przestrzeni w skończonym czasie.

Zobacz też

• Twierdzenie Bernoulliego
• Twierdzenie o obiegu Kelvina
• Równania Cauchy'ego
• Numer Froude'a
• Równania Madelunga
• Równania Naviera-Stokesa
• Równanie hamburgerów
• Równania dżinsów
• Idealny płyn

Źródła

•   Anderson, John (1995). Obliczeniowa dynamika płynów . Edukacja McGraw-Hill. ISBN 978-0-07-001685-9 .
•   Babinsky, Holger (listopad 2003), „Jak działają skrzydła?” (PDF) , Physics Education , 38 (6): 497–503, Bibcode : 2003PhyEd..38..497B , doi : 10.1088/0031-9120/38/6/001 , S2CID 1657792
•   Chorin, Alexandre J.; Marsden, Jerrold E. (2013). Matematyczne wprowadzenie do mechaniki płynów . Skoczek. ISBN 978-1-4612-0883-9 .
• Christodoulou, Demetrios (październik 2007). „Równania Eulera dotyczące przepływu płynu ściśliwego” (PDF) . Biuletyn Amerykańskiego Towarzystwa Matematycznego . 44 (4): 581–602. doi : 10.1090/S0273-0979-07-01181-0 .
• Eulera, Leonharda (1757). „Principes généraux du mouvement des fluides” [Ogólne zasady ruchu płynów]. Mémoires de l'académie des sciences de Berlin (w języku francuskim). 11 : 274–315.
•   Fay, James A. (1994). Wprowadzenie do mechaniki płynów . MIT Press. ISBN 978-0-262-06165-0 .
•   Friedlander S.; Serre, D., wyd. (2003). Podręcznik matematycznej dynamiki płynów - tom 2 . Elsevier. ISBN 978-0-444-51287-1 .
• Friedmann, A. (1934) [1922]. Kochin, Mikołaj (red.). Опыт гидромеханики сжимаемой жидкости [ Esej o hydrodynamice płynu ściśliwego ] (po rosyjsku). Piotrogród .
•   Gibon, JD; Moore, DR; Stuart, JT (2003). „Dokładne, nieskończonej energii, powiększone rozwiązania trójwymiarowych równań Eulera”. Nieliniowość . 16 (5): 1823–1831. Bibcode : 2003Nonli..16.1823G . doi : 10.1088/0951-7715/16/5/315 . S2CID 250797052 .
•   Henderson, LF (2000). „Ogólne prawa propagacji fal uderzeniowych przez materię” . W Ben-Dor, Gabi; Igra, Ozer; Elperin, Tov (red.). Podręcznik fal uderzeniowych, zestaw trzech tomów . Elsevier. ISBN 978-0-08-053372-8 .
• Hunter, John K. (25 września 2006), Wprowadzenie do nieściśliwych równań Eulera (PDF) , pobrane 2019-05-31
•   今井 功 (IMAI, Isao) (listopad 1973). 『流体力学(前編)』 [ Dynamika płynów 1 ] (po japońsku). 裳華房 (Shoukabou). ISBN 4-7853-2314-0 .
•   Landau, LD; Lifszyc, EM (2013). mechanika płynów . Elsevier. ISBN 978-1-4831-4050-6 .
•   Marchioro, C.; Pulvirenti, M. (1994). Matematyczna teoria nieściśliwych, nielepkich płynów . Stosowane nauki matematyczne. Tom. 96. Nowy Jork: Springer. ISBN 0-387-94044-8 .
•   Quartapelle, Luigi; Auteri, Franco (2013). Fluidodinamica comprimibile [ dynamika płynów ściśliwych ] (w języku włoskim). CEA. ISBN 978-88-08-18558-7 .
•   Toro, EF (1999). Solvers Riemanna i metody numeryczne dla dynamiki płynów: praktyczne wprowadzenie . Skoczek. ISBN 978-3-540-65966-2 .
• Valorani, Mauro; Nasuti, Francesco (nd), Metodi di analisi delle turbomachine (PDF) , Sapienza - Universit`a di Roma , pobrane 2019-05-31
• Zingale, M. (16 kwietnia 2013), Uwagi o równaniach Eulera (PDF) , dostęp 2019-05-31

Dalsza lektura

•    Badin, G.; Crisciani, F. (2018). Formułowanie wariacyjne płynów i geofizycznej dynamiki płynów - mechanika, symetrie i prawa zachowania - . Skoczek. P. 218. doi : 10.1007/978-3-319-59695-2 . ISBN 978-3-319-59694-5 . S2CID 125902566 .
•   Batchelor, GK (1967). Wprowadzenie do dynamiki płynów . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-66396-2 .
•   Thompson, Philip A. (1972). Przepływ płynu ściśliwego . Nowy Jork: McGraw-Hill. ISBN 0-07-064405-5 .