Strumień

Ten artykuł dotyczy pojęcia strumienia w naukach przyrodniczych i matematyce. W przypadku innych zastosowań zobacz Flux (ujednoznacznienie) .

Linie pola pola wektorowego F przechodzące przez powierzchnie o normalnej jednostkowej n , kąt od n do F wynosi θ . Strumień jest miarą tego, jaka część pola przechodzi przez daną powierzchnię. F rozkłada się na składowe prostopadłe (⊥) i równoległe (‖) do n . Tylko składowa równoległa przyczynia się do strumienia, ponieważ jest to maksymalny zasięg pola przechodzącego przez powierzchnię w punkcie, składowa prostopadła nie ma udziału. Góra: trzy linie pola przechodzące przez płaską powierzchnię, jedna normalna do powierzchni, jedna równoległa i jedna pośrednia. U dołu: Linia pola przechodząca przez zakrzywioną powierzchnię , pokazująca ustawienie normalnej jednostki i elementu powierzchni do obliczenia strumienia.

Aby obliczyć strumień pola wektorowego F (czerwone strzałki) przez powierzchnię S , powierzchnię dzieli się na małe obszary dS . Strumień przechodzący przez każdy skrawek jest równy normalnej (prostopadłej) składowej pola, iloczynowi skalarnemu F ( x ) z jednostkowym wektorem normalnym n ( x ) (niebieskie strzałki) w punkcie x pomnożonym przez powierzchnię dS . Suma F • n , dS dla każdej plamy na powierzchni jest strumieniem przechodzącym przez powierzchnię

Strumień opisuje każdy efekt, który wydaje się przechodzić lub podróżować (niezależnie od tego, czy faktycznie się porusza, czy nie) przez powierzchnię lub substancję. Strumień to pojęcie stosowane w matematyce stosowanej i rachunku wektorowym , które ma wiele zastosowań w fizyce . W przypadku zjawisk transportowych strumień jest wielkością wektorową opisującą wielkość i kierunek przepływu substancji lub właściwości. W rachunku wektorowym strumień jest wielkością skalarną , zdefiniowaną jako całka powierzchniowa składowej prostopadłej pola wektorowego po powierzchni.

Terminologia

Słowo flux pochodzi z łaciny : fluxus oznacza „płynąć”, a fluere to „płynąć”. Termin ten, jako fluksja , został wprowadzony do rachunku różniczkowego przez Izaaka Newtona .

Koncepcja strumienia ciepła była kluczowym wkładem Josepha Fouriera w analizę zjawisk wymiany ciepła. Jego nowatorski traktat Théorie analytique de la chaleur ( Analityczna teoria ciepła ) definiuje strumień jako wielkość centralną i wyprowadza dobrze znane obecnie wyrażenia strumienia w kategoriach różnic temperatur w płycie, a następnie bardziej ogólnie w kategoriach gradienty temperatury lub różnice temperatur w innych geometriach. Można argumentować, opierając się na pracy Jamesa Clerka Maxwella , że ​​definicja transportu poprzedza definicję strumienia używaną w elektromagnetyzmie . Konkretny cytat z Maxwell to:

W przypadku strumieni musimy wziąć całkę po powierzchni strumienia przechodzącego przez każdy element powierzchni. Wynik tej operacji nazywany jest całką powierzchniową strumienia. Reprezentuje ilość, która przechodzi przez powierzchnię.

— James Clerk Maxwell

Zgodnie z definicją transportu strumień może być pojedynczym wektorem lub polem wektorowym/funkcją położenia. W tym drugim przypadku strumień można łatwo scałkować na powierzchni. Natomiast zgodnie z definicją elektromagnetyzmu strumień jest całką po powierzchni; całkowanie strumienia drugiej definicji nie ma sensu, ponieważ całkowanie po powierzchni byłoby dwukrotne. Zatem cytat Maxwella ma sens tylko wtedy, gdy „strumień” jest używany zgodnie z definicją transportu (a ponadto jest to pole wektorowe, a nie pojedynczy wektor). Jest to ironiczne, ponieważ Maxwell był jednym z głównych twórców tego, co obecnie nazywamy „strumieniem elektrycznym” i „strumieniem magnetycznym” zgodnie z definicją elektromagnetyzmu. Ich nazwy zgodnie z cytatem (i definicją transportu) brzmiałyby „całka powierzchniowa strumienia elektrycznego” i „całka powierzchniowa strumienia magnetycznego”, w którym to przypadku „strumień elektryczny” byłby zamiast tego zdefiniowany jako „pole elektryczne” i „strumień magnetyczny " zdefiniowane jako "pole magnetyczne". Oznacza to, że Maxwell wyobrażał sobie te pola jako pewnego rodzaju przepływy/strumienie.

Biorąc pod uwagę strumień zgodnie z definicją elektromagnetyzmu, odpowiednia gęstość strumienia , jeśli jest używany ten termin, odnosi się do jego pochodnej wzdłuż powierzchni, która została zintegrowana. Zgodnie z fundamentalnym twierdzeniem rachunku różniczkowego odpowiednia gęstość strumienia jest strumieniem zgodnie z definicją transportu. Biorąc pod uwagę prąd , taki jak prąd elektryczny — ładunek w czasie, gęstość prądu byłaby również strumieniem zgodnie z definicją transportu — ładunek w czasie na obszar. Ze względu na sprzeczne definicje strumienia i wymienność słów strumień , przepływ i prąd w nietechnicznym języku angielskim, wszystkie terminy użyte w tym akapicie są czasami używane zamiennie i niejednoznacznie. Topniki do betonu w dalszej części tego artykułu będą używane zgodnie z ich szeroką akceptacją w literaturze, niezależnie od tego, której definicji topnika odpowiada ten termin.

Strumień jako natężenie przepływu na jednostkę powierzchni

W zjawiskach transportu ( wymiana ciepła , masa i dynamika płynów ) strumień definiuje się jako szybkość przepływu danej właściwości na jednostkę powierzchni, która ma wymiary [ilość]·[czas] ⁻¹ ·[powierzchnia] ⁻¹ . Obszar jest powierzchnią, przez którą właściwość przepływa „przez” lub „w poprzek”. Na przykład ilość wody przepływającej przez przekrój poprzeczny rzeki w ciągu sekundy podzielona przez pole tego przekroju lub ilość energii słonecznej padającej na skrawek ziemi w ciągu sekundy podzielona przez powierzchnię skrawka, są rodzajem strumienia.

Ogólna definicja matematyczna (transport)

Oto 3 definicje w rosnącej kolejności złożoności. Każdy jest szczególnym przypadkiem następujących. We wszystkich przypadkach częsty symbol j , (lub J ) jest używany dla strumienia, q dla wielkości fizycznej , która przepływa, t dla czasu, a A dla powierzchni. Identyfikatory te będą pisane pogrubioną czcionką wtedy i tylko wtedy, gdy są wektorami.

Najpierw strumień jako (pojedynczy) skalar:

$${\ Displaystyle j = {\ Frac {I} {A}},}$$

Gdzie

$${\ Displaystyle I = \ lim _ {\ Delta t \ do 0} {\ Frac {\ Delta q} {\ Delta t}} = {\ Frac {\ operatorname {d} q} {\ operatorname {d} t} }.}$$

W tym przypadku powierzchnia, na której mierzony jest strumień, jest stała i ma pole A . Zakłada się, że powierzchnia jest płaska, a przepływ jest wszędzie stały w odniesieniu do położenia i prostopadły do ​​powierzchni.

Po drugie, strumień jako pole skalarne określone wzdłuż powierzchni, czyli funkcja punktów na powierzchni:

$${\ Displaystyle j (\ mathbf {p}) = {\ Frac {\ częściowe I} {\ częściowe A}} (\ mathbf {p}),}$$

$${\ Displaystyle I (A, \ mathbf {p}) = {\ Frac {\ operatorname {d} q} {\ operatorname {d} t}} (A, \ mathbf {p}).}$$

Tak jak poprzednio, zakłada się, że powierzchnia jest płaska, a przepływ wszędzie jest do niej prostopadły. Jednak przepływ nie musi być stały. q jest teraz funkcją p , punktu na powierzchni i A , obszaru. Zamiast mierzyć całkowity przepływ przez powierzchnię, q mierzy przepływ przez dysk z obszarem A wyśrodkowanym na p wzdłuż powierzchni.

Wreszcie strumień jako pole wektorowe :

$${\ Displaystyle \ mathbf {j} (\ mathbf {p}) = {\ Frac {\ częściowy \ mathbf {I}} {\ częściowy A}} (\ mathbf {P} ),}$$

$${\ Displaystyle \ mathbf {I} (A, \ mathbf {p}) = {\ underset {\ mathbf {\ kapelusz {n}}} {\ operatorname {arg \, max}}} \ mathbf {\ kapelusz {n }} _ {\mathbf {p} }{\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p},\mathbf {\hat {n}}). }$$

W tym przypadku nie ma stałej powierzchni, na której mierzymy. q jest funkcją punktu, obszaru i kierunku (określonego przez wektor jednostkowy $mierzy$ przepływ przez dysk o obszarze A prostopadłym do tego wektor jednostkowy. I jest zdefiniowany przez wybranie wektora jednostkowego, który maksymalizuje przepływ wokół punktu, ponieważ prawdziwy przepływ jest maksymalizowany przez dysk, który jest do niego prostopadły. W ten sposób wektor jednostkowy w wyjątkowy sposób maksymalizuje funkcję, gdy wskazuje „prawdziwy kierunek” przepływu. (Ściśle mówiąc, jest to nadużycie notacji , ponieważ „arg max” nie może bezpośrednio porównywać wektorów; zamiast tego bierzemy wektor z największą normą.)

Nieruchomości

Te bezpośrednie definicje, zwłaszcza ostatnia, są raczej nieporęczne. Na przykład konstrukcja arg max jest sztuczna z punktu widzenia pomiarów empirycznych, kiedy za pomocą wiatrowskazu lub podobnego można łatwo wydedukować kierunek strumienia w punkcie. Zamiast bezpośrednio definiować strumień wektorowy, często bardziej intuicyjne jest określenie pewnych jego właściwości. Co więcej, na podstawie tych właściwości i tak można jednoznacznie określić strumień.

Jeśli strumień j przechodzi przez obszar pod kątem θ do normalnej powierzchni ${\ Displaystyle \ mathbf {\ hat {n}}}$ , to iloczyn skalarny

$${\ Displaystyle \ mathbf {j} \ cdot \ mathbf {\ kapelusz {n}} = j \ cos \ theta.}$$

Oznacza to, że składowa strumienia przechodzącego przez powierzchnię (tj. prostopadła do niej) to j cos θ , natomiast składowa strumienia przechodzącego stycznie do tego obszaru to j sin θ , ale nie ma strumienia faktycznie przechodzącego przez ten obszar w stycznej kierunek. Jedyną przechodzącą prostopadle do obszaru jest składowa kosinusowa.

W przypadku strumienia wektorowego całka powierzchniowa j po powierzchni S daje właściwy przepływ w jednostce czasu przez powierzchnię:

$${\ Displaystyle {\ Frac {\ operatorname {d} q} {\ operatorname {d} t}} = \ iint _ {S }\mathbf {j} \cdot \mathbf {\hat {n}} \,dA=\iint _{S}\mathbf {j} \cdot d\mathbf {A} ,}$$

gdzie A (i $jego$ mała) to wektora - kombinacja wielkości obszaru A , przez który i wektor jednostkowy $.$ do obszaru. W przeciwieństwie do drugiego zestawu równań, tutaj powierzchnia nie musi być

Na koniec możemy ponownie scałkować po czasie t ₁ do t ₂ , uzyskując całkowitą ilość właściwości przepływającej przez powierzchnię w tym czasie ( t ₂ − t ₁ ):

$${\ Displaystyle q = \ int _ {t_ {1}} ^ {t_ {2}} \ iint _ {S} \ mathbf {j} \ cdot d \ mathbf {A} \, dt.}$$

Strumienie transportowe

Osiem najpowszechniejszych form przepływu z literatury dotyczącej zjawisk transportowych jest zdefiniowanych w następujący sposób:

1. Strumień pędu , szybkość przenoszenia pędu na jednostkę powierzchni (N·s·m ⁻² ·s ⁻¹ ). ( Prawo lepkości Newtona )
2. Strumień ciepła , szybkość przepływu ciepła przez jednostkę powierzchni (J·m ⁻² ·s ⁻¹ ). ( Prawo przewodzenia Fouriera ) (Ta definicja strumienia ciepła pasuje do oryginalnej definicji Maxwella).
3. Strumień dyfuzji , szybkość ruchu cząsteczek na jednostkowym obszarze (mol·m ⁻² ·s ⁻¹ ). ( prawo dyfuzji Ficka )
4. Strumień objętościowy , natężenie przepływu objętościowego przez jednostkę powierzchni (m ³ ·m ^-2 ·s ^-1 ). ( Prawo przepływu wód gruntowych Darcy'ego )
5. Strumień masowy , natężenie przepływu masowego przez jednostkę powierzchni (kg·m ⁻² ·s ⁻¹ ). (Albo alternatywna forma prawa Ficka, która obejmuje masę cząsteczkową, albo alternatywna postać prawa Darcy'ego, która obejmuje gęstość.)
6. Strumień promieniowania , ilość energii przenoszonej w postaci fotonów w określonej odległości od źródła na jednostkę powierzchni na sekundę (J·m ⁻² ·s ⁻¹ ). Używany w astronomii do określania wielkości i klasy widmowej gwiazdy. Działa również jako uogólnienie strumienia ciepła, który jest równy strumieniowi promieniowania, gdy jest ograniczony do widma elektromagnetycznego.
7. Strumień energii , szybkość przepływu energii przez jednostkę powierzchni (J·m ⁻² ·s ⁻¹ ). Strumień promieniowania i strumień ciepła to szczególne przypadki strumienia energii.
8. Strumień cząstek, szybkość przenoszenia cząstek przez jednostkę powierzchni ([liczba cząstek] m ⁻² ·s ⁻¹ )

Te strumienie są wektorami w każdym punkcie przestrzeni i mają określoną wielkość i kierunek. Można również wziąć rozbieżność dowolnego z tych strumieni, aby określić szybkość akumulacji ilości w objętości kontrolnej wokół danego punktu w przestrzeni. Dla przepływu nieściśliwego rozbieżność strumienia objętościowego wynosi zero.

Dyfuzja chemiczna

Jak wspomniano powyżej, chemiczny strumień molowy składnika A w izotermicznym układzie izobarycznym jest zdefiniowany w prawie dyfuzji Ficka jako:

$${\ Displaystyle \ mathbf {J} _ {A} = -D_ {AB} \ nabla c_ {A}$$

gdzie symbol nabla ∇ oznacza operator gradientu , D _AB to współczynnik dyfuzji (m ² ·s ⁻¹ ) składnika A dyfundującego przez składnik B, c _A to stężenie ( mol /m ³ ) składnika A.

Strumień ten ma jednostki mol·m ⁻² ·s ⁻¹ i pasuje do oryginalnej definicji strumienia Maxwella.

W przypadku gazów rozcieńczonych kinetyczna teoria molekularna wiąże współczynnik dyfuzji D z gęstością cząstek n = N / V , masą cząsteczkową m , przekrojem poprzecznym zderzenia i temperaturą bezwzględną T przez ${\ displaystyle \ sigma}$

$${\ Displaystyle D = {\ Frac {2} {3n \ sigma}}} {\ sqrt {\ Frac {kT} {\ pi m}}}}$$

gdzie drugim czynnikiem jest średnia droga swobodna , a pierwiastek kwadratowy (ze stałą Boltzmanna k ) to średnia prędkość cząstek.

W przepływach turbulentnych transport ruchem wirowym można wyrazić jako rażąco zwiększony współczynnik dyfuzji.

Mechanika kwantowa

Główny artykuł: prąd prawdopodobieństwa

W mechanice kwantowej cząstki o masie m w stanie kwantowym ψ ( r , t ) mają gęstość prawdopodobieństwa zdefiniowaną jako

$${\ Displaystyle \ rho = \ psi ^ {*} \ psi = | \ psi | ^ {2}.}$$

Zatem prawdopodobieństwo znalezienia cząstki w elemencie o różnej objętości d ³ r wynosi

$${\ Displaystyle dP = | \ psi | ^ {2} \, d ^ {3} \ mathbf {r}.}$$

Wtedy liczba cząstek przechodzących prostopadle przez jednostkową powierzchnię przekroju poprzecznego w jednostce czasu jest strumieniem prawdopodobieństwa;

$${\ Displaystyle \ mathbf {J} = {\ Frac {i \ hbar} {2m}} \ lewo (\ psi \ nabla \ psi ^ {*} - \ psi ^ {*} \ nabla \ psi \ po prawej).}$$

Jest to czasami określane jako prąd prawdopodobieństwa lub gęstość prądu lub gęstość strumienia prawdopodobieństwa.

Strumień jako całka powierzchniowa

Wizualizacja strumienia. Pierścienie pokazują granice powierzchni. Czerwone strzałki oznaczają przepływ ładunków, cząstek płynu, cząstek subatomowych, fotonów itp. Liczba strzałek przechodzących przez każdy pierścień to strumień.

Ogólna definicja matematyczna (całka powierzchniowa)

Jako koncepcja matematyczna strumień jest reprezentowany przez całkę powierzchniową pola wektorowego ,

$Displaystyle \ Phi _ {F} = \ iint _ {A} \ mathbf {F} \ cdot \ operatorname {d} \ mathbf {A}} Φ$

${\ Displaystyle \ Phi _ {F} = \ iint _ {A} \ mathbf {F} \ cdot \ mathbf {n} \, \ operatorname {d} A}$

gdzie F jest polem wektorowym , a d A jest polem wektorowym powierzchni A , skierowanym jako normalna do powierzchni . Po drugie, n jest jednostkowym wektorem normalnym skierowanym na zewnątrz do powierzchni.

Powierzchnia musi być orientowalna , tzn. można wyróżnić dwie strony: powierzchnia nie zagina się z powrotem na siebie. Poza tym powierzchnia musi być rzeczywiście zorientowana, tzn. stosujemy konwencję co do tego, w którą stronę płynięcie liczy się jako dodatnie; przepływ wsteczny jest wtedy liczony jako ujemny.

Normalna powierzchni jest zwykle kierowana przez regułę prawej dłoni .

I odwrotnie, można uznać strumień za bardziej podstawową wielkość i nazwać pole wektorowe gęstością strumienia.

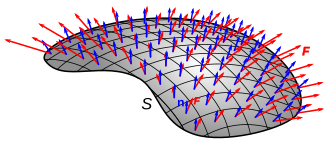
Często pole wektorowe jest rysowane przez krzywe (linie pola) podążające za „przepływem”; wielkość pola wektorowego jest wtedy gęstością linii, a strumień przez powierzchnię jest liczbą linii. Linie wychodzą z obszarów o dodatniej rozbieżności (źródła) i kończą się w obszarach o ujemnej rozbieżności (zlewiska).

Zobacz także obraz po prawej: liczba czerwonych strzałek przechodzących przez obszar jednostkowy to gęstość strumienia, krzywa otaczająca czerwone strzałki oznacza granicę powierzchni, a orientacja strzałek względem powierzchni oznacza znak iloczyn wewnętrzny pola wektorowego z normalnymi powierzchni.

Jeśli powierzchnia obejmuje obszar 3D, zwykle jest zorientowana tak, że napływ jest liczony jako dodatni; przeciwieństwem jest odpływ .

Twierdzenie o dywergencji stwierdza, że ​​odpływ netto przez zamkniętą powierzchnię, innymi słowy odpływ netto z obszaru 3D, znajduje się poprzez dodanie lokalnego odpływu netto z każdego punktu w regionie (co wyraża się rozbieżnością ) .

Jeśli powierzchnia nie jest zamknięta, jako granicę ma zorientowaną krzywą. Twierdzenie Stokesa mówi, że strumień zakrzywienia pola wektorowego jest całką liniową pola wektorowego na tej granicy. Ta całka po trajektorii jest również nazywana cyrkulacją , zwłaszcza w dynamice płynów. Zatem zwijanie jest gęstością cyrkulacji.

Możemy zastosować strumień i te twierdzenia do wielu dyscyplin, w których widzimy prądy, siły itp. Przyłożone przez obszary.

Elektromagnetyzm

Strumień elektryczny

„Ładunek elektryczny”, taki jak pojedynczy proton w przestrzeni, ma wielkość określoną w kulombach. Taki ładunek otacza pole elektryczne. W formie graficznej pole elektryczne z dodatniego ładunku punktowego można zwizualizować jako kropkę promieniującą linie pola elektrycznego (czasami nazywane także „liniami siły”). Koncepcyjnie strumień elektryczny można traktować jako „liczbę linii pola” przechodzących przez dany obszar. Z matematycznego punktu widzenia strumień elektryczny jest całką normalnej składowej pola elektrycznego na danym obszarze. Stąd jednostkami strumienia elektrycznego w systemie MKS są ^niutony na kulomb razy metry do kwadratu, czyli Nm 2 /C. (Gęstość strumienia elektrycznego jest strumieniem elektrycznym na jednostkę powierzchni i jest miarą siły normalnej składowej pola elektrycznego uśrednionej w obszarze całkowania. Jej jednostkami są N/C, tak samo jak pole elektryczne w jednostkach MKS. )

Stosowane są dwie formy strumienia elektrycznego , jedna dla pola E :

${\ Displaystyle \ Phi _ {E} =}$${\ Displaystyle {\ scriptstyle A}}$${\ Displaystyle \ mathbf {E} \ cdot {\ rm {d}} \ mathbf {A} }$

i jeden dla pola D (zwanego przemieszczeniem elektrycznym ):

${\ Displaystyle \ Phi _ {D} =}$${\ Displaystyle {\ scriptstyle A}}$${\ Displaystyle \ mathbf {D} \ cdot {\ rm {d}} \ mathbf {A} }$

Wielkość ta wynika z prawa Gaussa – które mówi, że strumień pola elektrycznego E z powierzchni zamkniętej jest proporcjonalny do ładunku elektrycznego Q _A zawartego w tej powierzchni (niezależnie od tego, jak ten ładunek jest rozłożony), całka ma postać:

${\ Displaystyle {\ scriptstyle A}}$${\ Displaystyle \ mathbf {E} \ cdot {\ rm {d}} \ mathbf {A} = {\ Frac {Q_ {A}$

₀ gdzie ε jest przenikalnością wolnej przestrzeni .

₀ Jeśli weźmie się pod uwagę strumień wektora pola elektrycznego E dla rury w pobliżu ładunku punktowego w polu ładunku, ale go nie zawierającej, której boki są utworzone przez linie styczne do pola, strumień dla boków wynosi zero i jest równy i przeciwny strumień na obu końcach rury. Jest to konsekwencja prawa Gaussa zastosowanego do odwrotnego pola kwadratowego. Strumień dla dowolnej powierzchni przekroju rury będzie taki sam. Całkowity strumień dla dowolnej powierzchni otaczającej ładunek q wynosi q / ε .

₀ W wolnej przestrzeni przemieszczenie elektryczne jest określone relacją konstytutywną D = ε E , więc dla dowolnej powierzchni ograniczającej strumień pola D jest równy znajdującemu się w niej ładunkowi Q _A. Tutaj wyrażenie „strumień” wskazuje na operację matematyczną i, jak widać, wynikiem niekoniecznie jest „przepływ”, ponieważ w rzeczywistości nic nie płynie wzdłuż linii pola elektrycznego.

Strumień magnetyczny

Gęstość strumienia magnetycznego ( pole magnetyczne ) wyrażoną w jednostce Wb/m ² ( Tesla ) oznaczamy przez B , a strumień magnetyczny definiujemy analogicznie:

${\ Displaystyle \ Phi _ {B} =}$${\ Displaystyle {\ scriptstyle A}}$${\ Displaystyle \ mathbf {B} \ cdot {\ rm {d}} \ mathbf {A} }$

z tym samym zapisem powyżej. Wielkość wynika z prawa indukcji Faradaya , gdzie strumień magnetyczny jest zależny od czasu, ponieważ granica jest zależna od czasu lub pole magnetyczne jest zależne od czasu. W formie integralnej:

${\ Displaystyle - {\ Frac {{\ rm {d}} \ Phi _ {B}} {{\ rm {d}} t}} = \ oint _{\częściowe A}\mathbf {E} \cdot d{\boldsymbol {\ell}}}$

gdzie re ℓ jest nieskończenie małym wektorowym elementem liniowym zamkniętej krzywej , o wielkości równej długości nieskończenie małego elementu liniowego i kierunku nadanym przez styczną do krzywej $częściowe A}$$\$$displaystyle \$ , ze znakiem określonym przez kierunek całkowania.

Tempo zmiany strumienia magnetycznego w pętli drutu jest pomniejszone o siłę elektromotoryczną wytworzoną w tym przewodzie. Kierunek jest taki, że jeśli prąd przepływa przez drut, siła elektromotoryczna spowoduje powstanie prądu, który „przeciwstawia się” zmianie pola magnetycznego, sam wytwarzając pole magnetyczne przeciwne do zmiany. Jest to podstawa cewek indukcyjnych i wielu generatorów elektrycznych .

Strumień Poyntinga

Korzystając z tej definicji, strumień wektora Poyntinga S na określonej powierzchni to szybkość, z jaką energia elektromagnetyczna przepływa przez tę powierzchnię, zdefiniowana jak poprzednio:

${\ Displaystyle \ Phi _ {S} =}$${\ Displaystyle {\ scriptstyle A}}$${\ Displaystyle \ mathbf {S} \ cdot {\ rm {d}} \ mathbf {A} }$

Strumień wektora Poyntinga przez powierzchnię to siła elektromagnetyczna lub energia w jednostce czasu przechodząca przez tę powierzchnię. Jest to powszechnie stosowane w analizie promieniowania elektromagnetycznego , ale ma również zastosowanie do innych układów elektromagnetycznych.

Myląco, wektor Poyntinga jest czasami nazywany strumieniem mocy , co jest przykładem pierwszego użycia strumienia powyżej. Ma jednostki watów na metr kwadratowy (W/m ² ).

Jednostki radiometrii SI

Jednostki radiometrii SI

Ilość		Jednostka		Wymiar	Notatki
Nazwa	Symbol	Nazwa	Symbol	Symbol
Energia promienista	P e	dżul	J	M ⋅ L 2 ⋅ T -2	Energia promieniowania elektromagnetycznego.
Gęstość energii promieniowania	my e	dżul na metr sześcienny	J/m 3	M ⋅ L -1 ⋅ T -2	Energia promieniowania na jednostkę objętości.
Strumień promieniowania	Φ e	wat	W = J/s	M ⋅ L 2 ⋅ T -3	Energia promieniowania emitowana, odbijana, przesyłana lub odbierana w jednostce czasu. Czasami nazywa się to również „mocą promieniowania”, aw astronomii nazywa się to jasnością .
Strumień widmowy	Φ e, ν	wat na herc	W/ Hz	M ⋅ L 2 ⋅ T -2	Strumień promieniowania na jednostkę częstotliwości lub długości fali. Ta ostatnia jest zwykle mierzona w W⋅nm −1 .
	Φ e, λ	wat na metr	W/m	M ⋅ L ⋅ T -3
Intensywność promieniowania	ja e,Ω	wat na steradian	W/ sr	M ⋅ L 2 ⋅ T -3	Strumień promieniowania emitowany, odbijany, przesyłany lub odbierany na jednostkę kąta bryłowego. Jest to kierunkowa .
Intensywność widmowa	ja e,Ω, ν	wat na steradian na herc	W⋅sr −1 ⋅Hz −1	M ⋅ L 2 ⋅ T -2	Intensywność promieniowania na jednostkę częstotliwości lub długości fali. Ta ostatnia jest zwykle mierzona w W⋅sr −1 ⋅nm −1 . Jest to kierunkowa .
	ja e, Ω, λ	wat na steradian na metr	W⋅sr −1 ⋅m −1	M ⋅ L ⋅ T -3
Blask	Le , Ω	wat na steradian na metr kwadratowy	W⋅sr −1 ⋅m −2	M ⋅ T −3	Strumień promieniowania emitowany, odbijany, transmitowany lub odbierany przez powierzchnię na jednostkę kąta bryłowego na jednostkę rzutowanej powierzchni. Jest to kierunkowa . Czasami jest to myląco nazywane „intensywnością”.
Widmowy blask Specyficzna intensywność	Le , Ω, ν	wat na steradian na metr kwadratowy na herc	W⋅sr −1 ⋅m −2 ⋅Hz −1	M ⋅ T −2	Promieniowanie powierzchni na jednostkę częstotliwości lub długości fali. Ta ostatnia jest zwykle mierzona w W⋅sr −1 ⋅m −2 ⋅nm −1 . Jest to kierunkowa . Czasami jest to również myląco nazywane „intensywnością widmową”.
	Le , Ω, λ	wat na steradian na metr kwadratowy, na metr	W⋅sr −1 ⋅m −3	M ⋅ L -1 ⋅ T -3
Gęstość strumienia promieniowania	E e	wata na metr kwadratowy	W/m 2	M ⋅ T −3	Strumień promieniowania odbierany przez powierzchnię na jednostkę powierzchni. Czasami jest to myląco nazywane „intensywnością”.
Widmowe natężenie promieniowania Widmowa gęstość strumienia	E e, v	wat na metr kwadratowy na herc	W⋅m −2 ⋅Hz −1	M ⋅ T −2	Natężenie promieniowania powierzchni na jednostkę częstotliwości lub długości fali. Czasami jest to również myląco nazywane „intensywnością widmową”. Jednostki gęstości strumienia widmowego spoza układu SI obejmują jansky (1 Jy = 10 −26 W⋅m −2 ⋅ Hz −1 ) i jednostkę strumienia słonecznego (1 sfu = 10 −22 W⋅m −2 ⋅ Hz −1 = 10 4 Jy).
	E e, λ	wat na metr kwadratowy, na metr	W/m 3	M ⋅ L -1 ⋅ T -3
Radiosity	J e	wata na metr kwadratowy	W/m 2	M ⋅ T −3	Strumień promieniowania opuszczający (emitowany, odbijany i przepuszczany przez) powierzchnię na jednostkę powierzchni. Czasami jest to myląco nazywane „intensywnością”.
Widmowa radiostacja	J e, ν	wat na metr kwadratowy na herc	W⋅m −2 ⋅Hz −1	M ⋅ T −2	Radiosity powierzchni na jednostkę częstotliwości lub długości fali. Ta ostatnia jest zwykle mierzona w W⋅m −2 ⋅nm −1 . Czasami jest to również myląco nazywane „intensywnością widmową”.
	J e, λ	wat na metr kwadratowy, na metr	W/m 3	M ⋅ L -1 ⋅ T -3
Promienne wyjście	ja e	wata na metr kwadratowy	W/m 2	M ⋅ T −3	Strumień promieniowania emitowany przez powierzchnię na jednostkę powierzchni. To jest emitowana składowa radiosity. „Emitancja promieniowania” to stare określenie tej wielkości. Czasami jest to myląco nazywane „intensywnością”.
Widmowe wyjście	Me , v	wat na metr kwadratowy na herc	W⋅m −2 ⋅Hz −1	M ⋅ T −2	Wyjście promieniowania powierzchni na jednostkę częstotliwości lub długości fali. Ta ostatnia jest zwykle mierzona w W⋅m −2 ⋅nm −1 . „Emitancja widmowa” to stare określenie tej wielkości. Czasami jest to również myląco nazywane „intensywnością widmową”.
	Me , λ	wat na metr kwadratowy, na metr	W/m 3	M ⋅ L -1 ⋅ T -3
Promienista ekspozycja	on e	dżul na metr kwadratowy	J/m 2	M ⋅ T −2	Energia promieniowania otrzymana przez powierzchnię na jednostkę powierzchni lub równoważne natężenie napromienienia powierzchni zintegrowane w czasie napromieniowania. Czasami nazywa się to również „fluencją promienistą”.
Ekspozycja widmowa	He , ν	dżul na metr kwadratowy na herc	J⋅m −2 ⋅Hz −1	M ⋅ T −1	Ekspozycja powierzchni na promieniowanie na jednostkę częstotliwości lub długości fali. Ta ostatnia jest zwykle mierzona w J⋅m −2 ⋅nm −1 . Jest to czasami nazywane „fluencją widmową”.
	He , λ	dżul na metr kwadratowy, na metr	J/m 3	M ⋅ L -1 ⋅ T -2
Zobacz też: SI · Radiometria · Fotometria

Zobacz też

• Wielkość AB
• Wybuchowo pompowany generator kompresji strumienia
• kowariancji wirów (inaczej korelacja wirów, strumień wirów)
• Zakład testowy Fast Flux
• Fluence (strumień pierwszego rodzaju dla wiązek cząstek)
• Dynamika płynów
• Ślad strumienia
• Przypinanie strumienia
• Kwantyzacja strumienia
• Prawo Gaussa
• Prawa odwrotnych kwadratów
• Jansky (jednostka gęstości strumienia widmowego spoza układu SI)
• Utajony strumień ciepła
• Strumień świetlny
• Strumień magnetyczny
• Kwant strumienia magnetycznego
• Strumień neutronów
• Strumień Poyntinga
• Twierdzenie Pontinga
• Strumień promieniowania
• Szybki kwant pojedynczego strumienia
• Strumień energii dźwięku
• Strumień objętościowy (strumień pierwszego rodzaju dla płynów)
• Objętościowe natężenie przepływu (strumień drugiego rodzaju dla płynów)

Notatki

•   Browne, Michael, dr (2010). Fizyka dla inżynierii i nauki, wydanie 2 . Kontury Schauma. Nowy Jork, Toronto: Wydawnictwo McGraw-Hill . ISBN 978-0-0716-1399-6 .
•   Purcell, Edward, dr (2013). Elektryczność i magnetyzm, wydanie 3 . Cambridge, Wielka Brytania: Cambridge University Press . ISBN 978110-7014022 .

Dalsza lektura

•    Stauffer, PH (2006). „Flux Flummoxed: propozycja konsekwentnego użytkowania”. Woda gruntowa . 44 (2): 125–128. doi : 10.1111/j.1745-6584.2006.00197.x . PMID 16556188 . S2CID 21812226 .

Linki zewnętrzne

• Słownikowa definicja strumienia w Wikisłowniku