Mechanika klasyczna

Aby zapoznać się z podręcznikami, zobacz Mechanika klasyczna (Goldstein) i Mechanika klasyczna (Kibble i Berkshire) .

Schemat ruchu orbitalnego satelity wokół Ziemi, przedstawiający prostopadłe wektory prędkości i przyspieszenia (siły), przedstawiony w klasycznej interpretacji.

Mechanika klasyczna to teoria fizyczna opisująca ruch obiektów makroskopowych , od pocisków po części maszyn i obiektów astronomicznych , takich jak statki kosmiczne , planety , gwiazdy i galaktyki . W przypadku obiektów rządzących się mechaniką klasyczną, jeśli znany jest stan obecny, można przewidzieć, jak będą się one poruszać w przyszłości ( determinizm ) i jak poruszały się w przeszłości (odwracalność).

Najwcześniejsze sformułowanie mechaniki klasycznej jest często określane jako mechanika Newtona . Składa się z koncepcji fizycznych opartych na fundamentalnych pracach Sir Isaaca Newtona oraz metod matematycznych wymyślonych przez Gottfrieda Wilhelma Leibniza , Josepha-Louisa Lagrange'a , Leonharda Eulera i innych współczesnych w XVII wieku w celu opisania ruchu ciał pod wpływem siły . Później opracowano bardziej abstrakcyjne metody, co doprowadziło do przeformułowania mechaniki klasycznej, znanej jako mechanika Lagrange'a i mechanika Hamiltona . Postępy te, poczynione głównie w XVIII i XIX wieku, znacznie wykraczają poza wcześniejsze prace, zwłaszcza dzięki zastosowaniu w nich mechaniki analitycznej . Są one, z pewnymi modyfikacjami, używane również we wszystkich dziedzinach współczesnej fizyki.

Mechanika klasyczna dostarcza dokładnych wyników podczas badania dużych obiektów, które nie są ekstremalnie masywne i poruszają się z prędkością nie zbliżającą się do prędkości światła . Kiedy badane obiekty mają rozmiary zbliżone do średnicy atomu, konieczne staje się wprowadzenie drugiej głównej poddziedziny mechaniki : mechaniki kwantowej . Aby opisać prędkości, które nie są małe w porównaniu z prędkością światła, potrzebna jest szczególna teoria względności . W przypadkach, gdy obiekty stają się niezwykle masywne, zastosowanie ma ogólna teoria względności . Jednak wiele współczesnych źródeł obejmuje mechanikę relatywistyczną w fizyce klasycznej, która ich zdaniem reprezentuje mechanikę klasyczną w jej najbardziej rozwiniętej i dokładnej formie.

Opis teorii

Analiza ruchu pocisku jest częścią mechaniki klasycznej.

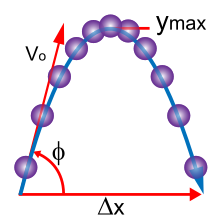
Poniżej przedstawiono podstawowe pojęcia mechaniki klasycznej. Dla uproszczenia często modeluje obiekty świata rzeczywistego jako cząstki punktowe (obiekty o znikomych rozmiarach). Ruch cząstki punktowej jest określony przez niewielką liczbę parametrów : jej położenie, masę i przyłożone do niej siły .

W rzeczywistości obiekty, które może opisać mechanika klasyczna, zawsze mają niezerowy rozmiar. (Zachowanie bardzo małych cząstek, takich jak elektron , jest dokładniej opisane przez mechanikę kwantową ). Obiekty o niezerowych rozmiarach mają bardziej skomplikowane zachowanie niż hipotetyczne cząstki punktowe, ze względu na dodatkowe stopnie swobody , np. puszka baseballowa . obracać się , gdy się porusza. Jednak wyniki dla cząstek punktowych można wykorzystać do badania takich obiektów, traktując je jako złożone , złożone z dużej liczby wspólnie działających cząstek punktowych. Środek masy obiektu złożonego zachowuje się jak cząstka punktowa.

Mechanika klasyczna wykorzystuje zdroworozsądkowe pojęcia dotyczące tego, jak materia i siły istnieją i oddziałują na siebie. Zakłada, że ​​materia i energia mają określone, poznawalne atrybuty, takie jak położenie w przestrzeni i prędkość. Mechanika nierelatywistyczna zakłada również, że siły działają natychmiast (patrz także Działanie na odległość ).

Pozycja i jej pochodne

Główny artykuł: Kinematyka

Jednostki „mechaniczne” ( to znaczy nie elektromagnetyczne ani termiczne ) pochodzące z układu SI z kg, m i s

pozycja	M
pozycja kątowa / kąt	bez jednostek (radian)
prędkość	m·s −1
prędkość kątowa	s -1
przyśpieszenie	m·s −2
przyspieszenie kątowe	s -2
szarpać	m·s −3
„kątowy skurcz”	s -3
specyficzna energia	m 2 ·s −2
moc dawki pochłoniętej	m 2 · s -3
moment bezwładności	kg·m 2
pęd	kg·m·s -1
moment pędu	kg·m 2 ·s -1
siła	kg·m·s −2
moment obrotowy	kg·m 2 ·s -2
energia	kg·m 2 ·s -2
moc	kg·m 2 ·s -3
ciśnienie i gęstość energii	kg·m −1 ·s −2
napięcie powierzchniowe	kg·s −2
stała sprężyny	kg·s −2
natężenie promieniowania i strumień energii	kg·s −3
lepkość kinematyczna	m 2 · s -1
lepkość dynamiczna	kg·m −1 ·s −1
gęstość (gęstość masy)	kg·m −3
ciężar właściwy (gęstość masy)	kg·m −2 ·s −2
gęstość liczb	m -3
działanie	kg·m 2 ·s -1

Położenie cząstki punktowej jest określone w odniesieniu do układu współrzędnych wyśrodkowanego w dowolnym ustalonym punkcie odniesienia w przestrzeni , zwanym początkiem O . Prosty układ współrzędnych mógłby opisać położenie cząstki P za pomocą wektora oznaczonego strzałką oznaczoną r , która wskazuje od początku O do punktu P . Ogólnie rzecz biorąc, cząstka punktowa nie musi być nieruchoma względem O . W przypadkach, gdy P porusza się względem O , r jest definiowane jako funkcja czasu t . W teorii względności sprzed Einsteina (znanej jako teoria względności Galileusza ) czas jest uważany za absolutny, tj. przedział czasu , jaki upływa między dowolną parą zdarzeń, jest taki sam dla wszystkich obserwatorów. Oprócz polegania na czasie absolutnym , mechanika klasyczna zakłada geometrię euklidesową dla struktury przestrzeni.

Szybkość i szybkość

Główne artykuły: Prędkość i prędkość

Prędkość , czyli szybkość zmiany przemieszczenia w czasie, definiuje się jako pochodną położenia względem czasu:

${\ Displaystyle \ mathbf {v} = {\ operatorname {d} \ mathbf {r} \ ponad \ operatorname {d} t} \, \!$ }

W mechanice klasycznej prędkości są bezpośrednio addytywne i odejmowane. Na przykład, jeśli jeden samochód jedzie na wschód z prędkością 60 km/h i wyprzedza inny samochód jadący w tym samym kierunku z prędkością 50 km/h, wolniejszy samochód postrzega szybszy samochód jako jadący na wschód z prędkością 60 − 50 = 10 km/ h . Jednak z perspektywy szybszego samochodu, wolniejszy samochód porusza się z prędkością 10 km/h na zachód, często oznaczaną jako -10 km/h, gdzie znak wskazuje kierunek przeciwny. Prędkości są bezpośrednio addytywne jako wielkości wektorowe ; należy się nimi zająć za pomocą analizy wektorowej .

Matematycznie, jeśli prędkość pierwszego obiektu w poprzednim omówieniu jest oznaczona przez wektor u = u d , a prędkość drugiego obiektu przez wektor v = v e , gdzie u jest prędkością pierwszego obiektu, v jest prędkość drugiego obiektu, a d i e są wektorami jednostkowymi odpowiednio w kierunkach ruchu każdego obiektu, to prędkość pierwszego obiektu widziana przez drugi obiekt wynosi:

${\ Displaystyle \ mathbf {u} '= \ mathbf {u} - \ mathbf {v} \,.}$

Podobnie, pierwszy obiekt widzi prędkość drugiego obiektu jako:

${\ Displaystyle \ mathbf {v '} = \ mathbf {v} - \ mathbf {u} \,.}$

Gdy oba obiekty poruszają się w tym samym kierunku, równanie to można uprościć do postaci:

${\ Displaystyle \ mathbf {u} '= (uv) \ mathbf {d} \,.}$

Lub, ignorując kierunek, różnicę można podać tylko pod względem prędkości:

${\ displaystyle u' = uv \,.}$

Przyśpieszenie

Główny artykuł: Przyspieszenie

Przyspieszenie , czyli szybkość zmiany prędkości, jest pochodną prędkości po czasie ( druga pochodna położenia po czasie):

${\ Displaystyle \ mathbf {a} = {\ operatorname {d} \ mathbf {v} \ nad \ operatorname {d} t} = {\ operatorname {d ^ {2}} \ mathbf {r} \ nad \ operatorname { d} t^{2}}.}$

Przyspieszenie reprezentuje zmianę prędkości w czasie. Prędkość może zmieniać się pod względem wielkości, kierunku lub obu. Czasami spadek wielkości prędkości „ v ” jest określany jako zwalnianie , ale ogólnie każda zmiana prędkości w czasie, w tym zwalnianie, jest określana jako przyspieszenie.

Ramy odniesienia

Główne artykuły: Inercjalny układ odniesienia i transformacja Galileusza

Podczas gdy położenie, prędkość i przyspieszenie cząstki można opisać w odniesieniu do dowolnego obserwatora w dowolnym stanie ruchu, mechanika klasyczna zakłada istnienie specjalnej rodziny układów odniesienia , w których mechaniczne prawa natury przyjmują stosunkowo prostą postać. Te specjalne układy odniesienia nazywane są układami inercjalnymi . Układ inercjalny to wyidealizowany układ odniesienia, w którym obiekt, na który działa zerowa siła wypadkowa, porusza się ze stałą prędkością; to znaczy jest albo w spoczynku, albo porusza się ruchem jednostajnym po linii prostej.

Kluczowym pojęciem układów inercjalnych jest sposób ich identyfikacji. Ze względów praktycznych układy odniesienia, które nie przyspieszają względem odległych gwiazd (skrajnie odległego punktu), są uważane za dobre przybliżenia układów inercjalnych. Nieinercjalne układy odniesienia przyspieszają względem istniejącego układu inercjalnego. Stanowią podstawę teorii względności Einsteina. Ze względu na ruch względny cząstki w układzie nieinercjalnym wydają się poruszać w sposób niewyjaśniony siłami z istniejących pól w układzie odniesienia. Wydaje się zatem, że istnieją inne siły, które wchodzą do równań ruchu wyłącznie w wyniku przyspieszenia względnego. Siły te nazywane są siłami fikcyjnymi , siłami bezwładności lub pseudosiłami.

Rozważmy dwa układy odniesienia S i S' . Dla obserwatorów w każdej z ramek odniesienia zdarzenie ma współrzędne czasoprzestrzenne ( x , y , z , t ) w klatce S i ( x' , y' , z' , t' ) w klatce S' . Zakładając, że czas jest mierzony tak samo we wszystkich układach odniesienia, jeśli wymagamy x = x', gdy t = 0 , to relacja między współrzędnymi czasoprzestrzennymi tego samego zdarzenia obserwowanego z układów odniesienia S' i S , które poruszają się z prędkość względna u w kierunku x wynosi:

${\ Displaystyle x '= x-ut \,}$

${\ Displaystyle y' = y \,}$

${\ Displaystyle z' = z \,}$

${\ displaystyle t '= t \,.}$

Ten zestaw formuł definiuje transformację grupową znaną jako transformacja Galileusza (nieformalnie transformacja Galileusza ). Ta grupa jest granicznym przypadkiem grupy Poincarégo używanej w szczególnej teorii względności . Przypadek graniczny ma zastosowanie, gdy prędkość u jest bardzo mała w porównaniu z c , czyli prędkością światła .

Transformacje mają następujące konsekwencje:

• v ′ = v − u (prędkość v ′ cząstki z perspektywy S ′ jest mniejsza o u niż jej prędkość v z perspektywy S )
• a ′ = a (przyspieszenie cząstki jest takie samo w każdym inercjalnym układzie odniesienia)
• F ′ = F (siła działająca na cząstkę jest taka sama w każdym bezwładnościowym układzie odniesienia)
• prędkość światła nie jest stałą w mechanice klasycznej, a szczególne miejsce, jakie przypisuje się prędkości światła w mechanice relatywistycznej, nie ma odpowiednika w mechanice klasycznej.

W przypadku niektórych problemów wygodnie jest użyć obracających się współrzędnych (układów odniesienia). W ten sposób można albo zachować odwzorowanie do wygodnego układu inercjalnego, albo wprowadzić dodatkowo fikcyjną siłę odśrodkową i siłę Coriolisa .

Siły i drugie prawo Newtona

Główne artykuły: Siła i prawa ruchu Newtona

Siła w fizyce to dowolne działanie, które powoduje zmianę prędkości obiektu; czyli przyspieszyć. Siła pochodzi z pola , takiego jak między innymi pole elektrostatyczne (spowodowane statycznymi ładunkami elektrycznymi), pole elektromagnetyczne (spowodowane przez poruszające się ładunki) lub pole grawitacyjne (spowodowane masą).

Newton jako pierwszy przedstawił matematycznie związek między siłą a pędem . Niektórzy fizycy interpretują drugą zasadę dynamiki Newtona jako definicję siły i masy, podczas gdy inni uważają ją za fundamentalny postulat, prawo natury. Każda interpretacja ma te same konsekwencje matematyczne, historycznie znane jako „drugie prawo Newtona”:

${\ Displaystyle \ mathbf {F} = {\ operatorname {d} \ mathbf {p} \ ponad \ operatorname {d} t} = {\ operatorname {d} (m \ mathbf {v}) \ ponad \ operatorname {d } T}.}$

Wielkość m v nazywana jest ( kanonicznym ) pędem . Siła wypadkowa działająca na cząstkę jest zatem równa szybkości zmiany pędu cząstki w czasie. Ponieważ definicja przyspieszenia to a = d v /d t , drugie prawo można zapisać w uproszczonej i bardziej znanej formie:

${\ Displaystyle \ mathbf {F} = m \ mathbf {a} \,.}$

Dopóki znana jest siła działająca na cząstkę, drugie prawo Newtona jest wystarczające do opisania ruchu cząstki. Gdy dostępne są niezależne relacje dla każdej siły działającej na cząstkę, można je podstawić do drugiego prawa Newtona, aby uzyskać zwykłe równanie różniczkowe , które nazywa się równaniem ruchu .

Jako przykład załóżmy, że jedyną siłą działającą na cząstkę jest tarcie i że można je modelować jako funkcję prędkości cząstki, na przykład:

${\ Displaystyle \ mathbf {F} _ {\ rm {R}} = - \ lambda \ mathbf {v} \,,}$

gdzie λ jest stałą dodatnią, znak ujemny oznacza, że ​​siła jest przeciwna do zwrotu prędkości. Wtedy równanie ruchu jest

${\ Displaystyle - \ lambda \ mathbf {v} = m \ mathbf {a} = m {\ operatorname {d} \ mathbf {v} \ ponad \ operatorname {d} t} \,.}$

Można to zintegrować , aby uzyskać

${\ Displaystyle \ mathbf {v} = \ mathbf {v} _ {0} e ^ {{- \ lambda t} / {m}}}$

₀ gdzie v jest prędkością początkową. Oznacza to, że prędkość tej cząstki maleje wykładniczo do zera w miarę upływu czasu. W tym przypadku równoważny punkt widzenia jest taki, że energia kinetyczna cząstki jest pochłaniana przez tarcie (które przekształca ją w energię cieplną zgodnie z zasadą zachowania energii ) , a cząstka zwalnia. Wyrażenie to można dalej scałkować, aby uzyskać pozycję r cząstki w funkcji czasu.

Do ważnych sił należą siła grawitacji i siła Lorentza dla elektromagnetyzmu . Ponadto trzecie prawo Newtona może być czasami wykorzystane do wydedukowania sił działających na cząstkę: jeśli wiadomo, że cząstka A wywiera siłę F na inną cząstkę B , wynika z tego, że B musi wywierać równą i przeciwną siłę reakcji , − F , na A. Silna postać trzeciego prawa Newtona wymaga, aby F i - F działały wzdłuż linii łączącej A i B , podczas gdy słaba forma nie. Często można znaleźć ilustracje słabej postaci trzeciego prawa Newtona dla sił magnetycznych.

Praca i energia

Główne artykuły: Praca (fizyka) , energia kinetyczna i energia potencjalna

do cząstki, która wykonuje przemieszczenie Δ r , przyłożona zostanie stała siła F , praca wykonana przez tę siłę jest zdefiniowana jako iloczyn skalarny wektorów siły i przemieszczenia:

${\ Displaystyle W = \ mathbf {F} \ cdot \ Delta \ mathbf {r} \,.}$

Mówiąc bardziej ogólnie, jeśli siła zmienia się w funkcji położenia, gdy cząstka porusza się od r ₁ do r ₂ wzdłuż toru C , praca wykonana nad cząstką jest określona przez całkę krzywoliniową

${\ Displaystyle W = \ int _ {C} \ mathbf {F} (\ mathbf {r}) \ cdot \ operatorname {d} \ mathbf {r} \,.}$

Jeśli praca wykonana podczas przemieszczania cząstki z r ₁ do r ₂ jest taka sama bez względu na wybraną ścieżkę, mówi się, że siła jest zachowawcza . Grawitacja jest siłą konserwatywną, podobnie jak siła wynikająca z wyidealizowanej sprężyny , zgodnie z prawem Hooke'a . Siła wywołana tarciem nie jest zachowawcza.

Energia kinetyczna E _k cząstki o masie m poruszającej się z prędkością v jest wyrażona wzorem

${\ Displaystyle E _ {\ operatorname {k}} = {\ tfrac {1} {2}} mv ^ {2} \,.}$

W przypadku rozciągłych obiektów złożonych z wielu cząstek energia kinetyczna ciała złożonego jest sumą energii kinetycznych cząstek.

pracy i energii mówi, że dla cząstki o stałej masie m całkowita praca W wykonana nad cząstką, gdy przemieszcza się ona z położenia r ₁ do r ₂ , jest równa zmianie energii kinetycznej E _k cząstki:

${\ Displaystyle W = \ Delta E _ {\ operatorname {k}} = E _ {\ operatorname {k_ {2}}} -E _ {\ operatorname {k_ {1}}} = {\ tfrac {1} {2}} m\lewo(v_{2}^{\,2}-v_{1}^{\,2}\prawo).}$

Siły zachowawcze można wyrazić jako gradient funkcji skalarnej, znanej jako energia potencjalna i oznaczanej jako E _p :

${\ Displaystyle \ mathbf {F} = - \ mathbf {\ nabla} E _ {\ operatorname {p}} \,.}$

Jeżeli wszystkie siły działające na cząstkę są zachowawcze, a Ep jest całkowitą energią potencjalną (którą definiuje się jako pracę zaangażowanych sił do przestawienia wzajemnych położeń ciał), otrzymaną przez zsumowanie energii potencjalnych odpowiadających każdej _sile

${\ Displaystyle \ mathbf {F} \ cdot \ Delta \ mathbf {r} = - \ mathbf {\ nabla} E _ {\ operatorname {p}} \ cdot \ Delta \ mathbf {r} = - \ Delta E_ {\ operatorname {P} }\,.}$

Spadek energii potencjalnej jest równy wzrostowi energii kinetycznej

${\ Displaystyle - \ Delta E _ {\ operatorname {p}} = \ Delta E _ {\ operatorname {k}} \ Strzałka w prawo \ Delta (E _ {\ operatorname {k}} + E _ {\ operatorname {p}}) = 0 \,.}$

Ten wynik jest znany jako zachowanie energii i stwierdza, że ​​całkowita energia ,

$\ Displaystyle \ suma E = E _ {\ operatorname {k}} + E _ {\ operatorname {p}} \,,}$

jest stała w czasie. Jest to często przydatne, ponieważ wiele powszechnie spotykanych sił ma charakter konserwatywny.

Poza prawami Newtona

Mechanika klasyczna opisuje również bardziej złożone ruchy rozciągniętych, niepunktowych obiektów. Prawa Eulera stanowią rozszerzenie praw Newtona w tej dziedzinie. Pojęcia momentu pędu opierają się na tym samym rachunku różniczkowym , który jest używany do opisu ruchu jednowymiarowego. Równanie rakiety rozszerza pojęcie szybkości zmiany pędu obiektu o skutki „utraty masy” przez obiekt. (Te uogólnienia/rozszerzenia wywodzą się z praw Newtona, powiedzmy, poprzez rozłożenie ciała stałego na zbiór punktów).

Istnieją dwa ważne alternatywne sformułowania mechaniki klasycznej: mechanika Lagrange'a i mechanika Hamiltona . Te i inne współczesne sformułowania zwykle pomijają pojęcie „siły”, zamiast tego odwołują się do innych wielkości fizycznych, takich jak energia, prędkość i pęd, do opisu układów mechanicznych we współrzędnych uogólnionych . Są to w zasadzie matematyczne przepisanie praw Newtona, ale skomplikowane problemy mechaniczne są znacznie łatwiejsze do rozwiązania w tych formach. Również analogia z mechaniką kwantową jest bardziej wyraźna w formalizmie hamiltonowskim.

Podane powyżej wyrażenia dotyczące pędu i energii kinetycznej są ważne tylko wtedy, gdy nie ma znaczącego wkładu elektromagnetycznego. W elektromagnetyzmie drugie prawo Newtona dotyczące przewodów przewodzących prąd załamuje się, chyba że uwzględni się wpływ pola elektromagnetycznego na pęd układu wyrażony wektorem Poyntinga podzielonym przez c ² , gdzie c jest prędkością światła w wolnej przestrzeni.

Granice ważności

Dziedzina ważności dla mechaniki klasycznej

Wiele gałęzi mechaniki klasycznej to uproszczenia lub przybliżenia dokładniejszych form; dwie z najdokładniejszych to ogólna teoria względności i relatywistyczna mechanika statystyczna . Optyka geometryczna jest przybliżeniem kwantowej teorii światła i nie ma nadrzędnej „klasycznej” formy.

Kiedy nie można zastosować zarówno mechaniki kwantowej, jak i mechaniki klasycznej, na przykład na poziomie kwantowym z wieloma stopniami swobody, przydatna jest kwantowa teoria pola (QFT). QFT zajmuje się małymi odległościami i dużymi prędkościami z wieloma stopniami swobody oraz możliwością dowolnej zmiany liczby cząstek w trakcie oddziaływania. Podczas traktowania dużych stopni swobody na poziomie makroskopowym przydatna staje się mechanika statystyczna . Mechanika statystyczna opisuje zachowanie dużej (ale policzalnej) liczby cząstek i ich interakcji jako całości na poziomie makroskopowym. Mechanika statystyczna jest stosowana głównie w termodynamice dla układów leżących poza granicami założeń termodynamiki klasycznej. W przypadku obiektów o dużych prędkościach , zbliżających się do prędkości światła, mechanikę klasyczną wspiera szczególna teoria względności . W przypadku, gdy obiekty stają się bardzo ciężkie (tj. ich promień Schwarzschilda nie jest pomijalnie mały dla danego zastosowania), odchylenia od mechaniki Newtona stają się widoczne i można je określić ilościowo za pomocą sparametryzowanego formalizmu postnewtonowskiego . W takim przypadku zastosowanie ma ogólna teoria względności (GR). Jednak do tej pory nie ma teorii grawitacji kwantowej łączącej GR i QFT w tym sensie, że można by ją wykorzystać, gdy obiekty stają się bardzo małe i ciężkie. ^{[4] [5]}

Newtonowskie przybliżenie do szczególnej teorii względności

W szczególnej teorii względności pęd cząstki wyraża się wzorem

${\ Displaystyle \ mathbf {p} = {\ Frac {m \ mathbf {v}}} {\ sqrt {1- {\ Frac {v ^ {2}}} {c ^ {2}}}}}}\,,}$

gdzie m to masa spoczynkowa cząstki, v jej prędkość, v to moduł v , a c to prędkość światła.

Jeśli v jest bardzo małe w porównaniu z c , v ² / c ² jest w przybliżeniu równe zeru i tak dalej

${\ Displaystyle \ mathbf {p} \ około m \ mathbf {v} \,.}$

Zatem równanie Newtona p = m v jest przybliżeniem równania relatywistycznego dla ciał poruszających się z małymi prędkościami w porównaniu z prędkością światła.

Na przykład relatywistyczna częstotliwość cyklotronu cyklotronu , żyrotronu lub magnetronu wysokiego napięcia jest określona wzorem

${\ Displaystyle f = f _ {\ operatorname {c}} {\ Frac {m_ {0}} {m_ {0} + {\ Frac {T} {c ^ {2 }}}}}\,,}$

₀ gdzie f _c jest klasyczną częstotliwością elektronu (lub innej naładowanej cząstki) o energii kinetycznej T i ( spoczynkowej ) masie m krążącej w polu magnetycznym. Masa (spoczynkowa) elektronu wynosi 511 keV. Tak więc poprawka częstotliwości wynosi 1% dla magnetycznej lampy próżniowej z napięciem przyspieszającym prądu stałego 5,11 kV.

Klasyczne przybliżenie mechaniki kwantowej

Przybliżenie promienia mechaniki klasycznej załamuje się, gdy długość fali de Broglie'a jest niewiele mniejsza niż inne wymiary układu. Dla cząstek nierelatywistycznych ta długość fali wynosi

${\ Displaystyle \ lambda = {\ Frac {h} {p}}}$

gdzie h to stała Plancka , a p to pęd.

Ponownie dzieje się tak z elektronami , zanim stanie się to z cięższymi cząstkami. Na przykład elektrony użyte przez Clintona Davissona i Lestera Germera w 1927 r., Przyspieszone o 54 V, miały długość fali 0,167 nm, która była wystarczająco długa, aby wykazywać pojedynczy płat boczny dyfrakcji podczas odbijania się od powierzchni kryształu niklu z odstępami atomowymi 0,215 nm. Przy większej komorze próżniowej stosunkowo łatwo byłoby zwiększyć rozdzielczość kątową z około radiana do miliradiana i zobaczyć dyfrakcję kwantową z okresowych wzorców pamięci komputera z układem scalonym .

Bardziej praktycznymi przykładami niepowodzeń mechaniki klasycznej w skali inżynierskiej jest przewodzenie przez tunelowanie kwantowe w diodach tunelowych i bardzo wąskie bramki tranzystorowe w układach scalonych .

Mechanika klasyczna jest tym samym przybliżeniem ekstremalnych wysokich częstotliwości , co optyka geometryczna . Częściej jest trafna, ponieważ opisuje cząstki i ciała z masą spoczynkową . Mają one większy pęd, a zatem krótsze długości fal De Broglie'a niż cząstki bezmasowe, takie jak światło, o tych samych energiach kinetycznych.

Historia

Osobny artykuł: Historia mechaniki klasycznej

Zobacz także: Kalendarium mechaniki klasycznej

Badanie ruchu ciał jest starożytne, co czyni mechanikę klasyczną jedną z najstarszych i największych dziedzin nauki , inżynierii i technologii .

Niektórzy starożytni filozofowie greccy , wśród nich Arystoteles , twórca fizyki Arystotelesa , mogli być pierwszymi, którzy podtrzymywali ideę, że „wszystko dzieje się z jakiegoś powodu” i że zasady teoretyczne mogą pomóc w zrozumieniu natury. Chociaż dla współczesnego czytelnika wiele z tych zachowanych idei wydaje się wybitnie rozsądnych, zauważalny jest brak zarówno teorii matematycznej , jak i kontrolowanego eksperymentu , jakie znamy. Stały się one później decydującymi czynnikami w kształtowaniu się współczesnej nauki, a ich wczesne zastosowanie stało się znane jako mechanika klasyczna. W swoim Elementa super demonstrationem ponderum , średniowieczny matematyk Jordanus de Nemore przedstawił koncepcję „ grawitacji pozycyjnej ” i użycia sił składowych .

Trójstopniowa teoria impetu według Alberta Saskiego .

Pierwszym opublikowanym przyczynowym wyjaśnieniem ruchu planet była Astronomia nova , opublikowana w 1609 roku. Na podstawie obserwacji Johannesa Keplera Tycho Brahe na orbicie Marsa doszedł do wniosku, że orbity planety są elipsami . To zerwanie ze starożytną myślą miało miejsce mniej więcej w tym samym czasie, gdy Galileusz proponował abstrakcyjne matematyczne prawa ruchu obiektów. Mógł (lub nie) przeprowadzić słynny eksperyment polegający na zrzuceniu dwóch kul armatnich o różnej masie z wieży w Pizie , pokazując, że obie spadły na ziemię w tym samym czasie. Rzeczywistość tego konkretnego eksperymentu jest kwestionowana, ale przeprowadził eksperymenty ilościowe, tocząc piłki po pochyłej płaszczyźnie . Jego teoria ruchu przyspieszonego wywodzi się z wyników takich eksperymentów i stanowi kamień węgielny mechaniki klasycznej. W 1673 roku Christiaan Huygens opisał w swoim Horologium Oscillatorium pierwsze dwa prawa ruchu . Praca jest również pierwszym współczesnym traktatem, w którym problem fizyczny (przyspieszony ruch spadającego ciała) jest idealizowany przez zestaw parametrów, a następnie analizowany matematycznie i stanowi jedno z przełomowych dzieł matematyki stosowanej .

Sir Isaac Newton (1643–1727), wpływowa postać w historii fizyki, którego trzy prawa ruchu stanowią podstawę mechaniki klasycznej

Newton oparł swoje zasady filozofii przyrody na trzech proponowanych prawach ruchu : prawie bezwładności , swoim drugim prawie przyspieszenia (wspomnianym powyżej) oraz prawie akcji i reakcji ; i tym samym położył podwaliny pod mechanikę klasyczną. Zarówno drugie, jak i trzecie prawo Newtona zostały odpowiednio potraktowane naukowo i matematycznie w Newton's Philosophiæ Naturalis Principia Mathematica . Tutaj różnią się one od wcześniejszych prób wyjaśnienia podobnych zjawisk, które były albo niepełne, niepoprawne, albo miały mało dokładnego wyrażenia matematycznego. Newton sformułował również zasady zachowania pędu i momentu pędu . W mechanice Newton był również pierwszym, który dostarczył pierwszego poprawnego naukowego i matematycznego sformułowania grawitacji w prawie powszechnego ciążenia Newtona . Połączenie praw ruchu i grawitacji Newtona zapewnia najpełniejszy i najdokładniejszy opis mechaniki klasycznej. Wykazał, że prawa te mają zastosowanie zarówno do przedmiotów codziennego użytku, jak i ciał niebieskich. W szczególności uzyskał teoretyczne wyjaśnienie ruchu planet Keplera .

Newton wcześniej wynalazł rachunek matematyczny i używał go do wykonywania obliczeń matematycznych. Aby uzyskać akceptację, jego książka, Principia , została sformułowana całkowicie w kategoriach ustalonych od dawna metod geometrycznych, które wkrótce zostały przyćmione przez jego rachunek różniczkowy. Jednak to Leibniz opracował preferowany dziś zapis pochodnej i całki . Newton i większość jemu współczesnych, z godnym uwagi wyjątkiem Huygensa , pracowali przy założeniu, że mechanika klasyczna będzie w stanie wyjaśnić wszystkie zjawiska, w tym światło , w postaci optyki geometrycznej . Nawet odkrywając tzw. pierścienie Newtona ( zjawisko interferencji fal ) utrzymywał własną korpuskularną teorię światła .

Lagrange'a było urzeczywistnienie idei Newtona w języku współczesnej matematyki, zwanej obecnie mechaniką Lagrange'a .

Po Newtonie mechanika klasyczna stała się głównym kierunkiem studiów w matematyce i fizyce. Sformułowania matematyczne stopniowo pozwoliły znaleźć rozwiązania znacznie większej liczby problemów. Pierwszy znaczący zabieg matematyczny został przeprowadzony w 1788 roku przez Josepha Louisa Lagrange'a . Z kolei mechanika Lagrange'a została ponownie sformułowana w 1833 roku przez Williama Rowana Hamiltona .

Hamiltona jest prawdopodobnie przeformułowanie mechaniki Lagrange'a , obecnie nazywanej mechaniką Hamiltona , stanowiącej preferowany wybór wielu wybitnych sformułowań fizyki matematycznej.

Pod koniec XIX wieku odkryto pewne trudności, które można było rozwiązać jedynie dzięki bardziej nowoczesnej fizyce. Niektóre z tych trudności dotyczyły zgodności z teorią elektromagnetyczną i słynnym eksperymentem Michelsona-Morleya . Rozwiązanie tych problemów doprowadziło do powstania szczególnej teorii względności , często nadal uważanej za część mechaniki klasycznej.

Drugi zestaw trudności dotyczył termodynamiki. W połączeniu z termodynamiką mechanika klasyczna prowadzi do paradoksu Gibbsa klasycznej mechaniki statystycznej , w którym entropia nie jest wielkością dobrze zdefiniowaną. Promieniowania ciała doskonale czarnego nie wyjaśniono bez wprowadzenia kwantów . Kiedy eksperymenty osiągnęły poziom atomowy, mechanika klasyczna nie potrafiła wyjaśnić, nawet w przybliżeniu, tak podstawowych rzeczy, jak poziomy energetyczne i rozmiary atomów oraz efekt fotoelektryczny . Wysiłek zmierzający do rozwiązania tych problemów doprowadził do rozwoju mechaniki kwantowej .

Od końca XX wieku mechanika klasyczna w fizyce nie jest już niezależną teorią. Zamiast tego mechanika klasyczna jest obecnie uważana za teorię przybliżoną do bardziej ogólnej mechaniki kwantowej. Nacisk przesunął się na zrozumienie podstawowych sił natury, jak w modelu standardowym i jego bardziej nowoczesnych rozszerzeniach w ujednoliconą teorię wszystkiego . Mechanika klasyczna jest teorią przydatną do badania ruchu niekwantowych cząstek mechanicznych, niskoenergetycznych w słabych polach grawitacyjnych. Została również rozszerzona na złożoną dziedzinę , w której złożona mechanika klasyczna wykazuje zachowania bardzo podobne do mechaniki kwantowej.

Gałęzie

Mechanika klasyczna była tradycyjnie podzielona na trzy główne gałęzie:

• Statyka , nauka o równowadze i jej związku z siłami
• Dynamika , nauka o ruchu i jego związku z siłami
• Kinematyka , zajmująca się implikacjami obserwowanych ruchów bez względu na okoliczności, które je powodują

Kolejny podział opiera się na wyborze formalizmu matematycznego:

• Mechanika Newtona
• Mechanika Lagrange'a
• mechanika Hamiltona

Alternatywnie można dokonać podziału według regionu zastosowania:

• Mechanika nieba , odnosząca się do gwiazd , planet i innych ciał niebieskich
• Mechanika ośrodków ciągłych , dla materiałów modelowanych jako kontinuum, np. ciał stałych i płynów (tj. cieczy i gazów ).
• Mechanika relatywistyczna (tj. obejmująca szczególną i ogólną teorię względności) dla ciał, których prędkość jest bliska prędkości światła.
• Mechanika statystyczna , która zapewnia ramy do powiązania mikroskopowych właściwości poszczególnych atomów i cząsteczek z makroskopowymi lub masowymi właściwościami termodynamicznymi materiałów.

Zobacz też

• Układ dynamiczny
• Historia mechaniki klasycznej
• Lista równań w mechanice klasycznej
• Wykaz publikacji z mechaniki klasycznej
• Wykaz podręczników mechaniki klasycznej i mechaniki kwantowej
• Dynamika molekularna
• Prawa ruchu Newtona
• Szczególna teoria względności
• Mechanika kwantowa
• Kwantowa teoria pola

Dalsza lektura

• Alonso, M.; Finn, J. (1992). Podstawowa fizyka uniwersytecka . Addison-Wesley.
•   Feynman, Richard (1999). Wykłady Feynmana z fizyki . Wydawnictwo Perseusz. ISBN 978-0-7382-0092-7 .
•   Feynman, Richard; Phillips, Richard (1998). Sześć łatwych utworów . Wydawnictwo Perseusz. ISBN 978-0-201-32841-7 .
•   Goldstein, Herbert ; Charles P. Poole; John L. Safko (2002). Mechanika klasyczna (wyd. 3). Addisona Wesleya. ISBN 978-0-201-65702-9 .
•   Kibble, Tom WB ; Berkshire, Frank H. (2004). Mechanika klasyczna (wyd. 5) . Imperial College Press . ISBN 978-1-86094-424-6 .
•   Kleppner D.; Kolenkow, RJ (1973). Wprowadzenie do mechaniki . McGraw-Hill. ISBN 978-0-07-035048-9 .
•   Landau, LD; Lifszyc, EM (1972). Kurs fizyki teoretycznej, tom. 1 – Mechanika . Firma Księgowa Franklin. ISBN 978-0-08-016739-8 .
•   Morin, Dawid (2008). Wprowadzenie do mechaniki klasycznej: z problemami i rozwiązaniami (wyd. 1). Cambridge: Cambridge University Press. ISBN 978-0-521-87622-3 .
•   Geralda Jaya Sussmana ; Jack Mądrość (2001). Struktura i interpretacja mechaniki klasycznej . MIT Press. ISBN 978-0-262-19455-6 .
•   O'Donnell, Peter J. (2015). Podstawowa dynamika i teoria względności . Prasa CRC. ISBN 978-1-4665-8839-4 .
•   Thornton, Stephen T.; Marion, Jerry B. (2003). Klasyczna dynamika cząstek i układów (wyd. 5) . Brooksa Cole'a. ISBN 978-0-534-40896-1 .

Linki zewnętrzne

• Crowell, Benjamin. Light and Matter (tekst wprowadzający, wykorzystuje algebrę z opcjonalnymi sekcjami dotyczącymi rachunku różniczkowego)
• Fitzpatrick, Ryszard. Mechanika klasyczna (wykorzystuje rachunek różniczkowy)
• Hoiland, Paweł (2004). Preferowane układy odniesienia i teoria względności
• Horbatsch, Marko, „ Notatki z kursu mechaniki klasycznej ”.
• Rosu, Haret C., „ Mechanika klasyczna ”. Edukacja fizyczna. 1999. [arxiv.org: fizyka/9909035]
• Shapiro, Joel A. (2003). Mechanika klasyczna
• Sussman, Gerald Jay & Wisdom, Jack & Mayer, Meinhard E. (2001). Struktura i interpretacja mechaniki klasycznej
• Ton, Dawid. Dynamika klasyczna (notatki z wykładów w Cambridge na temat formalizmu lagranżowskiego i hamiltonowskiego)
• 
  Kinematic Models for Design Digital Library (KMODDL) Filmy i zdjęcia setek działających modeli systemów mechanicznych na Cornell University . Zawiera również bibliotekę e-booków z klasycznymi tekstami na temat projektowania mechanicznego i inżynierii.
• MIT OpenCourseWare 8.01: Classical Mechanics Darmowe filmy z wykładami z rzeczywistych kursów z linkami do notatek z wykładów, zadań i egzaminów.
• Alejandro A. Torassa, O mechanice klasycznej