Tunelowanie kwantowe

W fizyce tunelowanie kwantowe ( tunelowanie kwantowe w języku angielskim amerykańskim ), penetracja bariery lub po prostu tunelowanie to zjawisko mechaniki kwantowej , w którym obiekt, taki jak elektron lub atom, przechodzi przez barierę energii potencjalnej , którą zgodnie z mechaniką klasyczną obiekt robi nie mają wystarczającej energii, aby wejść lub pokonać.

Tunelowanie jest konsekwencją falowej natury materii , gdzie kwantowa funkcja falowa opisuje stan cząstki lub innego układu fizycznego , a równania falowe, takie jak równanie Schrödingera, opisują ich zachowanie. Prawdopodobieństwo przeniesienia pakietu fal przez barierę maleje wykładniczo wraz z wysokością bariery, szerokością bariery i masą tunelującej cząstki, więc tunelowanie jest najbardziej widoczne w cząstkach o małej masie, takich jak elektrony lub protony tunelowanie przez mikroskopijnie wąskie bariery. Tunelowanie jest łatwo wykrywalne przy barierach o grubości około 1–3 nm lub mniejszej dla elektronów i około 0,1 nm lub mniejszej dla cięższych cząstek, takich jak protony lub atomy wodoru. Niektóre źródła opisują samo przenikanie funkcji falowej do bariery, bez transmisji po drugiej stronie, jako efekt tunelowania.

Tunelowanie odgrywa zasadniczą rolę w zjawiskach fizycznych, takich jak synteza jądrowa i rozpad promieniotwórczy alfa jąder atomowych. Zastosowania tunelowania obejmują diodę tunelową , obliczenia kwantowe , pamięć flash i skaningowy mikroskop tunelowy . Tunelowanie ogranicza minimalny rozmiar urządzeń stosowanych w mikroelektronice , ponieważ elektrony łatwo tunelują przez warstwy izolacyjne i tranzystory , które są cieńsze niż około 1 nm.

Efekt przewidywano na początku XX wieku. Jego akceptacja jako ogólnego zjawiska fizycznego nastąpiła w połowie wieku.

Historia

Tunelowanie kwantowe zostało opracowane na podstawie badań radioaktywności, które zostały odkryte w 1896 roku przez Henri Becquerela . Radioaktywność była dalej badana przez Marie Curie i Piotra Curie , za co otrzymali Nagrodę Nobla w dziedzinie fizyki w 1903 roku. Ernest Rutherford i Egon Schweidler badali jej naturę, co zostało później zweryfikowane empirycznie przez Friedricha Kohlrauscha . Idea półtrwania i możliwość przewidywania rozpadu zrodziła się z ich pracy.

W 1901 roku Robert Francis Earhart odkrył nieoczekiwany reżim przewodzenia, badając przewodzenie gazów między blisko rozmieszczonymi elektrodami za pomocą interferometru Michelsona . JJ Thomson skomentował, że odkrycie uzasadnia dalsze dochodzenie. W 1911, a następnie w 1914 roku ówczesny doktorant Franz Rother bezpośrednio zmierzył prądy emisji pola stałego. Zastosował metodę Earharta do kontrolowania i pomiaru separacji elektrod, ale z czułym galwanometrem platformowym . W 1926 r. Rother zmierzył prądy emisji polowej w „twardej” próżni między blisko rozmieszczonymi elektrodami .

Tunelowanie kwantowe zostało po raz pierwszy zauważone w 1927 roku przez Friedricha Hunda , gdy obliczał stan podstawowy potencjału podwójnej studni . Leonid Mandelstam i Michaił Leontowicz odkryli go niezależnie w tym samym roku. Analizowali implikacje nowego wówczas równania falowego Schrödingera .

Jego pierwszym zastosowaniem było matematyczne wyjaśnienie rozpadu alfa , które zostało opracowane w 1928 roku przez George'a Gamowa (który był świadomy odkryć Mandelstama i Leontovicha) oraz niezależnie przez Ronalda Gurneya i Edwarda Condona . Ci ostatni badacze jednocześnie rozwiązali równanie Schrödingera dla modelowego potencjału jądrowego i wyprowadzili zależność między okresem półtrwania cząstki a energią emisji, która zależała bezpośrednio od matematycznego prawdopodobieństwa tunelowania.

Po wzięciu udziału w seminarium Gamowa, Max Born rozpoznał powszechność tunelowania. Zdał sobie sprawę, że nie ogranicza się to do fizyki jądrowej , ale jest ogólnym wynikiem mechaniki kwantowej , która ma zastosowanie do wielu różnych systemów. Wkrótce potem obie grupy rozważały przypadek tunelowania cząstek do jądra. Badania półprzewodników oraz rozwój tranzystorów i diod doprowadziły do ​​zaakceptowania tunelowania elektronów w ciałach stałych w 1957 roku. Leo Esaki , Ivar Giaever i Brian Josephson przewidział tunelowanie nadprzewodzących par Coopera , za co otrzymali Nagrodę Nobla w dziedzinie fizyki w 1973 roku. W 2016 roku odkryto kwantowe tunelowanie wody .

Wprowadzenie do koncepcji

Animacja przedstawiająca efekt tunelu i jego zastosowanie w STM

Tunelowanie kwantowe należy do dziedziny mechaniki kwantowej : badania tego, co dzieje się w skali kwantowej . Tunelowanie nie może być bezpośrednio postrzegane. Znaczna część jego zrozumienia jest kształtowana przez mikroskopijny świat, którego mechanika klasyczna nie potrafi wyjaśnić. Aby zrozumieć to zjawisko , cząstki próbujące pokonać barierę potencjału można porównać do piłki próbującej przetoczyć się po zboczu.

Mechanika kwantowa i mechanika klasyczna różnią się podejściem do tego scenariusza. Mechanika klasyczna przewiduje, że cząstki, które nie mają wystarczającej energii, aby w klasyczny sposób pokonać barierę, nie mogą przedostać się na drugą stronę. W ten sposób piłka bez wystarczającej energii do pokonania wzgórza stoczyłaby się z powrotem. Piłka, której brakuje energii na przebicie ściany, odbija się. Alternatywnie, piłka może stać się częścią ściany (wchłanianie).

W mechanice kwantowej cząstki te mogą z niewielkim prawdopodobieństwem tunelować na drugą stronę, przekraczając w ten sposób barierę. Piłka w pewnym sensie pożycza energię z otoczenia, aby przejść przez ścianę. Następnie zwraca energię, czyniąc odbite elektrony bardziej energetycznymi, niż byłyby w innym przypadku.

Przyczyna tej różnicy wynika z traktowania materii jako posiadającej właściwości fal i cząstek . Jedna z interpretacji tej dwoistości dotyczy zasady nieoznaczoności Heisenberga , która określa granicę tego, jak dokładnie położenie i pęd cząstki można jednocześnie poznać. Oznacza to, że żadne rozwiązanie nie ma prawdopodobieństwa równego dokładnie zero (lub jeden), chociaż może zbliżać się do nieskończoności. Gdyby na przykład obliczenie jego położenia przyjęto jako prawdopodobieństwo 1, jego prędkość musiałaby wynosić nieskończoność (niemożliwość). Stąd prawdopodobieństwo istnienia danej cząstki po przeciwnej stronie pośredniej bariery jest niezerowe, a takie cząstki pojawią się po „drugiej” (słowo semantycznie w tym przypadku trudne) proporcjonalnie do tego prawdopodobieństwa.

Problem z tunelowaniem

Symulacja zdarzenia pakietu falowego na barierze potencjału. W jednostkach względnych energia bariery wynosi 20, czyli jest większa niż średnia energia pakietu fal wynosząca 14. Część pakietu fal przechodzi przez barierę.

Pakiet fal elektronowych skierowany na barierę potencjału. Słaba plama po prawej to część funkcji falowej, która przeszła przez barierę.

Funkcja falowa fizycznego układu cząstek określa wszystko, co można wiedzieć o układzie. Dlatego problemy mechaniki kwantowej analizują funkcję falową systemu. Korzystając ze sformułowań matematycznych, takich jak równanie Schrödingera , można wywnioskować ewolucję znanej funkcji falowej w czasie. Kwadrat wartości bezwzględnej tej funkcji falowej jest bezpośrednio związany z rozkładem prawdopodobieństwa położeń cząstek, który opisuje prawdopodobieństwo, że cząstki znajdują się w danych miejscach.

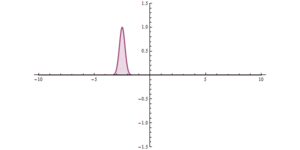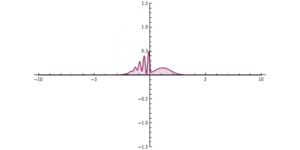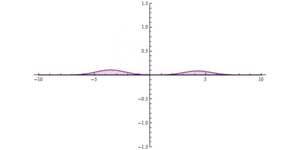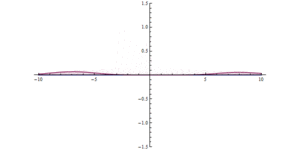
Na obu ilustracjach, gdy pojedynczy pakiet fal uderza w barierę, większość z nich jest odbijana, a część jest przepuszczana przez barierę. Pakiet fal staje się bardziej zdelokalizowany: znajduje się teraz po obu stronach bariery i ma niższą maksymalną amplitudę, ale ma taką samą zintegrowaną wielkość kwadratową, co oznacza, że ​​prawdopodobieństwo, że cząstka gdzieś się znajduje, pozostaje jednością . Im szersza bariera i im wyższa energia bariery, tym mniejsze prawdopodobieństwo tunelowania.

Niektóre modele barier tunelowych, takie jak pokazane bariery prostokątne , można analizować i rozwiązywać algebraicznie. Większość problemów nie ma rozwiązania algebraicznego, dlatego stosuje się rozwiązania numeryczne. „ Metody półklasyczne ” oferują przybliżone rozwiązania, które są łatwiejsze do obliczenia, takie jak przybliżenie WKB .

Tunelowanie dynamiczne

Kwantowe oscylacje tunelowe prawdopodobieństwa w całkowalnej podwójnej studni potencjału, widoczne w przestrzeni fazowej.

Koncepcję tunelowania kwantowego można rozszerzyć na sytuacje, w których istnieje transport kwantowy między regionami, które nie są klasycznie połączone, nawet jeśli nie ma związanej z nimi bariery potencjału. Zjawisko to znane jest jako tunelowanie dynamiczne.

Tunelowanie w przestrzeni fazowej

Koncepcja tunelowania dynamicznego jest szczególnie odpowiednia do rozwiązania problemu tunelowania kwantowego w dużych wymiarach (d>1). W przypadku układu całkowalnego , w którym ograniczone trajektorie klasyczne są ograniczone do torusa w przestrzeni fazowej , tunelowanie można rozumieć jako transport kwantowy między stanami półklasycznymi zbudowanymi na dwóch odrębnych, ale symetrycznych torusach.

Tunelowanie wspomagane chaosem

Wspomagane chaosem oscylacje tunelowe między dwoma regularnymi tori osadzonymi w chaotycznym morzu, widziane w przestrzeni fazowej

W prawdziwym życiu większość systemów nie jest integrowalna i wykazuje różne stopnie chaosu. Mówi się wtedy, że klasyczna dynamika jest mieszana, a przestrzeń fazowa systemu składa się zazwyczaj z wysp o regularnych orbitach otoczonych dużym morzem chaotycznych orbit. Istnienie chaotycznego morza, w którym transport jest klasycznie dozwolony, między dwoma symetrycznymi torusami, wspomaga następnie kwantowe tunelowanie między nimi. Zjawisko to nazywane jest tunelowaniem wspomaganym chaosem. i charakteryzuje się ostrymi rezonansami szybkości tunelowania przy zmianie dowolnego parametru systemu.

Tunelowanie wspomagane rezonansem

Kiedy jest $.$ w stosunku do rozmiarów regularnych wysp, drobna struktura klasycznej przestrzeni fazowej odgrywa kluczową rolę w tunelowaniu W szczególności dwa symetryczne torusy są połączone „poprzez szereg klasycznie zabronionych przejść przez nieliniowe rezonanse” otaczające dwie wyspy.

Powiązane zjawiska

Kilka zjawisk ma takie samo zachowanie jak tunelowanie kwantowe i można je dokładnie opisać za pomocą tunelowania. Przykłady obejmują tunelowanie klasycznej asocjacji fala-cząstka, zanikające sprzężenie fal (zastosowanie równania fali Maxwella do światła ) oraz zastosowanie niedyspersyjnego równania fali z akustyki zastosowane do „fal na strunach” . Sprzężenie fal zanikających do niedawna było nazywane tylko „tunelowaniem” w mechanice kwantowej; teraz jest używany w innych kontekstach.

Efekty te są modelowane podobnie do prostokątnej bariery potencjału . W takich przypadkach jedno medium transmisyjne , przez które rozchodzi się fala , jest takie samo lub prawie takie samo przez cały czas, a drugie medium, przez które fala rozchodzi się inaczej. Można to opisać jako cienki obszar ośrodka B między dwoma obszarami ośrodka A. Analiza prostokątnej bariery za pomocą równania Schrödingera może być dostosowana do tych innych efektów, pod warunkiem, że równanie falowe ma rozwiązania fali biegnącej w ośrodku A, ale prawdziwy wykładniczy rozwiązania w medium B.

W optyce ośrodek A to próżnia, a ośrodek B to szkło. W akustyce ośrodek A może być cieczą lub gazem, a ośrodek B ciałem stałym. całkowita energia cząstki jest większa niż jej energia potencjalna , a ośrodek B stanowi barierę potencjału. Mają one nadchodzącą falę i wynikowe fale w obu kierunkach. Może być więcej mediów i barier, a bariery nie muszą być dyskretne. Przybliżenia są w tym przypadku przydatne.

Aplikacje

Tunelowanie jest przyczyną niektórych ważnych makroskopowych zjawisk fizycznych. Tunelowanie kwantowe ma istotne implikacje dla funkcjonowania nanotechnologii .

Elektronika

Tunelowanie jest źródłem upływu prądu w elektronice integracji na bardzo dużą skalę (VLSI) i powoduje znaczny pobór mocy i efekty cieplne, które są plagą takich urządzeń. Uważa się, że jest to dolna granica, w jaki sposób można wykonać elementy urządzeń mikroelektronicznych. Tunelowanie jest podstawową techniką używaną do programowania pływających bramek pamięci flash .

Zimna emisja

Główny artykuł: Urządzenia półprzewodnikowe

Zimna emisja elektronów ma znaczenie dla fizyki półprzewodników i nadprzewodników . Jest to podobne do emisji termojonowej , w której elektrony losowo wyskakują z powierzchni metalu, podążając za polaryzacją napięcia, ponieważ statystycznie mają więcej energii niż bariera, w wyniku losowych zderzeń z innymi cząstkami. Kiedy pole elektryczne jest bardzo duże, bariera staje się wystarczająco cienka, aby elektrony mogły wydostać się ze stanu atomowego, prowadząc do prądu, który zmienia się w przybliżeniu wykładniczo wraz z polem elektrycznym. Te materiały są ważne dla pamięć flash , lampy próżniowe, a także niektóre mikroskopy elektronowe.

Węzeł tunelowy

Główny artykuł: skrzyżowanie tuneli

Prostą barierę można stworzyć oddzielając dwa przewody bardzo cienkim izolatorem . Są to skrzyżowania tuneli, których badanie wymaga zrozumienia tunelowania kwantowego. Złącza Josephsona wykorzystują tunelowanie kwantowe i nadprzewodnictwo do stworzenia efektu Josephsona . Ma to zastosowanie w precyzyjnych pomiarach napięć i pól magnetycznych , a także w wielozłączowych ogniwach słonecznych .

Automaty komórkowe z kropkami kwantowymi

QCA to technologia molekularnej syntezy binarnej, która działa w systemie tunelowania elektronów między wyspami. Jest to urządzenie o bardzo małej mocy i szybkości, które może pracować z maksymalną częstotliwością 15 Phz .

Dioda tunelowa

Główny artykuł: dioda tunelowa

Mechanizm działania rezonansowego urządzenia z diodą tunelującą , oparty na zjawisku tunelowania kwantowego przez bariery potencjału.

Diody to elektryczne urządzenia półprzewodnikowe , które umożliwiają przepływ prądu elektrycznego w jednym kierunku bardziej niż w drugim. Urządzenie zależy od warstwy zubożonej między półprzewodnikami typu N i typu P, aby spełniać swoje zadanie. Gdy są one silnie domieszkowane, warstwa zubożona może być wystarczająco cienka do tunelowania. Po zastosowaniu niewielkiego przesunięcia do przodu prąd wynikający z tunelowania jest znaczny. Ma to maksimum w punkcie, w którym odchylenie napięcia jest takie, że poziom energii pasm przewodnictwa p i n są takie same. Wraz ze wzrostem polaryzacji napięcia dwa pasma przewodzenia nie są już wyrównane, a dioda działa normalnie.

Ponieważ prąd tunelowania szybko spada, można stworzyć diody tunelowe, które mają zakres napięć, dla których prąd maleje wraz ze wzrostem napięcia. Ta szczególna właściwość jest wykorzystywana w niektórych zastosowaniach, takich jak urządzenia o dużej prędkości, w których charakterystyczne prawdopodobieństwo tunelowania zmienia się tak szybko, jak napięcie polaryzacji.

Rezonansowa dioda tunelowa wykorzystuje tunelowanie kwantowe w zupełnie inny sposób, aby osiągnąć podobny wynik. Ta dioda ma napięcie rezonansowe, dla którego duży prąd faworyzuje określone napięcie, osiągnięte przez umieszczenie blisko siebie dwóch cienkich warstw z pasmem o wysokiej przewodności energetycznej. potencjału kwantowego, która ma dyskretny najniższy poziom energii . Kiedy ten poziom energii jest wyższy niż poziom energii elektronów, tunelowanie nie występuje, a dioda jest spolaryzowana zaporowo. Po wyrównaniu dwóch energii napięcia elektrony płyną jak otwarty drut. W miarę dalszego wzrostu napięcia tunelowanie staje się nieprawdopodobne, a dioda znów zachowuje się jak normalna dioda, zanim drugi poziom energii stanie się zauważalny.

Tunelowe tranzystory polowe

Główny artykuł: tunelowy tranzystor polowy

W ramach europejskiego projektu badawczego zademonstrowano tranzystory polowe , w których bramka (kanał) jest sterowana za pomocą tunelowania kwantowego, a nie wtrysku termicznego, zmniejszając napięcie bramki z ≈1 wolta do 0,2 wolta i zmniejszając zużycie energii nawet o 100 razy. Gdyby te tranzystory można było przeskalować do układów scalonych VLSI , poprawiłyby one wydajność w przeliczeniu na moc układów scalonych .

Fuzja nuklearna

Główny artykuł: Fuzja jądrowa

Tunelowanie kwantowe jest kluczowym zjawiskiem dla syntezy jądrowej. Temperatura w jądrach gwiazd jest na ogół niewystarczająca, aby jądra atomowe mogły pokonać barierę kulombowską i osiągnąć syntezę termojądrową . Tunelowanie kwantowe zwiększa prawdopodobieństwo przebicia tej bariery. Chociaż prawdopodobieństwo to jest nadal niskie, niezwykle duża liczba jąder w jądrze gwiazdy wystarcza do podtrzymania stabilnej reakcji syntezy jądrowej.

Rozpad promieniotwórczy

Główny artykuł: rozpad promieniotwórczy

Rozpad promieniotwórczy to proces emisji cząstek i energii z niestabilnego jądra atomu w celu utworzenia stabilnego produktu. Odbywa się to poprzez tunelowanie cząstki z jądra (elektron tunelujący do jądra to wychwytywanie elektronów ). Było to pierwsze zastosowanie tunelowania kwantowego. Rozpad radioaktywny jest istotnym zagadnieniem dla astrobiologii , ponieważ ta konsekwencja tunelowania kwantowego tworzy stałe źródło energii w dużym przedziale czasu dla środowisk poza ekosferą okołogwiazdową , gdzie nasłonecznienie nie byłoby możliwe ( oceany podpowierzchniowe ) lub skuteczne.

Tunelowanie kwantowe może być jednym z mechanizmów hipotetycznego rozpadu protonu .

Astrochemia w obłokach międzygwiazdowych

Uwzględniając tunelowanie kwantowe, można wyjaśnić astrochemiczne syntezy różnych cząsteczek w obłokach międzygwiazdowych , takie jak synteza wodoru cząsteczkowego , wody ( lód ) i ważnego prebiotyku formaldehydu . W laboratorium zaobserwowano tunelowanie wodoru cząsteczkowego.

Biologia kwantowa

Tunelowanie kwantowe należy do głównych nietrywialnych efektów kwantowych w biologii kwantowej . Tutaj ważne jest zarówno tunelowanie elektronów, jak i tunelowanie protonów . Tunelowanie elektronów jest kluczowym czynnikiem w wielu biochemicznych reakcjach redoks ( fotosynteza , oddychanie komórkowe ) oraz katalizie enzymatycznej. Tunelowanie protonów jest kluczowym czynnikiem spontanicznej DNA .

Spontaniczna mutacja występuje, gdy normalna replikacja DNA ma miejsce po tunelowaniu szczególnie znaczącego protonu. Wiązanie wodorowe łączy pary zasad DNA. Potencjał podwójnej studni wzdłuż wiązania wodorowego oddziela potencjalną barierę energetyczną. Uważa się, że potencjał podwójnej studni jest asymetryczny, z jedną studnią głębszą od drugiej, tak że proton normalnie spoczywa w głębszej studni. Aby nastąpiła mutacja, proton musiał tunelować do płytszej studni. Ruch protonu z jego normalnej pozycji nazywa się przejściem tautomerycznym . Jeśli replikacja DNA ma miejsce w tym stanie, reguła parowania zasad DNA może być zagrożona, powodując mutację. Per-Olov Lowdin jako pierwszy rozwinął teorię spontanicznej mutacji w obrębie podwójnej helisy . Uważa się, że inne przypadki mutacji wywołanych tunelowaniem kwantowym w biologii są przyczyną starzenia się i raka.

Przewodnictwo kwantowe

Podczas gdy model przewodnictwa elektrycznego Drude-Lorentza zapewnia doskonałe przewidywania natury elektronów przewodzących w metalach, można go rozwinąć, stosując tunelowanie kwantowe, aby wyjaśnić naturę zderzeń elektronów. Kiedy swobodny pakiet fali elektronowej napotyka długi szereg równomiernie rozmieszczonych barier , odbita część pakietu falowego interferuje równomiernie z pakietem przesyłanym pomiędzy wszystkimi barierami, dzięki czemu możliwa jest 100% transmisja. Teoria przewiduje, że jeśli dodatnio naładowane jądra tworzą idealnie prostokątny układ, elektrony będą tunelować przez metal jako wolne elektrony, prowadząc do ekstremalnie wysokiego przewodnictwa , a zanieczyszczenia w metalu znacznie go zakłócą.

Skanowanie mikroskopu tunelującego

Główny artykuł: Skaningowy mikroskop tunelowy

Skaningowy mikroskop tunelowy (STM), wynaleziony przez Gerda Binniga i Heinricha Rohrera , może umożliwić obrazowanie pojedynczych atomów na powierzchni materiału. Działa, wykorzystując związek między tunelowaniem kwantowym a odległością. Gdy końcówka igły STM zostanie zbliżona do powierzchni przewodzącej, która ma polaryzację napięcia, pomiar prądu elektronów tunelujących między igłą a powierzchnią ujawnia odległość między igłą a powierzchnią. Za pomocą prętów piezoelektrycznych które zmieniają rozmiar po przyłożeniu napięcia, wysokość końcówki można regulować, aby utrzymać stały prąd tunelowania. Zmienne w czasie napięcia przykładane do tych prętów można rejestrować i wykorzystywać do obrazowania powierzchni przewodnika. STM mają dokładność do 0,001 nm, czyli około 1% średnicy atomowej.

Kinetyczny efekt izotopowy

Główny artykuł: Kinetyczny efekt izotopowy

W kinetyce chemicznej zastąpienie lekkiego izotopu pierwiastka cięższym zwykle skutkuje wolniejszą szybkością reakcji. Jest to ogólnie przypisywane różnicom w energiach drgań punktu zerowego dla wiązań chemicznych zawierających lżejsze i cięższe izotopy i jest ogólnie modelowane przy użyciu teorii stanu przejściowego . Jednak w niektórych przypadkach obserwuje się duże efekty izotopowe, których nie można wyjaśnić za pomocą półklasycznego traktowania, i wymagane jest tunelowanie kwantowe. RP Dzwon opracowali zmodyfikowane podejście do kinetyki Arrheniusa, które jest powszechnie stosowane do modelowania tego zjawiska.

Szybszy niż światło

Zobacz też: Szybszy od światła

Niektórzy fizycy twierdzą, że cząstki o spinie zerowym mogą podróżować szybciej niż prędkość światła podczas tunelowania. Wydaje się to naruszać zasadę przyczynowości , ponieważ istnieje wówczas układ odniesienia , w którym cząstka przybywa, zanim ją opuści. W 1998 roku Francis E. Low dokonał krótkiego przeglądu zjawiska tunelowania w czasie zerowym. Niedawno Günter Nimtz opublikował eksperymentalne dane dotyczące czasu tunelowania fononów , fotonów i elektronów .

Inni fizycy, tacy jak Herbert Winful , zakwestionował te roszczenia. Winful argumentował, że pakiet fal tunelującej cząstki rozchodzi się lokalnie, więc cząstka nie może tunelować przez barierę nielokalnie. Winful argumentował również, że eksperymenty, które rzekomo wykazują propagację nielokalną, zostały błędnie zinterpretowane. W szczególności prędkość grupowa pakietu falowego nie mierzy jego prędkości, ale jest związana z ilością czasu, przez jaki pakiet falowy jest przechowywany w barierze. Problem polega jednak na tym, że funkcja falowa wciąż rośnie wewnątrz bariery we wszystkich punktach jednocześnie. Innymi słowy, w każdym regionie niedostępnym do pomiaru propagacja nielokalna jest nadal matematycznie pewna.

Eksperyment przeprowadzony w 2020 roku, nadzorowany przez Aephraima Steinberga, wykazał, że cząstki powinny być w stanie tunelować z pozornymi prędkościami szybszymi niż światło.

Dyskusja matematyczna

Kwantowe tunelowanie przez barierę. Energia tunelowanej cząstki jest taka sama, ale amplituda prawdopodobieństwa jest zmniejszona.

Równanie Schrödingera

Niezależne od czasu równanie Schrödingera dla jednej cząstki w jednym wymiarze można zapisać jako

$${\ Displaystyle - {\ Frac {\ hbar ^ {2}} {2m}}} {\ frac {d^{2}}{dx^{2}}}\Psi (x)+V(x)\Psi (x)=E\Psi (x)}$$

Lub

$${\ Displaystyle {\ Frac {d ^ { 2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)\Psi (x)\ równoważne {\frac {2m}{\hbar ^{2}}}M(x)\psi(x)}$$

Gdzie

• ${\ Displaystyle \ hbar}$ to zredukowana stała Plancka ,
• m to masa cząstki,
• x reprezentuje odległość mierzoną w kierunku ruchu cząstki,
• Ψ jest funkcją falową Schrödingera,
• V to energia potencjalna cząstki (mierzona względem dowolnego dogodnego poziomu odniesienia),
• E to energia cząstki związana z ruchem w osi x (mierzona względem V ),
• M ( x ) to wielkość zdefiniowana przez V ( x ) − E , która nie ma przyjętej nazwy w fizyce.

Rozwiązania równania Schrödingera przybierają różne postacie dla różnych wartości x , w zależności od tego, czy M ( x ) jest dodatnie, czy ujemne. Gdy M ( x ) jest stałe i ujemne, to równanie Schrödingera można zapisać w postaci

${\ Displaystyle {\ Frac {d ^ {2}} {dx ^ {2}}} \ Psi (x) = {\ Frac {2m} {\ hbar ^ {2}}} M (x) \ Psi (x )=-k^{2}\Psi (x),\qquad {\text{gdzie}}\quad k^{2}=-{\frac {2m}{\hbar ^{2}}}M.}$

Rozwiązania tego równania reprezentują fale biegnące ze stałą fazową + k lub - k . Alternatywnie, jeśli M ( x ) jest stałe i dodatnie, to równanie Schrödingera można zapisać w postaci

${\ Displaystyle {\ Frac {d ^ {2}} {dx ^ {2}}} \ Psi (x) = {\ Frac {2m} {\ hbar ^ {2}}} M (x) \ Psi (x )={\kappa}^{2}\Psi (x),\qquad {\text{gdzie}}\quad {\kappa}^{2}={\frac {2m}{\hbar ^{2}} }M.}$

Rozwiązaniem tego równania są wznoszące się i opadające wykładniki w postaci zanikających fal . Kiedy M ( x ) zmienia się wraz z pozycją, występuje taka sama różnica w zachowaniu, w zależności od tego, czy M(x) jest ujemne, czy dodatnie. Wynika z tego, że znak M ( x ) określa naturę ośrodka, przy czym ujemny M (x) odpowiada ośrodkowi A, a dodatni M ( x ) odpowiada ośrodkowi B. Wynika z tego, że sprzężenie fal zanikających może wystąpić, jeśli obszar dodatniego M ( x ) jest umieszczony pomiędzy dwoma regionami ujemnego M ( x ), tworząc w ten sposób potencjalną barierę.

Matematyka radzenia sobie z sytuacją, w której M ( x ) zmienia się wraz z x , jest trudna, z wyjątkiem szczególnych przypadków, które zwykle nie odpowiadają fizycznej rzeczywistości. Pełne podejście matematyczne pojawia się w monografii Frömana i Frömana z 1965 roku. Ich pomysły nie zostały włączone do podręczników fizyki, ale ich poprawki mają niewielki efekt ilościowy.

Przybliżenie WKB

Główny artykuł: przybliżenie WKB

Funkcja falowa jest wyrażona jako wykładniczy funkcji:

$${\ Displaystyle \ Psi (x) = e ^ {\ Phi (x)},}$$

Gdzie

$${\ Displaystyle \ Phi '' (x) + \ Phi '(x) ^ {2} = {\ Frac {2m} {\ hbar ^ {2}}} \ lewo (V (x) -E \ prawo). }$$

${\ Displaystyle \ Phi '(x)}$ jest następnie dzielony na części rzeczywiste i urojone: Φ ′ ( x ) {\ Displaystyle \ Phi '(x)}

$${\ Displaystyle \ Phi '(x) = A (x) + iB (x),}$$

gdzie A ( x ) i B ( x ) są funkcjami o wartościach rzeczywistych.

Podstawiając drugie równanie do pierwszego i wykorzystując fakt, że część rzeczywista musi wynosić 0, otrzymujemy:

$${\ Displaystyle A' (x) + A (x) ^ {2} -B (x) ^ {2} = {\ Frac {2m} {\ hbar ^ {2}}} \ lewo (V (x) - E\prawo).}$$

Tunelowanie kwantowe w formułowaniu przestrzeni fazowej mechaniki kwantowej. Funkcja $_$ tunelowania potencjału Linie ciągłe przedstawiają poziomów hamiltonianu / ${\ Displaystyle H (x, p) = p ^ {2}/2 + U (x)}$ .

$potęgowy$ za pomocą przybliżenia półklasycznego, każdą funkcję należy rozwinąć jako szereg w . Z równań szereg potęgowy musi zaczynać się od co najmniej rzędu ${\ displaystyle \ hbar ^ {-1}},$ aby spełnić część rzeczywistą równania; dla dobra klasyczna granica zaczynająca się od najwyższej możliwej potęgi stałej Plancka jest preferowana, co prowadzi do

$${\ Displaystyle A (x) = {\ Frac {1} {\ hbar}} \ suma _ {k = 0} ^ {\ infty} \hbar ^{k}A_{k}(x)}$$

I

$${\ Displaystyle B (x) = {\ Frac {1} {\ hbar}} \ suma _ {k = 0} ^ {\ infty }\hbar ^{k}B_{k}(x),}$$

z następującymi ograniczeniami na warunkach najniższego rzędu,

$${\ Displaystyle A_ {0} (x) ^ {2} -B_ {0} (x) ^ {2} = 2 m \left(V(x)-E\right)}$$

I

$${\ Displaystyle A_ {0} (x) B_ {0} (x) = 0.}$$

W tym miejscu można rozważyć dwa skrajne przypadki.

Przypadek 1

Jeśli amplituda zmienia się powoli w porównaniu z fazą ${\ Displaystyle A_ {0} (x) = 0}$ i

$${\ Displaystyle B_ {0} (x) = \ pm {\ sqrt {2 m \ lewo (EV (x) \ prawo)}}}$$

co odpowiada ruchowi klasycznemu. Rozwiązanie następnej kolejności wydajności ekspansji

$${\ Displaystyle \ Psi (x) \ około C { \frac {e^{i\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(EV(x)\right)}}+\theta }}{\sqrt[ {4}] {{\frac {2m}{\hbar ^{2}}}\left(EV(x)\right)}}}}$$

Przypadek 2

Jeśli faza zmienia się powoli w porównaniu z amplitudą, ${\ Displaystyle B_ {0} (x) = 0}$ i

$${\ Displaystyle A_ {0} (x) = \ pm {\ sqrt {2 m \ lewo (V (x) -E \ prawo)}}}$$

co odpowiada tunelowaniu. Rozwiązanie następnej kolejności wydajności ekspansji

$${\ Displaystyle \ Psi (x) \ około {\ Frac {C_ {+} e ^ {+ \ int dx {\ sqrt {{\ Frac {2m} {\ hbar ^ {2}}} \ lewo (V(x)-E\right)}}}+C_{-}e^{-\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x )-E\right)}}}}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}$$

W obu przypadkach z mianownika widać, że oba te przybliżone rozwiązania są złe w pobliżu klasycznych punktów zwrotnych ${\ Displaystyle E = V (x)}$ . Z dala od potencjalnego wzgórza cząstka zachowuje się podobnie do swobodnej i oscylującej fali; poniżej potencjalnego wzgórza cząstka podlega wykładniczym zmianom amplitudy. Rozważając zachowanie w tych granicach i klasycznych punktach zwrotnych, można stworzyć globalne rozwiązanie.

wybiera się klasyczny punkt zwrotny ${\ Displaystyle {\ Frac {2m} {\ hbar ^$$)$ jest rozwinięte w szereg potęgowy o : ${\ Displaystyle x_ {1}}$ :

$${\ Displaystyle {\ Frac {2m} {\ hbar ^ {2}} }\left(V(x)-E\right)=v_{1}(x-x_{1})+v_{2}(x-x_{1})^{2}+\cdots }$$

Zachowanie tylko terminu pierwszego rzędu zapewnia liniowość:

$${\ Displaystyle {\ Frac {2m} {\ hbar ^ {2}}} \ lewo (V (x) -E \ prawo) = v_ {1} (xx_ {1}).}$$

Korzystając z tego przybliżenia, równanie w pobliżu staje się równaniem różniczkowym : ${\ displaystyle x_ {1}}$

$${\ Displaystyle {\ Frac {d ^ {2}} {dx ^ {2}}} \ psi (x) = v_ {1} (xx_ {1}) \ psi (x).}$$

Można to rozwiązać za pomocą funkcji Airy'ego jako rozwiązań.

$$\ Displaystyle \ Psi (x) = C_ {A} Ai \left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)+C_{B}Bi\left({\sqrt[{3}]{v_{1 }}}(x-x_{1})\prawo)}$$

Biorąc te rozwiązania dla wszystkich klasycznych punktów zwrotnych, można utworzyć globalne rozwiązanie, które łączy rozwiązania ograniczające. Biorąc pod uwagę dwa współczynniki po jednej stronie klasycznego punktu zwrotnego, dwa współczynniki po drugiej stronie klasycznego punktu zwrotnego można określić, używając tego lokalnego rozwiązania do ich połączenia.

Stąd rozwiązania funkcji Airy'ego będą asymptotować do funkcji sinusoidalnych, cosinusowych i wykładniczych we właściwych granicach. Relacje między ${\ Displaystyle C, \ theta}$ i $, C_ {-}}$ }

$$\ Displaystyle C_ {+} = {\ Frac {1} {2}} C \ sałata {\ lewo (\ teta - {\ Frac {\ pi}} 4}}\w prawo)}}$$

I

Kwantowe tunelowanie przez barierę. Na początku ( x = 0) znajduje się bardzo wysoka, ale wąska bariera potencjału. Można zauważyć znaczny efekt tunelowania.

${\ Displaystyle C_ {-} = - C \ sin {\ lewo (\ teta - {\ Frac {\ pi} {4}} \ prawej)}$

Po znalezieniu współczynników można znaleźć rozwiązanie globalne. Dlatego współczynnik transmisji dla cząstki tunelującej przez pojedynczą barierę potencjału wynosi

$${\ Displaystyle T (E) = e ^ {- 2 \ int _ {x_ {1}} ^{x_{2}}dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left[V(x)-E\right]}}},}$$

gdzie ${\ displaystyle x_ {1}, x_ {2}}$ to dwa klasyczne punkty zwrotne dla bariery potencjału.

W przypadku bariery prostokątnej wyrażenie to upraszcza się do:

$${\ Displaystyle T (E) = e ^ {- 2 {\ sqrt {{\ Frac {2m} {\ hbar ^ {2}}} (V_ {0} -E)}} (x_ {2} -x_ { 1})}.}$$

Zobacz też

• Wyładowanie bariery dielektrycznej
• Emisja elektronów polowych
• Metoda Holsztyńsko-Śledziowa
• Tunelowanie protonów
• Klonowanie kwantowe
• Nadprzewodnikowe złącze tunelowe
• Dioda tunelowa
• Węzeł tunelowy
• Biała dziura

Dalsza lektura

• N. Fröman i P.-O. Frömana (1965). JWKB Aproksymacja: wkład w teorię . Amsterdam: Holandia Północna.
•   Razavy, Mohsen (2003). Kwantowa teoria tunelowania . Świat naukowy. ISBN 978-981-238-019-7 .
•   Griffiths, David J. (2004). Wprowadzenie do mechaniki kwantowej (wyd. 2). Sala Prentice'a. ISBN 978-0-13-805326-0 .
•   James Binney i Skinner, D. (2010). Fizyka mechaniki kwantowej: wprowadzenie (wyd. 3). Archiwum Cappelli. ISBN 978-1-902918-51-8 .
•   Liboff, Richard L. (2002). Wprowadzenie do mechaniki kwantowej . Addison-Wesley. ISBN 978-0-8053-8714-8 .
•   Wileńkin, Aleksander; Wileńkin, Aleksander; Winitzki, Serge (2003). „Tworzenie cząstek we wszechświecie tunelowym”. Przegląd fizyczny D. 68 (2): 023520. arXiv : gr-qc/0210034 . Bibcode : 2003PhRvD..68b3520H . doi : 10.1103/PhysRevD.68.023520 . S2CID 118969589 .
• HJW Müller-Kirsten (2012). Wprowadzenie do mechaniki kwantowej: równanie Schrödingera i całka po ścieżce, wyd . Singapur: świat naukowy.

Linki zewnętrzne

• Animacja, aplikacje i badania związane z efektem tunelu i innymi zjawiskami kwantowymi (Université Paris Sud)
• Animowana ilustracja tunelowania kwantowego
• Animowana ilustracja tunelowania kwantowego w urządzeniu RTD
• Interaktywne rozwiązanie równania tunelu Schrodingera