Wprowadzenie do mechaniki kwantowej

Ten artykuł jest nietechnicznym wprowadzeniem do tematu. Aby zapoznać się z głównym artykułem w encyklopedii, zobacz Mechanika kwantowa .

Aby zapoznać się z książką Davida J. Griffithsa, zobacz Wprowadzenie do mechaniki kwantowej (książka) .

Mechanika kwantowa to nauka o materii i jej oddziaływaniach z energią w skali cząstek atomowych i subatomowych . Z kolei fizyka klasyczna wyjaśnia materię i energię jedynie w skali znanej ludzkiemu doświadczeniu, włączając w to zachowanie ciał astronomicznych, takich jak Księżyc. Fizyka klasyczna jest nadal używana w większości współczesnej nauki i technologii. Jednak pod koniec XIX wieku naukowcy odkryli zjawiska zarówno w dużych ( makro ), jak i małych ( mikro) ) światów, których fizyka klasyczna nie potrafiła wyjaśnić. Chęć rozwiązania niespójności między obserwowanymi zjawiskami a teorią klasyczną doprowadziła do dwóch głównych rewolucji w fizyce, które spowodowały zmianę pierwotnego paradygmatu naukowego : teorii względności i rozwoju mechaniki kwantowej . W tym artykule opisano, w jaki sposób fizycy odkryli ograniczenia fizyki klasycznej i opracowali główne koncepcje teorii kwantowej, która zastąpiła ją na początku XX wieku. Opisuje te koncepcje w przybliżeniu w kolejności, w jakiej zostały odkryte. Aby uzyskać pełniejszą historię tego tematu, zobacz Historia mechaniki kwantowej .

Światło zachowuje się pod pewnymi względami jak cząstki, a pod innymi jak fale. Materia — „materiał” wszechświata składający się z cząstek, takich jak elektrony i atomy — również wykazuje zachowanie falowe . Niektóre źródła światła, takie jak neony , emitują tylko określone częstotliwości światła, mały zestaw wyraźnych czystych kolorów określonych przez strukturę atomową neonu. Mechanika kwantowa pokazuje, że światło, wraz ze wszystkimi innymi formami promieniowania elektromagnetycznego , występuje w oddzielnych jednostkach, zwanych fotonami , i przewiduje jego spektralne (odpowiadające czystym kolorom) i intensywności wiązek światła. Pojedynczy foton jest kwantem , czyli najmniejszą obserwowalną cząstką pola elektromagnetycznego. Częściowego fotonu nigdy nie obserwuje się eksperymentalnie. Mówiąc szerzej, mechanika kwantowa pokazuje, że wiele właściwości obiektów, takich jak położenie, prędkość i moment pędu , które wydawały się ciągłe w powiększonym widoku mechaniki klasycznej, okazuje się być (w bardzo małej, powiększonej skali mechanika kwantowa) skwantowane . Takie właściwości cząstek elementarnych muszą przyjąć jedną z zestawu małych, dyskretnych dopuszczalnych wartości, a ponieważ różnica między tymi wartościami jest również niewielka, nieciągłości są widoczne tylko w bardzo małych (atomowych) skalach.

Wiele aspektów mechaniki kwantowej jest sprzecznych z intuicją i może wydawać się paradoksalne , ponieważ opisują zachowanie zupełnie inne niż obserwowane w większej skali. Mówiąc słowami fizyka kwantowego Richarda Feynmana , mechanika kwantowa zajmuje się „naturą taką, jaka jest – absurdalna”. Jednym z głównych „paradoksów” jest pozorna niespójność między prawami Newtona a mechaniką kwantową, którą można wyjaśnić za pomocą twierdzenia Ehrenfesta , co pokazuje, że wartości średnie otrzymane z mechaniki kwantowej (np. położenie i pęd) są zgodne z prawami klasycznymi. Jednak twierdzenie Ehrenfesta jest dalekie od wyjaśnienia wszystkich obserwowanych zjawisk sprzecznych z intuicją ( dziwactwa kwantowe ), ale jest raczej matematycznym wyrazem zasady zgodności .

Na przykład zasada nieoznaczoności mechaniki kwantowej oznacza, że ​​im dokładniej ustala się jeden pomiar (taki jak położenie cząstki), tym mniej dokładny musi być inny pomiar uzupełniający dotyczący tej samej cząstki (taki jak jej prędkość ).

Innym przykładem jest splątanie , w którym pomiar dowolnego dwuwartościowego stanu cząstki (takiego jak światło spolaryzowane w górę lub w dół) dokonany na jednej z dwóch „splątanych” cząstek, które są bardzo daleko od siebie, powoduje późniejszy pomiar na drugiej cząstce zawsze będzie drugą z dwóch wartości (np. spolaryzowana w przeciwnym kierunku).

Ostatnim przykładem jest nadciekłość , w której ciekły hel w pojemniku, schłodzony do temperatury bliskiej zera absolutnego , spontanicznie przepływa (powoli) w górę i przez otwór pojemnika, wbrew sile grawitacji.

Pierwsza teoria kwantowa: Max Planck i promieniowanie ciała doskonale czarnego

Główny artykuł: Katastrofa ultrafioletowa

Boczny portret Plancka jako młodego dorosłego, ok. 1878

Gorąca metaloplastyka. Żółto-pomarańczowa poświata jest widoczną częścią promieniowania cieplnego emitowanego pod wpływem wysokiej temperatury. Wszystko inne na zdjęciu również świeci promieniowaniem cieplnym, ale mniej jasno i na dłuższych falach, niż ludzkie oko może wykryć. Kamera dalekiej podczerwieni może obserwować to promieniowanie.

Promieniowanie cieplne to promieniowanie elektromagnetyczne emitowane z powierzchni obiektu w wyniku energii wewnętrznej obiektu. Jeśli obiekt jest wystarczająco ogrzany, zaczyna emitować światło na czerwonym końcu widma , gdy staje się czerwony .

Podgrzanie go dodatkowo powoduje zmianę koloru z czerwonego na żółty, biały i niebieski, ponieważ emituje światło o coraz krótszych długościach fal (wyższych częstotliwościach). Idealny emiter to także doskonały pochłaniacz: gdy jest zimno, taki obiekt wygląda idealnie czarny, ponieważ pochłania całe padające na niego światło i nie emituje żadnego. W związku z tym idealny emiter ciepła jest znany jako ciało doskonale czarne , a emitowane przez niego promieniowanie nazywane jest promieniowaniem ciała doskonale czarnego .

Prognozy ilości promieniowania cieplnego o różnych częstotliwościach emitowanego przez ciało. Prawidłowe wartości przewidywane przez prawo Plancka (kolor zielony) kontrastowały z klasycznymi wartościami prawa Rayleigha-Jeansa (kolor czerwony) i przybliżeniem Wiena (kolor niebieski).

Pod koniec XIX wieku promieniowanie cieplne zostało dość dobrze scharakteryzowane eksperymentalnie. Jednak fizyka klasyczna doprowadziła do powstania prawa Rayleigha-Jeansa , które, jak pokazano na rysunku, dobrze zgadza się z wynikami eksperymentów przy niskich częstotliwościach, ale zdecydowanie nie zgadza się przy wysokich częstotliwościach. Fizycy szukali jednej teorii, która wyjaśniałaby wszystkie wyniki eksperymentów.

Pierwszy model, który był w stanie wyjaśnić pełne widmo promieniowania cieplnego, przedstawił Max Planck w 1900 roku. Zaproponował on model matematyczny, w którym promieniowanie cieplne było w równowadze z zestawem oscylatorów harmonicznych . Aby odtworzyć wyniki eksperymentu, musiał założyć, że każdy oscylator emituje całkowitą liczbę jednostek energii przy swojej jednej charakterystycznej częstotliwości, zamiast być w stanie emitować dowolną ilość energii. Innymi słowy, energia emitowana przez oscylator została skwantowana . Kwant _ energia dla każdego oscylatora, według Plancka, była proporcjonalna do częstotliwości oscylatora; stała proporcjonalności jest obecnie znana jako stała Plancka . Stała Plancka, zwykle zapisywana jako h , ma wartość 6,63 × 10 ⁻³⁴ J⋅s . Zatem energia E oscylatora o częstotliwości f jest dana przez

${\ Displaystyle E = nhf, \ quad {\ tekst {gdzie}} \ quad n = 1,2,3, \ ldots}$

Aby zmienić kolor takiego promieniującego ciała, konieczna jest zmiana jego temperatury. Prawo Plancka wyjaśnia, dlaczego: zwiększenie temperatury ciała pozwala mu ogólnie emitować więcej energii i oznacza, że ​​większa część energii znajduje się w kierunku fioletowego końca widma.

Prawo Plancka było pierwszą teorią kwantową w fizyce, a Planck zdobył Nagrodę Nobla w 1918 r. „w uznaniu zasług, jakie wyświadczył rozwojowi fizyki poprzez odkrycie kwantów energii”. Jednak w tamtym czasie Planck uważał, że kwantyzacja była czysto heurystyczną konstrukcją matematyczną, a nie (jak się obecnie uważa) fundamentalną zmianą w naszym rozumieniu świata.

Fotony: kwantyzacja światła

Alberta Einsteina C. 1905

W 1905 roku Albert Einstein zrobił dodatkowy krok. Zasugerował, że kwantyzacja nie jest tylko konstrukcją matematyczną, ale że energia w wiązce światła faktycznie występuje w pojedynczych pakietach, które obecnie nazywa się fotonami . Energia pojedynczego fotonu $f}$ o częstotliwości jest dana przez częstotliwość pomnożoną przez $\ displaystyle$ Plancka (niezwykle małą liczbę dodatnią): fa {

${\ Displaystyle E = hf}$

Przez wieki naukowcy dyskutowali między dwiema możliwymi teoriami światła: czy jest to fala , czy raczej składa się ze strumienia drobnych cząstek ? W XIX wieku powszechnie uważano, że debata została rozstrzygnięta na korzyść teorii fal, ponieważ była w stanie wyjaśnić obserwowane efekty, takie jak załamanie , dyfrakcja , interferencja i polaryzacja . James Clerk Maxwell wykazał, że elektryczność, magnetyzm i światło są przejawami tego samego zjawiska: pola elektromagnetycznego . Równania Maxwella , które są kompletnym zbiorem praw klasycznego elektromagnetyzmu , opisują światło jako fale: kombinację oscylujących pól elektrycznych i magnetycznych. Ze względu na przewagę dowodów przemawiających za teorią fal, idee Einsteina spotkały się początkowo z wielkim sceptycyzmem. Ostatecznie jednak model fotonowy stał się preferowany. Jednym z najbardziej znaczących dowodów na jego korzyść była jego zdolność do wyjaśnienia kilku zagadkowych właściwości efektu fotoelektrycznego , opisane w następnej sekcji. Niemniej jednak analogia falowa pozostała niezbędna do zrozumienia innych cech światła: dyfrakcji , załamania i interferencji .

Efekt fotoelektryczny

Światło pada na powierzchnię z lewej strony. Jeśli częstotliwość światła jest wystarczająco wysoka, tj. dostarcza wystarczającą energię, ujemnie naładowane elektrony są wyrzucane z metalu.

Główny artykuł: efekt fotoelektryczny

W 1887 roku Heinrich Hertz zauważył, że gdy światło o wystarczającej częstotliwości uderza w metalową powierzchnię, powierzchnia ta emituje elektrony. W 1902 roku Philipp Lenard odkrył, że maksymalna możliwa energia wyrzuconego elektronu jest związana z częstotliwością światła, a nie z jego intensywnością : jeśli częstotliwość jest zbyt niska, żadne elektrony nie są wyrzucane niezależnie od intensywności. Silne wiązki światła w kierunku czerwonego końca widma mogą w ogóle nie wytwarzać potencjału elektrycznego, podczas gdy słabe wiązki światła w kierunku fioletowego końca widma wytwarzałyby coraz wyższe napięcia. Najniższa częstotliwość światła, która może powodować emisję elektronów, zwana częstotliwością progową, jest różna dla różnych metali. Ta obserwacja jest sprzeczna z klasycznym elektromagnetyzmem, który przewiduje, że energia elektronu powinna być proporcjonalna do natężenia padającego promieniowania. Kiedy więc fizycy po raz pierwszy odkryli urządzenia wykazujące efekt fotoelektryczny, początkowo spodziewali się, że większa intensywność światła wytworzy wyższe napięcie z urządzenia fotoelektrycznego.

Einstein wyjaśnił ten efekt postulując, że wiązka światła jest strumieniem cząstek („ fotonów ”) i że jeśli wiązka ma częstotliwość f , to każdy foton ma energię równą hf . Elektron może zostać uderzony tylko przez pojedynczy foton, który przekazuje elektronowi co najwyżej energię hf . Dlatego intensywność wiązki nie ma wpływu i tylko jej częstotliwość określa maksymalną energię, jaką można przekazać elektronowi.

usunięcie elektronu z metalu wymaga pewnej ilości energii, zwanej pracą wyjścia i oznaczonej przez φ . Ta ilość energii jest inna dla każdego metalu. Jeśli energia fotonu jest mniejsza niż praca wyjścia, to nie przenosi on energii wystarczającej do usunięcia elektronu z metalu. Częstotliwość progowa f ₀ jest częstotliwością fotonu, którego energia jest równa pracy wyjścia:

${\ Displaystyle \ varphi = hf_ {0}.}$

Jeśli f jest większe niż f ₀ , energia hf jest wystarczająca do usunięcia elektronu. Wyrzucony elektron ma energię kinetyczną EK _: , która jest co najwyżej równa energii fotonu pomniejszonej o energię potrzebną do oderwania elektronu od metalu

${\ Displaystyle E_ {K} = hf - \ varphi = h (ff_ {0}).}$

Opis światła złożony przez Einsteina jako złożonego z cząstek rozszerzył pojęcie skwantowanej energii Plancka, zgodnie z którym pojedynczy foton o danej częstotliwości f dostarcza niezmienną ilość energii hf . Innymi słowy, pojedyncze fotony mogą dostarczać mniej lub więcej energii, ale tylko w zależności od ich częstotliwości. W naturze pojedyncze fotony są rzadko spotykane. Słońce i źródła emisji dostępne w XIX wieku emitowały ogromną liczbę fotonów na sekundę, więc znaczenie energii przenoszonej przez każdy foton nie było oczywiste. Pomysł Einsteina, że ​​energia zawarta w poszczególnych jednostkach światła zależy od ich częstotliwości, umożliwił wyjaśnienie wyników eksperymentów, które wydawały się sprzeczne z intuicją. Jednak chociaż foton jest cząstką, nadal opisywano go jako mający falową właściwość częstotliwości. W rzeczywistości opis światła jako cząstki jest niewystarczający, a jego falowa natura jest nadal wymagana.

Konsekwencje kwantyzacji światła

Zależność między częstotliwością promieniowania elektromagnetycznego a energią każdego fotonu jest powodem, dla którego światło ultrafioletowe może powodować oparzenia słoneczne , ale światło widzialne lub podczerwone nie. Foton światła ultrafioletowego dostarcza dużą ilość energii — wystarczającą, aby przyczynić się do uszkodzenia komórek, na przykład w wyniku oparzenia słonecznego. Foton światła podczerwonego dostarcza mniej energii — tylko tyle, aby ogrzać skórę. Tak więc lampa na podczerwień może ogrzać dużą powierzchnię, być może wystarczająco dużą, aby zapewnić ludziom komfort w zimnym pomieszczeniu, ale nie może spowodować oparzeń słonecznych.

Wszystkie fotony o tej samej częstotliwości mają identyczną energię, a wszystkie fotony o różnych częstotliwościach proporcjonalnie (rząd 1, _foton E = hf ) różne energie. Jednakże, chociaż energia przekazywana przez fotony jest niezmienna przy danej częstotliwości, początkowy stan energetyczny elektronów w urządzeniu fotoelektrycznym przed absorpcją światła niekoniecznie jest jednolity. W przypadku pojedynczych elektronów mogą wystąpić anomalie. Na przykład elektron, który był już wzbudzony powyżej poziomu równowagi urządzenia fotoelektrycznego, może zostać wyrzucony, gdy pochłonie oświetlenie o nietypowo niskiej częstotliwości. Statystycznie jednak charakterystyczne zachowanie urządzenia fotoelektrycznego odzwierciedla zachowanie ogromnej większości jego elektronów, które znajdują się na poziomie równowagi. Ten punkt pomaga wyjaśnić różnicę między badaniem małych pojedynczych cząstek w dynamice kwantowej a badaniem masywnych pojedynczych cząstek w fizyce klasycznej.

Kwantyzacja materii: model atomu Bohra

Główny artykuł: model Bohra

Na początku XX wieku dowody wymagały modelu atomu z rozproszoną chmurą ujemnie naładowanych elektronów otaczających małe, gęste, dodatnio naładowane jądro . Te właściwości sugerowały model, w którym elektrony krążą wokół jądra jak planety krążące wokół gwiazdy. Jednak wiadomo było również, że atom w tym modelu będzie niestabilny: zgodnie z klasyczną teorią orbitujące elektrony podlegają przyspieszeniu dośrodkowemu i dlatego powinny emitować promieniowanie elektromagnetyczne, a utrata energii powoduje również ich spiralny ruch w kierunku jądra, zderzając się z nim w ułamku sekundy.

Drugą powiązaną zagadką było widmo emisyjne atomów. Gdy gaz jest podgrzewany, emituje światło tylko o dyskretnych częstotliwościach. Na przykład światło widzialne emitowane przez wodór składa się z czterech różnych kolorów, jak pokazano na poniższym rysunku. Intensywność światła przy różnych częstotliwościach jest również różna. Natomiast światło białe składa się z ciągłej emisji w całym zakresie widzialnych częstotliwości. Pod koniec XIX wieku prosta reguła znana jako formuła Balmera pokazał, w jaki sposób częstotliwości różnych linii są ze sobą powiązane, chociaż bez wyjaśnienia, dlaczego tak jest, ani bez przewidywania intensywności. Formuła przewidywała również dodatkowe linie widmowe w świetle ultrafioletowym i podczerwonym, których nie obserwowano w tamtym czasie. Linie te zostały później zaobserwowane eksperymentalnie, co wzbudziło zaufanie do wartości wzoru.

Widmo emisyjne wodoru . Po wzbudzeniu gazowy wodór emituje światło w czterech różnych kolorach (linie widmowe) w widmie widzialnym, a także szereg linii w podczerwieni i ultrafiolecie.

Wzór matematyczny opisujący widmo emisyjne wodoru

W 1885 roku szwajcarski matematyk Johann Balmer odkrył, że każda długość fali λ (lambda) w widzialnym widmie wodoru jest powiązana z pewną liczbą całkowitą n za pomocą równania

${\ Displaystyle \ lambda = B \ lewo ({\ Frac {n ^ {2}} {n ^ {2} -4}} \right)\qquad \qquad n=3,4,5,6}$

gdzie B jest stałą wyznaczoną przez Balmera i wynosi 364,56 nm.

W 1888 roku Johannes Rydberg uogólnił i znacznie zwiększył użyteczność wyjaśniającą wzoru Balmera. Przewidział, że λ jest powiązane z dwiema liczbami całkowitymi n i m zgodnie z tym, co jest obecnie znane jako wzór Rydberga :

${\ Displaystyle {\ Frac {1} {\ lambda}} = R \ lewo ({\ Frac {1} {m ^ {2}}} - {\ frac {1}{n^{2}}}\prawo),}$

gdzie R jest stałą Rydberga równą 0,0110 nm ⁻¹ , a n musi być większe od m .

Wzór Rydberga uwzględnia cztery widzialne długości fal wodoru, ustalając m = 2 i n = 3, 4, 5, 6 . Przewiduje również dodatkowe długości fal w widmie emisyjnym: dla m = 1 i dla n > 1 widmo emisyjne powinno zawierać określone długości fal ultrafioletowych, a dla m = 3 i n > 3 powinno również zawierać określone długości fal podczerwonych. Eksperymentalna obserwacja tych długości fal nastąpiła dwie dekady później: w 1908 roku Louis Paschen znalazł niektóre z przewidywanych długości fal w podczerwieni, aw 1914 roku Theodore Lyman znalazł niektóre z przewidywanych długości fal w ultrafiolecie.

Zarówno wzory Balmera, jak i Rydberga obejmują liczby całkowite: we współczesnych terminach sugerują, że pewna właściwość atomu jest skwantowana. Dokładne zrozumienie, czym jest ta właściwość i dlaczego została skwantowana, było główną częścią rozwoju mechaniki kwantowej, jak pokazano w dalszej części tego artykułu.

Model atomu Bohra , przedstawiający przejście elektronu z jednej orbity na drugą poprzez emisję fotonu

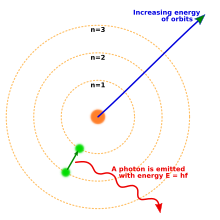
W 1913 roku Niels Bohr zaproponował nowy model atomu , który obejmował skwantowane orbity elektronów: elektrony nadal krążą wokół jądra, podobnie jak planety krążą wokół Słońca, ale mogą zamieszkiwać tylko określone orbity, a nie krążyć w dowolnej odległości. Kiedy atom emitował (lub pochłaniał) energię, elektron nie poruszał się po ciągłej trajektorii z jednej orbity wokół jądra na drugą, jak można by oczekiwać klasycznie. Zamiast tego elektron przeskakiwałby natychmiast z jednej orbity na drugą, emitując emitowane światło w postaci fotonu. Możliwe energie fotonów emitowanych przez każdy pierwiastek były określone przez różnice energii między orbitami, więc widmo emisji dla każdego pierwiastka zawierałoby pewną liczbę linii.

Niels Bohr jako młody człowiek

Wychodząc od tylko jednego prostego założenia dotyczącego zasady, której muszą przestrzegać orbity, model Bohra był w stanie powiązać obserwowane linie widmowe w widmie emisyjnym wodoru ze znanymi wcześniej stałymi. W modelu Bohra elektron nie mógł emitować energii w sposób ciągły i zderzać się z jądrem: gdy znalazł się na najbliższej dozwolonej orbicie, był stabilny na zawsze. Model Bohra nie wyjaśnił, dlaczego orbity powinny być kwantowane w ten sposób, ani nie był w stanie dokładnie przewidzieć atomów z więcej niż jednym elektronem ani wyjaśnić, dlaczego niektóre linie widmowe są jaśniejsze niż inne.

Wkrótce okazało się, że niektóre fundamentalne założenia modelu Bohra były błędne, ale kluczowy wniosek, że dyskretne linie w widmach emisyjnych wynikają z pewnych właściwości elektronów w kwantowanych atomach, jest prawidłowy. Sposób, w jaki faktycznie zachowują się elektrony, jest uderzająco różny od atomu Bohra i od tego, co widzimy w świecie naszego codziennego doświadczenia; ten nowoczesny kwantowo-mechaniczny model atomu omówiono poniżej .

Bardziej szczegółowe wyjaśnienie modelu Bohra

, że moment pędu L elektronu jest skwantowany:

${\ Displaystyle L = n {\ Frac {h} {2 \ pi}} = n \ hbar}$

gdzie n jest liczbą całkowitą, a h i ħ to odpowiednio stała Plancka i zredukowana stała Plancka. Wychodząc z tego założenia, prawo Coulomba i równania ruchu kołowego pokazują, że elektron o n jednostkach momentu pędu krąży wokół protonu w odległości r określonej przez

${\ Displaystyle R = {\ Frac {n ^ {2} h ^ {2}} {4 \ pi ^ {2} k_ {e} ja ^ {2 }}}}$ ,

gdzie k _e jest stałą kulombowską , m jest masą elektronu, a e jest ładunkiem elektronu . Dla uproszczenia jest to zapisane jako

${\ displaystyle r = n ^ {2} a_ {0}, \!}$

gdzie a ₀ , zwany promieniem Bohra , jest równe 0,0529 nm. Promień Bohra to promień najmniejszej dozwolonej orbity.

Energię elektronu można również obliczyć i jest ona podawana przez

${\ Displaystyle E = - {\ Frac {k _ {\ operatorname {e}} e ^ {2}} {2a_ {0}}} {\ Frac {1} n^{2}}}}$ .

₀ Zatem założenie Bohra, że ​​moment pędu jest skwantowany, oznacza, że ​​elektron może zajmować tylko określone orbity wokół jądra i że może mieć tylko określone energie. Konsekwencją tych ograniczeń jest to, że elektron nie uderza w jądro: nie może w sposób ciągły emitować energii i nie może zbliżyć się do jądra bliżej niż a (promień Bohra).

Elektron traci energię, przeskakując natychmiast ze swojej pierwotnej orbity na niższą; dodatkowa energia jest emitowana w postaci fotonu. I odwrotnie, elektron, który pochłonął foton, zyskuje energię, dzięki czemu przeskakuje na orbitę znajdującą się dalej od jądra.

rm _Każdy rn _foton świecącego wodoru atomowego jest spowodowany ruchem elektronu z wyższej orbity o promieniu na orbitę niższą . Energia E _γ tego fotonu jest różnicą energii E _n i E _m elektronu:

${\ Displaystyle E _ {\ gamma} = E_ {n} -E_ {m} = {\ Frac {k_ {\ matematyczna {e} }e^{2}}{2a_{0}}}\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}} \Prawidłowy)}$

Ponieważ równanie Plancka pokazuje, że energia fotonu jest związana z jego długością fali przez E _γ = hc / λ , długości fal światła, które mogą być emitowane, są określone wzorem

${\ Displaystyle {\ Frac {1} {\ lambda}} = {\ Frac {k _ {\ operatorname {e}} e ^ {2}} {2a_ {0} hc}} \ lewo ({\ Frac {1} {m^{2}}}-{\frac {1}{n^{2}}}\prawo).}$

To równanie ma taką samą postać jak wzór Rydberga i przewiduje, że stała R powinna być dana przez

${\ Displaystyle R = {\ Frac {k _ {\ operatorname {e}} e ^ {2}} {2a_ {0} hc}}.}$

Dlatego model atomu Bohra może przewidywać widmo emisyjne wodoru w kategoriach podstawowych stałych. Jednak nie był w stanie dokładnie przewidzieć atomów wieloelektronowych ani wyjaśnić, dlaczego niektóre linie widmowe są jaśniejsze niż inne.

Dualizm falowo-cząsteczkowy

Główny artykuł: dualizm falowo-cząsteczkowy

Louis de Broglie w 1929 r. De Broglie zdobył Nagrodę Nobla w dziedzinie fizyki za przewidywanie, że materia zachowuje się jak fala, poczynione w jego rozprawie doktorskiej z 1924 r.

Tak jak światło ma właściwości zarówno falowe, jak i cząsteczkowe, materia ma również właściwości falowe .

Materia zachowująca się jak fala została po raz pierwszy zademonstrowana eksperymentalnie dla elektronów: wiązka elektronów może wykazywać dyfrakcję , podobnie jak wiązka światła lub fala wodna. Podobne falowe zjawiska wykazano później dla atomów, a nawet cząsteczek.

Długość fali λ związana z dowolnym obiektem jest związana z jego pędem p poprzez stałą Plancka h :

${\ Displaystyle p = {\ Frac {h} {\ lambda}}.}$

Zależność, zwana hipotezą de Broglie'a, dotyczy wszystkich rodzajów materii: każda materia wykazuje właściwości zarówno cząstek, jak i fal.

Koncepcja dualizmu falowo-cząsteczkowego mówi, że ani klasyczne pojęcie „cząstki”, ani „fali” nie może w pełni opisać zachowania obiektów w skali kwantowej, ani fotonów, ani materii. Dualizm falowo-cząsteczkowy jest przykładem zasady komplementarności w fizyce kwantowej. Elegancki przykład dualizmu falowo-cząsteczkowego, eksperyment z podwójną szczeliną, omówiono w poniższej sekcji.

Eksperyment z podwójną szczeliną

Główny artykuł: Eksperyment z podwójną szczeliną

Obraz dyfrakcyjny powstający, gdy światło przechodzi przez jedną szczelinę (u góry) oraz obraz interferencyjny wytwarzany przez dwie szczeliny (u dołu). Znacznie bardziej złożony wzór z dwóch szczelin, z małymi prążkami interferencyjnymi, pokazuje falową propagację światła.

Eksperyment z podwójną szczeliną dla klasycznej cząstki, fali i cząstki kwantowej demonstrujący dualizm korpuskularno-falowy

W eksperymencie z podwójną szczeliną, przeprowadzonym pierwotnie przez Thomasa Younga w 1803 r., a dziesięć lat później przez Augustina Fresnela , wiązka światła jest kierowana przez dwie wąskie, blisko siebie rozmieszczone szczeliny, tworząc na ekranie wzór interferencyjny składający się z jasnych i ciemnych pasów . Jeśli jedna ze szczelin zostanie zakryta, można naiwnie oczekiwać, że intensywność prążków spowodowana interferencją zmniejszy się wszędzie o połowę. W rzeczywistości widoczny jest znacznie prostszy wzór, wzór dyfrakcyjny diametralnie naprzeciw otwartej szczeliny. To samo zachowanie można zademonstrować w falach wodnych, więc eksperyment z podwójną szczeliną był postrzegany jako demonstracja falowej natury światła.

Odmiany eksperymentu z podwójną szczeliną zostały przeprowadzone przy użyciu elektronów, atomów, a nawet dużych cząsteczek i zaobserwowano ten sam typ wzoru interferencji. W ten sposób wykazano, że cała materia posiada zarówno cechy cząstek, jak i fal.

Nawet jeśli intensywność źródła zostanie zmniejszona, tak że tylko jedna cząstka (np. foton lub elektron) przechodzi przez urządzenie naraz, ten sam wzór interferencji rozwija się w czasie. Cząstka kwantowa zachowuje się jak fala, gdy przechodzi przez podwójne szczeliny, ale jak cząstka, gdy zostanie wykryta. Jest to typowa cecha komplementarności kwantowej: cząstka kwantowa zachowuje się jak fala w eksperymencie mającym na celu zmierzenie jej właściwości falowych i jak cząstka w eksperymencie mającym na celu zmierzenie jej właściwości podobnych do cząstek. Punkt na ekranie detektora, w którym pojawia się pojedyncza cząstka, jest wynikiem przypadkowego procesu. Jednak wzór rozkładu wielu pojedynczych cząstek naśladuje wzór dyfrakcji wytwarzany przez fale.

Zastosowanie do modelu Bohra

De Broglie rozszerzył model atomu Bohra, pokazując, że elektron krążący wokół jądra może mieć właściwości falowe. W szczególności elektron obserwuje się tylko w sytuacjach, które pozwalają na falę stojącą wokół jądra . Przykładem fali stojącej jest struna skrzypiec, która jest zamocowana na obu końcach i może wibrować. Fale tworzone przez instrument strunowy wydają się oscylować w miejscu, poruszając się od grzbietu do doliny ruchem w górę iw dół. Długość fali fali stojącej jest związana z długością wibrującego obiektu i warunkami brzegowymi. $zamocowana na$ , może przenosić fale stojące o długości fali gdzie l jest długością, a n jest dodatnią liczbą całkowitą. De Broglie zasugerował, że dozwolone orbity elektronów to takie, dla których obwód orbity byłby całkowitą liczbą długości fal. Długość fali elektronu określa zatem, że możliwe są tylko orbity Bohra w określonych odległościach od jądra. Z kolei w dowolnej odległości od jądra mniejszej od określonej wartości ustalenie orbity byłoby niemożliwe. Minimalna możliwa odległość od jądra nazywana jest promieniem Bohra.

Traktowanie zdarzeń kwantowych przez De Broglie'a posłużyło jako punkt wyjścia dla Schrödingera, kiedy postanowił skonstruować równanie falowe do opisania zdarzeń kwantowo-teoretycznych.

Kręcić się

Główny artykuł: Spin (fizyka)

Zobacz także: eksperyment Sterna – Gerlacha

Spin kwantowy a magnes klasyczny w eksperymencie Sterna-Gerlacha

W 1922 roku Otto Stern i Walther Gerlach wystrzelili atomy srebra przez niejednorodne pole magnetyczne . W stosunku do bieguna północnego, skierowanego w górę, w dół lub gdzieś pomiędzy, w mechanice klasycznej magnes rzucony przez pole magnetyczne może zostać odchylony na małą lub dużą odległość w górę lub w dół. Atomy, które Sterna i Gerlacha wystrzelili w pole magnetyczne, zachowywały się podobnie. Jednakże, podczas gdy magnesy mogą być odchylane na różne odległości, atomy zawsze będą odchylane o stałą odległość w górę lub w dół. Oznaczało to, że właściwość atomu odpowiadająca orientacji magnesu musi być skwantowana, przyjmując jedną z dwóch wartości (w górę lub w dół), w przeciwieństwie do swobodnego wyboru pod dowolnym kątem.

Ralph Kronig zapoczątkował teorię, że cząstki, takie jak atomy lub elektrony, zachowują się tak, jakby obracały się lub „wirowały” wokół osi. Spin mógłby uwzględnić brakujący moment magnetyczny [ i pozwolić dwóm elektronom na tym samym orbicie zająć różne stany kwantowe gdyby „wirowały” w przeciwnych kierunkach, spełniając w ten sposób zasadę wykluczenia . Liczba kwantowa reprezentowała zwrot (dodatni lub ujemny) spinu.

Wybór orientacji pola magnetycznego zastosowanego w eksperymencie Sterna-Gerlacha jest arbitralny. Na pokazanej tutaj animacji pole jest pionowe, więc atomy są odchylane w górę lub w dół. Jeśli magnes zostanie obrócony o ćwierć obrotu, atomy zostaną odchylone w lewo lub w prawo. Użycie pola pionowego pokazuje, że spin wzdłuż osi pionowej jest skwantowany, a użycie pola poziomego pokazuje, że spin wzdłuż osi poziomej jest skwantowany.

Jeśli zamiast uderzać w ekran detektora, jedna z wiązek atomów wychodzących z aparatu Sterna-Gerlacha zostanie wprowadzona w inne (niejednorodne) pole magnetyczne zorientowane w tym samym kierunku, wszystkie atomy zostaną w tym drugim polu odchylone w ten sam sposób . Jeśli jednak drugie pole jest zorientowane pod kątem 90° do pierwszego, to połowa atomów jest odchylana w jedną stronę, a połowa w drugą, tak że wirowanie atomu wokół osi poziomej i pionowej jest od siebie niezależne. Jeśli jednak jedną z tych wiązek (np. atomy, które zostały odchylone w górę, a następnie w lewo) przepuścimy w trzecie pole magnetyczne, zorientowane w taki sam sposób jak pierwsza, połowa atomów porusza się w jedną stronę, a połowa w drugą, mimo że wszystkie pierwotnie poszedł w tym samym kierunku. Akcja pomiaru spinu atomów względem pola poziomego zmieniła ich spin względem pola pionowego.

Eksperyment Sterna – Gerlacha pokazuje kilka ważnych cech mechaniki kwantowej:

• Wykazano, że cecha świata przyrody jest skwantowana i może przyjmować tylko pewne dyskretne wartości.
• Cząstki posiadają wewnętrzny moment pędu , który jest bardzo podobny do momentu pędu klasycznie wirującego obiektu.
• Pomiar zmienia mierzony system w mechanice kwantowej. Można poznać tylko obrót obiektu w jednym kierunku, a obserwacja wirowania w innym kierunku niszczy pierwotną informację o wirowaniu.
• Mechanika kwantowa jest probabilistyczna: to, czy spin pojedynczego atomu wysłanego do aparatu jest dodatni, czy ujemny, jest przypadkowe.

Rozwój współczesnej mechaniki kwantowej

W 1925 roku Werner Heisenberg podjął próbę rozwiązania jednego z problemów, które model Bohra pozostawił bez odpowiedzi, wyjaśniając intensywność różnych linii w widmie emisji wodoru. Poprzez serię matematycznych analogii napisał kwantowo-mechaniczny analog do klasycznego obliczania intensywności. Wkrótce potem kolega Heisenberga, Max Born, zdał sobie sprawę, że metodę Heisenberga obliczania prawdopodobieństw przejść między różnymi poziomami energii można najlepiej wyrazić za pomocą matematycznej koncepcji macierzy .

W tym samym roku, opierając się na hipotezie de Broglie'a, Erwin Schrödinger opracował równanie opisujące zachowanie fali kwantowo-mechanicznej. Model matematyczny, nazwany równaniem Schrödingera , ma kluczowe znaczenie dla mechaniki kwantowej, określa dozwolone stany stacjonarne układu kwantowego i opisuje, jak stan kwantowy układu fizycznego zmienia się w czasie. Sama fala jest opisana przez funkcję matematyczną zwaną „ funkcją falową” . Schrödinger powiedział, że funkcja falowa zapewnia „środki do przewidywania prawdopodobieństwa wyników pomiarów”.

elektron atomu wodoru jako falę klasyczną poruszającą się w studni potencjału elektrycznego wytwarzanego przez proton. To obliczenie dokładnie odtworzyło poziomy energii modelu Bohra.

mechanika macierzowa Heisenberga i jego własna mechanika falowa dają te same przewidywania dotyczące właściwości i zachowania elektronu; z matematycznego punktu widzenia obie teorie miały wspólną formę. Jednak obaj mężczyźni nie zgadzali się co do interpretacji ich wspólnej teorii. Na przykład Heisenberg zaakceptował teoretyczne przewidywanie skoków elektronów między orbitalami w atomie, ale Schrödinger miał nadzieję, że teoria oparta na właściwościach fali ciągłej pozwoli uniknąć tego, co nazwał (parafrazując Wilhelma Wiena ) „ten nonsens o skokach kwantowych”. Ostatecznie zwyciężyło podejście Heisenberga i potwierdzono skoki kwantowe.

interpretacja kopenhaska

Główny artykuł: interpretacja kopenhaska

Instytut Nielsa Bohra w Kopenhadze, który był centralnym punktem dla badaczy mechaniki kwantowej i dziedzin pokrewnych w latach dwudziestych i trzydziestych XX wieku. Większość najbardziej znanych na świecie fizyków teoretyków spędzała tam czas.

Bohr, Heisenberg i inni próbowali wyjaśnić, co naprawdę oznaczają te wyniki eksperymentów i modele matematyczne. Ich opis, znany jako kopenhaska interpretacja mechaniki kwantowej, miał na celu opisanie natury rzeczywistości badanej przez pomiary i opisywanej matematycznymi sformułowaniami mechaniki kwantowej.

Główne zasady interpretacji kopenhaskiej to:

1. System jest całkowicie opisany funkcją falową , zwykle $reprezentowaną$ przez grecką literę „psi”). (Heisenberga)
2. $się$ jak zmienia w czasie, określa równanie Schrödingera.
3. Opis natury jest zasadniczo probabilistyczny. Prawdopodobieństwo zdarzenia — na przykład pojawienia się na ekranie cząstki w eksperymencie z podwójną szczeliną — jest związane z kwadratem wartości bezwzględnej amplitudy jej funkcji falowej. ( Reguła Borna , dzięki Maxowi Bornowi , która nadaje fizyczne znaczenie funkcji falowej w interpretacji kopenhaskiej: amplituda prawdopodobieństwa )
4. Nie jest możliwe jednoczesne poznanie wartości wszystkich właściwości systemu; te właściwości, które nie są dokładnie znane, muszą być opisane przez prawdopodobieństwa. zasada nieoznaczoności Heisenberga )
5. Materia, podobnie jak energia, wykazuje dualizm falowo-cząsteczkowy. Eksperyment może zademonstrować cząsteczkowe właściwości materii lub jej właściwości falowe; ale nie obie naraz. ( Zasada komplementarności ze względu na Bohra)
6. Urządzenia pomiarowe są zasadniczo urządzeniami klasycznymi i mierzą klasyczne właściwości, takie jak położenie i pęd.
7. Mechaniczny opis dużych systemów powinien być bardzo zbliżony do opisu klasycznego. ( Zasada korespondencji Bohra i Heisenberga)

Najróżniejsze następstwa tych zasad omówione zostaną dokładniej w poniższych podrozdziałach.

Zasada nieoznaczoności

Główny artykuł: Zasada niepewności

Werner Heisenberg w wieku 26 lat. Heisenberg zdobył Nagrodę Nobla w dziedzinie fizyki w 1932 roku za pracę, którą wykonał mniej więcej w tym czasie.

Załóżmy, że chcemy zmierzyć położenie i prędkość obiektu — na przykład samochodu przejeżdżającego przez fotoradar. Można przyjąć, że samochód ma określoną pozycję i prędkość w określonym momencie czasu. To, jak dokładnie można zmierzyć te wartości, zależy od jakości sprzętu pomiarowego. Poprawa precyzji sprzętu pomiarowego daje wynik bliższy rzeczywistej wartości. Można założyć, że prędkość samochodu i jego położenie można jednocześnie określić i zmierzyć operacyjnie, tak dokładnie, jak to tylko możliwe.

W 1927 roku Heisenberg udowodnił, że to ostatnie założenie jest błędne. Mechanika kwantowa pokazuje, że pewnych par właściwości fizycznych, na przykład położenia i prędkości, nie można jednocześnie zmierzyć ani zdefiniować w kategoriach operacyjnych z dowolną precyzją: im dokładniej mierzy się jedną właściwość lub definiuje w kategoriach operacyjnych, tym mniej dokładnie można inny. To stwierdzenie jest znane jako zasada nieoznaczoności . Zasada nieoznaczoności to nie tylko stwierdzenie o dokładności naszego sprzętu pomiarowego, ale głębiej dotyczy pojęciowego charakteru mierzonych wielkości – założenie, że samochód miał jednocześnie określoną pozycję i prędkość, nie działa w mechanice kwantowej. W skali samochodów i ludzi te niepewności są znikome, ale w przypadku atomów i elektronów stają się krytyczne.

Heisenberg podał jako ilustrację pomiar położenia i pędu elektronu za pomocą fotonu światła. Przy pomiarze położenia elektronu im wyższa częstotliwość fotonu, tym dokładniejszy jest pomiar położenia zderzenia fotonu z elektronem, ale większe jest zaburzenie elektronu. Dzieje się tak, ponieważ w wyniku zderzenia z fotonem elektron pochłania losową ilość energii, przez co uzyskany pomiar jego pędu jest coraz bardziej niepewny, ponieważ z konieczności mierzy się jego zaburzony pęd po zderzeniu na podstawie produktów zderzenia, a nie jego pierwotnego pędu ( pędu, który należy mierzyć jednocześnie z położeniem). W przypadku fotonu o niższej częstotliwości zaburzenie (a tym samym niepewność) pędu jest mniejsze, ale mniejsza jest też dokładność pomiaru położenia uderzenia.

Istotą zasady nieoznaczoności jest fakt, że dla każdej analizy matematycznej w dziedzinie położenia i prędkości uzyskanie ostrzejszej (bardziej precyzyjnej) krzywej w dziedzinie pozycji można uzyskać jedynie kosztem bardziej stopniowej (mniej precyzyjnej) krzywej w dziedzinie prędkości i odwrotnie. Większa ostrość w dziedzinie pozycji wymaga udziału większej liczby częstotliwości w dziedzinie prędkości, aby utworzyć węższą krzywą i odwrotnie. Jest to fundamentalny kompromis nieodłącznie związany z takimi powiązanymi lub uzupełniającymi się pomiarami, ale jest naprawdę zauważalny tylko w najmniejszej skali (Plancka), bliskiej wielkości cząstek elementarnych .

Zasada nieoznaczoności pokazuje matematycznie, że iloczyn niepewności położenia i pędu cząstki (pęd to prędkość pomnożona przez masę) nigdy nie może być mniejszy niż pewna wartość i że ta wartość jest związana ze stałą Plancka .

Załamanie funkcji falowej

Główny artykuł: upadek funkcji falowej

Załamanie funkcji falowej oznacza, że ​​pomiar wymusił lub przekształcił stan kwantowy (probabilistyczny lub potencjalny) w określoną zmierzoną wartość. Zjawisko to jest widoczne tylko w mechanice kwantowej, a nie w mechanice klasycznej.

Na przykład, zanim foton faktycznie „pojawi się” na ekranie detekcji, można go opisać tylko za pomocą zestawu prawdopodobieństw, gdzie może się pojawić. Kiedy pojawia się, na przykład w matrycy CCD aparatu elektronicznego, czas i przestrzeń, w której wchodzi w interakcję z urządzeniem, są znane w bardzo wąskich granicach. Jednak foton zniknął w procesie wychwytywania (mierzenia) i jego kwantowej funkcji falowej zniknął wraz z nim. W jej miejsce pojawiła się makroskopowa zmiana fizyczna na ekranie detekcyjnym, np. naświetlona plamka na arkuszu kliszy fotograficznej lub zmiana potencjału elektrycznego w jakiejś komórce matrycy CCD.

Stany własne i wartości własne

Dalsze informacje: Wprowadzenie do stanów własnych

Ze względu na zasadę nieoznaczoności stwierdzeniom dotyczącym zarówno położenia, jak i pędu cząstek można przypisać jedynie prawdopodobieństwo , że położenie lub pęd mają jakąś wartość liczbową. Dlatego konieczne jest jasne sformułowanie różnicy między stanem czegoś nieokreślonego, takiego jak elektron w chmurze prawdopodobieństwa, a stanem czegoś, co ma określoną wartość. Kiedy obiekt może być zdecydowanie „przygwożdżony” pod jakimś względem, mówi się, że posiada stan własny .

powyżej eksperymencie Sterna-Gerlacha obrót atomu wokół osi pionowej ma dwa stany własne: góra i dół. Zanim to zmierzymy, możemy tylko powiedzieć, że każdy pojedynczy atom ma takie samo prawdopodobieństwo, że będzie miał spin w górę lub w dół. Proces pomiaru powoduje załamanie funkcji falowej do jednego z dwóch stanów.

Stany własne spinu wokół osi pionowej nie są jednocześnie stanami własnymi spinu wokół osi poziomej, więc ten atom ma równe prawdopodobieństwo, że okaże się, że ma dowolną wartość spinu wokół osi poziomej. Jak opisano w powyższej sekcji , pomiar spinu wokół osi poziomej może pozwolić atomowi, który został obrócony w górę, na obrót w dół: pomiar jego spinu wokół osi poziomej załamuje jego funkcję falową do jednego ze stanów własnych tego pomiaru, co oznacza, że ​​jest nie jest już w stanie własnym wirowania wokół osi pionowej, więc może przyjąć dowolną wartość.

Zasada wykluczenia Pauliego

Wolfganga Pauliego

Główny artykuł: zasada wykluczenia Pauliego

W 1924 roku Wolfgang Pauli zaproponował nowy kwantowy stopień swobody (lub liczbę kwantową ) z dwiema możliwymi wartościami, aby rozwiązać niespójności między obserwowanymi widmami molekularnymi a przewidywaniami mechaniki kwantowej. W szczególności widmo wodoru atomowego miało dublet lub parę linii różniących się o niewielką wartość, podczas gdy oczekiwano tylko jednej linii. Pauli sformułował swoją zasadę wykluczenia , stwierdzając: „Atom nie może istnieć w takim stanie kwantowym, że dwa elektrony w nim [jego] mają ten sam zestaw liczb kwantowych”.

Rok później Uhlenbeck i Goudsmit zidentyfikowali nowy stopień swobody Pauliego z właściwością zwaną spinem , której efekty zaobserwowano w eksperymencie Sterna-Gerlacha.

Zastosowanie do atomu wodoru

Główny artykuł: Atomowy model orbitalny

Model atomu Bohra był zasadniczo modelem planetarnym, z elektronami krążącymi wokół jądrowego „słońca”. Jednak zasada nieoznaczoności mówi, że elektron nie może jednocześnie mieć dokładnego położenia i prędkości, tak jak ma to miejsce w przypadku planety. Mówi się, że zamiast klasycznych orbit elektrony zamieszkują orbitale atomowe . Orbital to „chmura” możliwych lokalizacji, w których można znaleźć elektron, rozkład prawdopodobieństw, a nie dokładna lokalizacja. Każdy orbital jest trójwymiarowy, a nie dwuwymiarowy, i często jest przedstawiany jako trójwymiarowy region, w którym istnieje 95-procentowe prawdopodobieństwo znalezienia elektronu.

elektron atomu wodoru jako falę, reprezentowaną przez „ funkcję falową ” Ψ , w studni potencjału elektrycznego , V , utworzonej przez proton. Rozwiązania równania Schrödingera są rozkładami prawdopodobieństw pozycji i lokalizacji elektronów. Orbitale mają szereg różnych kształtów w trzech wymiarach. Energie różnych orbitali można obliczyć i dokładnie odpowiadają one poziomom energii modelu Bohra.

Na obrazie Schrödingera każdy elektron ma cztery właściwości:

1. Oznaczenie „orbitalne”, wskazujące, czy fala cząstki znajduje się bliżej jądra z mniejszą energią, czy też dalej od jądra z większą energią;
2. „Kształt” orbitalny, kulisty lub inny;
3. „Nachylenie” orbity, określające moment magnetyczny orbity wokół osi z .
4. „Spin” elektronu.

Zbiorcza nazwa tych właściwości to stan kwantowy elektronu. Stan kwantowy można opisać, podając liczbę każdej z tych właściwości; liczby kwantowe elektronu . Stan kwantowy elektronu jest opisany przez jego funkcję falową. Zasada wykluczenia Pauliego wymaga, aby żadne dwa elektrony w atomie nie miały takich samych wartości wszystkich czterech liczb.

Kształty orbitali atomowych. Rzędy: 1 s , 2 p , 3 d i 4 f . Od lewej do prawej ${\ Displaystyle m = -l, \ ldots, l}$ . Kolory pokazują fazę funkcji falowej.

Pierwszą właściwością opisującą orbital jest główna liczba kwantowa , n , która jest taka sama jak w modelu Bohra. n oznacza poziom energii każdego orbitalu. Możliwe wartości n to liczby całkowite:

${\ Displaystyle n = 1,2,3 \ ldots}$

Następna liczba kwantowa, azymutalna liczba kwantowa , oznaczona jako l , opisuje kształt orbitalu. Kształt jest konsekwencją momentu pędu orbity. Moment pędu reprezentuje opór wirującego obiektu na przyspieszanie lub zwalnianie pod wpływem siły zewnętrznej. Azymutalna liczba kwantowa reprezentuje orbitalny moment pędu elektronu wokół jego jądra. Możliwe wartości l to liczby całkowite od 0 do n - 1 (gdzie n jest główną liczbą kwantową elektronu):

${\ Displaystyle l = 0,1, \ ldots, n-1.}$

Kształt każdego orbitalu jest zwykle określany za pomocą litery, a nie jego azymutalnej liczby kwantowej. Pierwszy kształt ( l = 0) jest oznaczony literą s ( mnemonikiem jest „ kula ”). Kolejny kształt jest oznaczony literą p i ma postać hantli. Pozostałe orbitale mają bardziej skomplikowane kształty (patrz orbital atomowy ) i są oznaczone literami d , f , g itd.

Trzecia liczba kwantowa, magnetyczna liczba kwantowa , opisuje moment magnetyczny elektronu i jest oznaczana przez ml ₍ lub po prostu m ). Możliwymi wartościami m _l są liczby całkowite od − l do l (gdzie l jest azymutalną liczbą kwantową elektronu):

${\ Displaystyle m_ {l} = -l, - (l-1), \ ldots, 0, \ ldots, (l-1), l.}$

Magnetyczna liczba kwantowa mierzy składową momentu pędu w określonym kierunku. Wybór kierunku jest dowolny; konwencjonalnie wybierany jest kierunek z.

Czwarta liczba kwantowa, spinowa liczba kwantowa (odnosząca się do „orientacji” spinu elektronu) jest oznaczana m _s , wartościami + 1 ⁄ 2 lub − 1 ⁄ 2 .

Chemik Linus Pauling napisał na przykład:

W przypadku atomu helu z dwoma elektronami na orbicie 1 s zasada wykluczenia Pauliego wymaga, aby dwa elektrony różniły się wartością jednej liczby kwantowej. Ich wartości n , l i ml _. są takie same W związku z tym muszą różnić się wartością m _s , która może mieć wartość + 1 ⁄ 2 dla jednego elektronu i − 1 ⁄ 2 dla drugiego”.

To podstawowa struktura i symetria orbitali atomowych oraz sposób, w jaki wypełniają je elektrony, prowadzi do organizacji układu okresowego pierwiastków . Sposób, w jaki orbitale atomowe na różnych atomach łączą się, tworząc orbitale molekularne, określa strukturę i siłę wiązań chemicznych między atomami.

Równanie falowe Diraca

Główny artykuł: równanie Diraca

Paul Dirac (1902–1984)

W 1928 roku Paul Dirac rozszerzył równanie Pauliego opisujące wirujące elektrony, aby uwzględnić szczególną teorię względności . Rezultatem była teoria, która właściwie radziła sobie ze zdarzeniami, takimi jak prędkość, z jaką elektron krąży wokół jądra, występująca przy znacznej części prędkości światła . Wykorzystując najprostsze oddziaływanie elektromagnetyczne , Dirac był w stanie przewidzieć wartość momentu magnetycznego związanego ze spinem elektronu i znaleźć zaobserwowaną eksperymentalnie wartość, która była zbyt duża, aby mogła być wartością wirującej naładowanej kuli regulowanej przez fizyka klasyczna . Był w stanie rozwiązać linie widmowe atomu wodoru i odtworzyć na podstawie pierwszych zasad fizycznych udany wzór Sommerfelda na subtelną strukturę widma wodoru.

Równania Diraca czasami dawały ujemną wartość energii, dla której proponował nowatorskie rozwiązanie: zakładał istnienie antyelektronu i dynamicznej próżni. Doprowadziło to do powstania wielocząstkowej kwantowej teorii pola .

Splątanie kwantowe

Główny artykuł: Splątanie kwantowe

Superpozycja dwóch charakterystyk kwantowych i dwie możliwości rozdzielczości

Zasada wykluczenia Pauliego mówi, że dwa elektrony w jednym układzie nie mogą znajdować się w tym samym stanie. Natura pozostawia jednak otwartą możliwość, że dwa elektrony mogą mieć oba stany „nałożone” na każdy z nich. Przypomnijmy, że funkcje falowe, które pojawiają się jednocześnie z podwójnych szczelin, docierają do ekranu detekcji w stanie superpozycji. Nic nie jest pewne, dopóki nałożone na siebie przebiegi nie „zapadną się”. W tym momencie elektron pojawia się gdzieś zgodnie z prawdopodobieństwem, które jest kwadratem wartości bezwzględnej sumy zespolonych amplitud dwóch nałożonych przebiegów. Tam sytuacja jest już bardzo abstrakcyjna. Konkretny sposób myślenia o fotonach splątanych, czyli fotonach, w których dwa przeciwne stany nakładają się na każdy z nich w tym samym zdarzeniu, jest następujący:

Wyobraź sobie, że mamy dwa oznaczone kolorami stany fotonów: jeden stan oznaczony jako niebieski , a drugi oznaczony jako czerwony . Niech superpozycja stanu czerwonego i niebieskiego pojawi się (w wyobraźni) jako purpura państwo. Rozważymy przypadek, w którym w wyniku pojedynczego zdarzenia atomowego powstają dwa fotony. Być może są one wytwarzane przez wzbudzenie kryształu, który w charakterystyczny sposób pochłania foton o określonej częstotliwości i emituje dwa fotony o połowie pierwotnej częstotliwości. W tym przypadku fotony są ze sobą połączone poprzez wspólne pochodzenie w pojedynczym zdarzeniu atomowym. Ta konfiguracja skutkuje nakładającymi się stanami fotonów. Więc dwa fotony wychodzą fioletowe. Jeśli eksperymentator przeprowadza teraz jakiś eksperyment, który określa, czy jeden z fotonów jest niebieski czy czerwony , to ten eksperyment zmienia zaangażowany foton z fotonu mającego superpozycję niebieskich i czerwonych cech na foton, który ma tylko jedną z tych cech. Problem, jaki miał Einstein z taką wyimaginowaną sytuacją, polegał na tym, że jeśli jeden z tych fotonów odbijał się między lustrami w laboratorium na Ziemi, a drugi przebył połowę drogi do najbliższej gwiazdy, kiedy jego bliźniak został ujawniony jako albo niebieski lub czerwony, oznaczało to, że odległy foton musiał teraz stracić swoją purpurę stan też. Więc ilekroć można by go zbadać po zmierzeniu jego bliźniaka, musiałby koniecznie pojawić się w stanie przeciwnym do tego, co ujawnił jego bliźniak.

Próbując wykazać, że mechanika kwantowa nie jest kompletną teorią, Einstein zaczął od przewidywania teorii, że dwie lub więcej cząstek, które oddziaływały w przeszłości, może wydawać się silnie skorelowane, gdy później zmierzy się ich różne właściwości. Starał się wyjaśnić tę pozorną interakcję klasycznie, poprzez ich wspólną przeszłość, a najlepiej nie jakimś „upiornym działaniem na odległość”. Argument ten został przedstawiony w słynnej pracy Einsteina, Podolsky'ego i Rosena (1935; w skrócie EPR) przedstawiającej to, co obecnie nazywa się paradoksem EPR . Zakładając to, co obecnie nazywa się lokalnym realizmem , EPR próbował wykazać na podstawie teorii kwantowej, że cząstka ma jednocześnie położenie i pęd, podczas gdy zgodnie z interpretacją kopenhaską tylko jedna z tych dwóch właściwości faktycznie istnieje i tylko w momencie jej pomiaru. EPR doszedł do wniosku, że teoria kwantowa jest niekompletna, ponieważ odmawia uwzględnienia właściwości fizycznych, które obiektywnie istnieją w przyrodzie. (Einstein, Podolsky, & Rosen 1935 jest obecnie najczęściej cytowaną publikacją Einsteina w czasopismach fizycznych). W tym samym roku Erwin Schrödinger użył słowa „splątanie” i oświadczył: „Nie nazwałbym tego jest raczej charakterystyczną cechą mechaniki kwantowej”. Odkąd irlandzki fizyk John Stewart Bell teoretycznie i eksperymentalnie obalił teorię „ukrytych zmiennych” Einsteina, Podolsky'ego i Rosena, większość fizyków zaakceptowała splątanie jako rzeczywiste zjawisko. Istnieją jednak pewne spór mniejszości Nierówności Bella są najpotężniejszym wyzwaniem dla twierdzeń Einsteina.

Kwantowa teoria pola

Główny artykuł: Kwantowa teoria pola

Idea kwantowej teorii pola rozpoczęła się pod koniec lat dwudziestych XX wieku od brytyjskiego fizyka Paula Diraca , który próbował skwantować energię pola elektromagnetycznego ; podobnie jak w mechanice kwantowej skwantyzowano energię elektronu w atomie wodoru. Kwantyzacja to procedura konstruowania teorii kwantowej wychodząc od teorii klasycznej.

Merriam-Webster definiuje dziedzinę fizyki jako „obszar lub przestrzeń, w której istnieje określony efekt (taki jak magnetyzm )”. Inne efekty, które objawiają się jako pola, to grawitacja i elektryczność statyczna . W 2008 roku fizyk Richard Hammond napisał:

Czasami rozróżniamy mechanikę kwantową (QM) i kwantową teorię pola (QFT). QM odnosi się do systemu, w którym liczba cząstek jest stała, a pola (takie jak pole elektromechaniczne) są ciągłymi jednostkami klasycznymi. QFT… idzie o krok dalej i pozwala na tworzenie i anihilację cząstek…

Dodał jednak, że mechanika kwantowa jest często używana w odniesieniu do „całego pojęcia widzenia kwantowego”.

W 1931 roku Dirac zaproponował istnienie cząstek, które później stały się znane jako antymateria . Dirac podzielił Nagrodę Nobla w dziedzinie fizyki za rok 1933 ze Schrödingerem „za odkrycie nowych produktywnych form teorii atomowej ”.

Na pierwszy rzut oka kwantowa teoria pola dopuszcza nieskończoną liczbę cząstek i pozostawia samej teorii przewidywanie, ile i z jakim prawdopodobieństwem lub liczbami powinny one istnieć. Po dalszym rozwinięciu teoria często zaprzecza obserwacji, tak że jej operatory tworzenia i anihilacji można empirycznie powiązać. Ponadto empiryczne prawa zachowania, takie jak prawo masy i energii zasugerować pewne ograniczenia matematycznej postaci teorii, które z matematycznego punktu widzenia są wybredne. Ten ostatni fakt utrudnia posługiwanie się kwantowymi teoriami pola, ale doprowadził również do dalszych ograniczeń dopuszczalnych form teorii; powikłania są wymienione poniżej w rubryce renormalizacja .

Elektrodynamika kwantowa

Główny artykuł: elektrodynamika kwantowa

Elektrodynamika kwantowa (QED) to nazwa kwantowej teorii siły elektromagnetycznej . Zrozumienie QED zaczyna się od zrozumienia elektromagnetyzmu . Elektromagnetyzm można nazwać „elektrodynamiką”, ponieważ jest to dynamiczna interakcja między siłami elektrycznymi i magnetycznymi . Elektromagnetyzm zaczyna się od ładunku elektrycznego .

Ładunki elektryczne są źródłem i tworzą pola elektryczne . Pole elektryczne to pole, które wywiera siłę na dowolne cząstki przenoszące ładunki elektryczne w dowolnym punkcie przestrzeni. Obejmuje to między innymi elektron, proton, a nawet kwarki . Gdy działa siła, poruszają się ładunki elektryczne, płynie prąd i wytwarzane jest pole magnetyczne. Z kolei zmieniające się pole magnetyczne wywołuje prąd elektryczny (często poruszające się elektrony). Fizyczny opis oddziałujących naładowanych cząstek , prądów elektrycznych, pól elektrycznych i pól magnetycznych nazywa się elektromagnetyzmem.

W 1928 roku Paul Dirac stworzył relatywistyczną kwantową teorię elektromagnetyzmu. To był prekursor współczesnej elektrodynamiki kwantowej, ponieważ zawierał podstawowe składniki współczesnej teorii. Jednak problem nierozwiązywalnych nieskończoności rozwinął się w tej relatywistycznej teorii kwantowej . Wiele lat później renormalizacja w dużej mierze rozwiązała ten problem. Początkowo postrzegana jako tymczasowa, podejrzana procedura przez niektórych jej twórców, renormalizacja ostatecznie została przyjęta jako ważne i samospójne narzędzie w QED i innych dziedzinach fizyki. Również pod koniec lat czterdziestych diagramy Feynmana zobrazował wszystkie możliwe interakcje na danym zdarzeniu. Diagramy pokazały w szczególności, że siła elektromagnetyczna to wymiana fotonów między oddziałującymi cząstkami.

Przesunięcie Lamba jest przykładem przewidywania elektrodynamiki kwantowej, które zostało zweryfikowane eksperymentalnie. Jest to efekt, w wyniku którego kwantowa natura pola elektromagnetycznego powoduje, że poziomy energii w atomie lub jonie nieznacznie odbiegają od tego, jaki byłby w innym przypadku. W rezultacie linie widmowe mogą się przesuwać lub rozdzielać.

Podobnie, w swobodnie rozchodzącej się fali elektromagnetycznej, prąd może być po prostu abstrakcyjnym prądem przesunięcia , zamiast obejmować nośniki ładunku. W QED jego pełny opis zasadniczo wykorzystuje krótkotrwałe cząstki wirtualne . Tam QED ponownie potwierdza wcześniejszą, raczej tajemniczą koncepcję.

Model standardowy

Główny artykuł: Model standardowy

W latach sześćdziesiątych fizycy zdali sobie sprawę, że QED rozpada się przy ekstremalnie wysokich energiach. Na podstawie tej niekonsekwencji odkryto Model Standardowy fizyki cząstek elementarnych, który teoretycznie zaradził załamaniu wyższych energii. Jest to kolejna rozszerzona kwantowa teoria pola, która łączy oddziaływania elektromagnetyczne i słabe w jedną teorię. Nazywa się to teorią elektrosłabą .

Dodatkowo Model Standardowy zawiera wysokoenergetyczną unifikację teorii elektrosłabej z oddziaływaniem silnym , opisanym przez chromodynamikę kwantową . Postuluje również związek z grawitacją jako kolejną teorię cechowania , ale związek ten jest nadal słabo poznany od 2015 roku. Udane przewidywanie przez teorię cząstki Higgsa w celu wyjaśnienia masy bezwładności zostało potwierdzone przez Wielki Zderzacz Hadronów , a zatem Model Standardowy jest obecnie uważany za podstawowy i mniej lub bardziej kompletny opis fizyki cząstek elementarnych , jaką znamy.

Interpretacje

Główny artykuł: Interpretacje mechaniki kwantowej

Fizyczne pomiary, równania i przewidywania dotyczące mechaniki kwantowej są spójne i posiadają bardzo wysoki poziom potwierdzenia. Jednak pytanie, co te abstrakcyjne modele mówią o naturze rzeczywistego świata, otrzymało konkurencyjne odpowiedzi. Te interpretacje są bardzo zróżnicowane, a czasem nieco abstrakcyjne. Na przykład interpretacja kopenhaska stwierdza, że ​​przed pomiarem twierdzenia o właściwościach cząstki są całkowicie bezsensowne, podczas gdy w interpretacji wielu światów opisuje istnienie multiwersu składa się z każdego możliwego wszechświata.

Aplikacje

Główny artykuł: Mechanika kwantowa: zastosowania

Zastosowania mechaniki kwantowej obejmują laser , tranzystor , mikroskop elektronowy i rezonans magnetyczny . Specjalna klasa zastosowań mechaniki kwantowej jest związana z makroskopowymi zjawiskami kwantowymi , takimi jak nadciekły hel i nadprzewodniki. Badania nad półprzewodnikami doprowadziły do ​​wynalezienia diody i tranzystora , które są nieodzowne we współczesnej elektronice .

Nawet w prostym przełączniku światła tunelowanie kwantowe jest absolutnie niezbędne, ponieważ w przeciwnym razie elektrony w prądzie elektrycznym nie mogłyby przeniknąć przez barierę potencjału złożoną z warstwy tlenku. Chipy pamięci flash znalezione w napędach USB również wykorzystują tunelowanie kwantowe, aby wymazać ich komórki pamięci.

Zobacz też

• Eksperymenty myślowe Einsteina
• Makroskopowe zjawiska kwantowe
• Filozofia fizyki
• Obliczenia kwantowe
• Wirtualna cząsteczka
• Wykaz podręczników mechaniki klasycznej i kwantowej

Bibliografia

• Bernstein, Jeremy (2005). „Max Born i teoria kwantowa”. American Journal of Physics . 73 (11): 999–1008. Bibcode : 2005AmJPh..73..999B . doi : 10.1119/1.2060717 .
• Beller, Mara (2001). Dialog kwantowy: tworzenie rewolucji . Wydawnictwo Uniwersytetu Chicagowskiego.
•    Bohr, Niels (1958). Fizyka atomowa i wiedza o człowieku . John Wiley & Synowie]. ISBN 0486479285 . OCLC 530611 .
•   de Broglie, Louis (1953). Rewolucja w fizyce . Prasa w południe. LCCN 53010401 .
•   Bronner, Patryk; Strunz, Andreas; Silberhorn, Krystyna; Meyn, Jan-Peter (2009). „Wykazanie losowości kwantowej za pomocą pojedynczych fotonów”. Europejski Dziennik Fizyki . 30 (5): 1189-1200. Bibcode : 2009EJPh...30.1189B . doi : 10.1088/0143-0807/30/5/026 . S2CID 7903179 .
•    Einstein, Albert (1934). Eseje w nauce . Biblioteka Filozoficzna . ISBN 0486470113 . LCCN 55003947 .
•    Feigl, Herbert ; Brodbeck, maj (1953). Odczyty z filozofii nauki . Appleton-Century-Crofts. ISBN 0390304883 . LCCN 53006438 .
• Feynman, Richard P. (1949). „Podejście czasoprzestrzenne do elektrodynamiki kwantowej” . Przegląd fizyczny . 76 (6): 769–89. Bibcode : 1949PhRv...76..769F . doi : 10.1103/PhysRev.76.769 .
•   Feynman, Richard P. (1990). QED, Dziwna teoria światła i materii . Książki o pingwinach. ISBN 978-0140125054 .
• Fowler, Michael (1999). Atom Bohra . Uniwersytet Wirginii.
•    Heisenberg, Werner (1958). Fizyka i Filozofia . Harper i bracia. ISBN 0061305499 . LCCN 99010404 .
•   Lakshmibala, S. (2004). „Heisenberg, mechanika macierzy i zasada nieoznaczoności”. Rezonans: Journal of Science Education . 9 (8): 46–56. doi : 10.1007/bf02837577 . S2CID 29893512 .
•   Liboff, Richard L. (1992). Wstępna mechanika kwantowa (wyd. 2). Pub Addison-Wesley. Co ISBN 9780201547153 .
•    Lindsay, Robert Bruce; Margenau, Henry (1957). Podstawy fizyki . Dover. ISBN 0918024188 . LCCN 57014416 .
•   McEvoy, JP; Zarate, Oscar (2004). Przedstawiamy teorię kwantową . ISBN 1874166374 .
• Nawa, Carl Rod (2005). „Fizyka kwantowa” . Hiperfizyka . Georgia State University.
• Torf, F. David (2002). Od pewności do niepewności: historia nauki i idei w XXI wieku . Józefa Henryka Pressa .
•    Reichenbach, Hans (1944). Filozoficzne podstawy mechaniki kwantowej . Wydawnictwo Uniwersytetu Kalifornijskiego. ISBN 0486404595 . LCCN a44004471 .
•   Schilpp, Paul Arthur (1949). Albert Einstein: filozof-naukowiec . Wydawnictwo Tudorów. LCCN 50005340 .
• Amerykański czytelnik naukowy , 1953.
•    Sears, Francis Weston (1949). Optyka (wyd. 3). Addison-Wesley. ISBN 0195046013 . LCCN 51001018 .
• Shimony, A. (1983). „(tytuł nie podany w cytacie)”. Podstawy mechaniki kwantowej w świetle nowych technologii (S. Kamefuchi i in., red.) . Tokio: Japońskie Towarzystwo Fizyczne. P. 225. ; cyt. w: Popescu, Sandu; Daniela Rohrlicha (1996). „Akcja i pasja na odległość: esej na cześć profesora Abnera Shimony'ego”. arXiv : kwant-ph/9605004 .
•   Tawel, Morton; Tavel, Judith (ilustracje) (2002). Fizyka współczesna i granice poznania . Rutgers University Press. ISBN 978-0813530772 .
• Van Vleck, JH, 1928, „Zasada zgodności w statystycznej interpretacji mechaniki kwantowej”, Proc. Natl. Acad. nauka 14: 179.
• Westmoreland; Benjamina Schumachera (1998). „Splątanie kwantowe i nieistnienie sygnałów nadświetlnych”. arXiv : kwant-ph/9801014 .
• Wheeler, John Archibald ; Feynman, Richard P. (1949). „Elektrodynamika klasyczna w kategoriach bezpośredniego działania międzycząsteczkowego” (PDF) . Recenzje współczesnej fizyki . 21 (3): 425–33. Bibcode : 1949RvMP...21..425W . doi : 10.1103/RevModPhys.21.425 .
• Wieman, Carl; Perkins, Katherine (2005). „Transformacja edukacji fizycznej”. Fizyka dzisiaj . 58 (11): 36. Bibcode : 2005PhT....58k..36W . doi : 10.1063/1.2155756 .

Dalsza lektura

Poniższe tytuły, wszystkie autorstwa pracujących fizyków, mają na celu przekazanie teorii kwantowej laikom przy użyciu minimalnej aparatury technicznej.

•   Jim Al-Khalili (2003). Quantum: przewodnik dla zakłopotanych . Weidenfelda i Nicolsona. ISBN 978-1780225340 .
•   Chester, Marvin (1987). Elementarz mechaniki kwantowej . Johna Wileya. ISBN 0486428788 .
•   Brian Cox i Jeff Forshaw (2011) Kwantowy Wszechświat . Allena Lane'a. ISBN 978-1846144325 .
•   Richarda Feynmana (1985). QED: Dziwna teoria światła i materii . Wydawnictwo Uniwersytetu Princeton. ISBN 0691083886 .
• Ford, Kenneth (2005). Świat kwantowy . Uniwersytet Harvarda Naciskać. Obejmuje fizykę cząstek elementarnych.
• Ghirardi, GianCarlo (2004). Ukradkowe spojrzenie na karty Boga , Gerald Malsbary, przeł. Uniwersytet Princeton Naciskać. Najbardziej techniczna z cytowanych tutaj prac. Fragmenty wykorzystujące algebrę , trygonometrię i notację bra-ket można pominąć przy pierwszym czytaniu.
•   Tony Hej i Walters, Patrick (2003). Nowy Wszechświat Kwantowy . Uniwersytet Cambridge Naciskać. Zawiera wiele informacji na temat technologii, które umożliwiła teoria kwantowa. ISBN 978-0521564571 .
•   Władimir G. Ivancevic, Tijana T. Ivancevic (2008). Skok kwantowy: od Diraca i Feynmana przez wszechświat do ludzkiego ciała i umysłu . Światowe Wydawnictwo Naukowe. Zapewnia intuicyjne wprowadzenie w kategoriach niematematycznych i wprowadzenie w stosunkowo podstawowych terminach matematycznych. ISBN 978-9812819277 .
•   JP McEvoy i Oscar Zarate (2004). Przedstawiamy teorię kwantową . Księgi totemów. ISBN 1840465778 '
•   N. David Mermin (1990). „Straszne działania na odległość: tajemnice QT” w jego Boojums przez całą drogę . Uniwersytet Cambridge Prasa: 110–76. Autor jest rzadkim fizykiem, który próbuje komunikować się z filozofami i humanistami. ISBN 978-0521388801 .
•   Rolanda Omnèsa (1999). Zrozumienie mechaniki kwantowej . Uniwersytet Princeton Naciskać. ISBN 978-0691004358 .
•   Victora Stengera (2000). Ponadczasowa rzeczywistość: symetria, prostota i wiele wszechświatów . Buffalo NY: Prometeusz Książki. rozdziały 5–8. ISBN 978-1573928595 .
•   Martinusa Veltmana (2003). Fakty i tajemnice w fizyce cząstek elementarnych . Światowe Wydawnictwo Naukowe. ISBN 978-9812381491 .

Linki zewnętrzne

• „ Świat mikroskopowy - wprowadzenie do mechaniki kwantowej”. autorstwa Takady, Kenjiro, emerytowanego profesora na Uniwersytecie Kyushu
• Quantum Exchange (samouczki i oprogramowanie do nauki typu open source).
• Atomy i układ okresowy pierwiastków
• Interferencja na pojedynczej i podwójnej szczelinie
• Ewolucja w czasie pakietu falowego w kwadratowej studni Animowana demonstracja rozproszenia pakietu falowego w czasie.
• Carroll, Sean M. „Mechanika kwantowa (wstyd)” . Sześćdziesiąt symboli . Brady Haran z Uniwersytetu w Nottingham.