Czarne ciało

Aby zapoznać się z promieniowaniem ciała doskonale czarnego w równowadze termicznej, zobacz Promieniowanie ciała doskonale czarnego . W przypadku kanadyjskiego filmu krótkometrażowego zobacz Black Bodies (film) .

Grzejnik typu Black Body stosowany w laboratorium CARLO w Polsce. Jest to przybliżenie modelu opisanego przez prawo Plancka stosowanego jako widmowy wzorzec natężenia napromienienia .

Wraz ze spadkiem temperatury ciała doskonale czarnego zmniejsza się również jego intensywność, a szczyt przesuwa się w kierunku dłuższych fal. Dla porównania pokazano klasyczne prawo Rayleigha-Jeansa i jego katastrofę w ultrafiolecie .

Ciało doskonale czarne lub ciało doskonale czarne to wyidealizowane ciało fizyczne , które pochłania całe padające promieniowanie elektromagnetyczne , niezależnie od częstotliwości lub kąta padania . Nazwa „ciało doskonale czarne” pochodzi od tego, że pochłania ono wszystkie kolory światła. Ciało doskonale czarne emituje również promieniowanie ciała doskonale czarnego . W przeciwieństwie do tego, białe ciało to takie, które ma „szorstką powierzchnię, która całkowicie i równomiernie odbija wszystkie padające promienie we wszystkich kierunkach”.

Ciało doskonale czarne w równowadze termicznej (to znaczy w stałej temperaturze) emituje promieniowanie elektromagnetyczne ciała doskonale czarnego. Promieniowanie jest emitowane zgodnie z prawem Plancka , co oznacza, że ​​jego widmo zależy wyłącznie od temperatury (patrz rysunek po prawej), a nie od kształtu czy składu ciała.

Idealne ciało doskonale czarne w równowadze termicznej ma dwie główne właściwości:

1. Jest idealnym emiterem: przy każdej częstotliwości emituje tyle samo lub więcej energii promieniowania cieplnego, co każde inne ciało w tej samej temperaturze.
2. Jest to emiter rozproszony: mierzona na jednostkę powierzchni prostopadle do kierunku, energia jest promieniowana izotropowo , niezależnie od kierunku.

Przybliżona realizacja czarnej powierzchni to otwór w ścianie dużej izolowanej obudowy ( na przykład piekarnika ). Każde światło wpadające do otworu jest odbijane lub pochłaniane na wewnętrznych powierzchniach ciała i jest mało prawdopodobne, aby ponownie się pojawiło, dzięki czemu otwór jest prawie idealnym pochłaniaczem. Kiedy promieniowanie zamknięte w takiej obudowie jest w równowadze termicznej, promieniowanie emitowane z otworu będzie tak duże, jak promieniowanie dowolnego ciała w tej temperaturze równowagi.

Rzeczywiste materiały emitują energię na poziomie ułamka — zwanego emisyjnością — poziomów energii ciała doskonale czarnego. Z definicji ciało doskonale czarne w równowadze termicznej ma emisyjność ε = 1 . Źródło o niższej emisyjności, niezależnej od częstotliwości, jest często określane jako ciało szare. Konstruowanie ciał czarnych o emisyjności jak najbliższej 1 pozostaje tematem aktualnego zainteresowania.

W astronomii promieniowanie gwiazd i planet jest czasami charakteryzowane za pomocą efektywnej temperatury , temperatury ciała doskonale czarnego, które emitowałoby ten sam całkowity strumień energii elektromagnetycznej.

Definicja

Idea ciała doskonale czarnego została pierwotnie przedstawiona przez Gustava Kirchhoffa w 1860 roku w następujący sposób:

... przypuszczenie, że można sobie wyobrazić ciała, które przy nieskończenie małych grubościach całkowicie pochłaniają wszystkie padające promienie i ani ich nie odbijają, ani nie przepuszczają. Takie ciała będę nazywał ciałami doskonale czarnymi lub, krócej, ciałami czarnymi .

Bardziej nowoczesna definicja odrzuca odniesienie do „nieskończenie małych grubości”:

Idealne ciało jest teraz zdefiniowane, zwane ciałem doskonale czarnym . Ciało doskonale czarne przepuszcza całe padające promieniowanie (brak odbitej energii) i wewnętrznie pochłania całe padające promieniowanie (brak energii przenoszonej przez ciało). Dotyczy to promieniowania o wszystkich długościach fal i dla wszystkich kątów padania. Stąd ciało doskonale czarne jest doskonałym pochłaniaczem dla całego padającego promieniowania.

Idealizacje

W tej sekcji opisano niektóre koncepcje opracowane w związku z ciałami doskonale czarnymi.

Przybliżona realizacja czarnego ciała jako małej dziury w izolowanej obudowie

Wnęka z otworem

Powszechnie stosowanym modelem czarnej powierzchni jest mały otwór we wnęce o ścianach nieprzezroczystych dla promieniowania. Promieniowanie padające na otwór przejdzie do wnęki i jest bardzo mało prawdopodobne, aby zostało ponownie wyemitowane, jeśli wnęka jest duża. Dziura nie jest idealnie czarną powierzchnią — w szczególności, jeśli długość fali padającego promieniowania jest większa niż średnica otworu, część zostanie odbita. Podobnie, nawet w doskonałej równowadze termicznej, promieniowanie wewnątrz wnęki o skończonych rozmiarach nie będzie miało idealnego widma Plancka dla długości fal porównywalnych lub większych niż rozmiar wnęki.

Załóżmy, że we wnęce utrzymywana jest stała temperatura T , a promieniowanie uwięzione wewnątrz obudowy jest w równowadze termicznej z obudową. Otwór w obudowie pozwoli na ucieczkę części promieniowania. Jeśli otwór jest mały, promieniowanie wchodzące i wychodzące z otworu ma znikomy wpływ na równowagę promieniowania wewnątrz wnęki. To uciekające promieniowanie będzie zbliżone do promieniowania ciała doskonale czarnego , które wykazuje rozkład energii charakterystyczny dla temperatury T i nie zależy od właściwości wnęki lub otworu, przynajmniej dla długości fal mniejszych niż rozmiar otworu. Zobacz rysunek we wprowadzeniu, aby zobaczyć widmo jako funkcję częstotliwości promieniowania, które jest powiązane z energią promieniowania równaniem E = hf , gdzie E = energia, h = stała Plancka , f = częstotliwość.

W dowolnym momencie promieniowanie we wnęce może nie znajdować się w równowadze termicznej, ale druga zasada termodynamiki mówi, że pozostawione w spokoju ostatecznie osiągnie równowagę, chociaż czas potrzebny na to może być bardzo długi. Zazwyczaj równowagę osiąga się przez ciągłą absorpcję i emisję promieniowania przez materiał wnęki lub jej ścian. Promieniowanie wchodzące do wnęki zostanie „ ztermalizowane ” przez ten mechanizm: energia będzie redystrybuowana, dopóki zespół fotonów nie osiągnie rozkładu Plancka . Czas potrzebny do termalizacji jest znacznie krótszy w przypadku obecności skondensowanej materii niż w przypadku materii rozrzedzonej, takiej jak rozcieńczony gaz. W temperaturach poniżej miliardów kelwinów bezpośrednie interakcje foton-foton są zwykle pomijalne w porównaniu z interakcjami z materią. Fotony są przykładem oddziałującego bozonowego i jak opisano w twierdzeniu H , w bardzo ogólnych warunkach każdy oddziałujący gaz bozonowy zbliży się do równowagi termicznej.

Transmisja, absorpcja i odbicie

Zachowanie ciała w odniesieniu do promieniowania cieplnego charakteryzuje się jego transmisją τ , absorpcją α i odbiciem ρ .

Granica ciała tworzy interfejs z otoczeniem, a interfejs ten może być szorstki lub gładki. Nieodbijająca granica międzyfazowa oddzielająca obszary o różnych współczynnikach załamania światła musi być zgrubna, ponieważ prawa odbicia i załamania rządzące równaniami Fresnela dla gładkiej granicy wymagają odbitego promienia, gdy współczynniki załamania materiału i jego otoczenia różnią się. Kilka wyidealizowanych typów zachowań ma określone nazwy:

Ciało nieprzezroczyste to takie, które nie przepuszcza żadnego docierającego do niego promieniowania, chociaż niektóre mogą zostać odbite. Oznacza to, że τ = 0 i α + ρ = 1.

Przezroczyste ciało to takie, które przepuszcza całe docierające do niego promieniowanie. Oznacza to, że τ = 1 i α = ρ = 0.

Ciało szare to takie, w którym α , ρ i τ są stałe dla wszystkich długości fal. Termin ten jest również używany do oznaczenia ciała, dla którego α jest niezależne od temperatury i długości fali.

Ciało białe to takie, w przypadku którego całe padające promieniowanie odbija się równomiernie we wszystkich kierunkach: τ = 0, α = 0 i ρ = ​​1.

Dla ciała doskonale czarnego τ = 0, α = 1 i ρ = ​​0. Planck oferuje teoretyczny model ciał doskonale czarnych, które, jak zauważył, nie istnieją w naturze: poza nieprzezroczystym wnętrzem mają interfejsy, które doskonale przepuszczają i nierefleksyjne.

Doskonałe czarne ciała Kirchhoffa

Kirchhoff w 1860 roku przedstawił teoretyczną koncepcję doskonale czarnego ciała z całkowicie absorbującą warstwą powierzchniową o nieskończenie małej grubości, ale Planck zauważył pewne poważne ograniczenia tego pomysłu. Planck zwrócił uwagę na trzy wymagania dotyczące ciała doskonale czarnego: ciało musi (i) przepuszczać promieniowanie, ale nie odbijać; (ii) posiadać minimalną grubość odpowiednią do pochłaniania padającego promieniowania i zapobiegania jego ponownej emisji; (iii) spełniać surowe ograniczenia dotyczące rozpraszania , aby zapobiec przedostawaniu się i odbijaniu promieniowania. W konsekwencji doskonałe czarne ciała Kirchhoffa, które pochłaniają całe padające na nie promieniowanie, nie mogą być zrealizowane w nieskończenie cienkiej warstwie powierzchniowej i narzucają warunki rozpraszania światła w ciele czarnym, które są trudne do spełnienia.

Realizacje

Realizacja czarnego ciała odnosi się do realnego świata, fizycznego ucieleśnienia. Tu jest kilka.

Wnęka z otworem

W 1898 roku Otto Lummer i Ferdinand Kurlbaum opublikowali opis źródła promieniowania wnękowego. Ich konstrukcja była używana w dużej mierze niezmieniona do pomiarów promieniowania do dnia dzisiejszego. Była to dziura w ścianie platynowej skrzynki, podzielona przesłonami, której wnętrze poczerniało od tlenku żelaza. Był ważnym składnikiem stopniowo udoskonalonych pomiarów, które doprowadziły do ​​odkrycia prawa Plancka. Wersja opisana w 1901 roku miała wnętrze poczerniałe mieszaniną tlenków chromu, niklu i kobaltu. Zobacz także Hohlraum .

Prawie czarne materiały

Istnieje zainteresowanie materiałami podobnymi do ciała czarnego do kamuflażu i materiałami pochłaniającymi radary, zapewniającymi niewidzialność radaru. Mają również zastosowanie jako kolektory energii słonecznej oraz detektory termiczne na podczerwień. Jako doskonały emiter promieniowania, gorący materiał zachowujący się jak ciało doskonale czarne stworzyłby wydajny grzejnik na podczerwień, szczególnie w kosmosie lub w próżni, gdzie ogrzewanie konwekcyjne jest niedostępne. Są również przydatne w teleskopach i kamerach jako powierzchnie przeciwodblaskowe w celu zmniejszenia rozproszonego światła i gromadzenia informacji o obiektach w obszarach o wysokim kontraście (na przykład obserwacja planet na orbicie wokół ich gwiazd), gdzie materiały podobne do ciała doskonale czarnego pochłaniają światło które pochodzi z niewłaściwych źródeł.

Od dawna wiadomo, że czarna jak lampa powłoka sprawi, że ciało będzie prawie czarne. W produkowanych nanorurkach węglowych można znaleźć poprawę w stosunku do czerni lampowej . Materiały nanoporowate mogą osiągnąć współczynniki załamania światła zbliżone do próżni, w jednym przypadku uzyskując średni współczynnik odbicia 0,045%. W 2009 roku zespół japońskich naukowców stworzył materiał o nazwie nanoblack, który jest bliski idealnemu ciału doskonale czarnemu, w oparciu o ustawione pionowo, jednościenne nanorurki węglowe . Pochłania to od 98% do 99% padającego światła w zakresie widmowym od ultrafioletu do dalekiej podczerwieni.

Inne przykłady niemal doskonałych czarnych materiałów to superczarne , przygotowane przez chemiczne wytrawianie stopu niklu i fosforu , ustawione pionowo układy nanorurek węglowych (jak VantaBlack ) i kwiatowe nanostruktury węglowe; wszystkie pochłaniają 99,9% światła lub więcej.

Gwiazdy i planety

Aby uzyskać więcej informacji na temat indeksu kolorów UBV, zobacz System fotometryczny .

Wyidealizowany widok przekroju poprzecznego gwiazdy. Fotosfera zawiera fotony światła prawie w równowadze termicznej, a niektóre uciekają w przestrzeń kosmiczną jako promieniowanie ciała bliskiego doskonale czarnemu .

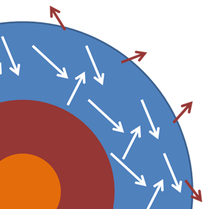
Gwiazda lub planeta jest często modelowana jako ciało doskonale czarne, a promieniowanie elektromagnetyczne emitowane z tych ciał jako promieniowanie ciała doskonale czarnego . Rysunek przedstawia bardzo schematyczny przekrój ilustrujący ten pomysł. Fotosfera , w której fotony światła oddziałują z materią w fotosferze i osiągają wspólną temperaturę T, która jest utrzymywana przez długi okres czasu . Niektóre fotony uciekają i są emitowane w przestrzeń kosmiczną, ale energia, którą przenoszą, jest zastępowana energią z wnętrza gwiazdy, dzięki czemu temperatura fotosfery jest prawie stała. Zmiany w jądrze prowadzą do zmian w dostawie energii do fotosfery, ale zmiany te są powolne w interesującej nas skali czasowej. Zakładając, że te okoliczności mogą zostać zrealizowane, zewnętrzna warstwa gwiazdy jest nieco analogiczna do przykładu obudowy z małym otworem, w którym otwór zastąpiono ograniczoną transmisją w przestrzeń na zewnątrz fotosfery. Przy wszystkich tych założeniach gwiazda emituje promieniowanie ciała doskonale czarnego w temperaturze fotosfery.

Efektywna temperatura ciała doskonale czarnego w porównaniu z indeksem koloru BV i UB gwiazd ciągu głównego i superolbrzymów na tak zwanym diagramie kolor-kolor .

Za pomocą tego modelu szacuje się efektywną temperaturę gwiazd, zdefiniowaną jako temperaturę ciała doskonale czarnego, które daje taki sam powierzchniowy strumień energii jak gwiazda. Gdyby gwiazda była ciałem czarnym, taka sama efektywna temperatura wynikałaby z dowolnego obszaru widma. Na przykład porównania w B (niebieskim) lub V (widocznym) prowadzą do tak zwanego indeksu koloru BV , który zwiększa stopień czerwieni gwiazdy, przy czym indeks Słońca wynosi +0,648 ± 0,006. Połączenie U (ultrafiolet) i B prowadzi do wskaźnika UB , który staje się bardziej ujemny, im gorętsza jest gwiazda i im więcej promieniowania UV. Zakładając, że Słońce jest gwiazdą typu G2 V, jego UB wynosi +0,12. Dwa wskaźniki dla dwóch typów najczęstszych sekwencji gwiazd porównano na rysunku (diagramie) z efektywną temperaturą powierzchni gwiazd, gdyby były one doskonale czarnymi ciałami. Istnieje surowa korelacja. Na przykład dla danego BV krzywe obu najpowszechniejszych sekwencji gwiazd (sekwencji głównej i nadolbrzymów) leżą poniżej odpowiedniego wskaźnika UB ciała doskonale czarnego , który obejmuje widmo ultrafioletowe, co pokazuje, że obie grupy gwiazd emitują mniej światło ultrafioletowe niż ciało doskonale czarne o tym samym wskaźniku BV . Być może zaskakujące jest to, że tak dobrze pasują do krzywej ciała doskonale czarnego, biorąc pod uwagę, że gwiazdy mają bardzo różne temperatury na różnych głębokościach. Na przykład Słońce ma efektywną temperaturę 5780 K, którą można porównać do temperatury jego fotosfery (obszaru generującego światło), która waha się od około 5000 K na jego zewnętrznej granicy z chromosferą do około 9500 K na jego zewnętrznej granicy z chromosferą. wewnętrzna granica ze strefą konwekcji o głębokości około 500 km (310 mil).

Czarne dziury

Zobacz też: Promieniowanie Hawkinga

Czarna dziura to obszar czasoprzestrzeni , z którego nic nie ucieka. Wokół czarnej dziury znajduje się matematycznie zdefiniowana powierzchnia zwana horyzontem zdarzeń , która wyznacza punkt bez powrotu. Nazywa się to „czarnym”, ponieważ pochłania całe światło padające na horyzont, niczego nie odbijając, co czyni go niemal idealnym ciałem czarnym (promieniowanie o długości fali równej lub większej niż średnica otworu może nie zostać pochłonięte, więc czarne dziury nie są ciałami doskonale czarnymi). Fizycy uważają, że dla obserwatora z zewnątrz czarne dziury mają niezerową temperaturę i emitują promieniowanie ciała doskonale czarnego , promieniowanie o prawie idealnym widmie ciała doskonale czarnego, które ostatecznie odparowuje . Mechanizm tej emisji jest związany z fluktuacjami próżni , w których wirtualna para cząstek jest rozdzielana przez grawitację otworu, przy czym jeden element jest zasysany do otworu, a drugi emitowany. Rozkład energii emisji opisuje prawo Plancka z temperaturą T :

${\ Displaystyle T = {\ Frac {\ hbar c ^ {3}} {8 \ pi Gk _ {\ tekst {B}} M}} \,}$

gdzie c to prędkość światła , ℏ to zredukowana stała Plancka , k _B to stała Boltzmanna , G to stała grawitacji , a M to masa czarnej dziury. Przewidywania te nie zostały jeszcze przetestowane ani obserwacyjnie, ani eksperymentalnie.

Kosmiczne mikrofalowe promieniowanie tła

Zobacz też: Wielki Wybuch i Kosmiczne mikrofalowe promieniowanie tła

Teoria Wielkiego Wybuchu opiera się na zasadzie kosmologicznej , która mówi, że w dużych skalach Wszechświat jest jednorodny i izotropowy. Zgodnie z teorią, Wszechświat mniej więcej sekundę po powstaniu był prawie idealnym ciałem czarnym w równowadze termicznej w temperaturze powyżej 10 10 ^K. Temperatura spadała wraz z rozszerzaniem się Wszechświata i ochładzaniem się materii i promieniowania. Obserwowane dzisiaj kosmiczne mikrofalowe promieniowanie tła jest „najdoskonalszym ciałem czarnym, jakie kiedykolwiek zmierzono w przyrodzie”. Ma prawie idealne widmo Plancka w temperaturze około 2,7 K. Odbiega od doskonałej izotropii prawdziwego promieniowania ciała doskonale czarnego przez obserwowaną anizotropię, która zmienia się wraz z kątem na niebie tylko do około jednej części na 100 000.

Chłodzenie radiacyjne

Wykresy log-log szczytowej długości fali emisji i wyjścia promieniowania w funkcji temperatury ciała doskonale czarnego – czerwone strzałki pokazują, że ciała czarne 5780 K mają szczytową długość fali 501 nm i 63,3 MW/m ² ; promienne wyjście

Zobacz też: Chłodzenie radiacyjne i Radiosity (wymiana ciepła)

Całkowanie prawa Plancka na wszystkich częstotliwościach zapewnia całkowitą energię na jednostkę czasu na jednostkę pola powierzchni wypromieniowaną przez ciało doskonale czarne utrzymywane w temperaturze T i jest znane jako prawo Stefana – Boltzmanna :

${\ Displaystyle P / A = \ sigma T ^ {4} \,}$

gdzie σ jest stałą Stefana-Boltzmanna , σ ≈ 5,67 × 10 ⁻⁸ W⋅m ⁻² ⋅K ⁻⁴ Aby pozostać w równowadze termicznej w stałej temperaturze T , ciało doskonale czarne musi zaabsorbować lub wewnętrznie wytworzyć taką ilość mocy P nad dany obszar A.

Chłodzenie ciała pod wpływem promieniowania cieplnego jest często aproksymowane za pomocą prawa Stefana-Boltzmanna uzupełnionego o emisyjność „ciała szarego” ε ≤ 1 ( P / A = εσT ⁴ ). Szybkość spadku temperatury ciała emitującego można oszacować na podstawie wypromieniowanej mocy i pojemności cieplnej ciała . To podejście jest uproszczeniem, które ignoruje szczegóły mechanizmów odpowiedzialnych za redystrybucję ciepła (co może obejmować zmianę składu, przemiany fazowe lub przebudowę ciała), które zachodzą w ciele podczas jego stygnięcia i zakłada, że ​​w każdym momencie ciało charakteryzuje się przez jedną temperaturę. Pomija również inne możliwe komplikacje, takie jak zmiany emisyjności wraz z temperaturą oraz rolę innych towarzyszących form emisji energii, np. emisji cząstek typu neutrin.

Jeśli założymy, że gorące ciało emitujące podlega prawu Stefana-Boltzmanna i znana jest jego emisja mocy P i temperatura T , to prawo to można wykorzystać do oszacowania wymiarów emitującego obiektu, ponieważ całkowita emitowana moc jest proporcjonalna do powierzchni powierzchnia emitująca. W ten sposób odkryto, że rozbłyski rentgenowskie obserwowane przez astronomów pochodzą z gwiazd neutronowych o promieniu około 10 km, a nie z czarnych dziur, jak pierwotnie przypuszczano. Dokładne oszacowanie wielkości wymaga pewnej wiedzy na temat emisyjności, w szczególności jej zależności widmowej i kątowej.

Zobacz też

• Prawo promieniowania cieplnego Kirchhoffa
• Vantablack , substancja wyprodukowana w 2014 roku i jedna z najczarniejszych znanych
• Locus Plancka , żarzenie ciała doskonale czarnego w danej przestrzeni chromatyczności

Bibliografia

• Chandrasekhar, S. (1950). Transfer radiacyjny . Oxford University Press .
•   Goody, RM; Yung, YL (1989). Promieniowanie atmosferyczne: podstawa teoretyczna (wyd. 2). Oxford University Press . ISBN 978-0-19-510291-8 .
•   Hermann, A. (1971). Geneza teorii kwantowej . Nash, CW (tłum.). MIT Naciśnij . ISBN 978-0-262-08047-7 . tłumaczenie Frühgeschichte der Quantentheorie (1899–1913) , Physik Verlag, Mosbach/Baden.
•   Kangro, H. (1976). Wczesna historia prawa promieniowania Plancka . Taylora i Franciszka . ISBN 978-0-85066-063-0 .
• Kirchhoff, G. (1860a). „Über die Fraunhofer'schen Linien”. Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin : 662–665.
• Kirchhoff, G. (1860b). „Über den Zusammenhang zwischen Emission und Absorption von Licht und Wärme”. Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin : 783–787.
• Kirchhoff, G. (1860c). „Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme and Licht” . Annalen der Physik und Chemie . 109 (2): 275–301. Bibcode : 1860AnP...185..275K . doi : 10.1002/andp.18601850205 . Przetłumaczone przez Guthrie, F. jako Kirchhoff, G. (1860). „O relacji między promieniującymi i pochłaniającymi mocami różnych ciał dla światła i ciepła” . Magazyn filozoficzny . Seria 4. 20 : 1–21.
• Kirchhoff, G. (1882) [1862]. „Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme und Licht”. Gessamelte Abhandlungen . Lipsk: Johann Ambrosius Barth. s. 571–598.
•   Kondepudi D.; Prigogine, I. (1998). Współczesna termodynamika. Od silników cieplnych do struktur rozpraszających . John Wiley & Synowie . ISBN 978-0-471-97393-5 .
•   Kragh, H. (1999). Generacje kwantowe: historia fizyki w XX wieku . Wydawnictwo Uniwersytetu Princeton . ISBN 978-0-691-01206-3 .
•   Kuhn, TS (1978). Teoria ciała doskonale czarnego i nieciągłość kwantowa . Oxford University Press . ISBN 978-0-19-502383-1 .
•   Loudon, R. (2000) [1973]. Kwantowa teoria światła (wyd. Trzecie). Wydawnictwo Uniwersytetu Cambridge . ISBN 978-0-19-850177-0 .
• Lummer, O .; Kurlbaum, F. (1898). "Der electrisch geglühte "absolut schwarze" Körper und seine Temperaturmessung". Verhandlungen der Deutschen Physikalischen Gesellschaft . 17 : 106–111.
• Lummer, O .; Kurlbaum, F. (1901). "Der elektrisch geglühte "schwarze" Körper" . Annalen der Physik . 310 (8): 829–836. Bibcode : 1901AnP...310..829L . doi : 10.1002/andp.19013100809 .
•   Mandel, L. ; Wilk, E. (1995). Spójność optyczna i optyka kwantowa . Wydawnictwo Uniwersytetu Cambridge . ISBN 978-0-521-41711-2 .
•   Mehra, J .; Rechenberg, H. (1982). Historyczny rozwój teorii kwantów . Tom. 1, część 1. Springer-Verlag . ISBN 978-0-387-90642-3 .
•   Mihałas, D .; Weibel-Mihalas, B. (1984). Podstawy hydrodynamiki promieniowania . Oxford University Press . ISBN 978-0-19-503437-0 .
• Milne, EA (1930). „Termodynamika gwiazd”. Handbuch der Astrophysik . 3, część 1: 63–255.
•   Planck, M. (1914). Teoria promieniowania cieplnego . Masius, M. (tłum.) (wyd. 2). P. Blakiston's Son & Co. OL 7154661M .
•   Rybicki, GB; Lightman, AP (1979). Procesy radiacyjne w astrofizyce . John Wiley & Synowie . ISBN 978-0-471-82759-7 .
• Schirrmacher, A. (2001). Teoria eksperymentów: dowody prawa promieniowania Kirchhoffa przed i po Plancku . Münchner Zentrum für Wissenschafts und Technikgeschichte.
•   Stewart, B. (1858). „Relacja z niektórych eksperymentów na promieniowaniu cieplnym” . Transakcje Towarzystwa Królewskiego w Edynburgu . 22 : 1–20. doi : 10.1017/S0080456800031288 . S2CID 122316368 .

Linki zewnętrzne

• Keesey, Lori J. (12 grudnia 2010). „Czarniejszy niż czarny” . NASA . Inżynierowie opracowują teraz materiał ciemniejszy niż smoła, który pomoże naukowcom zebrać trudne do uzyskania pomiary naukowe… materiał oparty na nanotechnologii jest obecnie opracowywany przez zespół 10 technologów z Centrum Lotów Kosmicznych NASA Goddard