Optyka
| Część serii |
| Fizyka |
|---|

|
Optyka to dziedzina fizyki , która bada zachowanie i właściwości światła , w tym jego interakcje z materią oraz budowę instrumentów , które je wykorzystują lub wykrywają . Optyka zwykle opisuje zachowanie widzialnego , ultrafioletowego i podczerwonego . Ponieważ światło jest falą elektromagnetyczną , inne formy promieniowania elektromagnetycznego, takie jak promieniowanie rentgenowskie , mikrofale i inne fale radiowe wykazują podobne właściwości.
Większość zjawisk optycznych można wytłumaczyć za pomocą klasycznego elektromagnetycznego opisu światła. Pełne elektromagnetyczne opisy światła są jednak często trudne do zastosowania w praktyce. Praktyczna optyka jest zwykle wykonywana przy użyciu uproszczonych modeli. Najpowszechniejsza z nich, optyka geometryczna , traktuje światło jako zbiór promieni poruszających się po liniach prostych i uginających się, gdy przechodzą przez lub odbijają się od powierzchni. Optyka fizyczna to bardziej kompleksowy model światła, który obejmuje efekty falowe , takie jak dyfrakcja i interferencja , której nie można wyjaśnić w optyce geometrycznej. Historycznie rzecz biorąc, najpierw opracowano oparty na promieniach model światła, a następnie falowy model światła. Postęp w teorii elektromagnetyzmu w XIX wieku doprowadził do odkrycia, że fale świetlne są w rzeczywistości promieniowaniem elektromagnetycznym.
Niektóre zjawiska zależą od światła, które ma zarówno właściwości falowe, jak i cząsteczkowe . Wyjaśnienie tych efektów wymaga mechaniki kwantowej . Rozważając właściwości podobne do cząstek światła, światło jest modelowane jako zbiór cząstek zwanych „ fotonami ”. Optyka kwantowa zajmuje się zastosowaniem mechaniki kwantowej do układów optycznych.
Nauki optyczne są istotne i badane w wielu pokrewnych dyscyplinach, w tym astronomii , różnych dziedzinach inżynierii , fotografii i medycynie (szczególnie okulistyce i optometrii , w których nazywa się to optyką fizjologiczną). Praktyczne zastosowania optyki znajdują się w różnych technologiach i przedmiotach codziennego użytku, w tym w lustrach , soczewkach , teleskopach , mikroskopach , laserach i światłowodach .
Historia
Optyka rozpoczęła się wraz z rozwojem soczewek przez starożytnych Egipcjan i mieszkańców Mezopotamii . Najwcześniejsze znane soczewki, wykonane z polerowanego kryształu, często kwarcu , pochodzą już z 2000 pne z Krety (Muzeum Archeologiczne w Heraklionie, Grecja). Soczewki z Rodos pochodzą z około 700 rpne, podobnie jak soczewki asyryjskie , takie jak soczewka Nimrud . Starożytni Rzymianie i Grecy szklane kule wypełnione wodą do robienia soczewek. Po tych praktycznych osiągnięciach nastąpił rozwój teorii światła i widzenia przez starożytnych greckich i indyjskich oraz rozwój optyki geometrycznej w świecie grecko-rzymskim . Słowo optyka pochodzi od starożytnego greckiego słowa ὀπτική ( optikē ), oznaczającego „wygląd, wygląd”.
Grecka filozofia optyki podzieliła się na dwie przeciwstawne teorie dotyczące działania widzenia, teorię intromisji i teorię emisji . Podejście intromisyjne postrzegało widzenie jako pochodzące od obiektów odrzucających swoje kopie (zwane eidolą), które zostały uchwycone przez oko. W przypadku wielu propagatorów, w tym Demokryta , Epikura , Arystotelesa i ich zwolenników, teoria ta wydaje się mieć pewien kontakt ze współczesnymi teoriami tego, czym naprawdę jest widzenie, ale pozostała jedynie spekulacją pozbawioną jakichkolwiek podstaw eksperymentalnych.
Platon jako pierwszy wyartykułował teorię emisji, ideę, że percepcja wzrokowa jest realizowana przez promienie emitowane przez oczy. Skomentował również parzystości luster w Timajosie . Jakieś sto lat później Euklides (IV – III wiek pne) napisał traktat zatytułowany Optyka , w którym połączył wizję z geometrią , tworząc optykę geometryczną . Oparł swoją pracę na teorii emisji Platona, w której opisał matematyczne zasady perspektywy i opisał skutki refrakcji , chociaż kwestionował, czy wiązka światła z oka może natychmiast oświetlić gwiazdy za każdym razem, gdy ktoś mrugnie. Euklides sformułował zasadę najkrótszej trajektorii światła i rozważał wielokrotne odbicia na zwierciadłach płaskich i kulistych. Ptolemeusz w swoim traktacie Optyka , wyznawał teorię widzenia ekstramisyjno-intromisyjnego: promienie (lub strumień) z oka tworzyły stożek, którego wierzchołek znajdował się w oku, a podstawa określała pole widzenia. Promienie były czułe i przekazywały informacje z powrotem do intelektu obserwatora o odległości i orientacji powierzchni. Podsumował większość Euklidesa i dalej opisał sposób pomiaru kąta załamania , chociaż nie zauważył empirycznego związku między tym a kątem padania. Plutarch (I – II wne) opisał wielokrotne odbicia na zwierciadłach sferycznych i omówił tworzenie powiększonych i pomniejszonych obrazów, zarówno rzeczywistych, jak i urojonych, w tym przypadek chiralności obrazów.
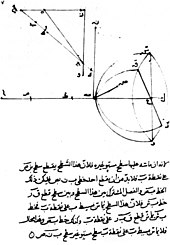
W średniowieczu greckie idee dotyczące optyki zostały wskrzeszone i rozszerzone przez pisarzy ze świata muzułmańskiego . Jednym z najwcześniejszych z nich był Al-Kindi (ok. 801–873), który pisał o zaletach arystotelesowskich i euklidesowych idei optyki, opowiadając się za teorią emisji, ponieważ może ona lepiej kwantyfikować zjawiska optyczne. W 984 roku perski matematyk Ibn Sahl napisał traktat „O spalaniu luster i soczewek”, poprawnie opisując prawo załamania równoważne prawu Snella. Użył tego prawa do obliczenia optymalnych kształtów soczewek i krzywe lusterka . Na początku XI wieku Alhazen (Ibn al-Haytham) napisał Księgę optyki ( Kitab al-manazir ), w którym badał odbicie i załamanie oraz zaproponował nowy system wyjaśniania widzenia i światła w oparciu o obserwacje i eksperymenty. Odrzucił „teorię emisji” optyki Ptolemeusza, w której promienie były emitowane przez oko, i zamiast tego wysunął ideę, że światło odbija się we wszystkich kierunkach po liniach prostych ze wszystkich punktów oglądanych obiektów, a następnie wpada do oka, chociaż on nie był w stanie poprawnie wyjaśnić, w jaki sposób oko wychwytuje promienie. Praca Alhazena była w dużej mierze ignorowana w świecie arabskim, ale została anonimowo przetłumaczona na łacinę około 1200 rne, a następnie podsumowana i rozwinięta przez polskiego mnicha Witelo czyniąc go standardowym tekstem dotyczącym optyki w Europie przez następne 400 lat.
W XIII wieku w średniowiecznej Europie angielski biskup Robert Grosseteste pisał na szeroki zakres tematów naukowych i omawiał światło z czterech różnych perspektyw: epistemologii światła , metafizyki lub kosmogonii światła, etiologii lub fizyki światła oraz teologię światła, opierając się na dziełach Arystotelesa i platonizmu. Najsłynniejszy uczeń Grosseteste'a, Roger Bacon , napisał prace cytujące wiele niedawno przetłumaczonych dzieł optycznych i filozoficznych, w tym prace Alhazena, Arystotelesa, Avicenna , Awerroes , Euklides, al-Kindi, Ptolemeusz, Tideus i Konstantyn Afrykanin . Bacon był w stanie użyć części szklanych kulek jako szkieł powiększających , aby wykazać, że światło odbija się od przedmiotów, a nie jest z nich uwalniane.
Pierwsze okulary do noszenia zostały wynalezione we Włoszech około 1286 roku. To był początek przemysłu optycznego polegającego na szlifowaniu i polerowaniu soczewek do tych „okularów”, najpierw w Wenecji i Florencji w XIII wieku, a później w ośrodkach produkcji okularów w obu krajach. Holandia i Niemcy. Twórcy okularów stworzyli ulepszone typy soczewek do korekcji wzroku, opierając się bardziej na wiedzy empirycznej zdobytej z obserwacji działania soczewek niż na podstawowej teorii optycznej tamtych czasów (teorii, która w większości nie potrafiła nawet odpowiednio wyjaśnić, jak działają okulary ). Ten praktyczny rozwój, mistrzostwo i eksperymenty z soczewkami doprowadziły bezpośrednio do wynalezienia związku mikroskop optyczny około 1595 r. i teleskop refrakcyjny w 1608 r., które pojawiły się w ośrodkach produkcji spektakli w Holandii.

Na początku XVII wieku Johannes Kepler rozszerzył w swoich pismach optykę geometryczną, obejmując soczewki, odbicie w płaskich i zakrzywionych zwierciadłach, zasady działania kamer otworkowych , prawo odwrotnych kwadratów regulujące intensywność światła oraz optyczne wyjaśnienia zjawisk astronomicznych, takich jak jak zaćmienia Księżyca i Słońca oraz paralaksa astronomiczna . Był również w stanie poprawnie wydedukować rolę siatkówki jako rzeczywisty organ, który rejestrował obrazy, w końcu będąc w stanie naukowo określić ilościowo wpływ różnych typów soczewek, które twórcy okularów obserwowali przez ostatnie 300 lat. Po wynalezieniu teleskopu Kepler przedstawił teoretyczne podstawy ich działania i opisał ulepszoną wersję, znaną jako teleskop Keplera , wykorzystującą dwie soczewki wypukłe do uzyskania większego powiększenia.
Teoria optyki rozwinęła się w połowie XVII wieku wraz z traktatami napisanymi przez filozofa René Descartesa , w których wyjaśniono różnorodne zjawiska optyczne, w tym odbicie i załamanie, zakładając, że światło jest emitowane przez obiekty, które je wytwarzają. Różniło się to zasadniczo od starożytnej greckiej teorii emisji. Pod koniec lat sześćdziesiątych i na początku lat siedemdziesiątych XVII wieku Izaak Newton rozwinął idee Kartezjusza w korpuskułową teorię światła , słynnie ustalając, że białe światło jest mieszanką kolorów, które można rozdzielić na części składowe za pomocą pryzmatu . w 1690 r. Christiaan Huygens zaproponował falową teorię światła opartą na sugestiach Roberta Hooke'a z 1664 roku. Sam Hooke publicznie skrytykował teorie światła Newtona, a spór między nimi trwał aż do śmierci Hooke'a. W 1704 roku Newton opublikował Opticks iw tamtym czasie, częściowo z powodu swoich sukcesów w innych dziedzinach fizyki, powszechnie uważano go za zwycięzcę debaty nad naturą światła.
Optyka newtonowska była ogólnie akceptowana do początku XIX wieku, kiedy Thomas Young i Augustin-Jean Fresnel przeprowadzili eksperymenty dotyczące interferencji światła, które mocno ustaliły falową naturę światła. Słynny eksperyment Younga z podwójną szczeliną wykazał, że światło podlega zasadzie superpozycji , która jest właściwością falową, której nie przewiduje teoria ciałek Newtona. Ta praca doprowadziła do teorii dyfrakcji światła i otworzyła cały obszar badań w optyce fizycznej. Optyka falowa została pomyślnie zunifikowana teoria elektromagnetyczna Jamesa Clerka Maxwella w latach 60. XIX wieku.
Następny rozwój teorii optycznej nastąpił w 1899 r., kiedy Max Planck prawidłowo modelował promieniowanie ciała doskonale czarnego , zakładając, że wymiana energii między światłem a materią zachodzi tylko w dyskretnych ilościach, które nazwał kwantami . W 1905 roku Albert Einstein opublikował teorię efektu fotoelektrycznego , która mocno ugruntowała kwantyzację samego światła. W 1913 roku Niels Bohr wykazał, że atomy mogą emitować tylko dyskretne ilości energii, wyjaśniając w ten sposób dyskretne linie widoczne w emisji i widma absorpcyjne . Zrozumienie interakcji między światłem a materią, które nastąpiło w wyniku tych odkryć, nie tylko stworzyło podstawę optyki kwantowej, ale miało również kluczowe znaczenie dla rozwoju mechaniki kwantowej jako całości. Ostateczna kulminacja, teoria elektrodynamiki kwantowej , wyjaśnia wszystkie procesy optyczne i elektromagnetyczne jako wynik wymiany fotonów rzeczywistych i wirtualnych . Optyka kwantowa zyskała praktyczne znaczenie wraz z wynalezieniem masera w 1953 roku i lasera w 1960 roku.
Po pracach Paula Diraca w kwantowej teorii pola , George Sudarshan , Roy J. Glauber i Leonard Mandel zastosowali teorię kwantową do pola elektromagnetycznego w latach pięćdziesiątych i sześćdziesiątych XX wieku, aby uzyskać bardziej szczegółowe zrozumienie fotodetekcji i statystyki światła .
Optyka klasyczna
Optyka klasyczna dzieli się na dwie główne gałęzie: optykę geometryczną (lub promieniową) i optykę fizyczną (lub falową). W optyce geometrycznej uważa się, że światło porusza się po liniach prostych, podczas gdy w optyce fizycznej światło jest uważane za falę elektromagnetyczną.
Optykę geometryczną można postrzegać jako przybliżenie optyki fizycznej, która ma zastosowanie, gdy długość fali użytego światła jest znacznie mniejsza niż rozmiar elementów optycznych w modelowanym układzie.
Optyka geometryczna
Optyka geometryczna lub optyka promieni opisuje rozchodzenie się światła za pomocą „promieni”, które poruszają się po liniach prostych i których torami rządzą prawa odbicia i załamania na styku różnych ośrodków. Prawa te zostały odkryte empirycznie już w 984 r. n.e. i od tego czasu aż do dnia dzisiejszego są wykorzystywane w projektowaniu elementów i przyrządów optycznych. Można je podsumować w następujący sposób:
Kiedy promień światła uderza w granicę między dwoma przezroczystymi materiałami, dzieli się na promień odbity i załamany.
- Prawo odbicia mówi, że promień odbity leży w płaszczyźnie padania, a kąt odbicia jest równy kątowi padania.
- Prawo załamania mówi, że załamany promień leży w płaszczyźnie padania, a sinus kąta padania podzielony przez sinus kąta załamania jest stałą: grzech
- ,
gdzie n jest stałą dla dowolnych dwóch materiałów i danej barwy światła. Jeśli pierwszym materiałem jest powietrze lub próżnia, n jest współczynnikiem załamania drugiego materiału.
Prawa odbicia i załamania światła można wyprowadzić z zasady Fermata, która mówi, że droga, jaką pokonuje promień światła między dwoma punktami, jest drogą, którą można pokonać w jak najkrótszym czasie.
przybliżenia
Optyka geometryczna jest często upraszczana poprzez przybliżenie przyosiowe lub „przybliżenie pod małym kątem”. Zachowanie matematyczne staje się wówczas liniowe, umożliwiając opisywanie elementów optycznych i systemów za pomocą prostych macierzy. Prowadzi to do technik optyki gaussowskiej i śledzenia promieni przyosiowych , które są wykorzystywane do znajdowania podstawowych właściwości układów optycznych, takich jak przybliżone położenie obrazu i obiektu oraz powiększenia .
Refleksje
Odbicia można podzielić na dwa rodzaje: odbicie lustrzane i odbicie rozproszone . Odbicie lustrzane opisuje połysk powierzchni takich jak lustra, które odbijają światło w prosty, przewidywalny sposób. Pozwala to na tworzenie odbitych obrazów, które można powiązać z rzeczywistym ( rzeczywistym ) lub ekstrapolowanym ( wirtualnym) . ) położenie w przestrzeni. Odbicie rozproszone opisuje materiały nie błyszczące, takie jak papier lub kamień. Odbicia od tych powierzchni można opisać jedynie statystycznie, przy czym dokładny rozkład odbitego światła zależy od mikroskopowej struktury materiału. Wiele odbłyśników rozproszonych jest opisanych lub można je przybliżyć za pomocą prawa kosinusów Lamberta , które opisuje powierzchnie, które mają taką samą luminancję , gdy patrzy się pod dowolnym kątem. Błyszczące powierzchnie mogą dawać zarówno lustrzane, jak i rozproszone odbicie.
W odbiciu zwierciadlanym kierunek promienia odbitego jest określony przez kąt, jaki promień padający tworzy z normalną powierzchnią , czyli linią prostopadłą do powierzchni w punkcie, w którym pada promień. Promień padający i odbity oraz normalna leżą w jednej płaszczyźnie, a kąt między promieniem odbitym a normalną powierzchni jest taki sam, jak między promieniem padającym a normalną. Jest to znane jako prawo odbicia .
W przypadku zwierciadeł płaskich prawo odbicia oznacza, że obrazy przedmiotów są ustawione pionowo i w takiej samej odległości za lustrem, w jakiej znajdują się przed lustrem. Rozmiar obrazu jest taki sam jak rozmiar obiektu. Prawo implikuje również, że odbicia lustrzane mają odwróconą parzystość, co postrzegamy jako inwersję lewo-prawo. Obrazy utworzone z odbicia w dwóch (lub dowolnej parzystej liczbie) lustrach nie mają odwróconej parzystości. Odbłyśniki narożne wytwarzają odbite promienie, które wracają w kierunku, z którego nadeszły promienie padające. Nazywa się to retrorefleksją .
Lustra o zakrzywionych powierzchniach można modelować za pomocą śledzenia promieni i prawa odbicia w każdym punkcie powierzchni. W przypadku zwierciadeł o powierzchniach parabolicznych równoległe promienie padające na zwierciadło wytwarzają promienie odbite, które zbiegają się we wspólnym ognisku . Inne zakrzywione powierzchnie mogą również skupiać światło, ale z aberracjami wynikającymi z rozbieżnego kształtu, powodując rozmycie ogniska w przestrzeni. W szczególności zwierciadła sferyczne wykazują aberrację sferyczną . Zakrzywione lustra mogą tworzyć obrazy o powiększeniu większym lub mniejszym niż jeden, a powiększenie może być ujemne, co wskazuje, że obraz jest odwrócony. Pionowy obraz utworzony przez odbicie w lustrze jest zawsze wirtualny, podczas gdy obraz odwrócony jest rzeczywisty i można go wyświetlić na ekranie.
Załamania
Załamanie występuje, gdy światło przechodzi przez obszar przestrzeni o zmiennym współczynniku załamania; ta zasada pozwala na soczewki i skupianie światła. , gdy istnieje interfejs między jednolitym ośrodkiem o współczynniku załamania ośrodkiem o współczynniku . W takich sytuacjach prawo Snella opisuje wynikające z tego ugięcie promienia świetlnego:
gdzie i odpowiednio kątami między normalną (do interfejsu) a
Współczynnik załamania ośrodka jest związany z prędkością v światła w tym ośrodku przez
- ,
gdzie c jest prędkością światła w próżni .
Prawo Snella można wykorzystać do przewidywania odchylenia promieni świetlnych przechodzących przez ośrodki liniowe, o ile znane są współczynniki załamania i geometria ośrodków. Na przykład rozchodzenie się światła przez pryzmat powoduje, że promień światła jest odchylany w zależności od kształtu i orientacji pryzmatu. W większości materiałów współczynnik załamania zmienia się wraz z częstotliwością światła. Biorąc to pod uwagę, prawo Snella można wykorzystać do przewidzenia, w jaki sposób pryzmat rozproszy światło w widmie. Odkrycie tego zjawiska podczas przepuszczania światła przez pryzmat przypisuje się słynnemu Izaakowi Newtonowi.
Niektóre ośrodki mają współczynnik załamania światła, który zmienia się stopniowo wraz z położeniem, dlatego promienie świetlne w ośrodku są zakrzywione. Zjawisko to odpowiada za miraże obserwowane w upalne dni: zmiana współczynnika załamania powietrza wraz z wysokością powoduje zakrzywienie promieni świetlnych, tworząc w oddali wrażenie zwierciadlanych odbić (jak na tafli wody). Materiały optyczne o różnych współczynnikach załamania światła nazywane są materiałami o współczynniku gradientu (GRIN). Takie materiały są używane do produkcji optyki gradientowej .
materiału o niskim współczynniku załamania światła, prawo Snella przewiduje, że nie ma kiedy jest duży. W takim przypadku transmisja nie występuje; odbija się całe światło. Zjawisko to nazywane jest całkowitym wewnętrznym odbiciem i pozwala na to technologia światłowodowa. Gdy światło przechodzi przez światłowód, podlega całkowitemu wewnętrznemu odbiciu, dzięki czemu zasadniczo nie traci światła na całej długości kabla.
soczewki
Urządzenie, które wytwarza zbieżne lub rozbieżne promienie świetlne w wyniku załamania, jest znane jako soczewka . Soczewki charakteryzują się ogniskową : soczewka skupiająca ma ogniskową dodatnią, a soczewka rozpraszająca ma ogniskową ujemną. Mniejsza ogniskowa wskazuje, że soczewka ma silniejszy efekt zbieżności lub rozbieżności. Ogniskowa prostej soczewki w powietrzu jest określona przez równanie producenta soczewek .
Śledzenie promieni może być wykorzystane do pokazania, w jaki sposób obrazy są tworzone przez soczewkę. W przypadku cienkiej soczewki w powietrzu położenie obrazu określa proste równanie
- ,
gdzie to odległość od obiektu do soczewki, to odległość od soczewki do obrazu, a to ogniskowa obiektywu. W konwencji znakowej odległości przedmiotu i obrazu są dodatnie, jeśli przedmiot i obraz znajdują się po przeciwnych stronach soczewki.
Przychodzące promienie równoległe są skupiane przez soczewkę skupiającą w punkcie znajdującym się w odległości jednej ogniskowej od soczewki, po drugiej stronie soczewki. Nazywa się to tylnym ogniskiem obiektywu. Promienie z obiektu znajdującego się w skończonej odległości są ogniskowane dalej od soczewki niż odległość ogniskowa; im bliżej soczewki znajduje się przedmiot, tym dalej obraz znajduje się od soczewki.
W przypadku soczewek rozbieżnych przychodzące równoległe promienie rozchodzą się po przejściu przez soczewkę w taki sposób, że wydaje się, że pochodzą z punktu o ogniskowej przed soczewką. To jest przednia ogniskowa obiektywu. Promienie z obiektu znajdującego się w skończonej odległości są powiązane z wirtualnym obrazem, który znajduje się bliżej soczewki niż ognisko i po tej samej stronie soczewki co przedmiot. Im bliżej soczewki znajduje się obiekt, tym bliżej soczewki znajduje się wirtualny obraz. Podobnie jak w przypadku luster, pionowe obrazy wytwarzane przez pojedynczą soczewkę są wirtualne, podczas gdy obrazy odwrócone są rzeczywiste.
Soczewki cierpią na aberracje , które zniekształcają obrazy. Aberracje monochromatyczne występują, ponieważ geometria soczewki nie kieruje idealnie promieni z każdego punktu obiektu do pojedynczego punktu na obrazie, podczas gdy aberracja chromatyczna występuje, ponieważ współczynnik załamania soczewki zmienia się wraz z długością fali światła.

Optyka fizyczna
W optyce fizycznej uważa się, że światło rozchodzi się jako fala. Model ten przewiduje zjawiska takie jak interferencja i dyfrakcja, których nie wyjaśnia optyka geometryczna. Prędkość świetlnych w powietrzu wynosi około 3,0⋅10 8 m/s (dokładnie 299 792 458 m/s w próżni ). Długość fali światła widzialnego waha się między 400 a 700 nm, ale termin „światło” jest również często stosowany do promieniowania podczerwonego (0,7–300 μm) i ultrafioletowego (10–400 nm).
Model falowy można wykorzystać do przewidywania zachowania układu optycznego bez konieczności wyjaśniania, co „faluje” w jakim ośrodku. Do połowy XIX wieku większość fizyków wierzyła w „eteryczne” medium, w którym rozchodzi się zaburzenie światła. Istnienie fal elektromagnetycznych zostało przewidziane w 1865 r. za pomocą równań Maxwella . Fale te rozchodzą się z prędkością światła i mają zmienne pola elektryczne i magnetyczne, które są prostopadłe do siebie, a także do kierunku propagacji fal. Fale świetlne są obecnie ogólnie traktowane jako fale elektromagnetyczne, z wyjątkiem przypadków należy wziąć pod uwagę efekty mechaniki kwantowej .
Modelowanie i projektowanie układów optycznych z wykorzystaniem optyki fizycznej
Dostępnych jest wiele uproszczonych przybliżeń do analizy i projektowania systemów optycznych. Większość z nich wykorzystuje pojedynczą skalarną do reprezentowania pola elektrycznego fali świetlnej, zamiast używać modelu wektorowego z ortogonalnymi wektorami elektrycznymi i magnetycznymi. Równanie Huygensa -Fresnela jest jednym z takich modeli. Zostało to wyprowadzone empirycznie przez Fresnela w 1815 r., Opierając się na hipotezie Huygensa, że każdy punkt czoła fali generuje wtórne sferyczne czoło fali, które Fresnel połączył z zasadą superpozycji fal . Równanie dyfrakcyjne Kirchhoffa , które wyprowadzono za pomocą równań Maxwella, stawia równanie Huygensa-Fresnela na mocniejszym fundamencie fizycznym. Przykłady zastosowania zasady Huygensa-Fresnela można znaleźć w artykułach dotyczących dyfrakcji i dyfrakcji Fraunhofera .
Bardziej rygorystyczne modele, obejmujące modelowanie zarówno pola elektrycznego, jak i magnetycznego fali świetlnej, są wymagane w przypadku materiałów, których właściwości elektryczne i magnetyczne wpływają na interakcję światła z materiałem. Na przykład zachowanie fali świetlnej oddziałującej z metalową powierzchnią jest zupełnie inne niż to, co dzieje się, gdy oddziałuje ona z materiałem dielektrycznym. Model wektorowy musi być również używany do modelowania światła spolaryzowanego.
modelowania numerycznego, takie jak metoda elementów skończonych , metoda elementów brzegowych i metoda macierzy linii transmisyjnych, mogą być wykorzystywane do modelowania propagacji światła w układach, których nie można rozwiązać analitycznie. Takie modele są wymagające obliczeniowo i są zwykle używane tylko do rozwiązywania problemów na małą skalę, które wymagają dokładności większej niż ta, którą można osiągnąć za pomocą rozwiązań analitycznych.
Wszystkie wyniki optyki geometrycznej można odzyskać za pomocą technik optyki Fouriera , które wykorzystują wiele takich samych technik matematycznych i analitycznych, jakie są stosowane w inżynierii akustycznej i przetwarzaniu sygnałów .
Propagacja wiązki Gaussa to prosty model optyki fizycznej przyosiowej do propagacji promieniowania spójnego, takiego jak wiązki laserowe. Technika ta częściowo uwzględnia dyfrakcję, umożliwiając dokładne obliczenie szybkości, z jaką wiązka lasera rozszerza się wraz z odległością, oraz minimalnego rozmiaru, na jakim wiązka może zostać skupiona. Propagacja wiązki Gaussa wypełnia zatem lukę między optyką geometryczną i fizyczną.
Superpozycja i interferencja
W przypadku braku efektów nieliniowych zasadę superpozycji można wykorzystać do przewidywania kształtu oddziałujących przebiegów poprzez proste dodanie zakłóceń. Ta interakcja fal w celu wytworzenia wynikowego wzoru jest ogólnie nazywana „interferencją” i może skutkować różnymi skutkami. Jeśli dwie fale o tej samej długości fali i częstotliwości są w fazie , zarówno grzbiety, jak i doliny fal są wyrównane. Powoduje to konstruktywną interferencję oraz wzrost amplitudy fali, co dla światła wiąże się z rozjaśnieniem kształtu fali w tym miejscu. Alternatywnie, jeśli dwie fale o tej samej długości fali i częstotliwości są przesunięte w fazie, grzbiety fal zrównają się z dolinami fal i odwrotnie. Powoduje to destrukcyjną interferencję i spadek amplitudy fali, co dla światła wiąże się ze ściemnieniem przebiegu w tym miejscu. Zobacz poniżej ilustrację tego efektu.
|
połączony kształt fali |

|
|
| fala 1 | ||
| fala 2 | ||
| Dwie fale w fazie |
w fazie o 180° |
|
Ponieważ zasada Huygensa-Fresnela stwierdza, że każdy punkt czoła fali jest powiązany z wytwarzaniem nowego zakłócenia, możliwe jest, że czoło fali będzie sobie konstruktywnie lub destrukcyjnie interferować w różnych miejscach, tworząc jasne i ciemne prążki w regularnych i przewidywalnych wzorach. Interferometria to nauka zajmująca się pomiarem tych wzorców, zwykle jako środek do precyzyjnego określania odległości lub rozdzielczości kątowych . Interferometr Michelsona był słynnym instrumentem, który wykorzystywał efekty interferencyjne do dokładnego pomiaru prędkości światła.
Na wygląd cienkich warstw i powłok mają bezpośredni wpływ efekty interferencyjne. Powłoki antyrefleksyjne wykorzystują destrukcyjną interferencję, aby zmniejszyć współczynnik odbicia powierzchni, które pokrywają, i mogą być używane do minimalizowania odblasków i niepożądanych odbić. Najprostszym przypadkiem jest pojedyncza warstwa o grubości równej jednej czwartej długości fali padającego światła. Fala odbita od góry filmu i fala odbita od granicy filmu/materiału są wtedy przesunięte w fazie dokładnie o 180°, powodując destrukcyjną interferencję. Fale są dokładnie przesunięte w fazie tylko dla jednej długości fali, która zazwyczaj byłaby wybierana tak, aby znajdowała się blisko środka widma widzialnego, około 550 nm. Bardziej złożone projekty wykorzystujące wiele warstw mogą osiągnąć niski współczynnik odbicia w szerokim paśmie lub bardzo niski współczynnik odbicia przy jednej długości fali.
Konstruktywna interferencja w cienkich warstwach może powodować silne odbicie światła w zakresie długości fal, które mogą być wąskie lub szerokie, w zależności od konstrukcji powłoki. Folie te wykorzystywane są do wykonywania zwierciadeł dielektrycznych , filtrów interferencyjnych , reflektorów ciepła oraz filtrów do separacji barw w kamerach telewizji kolorowej . Ten efekt interferencji jest również przyczyną kolorowych tęczowych wzorów widocznych w plamach ropy.
Dyfrakcja i rozdzielczość optyczna
Dyfrakcja to proces, w którym najczęściej obserwuje się interferencję światła. Efekt ten został po raz pierwszy opisany w 1665 roku przez Francesco Marię Grimaldi , który również ukuł termin z łacińskiego diffringere , „rozpaść się na kawałki”. Później tego stulecia Robert Hooke i Isaac Newton również opisali zjawiska znane obecnie jako dyfrakcja w pierścieniach Newtona, podczas gdy James Gregory odnotował swoje obserwacje wzorów dyfrakcji z ptasich piór.
Pierwszy model optyki fizycznej dyfrakcji, który opierał się na zasadzie Huygensa-Fresnela, został opracowany w 1803 roku przez Thomasa Younga w jego eksperymentach z interferencją z wzorami interferencji dwóch blisko rozmieszczonych szczelin. Young wykazał, że jego wyniki można wyjaśnić tylko wtedy, gdy dwie szczeliny działają raczej jako dwa unikalne źródła fal niż cząsteczki. W 1815 i 1818 roku Augustin-Jean Fresnel mocno ustalił matematykę, w jaki sposób interferencja fal może wyjaśniać dyfrakcję.
Najprostsze fizyczne modele dyfrakcji wykorzystują równania, które opisują separację kątową jasnych i ciemnych prążków pod wpływem światła o określonej długości fali (λ). Ogólnie równanie ma postać
gdzie dwoma źródłami czoła fali (w przypadku eksperymentów Younga były to szczeliny ), jest kątowym między środkowym obrzeżem a krawędzią prążek rzędu, gdzie centralne maksimum to .
To równanie zostało nieznacznie zmodyfikowane, aby uwzględnić różne sytuacje, takie jak dyfrakcja przez pojedynczą szczelinę, dyfrakcja przez wiele szczelin lub dyfrakcja przez siatkę dyfrakcyjną zawierającą dużą liczbę szczelin w równych odstępach. Bardziej skomplikowane modele dyfrakcji wymagają pracy z matematyką Fresnela lub Fraunhofera.
Dyfrakcja rentgenowska wykorzystuje fakt, że atomy w krysztale mają regularne odstępy w odległościach rzędu jednego angstrema . Aby zobaczyć wzory dyfrakcyjne, przez kryształ przepuszcza się promienie rentgenowskie o długości fali podobnej do tej odległości. Ponieważ kryształy są obiektami trójwymiarowymi, a nie dwuwymiarowymi siatkami, powiązany wzór dyfrakcyjny zmienia się w dwóch kierunkach zgodnie z , przy czym powiązane jasne plamy występują w unikalnych wzorach , a odstępy między atomami są dwukrotnie większe.
Efekty dyfrakcyjne ograniczają zdolność detektora optycznego do optycznego rozdzielania oddzielnych źródeł światła. Ogólnie rzecz biorąc, światło przechodzące przez aperturę podlega dyfrakcji, a najlepsze obrazy, jakie można stworzyć (jak opisano w optyce z ograniczoną dyfrakcją ), pojawiają się jako centralna plamka z otaczającymi ją jasnymi pierścieniami, oddzielonymi ciemnymi zerami; ten wzór jest znany jako wzór Airy'ego , a środkowy jasny płat jako dysk Airy'ego . Rozmiar takiego dysku jest określony przez
gdzie θ to rozdzielczość kątowa, λ to długość fali światła, a D to średnica otworu obiektywu. Jeśli kątowa separacja dwóch punktów jest znacznie mniejsza niż promień kątowy dysku Airy'ego, to tych dwóch punktów nie można rozdzielić na obrazie, ale jeśli ich separacja kątowa jest znacznie większa, powstają odrębne obrazy dwóch punktów i one można zatem rozwiązać. Rayleigh zdefiniował nieco arbitralne kryterium Rayleigha „że dwa punkty, których separacja kątowa jest równa promieniowi dysku Airy'ego (mierzonemu do pierwszego zera, to znaczy do pierwszego miejsca, w którym nie widać światła) można uznać za rozwiązane. Można zauważyć, że im większa średnica soczewka lub jej apertura, tym lepsza rozdzielczość Interferometria , ze swoją zdolnością do naśladowania bardzo dużych apertur linii bazowej, pozwala na największą możliwą rozdzielczość kątową.
W przypadku obrazowania astronomicznego atmosfera uniemożliwia osiągnięcie optymalnej rozdzielczości w zakresie widzialnym z powodu rozpraszania i dyspersji atmosferycznej, które powodują migotanie gwiazd . Astronomowie określają ten efekt jako jakość widzenia astronomicznego . Techniki znane jako optyka adaptacyjna zostały wykorzystane do wyeliminowania zakłóceń atmosferycznych obrazów i uzyskania wyników zbliżonych do granicy dyfrakcji.
Dyspersja i rozpraszanie
Procesy refrakcyjne zachodzą w granicach optyki fizycznej, gdzie długość fali światła jest podobna do innych odległości, jako rodzaj rozpraszania. Najprostszym rodzajem rozpraszania jest rozpraszanie Thomsona , które występuje, gdy fale elektromagnetyczne są odchylane przez pojedyncze cząstki. W granicach rozpraszania Thomsona, w którym oczywista jest falowa natura światła, światło jest rozpraszane niezależnie od częstotliwości, w przeciwieństwie do rozpraszania Comptona , które jest zależne od częstotliwości i ściśle mechaniki kwantowej proces, obejmujący naturę światła jako cząstek. W sensie statystycznym elastyczne rozpraszanie światła przez liczne cząstki znacznie mniejsze niż długość fali światła jest procesem znanym jako rozpraszanie Rayleigha, podczas gdy podobny proces rozpraszania przez cząstki o podobnej lub większej długości fali jest znany jako rozpraszanie Mie z Tyndallem efekt jest powszechnie obserwowanym wynikiem. Niewielka część światła rozpraszanego przez atomy lub cząsteczki może podlegać rozpraszaniu ramanowskiemu , w którym częstotliwość zmienia się w wyniku wzbudzenia atomów i cząsteczek. Rozpraszanie Brillouina występuje, gdy częstotliwość światła zmienia się w wyniku lokalnych zmian w czasie i ruchów gęstego materiału.
Dyspersja występuje, gdy różne częstotliwości światła mają różne prędkości fazowe , ze względu na właściwości materiału ( dyspersja materiału ) lub geometrię światłowodu ( dyspersja falowodu ). Najbardziej znaną formą dyspersji jest spadek współczynnika załamania światła wraz ze wzrostem długości fali, który obserwuje się w większości przezroczystych materiałów. Nazywa się to „normalną dyspersją”. Występuje we wszystkich materiałach dielektrycznych , w zakresach długości fal, w których materiał nie pochłania światła. W zakresach długości fal, w których ośrodek ma znaczną absorpcję, współczynnik załamania może rosnąć wraz z długością fali. Nazywa się to „nieprawidłową dyspersją”.
Rozdzielenie kolorów przez pryzmat jest przykładem normalnej dyspersji. Na powierzchniach pryzmatu prawo Snella przewiduje, że światło padające pod kątem θ do normalnej zostanie załamane pod kątem arcsin(sin (θ) / n ). Zatem światło niebieskie, o wyższym współczynniku załamania światła, jest załamywane silniej niż światło czerwone, co daje dobrze znany tęczy .
Dyspersję materiału często charakteryzuje liczba Abbego , która daje prostą miarę dyspersji opartą na współczynniku załamania światła przy trzech określonych długościach fal. Dyspersja falowodu zależy od stałej propagacji . Oba rodzaje dyspersji powodują zmiany charakterystyk grupowych fali, cech pakietu falowego, które zmieniają się z tą samą częstotliwością co amplituda fali elektromagnetycznej. „Grupowa dyspersja prędkości” przejawia się jako rozprzestrzenianie się sygnału „obwiedni” promieniowania i może być określona ilościowo za pomocą parametru opóźnienia dyspersji grupowej:
gdzie grupową Dla ośrodka jednorodnego prędkość grupowa wynosi
gdzie n to współczynnik załamania, a c to prędkość światła w próżni. Daje to prostszą postać parametru opóźnienia dyspersji:
Jeśli D jest mniejsze od zera, mówi się, że ośrodek ma dyspersję dodatnią lub dyspersję normalną. Jeśli D jest większe od zera, ośrodek ma ujemną dyspersję . Jeśli impuls światła jest propagowany przez ośrodek normalnie dyspersyjny, wynikiem jest to, że składowe o wyższej częstotliwości spowalniają bardziej niż składowe o niższej częstotliwości. W związku z tym puls staje się dodatnio ćwierkający lub ćwierkający , zwiększając częstotliwość w czasie. Powoduje to, że widmo wychodzące z pryzmatu wydaje się mieć najmniej załamane światło czerwone, a najbardziej załamane światło niebiesko-fioletowe. I odwrotnie, jeśli impuls przechodzi przez ośrodek o anomalnej (ujemnej) dyspersji, składowe o wysokiej częstotliwości poruszają się szybciej niż te o niższej częstotliwości, a impuls staje się ćwierkany ujemnie lub ściśnięty , a częstotliwość zmniejsza się z czasem.
Rezultatem dyspersji prędkości grupowej, czy to ujemnej, czy dodatniej, jest ostatecznie czasowe rozłożenie impulsu. To sprawia, że zarządzanie dyspersją jest niezwykle ważne w systemach komunikacji optycznej opartych na światłowodach , ponieważ jeśli dyspersja jest zbyt wysoka, każda grupa impulsów reprezentujących informacje będzie się rozprzestrzeniać w czasie i łączyć, uniemożliwiając wydobycie sygnału.
Polaryzacja
Polaryzacja jest ogólną właściwością fal, która opisuje orientację ich oscylacji. W przypadku fal poprzecznych, takich jak wiele fal elektromagnetycznych, opisuje orientację oscylacji w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali. Oscylacje mogą być zorientowane w jednym kierunku ( polaryzacja liniowa ) lub kierunek oscylacji może zmieniać się wraz z przemieszczaniem się fali ( polaryzacja kołowa lub eliptyczna ). Fale spolaryzowane kołowo mogą obracać się w prawo lub w lewo w kierunku ruchu, a która z tych dwóch rotacji jest obecna w fali, nazywana jest chiralnością fali .
Typowym sposobem uwzględnienia polaryzacji jest śledzenie orientacji wektora pola elektrycznego podczas rozchodzenia się fali elektromagnetycznej. Wektor pola elektrycznego fali płaskiej można dowolnie podzielić na dwie prostopadłe składowe oznaczone x i y (gdzie z wskazuje kierunek rozchodzenia się). Kształt wytyczony w płaszczyźnie xy przez wektor pola elektrycznego jest figurą Lissajous opisującą stan polaryzacji . Poniższe rysunki przedstawiają przykłady ewolucji wektora pola elektrycznego (kolor niebieski) w czasie (osie pionowe) w określonym punkcie przestrzeni wraz z jego składowymi x i y (czerwony/lewy i zielony / prawy ) , oraz ścieżka wytyczona przez wektor w płaszczyźnie (fioletowy): Ta sama ewolucja miałaby miejsce, patrząc na pole elektryczne w określonym czasie, podczas ewolucji punktu w przestrzeni, wzdłuż kierunku przeciwnego do propagacji.
Na powyższym rysunku po lewej stronie składowe x i y fali świetlnej są w fazie. W tym przypadku stosunek ich sił jest stały, więc kierunek wektora elektrycznego (suma wektorów tych dwóch składowych) jest stały. Ponieważ wierzchołek wektora wyznacza pojedynczą linię na płaszczyźnie, ten szczególny przypadek nazywa się polaryzacją liniową. Kierunek tej linii zależy od względnych amplitud obu składowych.
Na środkowym rysunku dwie prostopadłe składowe mają te same amplitudy i są przesunięte w fazie o 90°. W tym przypadku jedna składowa ma wartość zero, gdy druga składowa ma maksymalną lub minimalną amplitudę. Istnieją dwie możliwe zależności fazowe, które spełniają to wymaganie: x może znajdować się 90° przed składową y lub może być 90° za składową y . W tym szczególnym przypadku wektor elektryczny zakreśla okrąg na płaszczyźnie, więc ta polaryzacja nazywana jest polaryzacją kołową. Kierunek obrotu w okręgu zależy od tego, która z zależności dwufazowych istnieje i odpowiada polaryzacja kołowa prawoskrętna i polaryzacja kołowa lewoskrętna .
We wszystkich innych przypadkach, gdy dwie składowe albo nie mają takich samych amplitud i/lub ich różnica faz nie jest ani zerem, ani wielokrotnością 90°, polaryzację nazywamy polaryzacją eliptyczną, ponieważ wektor elektryczny zakreśla elipsę w płaszczyźnie ( elipsa polaryzacyjna ). Pokazano to na powyższym rysunku po prawej stronie. Szczegółowa matematyka polaryzacji jest wykonywana za pomocą rachunku Jonesa i jest scharakteryzowana parametrami Stokesa .
Zmiana polaryzacji
Ośrodki, które mają różne współczynniki załamania dla różnych trybów polaryzacji, nazywane są dwójłomnymi . Dobrze znane przejawy tego efektu pojawiają się w płytach /retarderach fali optycznej (mody liniowe) oraz w rotacji Faradaya / rotacji optycznej (mody kołowe). Jeśli długość ścieżki w ośrodku dwójłomnym jest wystarczająca, fale płaskie opuszczą materiał ze znacznie innym kierunkiem propagacji z powodu załamania. Tak jest na przykład w przypadku makroskopowych kryształów kalcytu , które przedstawiają widzowi dwa przesunięte, ortogonalnie spolaryzowane obrazy tego, co jest przez nie oglądane. To właśnie ten efekt zapewnił pierwsze odkrycie polaryzacji przez Erazma Bartholinusa w 1669 r. Ponadto przesunięcie fazowe, a tym samym zmiana stanu polaryzacji, jest zwykle zależna od częstotliwości, co w połączeniu z dichroizmem często powoduje powstawanie jasnych kolory i efekty przypominające tęczę. W mineralogii takie właściwości określa się mianem pleochroizmu , są często wykorzystywane do identyfikacji minerałów za pomocą mikroskopów polaryzacyjnych. Ponadto wiele tworzyw sztucznych, które normalnie nie są dwójłomne, stanie się nimi pod wpływem naprężeń mechanicznych , zjawiska będącego podstawą fotosprężystości . Metody niedwójłomne do obracania liniowej polaryzacji wiązek światła obejmują zastosowanie pryzmatycznych rotatorów polaryzacji , które wykorzystują całkowite wewnętrzne odbicie w zestawie pryzmatów zaprojektowanym do wydajnej transmisji współliniowej.
Media, które zmniejszają amplitudę niektórych trybów polaryzacji, nazywane są dichroicznymi , a urządzenia, które blokują prawie całe promieniowanie w jednym trybie, znane są jako filtry polaryzacyjne lub po prostu „ polaryzatory ”. Prawo Malusa, które zostało nazwane na cześć Étienne-Louisa Malusa , mówi, że kiedy doskonały polaryzator jest umieszczony w liniowo spolaryzowanej wiązce światła, intensywność I światła przechodzącego przez nie jest określona wzorem
Gdzie
- 0 I to intensywność początkowa,
- a θ i to kąt między początkowym kierunkiem polaryzacji światła a osią polaryzatora.
Wiązkę światła niespolaryzowanego można traktować jako zawierającą jednolitą mieszaninę liniowych polaryzacji pod wszystkimi możliwymi kątami. wartość transmisji staje
W praktyce część światła jest tracona w polaryzatorze, a rzeczywista przepuszczalność światła niespolaryzowanego będzie nieco niższa, około 38% dla polaryzatorów typu polaroid, ale znacznie wyższa (>49,9%) dla niektórych typów pryzmatów dwójłomnych.
Oprócz dwójłomności i dichroizmu w ośrodkach rozszerzonych, efekty polaryzacji mogą również wystąpić na (odblaskowej) granicy faz między dwoma materiałami o różnym współczynniku załamania światła. Efekty te są traktowane przez równania Fresnela . Część fali jest przepuszczana, a część odbijana, przy czym stosunek zależy od kąta padania i kąta załamania. W ten sposób optyka fizyczna odzyskuje kąt Brewstera . Kiedy światło odbija się od cienkiej warstwy na powierzchni, interferencja między odbiciami od powierzchni folii może powodować polaryzację światła odbitego i przechodzącego.
Naturalne światło

Większość źródeł promieniowania elektromagnetycznego zawiera dużą liczbę atomów lub cząsteczek emitujących światło. Orientacja pól elektrycznych wytwarzanych przez te emitery może nie być skorelowana , w takim przypadku mówi się, że światło jest niespolaryzowane . Jeśli istnieje częściowa korelacja między emiterami, światło jest częściowo spolaryzowane . Jeśli polaryzacja jest stała w całym spektrum źródła, światło częściowo spolaryzowane można opisać jako superpozycję składowej całkowicie niespolaryzowanej i składowej całkowicie spolaryzowanej. Można więc opisać światło w kategoriach stopnia polaryzacji , oraz parametry elipsy polaryzacyjnej.
Światło odbite od błyszczących przezroczystych materiałów jest częściowo lub całkowicie spolaryzowane, z wyjątkiem sytuacji, gdy światło jest prostopadłe do powierzchni. To właśnie ten efekt umożliwił matematykowi Étienne-Louisowi Malusowi wykonanie pomiarów, które umożliwiły mu opracowanie pierwszych modeli matematycznych światła spolaryzowanego. Polaryzacja występuje, gdy światło jest rozpraszane w atmosferze . Rozproszone światło daje jasność i kolor czystego nieba . Tę częściową polaryzację rozproszonego światła można wykorzystać przy użyciu filtrów polaryzacyjnych do przyciemnienia nieba na zdjęciach . Polaryzacja optyczna ma zasadnicze znaczenie w chemii ze względu na dichroizm kołowy i skręcalność optyczną („ dwójłomność kołowa ”) wykazywaną przez cząsteczki optycznie czynne ( chiralne ) .
Nowoczesna optyka
Nowoczesna optyka obejmuje dziedziny optyki i inżynierii, które stały się popularne w XX wieku. Te dziedziny optyki zazwyczaj odnoszą się do elektromagnetycznych lub kwantowych właściwości światła, ale obejmują inne tematy. Główna poddziedzina współczesnej optyki, optyka kwantowa , zajmuje się specyficznie kwantowymi mechanicznymi właściwościami światła. Optyka kwantowa jest nie tylko teoretyczna; niektóre nowoczesne urządzenia, takie jak lasery, mają zasady działania zależne od mechaniki kwantowej. Detektory światła, takie jak fotopowielacze i channeltrony , reagują na pojedyncze fotony. Elektroniczny czujniki obrazu , takie jak matryce CCD , wykazują szum śrutowy odpowiadający statystykom poszczególnych zdarzeń fotonowych. Diody elektroluminescencyjne i ogniwa fotowoltaiczne również nie mogą być zrozumiane bez mechaniki kwantowej. W badaniu tych urządzeń optyka kwantowa często pokrywa się z elektroniką kwantową .
Specjalistyczne obszary badań optyki obejmują badanie interakcji światła z określonymi materiałami, jak w optyce kryształów i metamateriałach . Inne badania koncentrują się na fenomenologii fal elektromagnetycznych, jak w optyce pojedynczej , optyce nieobrazowej , optyce nieliniowej , optyce statystycznej i radiometrii . Ponadto inżynierowie komputerowi zainteresowali się optyką zintegrowaną , wizją maszynową i obliczeniami fotonicznymi jako możliwe komponenty „następnej generacji” komputerów.
Dziś czysta nauka optyki nazywana jest nauką optyczną lub fizyką optyczną , aby odróżnić ją od stosowanych nauk optycznych, które określa się mianem inżynierii optycznej . Wybitne poddziedziny inżynierii optycznej obejmują inżynierię oświetlenia , fotonikę i optoelektronikę z praktycznymi zastosowaniami, takimi jak projektowanie soczewek , wytwarzanie i testowanie elementów optycznych oraz przetwarzanie obrazu . Niektóre z tych dziedzin nakładają się na siebie, z niejasnymi granicami między terminami przedmiotowymi, które oznaczają nieco różne rzeczy w różnych częściach świata iw różnych obszarach przemysłu. Profesjonalna społeczność naukowców zajmujących się optyką nieliniową rozwinęła się w ciągu ostatnich kilkudziesięciu lat dzięki postępowi w technologii laserowej.
Lasery

Laser to urządzenie, które emituje światło, rodzaj promieniowania elektromagnetycznego, w procesie zwanym emisją wymuszoną . Termin laser jest skrótem od Light Amplification by Stimulated Emission of Radiation (wzmacnianie światła przez stymulowaną emisję promieniowania) . Światło lasera jest zwykle przestrzennie spójne , co oznacza, że albo jest emitowane w postaci wąskiej wiązki o niskiej rozbieżności , albo może zostać przekształcone w wiązkę za pomocą elementów optycznych, takich jak soczewki. Bo to mikrofalowy odpowiednik lasera, maser , został opracowany jako pierwszy, urządzenia emitujące mikrofale i częstotliwości radiowe są zwykle nazywane maserami .

Pierwszy działający laser został zademonstrowany 16 maja 1960 roku przez Theodore'a Maimana w Hughes Research Laboratories . Kiedy po raz pierwszy zostały wynalezione, nazywano je „rozwiązaniem szukającym problemu”. Od tego czasu lasery stały się przemysłem wartym wiele miliardów dolarów, znajdującym zastosowanie w tysiącach bardzo różnorodnych zastosowań. Pierwszym zastosowaniem laserów widocznym w życiu codziennym ogółu społeczeństwa był kodów kreskowych w supermarkecie , wprowadzony w 1974 r. Laserowy odtwarzacz dysków, wprowadzony w 1978 r., był pierwszym udanym produktem konsumenckim zawierającym laser, ale płyt kompaktowych był pierwszym urządzeniem wyposażonym w laser, które stało się naprawdę powszechne w domach konsumentów począwszy od 1982 roku. Te optyczne urządzenia pamięci masowej wykorzystują laser półprzewodnikowy o szerokości mniejszej niż milimetr do skanowania powierzchni dysku w celu odzyskania danych. Komunikacja światłowodowa opiera się na laserach do przesyłania dużych ilości informacji z prędkością światła. Inne powszechne zastosowania laserów obejmują drukarki laserowe i wskaźniki laserowe . Lasery znajdują zastosowanie w medycynie w takich dziedzinach jak bezkrwawa chirurgia , chirurgii laserowej oka i mikrodysekcji przechwytywania laserowego oraz w zastosowaniach wojskowych, takich jak systemy obrony przeciwrakietowej , elektrooptyczne środki zaradcze (EOCM) i lidar . Lasery są również wykorzystywane w hologramach , bąbelkach , pokazach światła laserowego i depilacji laserowej .
Efekt Kapicy-Diraca
Kapitsy -Diraca powoduje dyfrakcję wiązek cząstek w wyniku napotkania stojącej fali światła. Światło może być używane do pozycjonowania materii za pomocą różnych zjawisk (patrz pęseta optyczna ).
Aplikacje
Optyka jest częścią codziennego życia. Wszechobecność systemów wizualnych w biologii wskazuje na centralną rolę optyki jako nauki o jednym z pięciu zmysłów . Wiele osób korzysta z okularów lub soczewek kontaktowych , a optyka jest integralną częścią funkcjonowania wielu dóbr konsumpcyjnych, w tym aparatów fotograficznych . Tęcze i miraże to przykłady zjawisk optycznych. Łączność optyczna stanowi podstawę zarówno Internetu , jak i nowoczesnej telefonii .
Ludzkie oko

Ludzkie oko działa poprzez skupianie światła na warstwie komórek fotoreceptorów zwanej siatkówką, która tworzy wewnętrzną wyściółkę tylnej części oka. Ogniskowanie odbywa się za pomocą szeregu przezroczystych mediów. Światło wpadające do oka przechodzi najpierw przez rogówkę, która zapewnia znaczną część mocy optycznej oka. Światło następnie przechodzi przez płyn tuż za rogówką — komorę przednią , a następnie przechodzi przez źrenicę . Następnie światło przechodzi przez soczewkę , który dodatkowo skupia światło i umożliwia regulację ostrości. Światło następnie przechodzi przez główny płyn w oku - ciało szkliste i dociera do siatkówki. Komórki siatkówki wyścielają tylną część oka, z wyjątkiem miejsca, w którym wychodzi nerw wzrokowy; skutkuje to martwym punktem .
Istnieją dwa rodzaje komórek fotoreceptorów, pręciki i czopki, które są wrażliwe na różne aspekty światła. Pręciki są wrażliwe na intensywność światła w szerokim zakresie częstotliwości, dlatego odpowiadają za widzenie czarno-białe . Pręciki nie występują w dołku, obszarze siatkówki odpowiedzialnym za widzenie centralne, i nie reagują tak jak czopki na przestrzenne i czasowe zmiany światła. W siatkówce jest jednak dwadzieścia razy więcej pręcików niż czopków, ponieważ pręciki są obecne na większym obszarze. Ze względu na ich szersze rozmieszczenie pręciki odpowiadają za widzenie peryferyjne .
Natomiast komórki czopków są mniej wrażliwe na ogólną intensywność światła, ale występują w trzech odmianach, które są wrażliwe na różne zakresy częstotliwości, a zatem są wykorzystywane do postrzegania kolorów i widzenia fotopowego . Komórki czopków są silnie skoncentrowane w dołku i mają wysoką ostrość widzenia, co oznacza, że mają lepszą rozdzielczość przestrzenną niż pręciki. Ponieważ czopki nie są tak wrażliwe na słabe światło jak pręciki, większość noktowizorów ogranicza się do pręcików. Podobnie, ponieważ komórki czopków znajdują się w dołku, widzenie centralne (w tym widzenie potrzebne do większości czytania, drobnych prac szczegółowych, takich jak szycie lub dokładne badanie przedmiotów) jest wykonywane przez komórki czopków.
Mięśnie rzęskowe wokół soczewki umożliwiają regulację ostrości oka. Ten proces jest znany jako akomodacja . Punkt bliski i punkt daleki określają najbliższą i najdalszą odległość od oka, w której można ustawić ostrość obiektu. Dla osoby o normalnym wzroku daleki punkt znajduje się w nieskończoności. Lokalizacja punktu bliży zależy od tego, jak bardzo mięśnie mogą zwiększyć krzywiznę soczewki i jak mało elastyczna stała się soczewka z wiekiem. Optometryści , okuliści i optycy zwykle uważaj, że odpowiedni punkt do bliży znajduje się bliżej niż normalna odległość czytania — około 25 cm.
Wady wzroku można wyjaśnić za pomocą zasad optycznych. Wraz z wiekiem soczewka staje się mniej elastyczna, a punkt bliży oddala się od oka, co jest stanem znanym jako starczowzroczność . Podobnie osoby cierpiące na nadwzroczność nie mogą zmniejszyć ogniskowej soczewki na tyle, aby umożliwić obrazowanie pobliskich obiektów na ich siatkówce. I odwrotnie, ludzie, którzy nie mogą zwiększyć ogniskowej swojego obiektywu na tyle, aby umożliwić obrazowanie odległych obiektów na siatkówce, cierpią na krótkowzroczność i mają daleki punkt, który jest znacznie bliżej niż nieskończoność. Stan znany jako astygmatyzm powstaje, gdy rogówka nie jest kulista, lecz bardziej zakrzywiona w jednym kierunku. Powoduje to, że obiekty rozciągające się w poziomie skupiają się na innych częściach siatkówki niż obiekty rozciągające się w pionie, co skutkuje zniekształconymi obrazami.
Wszystkie te wady można skorygować za pomocą soczewek korekcyjnych . W przypadku starczowzroczności i nadwzroczności soczewka skupiająca zapewnia dodatkową krzywiznę niezbędną do zbliżenia punktu bliży do oka, podczas gdy w przypadku krótkowzroczności soczewka rozpraszająca zapewnia krzywiznę niezbędną do przesunięcia punktu dalekiego w nieskończoność. Astygmatyzm koryguje się cylindrycznej powierzchni , która zakrzywia się mocniej w jednym kierunku niż w drugim, kompensując niejednorodność rogówki.
Moc optyczna soczewek korekcyjnych mierzona jest w dioptriach , czyli wartości równej odwrotności ogniskowej mierzonej w metrach; z dodatnią ogniskową odpowiadającą soczewce skupiającej i ujemną ogniskową odpowiadającą soczewce rozpraszającej. W przypadku soczewek, które również korygują astygmatyzm, podane są trzy liczby: jedna dla mocy sferycznej, jedna dla mocy cylindrycznej i jedna dla kąta orientacji astygmatyzmu.
Efekty wizualne
Złudzenia optyczne (zwane także złudzeniami wizualnymi) charakteryzują się postrzeganymi wizualnie obrazami, które różnią się od obiektywnej rzeczywistości. Informacje zebrane przez oko są przetwarzane w mózgu w celu uzyskania perceptu , który różni się od obrazu obiektu. Złudzenia optyczne mogą być wynikiem różnych zjawisk, w tym efektów fizycznych, które tworzą obrazy różniące się od przedmiotów, które je tworzą, fizjologicznych skutków nadmiernej stymulacji dla oczu i mózgu (np. jasność, nachylenie, kolor, ruch) oraz iluzje poznawcze, w których oko i mózg wyciągają nieświadome wnioski .
Złudzenia poznawcze obejmują takie, które wynikają z nieświadomego niewłaściwego zastosowania pewnych zasad optycznych. Na przykład pokoju Amesa , Heringa , Müllera-Lyera , Orbisona , Ponzo , Sandera i Wundta opierają się na sugestii pojawienia się odległości za pomocą zbieżnych i rozbieżnych linii, w taki sam sposób, w jaki równoległe promienie światła (lub w rzeczywistości dowolny zestaw równoległych linii) wydają się zbiegać w punkcie zbiegu w nieskończoności w dwuwymiarowych renderowanych obrazach z artystyczną perspektywą. Ta sugestia jest również odpowiedzialna za słynną iluzję księżyca , w której księżyc, pomimo zasadniczo tego samego rozmiaru kątowego, wydaje się znacznie większy w pobliżu horyzontu niż w zenicie . Ta iluzja tak zmyliła Ptolemeusza , że błędnie przypisał ją refrakcji atmosferycznej, opisując ją w swoim traktacie Optyka .
Inny rodzaj iluzji optycznej wykorzystuje zepsute wzorce, aby oszukać umysł w celu dostrzeżenia symetrii lub asymetrii, których nie ma. Przykłady obejmują ścianę kawiarni , iluzje Ehrensteina , spirali Frasera , Poggendorffa i Zöllnera . Pokrewne, ale nie ściśle złudzenia, to wzorce, które pojawiają się w wyniku nakładania się struktur okresowych. Na przykład przezroczyste tkanki o strukturze siatki tworzą kształty znane jako wzory mory , podczas gdy nakładanie okresowych przezroczystych wzorów zawierających równoległe nieprzezroczyste linie lub krzywe tworzy liniowe wzory mory.
Instrumenty optyczne
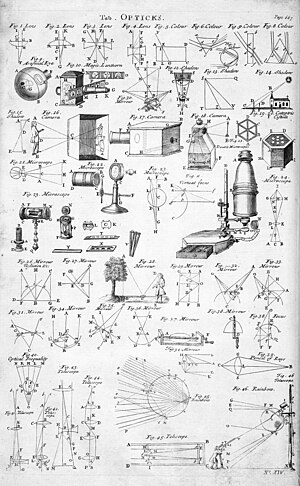
Pojedyncze soczewki mają różnorodne zastosowania, w tym soczewki fotograficzne , soczewki korekcyjne i szkła powiększające, podczas gdy pojedyncze lustra są używane w reflektorach parabolicznych i lusterkach wstecznych . Połączenie wielu zwierciadeł, pryzmatów i soczewek tworzy złożone instrumenty optyczne, które mają praktyczne zastosowania. Na przykład peryskop to po prostu dwa płaskie lustra ustawione tak, aby umożliwić oglądanie wokół przeszkód. Najbardziej znanymi złożonymi instrumentami optycznymi w nauce są mikroskop i teleskop, które zostały wynalezione przez Holendrów pod koniec XVI wieku.
Mikroskopy zostały po raz pierwszy opracowane z zaledwie dwiema soczewkami: soczewką obiektywową i okularem . Obiektyw jest zasadniczo szkłem powiększającym i został zaprojektowany z bardzo małą ogniskową, podczas gdy okular ma zazwyczaj dłuższą ogniskową. Powoduje to tworzenie powiększonych obrazów bliskich obiektów. Zwykle stosuje się dodatkowe źródło oświetlenia, ponieważ powiększone obrazy są ciemniejsze ze względu na zachowanie energii i rozchodzenie się promieni świetlnych na większej powierzchni. Współczesne mikroskopy, zwane mikroskopami złożonymi mieć w sobie wiele obiektywów (zwykle cztery), aby zoptymalizować funkcjonalność i zwiększyć stabilność obrazu. Nieco inna odmiana mikroskopu, mikroskop porównawczy , patrzy na obrazy obok siebie, aby uzyskać stereoskopowy widok obuoczny , który wydaje się trójwymiarowy, gdy jest używany przez ludzi.
Pierwsze teleskopy, zwane teleskopami refrakcyjnymi, również zostały opracowane z pojedynczym obiektywem i okularem. W przeciwieństwie do mikroskopu, obiektyw teleskopu został zaprojektowany z dużą ogniskową, aby uniknąć aberracji optycznych. Obiektyw skupia obraz odległego obiektu w jego ognisku, które jest ustawione tak, aby znajdowało się w ognisku okularu o znacznie mniejszej ogniskowej. Głównym celem teleskopu niekoniecznie jest powiększenie, ale raczej zbieranie światła, które jest określone przez fizyczny rozmiar soczewki obiektywu. W związku z tym teleskopy są zwykle wskazywane przez średnice ich obiektywów, a nie przez powiększenie, które można zmienić, zmieniając okulary. Ponieważ powiększenie teleskopu jest równe ogniskowej obiektywu podzielonej przez ogniskową okularu, okulary o mniejszej ogniskowej powodują większe powiększenie.
Ponieważ wytwarzanie dużych soczewek jest znacznie trudniejsze niż tworzenie dużych luster, większość nowoczesnych teleskopów to teleskopy zwierciadlane , czyli teleskopy, które wykorzystują zwierciadło główne zamiast soczewki obiektywowej. W przypadku teleskopów zwierciadlanych stosuje się te same ogólne zasady optyczne, co w przypadku teleskopów refrakcyjnych, mianowicie im większe zwierciadło główne, tym więcej zbieranego światła, a powiększenie jest nadal równe ogniskowej zwierciadła głównego podzielonej przez ogniskową okularu . Profesjonalne teleskopy na ogół nie mają okularów i zamiast tego umieszczają instrument (często urządzenie ze sprzężeniem ładunkowym) w ognisku.
Fotografia
Optyka fotografii obejmuje zarówno soczewki, jak i medium, w którym rejestrowane jest promieniowanie elektromagnetyczne, czy to płyta , film , czy urządzenie ze sprzężeniem ładunkowym. Fotografowie muszą wziąć pod uwagę wzajemność aparatu i ujęcia, które podsumowuje relacja
- Ekspozycja ∝ ApertureArea × ExposureTime × SceneLuminance
Innymi słowy, im mniejszy otwór przysłony (zapewniający większą głębię ostrości), tym mniej wpadającego światła, więc czas musi zostać zwiększony (co prowadzi do możliwego rozmycia w przypadku ruchu). Przykładem zastosowania prawa wzajemności jest reguła Sunny 16 , która daje przybliżone oszacowanie ustawień potrzebnych do oszacowania właściwej ekspozycji w świetle dziennym.
Przysłona aparatu jest mierzona liczbą bez jednostek, zwaną liczbą f lub f-stop, f / #, często zapisywaną jako i podawana przez
gdzie a źrenicy wejściowej Zgodnie z konwencją „ f /#” jest traktowane jako pojedynczy symbol, a określone wartości f /# są zapisywane przez zastąpienie znaku liczby wartością. Dwa sposoby na zwiększenie przysłony to albo zmniejszenie średnicy źrenicy wejściowej, albo zmiana ogniskowej na dłuższą (w przypadku obiektywu zmiennoogniskowego można to zrobić po prostu regulując obiektyw). Wyższe liczby f mają również większe głębia ostrości obiektywu zbliża się do granic możliwości aparatu otworkowego, który jest w stanie idealnie ustawić ostrość wszystkich obrazów, niezależnie od odległości, ale wymaga bardzo długich czasów naświetlania.
Pole widzenia, które zapewnia obiektyw, zmienia się wraz z ogniskową obiektywu. Istnieją trzy podstawowe klasyfikacje oparte na stosunku do przekątnej filmu lub rozmiaru czujnika aparatu do ogniskowej obiektywu:
- Normalna soczewka : kąt widzenia około 50° (nazywany normalnym , ponieważ ten kąt jest uważany za mniej więcej równoważny ludzkiemu widzeniu) i ogniskowa w przybliżeniu równa przekątnej kliszy lub czujnika.
- Obiektyw szerokokątny : kąt widzenia szerszy niż 60° i ogniskowa krótsza niż normalny obiektyw.
- Obiektyw o długiej ogniskowej : kąt widzenia węższy niż normalny obiektyw. Jest to dowolny obiektyw o ogniskowej dłuższej niż przekątna filmu lub czujnika. Najpopularniejszym typem obiektywu o długim ogniskowaniu jest teleobiektyw , konstrukcja wykorzystująca specjalną grupę teleobiektywów , aby była fizycznie krótsza niż długość ogniskowej.
Nowoczesne obiektywy zmiennoogniskowe mogą mieć niektóre lub wszystkie z tych cech.
Wartość bezwzględna wymaganego czasu naświetlania zależy od czułości używanego nośnika na światło (mierzonej na podstawie czułości filmu lub, w przypadku nośników cyfrowych, wydajności kwantowej ). Wczesna fotografia wykorzystywała nośniki o bardzo niskiej czułości na światło, dlatego czasy naświetlania musiały być długie, nawet w przypadku bardzo jasnych ujęć. Wraz z rozwojem technologii poprawiła się również czułość aparatów na kliszę i aparatów cyfrowych.
Inne wyniki optyki fizycznej i geometrycznej dotyczą optyki aparatu. Na przykład maksymalna rozdzielczość określonej konfiguracji kamery jest określona przez granicę dyfrakcji związaną z rozmiarem źrenicy i określoną w przybliżeniu przez kryterium Rayleigha.
Optyka atmosferyczna

Unikalne właściwości optyczne atmosfery powodują szeroki wachlarz spektakularnych zjawisk optycznych. Niebieski kolor nieba jest bezpośrednim wynikiem rozpraszania Rayleigha, które przekierowuje światło słoneczne o wyższej częstotliwości (niebieskie) z powrotem w pole widzenia obserwatora. Ponieważ światło niebieskie rozprasza się łatwiej niż światło czerwone, słońce przybiera czerwonawy odcień, gdy jest obserwowane przez gęstą atmosferę, na przykład podczas wschodu lub zachodu słońca . Dodatkowe cząstki stałe na niebie mogą rozpraszać różne kolory pod różnymi kątami, tworząc kolorowe świecące niebo o zmierzchu i świcie. Rozpraszanie kryształków lodu i innych cząstek w atmosferze jest odpowiedzialne za aureole , poświaty , korony , promienie słoneczne i psy słoneczne . Zmienność tego rodzaju zjawisk wynika z różnych rozmiarów i geometrii cząstek.
Miraże to zjawiska optyczne, w których promienie świetlne są zakrzywiane w wyniku zmian termicznych współczynnika załamania światła powietrza, tworząc przesunięte lub mocno zniekształcone obrazy odległych obiektów. Inne dramatyczne zjawiska optyczne z tym związane obejmują efekt Novaya Zemlya , w którym słońce wydaje się wschodzić wcześniej niż przewidywano ze zniekształconym kształtem. Spektakularna forma załamania występuje wraz z inwersją temperatury zwaną Fata Morgana , w której obiekty na horyzoncie, a nawet poza nim, takie jak wyspy, klify, statki lub góry lodowe, wydają się wydłużone i wzniesione, jak „zamki z bajki”.
Tęcze są wynikiem połączenia wewnętrznego odbicia i rozproszonego załamania światła w kroplach deszczu. Pojedyncze odbicie od grzbietu szeregu kropel deszczu tworzy tęczę o rozmiarze kątowym na niebie, który waha się od 40° do 42° z czerwienią na zewnątrz. Podwójne tęcze są wytwarzane przez dwa wewnętrzne odbicia o wielkości kątowej od 50,5° do 54° z fioletem na zewnątrz. Ponieważ tęczę widać, gdy słońce znajduje się 180° od środka tęczy, tęcze są bardziej widoczne, im bliżej horyzontu znajduje się słońce.
Zobacz też
- Dalsza lektura
- Urodzony, Maks; Wilk, Emil (2002). Zasady optyki . Wydawnictwo Uniwersytetu Cambridge. ISBN 978-1-139-64340-5 .
- Hecht, Eugeniusz (2002). Optyka (4 wyd.). Addison-Wesley Longman, Incorporated. ISBN 978-0-8053-8566-3 .
- Serway, Raymond A.; Jewett, John W. (2004). Fizyka dla naukowców i inżynierów (6, wyd. Ilustrowane). Belmont, Kalifornia: Thomson-Brooks/Cole. ISBN 978-0-534-40842-8 .
- Tipler, Paweł A.; Mosca, Gene (2004). Fizyka dla naukowców i inżynierów: elektryczność, magnetyzm, światło i elementarna fizyka współczesna . Tom. 2. WH Freemana. ISBN 978-0-7167-0810-0 .
- Lipson, Stephen G.; Lipson, Henry; Tannhauser, David Stefan (1995). Fizyka optyczna . Wydawnictwo Uniwersytetu Cambridge. ISBN 978-0-521-43631-1 .
- Fowles, Grant R. (1975). Wprowadzenie do współczesnej optyki . Publikacje kurierskie Dover. ISBN 978-0-486-65957-2 .
Linki zewnętrzne
- Odpowiednie dyskusje
- Optyka na temat In Our Time w BBC
- podręcznikach i samouczkach
- Light and Matter - podręcznik typu open source, zawierający omówienie optyki w rozdz. 28-32
- Optics2001 — biblioteka optyki i społeczność
- Optyka podstawowa — przewodnik techniczny Melles Griot
- Fizyka światła i optyki - książka licencjacka Uniwersytetu Brighama Younga
- Optyka dla PV – wprowadzenie krok po kroku do optyki klasycznej
- Moduły Wikibooks
- Dalsze lektury
- Towarzystwa
|
|