Rozpraszanie Mie

Rozpraszanie Mie jako funkcja promienia cząstki. W jednym cyklu średnica cząstek zmienia się od 0,1 długości fali do 1 długości fali. Współczynnik załamania kuli wynosi 1,5

Rozpraszanie Mie, widok artystyczny (pod padającą falą płaszczyzny spolaryzowanej liniowo)

Rezonanse Mie a promień

Przekrój poprzeczny radaru monostatycznego (RCS) doskonale przewodzącej metalowej kuli w funkcji częstotliwości (obliczonej teorią Mie). W granicy rozpraszania Rayleigha dla niskich częstotliwości , gdzie obwód jest mniejszy niż długość fali, znormalizowany RCS wynosi σ/(π R ² ) ~ 9 ( kR ) ⁴ . W zakresie optycznym wysokiej częstotliwości σ/(π R ² ) ~ 1.

Rozwiązanie Mie do równań Maxwella (znane również jako rozwiązanie Lorenza – Mie , rozwiązanie Lorenza – Mie – Debye'a lub rozpraszanie Mie ) opisuje rozpraszanie płaskiej fali elektromagnetycznej przez jednorodną kulę . Rozwiązanie ma postać nieskończonej serii kulistych wielobiegunowych fal cząstkowych . Nosi imię Gustava Mie .

Termin rozwiązanie Mie jest również używany do określania rozwiązań równań Maxwella dla rozpraszania przez sfery uwarstwione lub nieskończone cylindry lub inne geometrie, w których można zapisać osobne równania dla promieniowej i kątowej zależności rozwiązań. Termin teoria Mie jest czasami używany w odniesieniu do tego zbioru rozwiązań i metod; nie odnosi się do niezależnej teorii fizycznej ani prawa. Mówiąc szerzej, wzory „rozpraszania Mie” są najbardziej przydatne w sytuacjach, w których rozmiar cząstek rozpraszających jest porównywalny z długością fali światła, a nie znacznie mniejszy lub znacznie większy.

Rozpraszanie Mie (czasami określane jako rozpraszanie niemolekularne lub rozpraszanie cząstek aerozolu ) ma miejsce w dolnych 4500 m (15 000 stóp) atmosfery, gdzie wiele zasadniczo kulistych cząstek o średnicach w przybliżeniu równych długości fali padającego promienia może być obecny. Teoria rozpraszania Mie nie ma górnego ograniczenia rozmiaru i jest zbieżna do granic optyki geometrycznej dla dużych cząstek.

Wstęp

Część kątowa sferycznych harmonicznych wektorów magnetycznych i elektrycznych. Czerwone i zielone strzałki pokazują kierunek pola. Przedstawiono również generowanie funkcji skalarnych, pokazano tylko trzy pierwsze rzędy (dipole, kwadrupole, oktupole).

Nowoczesne sformułowanie rozwiązania Mie dotyczącego problemu rozpraszania na kuli można znaleźć w wielu książkach, np. JA Stratton 's Electromagnetic Theory . W tym sformułowaniu padająca fala płaska, jak również pole rozpraszające, są rozszerzane na promieniujące sferyczne wektory sferyczne harmoniczne . Pole wewnętrzne jest rozszerzane na sferyczne harmoniczne wektorów regularnych. Wymuszając warunek brzegowy na powierzchni sferycznej, można obliczyć współczynniki rozszerzalności pola rozproszonego.

Dla cząstek znacznie większych lub znacznie mniejszych niż długość fali światła rozproszonego istnieją proste i dokładne przybliżenia, które wystarczą do opisania zachowania układu. Jednak w przypadku obiektów, których rozmiar mieści się w granicach kilku rzędów wielkości długości fali, np. kropelek wody w atmosferze, cząstek lateksu w farbie, kropelek w emulsjach, w tym w mleku, oraz komórek biologicznych i składników komórkowych, konieczne jest bardziej szczegółowe podejście.

Rozwiązanie Mie nosi imię jego twórcy, niemieckiego fizyka Gustava Mie . Duński fizyk Ludvig Lorenz i inni niezależnie opracowali teorię rozpraszania elektromagnetycznej fali płaskiej przez kulę dielektryczną .

Formalizm umożliwia obliczenie pól elektrycznych i magnetycznych wewnątrz i na zewnątrz kulistego obiektu i jest zwykle używany do obliczania, ile światła jest rozproszone (całkowity przekrój optyczny ) lub dokąd zmierza (współczynnik kształtu). Godnymi uwagi cechami tych wyników są rezonanse Mie, rozmiary, które rozpraszają się szczególnie silnie lub słabo. Kontrastuje to z rozpraszaniem Rayleigha dla małych cząstek i rozpraszaniem Rayleigha-Gansa-Debye'a (za Lordem Rayleighem , Richardem Gansem i Peterem Debye'em ) dla dużych cząstek. Istnienie rezonansów i innych cech rozpraszania Mie sprawia, że ​​jest to szczególnie przydatny formalizm przy stosowaniu światła rozproszonego do pomiaru wielkości cząstek.

przybliżenia

Przybliżenie Rayleigha (rozpraszanie)

Główny artykuł: rozpraszanie Rayleigha

Zmiana koloru nieba o zachodzie słońca (czerwony najbliżej słońca, niebieski najdalej) jest spowodowana rozpraszaniem Rayleigha przez cząsteczki gazów atmosferycznych, które są znacznie mniejsze niż długości fal światła widzialnego. Szaro-biały kolor chmur jest spowodowany przez rozpraszanie Mie przez kropelki wody, których rozmiar jest porównywalny z długością fali światła widzialnego.

Rozpraszanie Rayleigha opisuje elastyczne rozpraszanie światła przez kule, które są znacznie mniejsze niż długość fali światła. Natężenie I promieniowania rozproszonego jest określone wzorem

${\ Displaystyle I = I_ {0} \ lewo ({{{ \frac {1+\cos ^{2}\theta }{2R^{2}}}\right)\left({\frac {2\pi }{\lambda }}\right)^{4}\left ({\frac {n^{2}-1}{n^{2}+2}}\right)^{2}\left({\frac {d}{2}}\right)^{6} ,}$

gdzie I ₀ to natężenie światła przed oddziaływaniem z cząstką, R to odległość między cząstką a obserwatorem, θ to kąt rozpraszania, λ to długość fali rozważanego światła, n to współczynnik załamania światła cząstki, a d jest średnicą cząstki.

Z powyższego równania widać, że rozpraszanie Rayleigha jest silnie zależne od rozmiaru cząstki i długości fali. Intensywność promieniowania rozproszonego Rayleigha gwałtownie wzrasta wraz ze wzrostem stosunku wielkości cząstek do długości fali. Ponadto intensywność promieniowania rozproszonego Rayleigha jest identyczna w kierunku do przodu i do tyłu.

Model rozpraszania Rayleigha załamuje się, gdy rozmiar cząstek staje się większy niż około 10% długości fali padającego promieniowania. W przypadku cząstek o wymiarach większych niż ten, model rozpraszania Mie może być użyty do znalezienia intensywności rozproszonego promieniowania. Intensywność promieniowania rozproszonego Mie jest dana sumą nieskończonej serii terminów, a nie prostym wyrażeniem matematycznym. Można jednak wykazać, że rozpraszanie w tym zakresie rozmiarów cząstek różni się od rozpraszania Rayleigha pod kilkoma względami: jest z grubsza niezależne od długości fali i jest większe w kierunku do przodu niż w kierunku odwrotnym. Im większy rozmiar cząstek, tym więcej światła jest rozpraszane w kierunku do przodu.

Niebieski kolor nieba wynika z rozpraszania Rayleigha, ponieważ rozmiar cząstek gazu w atmosferze jest znacznie mniejszy niż długość fali światła widzialnego. Rozpraszanie Rayleigha jest znacznie większe dla światła niebieskiego niż dla innych kolorów ze względu na jego krótszą długość fali. Gdy światło słoneczne przechodzi przez atmosferę, jego składowa niebieska jest silnie rozpraszana przez gazy atmosferyczne, natomiast składowa o większej długości fali (np. czerwona/żółta) nie. Dlatego światło słoneczne docierające bezpośrednio ze Słońca wydaje się być lekko żółte, podczas gdy światło rozproszone na pozostałej części nieba wydaje się niebieskie. Podczas wschodów i zachodów słońca wpływ rozpraszania Rayleigha na widmo przepuszczanego światła jest znacznie większy ze względu na większą odległość, jaką promienie świetlne muszą pokonać w gęstym powietrzu w pobliżu powierzchni Ziemi.

W przeciwieństwie do tego, kropelki wody tworzące chmury mają rozmiar porównywalny do długości fal w świetle widzialnym, a rozpraszanie jest opisane raczej przez model Mie niż Rayleigha. Tutaj wszystkie długości fal światła widzialnego są rozproszone w przybliżeniu identycznie, dlatego chmury wydają się być białe lub szare.

Przybliżenie Rayleigha-Gansa

Rayleigha -Gansa jest przybliżonym rozwiązaniem rozpraszania światła, gdy względny współczynnik załamania światła cząstki jest zbliżony do współczynnika otoczenia, a jej rozmiar jest znacznie mniejszy w porównaniu z długością fali światła podzieloną przez | n − 1|, gdzie n jest współczynnikiem załamania :

${\ Displaystyle | n-1 | \ ll 1}$

${\ displaystyle kd | n-1 | \ ll 1}$

gdzie ${\ textstyle k}$ jest wektorem falowym światła ( ( ${\ textstyle k = {\ Frac {2 \ pi} {\ lambda}}}$$)$ odnosi do wymiar liniowy cząstki. Pierwszy warunek jest często określany jako „miękkość optyczna”, a przybliżenie to dotyczy cząstek o dowolnym kształcie.

Anomalne przybliżenie dyfrakcyjne van de Hulsta

Przybliżenie anomalnej dyfrakcji jest ważne dla dużych (w porównaniu z długością fali) i optycznie miękkich kul; miękkie w kontekście optyki oznacza, że ​​współczynnik załamania światła cząstki (m) różni się tylko nieznacznie od współczynnika załamania światła otoczenia, a cząstka poddaje fali tylko niewielkiemu przesunięciu fazowemu. Efektywność ekstynkcji w tym przybliżeniu jest dana przez

${\ Displaystyle Q = 2 - {\ Frac {4} {p}} \ sin p + {\ Frac {4} {p ^ {2}}}(1-\cos p),}$

gdzie Q jest współczynnikiem efektywności rozpraszania, który definiuje się jako stosunek przekroju poprzecznego rozpraszania do przekroju geometrycznego π a ² .

Termin p = 4πa( n − 1)/λ ma fizyczne znaczenie opóźnienia fazowego fali przechodzącej przez środek kuli, gdzie a to promień kuli, n to stosunek współczynników załamania wewnątrz i na zewnątrz kuli kula, a λ długość fali światła.

Ten zestaw równań został po raz pierwszy opisany przez van de Hulsta w (1957).

Matematyka

Rozpraszanie fali płaskiej, kierunek padania równoległy do ​​osi z , polaryzacja równoległa do osi x , promień nanocząstki to

Rozpraszanie przez sferyczną nanocząstkę jest rozwiązywane dokładnie niezależnie od wielkości cząstki. Rozważamy rozpraszanie przez falę płaską rozchodzącą się wzdłuż osi z spolaryzowaną wzdłuż osi x . Przepuszczalność dielektryczna i magnetyczna cząstki wynosi ${\ Displaystyle \ varepsilon _ {1}}$ i ${\ Displaystyle \ mu _ {1}}$ i i $1 {\ Displaystyle \ mu _ {1}}$ i ${\ Displaystyle \ varepsilon}$ dla środowiska.

Aby rozwiązać problem rozpraszania, najpierw zapisujemy rozwiązania wektorowego równania Helmholtza we współrzędnych sferycznych, ponieważ pola wewnątrz i na zewnątrz cząstek muszą to spełniać. Równanie Helmholtza:

${\ Displaystyle \ nabla ^ {2} \ mathbf {E} + {k} ^ {2} \ mathbf {E} = 0, \ \ \ \ \nabla ^{2}\mathbf {H} +{k}^{2}\mathbf {H} =0.}$

Oprócz równania Helmholtza pola muszą spełniać warunki ${\ Displaystyle \ nabla \ cdot \ mathbf {E} = \ nabla \ cdot \ mathbf {H} = 0}$ i ${\ Displaystyle \ nabla \ razy \ mathbf {E} = i \ omega \ mu \ mathbf {H}}$ , ${\ Displaystyle \ nabla \ razy \ mathbf {H. } =-i\omega \varepsilon \mathbf {E} }$ . Wektorowe harmoniczne sferyczne posiadają wszystkie niezbędne właściwości, wprowadzone w następujący sposób:

${\ Displaystyle \ mathbf {M} _ {^ {e} _ {o} mn} = \ nabla \ razy \ lewo (\ mathbf {r} \ psi _ {^ {e} _ {o} mn} \ prawej)}$ - harmoniczne magnetyczne (TE) ,

${\ Displaystyle \ mathbf {N} _ {^ { e}_{o}mn}={\frac {\nabla \times \mathbf {M} _{^{e}_{o}mn}}{k}}} — elektryczne harmoniczne (TM)$ ,

Gdzie

${\ Displaystyle {\ psi _ {emn} = \ bos m \ varphi P_ {n} ^ {m} (\ sałata \vartheta )z_{n}({k}r),}}$

$\ Displaystyle {\ psi _ {omn} = \ sin m \ varphi P_ {n} ^ {m} (\ cos \ vartheta) z_ {n} ({k} r),}}$

i ${\ Displaystyle P_ {n} ^ {m} (\ cos \ theta)}$ - Powiązane wielomiany Legendre'a i ${\ Displaystyle z_ {n} ({k} r)}$ — dowolna ze sferycznych funkcji Bessela .

Następnie rozszerzamy padającą falę płaską w sferycznych harmonicznych wektorowych:

${\ Displaystyle \ mathbf {E} _ {inc} = E_ {0} e ^ {ikr \ cos \ theta} \ mathbf {e} _ {x} = E_ {0} \sum _{n=1}^{\infty}i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{o1n}^{( 1)}(k,\mathbf {r} )-i\mathbf {N} _{e1n}^{(1)}(k,\mathbf {r} )\right),}$

${\ Displaystyle \ mathbf {H} _ {inc} = {\ Frac {-k} {\ omega \ mu}} E_ {0} \ suma _ {n = 1} ^ {\ infty} i ^ {n} \frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{e1n}^{(1)}(k,\mathbf {r} )+i\mathbf {N} _{o1n}^{(1)}(k,\mathbf {r} )\prawo).}$

Tutaj indeks górny oznacza $}$ funkcji są sferyczne funkcje Bessela o $Displaystyle (1)$ pierwszy rodzaj. Współczynniki rozszerzalności uzyskuje się, biorąc całek postaci

${\ Displaystyle {\ Frac {\ int _ {0} ^ {2 \ pi} \ int _ {0} ^ {\ pi} \ mathbf {E} _ {inc} \ cdot \ mathbf {M} _ {^ { e}_{o}mn}^{(1)}\sin \theta d\theta d\varphi }{\int _{0}^{2\pi }\int _{0}^{\pi }| \mathbf {M} _{^{e}_{o}mn}^{(1)}|^{2}\sin \theta d\theta d\varphi }}.}$

W tym przypadku wszystkie współczynniki w $liczniku wynoszą zero,$ całka po kącie $wynosi$ .

Następnie nakładane są następujące warunki:

1) Warunki interfejsowe na granicy sfery i otoczenia (pozwalające na powiązanie współczynników rozszerzalności pola padającego, wewnętrznego i rozproszonego)

2) Warunek, że rozwiązanie jest ograniczone na początku (dlatego w promieniowej części funkcji generujących sferyczne funkcje Bessela ${\ Displaystyle \ psi _ {^ {e} _ {o} mn}}$ pierwszego rodzaju są wybierane do pola wewnętrznego),

3) Dla pola rozproszonego asymptotyka w nieskończoności odpowiada rozbieżnej fali sferycznej (w związku z tym dla pola rozproszonego w promieniowej części funkcji generujących ψ o mi m n {\ $^ {e wybrano }_{o}mn}}$ sferycznych funkcji Hankla pierwszego rodzaju).

Pola rozproszone są zapisywane w postaci wektorowego rozwinięcia harmonicznego jako

${\ Displaystyle \ mathbf {E} _ {s} = \ suma _ {n = 1} ^ {\ infty} E_ {n} \ lewo (ia_ {n} \ mathbf {N} _ {e1n} ^ {(3 )}(k,\mathbf {r} )-b_{n}\mathbf {M} _{o1n}^{(3)}(k,\mathbf {r} )\right),}$

${\ Displaystyle \ mathbf {H} _ {s} = {\ Frac {k} {\ omega \ mu}} \ suma _ {n = 1} ^ {\ infty} E_ {n} \ lewo (a_ {n} \mathbf {M} _{e1n}^{(3)}(k,\mathbf {r} )+ib_{n}\mathbf {N} _{o1n}^{(3)}(k,\mathbf { r} )\prawo).}$

$} pierwszy rodzaj$ indeks górny oznacza, funkcji są sferyczne funkcje Hankla o ${\ Displaystyle (3$$mi$ rodzaju miałyby i ${\ Displaystyle E_ {n} = {\ Frac {i ^ {n} E_ {0} (2n + 1)} {n (n + 1)}}}$ ,

Pola wewnętrzne:

${\ Displaystyle \ mathbf {E} _{1}=\suma_{n=1}^{\infty}E_{n}\left(-id_{n}\mathbf {N} _{e1n}^{(1)}( k_{1},\mathbf {r} )+c_{n}\mathbf {M} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right),}$

${\ Displaystyle \ mathbf {H} _ {1} = {\ Frac {-k_ {1}}} {\ omega \ mu _ {1}}} \ suma _ {n = 1} ^ {\ infty} E_ {n }\left(d_{n}\mathbf {M} _{e1n}^{(1)}(k_{1},\mathbf {r} )+ic_{n}\mathbf {N} _{o1n}^ {(1)}(k_{1},\mathbf {r} )\right).}$

${\ Displaystyle k = {\ Frac {\ omega} {c}} n}$ jest wektorem falowym na zewnątrz cząstki ${\ Displaystyle k_ {1} = {\ Frac {\ omega } {c}} {n_ {1}}}$ to wektor falowy w ośrodku z materiału cząsteczkowego, $ośrodka$ i to współczynniki załamania światła i ${\ displaystyle n_ {1}}$ cząsteczka.

Po zastosowaniu warunków interfejsu otrzymujemy wyrażenia na współczynniki:

${\ Displaystyle c_ {n} (\ omega) = {\ Frac {\ mu _ {1} \ lewo [\ rho h_ {n}(\rho )\right]'j_{n}(\rho )-\mu _{1}\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1} j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

${\ Displaystyle d_ {n} (\ omega) = {\ Frac {\ mu _ {1} n_ {1} n\left[\rho h_{n}(\rho )\right]'j_{n}(\rho)-\mu _{1}n_{1}n\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _ {1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho)} },}$

${\ Displaystyle b_ {n} (\ omega) = {\ Frac {\ mu _ {1} \ lewo [\ rho j_ {n} (\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'j_{ n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho)\right]'j_{n}(\rho _{1})-\mu \left[\ rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

${\ Displaystyle a_ {n} (\ omega) = {\ Frac {\ mu n_ {1} ^ {2} \ left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_ {n}(\rho _{1})\right]'j_{n}(\rho)}{\mu n_{1}^{2}\left[\rho h_{n}(\rho)\right ]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right] 'h_{n}(\rho )}},}$

Gdzie

${\ Displaystyle \ rho = ka,}$

${\ Displaystyle \ rho _ {1} = k_ {1} a}$ gdzie ${\ Displaystyle a}$ jest promieniem kuli.

$}}$$n$ i reprezentują sferyczne funkcje Bessela i Hankla pierwszego rodzaju

Przekroje rozpraszania i ekstynkcji

Wielobiegunowe widmo dekompozycji przekroju poprzecznego rozpraszania przez nanosferę złota o promieniu 100 nm

Widmo dekompozycji wielobiegunowej przekroju poprzecznego rozpraszania przez nanosferę o promieniu 100 nm i współczynniku załamania światła n=4

Wielobiegunowe widmo dekompozycji przekroju poprzecznego rozpraszania przez nanosferę krzemu o promieniu 100 nm

$Wartości$ powszechnie $obliczane$ użyciu teorii $Mie$ obejmują wydajności wygaszania absorpcji $a$ to stosunki przekroju poprzecznego odpowiedniego procesu obszaru chronionego przed cząstkami gdzie a jest promieniem $.$ Zgodnie z definicją wyginięcia,

${\ Displaystyle \ sigma _ {e} = \ sigma _ {s} + \ sigma _ {a}}$ i ${\ Displaystyle Q_ {e} = Q_ {s}+Q_{a}}$ .

Współczynniki rozpraszania i ekstynkcji można przedstawić jako nieskończoną serię:

${\ Displaystyle Q_ {s} = {\ Frac {2} {k ^ { 2}a^{2}}}\suma _{n=1}^{\infty }(2n+1)(|a_{n}|^{2}+|b_{n}|^{2}) }$

${\ Displaystyle Q_ {e} = {\ Frac {2} {k ^ {2} a ^ {2}}} \ suma _ {n = 1} ^ {\infty}(2n+1)\Re (a_{n}+b_{n})}$

Udziały w tych sumach, indeksowane przez n , odpowiadają rzędom rozwinięcia wielobiegunowego , gdzie n=1 jest wyrazem dipolowym, n=2 jest wyrazem kwadransowym i tak dalej.

Aplikacja na większe cząstki

Jeśli rozmiar cząstki jest równy kilku długościom fali w materiale, to pola rozproszone mają pewne cechy. Ponadto porozmawiamy o postaci pola elektrycznego, ponieważ pole magnetyczne uzyskuje się z niego, biorąc wirnik.

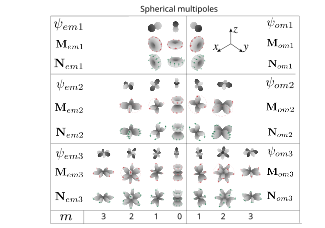
Wszystkie współczynniki Mie zależą od częstotliwości i osiągają maksimum, gdy mianownik jest bliski zeru (dokładna równość do zera jest osiągana dla częstotliwości zespolonych). W tym przypadku możliwe jest, że w rozpraszaniu dominuje udział jednej określonej harmonicznej. Wtedy przy dużych odległościach od cząstki charakterystyka promieniowania pola rozproszonego będzie podobna do odpowiedniej charakterystyki promieniowania kątowej części wektorowych sferycznych harmonicznych. $mathbf {N} _ {^ {e} _ {o} m1}}$ \ odpowiadają dipolom elektrycznym (jeśli udział tej harmonicznej dominuje w rozszerzaniu się pola elektrycznego, to pole jest podobne do elektrycznego pola dipolowego), M o mi m 1 {\ $} _ {^ {e } _ {o} m1}}$ odpowiadają polu elektrycznemu dipola magnetycznego i ${\ Displaystyle \ mathbf {M} _ {^ {e} _ {o} m2}}$$}}$ - kwadrupole elektryczne i magnetyczne, ${\ Displaystyle \ mathbf {N} _ {^ {e} _ {o} m3}}$ i ${\ Displaystyle \ mathbf {M} _ {^ {e} _ {o} m3 }}$ - oktupole i tak dalej. Maksima współczynników rozpraszania (a także zmiana ich fazy na $nazywane$ są rezonansami wielobiegunowymi .

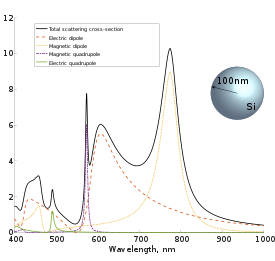
Zależność przekroju poprzecznego rozpraszania od długości fali i udziału właściwych rezonansów silnie zależy od materiału cząstki. Na przykład dla cząstki złota o promieniu 100 nm udział dipola elektrycznego w rozpraszaniu przeważa w zakresie optycznym, podczas gdy dla cząstki krzemu występują wyraźne rezonanse dipolowe i kwadrupolowe magnetyczne. W przypadku cząstek metali pik widoczny w przekroju poprzecznym rozpraszania nazywany jest również zlokalizowanym rezonansem plazmonowym .

W granicach małych cząstek lub długich fal , w przekroju poprzecznym rozpraszania dominuje udział dipola elektrycznego.

Inne kierunki padającej fali płaskiej

W przypadku fali płaskiej spolaryzowanej x , padającej wzdłuż osi z , rozkłady wszystkich pól zawierały tylko harmoniczne o m=1 , ale dla dowolnej fali padającej tak nie jest. Dla obróconej fali płaskiej współczynniki rozszerzalności można uzyskać, na przykład, wykorzystując fakt, że podczas obrotu sferyczne harmoniczne wektorów są wzajemnie przekształcane przez macierze D Wignera .

W takim przypadku pole rozproszone zostanie rozłożone na wszystkie możliwe harmoniczne:

${\ Displaystyle \ mathbf {E} _ {s} = \ suma _ {n = 1} ^ {\ infty} \ suma _ {m = 0} ^ {n} E_ {0} (D_ {Memn} \ mathbf { M} _{emn}^{(3)}(k,\mathbf {r} )+D_{Momn}\mathbf {M} _{omn}^{(3)}(k,\mathbf {r} ) +D_{Nemn}\mathbf {N} _{emn}^{(3)}(k,\mathbf {r} )+D_{Nomn}\mathbf {N} _{omn}^{(3)}( k,\mathbf {r} })}$

Wtedy przekrój poprzeczny rozpraszania będzie wyrażony za pomocą współczynników w następujący sposób:

${\ Displaystyle C_ {sca} = {\ Frac {2 \ pi} {\ pi a ^ {2} k ^ {2}}} \ suma _ {n = 1} ^ {\ infty} {\ frac {n ( n+1)}{(2n+1)}}\times {\Bigl [}\sum \limits _{m=1}^{n}{\frac {(n+m)!}{(nm)! }}(|D_{Nazwa}|^{2}+|D_{Nazwa}|^{2}+|D_{Nazwa}|^{2}+|D_{Nazwa}|^{2})+2| D_{Me0n}|^{2}+2|D_{Ne0n}|^{2}{\Bigr ]}.}$

Efekt Kerkera

Efekt Kerkera to zjawisko w kierunkowości rozpraszania, które występuje, gdy prezentowane są różne odpowiedzi wielobiegunowe i nie można ich pominąć.

Szczególny (dipolarny) przypadek efektu Kerkera. Całkowite pole elektryczne skrzyżowanych dipoli magnetycznych i elektrycznych promieniujących w fazie. Charakter promieniowania jest asymetryczny, w jednym kierunku pola wzajemnie się niszczą, aw drugim sumują się.

W 1983 roku w pracy Kerkera , Wanga i Gilesa zbadano kierunek rozpraszania przez cząstki o ${\ displaystyle \ mu \ neq 1} .$ W szczególności wykazano, że dla hipotetycznych cząstek z ${\ Displaystyle \ mu = \ varepsilon}$ rozpraszanie wsteczne jest całkowicie stłumione. Można to postrzegać jako rozszerzenie sferycznej powierzchni wyników Gilesa i Wilda dla odbicia na płaskiej powierzchni o równych współczynnikach załamania światła, gdzie odbicie i transmisja są stałe i niezależne od kąta padania.

Ponadto przekroje poprzeczne rozpraszania w kierunku do przodu i do tyłu są po prostu wyrażone za pomocą współczynników Mie:

${\ Displaystyle C_ {sca} ^ {\ rm {wstecz}} = {\ Frac {1} {a ^ {2} k ^ {2}}} {\ bigg |} \ suma _ {n = 1} ^ { \infty}{(2n+1)}(-1)^{n}(a_{n}-b_{n}){\bigg |}^{2}}$

${\ Displaystyle C_ {sca} ^ {\ rm {do przodu}} = {\ Frac {1} {a ^ {2} k ^ {2}}} {\ bigg |} \ suma _ {n = 1} ^ { \infty}{(2n+1)}(a_{n}+b_{n}){\bigg |}^{2}}$

W przypadku niektórych kombinacji współczynników powyższe wyrażenia można zminimalizować.

Na przykład, gdy terminy z $\ Displaystyle (a_ {1} -b_ {1})$ zaniedbać ( przybliżenie dipolowe ), $)$, corresponds to the minimum in backscattering (magnetic and electric dipoles are equal in magnitude and are in phase, this is also called 'first Kerker' or 'zero-backward intensity condition'). And ${\ displaystyle (a_ {1} + b_ {1}) = 0}$ odpowiada minimum w rozpraszaniu do przodu, jest to również nazywane „drugim warunkiem Kerkera” (lub „warunkiem intensywności bliskiej zeru”). Z twierdzenia optycznego wynika, że ​​dla cząstki pasywnej ${\ Displaystyle (a_ {1} = - b_ {1})}$ jest możliwe. Dla dokładnego rozwiązania problemu konieczne jest uwzględnienie wkładów wszystkich multipoli. Suma dipoli elektrycznych i magnetycznych tworzy źródło Huygensa

W przypadku cząstek dielektrycznych maksymalne rozpraszanie do przodu obserwuje się przy długościach fal dłuższych niż długość fali magnetycznego rezonansu dipolowego, a maksymalne rozpraszanie do tyłu przy krótszych. .

Później odkryto inne odmiany tego efektu. Na przykład poprzeczny efekt Kerkera, z prawie całkowitym równoczesnym tłumieniem pól rozproszonych zarówno do przodu, jak i do tyłu (wzory rozpraszania bocznego), optomechaniczny efekt Kerkera w rozpraszaniu akustycznym, a także występujący w roślinach.

Na YouTube znajduje się również krótki film z wyjaśnieniem efektu.

Funkcja sfery Diadic Greena

Funkcja Greena jest rozwiązaniem następującego równania:

${\ Displaystyle \ nabla \ razy \ nabla \ razy {\ bf {\ kapelusz {G}}} (\ omega \ mathbf {r} \ mathbf {r} ') = \ lewo ({\ frac {\ omega} {c}}\right)^{2}\varepsilon (\mathbf {r},\omega){\bf {\hat {G}}}(\omega,\mathbf {r},\mathbf {r} ' )+{\bf {\kapelusz {1}}}\delta (\mathbf {r} -\mathbf {r} '),}$

gdzie ${\ Displaystyle {\ kapelusz {\ bf {1}}}}$ - macierz tożsamości ${\ Displaystyle \ varepsilon (\ mathbf {r}, \ omega) = \ varepsilon _ {1} (\ omega)}$ dla ${\ Displaystyle r <a}$ ε $\ Displaystyle \ varepsilon (\ mathbf {r}, \ omega) = \ varepsilon}$ dla ${\ displaystyle r> a}$ . Ponieważ wszystkie pola są wektorowe, funkcja Greena jest macierzą 3 na 3 i nazywana jest diadą. Jeśli polaryzacja jest indukowana w systemie, gdy pola są zapisywane jako ${\ Displaystyle \ mathbf {P} (\ mathbf {r})}$

${\ Displaystyle \ mathbf {E} ^ {\ omega} ({\ mathbf {r} })=\omega ^{2}\mu \int \limits _{V}dV'{\hat {\bf {G}}}({\bf {r,r'}},k)\mathbf {P } ^{\omega}(\mathbf {r} ')}$

W taki sam sposób jak pola, funkcję Greena można rozłożyć na wektorowe sferyczne harmoniczne. Funkcja Dyadic Greena wolnej przestrzeni а:

${\ Displaystyle {\ kapelusz {\ bf {G}}} ^ {0} ({\ mathbf {r}, \ mathbf {r} ', k}) = {\ Frac {\ mathbf {e_ {r}} \otimes \mathbf {e_{r}} }{k^{2}}}\delta (\mathbf {r} -\mathbf {r} ')+{\frac {ik}{4\pi }}\sum _{n=1}^{\infty}\suma _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1) }}{\frac {(nm)!}{(n+m)!}}\cdot }$

${\ Displaystyle \ lewo \ {{\ rozpocząć {tablica} {l} \ cdot {\ Bigl (} (\ mathbf {M} _ {emn} ^ {(1)} [k, \ mathbf {r}] \ czasami {\mathbf {M}}_{emn}^{(3)}[k,\mathbf {r} ']+\mathbf {M} _{omn}^{(1)}[k,\mathbf {r } ]\otimes {\mathbf {M}}_{omn}^{(3)}[k,\mathbf {r} '])+({\mathbf {N}}_{emn}^{(1) }[k,\mathbf {r} ]\otimes {\mathbf {N}}_{emn}^{(3)}[k,\mathbf {r} ']+\mathbf {N} _{omn}^ {(1)}[k,\mathbf {r}]\otimes {\mathbf {N}}_{omn}^{(3)}[k,\mathbf {r} ']){\Bigr)}, {\text{if}}r<r'\\\cdot {\Bigl (}(\mathbf {M} _{emn}^{(3)}[k,\mathbf {r}]\otimes {\mathbf {M}}_{emn}^{(1)}[k,\mathbf {r} ']+\mathbf {M} _{omn}^{(3)}[k,\mathbf {r} ]\ czasami {\mathbf {M}}_{omn}^{(1)}[k,\mathbf {r} '])+({\mathbf {N}}_{emn}^{(3)}[k ,\mathbf {r} ]\otimes {\mathbf {N}}_{emn}^{(1)}[k,\mathbf {r} ']+\mathbf {N} _{omn}^{(3 )}[k,\mathbf {r} ]\otimes {\mathbf {N}}_{omn}^{(1)}[k,\mathbf {r} ']){\Bigr )},{\text {if }}r>r'\koniec{tablica}}\prawo.}$

W obecności kuli funkcja Greena jest również rozkładana na sferyczne harmoniczne wektorowe. $\ mathbf {r} '} .$ znajdują się punkty i $displaystyle$

Gdy oba punkty znajdują się poza sferą ( ${\ displaystyle r> a, r'> a}$ ):

${\ Displaystyle {\ kapelusz {\ bf {G}}} ^ {00} ({\ mathbf {r}, \ mathbf {r} ', k, k_ {1}}) = {\ kapelusz {\ bf { G}}}^{0}({\mathbf {r} ,\mathbf {r} ',k})+{\frac {ik}{4\pi}}\suma _{n=1}^{\ infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(nm) !}{(n+m)!}}\cdot }$

${\ Displaystyle \ cdot {\ Bigl (} a_ {n} ^ {(0)} (\ omega) (\ mathbf {M} _ {^ {e} _ {o} mn }^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M}}_{^{e}_{o}mn}^{(3)}[k,\mathbf {r } '])+b_{n}^{(0)}(\omega)({\mathbf {N}}_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N}}_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ']){\Bigr )}}$

gdzie współczynniki to:

${\ Displaystyle a_ {n} ^ {(0)} (\ omega) = {\ Frac { \mu /\mu _{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )-\left[\rho j_{ n}(\rho )\right]'j_{n}(\rho _{1})}{\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{ 1})-\mu /\mu _{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

${\ Displaystyle b_ {n} ^ {(0)} (\ omega) = {\ Frac {n ^ {2} \ mu _ {1} / \ mu \ lewo [\ rho _ {1} j_ {n} ( \rho _{1})\right]'j_{n}(\rho)-n_{1}^{2}\left[\rho j_{n}(\rho)\right]'j_{n}( \rho _{1})}{n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-n^{ 2}\mu _{1}/\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho)}}.}$

Gdy oba punkty znajdują się wewnątrz kuli ( ${\ displaystyle r <a, r' <a}$ ):

${\ Displaystyle {\ kapelusz {\ bf {G}}} ^ {11} ({\ mathbf {r}, \ mathbf {r} ', k, k_ {1}}) = {\ kapelusz {\ bf { G}}}^{0}({\mathbf {r} ,\mathbf {r} ',k_{1}})+{\frac {ik_{1}}{4\pi}}\sum _{n =1}^{\infty}\suma _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{ \frac {(nm)!}{(n+m)!}}\cdot }$

${\ Displaystyle \ cdot {\ Bigl (} c_ {n} ^ {(1)} (\ omega) (\ mathbf {M} _ { ^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r}]\oraz {\mathbf {M}}_{^{e}_{o}mn}^ {(1)}[k_{1},\mathbf {r} '])+d_{n}^{(1)}(\omega)({\mathbf {N}}_{^{e}_{ o}mn}^{(1)}[k_{1},\mathbf {r} ]\oraz {\mathbf {N}}_{^{e}_{o}mn}^{(1)}[ k_{1},\mathbf {r} ']){\Bigr )},}$

Współczynniki:

${\ Displaystyle c_ {n} ^ {(1)} (\ omega) = {\ frac {\mu _{1}/\mu \left[\rho h_{n}(\rho )\right]'h_{n}(\rho _{1})-\left[\rho _{1}h_ {n}(\rho _{1})\right]'h_{n}(\rho )}{\left[\rho _{1}j_{n}(\rho _{1})\right]' h_{n}(\rho )-\mu _{1}/\mu \left[\rho h_{n}(\rho)\right]'j_{n}(\rho _{1})}}, }$

${\ Displaystyle d_ {n} ^ {(1)} (\ omega) = {\ Frac {n_ {1} ^ {2} \ mu / \ mu _ {1} \ lewo [\ rho h_ {n} (\ rho )\right]'h_{n}(\rho _{1})-n^{2}\left[\rho _{1}h_{n}(\rho _{1})\right]'h_ {n}(\rho )}{n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-n_{ 1}^{2}\mu /\mu _{1}\left[\rho h_{n}(\rho)\right]'j_{n}(\rho _{1})}}.}$

Źródło znajduje się wewnątrz kuli, a punkt obserwacyjny na zewnątrz ( ${\ displaystyle r> a, r' <a}$ ):

${\ Displaystyle {\ kapelusz {\ bf {G}}} ^ {01} ({\ mathbf {r}, \ mathbf {r} ', k, k_ {1}}) = {\ Frac {ik_ {1} }}{4\pi }}\sum _{n=1}^{\infty}\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n +1}{n(n+1)}}{\frac {(nm)!}{(n+m)!}}\cdot}$

${\ Displaystyle \ cdot {\ Bigl (} a_ {n} ^ {(1)} (\ omega) (\ mathbf {M} _ {^ {e} _ {o} mn} ^ {(3)} [k ,\mathbf {r} ]\otimes {\mathbf {M}}_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} '])+b_ {n}^{(1)}(\omega)({\mathbf {N}}_{^{e}_{o}mn}^{(3)}[k,\mathbf {r}]\oraz {\mathbf {N}}_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ']){\bigr)}}$

współczynniki:

${\ Displaystyle a_ {n} ^ {(1)} (\ omega) = {\ Frac { \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho _{1})-\left[\rho _{1}h_{n }(\rho _{1})\right]'j_{n}(\rho _{1})}{\left[\rho _{1}j_{n}(\rho _{1})\right ]'h_{n}(\rho )-\mu _{1}/\mu \left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})} },}$

${\ Displaystyle b_ {n} ^ {(1)} (\ omega) = {\ Frac {nn_ {1} \ lewo [\ rho _ {1} j_ {n} (\ rho _ {1}) \ prawo] 'h_{n}(\rho _{1})-nn_{1}\left[\rho _{1}h_{n}(\rho _{1})\right]'j_{n}(\rho _{1})}{n^{2}\mu _{1}/\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n} (\rho )-n_{1}^{2}\left[\rho h_{n}(\rho)\right]'j_{n}(\rho _{1})}}.}$

Źródło znajduje się na zewnątrz kuli, a punkt obserwacyjny znajduje się w środku ( ${\ displaystyle r <a, r'> a}$ ):

${\ Displaystyle {\ kapelusz {\ bf {G}}} ^ {10} ({\ mathbf {r}, \ mathbf {r} ', k, k_ {1}}) = {\ Frac {ik} 4\pi }}\sum _{n=1}^{\infty}\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1} {n(n+1)}}{\frac {(nm)!}{(n+m)!}}\cdot}$

${\ Displaystyle \ cdot {\ Bigl (} c_ {n} ^ {(0)} (\ omega) (\ mathbf {M} _ {^ {e} _ {o} mn} ^ {(1)} [k ,\mathbf {r} ]\otimes {\mathbf {M}}_{^{e}_{o}mn}^{(3)}[k_{1},\mathbf {r} '])+d_ {n}^{(0)}(\omega)({\mathbf {N}}_{^{e}_{o}mn}^{(1)}[k,\mathbf {r}]\oraz {\mathbf {N}}_{^{e}_{o}mn}^{(3)}[k_{1},\mathbf {r} ']){\bigr)}}$

współczynniki:

${\ Displaystyle c_ {n} ^ {(0)} (\ omega) = {\ Frac {\ lewo [\ rho h_ { n}(\rho)\right]'j_{n}(\rho)-\left[\rho j_{n}(\rho)\right]'h_{n}(\rho)}{\left[\ rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu /\mu _{1}\left[\rho _{1}j_{n}(\ rho _{1})\right]'h_{n}(\rho )}},}$

${\ Displaystyle d_ {n} ^ {(0)} (\ omega) = {\ Frac {nn_ {1} \ lewo [\ rho h_ {n} (\ rho) \ prawej] 'j_ {n} (\ rho )-nn_{1}\left[\rho j_{n}(\rho )\right]'h_{n}(\rho)}{n_{1}^{2}\mu /\mu _{1} \left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-n^{2}\left[\rho _{1}j_{n}(\ rho _{1})\right]'j_{n}(\rho)}}.}$

Kody obliczeniowe

Rozwiązania Mie są implementowane w wielu programach napisanych w różnych językach komputerowych, takich jak Fortran , MATLAB i Mathematica . Rozwiązania te rozwiązują nieskończone szeregi i dostarczają jako dane wyjściowe obliczenia funkcji fazy rozpraszania, wydajności ekstynkcji, rozpraszania i absorpcji oraz innych parametrów, takich jak parametry asymetrii lub moment promieniowania. Obecne użycie terminu „rozwiązanie Mie” wskazuje na szeregowe przybliżenie rozwiązania równań Maxwella. Istnieje kilka znanych obiektów, które pozwalają na takie rozwiązanie: kule, koncentryczne kule, nieskończone cylindry, skupiska kul i skupiska walców. Znane są również szeregowe rozwiązania rozpraszania przez cząstki elipsoidalne. Lista kodów implementujących te specjalistyczne rozwiązania znajduje się poniżej:

• Kody rozpraszania elektromagnetycznego przez kule – rozwiązania dla pojedynczej kuli, kul powlekanych, kuli wielowarstwowej i klastra kul;
• Kody rozpraszania elektromagnetycznego przez walce – rozwiązania dla pojedynczego walca, walców wielowarstwowych i klastra walców.

Uogólnieniem, które pozwala na traktowanie cząstek o bardziej ogólnym kształcie, jest metoda macierzy T , która również opiera się na szeregowym przybliżeniu rozwiązań równań Maxwella.

Zobacz także zewnętrzne linki do innych kodów i kalkulatorów.

Aplikacje

Teoria Mie jest bardzo ważna w optyce meteorologicznej , gdzie stosunki średnicy do długości fali rzędu jedności i większe są charakterystyczne dla wielu problemów dotyczących zamglenia i rozpraszania chmur . Kolejnym zastosowaniem jest charakteryzacja cząstek za pomocą pomiarów rozpraszania optycznego. Rozwiązanie Mie jest również ważne dla zrozumienia wyglądu popularnych materiałów, takich jak mleko , tkanka biologiczna i farba lateksowa .

Nauka o atmosferze

Rozpraszanie Mie występuje, gdy średnice cząstek atmosferycznych są podobne lub większe niż długości fal światła. Kurz , pyłki , dym i mikroskopijne kropelki wody tworzące chmury są częstymi przyczynami rozpraszania Mie. Rozpraszanie Mie występuje głównie w niższych partiach atmosfery, gdzie większe cząstki są bardziej obfite i dominuje w pochmurnych warunkach.

Wykrywanie i badania przesiewowe raka

Teoria Mie została wykorzystana do określenia, czy rozproszone światło z tkanki odpowiada zdrowym lub nowotworowym jądrom komórkowym przy użyciu interferometrii o niskiej koherencji z rozdzielczością kątową .

Kliniczna analiza laboratoryjna

Teoria Mie jest główną zasadą stosowania testów nefelometrycznych , szeroko stosowanych w medycynie do pomiaru różnych białek osocza . Za pomocą nefelometrii można wykrywać i oznaczać ilościowo szeroką gamę białek osocza .

Cząsteczki magnetyczne

W przypadku kul magnetycznych występuje szereg niezwykłych efektów rozpraszania elektromagnetycznego. Gdy względna przenikalność jest równa przepuszczalności , wzmocnienie rozproszenia wstecznego wynosi zero. Ponadto promieniowanie rozproszone jest spolaryzowane w tym samym kierunku, co promieniowanie padające. W granicy małych cząstek (lub długich fal) mogą wystąpić warunki dla zerowego rozproszenia w przód, pełnej polaryzacji promieniowania rozproszonego w innych kierunkach oraz asymetrii rozproszenia w przód do rozproszenia wstecznego. Szczególny przypadek w granicy małych cząstek zapewnia interesujące szczególne przypadki pełnej polaryzacji i asymetrii rozpraszania do przodu do rozpraszania wstecznego.

Metamateriał

Teoria Mie została wykorzystana do projektowania metamateriałów . Zwykle składają się z trójwymiarowych kompozytów metalowych lub niemetalicznych wtrąceń okresowo lub losowo osadzonych w matrycy o niskiej przenikalności. W takim schemacie ujemne parametry konstytutywne są zaprojektowane tak, aby pojawiały się wokół rezonansów Mie wtrąceń: ujemna efektywna przenikalność elektryczna jest zaprojektowana wokół rezonansu współczynnika rozpraszania dipola elektrycznego Mie, podczas gdy ujemna efektywna przepuszczalność jest zaprojektowany wokół rezonansu współczynnika rozpraszania dipola magnetycznego Mie, a materiał podwójnie ujemny (DNG) jest zaprojektowany wokół nakładania się rezonansów współczynników rozpraszania dipola elektrycznego i magnetycznego Mie. Cząstka ma zwykle następujące kombinacje:

1. jeden zestaw cząstek magnetodielektrycznych o wartościach względnej przenikalności i przenikalności znacznie większych od jedności i bliskich sobie;
2. dwie różne cząstki dielektryczne o równej przenikalności elektrycznej, ale różnej wielkości;
3. dwie różne cząstki dielektryczne o jednakowej wielkości, ale różnej przenikalności elektrycznej.

Teoretycznie cząstki analizowane za pomocą teorii Mie są zwykle kuliste, ale w praktyce cząstki są zwykle wytwarzane w postaci sześcianów lub cylindrów dla ułatwienia wytwarzania. Aby spełnić kryteria homogenizacji, które można stwierdzić w postaci, że stała sieciowa jest znacznie mniejsza od roboczej długości fali, względna przenikalność cząstek dielektryka powinna być znacznie większa niż 1, np. ε $\ displaystyle \varepsilon _{\text{r}}>78(38)}$ aby osiągnąć ujemną efektywną przenikalność (przepuszczalność).

Wielkość cząstek

Teoria Mie jest często stosowana w analizie dyfrakcji laserowej w celu sprawdzenia efektu wielkości cząstek. Podczas gdy wczesne komputery w latach 70. były w stanie obliczyć dane dyfrakcyjne tylko z prostszym przybliżeniem Fraunhofera, Mie jest szeroko stosowany od lat 90. XX wieku i oficjalnie zalecany dla cząstek poniżej 50 mikrometrów w wytycznych ISO 13320:2009.

Teoria Mie została wykorzystana do wykrywania stężenia oleju w zanieczyszczonej wodzie.

Rozpraszanie Mie jest podstawową metodą określania wielkości pojedynczych sonoluminescencyjnych pęcherzyków powietrza w wodzie i jest ważne dla wnęk w materiałach, a także cząstek w materiałach, o ile otaczający materiał jest zasadniczo nieabsorbujący.

Parazytologia

Wykorzystywano go również do badania struktury Plasmodium falciparum , szczególnie patogennej postaci malarii .

Rozszerzenia

W 1986 roku PA Bobbert i J. Vlieger rozszerzyli model Mie, aby obliczyć rozpraszanie przez kulę w jednorodnym ośrodku umieszczonym na płaskiej powierzchni. Podobnie jak model Mie, rozszerzony model można zastosować do sfer o promieniu zbliżonym do długości fali padającego światła. Istnieje kod C++ implementujący model Bobberta-Vliegera (BV). Ostatnie osiągnięcia są związane z rozpraszaniem przez elipsoidę. Współczesne badania sięgają do dobrze znanych badań Rayleigha.

Zobacz też

• Elektromagnetyka obliczeniowa
• Rozpraszanie światła przez cząstki
• Lista kodów przenoszenia promieniowania atmosferycznego
• Kody rozpraszania elektromagnetycznego przez kule
• Właściwości optyczne wody i lodu

Dalsza lektura

• Kerker, M. (1969). Rozpraszanie światła i innego promieniowania elektromagnetycznego . Nowy Jork: akademicki.
•   Fryzjer PW; Hill, SS (1990). Rozpraszanie światła przez cząstki: metody obliczeniowe . Singapur: świat naukowy. ISBN 978-9971-5-0813-5 .
•   Miszczenko, M.; Travis, L.; Lacis, A. (2002). Rozpraszanie, absorpcja i emisja światła przez małe cząstki . Nowy Jork: Cambridge University Press. ISBN 978-0-521-78252-4 .
• Frisvad, J.; Christensen, N.; Jensen, H. (2007). „Obliczanie właściwości rozpraszania uczestniczących mediów przy użyciu teorii Lorenza-Mie” (PDF) . Transakcje ACM na grafice . 26 (3): 60. doi : 10.1145/1276377.1276452 .
• Wriedt, Thomas (2008). „Teoria Mie 1908, na telefon komórkowy 2008”. Journal of Quantitative Spectroscopy & Radiative Transfer . 109 (8): 1543–1548. Bibcode : 2008JQSRT.109.1543W . doi : 10.1016/j.jqsrt.2008.01.009 .
• Lorenz, Ludwig (1890). „Lysbevægelsen i og uden for en af ​​plane Lysbølger belyst Kugle”. Det Kongelige Danske Videnskabernes Selskabs Skrifter . 6 (6): 1–62.

Linki zewnętrzne

• SCATTERLIB i scattport.org to zbiory kodów rozpraszania światła z implementacjami rozwiązań Mie w FORTRAN , C++ , IDL , Pascal , Mathematica i Mathcad
• JMIE (kod 2D C++ do obliczania pól analitycznych wokół nieskończonego cylindra, opracowany przez Jeffreya M. McMahona)
• ScatLab . Oprogramowanie rozpraszające Mie dla systemu Windows.
• STRATIFY MatLab kod rozpraszania z wielowarstwowych sfer w przypadkach, gdy źródłem jest dipol punktowy i fala płaska. Opis w arXiv:2006.06512
• Scattnlay , pakiet rozwiązań C++ Mie typu open source z opakowaniami Python i JavaScript . Zapewnia wyniki symulacji pola dalekiego i bliskiego dla sfer wielowarstwowych.
• Internetowy kalkulator rozpraszania Mie zapewnia symulację właściwości rozpraszania (w tym dekompozycję wielobiegunową) oraz mapy bliskiego pola dla kul masowych, rdzeniowo-powłokowych i wielowarstwowych. Parametry materiału obejmują wszystkie pliki nk-data ze refractiveindex.info . Kod źródłowy jest częścią Scattnlay .
• internetowy kalkulator rozwiązań Mie z dokumentacją w języku niemieckim i angielskim.
• Internetowy kalkulator rozpraszania Mie tworzy piękne wykresy dla różnych parametrów.
• phpMie Online Kalkulator rozpraszania Mie napisany w PHP .
• Rozpraszanie światła za pośrednictwem rezonansu Mie i losowe laserowanie.
• Rozwiązanie Mie dla cząstek kulistych .
• PyMieScatt , pakiet rozwiązań Mie napisany w Pythonie .
• pyMieForAll , pakiet rozwiązania C++ Mie typu open source z opakowaniem języka Python .