Obiektyw

W przypadku innych zastosowań zobacz Obiektyw (ujednoznacznienie) .

Soczewka dwuwypukła

Soczewki mogą służyć do skupiania światła

Soczewka to przepuszczalne urządzenie optyczne , które skupia lub rozprasza wiązkę światła za pomocą załamania . Prosta soczewka składa się z jednego kawałka przezroczystego materiału , podczas gdy złożona soczewka składa się z kilku prostych soczewek ( elementów ), zwykle ułożonych wzdłuż wspólnej osi . Soczewki są wykonane z materiałów takich jak szkło lub plastik i są szlifowane , polerowane lub formowane do wymaganego kształtu. Soczewka może skupiać światło, tworząc obraz , w przeciwieństwie do pryzmatu , który załamuje światło bez ogniskowania. Urządzenia, które podobnie skupiają lub rozpraszają fale i promieniowanie inne niż światło widzialne, są również nazywane „soczewkami”, takimi jak soczewki mikrofalowe , soczewki elektronowe , soczewki akustyczne lub soczewki wybuchowe .

Soczewki są używane w różnych urządzeniach do przetwarzania obrazu, takich jak teleskopy , lornetki i aparaty fotograficzne . Są również używane jako pomoce wizualne w okularach do korygowania wad wzroku, takich jak krótkowzroczność i nadwzroczność .

Historia

Zobacz też: Historia optyki i Obiektyw aparatu

Światło załamuje się w kulistym szklanym pojemniku wypełnionym wodą. Rogera Bacona , XIII wiek

Obiektyw do LSST , planowanego teleskopu do obserwacji nieba

Słowo soczewka pochodzi od lēns , łacińskiej nazwy soczewicy ( nasiona rośliny soczewicy), ponieważ soczewka podwójnie wypukła ma kształt soczewicy. Soczewica nadaje również nazwę figurze geometrycznej .

Niektórzy uczeni twierdzą, że dowody archeologiczne wskazują, że soczewki były szeroko stosowane w starożytności przez kilka tysiącleci. Tak zwana soczewka Nimrud to artefakt z kryształu górskiego datowany na VII wiek pne, który mógł być używany jako szkło powiększające lub płonące szkło lub nie. Inni sugerowali, że niektóre egipskie hieroglify przedstawiają „proste szklane soczewki meniskalne”.

Najstarsza pewna wzmianka o używaniu soczewek pochodzi z sztuki Arystofanesa Chmury (424 pne), w której wspomina się o płonącym szkle. Pliniusz Starszy (I w.) potwierdza, że ​​płonące kielichy były znane już w okresie rzymskim. Pliniusz ma również najwcześniejszą znaną wzmiankę o używaniu soczewek korekcyjnych , kiedy wspomina, że ​​Nero miał oglądać mecze gladiatorów za pomocą szmaragdu (prawdopodobnie wklęsłego , aby skorygować krótkowzroczność , chociaż wzmianka jest niejasna). Zarówno Pliniusz, jak i Seneka Młodszy (3 pne – 65 ne) opisali powiększający efekt szklanej kuli wypełnionej wodą.

Ptolemeusz (II wiek) napisał książkę o optyce , która jednak przetrwała tylko w łacińskim tłumaczeniu niekompletnego i bardzo słabego tłumaczenia arabskiego. Książka została jednak przyjęta przez średniowiecznych uczonych w świecie islamskim i skomentowana przez Ibn Sahla (X wiek), który z kolei został ulepszony przez Alhazena ( Księga Optyki , XI wiek). Arabskie tłumaczenie Optyki Ptolemeusza stało się dostępne w tłumaczeniu łacińskim w XII wieku ( Eugeniusz z Palermo 1154). Między XI a XIII wiekiem” kamienie do czytania . Były to prymitywne soczewki płasko-wypukłe, początkowo wykonane przez przecięcie szklanej kuli na pół. Średniowieczne (XI lub XII w.) soczewki Visby z kryształu górskiego mogły być przeznaczone do użytku jako płonące okulary lub nie.

Okulary zostały wynalezione jako ulepszenie „kamieni do czytania” z okresu średniowiecza w północnych Włoszech w drugiej połowie XIII wieku. To był początek przemysłu optycznego polegającego na szlifowaniu i polerowaniu soczewek do okularów, najpierw w Wenecji i Florencji pod koniec XIII wieku, a później w ośrodkach produkcji okularów w Holandii i Niemczech . Twórcy okularów stworzyli ulepszone typy soczewek do korekcji wzroku, opierając się bardziej na wiedzy empirycznej uzyskanej z obserwacji działania soczewek (prawdopodobnie bez znajomości ówczesnej podstawowej teorii optycznej). Praktyczny rozwój i eksperymenty z soczewkami doprowadziły do ​​wynalezienia złożonego mikroskopu optycznego około 1595 r., a teleskopu refrakcyjnego w 1608 r., które pojawiły się w ośrodkach produkcji okularów w Holandii .

Dalsze informacje: Historia teleskopu

Wraz z wynalezieniem teleskopu i mikroskopu w XVII i na początku XVIII wieku przeprowadzono wiele eksperymentów z kształtami soczewek przez tych, którzy próbowali korygować błędy chromatyczne widoczne w soczewkach. Optycy próbowali konstruować soczewki o różnych formach krzywizny, błędnie zakładając, że błędy wynikają z defektów sferycznego kształtu ich powierzchni. Optyczna teoria refrakcji i eksperymenty wykazały, że żadna jednoelementowa soczewka nie może skupić wszystkich kolorów. Doprowadziło to do wynalezienia złożonej soczewki achromatycznej przez Chestera Moore'a Halla w Anglii w 1733 r. wynalazek, do którego również zgłosił się inny Anglik John Dollond w patencie z 1758 r.

Budowa soczewek prostych

Większość soczewek to soczewki sferyczne : ich dwie powierzchnie są częściami powierzchni sfer. Każda powierzchnia może być wypukła (wybrzuszona na zewnątrz soczewki), wklęsła (wciśnięta w soczewkę) lub płaska (płaska). Linia łącząca środki kul tworzących powierzchnie soczewki nazywana jest osią soczewki . Zazwyczaj oś soczewki przechodzi przez fizyczny środek soczewki, ze względu na sposób ich produkcji. Soczewki mogą być cięte lub szlifowane po wyprodukowaniu, aby nadać im inny kształt lub rozmiar. Oś soczewki może wówczas nie przechodzić przez fizyczny środek soczewki.

toryczne lub sfero-cylindryczne mają powierzchnie o dwóch różnych promieniach krzywizny w dwóch prostopadłych płaszczyznach. Mają różną moc skupienia w różnych meridianach. Tworzy to astygmatyczną . Przykładem są soczewki okularowe, które służą do korygowania astygmatyzmu w czyimś oku.

Rodzaje soczewek prostych

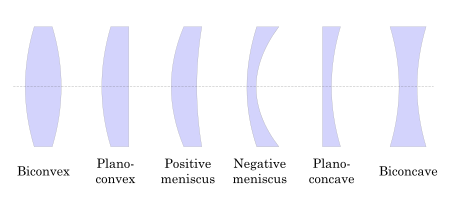
Soczewki są klasyfikowane według krzywizny dwóch powierzchni optycznych. Soczewka jest dwuwypukła (lub podwójnie wypukła lub tylko wypukła ), jeśli obie powierzchnie są wypukłe . Jeśli obie powierzchnie mają ten sam promień krzywizny, soczewka jest równowypukła . Soczewka z dwiema wklęsłymi powierzchniami jest dwuwklęsła (lub po prostu wklęsła ). Jeśli jedna z powierzchni jest płaska, soczewka jest płasko-wypukła lub płasko-wklęsła w zależności od krzywizny drugiej powierzchni. Soczewka z jednym wypukłym i jednym wklęsłym bokiem jest wypukła-wklęsła lub menisk . To właśnie ten typ soczewek jest najczęściej stosowany w soczewkach korekcyjnych .

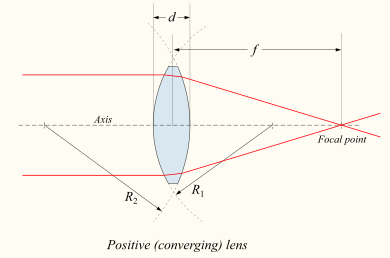
Jeśli soczewka jest dwuwypukła lub płasko-wypukła, skolimowana wiązka światła przechodząca przez soczewkę skupia się w punkcie (ognisku ) za soczewką. W tym przypadku soczewka nazywana jest dodatnią lub skupiającą . W przypadku cienkiej soczewki w powietrzu odległość od soczewki do plamki jest ogniskową soczewki, która jest zwykle reprezentowana przez f na diagramach i równaniach. Rozszerzona półkulista soczewka to specjalny rodzaj soczewki płasko-wypukłej, w której zakrzywiona powierzchnia soczewki jest pełną półkulą, a soczewka jest znacznie grubsza niż promień krzywizny.

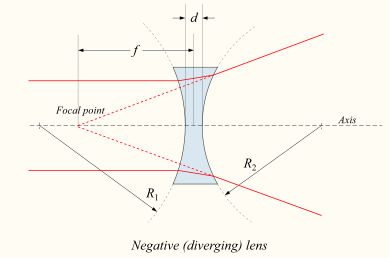
Jeśli soczewka jest dwuwklęsła lub płaskowklęsła, skolimowana wiązka światła przechodząca przez soczewkę jest rozbieżna (rozproszona); soczewka jest zatem nazywana ujemną lub rozpraszającą . Wiązka po przejściu przez soczewkę wydaje się wychodzić z określonego punktu na osi przed soczewką. W przypadku cienkiej soczewki w powietrzu odległość od tego punktu do soczewki jest ogniskową, chociaż jest ujemna w stosunku do ogniskowej soczewki skupiającej.

Soczewki wypukłe wklęsłe (menisk) mogą być dodatnie lub ujemne, w zależności od względnych krzywizn obu powierzchni. Ujemna menisku ma bardziej stromą wklęsłą powierzchnię i jest cieńsza w środku niż na obrzeżach. I odwrotnie, dodatnia soczewka menisku ma bardziej stromą wypukłą powierzchnię i jest grubsza w środku niż na obrzeżach. Idealna cienka soczewka z dwiema powierzchniami o równej krzywiźnie miałaby zerową moc optyczną , co oznacza, że ​​nie będzie ani zbiegać, ani rozpraszać światła. Wszystkie prawdziwe soczewki mają jednak niezerową grubość, co sprawia, że ​​prawdziwa soczewka z identycznymi zakrzywionymi powierzchniami jest nieco dodatnia. Aby uzyskać dokładnie zerową moc optyczną, soczewka menisku musi mieć nieco nierówne krzywizny, aby uwzględnić wpływ grubości soczewki.

Równanie Lensmakera

Położenie ogniska soczewki sferycznej zależy od promieni krzywizny obu ścianek.

Ogniskową soczewki w powietrzu można obliczyć z równania producenta soczewek :

${\ Displaystyle {\ Frac {1} {f}} = (n-1) \ lewo[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)d}{nR_{1}R_{2} }}\Prawidłowy],}$

Gdzie

${\ displaystyle f}$ to ogniskowa soczewki,

$.$ to współczynnik załamania materiału soczewki,

ze znakiem, patrz $poniżej$ promień krzywizny ) powierzchni soczewki bliżej źródła światła,

to promień krzywizny powierzchni soczewki dalej od źródła światła $($

$grubość$ to odległość wzdłuż osi soczewki między nimi wierzchołki powierzchni ).

Ogniskowa f jest dodatnia dla soczewek skupiających i ujemna dla soczewek rozpraszających. Odwrotność ogniskowej, 1/ f , jest mocą optyczną soczewki. Jeśli ogniskowa jest w metrach, daje to moc optyczną w dioptriach (metrach odwrotnych).

Soczewki mają taką samą ogniskową, gdy światło przemieszcza się od tyłu do przodu, jak gdy światło przechodzi od przodu do tyłu. Inne właściwości soczewki, takie jak aberracje , nie są takie same w obu kierunkach.

Konwencja znakowa dla promieni krzywizny R ₁ i R ₂

Główny artykuł: Promień krzywizny (optyka)

Znaki promieni krzywizny soczewki wskazują, czy odpowiednie powierzchnie są wypukłe, czy wklęsłe. Konwencja znaków używana do przedstawienia tego jest różna, ale w tym artykule dodatnie R wskazuje, że środek krzywizny powierzchni znajduje się dalej w kierunku przemieszczania się promienia (po prawej, na załączonych diagramach), podczas gdy ujemne R oznacza, że ​​promienie docierają do powierzchni minęły już środek krzywizny. W konsekwencji, dla zewnętrznych powierzchni soczewek, jak pokazano na powyższym schemacie > ₁ > 0 and , _R1 < 0 oznacza powierzchnie wypukłe (służące do skupiania światła w soczewce dodatniej), natomiast R ₁ < 0 i R ₂ > 0 oznaczają powierzchnie wklęsłe . Odwrotność promienia krzywizny nazywa się krzywizną . Płaska powierzchnia ma zerową krzywiznę, a jej promień krzywizny jest nieskończony .

Przybliżenie cienkiej soczewki

Jeśli d jest małe w porównaniu z _{R1 i} R2 , to można wykonać przybliżenie cienkiej soczewki . Dla soczewki w powietrzu f jest wtedy podane przez

${\ Displaystyle {\ Frac {1} {f}} \ około \ lewo (n-1 \ prawo) \ lewo [{\ Frac {1} {1} R_ {1}}} - {\ Frac {1} {R_ { 2}}}\prawo].}$

Właściwości obrazu

Jak wspomniano powyżej, soczewka dodatnia lub skupiająca w powietrzu skupia skolimowaną wiązkę poruszającą się wzdłuż osi soczewki do punktu (znanego jako ognisko ) w odległości f od soczewki. I odwrotnie, punktowe źródło światła umieszczone w ognisku jest przekształcane przez soczewkę w skolimowaną wiązkę. Te dwa przypadki są przykładami obrazu powstawanie w soczewkach. W pierwszym przypadku obiekt znajdujący się w nieskończonej odległości (reprezentowanej przez skolimowaną wiązkę fal) jest ogniskowany na obrazie w ognisku soczewki. W tym drugim przypadku obiekt znajdujący się w odległości ogniskowej od obiektywu jest obrazowany w nieskończoności. Płaszczyzna prostopadła do osi soczewki znajdująca się w odległości f od soczewki nazywana jest płaszczyzną ogniskową .

Jeżeli odległości od przedmiotu do soczewki i od soczewki do obrazu wynoszą odpowiednio S ₁ i S ₂ , to dla soczewki o znikomej grubości ( cienka soczewka ) w powietrzu odległości te są powiązane wzorem cienkiej soczewki :

${\ Displaystyle {\ Frac {1} {1} {1}} + {\ Frac {1} {1} {2}}} = {\ Frac {1} {f}}.}$

Można to również zapisać w formie „newtonowskiej”:

${\ Displaystyle x_ {1} x_ {2} = f ^ {2}, \!}$

gdzie ${\ Displaystyle x_ {1} = S_ {1} -f}$ i ${\ Displaystyle x_ {2} = S_ {2} -f}$ .

Obiektyw aparatu tworzy rzeczywisty obraz odległego obiektu.

Dlatego, jeśli przedmiot jest umieszczony w odległości S ₁ > f od dodatniej soczewki o ogniskowej f , to zgodnie z tym wzorem obliczymy odległość obrazu S _{2 .} Jeśli ekran jest umieszczony w odległości S ₂ po przeciwnej stronie soczewki, powstaje na nim obraz. Ten rodzaj obrazu, który można wyświetlić na ekranie lub na czujniku obrazu , nazywany jest obrazem rzeczywistym . Taka jest zasada działania aparatu , a także ludzkiego oka , w którym siatkówka służy jako czujnik obrazu.

Regulacja ogniskowania kamery dostosowuje S ₂ , ponieważ użycie odległości obrazu innej niż wymagana przez ten wzór daje nieostry (rozmyty) obraz obiektu w odległości S ₁ od kamery. Innymi słowy, modyfikacja S ₂ powoduje, że obiekty w innym S ₁ mają idealną ostrość.

Tworzenie wirtualnego obrazu przy użyciu soczewki pozytywowej jako szkła powiększającego.

W niektórych przypadkach S ₂ jest ujemne, co wskazuje, że obraz jest tworzony po przeciwnej stronie soczewki, z której rozważane są te promienie. Ponieważ rozbieżne promienie światła wychodzące z soczewki nigdy nie stają się ogniskowe, a promienie te nie są fizycznie obecne w punkcie, w którym wydają się tworzyć obraz, nazywa się to obrazem wirtualnym . W przeciwieństwie do rzeczywistych obrazów, wirtualny obraz nie może być wyświetlany na ekranie, ale wydaje się obserwatorowi patrzącemu przez obiektyw tak, jakby był prawdziwym obiektem w miejscu tego wirtualnego obrazu. Podobnie, kolejna soczewka wydaje się być obiektem w tym miejscu, tak że druga soczewka może ponownie skupić to światło na rzeczywistym obrazie, a _następnie S1 jest mierzona od wirtualnej lokalizacji obrazu za pierwszą soczewką do drugiej soczewki . To właśnie robi oko, gdy patrzy przez szkło powiększające . Szkło powiększające tworzy (powiększony) wirtualny obraz za szkłem powiększającym, ale promienie te są następnie odtwarzane przez soczewkę oka , tworząc rzeczywisty obraz na siatkówce .

Obiektyw negatywowy tworzy pozorny obraz pomniejszony.

Soczewka Barlowa (B) odtwarza obraz wirtualnego obiektu (ognisko toru czerwonego promienia) na powiększony obraz rzeczywisty (zielone promienie w ognisku)

Stosując dodatnią soczewkę o ogniskowej f , powstaje wirtualny obraz, gdy S ₁ < f , soczewka jest zatem używana jako szkło powiększające (a nie, gdy S ₁ >> f jak w aparacie). Używając soczewki ujemnej ( f < 0 ) z obiektem rzeczywistym ( S ₁ > 0 ) można uzyskać jedynie wirtualny obraz ( S ₂ < 0 ), zgodnie z powyższym wzorem. Jest to również możliwe dla odległości obiektu S ₁ być ujemna, w którym to przypadku soczewka widzi tak zwany obiekt wirtualny . Dzieje się tak, gdy soczewka jest włożona w zbieżną wiązkę (ogniskowaną przez poprzednią soczewkę) przed położeniem jej rzeczywistego obrazu. W takim przypadku nawet soczewka negatywowa może wyświetlać rzeczywisty obraz, tak jak robi to soczewka Barlowa .

Rzeczywisty obraz lampy jest rzutowany na ekran (odwrócony). Widoczne są odbicia światła od obu powierzchni soczewki dwuwypukłej.

Soczewka wypukła ( f ≪ S ₁ ) tworząca rzeczywisty, odwrócony obraz (jak obraz tworzony przez obiektyw teleskopu lub lornetki), a nie prosty, wirtualny obraz widziany w lupie ( f > S 1 ₎ . Ten rzeczywisty obraz można również oglądać po umieszczeniu na ekranie.

W przypadku cienkiej soczewki odległości S1 i S2 są mierzone od przedmiotu i obrazu do położenia soczewki, jak opisano _{powyżej .} Gdy grubość soczewki jest niewiele mniejsza niż S ₁ i S ₂ lub występuje wiele elementów soczewki ( soczewka złożona ), zamiast tego należy mierzyć od obiektu i obrazu do głównych płaszczyzn soczewki. Jeżeli odległości S ₁ lub S ₂ przechodzą przez ośrodek inne niż powietrze lub próżnia, wymagana jest bardziej skomplikowana analiza.

Powiększenie

Powiększenie liniowe systemu obrazowania przy użyciu pojedynczej soczewki jest określone wzorem

${\ Displaystyle M = - {\ Frac {S_ {2}} {S_ {1}}} = {\ Frac {f} {f-S_ {1} }},}$

gdzie M jest współczynnikiem powiększenia zdefiniowanym jako stosunek wielkości obrazu do wielkości przedmiotu. Konwencja znakowa tutaj mówi, że jeśli M jest ujemne, tak jak w przypadku rzeczywistych obrazów, obraz jest odwrócony w stosunku do obiektu. W przypadku obrazów wirtualnych M jest dodatnie, więc obraz jest pionowy.

Ten wzór na powiększenie pozwala na dwa proste sposoby rozróżnienia soczewek skupiających ( f > 0 ) i rozpraszających ( f < 0 ): W przypadku obiektu bardzo blisko soczewki ( 0 < S ₁ < |f| ), soczewka skupiająca utworzyłaby powiększony (większy) obraz wirtualny, podczas gdy soczewka rozpraszająca utworzyłaby obraz zdepowiększony (mniejszy); W przypadku obiektu znajdującego się bardzo daleko od soczewki ( S ₁ > |f| > 0 ), soczewka skupiająca utworzyłaby obraz odwrócony, podczas gdy soczewka rozpraszająca utworzyłaby obraz prosty.

Powiększenie liniowe M nie zawsze jest najbardziej użyteczną miarą siły powiększenia. Na przykład przy charakteryzowaniu teleskopu optycznego lub lornetki, które wytwarzają tylko wirtualny obraz, należy bardziej zainteresować się powiększeniem kątowym — które wyraża, o ile większy odległy obiekt wydaje się przez teleskop w porównaniu z gołym okiem. W przypadku aparatu należałoby podać skalę płytową , który porównuje pozorny (kątowy) rozmiar odległego obiektu z rozmiarem rzeczywistego obrazu wytwarzanego w ognisku. Skala płyty jest odwrotnością ogniskowej obiektywu aparatu; obiektywy są klasyfikowane jako obiektywy o długiej ogniskowej lub obiektywy szerokokątne zgodnie z ich ogniskowymi.

Użycie niewłaściwego pomiaru powiększenia może być formalnie poprawne, ale dać bezsensowną liczbę. Na przykład, używając szkła powiększającego o ogniskowej 5 cm, trzymanego w odległości 20 cm od oka i 5 cm od przedmiotu, powstaje wirtualny obraz w nieskończoności o nieskończonej wielkości liniowej: M = ∞ . Ale powiększenie kątowe wynosi 5, co oznacza, że ​​obiekt wydaje się 5 razy większy dla oka niż bez soczewki. Robiąc zdjęcie księżyca aparatem z obiektywem 50 mm nie zależy nam na powiększeniu liniowym M ≈ −50 mm / 380 000 km = −1,3 × 10 ⁻¹⁰ . Skala płyty aparatu wynosi raczej około 1°/mm, z czego można wywnioskować, że obraz 0,5 mm na kliszy odpowiada rozmiarowi kątowemu Księżyca widzianego z Ziemi około 0,5°.

W skrajnym przypadku, gdy obiekt znajduje się w nieskończonej odległości, S ₁ = ∞ , S ₂ = f i M = − f /∞= 0 , co wskazuje, że obiekt zostałby zobrazowany w jednym punkcie na płaszczyźnie ogniskowej. W rzeczywistości średnica rzutowanej plamki nie jest w rzeczywistości równa zeru, ponieważ dyfrakcja wyznacza dolną granicę wielkości funkcji rozrzutu punktów . Nazywa się to granicą dyfrakcji .

Obrazy czarnych liter w cienkiej wypukłej soczewce o ogniskowej f są pokazane na czerwono. Wybrane promienie są pokazane dla liter E , I i K odpowiednio w kolorze niebieskim, zielonym i pomarańczowym. Zauważ, że E (przy 2 f ) ma równy rozmiar, rzeczywisty i odwrócony obraz; I (w f ) ma swój obraz w nieskończoności ; i K (przy f /2) ma podwójny rozmiar, wirtualny i pionowy obraz.

Aberracje

Aberracja optyczna
Rozogniskowanie Pochylenie Aberracja sferyczna Astygmatyzm Koma Dystorsja Krzywizna pola Petzvala Aberracja chromatyczna

Główny artykuł: aberracja optyczna

Soczewki nie tworzą doskonałych obrazów, a soczewka zawsze wprowadza pewien stopień zniekształcenia lub aberracji , które sprawiają, że obraz jest niedoskonałą repliką obiektu. Staranne zaprojektowanie systemu soczewek dla konkretnego zastosowania minimalizuje aberrację. Na jakość obrazu wpływa kilka rodzajów aberracji, w tym aberracja sferyczna, koma i aberracja chromatyczna.

Aberracja sferyczna

Główny artykuł: aberracja sferyczna

Aberracja sferyczna występuje, ponieważ sferyczne powierzchnie nie mają idealnego kształtu dla soczewki, ale są zdecydowanie najprostszym kształtem, do jakiego można szlifować i polerować szkło , i tak są często używane. Aberracja sferyczna powoduje, że wiązki równoległe do osi obiektywu, ale oddalone od niej, są ogniskowane w nieco innym miejscu niż wiązki blisko osi. Objawia się to rozmyciem obrazu. Aberrację sferyczną można zminimalizować przy normalnych kształtach soczewek, starannie dobierając krzywizny powierzchni do konkretnego zastosowania. Na przykład soczewka płasko-wypukła, która służy do skupiania skolimowanej wiązki, tworzy ostrzejsze ognisko, gdy jest używana wypukłą stroną skierowaną w stronę źródła wiązki.

Śpiączka

Główny artykuł: Coma (optyka)

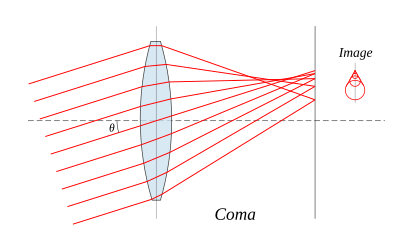
Koma , czyli aberracja komatyczna , wywodzi swoją nazwę od kometowatego wyglądu aberrowanego obrazu. Koma występuje, gdy obrazowany jest obiekt znajdujący się poza osią optyczną soczewki, gdy promienie przechodzą przez soczewkę pod kątem do osi θ. Promienie przechodzące przez środek soczewki o ogniskowej f skupiają się w punkcie o odległości f tan θ od osi. Promienie przechodzące przez zewnętrzne krawędzie soczewki skupiają się w różnych punktach, dalej od osi (koma dodatnia) lub bliżej osi (koma ujemna). Ogólnie rzecz biorąc, wiązka równoległych promieni przechodzących przez soczewkę w ustalonej odległości od środka soczewki jest ogniskowana na obrazie w kształcie pierścienia w płaszczyźnie ogniskowej, znanym jako koło komatyczne . Suma wszystkich tych okręgów daje rozbłysk w kształcie litery V lub podobny do komety. Podobnie jak w przypadku aberracji sferycznej, komę można zminimalizować (a w niektórych przypadkach wyeliminować), wybierając krzywiznę dwóch powierzchni soczewek w celu dopasowania do zastosowania. Soczewki, w których zminimalizowana jest zarówno aberracja sferyczna, jak i koma, nazywane są soczewkami bestform .

Aberracja chromatyczna

Główny artykuł: aberracja chromatyczna

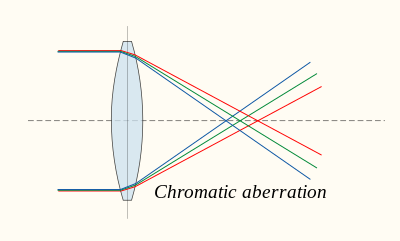
Aberracja chromatyczna jest spowodowana dyspersją materiału soczewki — zmianą jej współczynnika załamania światła n wraz z długością fali światła. Ponieważ z powyższych wzorów f jest zależne od n , wynika z tego, że światło o różnych długościach fali skupia się w różnych pozycjach. Aberracja chromatyczna obiektywu jest postrzegana jako kolorowe obwódki wokół obrazu. Można go zminimalizować, stosując dublet achromatyczny (lub achromat ), w którym dwa materiały o różnej dyspersji są połączone ze sobą, tworząc pojedynczą soczewkę. Zmniejsza to ilość aberracji chromatycznej w pewnym zakresie długości fal, chociaż nie zapewnia idealnej korekcji. Zastosowanie achromatów było ważnym krokiem w rozwoju mikroskopu optycznego. Apochromat to soczewka lub układ soczewek o jeszcze lepszej korekcji aberracji chromatycznej, połączonej z ulepszoną korekcją aberracji sferycznej . Apochromaty są znacznie droższe niż achromaty.

Aby zminimalizować aberrację chromatyczną, można również zastosować różne materiały soczewek, takie jak specjalistyczne powłoki lub soczewki wykonane z krystalicznego fluorytu . Ta naturalnie występująca substancja ma najwyższą znaną liczbę Abbego , co wskazuje, że materiał ma niską dyspersję.

Inne rodzaje aberracji

Inne rodzaje aberracji obejmują krzywiznę pola , zniekształcenie beczkowate i poduszkowate oraz astygmatyzm .

Dyfrakcja przysłony

Nawet jeśli obiektyw został zaprojektowany tak, aby minimalizować lub eliminować aberracje opisane powyżej, jakość obrazu jest nadal ograniczona dyfrakcją światła przechodzącego przez ograniczoną aperturę obiektywu . Obiektyw z ograniczoną dyfrakcją to taki, w którym aberracje zostały zredukowane do punktu, w którym jakość obrazu jest ograniczona przede wszystkim przez dyfrakcję w warunkach projektowych.

Soczewki złożone

Zobacz też: obiektyw fotograficzny , soczewka dubletowa (soczewka) , soczewka potrójna i soczewka achromatyczna

Proste soczewki podlegają omówionym powyżej aberracjom optycznym . W wielu przypadkach aberracje te można w znacznym stopniu skompensować, stosując kombinację prostych soczewek z aberracjami uzupełniającymi. Soczewka złożona to zbiór prostych soczewek o różnych kształtach, wykonanych z materiałów o różnych współczynnikach załamania światła, ułożonych jedna za drugą według wspólnej osi.

Najprostszym przypadkiem jest sytuacja, gdy soczewki są umieszczone w kontakcie: jeśli soczewki o ogniskowych f ₁ i f ₂ są „ cienkie ”, łączna ogniskowa f soczewek jest dana wzorem

${\ Displaystyle {\ Frac {1} {f}} = {\ Frac {1} {f_ {1}}} + {\ Frac {1} {f_ {2}}}.}$

Ponieważ 1/ f to moc soczewki, można zauważyć, że moce cienkich soczewek w kontakcie są addytywne.

Jeśli dwie cienkie soczewki są oddalone w powietrzu o pewną odległość d , ogniskowa dla połączonego układu jest określona wzorem

${\ Displaystyle {\ Frac {1} {f}} = {\ Frac {1} {f_ {1}}} + {\ Frac {1} {f_ {2}}} - {\ Frac {d} {f_ {1}f_{2}}}.}$

Odległość od przedniego ogniska połączonych soczewek do pierwszego obiektywu nazywana jest przednią ogniskową (FFL):

${\ Displaystyle {\ tekst {FFL}} = {\ Frac {f_ {1} (f_ {2} -d)} {(f_ {1} + f_ {2}) -d}}.}$

Podobnie odległość od drugiego obiektywu do tylnego ogniska połączonego systemu to tylna ogniskowa (BFL):

${\ Displaystyle {\ tekst {BFL}} = {\ Frac {f_ {2} (d-f_ {1})} {d- (f_ {1} + f_ {2})}}.}$

Ponieważ d dąży do zera, ogniskowe dążą do wartości f podanej dla cienkich soczewek w kontakcie.

Jeśli odległość separacji jest równa sumie ogniskowych ( d = f ₁ + f ₂ ), FFL i BFL są nieskończone. Odpowiada to parze soczewek, które przekształcają równoległą (skolimowaną) wiązkę w inną skolimowaną wiązkę. Ten typ systemu nazywany jest systemem afokalnym , ponieważ nie powoduje zbieżności ani rozbieżności netto wiązki. Dwie soczewki w tej separacji tworzą najprostszy typ teleskopu optycznego . Chociaż system nie zmienia rozbieżności skolimowanej wiązki, zmienia szerokość wiązki. Powiększenie takiego teleskopu jest podane przez

${\ Displaystyle M = - {\ Frac {f_ {2}} {f_ {1}}}}$

który jest stosunkiem szerokości wiązki wyjściowej do szerokości wiązki wejściowej. Zwróć uwagę na konwencję znaku: teleskop z dwiema soczewkami wypukłymi ( f ₁ > 0, f ₂ > 0) daje powiększenie ujemne, wskazujące na odwrócony obraz. Soczewka wypukła i wklęsła ( f ₁ > 0 > f ₂ ) dają dodatnie powiększenie i obraz jest prosty. Aby uzyskać więcej informacji na temat prostych teleskopów optycznych, zobacz Teleskop refrakcyjny § Konstrukcje teleskopów refrakcyjnych .

Typy niekuliste

Asferyczna soczewka dwuwypukła.

Soczewki cylindryczne mają krzywiznę tylko wzdłuż jednej osi. Służą do skupiania światła w linii lub przekształcania światła eliptycznego z diody laserowej w okrągłą wiązkę. Są one również używane w obiektywach anamorficznych do filmów .

Soczewki asferyczne mają co najmniej jedną powierzchnię, która nie jest ani sferyczna, ani cylindryczna. Bardziej skomplikowane kształty pozwalają takim soczewkom tworzyć obrazy z mniejszą aberracją niż standardowe proste soczewki, ale są trudniejsze i droższe w produkcji. Były one wcześniej skomplikowane w wykonaniu i często bardzo drogie, ale postęp technologiczny znacznie obniżył koszty produkcji takich soczewek.

Zbliżenie płaskiej soczewki Fresnela .

Soczewka Fresnela ma powierzchnię optyczną podzieloną na wąskie pierścienie, dzięki czemu soczewka jest znacznie cieńsza i lżejsza niż konwencjonalne soczewki. Trwałe soczewki Fresnela można formować z tworzywa sztucznego i są niedrogie.

Soczewki soczewkowe to układy mikrosoczewek , które są używane w druku soczewkowym do tworzenia obrazów, które mają iluzję głębi lub które zmieniają się, gdy patrzy się na nie pod różnymi kątami.

Soczewka dwuogniskowa ma dwie lub więcej ogniskowych lub stopniowaną ogniskową wbudowaną w soczewkę.

Soczewka gradientowa ma płaskie powierzchnie optyczne, ale ma promieniową lub osiową zmianę współczynnika załamania światła, która powoduje skupienie światła przechodzącego przez soczewkę.

Aksikon ma stożkową powierzchnię optyczną . Obrazuje źródło punktowe w linię wzdłuż osi optycznej lub przekształca wiązkę laserową w pierścień.

Dyfrakcyjne elementy optyczne mogą działać jako soczewki.

Supersoczewki są wykonane z metamateriałów o ujemnym indeksie i mają tworzyć obrazy w rozdzielczości przestrzennej przekraczającej granicę dyfrakcji . Pierwsze supersoczewki powstały w 2004 roku przy użyciu takiego metamateriału dla mikrofal. Ulepszone wersje zostały stworzone przez innych badaczy. Od 2014 roku supersoczewka nie została jeszcze zademonstrowana w widzialnym lub bliskiej podczerwieni .

Opracowano prototyp płaskiej ultracienkiej soczewki bez krzywizny.

Używa

Pojedyncza soczewka wypukła osadzona w oprawce z uchwytem lub podstawką to szkło powiększające .

Soczewki są wykorzystywane jako protetyka do korekcji wad refrakcji, takich jak krótkowzroczność , nadwzroczność , starczowzroczność i astygmatyzm . (Patrz soczewki korekcyjne , soczewki kontaktowe , okulary .) Większość soczewek używanych do innych celów ma ścisłą symetrię osiową ; soczewki okularowe są tylko w przybliżeniu symetryczne. Zwykle mają kształt dopasowany do mniej więcej owalnej, a nie okrągłej ramy; ośrodki optyczne są umieszczone nad gałkami ocznymi ; ich krzywizna może nie być osiowo symetryczna, aby skorygować astygmatyzm . Soczewki okularów przeciwsłonecznych mają za zadanie tłumić światło; soczewki przeciwsłoneczne, które również korygują wady wzroku, mogą być wykonane na zamówienie.

Inne zastosowania to systemy obrazowania, takie jak monokulary , lornetki , teleskopy , mikroskopy , kamery i projektory . Niektóre z tych instrumentów wytwarzają wirtualny obraz po nałożeniu na ludzkie oko; inne wytwarzają rzeczywisty obraz , który można zarejestrować na kliszy fotograficznej lub czujniku optycznym lub wyświetlić na ekranie. W tych urządzeniach soczewki są czasami łączone z zakrzywionymi lustrami , aby uzyskać efekt system katadioptryczny , w którym aberracja sferyczna soczewki koryguje przeciwną aberrację w lustrze (taki jak korektory Schmidta i łąkotki ).

Soczewki wypukłe wytwarzają obraz obiektu w nieskończoności w ich ognisku; jeśli słońce , większość światła widzialnego i podczerwonego padającego na soczewkę jest skoncentrowana na małym obrazie. Duża soczewka wytwarza wystarczającą intensywność, aby spalić łatwopalny przedmiot w ognisku. Ponieważ zapłon można osiągnąć nawet przy źle wykonanej soczewce, soczewki były używane jako płonące okulary od co najmniej 2400 lat. Nowoczesną aplikacją jest wykorzystanie stosunkowo dużych soczewek do skupienia energii słonecznej na stosunkowo małych ogniwach fotowoltaicznych , uzyskując więcej energii bez konieczności stosowania większych i droższych ogniw.

radioastronomiczne i radarowe często wykorzystują soczewki dielektryczne , powszechnie nazywane anteną soczewkową , do załamywania promieniowania elektromagnetycznego w antenie kolektora.

Soczewki mogą zostać porysowane i wytarte. Dostępne są powłoki odporne na ścieranie , które pomagają to kontrolować.

Zobacz też

• Powłoka zapobiegająca parowaniu powierzchni optycznych
• Tylna płaszczyzna ogniskowa
• bokeh
• Punkt kardynalny (optyka)
• Żrący (optyka)
• Okular
• liczba F
• Soczewka grawitacyjna
• Soczewka (anatomia)
• Lista projektów soczewek
• Apertura numeryczna
• Powłoki optyczne
• Konstrukcja soczewki optycznej
• Soczewka fotochromowa
• Pryzmat (optyka)
• Śledzenie promienia
• Analiza macierzy transferu promieni

Bibliografia

•   Hecht, Eugeniusz (1987). Optyka (wyd. 2). Addisona Wesleya. ISBN 978-0-201-11609-0 . Rozdziały 5 i 6.
•   Hecht, Eugeniusz (2002). Optyka (wyd. 4). Addisona Wesleya. ISBN 978-0-321-18878-6 .
•   Greivenkamp, ​​John E. (2004). Przewodnik terenowy po optyce geometrycznej . Przewodniki terenowe SPIE, tom. FG01 . SZPIEC. ISBN 978-0-8194-5294-8 .

Linki zewnętrzne

• Rozdział z internetowego podręcznika na temat refrakcji i soczewek
• Cienkie soczewki sferyczne (.pdf) w projekcie PHYSNET .
• Artykuł o obiektywie na digitalartform.com
• Artykuł o soczewkach starożytnego Egiptu
• Animacja FDTD propagacji elektromagnetycznej przez soczewkę wypukłą (w osi i poza osią) Wideo na YouTube
• Zastosowanie soczewek powiększających w świecie klasycznym
• Henker, Otto (1911). „Obiektyw” . Encyklopedia Britannica . Tom. 16 (wyd. 11). s. 421–427. (z 21 diagramami)

Symulacje

• Nauka przez symulacje – soczewki wklęsłe i wypukłe
• OpticalRayTracer – symulator obiektywu typu open source (java do pobrania)
• Wideo z symulacją światła przechodzącego przez soczewkę wypukłą Wideo na YouTube
• Animacje przedstawiające obiektyw firmy QED