Krystalografia rentgenowska

Proszkowy dyfraktometr rentgenowski w ruchu

Krystalografia rentgenowska to nauka eksperymentalna określająca atomową i molekularną strukturę kryształu , w której struktura krystaliczna powoduje, że wiązka padających promieni rentgenowskich załamuje się w wielu określonych kierunkach. Mierząc kąty i natężenia tych ugiętych wiązek, krystalograf może uzyskać trójwymiarowy obraz gęstości elektronów w krysztale. Na podstawie tej gęstości elektronowej można określić średnie pozycje atomów w krysztale, a także ich położenie wiązania chemiczne , ich nieład krystalograficzny i różne inne informacje.

Ponieważ wiele materiałów może tworzyć kryształy - takie jak sole , metale , minerały , półprzewodniki , a także różne cząsteczki nieorganiczne, organiczne i biologiczne - krystalografia rentgenowska ma fundamentalne znaczenie dla rozwoju wielu dziedzin nauki. W pierwszych dziesięcioleciach stosowania metoda ta określała wielkość atomów, długości i rodzaje wiązań chemicznych oraz różnice w skali atomowej między różnymi materiałami, zwłaszcza minerałami i stopami . Metoda ujawniła również strukturę i funkcję wielu cząsteczek biologicznych, w tym witamin , leki, białka i kwasy nukleinowe, takie jak DNA . Krystalografia rentgenowska jest nadal podstawową metodą charakteryzowania struktury atomowej nowych materiałów i rozróżniania materiałów, które wydają się podobne w innych eksperymentach . Struktury kryształów rentgenowskich mogą również wyjaśniać niezwykłe właściwości elektroniczne lub elastyczne materiału, rzucać światło na interakcje i procesy chemiczne lub służyć jako podstawa do projektowania leków przeciw chorobom .

W pomiarze dyfrakcji rentgenowskiej pojedynczego kryształu kryształ jest montowany na goniometrze . Goniometr służy do ustawiania kryształu w wybranych orientacjach. Kryształ jest oświetlany precyzyjnie zogniskowaną monochromatyczną wiązką promieni rentgenowskich, tworząc wzór dyfrakcyjny składający się z regularnie rozmieszczonych plam, zwanych odbiciami . Dwuwymiarowe obrazy wykonane w różnych orientacjach są przekształcane w trójwymiarowy model gęstości elektronów w krysztale za pomocą matematycznej metody transformacji Fouriera , w połączeniu z danymi chemicznymi znanymi dla próbki. Słaba rozdzielczość (nieostrość) lub nawet błędy mogą wystąpić, jeśli kryształy są zbyt małe lub nie są wystarczająco jednolite w swoim wewnętrznym składzie.

Krystalografia rentgenowska jest powiązana z kilkoma innymi metodami określania struktur atomowych. Podobne obrazy dyfrakcyjne można uzyskać przez rozpraszanie elektronów lub neutronów , a rozpraszanie neutronów można podobnie interpretować za pomocą transformacji Fouriera . Jeśli nie można uzyskać monokryształów o wystarczających rozmiarach, można zastosować różne inne metody rentgenowskie w celu uzyskania mniej szczegółowych informacji; takie metody obejmują dyfrakcję światłowodową , dyfrakcję proszkową i (jeśli próbka nie jest skrystalizowana) rozpraszanie promieni rentgenowskich pod małymi kątami (SAXS). Jeśli badany materiał jest dostępny tylko w postaci nanokrystalicznych lub ma słabą krystaliczność, do określenia struktury atomu można zastosować metody dyfrakcji elektronowej , transmisyjnej mikroskopii elektronowej i krystalografii elektronowej .

Dla wszystkich wyżej wymienionych metod dyfrakcji rentgenowskiej rozpraszanie jest elastyczne ; rozproszone promienie rentgenowskie mają taką samą długość fali jak przychodzące promieniowanie rentgenowskie. Z kolei nieelastycznego rozpraszania promieniowania rentgenowskiego są przydatne w badaniu wzbudzeń próbki, takich jak plazmony , wzbudzenia pola krystalicznego i orbitalnego, magnony i fonony , zamiast rozkładu jej atomów.

Historia

Wczesna historia naukowa kryształów i promieni rentgenowskich

Rysunek kwadratowego (A) i sześciokątnego (B) opakowania z pracy Keplera Strena seu de Nive Sexangula .

Sześciokątna symetria płatków śniegu wynika z czworościennego układu wiązań wodorowych wokół każdej cząsteczki wody.

Kryształy, choć od dawna podziwiane za ich regularność i symetrię, nie były badane naukowo aż do XVII wieku. Johannes Kepler postawił hipotezę w swojej pracy Strena seu de Nive Sexangula (Noworoczny prezent sześciokątnego śniegu) (1611), że sześciokątna symetria kryształów płatków śniegu wynika z regularnego upakowania kulistych cząstek wody. Duński naukowiec Nicolas Steno (1669) był pionierem eksperymentalnych badań symetrii kryształów. Steno wykazał, że kąty między ścianami są takie same w każdym egzemplarzu określonego rodzaju kryształu. René Just Haüy (1784) odkrył, że każdą ścianę kryształu można opisać za pomocą prostych wzorów ułożonych w stos bloków o tym samym kształcie i rozmiarze. Dlatego William Hallowes Miller w 1839 roku był w stanie nadać każdej twarzy unikalną etykietę trzech małych liczb całkowitych, indeksów Millera , które nadal są używane do identyfikacji twarzy kryształów. Badania Haüya doprowadziły do ​​​​pomysłu, że kryształy są regularnym trójwymiarowym układem ( siecią Bravais'go ) atomów i cząsteczek ; pojedyncza komórka elementarna powtarza się w nieskończoność wzdłuż trzech głównych kierunków. W XIX wieku pełny katalog możliwych symetrii kryształu opracowali Johan Hessel , Auguste Bravais , Evgraf Fedorov , Arthur Schönflies i (z opóźnieniem) William Barlow (1894). Barlow zaproponował kilka struktur krystalicznych w latach osiemdziesiątych XIX wieku, które zostały później potwierdzone przez krystalografię rentgenowską; jednak dostępne dane były zbyt skąpe w latach osiemdziesiątych XIX wieku, aby uznać jego modele za rozstrzygające.

Model rozmieszczenia cząsteczek wody w lodzie, ukazujący wiązania wodorowe (1), które utrzymują bryłę razem.

Wilhelm Röntgen odkrył promieniowanie rentgenowskie w 1895 roku. Fizycy nie byli pewni natury promieni rentgenowskich, ale wkrótce podejrzewali, że są to fale promieniowania elektromagnetycznego . Teoria promieniowania elektromagnetycznego Maxwella została dobrze przyjęta, a eksperymenty Charlesa Glovera Barkli wykazały, że promieniowanie rentgenowskie wykazuje zjawiska związane z falami elektromagnetycznymi, w tym polaryzację poprzeczną i linie widmowe podobne do obserwowanych w zakresie widzialnym. Barkla stworzył również notację rentgenowską, odnotowując w 1909 roku dwa odrębne typy wiązek dyfrakcyjnych, najpierw nazywając je „A” i „B”, a następnie zakładając, że mogą istnieć linie poprzedzające „A”, rozpoczął numeracja alfabetyczna rozpoczynająca się na literę „K”. Eksperymenty z pojedynczą szczeliną w laboratorium Arnolda Sommerfelda sugerowały, że promieniowanie rentgenowskie ma długość fali około 1 angstremów . Promienie rentgenowskie to nie tylko fale, ale także fotony i mają właściwości cząstek, co spowodowało, że Sommerfeld ukuł nazwę Bremsstrahlung dla tego falowego typu dyfrakcji. Albert Einstein przedstawił koncepcję fotonu w 1905 r., ale została ona powszechnie zaakceptowana dopiero w 1922 r., kiedy Arthur Compton potwierdził ją przez rozproszenie promieni rentgenowskich z elektronów. Cząsteczkowe właściwości promieni rentgenowskich, takie jak jonizacja gazów, skłoniły Williama Henry'ego Bragga do argumentowania w 1907 r., Że promienie rentgenowskie nie są promieniowaniem elektromagnetycznym. Pogląd Bragga okazał się niepopularny, a obserwacja dyfrakcji rentgenowskiej wg Max von Laue w 1912 roku potwierdził dla większości naukowców, że promieniowanie rentgenowskie jest formą promieniowania elektromagnetycznego.

Dyfrakcja rentgenowska

Nadchodząca wiązka (pochodząca z lewego górnego rogu) powoduje, że każdy rozpraszacz ponownie wypromieniowuje niewielką część swojej intensywności jako falę sferyczną. Jeśli rozpraszacze są rozmieszczone symetrycznie z odstępem d , te fale sferyczne będą zsynchronizowane (dodane konstruktywnie) tylko w kierunkach, w których różnica długości dróg 2 d sin θ jest równa całkowitej wielokrotności długości fali λ. W takim przypadku część padającej wiązki jest odchylana o kąt 2θ, tworząc plamkę odbicia na obrazie dyfrakcyjnym .

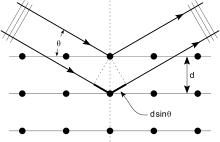
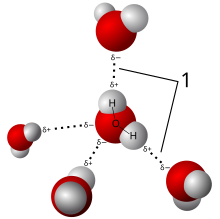
Kryształy to regularne układy atomów, a promieniowanie rentgenowskie można uznać za fale promieniowania elektromagnetycznego. Atomy rozpraszają fale rentgenowskie, głównie przez elektrony atomów. Tak jak fala oceaniczna uderzająca w latarnię morską wytwarza wtórne fale kołowe emanujące z latarni morskiej, tak promieniowanie rentgenowskie uderzające w elektron wytwarza wtórne fale sferyczne emanujące z elektronu. Zjawisko to znane jest jako rozpraszanie sprężyste , a elektron (lub latarnia morska) jako rozpraszacz . Regularny układ rozpraszaczy wytwarza regularny układ fal sferycznych. Chociaż te fale znoszą się nawzajem w większości kierunków destrukcyjną ingerencję , dodają konstruktywnie w kilku określonych kierunkach, określonych przez prawo Bragga :

${\ Displaystyle n \ lambda = 2d \ sin \ teta}$

Tutaj d to odległość między dyfrakcyjnymi płaszczyznami, $kąt padania$ , n to dowolna liczba całkowita, a λ to długość fali wiązki. Te określone kierunki pojawiają się jako plamki na obrazie dyfrakcyjnym zwanym odbiciami . Zatem dyfrakcja promieniowania rentgenowskiego wynika z fali elektromagnetycznej (promieniowanie rentgenowskie) padającej na regularny układ rozpraszaczy (powtarzające się układy atomów w krysztale).

Promienie rentgenowskie są używane do wytworzenia wzoru dyfrakcyjnego, ponieważ ich długość fali λ jest zwykle tego samego rzędu wielkości (1–100 angstremów), co odległość d między płaszczyznami w krysztale. W zasadzie każda fala uderzająca w regularny układ rozpraszaczy powoduje dyfrakcję , jak po raz pierwszy przewidział Francesco Maria Grimaldi w 1665 r. Aby wytworzyć znaczącą dyfrakcję, odległość między rozpraszaczami i długość fali uderzającej fali powinny być podobne pod względem wielkości. Dla ilustracji, dyfrakcja światła słonecznego przez ptasie pióro została po raz pierwszy opisana przez Jamesa Gregory'ego w późniejszym wieku XVII. Pierwsze sztuczne siatki dyfrakcyjne dla światła widzialnego zostały skonstruowane przez Davida Rittenhouse'a w 1787 r. I Josepha von Fraunhofera w 1821 r. Jednak światło widzialne ma zbyt dużą długość fali (zwykle 5500 angstremów), aby obserwować dyfrakcję na kryształach. Przed pierwszymi eksperymentami dyfrakcji rentgenowskiej odstępy między płaszczyznami sieci w krysztale nie były znane z całą pewnością.

Pomysł, że kryształy mogą być użyte jako siatka dyfrakcyjna dla promieni rentgenowskich, pojawił się w 1912 roku podczas rozmowy pomiędzy Paulem Peterem Ewaldem i Maxem von Laue w Ogrodzie Angielskim w Monachium . Ewald zaproponował model rezonatora kryształów do swojej pracy magisterskiej, ale model ten nie mógł zostać zweryfikowany przy użyciu światła widzialnego , ponieważ długość fali była znacznie większa niż odległość między rezonatorami. Von Laue zdał sobie sprawę, że do obserwacji tak małych odległości potrzebne jest promieniowanie elektromagnetyczne o krótszej długości fali i zasugerował, że promieniowanie rentgenowskie może mieć długość fali porównywalną z odległością między komórkami elementarnymi w kryształach. Von Laue współpracował z dwoma technikami, Walterem Friedrichem i jego asystentem Paulem Knippingiem, aby przepuścić wiązkę promieni rentgenowskich przez kryształ siarczanu miedzi i zarejestrować jego dyfrakcję na kliszy fotograficznej . Po wywołaniu płyta pokazała dużą liczbę dobrze zdefiniowanych plamek ułożonych we wzór przecinających się okręgów wokół plamki wytworzonej przez wiązkę centralną. Von Laue opracował prawo, które łączy kąty rozpraszania z rozmiarem i orientacją odstępów między komórkami elementarnymi w krysztale, za co otrzymał Nagrodę Nobla w dziedzinie fizyki w 1914 roku.

Rozpraszanie

Jak opisano w wywodzie matematycznym poniżej , rozpraszanie promieniowania rentgenowskiego jest określone przez gęstość elektronów w krysztale. Ponieważ energia promieniowania rentgenowskiego jest znacznie większa niż energia elektronu walencyjnego, rozpraszanie można modelować jako rozpraszanie Thomsona , oddziaływanie promienia elektromagnetycznego ze swobodnym elektronem. Model ten jest ogólnie przyjęty do opisu polaryzacji promieniowania rozproszonego.

Intensywność rozpraszania Thomsona dla jednej cząstki o masie m i ładunku elementarnym q wynosi:

$I_ {o} = ja_ {e}\left({\frac {q^{4}}{m^{2}c^{4}}}\right){\frac {1+\cos ^{2}2\theta}{2 }}=I_{e}7,94,10^{-26}{\frac {1+\cos ^{2}2\theta }{2}}=I_{e}f}$

Stąd jądra atomowe, które są znacznie cięższe od elektronu, mają znikomy udział w rozproszeniu promieniowania rentgenowskiego. W związku z tym spójne rozpraszanie wykryte na atomie można dokładnie przybliżyć, analizując zbiorowe rozpraszanie elektronów w układzie.

Rozwój od 1912 do 1920 roku

Chociaż diamenty (u góry po lewej) i grafit (u góry po prawej) mają identyczny skład chemiczny – oba są czystym węglem – krystalografia rentgenowska ujawniła, że ​​układ ich atomów (u dołu) odpowiada za ich różne właściwości. W diamencie atomy węgla są ułożone czworościennie i utrzymywane razem pojedynczymi wiązaniami kowalencyjnymi , czyniąc go silnym we wszystkich kierunkach. Natomiast grafit składa się z ułożonych w stos arkuszy. Wewnątrz arkusza wiązanie jest kowalencyjne i ma symetrię heksagonalną, ale nie ma wiązań kowalencyjnych między arkuszami, co ułatwia rozszczepianie grafitu na płatki.

Po pionierskich badaniach Von Laue dziedzina szybko się rozwijała, przede wszystkim dzięki fizykom Williamowi Lawrence'owi Braggowi i jego ojcu Williamowi Henry'emu Braggowi . W latach 1912–1913 młodszy Bragg opracował prawo Bragga , które łączy obserwowane rozpraszanie z odbiciami od równomiernie rozmieszczonych płaszczyzn w krysztale. Braggowie, ojciec i syn, otrzymali w 1915 roku Nagrodę Nobla w dziedzinie fizyki za pracę w dziedzinie krystalografii. Najwcześniejsze struktury były na ogół proste i odznaczały się jednowymiarową symetrią. Jednak wraz z poprawą metod obliczeniowych i eksperymentalnych w następnych dziesięcioleciach stało się możliwe wydedukowanie wiarygodnych pozycji atomów dla bardziej skomplikowanych dwu- i trójwymiarowych układów atomów w komórce elementarnej.

Potencjał krystalografii rentgenowskiej do określania struktury cząsteczek i minerałów - wówczas znany tylko niejasno z eksperymentów chemicznych i hydrodynamicznych - został natychmiast zrealizowany. Najwcześniejsze struktury były prostymi nieorganicznymi kryształami i minerałami, ale nawet one ujawniały podstawowe prawa fizyki i chemii. Pierwszą strukturą o rozdzielczości atomowej, którą „rozwiązano” (tzn. wyznaczono) w 1914 r., była struktura soli kuchennej . Rozkład elektronów w strukturze soli kuchennej wykazał, że kryształy niekoniecznie składają się z związanych kowalencyjnie i udowodnił istnienie związków jonowych . W tym samym roku rozwiązano strukturę diamentu , udowadniając czworościenny układ jego wiązań chemicznych i wykazując, że długość pojedynczego wiązania C – C wynosiła 1,52 angstremów. Inne wczesne struktury obejmowały miedź , fluorek wapnia (CaF ₂ , znany również jako fluoryt ), kalcyt (CaCO ₃ ) i piryt (FeS ₂ ) w 1914 roku; spinel (MgAl ₂ O ₄ ) w 1915 r.; rutyl i anataz _ formy dwutlenku tytanu (TiO ₂ ) w 1916 r.; pirochroit Mn(OH) ₂ i, co za tym idzie, brucyt Mg(OH) ₂ w 1919 r. Również w 1919 r. Ralph Walter Graystone Wyckoff określił azotan sodu (NaNO ₃ ) i dichlorojodek cezu (CsICl _{2 )} , a wurcyt (heksagonalny ZnS) stała się znana w 1920 roku.

Strukturę grafitu rozwiązano w 1916 r. pokrewną metodą dyfrakcji proszkowej , którą opracowali Peter Debye i Paul Scherrer oraz niezależnie Albert Hull w 1917 r. Strukturę grafitu określono na podstawie dyfrakcji monokrystalicznej w 1924 r. dwoma grupy niezależnie. Hull wykorzystał również metodę proszkową do określenia struktur różnych metali, takich jak żelazo i magnez.

Znaczenie kulturowe i estetyczne

W 1951 roku Festival Pattern Group na Festival of Britain gościła współpracującą grupę producentów tekstyliów i doświadczonych krystalografów w celu zaprojektowania koronek i nadruków w oparciu o krystalografię rentgenowską insuliny , glinki chińskiej i hemoglobiny . Jednym z czołowych naukowców projektu była Helen Megaw , ówczesny zastępca dyrektora ds. badań w Cavendish Laboratory w Cambridge. Megaw jest uznawany za jedną z głównych postaci, która czerpała inspirację z diagramów kryształów i dostrzegła ich potencjał w projektowaniu. W 2008 roku Wellcome Collection w Londynie była kuratorem wystawy w Festival Pattern Group zatytułowanej „From Atom to Patterns”.

Wkład w chemię i materiałoznawstwo

Krystalografia rentgenowska doprowadziła do lepszego zrozumienia wiązań chemicznych i oddziaływań niekowalencyjnych . Wstępne badania ujawniły typowe promienie atomów i potwierdziły wiele teoretycznych modeli wiązań chemicznych, takich jak tetraedryczne wiązanie węgla w strukturze diamentu, oktaedryczne wiązanie metali obserwowane w heksachloroplatynianie (IV) amonu oraz rezonans obserwowany w płaska grupa węglanowa i w cząsteczkach aromatycznych. Struktura heksametylobenzenu Kathleen Lonsdale z 1928 r . Ustanowiła heksagonalną symetrię benzenu i wykazał wyraźną różnicę w długości wiązań między alifatycznymi wiązaniami C – C i aromatycznymi wiązaniami C – C; odkrycie to doprowadziło do idei rezonansu między wiązaniami chemicznymi, co miało głębokie konsekwencje dla rozwoju chemii. Jej wnioski przewidział William Henry Bragg , który w 1921 roku opublikował modele naftalenu i antracenu oparte na innych cząsteczkach, wczesnej formie wymiany molekularnej .

Również w latach dwudziestych XX wieku Victor Moritz Goldschmidt , a później Linus Pauling, opracowali zasady eliminacji chemicznie nieprawdopodobnych struktur i określania względnych rozmiarów atomów. Zasady te doprowadziły do ​​​​struktury brukitu (1928) i zrozumienia względnej stabilności form rutylu , brukitu i anatazu dwutlenku tytanu .

Odległość między dwoma związanymi atomami jest czułą miarą siły wiązania i kolejności wiązań ; w ten sposób badania krystalograficzne rentgenowskie doprowadziły do ​​​​odkrycia jeszcze bardziej egzotycznych typów wiązań w chemii nieorganicznej , takich jak podwójne wiązania metal-metal, poczwórne wiązania metal-metal i trójśrodkowe wiązania dwuelektronowe. Krystalografia rentgenowska - lub, ściśle mówiąc, eksperyment nieelastycznego rozpraszania Comptona - również dostarczyła dowodów na częściowo kowalencyjny charakter wiązań wodorowych . W dziedzinie chemii metaloorganicznej struktura rentgenowska ferrocen zapoczątkował badania naukowe nad związkami warstwowymi , podczas gdy sól Zeise'a stymulowała badania nad „powrotnymi wiązaniami” i kompleksami metal-pi. Wreszcie krystalografia rentgenowska odegrała pionierską rolę w rozwoju chemii supramolekularnej , zwłaszcza w wyjaśnianiu struktur eterów koronowych i zasad chemii gospodarz-gość .

Dyfrakcja rentgenowska jest bardzo potężnym narzędziem w rozwoju katalizatorów . Pomiary ex-situ są rutynowo przeprowadzane w celu sprawdzenia struktury krystalicznej materiałów lub odkrycia nowych struktur. Eksperymenty in-situ dają wszechstronne zrozumienie stabilności strukturalnej katalizatorów w warunkach reakcji.

W naukach o materiałach analizowano wiele skomplikowanych układów nieorganicznych i metaloorganicznych przy użyciu metod monokrystalicznych, takich jak fulereny , metaloporfiryny i inne skomplikowane związki. Dyfrakcja monokrystaliczna jest również stosowana w przemyśle farmaceutycznym ze względu na niedawne problemy z polimorfami . Głównymi czynnikami wpływającymi na jakość struktur monokrystalicznych są wielkość i regularność kryształu; rekrystalizacja jest powszechnie stosowaną techniką poprawy tych czynników w kryształach małocząsteczkowych. Baza danych strukturalnych Cambridge zawiera ponad 1 000 000 struktur według stanu na czerwiec 2019 r .; ponad 99% tych struktur określono metodą dyfrakcji rentgenowskiej.

Mineralogia i metalurgia

marsjańskiej gleby metodą dyfrakcji rentgenowskiej – analiza CheMin ujawnia skaleń , pirokseny , oliwin i więcej ( łazik Curiosity w „ Rocknest ”, 17 października 2012).

Od lat dwudziestych XX wieku dyfrakcja rentgenowska jest główną metodą określania rozmieszczenia atomów w minerałach i metalach . Zastosowanie krystalografii rentgenowskiej w mineralogii rozpoczęło się od struktury granatu , którą określił w 1924 roku Menzer. Systematyczne badanie krystalograficzne rentgenowskie krzemianów przeprowadzono w latach dwudziestych XX wieku. Badanie to wykazało, że wraz ze Si / O kryształy krzemianu wykazują znaczące zmiany w ich rozmieszczeniu atomowym. Machatschki rozszerzył te spostrzeżenia na minerały, w których glinowe zamienniki atomów krzemu w krzemianach. Pierwsze zastosowanie krystalografii rentgenowskiej w metalurgii miało również miejsce w połowie lat dwudziestych XX wieku. Przede wszystkim struktura stopu Mg _{2 Sn} Linusa Paulinga doprowadziła do jego teorii stabilności i struktury złożonych kryształów jonowych.

17 października 2012 r. łazik Curiosity na Marsie w „ Rocknest ” wykonał pierwszą analizę dyfrakcji rentgenowskiej marsjańskiej gleby . Wyniki z analizatora CheMin łazika ujawniły obecność kilku minerałów, w tym skalenia , piroksenów i oliwinu , i zasugerowały, że marsjańska gleba w próbce była podobna do „zwietrzałych gleb bazaltowych ” hawajskich wulkanów .

Wczesne cząsteczki organiczne i małe cząsteczki biologiczne

Trójwymiarowa struktura penicyliny , rozwiązana przez Dorothy Crowfoot Hodgkin w 1945 roku. Zielone, czerwone, żółte i niebieskie kule reprezentują odpowiednio atomy węgla , tlenu , siarki i azotu . Białe kule reprezentują wodór , który został określony raczej matematycznie niż za pomocą analizy rentgenowskiej.

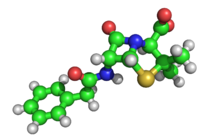
Pierwszą strukturę związku organicznego, heksametylenotetraminy , odkryto w 1923 roku. Następnie przeprowadzono kilka badań nad długołańcuchowymi kwasami tłuszczowymi , które są ważnym składnikiem błon biologicznych . W latach trzydziestych XX wieku zaczęto rozwiązywać struktury znacznie większych cząsteczek o dwuwymiarowej złożoności. Znaczącym postępem była struktura ftalocyjaniny , dużej płaskiej cząsteczki, która jest blisko spokrewniona z cząsteczkami porfiryny ważnymi w biologii, takimi jak hem , koryna i chlorofil .

Krystalografia rentgenowska cząsteczek biologicznych wystartowała z Dorothy Crowfoot Hodgkin , która rozwiązała struktury cholesterolu (1937), penicyliny (1946) i witaminy B12 _{( 1956), za co} w 1964 roku otrzymała Nagrodę Nobla w dziedzinie chemii . W 1969 roku udało jej się rozwiązać strukturę insuliny , nad którą pracowała przez ponad trzydzieści lat.

Biologiczna krystalografia makrocząsteczkowa

Diagram wstążkowy struktury mioglobiny , przedstawiający helisy alfa . Takie białka to długie, liniowe cząsteczki o tysiącach atomów; jednak względne położenie każdego atomu zostało określone z rozdzielczością subatomową za pomocą krystalografii rentgenowskiej. szkieletu białka od jego N-końca do C-końca.

Struktury krystaliczne białek ( które są nieregularne i setki razy większe niż cholesterol) zaczęto rozwiązywać pod koniec lat 50 . Perutza w 1962 roku. Od tego sukcesu określono ponad 130 000 rentgenowskich struktur krystalicznych białek, kwasów nukleinowych i innych cząsteczek biologicznych. Najbliżej konkurencyjną metodą pod względem liczby analizowanych struktur jest spektroskopia magnetycznego rezonansu jądrowego (NMR). , który rozwiązał mniej niż jedną dziesiątą tego. Krystalografia może rozwiązywać struktury dowolnie dużych cząsteczek, podczas gdy NMR w stanie roztworu jest ograniczony do stosunkowo małych (poniżej 70 k Da ). Krystalografia rentgenowska jest rutynowo stosowana do określenia, w jaki sposób lek farmaceutyczny oddziałuje z docelowym białkiem i jakie zmiany mogą go poprawić. Jednak wewnętrzne białka błonowe pozostają trudne do krystalizacji, ponieważ wymagają detergentów lub innych denaturantów do ich rozpuszczenia w izolacji, a takie detergenty często zakłócają krystalizację. Białka błonowe są dużym składnikiem genomu i obejmują wiele białek o dużym znaczeniu fizjologicznym, takich jak kanały jonowe i receptory . Kriogenika helowa służy do zapobiegania uszkodzeniom kryształów białek przez promieniowanie.

Na drugim końcu skali nawet stosunkowo małe cząsteczki mogą stanowić wyzwanie dla zdolności rozdzielczej krystalografii rentgenowskiej. Struktura przypisana w 1991 r. antybiotykowi wyizolowanemu z organizmu morskiego, diazonamidowi A (C ₄₀ H ₃₄ Cl ₂ N ₆ O ₆ , masa molowa 765,65 g/mol), okazała się błędna na podstawie klasycznego dowodu struktury: próbki syntetycznej nie był identyczny z produktem naturalnym. Błąd został przypisany niezdolności krystalografii rentgenowskiej do rozróżnienia prawidłowego -OH / -NH i zamienionego -NH ₂ / -O- grupy w nieprawidłowej strukturze. Jednak dzięki postępowi w oprzyrządowaniu podobne grupy można rozróżnić za pomocą nowoczesnych monokrystalicznych dyfraktometrów rentgenowskich.

Pomimo tego, że jest nieocenionym narzędziem w biologii strukturalnej , krystalografia białek niesie ze sobą pewne nieodłączne problemy w swojej metodologii, które utrudniają interpretację danych. Sieć krystaliczna, która powstaje w procesie krystalizacji, zawiera liczne jednostki oczyszczonego białka, które są gęsto i symetrycznie upakowane w krysztale. Szukając nieznanego wcześniej białka, ustalenie jego kształtu i granic w sieci krystalicznej może być trudne. Białka zwykle składają się z mniejszych podjednostek, a zadanie rozróżnienia podjednostek i zidentyfikowania właściwego białka może być wyzwaniem nawet dla doświadczonych krystalografów. Niebiologiczne interfejsy, które występują podczas krystalizacji, są znane jako styki upakowania kryształów (lub po prostu styki kryształów) i nie można ich rozróżnić za pomocą środków krystalograficznych. Kiedy nowa struktura białka zostanie rozwiązana za pomocą krystalografii rentgenowskiej i osadzona w Protein Data Bank , jego autorzy proszeni są o określenie „zespołu biologicznego”, który stanowiłby funkcjonalne, biologicznie istotne białko. Jednak błędy, brakujące dane i niedokładne adnotacje podczas przesyłania danych prowadzą do powstania niejasnych struktur i zagrażają wiarygodności bazy danych. Zgłoszono, że poziom błędu w przypadku samych błędnych adnotacji wynosi ponad 6,6% lub około 15%, co prawdopodobnie jest wielkością nietrywialną, biorąc pod uwagę liczbę zdeponowanych struktur. Ten „problem klasyfikacji interfejsów” jest zwykle rozwiązywany za pomocą metod obliczeniowych i stał się uznanym tematem w bioinformatyka strukturalna .

Techniki rozpraszania

Dalsze informacje: Techniki rozpraszania promieniowania rentgenowskiego

Rozpraszanie elastyczne a nieelastyczne

Krystalografia rentgenowska jest formą rozpraszania sprężystego ; wychodzące promienie rentgenowskie mają taką samą energię, a zatem tę samą długość fali, co przychodzące promienie rentgenowskie, tylko ze zmienionym kierunkiem. Natomiast rozpraszanie nieelastyczne występuje, gdy energia jest przenoszona z nadchodzącego promieniowania rentgenowskiego do kryształu, np. poprzez wzbudzenie elektronu w powłoce wewnętrznej do wyższego poziomu energii . Takie nieelastyczne rozpraszanie zmniejsza energię (lub zwiększa długość fali) wychodzącej wiązki. Rozpraszanie nieelastyczne jest przydatne do badania takich wzbudzeń materii, ale nie do określania rozkładu rozpraszaczy w materii, co jest celem krystalografii rentgenowskiej.

Promieniowanie rentgenowskie ma długość fali od 10 do 0,01 nanometra ; typowa długość fali stosowana w krystalografii to 1 Å (0,1 nm), co odpowiada skali kowalencyjnych wiązań chemicznych i promienia pojedynczego atomu. Fotony o większej długości fali (takie jak promieniowanie ultrafioletowe ) nie miałyby wystarczającej rozdzielczości do określenia pozycji atomów. Z drugiej strony fotony o krótszej długości fali, takie jak promienie gamma, są trudne do wytworzenia w dużych ilościach, trudne do skupienia i zbyt silnie oddziałują z materią, wytwarzając pary cząstka-antycząstka . Dlatego promieniowanie rentgenowskie jest „słodkim punktem” dla długości fali przy określaniu struktur o rozdzielczości atomowej na podstawie rozpraszania promieniowania elektromagnetycznego .

Inne techniki rentgenowskie

Inne formy elastycznego rozpraszania promieniowania rentgenowskiego oprócz dyfrakcji monokrystalicznej obejmują dyfrakcję proszkową , rozpraszanie promieni rentgenowskich pod małymi kątami ( SAXS ) i kilka rodzajów dyfrakcji włókien rentgenowskich , które zostały wykorzystane przez Rosalind Franklin do określenia struktury podwójnej helisy DNA . _ Ogólnie rzecz biorąc, dyfrakcja rentgenowska monokryształu dostarcza więcej informacji strukturalnych niż te inne techniki; wymaga jednak odpowiednio dużego i regularnego kryształu, który nie zawsze jest dostępny.

Te metody rozpraszania generalnie wykorzystują monochromatyczne promieniowanie rentgenowskie, które jest ograniczone do jednej długości fali z niewielkimi odchyleniami. Szerokie spektrum promieni rentgenowskich (tj. połączenie promieni rentgenowskich o różnych długościach fal) można również wykorzystać do przeprowadzenia dyfrakcji rentgenowskiej, techniki znanej jako metoda Laue. Jest to metoda zastosowana w pierwotnym odkryciu dyfrakcji rentgenowskiej. Rozpraszanie Laue'a dostarcza wielu informacji strukturalnych przy krótkiej ekspozycji na wiązkę promieniowania rentgenowskiego i dlatego jest wykorzystywane w badaniach strukturalnych bardzo szybkich zdarzeń ( Krystalografia rozdzielcza w czasie ). Jednak nie nadaje się tak dobrze jak rozpraszanie monochromatyczne do określania pełnej struktury atomowej kryształu i dlatego działa lepiej w przypadku kryształów o stosunkowo prostych układach atomowych.

Tryb odbicia wstecznego Laue rejestruje promienie rentgenowskie rozproszone do tyłu ze źródła o szerokim spektrum. Jest to przydatne, jeśli próbka jest zbyt gruba, aby promienie rentgenowskie mogły przez nią przejść. Płaszczyzny dyfrakcyjne w krysztale określa się, wiedząc, że normalna do płaszczyzny dyfrakcyjnej dzieli kąt między wiązką padającą a wiązką ugiętą na pół. Wykres Greningera może być użyty do interpretacji fotografii odbicia wstecznego Laue.

Dyfrakcja elektronów i neutronów

Inne cząstki, takie jak elektrony i neutrony , mogą być użyte do wytworzenia obrazu dyfrakcyjnego . Chociaż rozpraszanie elektronów, neutronów i promieni rentgenowskich opiera się na różnych procesach fizycznych, uzyskane wzory dyfrakcyjne są analizowane przy użyciu tych samych technik dyfrakcyjnych .

Jak wyprowadzono poniżej, gęstość elektronów w krysztale i wzorach dyfrakcyjnych są często powiązane prostą metodą matematyczną, transformatą Fouriera , która umożliwia stosunkowo łatwe obliczenie gęstości na podstawie wzorów. Jednak działa to tylko wtedy, gdy rozpraszanie jest słabe , tj. jeśli wiązki rozproszone są znacznie mniej intensywne niż wiązka przychodząca. Słabo rozproszone promienie rentgenowskie lub wiązki neutronów przechodzą przez pozostałą część kryształu bez drugiego zdarzenia rozpraszania. Takie ponownie rozproszone fale nazywane są „rozpraszaniem wtórnym” lub „dyfrakcją dynamiczną” i zmieniają analizę. Każdy wystarczająco gruby kryształ wytworzy dynamiczną dyfrakcję, ale ponieważ promienie rentgenowskie i neutrony oddziałują stosunkowo słabo z materią, generalnie nie stanowi to istotnego problemu, gdy są używane.

Ponieważ oddziałują one poprzez siły Coulomba, rozpraszanie elektronów przez materię jest 1000 lub więcej razy silniejsze niż w przypadku promieniowania rentgenowskiego. Stąd wiązki elektronów wytwarzają silne dynamiczne rozpraszanie nawet w przypadku stosunkowo cienkich kryształów (>10 nm). Chociaż istnieją podobieństwa między dyfrakcją promieni rentgenowskich i elektronów, co można znaleźć w książce Johna M. Cowleya , podejście jest zazwyczaj inne, ponieważ opiera się na oryginalnym podejściu Hansa Bethe i rozwiązaniu równania Schrödingera dla relatywistycznych elektronów , a nie kinematyczny lub zgodne z prawem Bragga . Możliwe są informacje o bardzo małych obszarach, aż do pojedynczych atomów. Zakres zastosowań dyfrakcji elektronów , transmisyjnej mikroskopii elektronowej i transmisyjnej krystalografii elektronowej z elektronami o wysokiej energii jest szeroki; zobacz odpowiednie linki, aby uzyskać więcej informacji i cytatów. Oprócz metod transmisji, niskoenergetyczna dyfrakcja elektronów jest techniką, w której elektrony są wstecznie rozpraszane na powierzchniach i była szeroko stosowana do określania struktur powierzchniowych w skali atomowej oraz odbicie, dyfrakcja elektronów o wysokiej energii to kolejna metoda, która jest szeroko stosowana do monitorowania wzrostu cienkich warstw.

Dyfrakcja neutronów jest doskonałą metodą określania struktury, chociaż trudno było uzyskać intensywne, monochromatyczne wiązki neutronów w wystarczających ilościach. Tradycyjnie wykorzystywano reaktory jądrowe , chociaż źródła wytwarzające neutrony metodą spallacji stają się coraz bardziej dostępne. Będąc nienaładowanymi, neutrony znacznie łatwiej rozpraszają się od jąder atomowych niż od elektronów. Dlatego rozpraszanie neutronów jest bardzo przydatne do obserwacji pozycji lekkich atomów z niewielką liczbą elektronów, zwłaszcza wodoru , który jest zasadniczo niewidoczny w dyfrakcji rentgenowskiej. Rozpraszanie neutronów ma również niezwykłą właściwość polegającą na tym, że rozpuszczalnik można uczynić niewidocznym, dostosowując stosunek zwykłej wody H ₂ O do ciężkiej wody D ₂ O.

Metody

Omówienie dyfrakcji rentgenowskiej monokryształu

Przepływ pracy do rozwiązywania struktury cząsteczki za pomocą krystalografii rentgenowskiej.

krystalografii rentgenowskiej jest dyfrakcja rentgenowska monokryształu , w której wiązka promieni rentgenowskich uderza w pojedynczy kryształ, tworząc rozproszone wiązki. Kiedy docierają do kawałka filmu lub innego detektora, wiązki te tworzą dyfrakcyjny wzór plam; siły i kąty tych wiązek są rejestrowane, gdy kryształ jest stopniowo obracany. Każde miejsce nazywa się odbiciem , ponieważ odpowiada odbiciu promieni rentgenowskich od jednego zestawu równomiernie rozmieszczonych płaszczyzn w krysztale. W przypadku monokryształów o wystarczającej czystości i regularności dane z dyfrakcji rentgenowskiej mogą określić średnie długości wiązań chemicznych i kąty odpowiednio z dokładnością do kilku tysięcznych angstremów i do kilku dziesiątych stopnia . Atomy w krysztale nie są statyczne, ale oscylują wokół swoich średnich pozycji, zwykle o mniej niż kilka dziesiątych angstremów. Krystalografia rentgenowska pozwala zmierzyć wielkość tych oscylacji.

Procedura

Technika krystalografii rentgenowskiej monokryształu składa się z trzech podstawowych etapów. Pierwszym – i często najtrudniejszym – krokiem jest uzyskanie odpowiedniego kryształu badanego materiału. Kryształ powinien być wystarczająco duży (zwykle większy niż 0,1 mm we wszystkich wymiarach), czysty pod względem składu i regularnej struktury, bez znaczących wewnętrznych niedoskonałości , takich jak pęknięcia lub zbliźniaczenia .

W drugim etapie kryształ umieszcza się w intensywnej wiązce promieni rentgenowskich, zwykle o jednej długości fali ( monochromatyczne promienie rentgenowskie ), wytwarzając regularny wzór odbić. Mierzone są kąty i natężenia ugiętych promieni rentgenowskich, przy czym każdy związek ma unikalny wzór dyfrakcji. Gdy kryształ jest stopniowo obracany, poprzednie odbicia znikają i pojawiają się nowe; intensywność każdej plamki jest rejestrowana przy każdej orientacji kryształu. Może być konieczne zebranie wielu zestawów danych, przy czym każdy zestaw obejmuje nieco ponad połowę pełnego obrotu kryształu i zazwyczaj zawiera dziesiątki tysięcy odbić.

W trzecim etapie dane te są łączone obliczeniowo z uzupełniającymi informacjami chemicznymi w celu stworzenia i udoskonalenia modelu rozmieszczenia atomów w krysztale. Ostateczny, udoskonalony model układu atomowego — obecnie nazywany strukturą krystaliczną — jest zwykle przechowywany w publicznej bazie danych.

Ograniczenia

Zobacz też: Rozdzielczość (gęstość elektronów)

Ponieważ powtarzająca się jednostka kryształu, jego komórka elementarna, staje się większa i bardziej złożona, obraz na poziomie atomowym dostarczany przez krystalografię rentgenowską staje się mniej rozdzielczy (bardziej „rozmyty”) dla danej liczby obserwowanych odbić. Często rozróżnia się dwa ograniczające przypadki krystalografii rentgenowskiej - krystalografię „małocząsteczkową” (która obejmuje ciągłe nieorganiczne ciała stałe) i krystalografię „makromolekularną”. Krystalografia małocząsteczkowa zazwyczaj obejmuje kryształy o mniej niż 100 atomach w ich jednostce asymetrycznej ; takie struktury krystaliczne są zwykle tak dobrze rozdzielone, że atomy można rozpoznać jako izolowane „plamki” o gęstości elektronowej. Z kolei krystalografia makrocząsteczkowa często obejmuje dziesiątki tysięcy atomów w komórce elementarnej. Takie struktury krystaliczne są generalnie gorzej rozdzielone (bardziej „rozmazane”); atomy i wiązania chemiczne pojawiają się jako rurki o gęstości elektronowej, a nie jako pojedyncze atomy. Ogólnie rzecz biorąc, małe cząsteczki są również łatwiejsze do krystalizacji niż makrocząsteczki; jednak krystalografia rentgenowska okazała się możliwa nawet w przypadku wirusów i białka z setkami tysięcy atomów, dzięki ulepszonemu obrazowaniu krystalograficznemu i technologii. Chociaż zwykle krystalografię rentgenowską można przeprowadzić tylko wtedy, gdy próbka ma postać krystaliczną, przeprowadzono nowe badania nad próbkowaniem próbek niekrystalicznych.

Krystalizacja

Dalsze informacje: Krystalizacja , Rekrystalizacja (chemia) § Pojedyncze doskonałe kryształy (do analizy rentgenowskiej) i Krystalizacja białek

Kryształ białka widziany pod mikroskopem . Kryształy stosowane w krystalografii rentgenowskiej mogą mieć średnicę mniejszą niż milimetr.

Chociaż krystalografia może być wykorzystana do scharakteryzowania zaburzenia w zanieczyszczonym lub nieregularnym krystalografii, krystalografia generalnie wymaga czystego kryształu o wysokiej regularności, aby rozwiązać strukturę skomplikowanego układu atomów. Czyste, regularne kryształy można czasami uzyskać z materiałów naturalnych lub syntetycznych, takich jak próbki metali , minerałów lub innych materiałów makroskopowych. Regularność takich kryształów można czasami poprawić za pomocą makromolekularnego wyżarzania kryształów i innych metod. Jednak w wielu przypadkach uzyskanie kryształu o jakości dyfrakcyjnej jest główną przeszkodą w rozwiązaniu jego struktury o rozdzielczości atomowej.

Krystalografia małocząsteczkowa i makrocząsteczkowa różnią się zakresem możliwych technik stosowanych do wytwarzania kryształów o jakości dyfrakcyjnej. Małe cząsteczki na ogół mają kilka stopni swobody konformacyjnej i mogą być krystalizowane za pomocą szerokiego zakresu metod, takich jak chemiczne osadzanie z fazy gazowej i rekrystalizacja . Z kolei makrocząsteczki mają na ogół wiele stopni swobody i ich krystalizacja musi być przeprowadzona tak, aby zachować stabilną strukturę. Na przykład białka i większe RNA nie mogą krystalizować, jeśli ich trzeciorzędowa struktura została rozwinięta ; dlatego zakres warunków krystalizacji jest ograniczony do warunków roztworu, w których takie cząsteczki pozostają sfałdowane.

Trzy metody przygotowania kryształów, A: Wisząca kropla. B: Spadek na siedząco. C: Mikrodializa

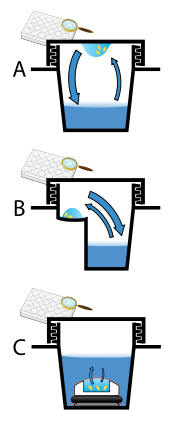
Kryształy białka są prawie zawsze hodowane w roztworze. Najczęstszym podejściem jest bardzo stopniowe obniżanie rozpuszczalności jego cząsteczek składowych; jeśli zostanie to zrobione zbyt szybko, cząsteczki wytrącą się z roztworu, tworząc bezużyteczny pył lub bezpostaciowy żel na dnie pojemnika. Wzrost kryształów w roztworze charakteryzuje się dwoma etapami: zarodkowaniem mikroskopijnego krystalitu (prawdopodobnie mającego tylko 100 cząsteczek), po którym następuje wzrost tego krystalitu, najlepiej do kryształu o jakości dyfrakcyjnej. Warunki rozwiązania, które sprzyjają pierwszemu etapowi (zarodkowanie), nie zawsze są tymi samymi warunkami, które sprzyjają drugiemu etapowi (kolejny wzrost). Celem krystalografa jest określenie warunków roztworu, które sprzyjają rozwojowi pojedynczego, dużego kryształu, ponieważ większe kryształy zapewniają lepszą rozdzielczość cząsteczki. W związku z tym warunki rozwiązania powinny odrzucają pierwszy etap (zarodkowanie), ale faworyzują drugi (wzrost), tak że na kroplę tworzy się tylko jeden duży kryształ. Jeśli zarodkowanie jest zbyt sprzyjane, w kropli utworzy się deszcz małych krystalitów zamiast jednego dużego kryształu; jeśli faworyzuje się go za mało, żaden kryształ nie powstanie. Inne podejścia obejmują krystalizację białek pod olejem, gdzie wodne roztwory białek są dozowane pod ciekłym olejem, a woda odparowuje przez warstwę oleju. Różne oleje mają różną przepuszczalność parowania, co powoduje zmiany w szybkościach stężeń z różnych mieszanin substancji percypcyjnej/białkowej.

Niezwykle trudno jest przewidzieć dobre warunki do zarodkowania lub wzrostu dobrze uporządkowanych kryształów. W praktyce sprzyjające warunki są identyfikowane przez badanie przesiewowe ; przygotowywana jest bardzo duża partia cząsteczek i testowana jest szeroka gama roztworów krystalizacyjnych. Na ogół wypróbowuje się setki, a nawet tysiące warunków rozwiązania, zanim znajdzie się ten, który zakończy się sukcesem. Różne warunki mogą wykorzystywać jeden lub więcej mechanizmów fizycznych do obniżania rozpuszczalności cząsteczki; na przykład niektóre mogą zmieniać pH, niektóre zawierają sole serii Hofmeistera lub chemikalia, które obniżają stałą dielektryczną roztworu, a jeszcze inne zawierają duże polimery, takie jak glikol polietylenowy , które wypychają cząsteczkę z roztworu przez efekty entropiczne. Powszechne jest również wypróbowywanie kilku temperatur w celu pobudzenia krystalizacji lub stopniowe obniżanie temperatury, aby roztwór stał się przesycony. Metody te wymagają dużych ilości cząsteczki docelowej, ponieważ wykorzystują wysokie stężenie cząsteczki (cząsteczek) do krystalizacji. Ze względu na trudność w uzyskaniu tak dużych ilości ( miligramów ) białka krystalizacyjnego opracowano roboty, które są w stanie dokładnie dozować próbne krople krystalizacyjne o objętości rzędu 100 nanolitrów . Oznacza to, że w jednym eksperymencie zużywa się 10-krotnie mniej białka w porównaniu z ręcznymi próbami krystalizacji (rzędu 1 mikrolitra ).

Wiadomo, że kilka czynników hamuje lub zakłóca krystalizację. Rosnące kryształy są zwykle utrzymywane w stałej temperaturze i chronione przed wstrząsami lub wibracjami, które mogłyby zakłócić ich krystalizację. Zanieczyszczenia w cząsteczkach lub w roztworach krystalizacyjnych często nie sprzyjają krystalizacji. Elastyczność konformacyjna cząsteczki również zmniejsza prawdopodobieństwo krystalizacji z powodu entropii. Cząsteczki, które mają tendencję do samodzielnego składania się w regularne helisy, często nie chcą składać się w kryształy. Kryształy mogą zostać zniszczone przez zbliźniaczenie , co może wystąpić, gdy komórka elementarna może upakować się równie korzystnie w wielu orientacjach; chociaż ostatnie postępy w metodach obliczeniowych mogą pozwolić na rozwiązanie struktury niektórych bliźniaczych kryształów. Po nieudanej krystalizacji cząsteczki docelowej krystalograf może spróbować ponownie z nieco zmodyfikowaną wersją cząsteczki; nawet niewielkie zmiany właściwości molekularnych mogą prowadzić do dużych różnic w zachowaniu krystalizacji.

Zbieranie danych

Montaż kryształu

Animacja przedstawiająca pięć ruchów możliwych za pomocą czterokołowego goniometru kappa. Obroty wokół każdego z czterech kątów φ, κ, ω i 2θ pozostawiają kryształ w wiązce promieniowania rentgenowskiego, ale zmieniają orientację kryształu. Detektor (czerwone pole) można przesuwać bliżej lub dalej od kryształu, co pozwala na uzyskanie danych o wyższej rozdzielczości (jeśli jest bliżej) lub lepsze rozróżnienie pików Bragga (jeśli jest dalej).

Kryształ jest mocowany do pomiarów w taki sposób, że można go trzymać w wiązce promieniowania rentgenowskiego i obracać. Istnieje kilka metod montażu. W przeszłości kryształy wprowadzano do szklanych kapilar wraz z roztworem krystalizacyjnym ( roztworem macierzystym ). Obecnie kryształy małych cząsteczek są zwykle mocowane za pomocą oleju lub kleju do włókna szklanego lub pętli, która jest wykonana z nylonu lub tworzywa sztucznego i są mocowane do litego pręta. Kryształy białka są zbierane przez pętlę, a następnie błyskawicznie zamrażane ciekłym azotem . To zamrożenie zmniejsza uszkodzenia spowodowane promieniowaniem rentgenowskim, a także szum w pikach Bragga spowodowany ruchem termicznym (efekt Debye-Waller). Jednak nietraktowane kryształy białka często pękają, jeśli zostaną szybko zamrożone; w związku z tym przed zamrożeniem są one na ogół wstępnie moczone w roztworze środka krioochronnego. Niestety, to wstępne namaczanie może samo w sobie spowodować pęknięcie kryształu, niszcząc go dla krystalografii. Ogólnie rzecz biorąc, udane krio-warunki są identyfikowane metodą prób i błędów.

Kapilara lub pętla jest zamontowana na goniometrze , co umożliwia jej dokładne ustawienie w wiązce promieniowania rentgenowskiego i obracanie. Ponieważ zarówno kryształ, jak i wiązka są często bardzo małe, kryształ musi być wyśrodkowany w wiązce z dokładnością do ~ 25 mikrometrów, co jest wspomagane przez kamerę skupioną na krysztale. Najpopularniejszym typem goniometru jest „goniometr kappa”, który oferuje trzy kąty obrotu: kąt ω, który obraca się wokół osi prostopadłej do belki; kąt κ wokół osi położonej ~50° do osi ω; i wreszcie kąt φ wokół osi pętli/kapilary. Gdy kąt κ wynosi zero, osie ω i φ są wyrównane. Obrót κ pozwala na wygodne zamontowanie kryształu, ponieważ ramię, w którym osadzony jest kryształ, może być wychylone w kierunku krystalografa. Oscylacje przeprowadzane podczas zbierania danych (wymienione poniżej) dotyczą tylko osi ω. Starszym typem goniometru jest goniometr czterokołowy i jego krewni, tacy jak goniometr sześciokołowy.

Źródła promieniowania rentgenowskiego

Dalsze informacje: dyfraktometr , synchrotronowe źródło światła i laser na swobodnych elektronach

Obrotowa anoda

Krystalografię na małą skalę można wykonać za pomocą lokalnego źródła lampy rentgenowskiej , zwykle połączonego z detektorem płyt obrazowych . Mają one tę zaletę, że są stosunkowo niedrogie i łatwe w utrzymaniu oraz umożliwiają szybkie badanie przesiewowe i pobieranie próbek. Jednak długość fali wytwarzanego światła jest ograniczona dostępnością różnych anodowych . Ponadto intensywność jest ograniczona przez przyłożoną moc i dostępną wydajność chłodzenia, aby uniknąć stopienia anody. W takich układach elektrony są odparowywane z katody i przyspieszane przez silny potencjał elektryczny ~50 kV ; po osiągnięciu dużej prędkości elektrony zderzają się z metalową płytką, emitując bremsstrahlung i kilka silnych linii widmowych odpowiadających wzbudzeniu elektronów wewnętrznej powłoki metalu. Najczęściej stosowanym metalem jest miedź , którą można łatwo schłodzić ze względu na wysoką przewodność cieplną i która wytwarza silne linie K _α i K _{β . Linia} K _β jest czasami tłumiona cienką (~10 µm) folią niklową. Najprostsza i najtańsza odmiana zamkniętej lampy rentgenowskiej ma stacjonarną anodę (tzw Crookesa ) i uruchomić z ~2 kW mocy wiązki elektronów. Droższa odmiana ma źródło typu obracającej się anody , które działa z ~ 14 kW mocy e-beam.

Promienie rentgenowskie są generalnie filtrowane (za pomocą filtrów rentgenowskich ) do pojedynczej długości fali (monochromatyczne) i kolimowane w jednym kierunku, zanim uderzą w kryształ. Filtrowanie nie tylko upraszcza analizę danych, ale także usuwa promieniowanie, które degraduje kryształ bez dostarczania użytecznych informacji. Kolimację wykonuje się albo kolimatorem (w zasadzie długim tubusem), albo sprytnym układem delikatnie zakrzywionych luster. Systemy lustrzane są preferowane w przypadku małych kryształów (poniżej 0,3 mm) lub z dużymi komórkami elementarnymi (powyżej 150 Å).

Anody obrotowe zostały użyte przez Joannę (Joka) Marię Vandenberg w pierwszych eksperymentach, które wykazały moc promieni rentgenowskich do szybkiego (w produkcji w czasie rzeczywistym) przesiewania dużych płytek cienkowarstwowych InGaAsP do kontroli jakości laserów studni kwantowych .

Tubus mikrofokusa

Nowszym wynalazkiem jest rura mikroogniskowa , która może zapewnić co najmniej tak wysoki strumień wiązki (po kolimacji) jak źródła z obracającą się anodą, ale wymaga jedynie mocy wiązki kilkudziesięciu lub setek watów, a nie kilku kilowatów.

Promieniowanie synchrotronowe

promieniowania synchrotronowego są jednymi z najjaśniejszych źródeł światła na Ziemi i jednymi z najpotężniejszych narzędzi dostępnych dla krystalografów rentgenowskich. Wiązki rentgenowskie generowane w dużych maszynach zwanych synchrotronami , które przyspieszają naładowane elektrycznie cząstki, często elektrony, do prędkości bliskiej prędkości światła i zamykają je w (z grubsza) kołowej pętli za pomocą pól magnetycznych.

Synchrotrony to na ogół obiekty krajowe, z których każdy ma kilka dedykowanych linii badawczych , w których dane są gromadzone bez przerwy. Synchrotrony zostały pierwotnie zaprojektowane do użytku przez fizyków wysokich energii badających cząstki subatomowe i zjawiska kosmiczne . Największym elementem każdego synchrotronu jest jego pierścień magazynujący elektrony. Ten pierścień w rzeczywistości nie jest idealnym kołem, ale wielokątem o wielu bokach. W każdym rogu wielokąta lub sektora dokładnie ustawione magnesy zakrzywiają strumień elektronów. Gdy ścieżka elektronów jest zakrzywiona, emitują one wybuchy energii w postaci promieni rentgenowskich.

Korzystanie z promieniowania synchrotronowego często wiąże się ze specyficznymi wymaganiami dla krystalografii rentgenowskiej. Intensywne promieniowanie jonizujące może spowodować uszkodzenie próbek, zwłaszcza kryształów wielkocząsteczkowych. Krystalografia kriogeniczna chroni próbkę przed uszkodzeniem przez promieniowanie, zamrażając kryształ w temperaturach ciekłego azotu (~100 K ). Metody kriokrystalograficzne stosuje się również do domowych źródeł obrotowych anod. Jednak promieniowanie synchrotronowe często ma tę zaletę, że wybierane przez użytkownika długości fal pozwalają na anomalne rozpraszanie eksperymenty, które maksymalizują anomalny sygnał. Ma to kluczowe znaczenie w eksperymentach, takich jak dyspersja anomalna na jednej długości fali (SAD) i dyspersja anomalna na wielu długościach fal (MAD).

Laser na swobodnych elektronach

Lasery na swobodnych elektronach zostały opracowane do użytku w krystalografii rentgenowskiej. Są to najjaśniejsze obecnie dostępne źródła promieniowania rentgenowskiego; z promieniami rentgenowskimi nadchodzącymi w femtosekundowych . Intensywność źródła jest taka, że ​​wzory dyfrakcyjne z rozdzielczością atomową można rozdzielić dla kryształów, które w przeciwnym razie byłyby zbyt małe, aby je zebrać. Jednak intensywne źródło światła również niszczy próbkę, co wymaga wystrzelenia wielu kryształów. Ponieważ każdy kryształ jest losowo zorientowany w wiązce, należy zebrać setki tysięcy pojedynczych obrazów dyfrakcyjnych, aby uzyskać pełny zestaw danych. Ta metoda to seryjna krystalografia femtosekundowa , został wykorzystany do rozwiązania struktury wielu struktur krystalicznych białek, czasami odnotowując różnice z równoważnymi strukturami zebranymi ze źródeł synchrotronowych.

Rejestrowanie odbić

Dyfraktogram rentgenowski skrystalizowanego enzymu. Wzór plamek ( odbicia ) i względna siła każdej plamki ( intensywności ) mogą być wykorzystane do określenia struktury enzymu.

Kiedy kryształ jest zamontowany i wystawiony na działanie intensywnej wiązki promieni rentgenowskich, rozprasza promienie rentgenowskie na wzór plamek lub odbić , które można zaobserwować na ekranie za kryształem. Podobny wzór można zobaczyć, kierując wskaźnik laserowy na płytę kompaktową . Względne intensywności tych plam dostarczają informacji do określenia rozmieszczenia cząsteczek w krysztale w szczegółach atomowych. Intensywność tych odbić można rejestrować za pomocą kliszy fotograficznej , detektora powierzchni (takiego jak detektor pikseli ) lub urządzenia ze sprzężeniem ładunkowym (CCD) czujnik obrazu. Piki pod małymi kątami odpowiadają danym o niskiej rozdzielczości, podczas gdy piki pod dużymi kątami reprezentują dane o wysokiej rozdzielczości; w ten sposób górną granicę ostatecznej rozdzielczości struktury można określić na podstawie kilku pierwszych obrazów. W tym momencie można określić niektóre miary jakości dyfrakcji, takie jak mozaikowatość kryształu i jego ogólny nieład, obserwowany w szerokościach pików. Na tym etapie można również szybko zdiagnozować niektóre patologie kryształu, które czynią go niezdolnym do rozwiązania struktury.

Jeden obraz plamek to za mało, aby zrekonstruować cały kryształ; reprezentuje tylko mały wycinek pełnej transformaty Fouriera. Aby zebrać wszystkie niezbędne informacje, kryształ należy krok po kroku obracać o 180°, rejestrując obraz przy każdym kroku; odwrotnej przestrzeni potrzeba nieco więcej niż 180 ° , ze względu na krzywiznę kuli Ewalda . Jednakże, jeśli kryształ ma wyższą symetrię, można zarejestrować mniejszy zakres kątowy, taki jak 90° lub 45°. Oś obrotu należy zmienić przynajmniej raz, aby uniknąć powstania „martwego punktu” w przestrzeni odwrotnej blisko osi obrotu. Zwykle lekko kołysze się kryształem (o 0,5–2 °), aby uchwycić szerszy obszar wzajemnej przestrzeni.

fazowania może być potrzebnych wiele zestawów danych . Na przykład anomalnej dyspersji o wielu długościach fal wymaga zarejestrowania rozpraszania na co najmniej trzech (a zwykle czterech, w przypadku redundancji) długości fal przychodzącego promieniowania rentgenowskiego. Pojedynczy kryształ może ulec zbyt dużej degradacji podczas zbierania jednego zestawu danych z powodu uszkodzeń spowodowanych promieniowaniem; w takich przypadkach należy pobrać zestawy danych dotyczące wielu kryształów.

Analiza danych

Symetria kryształów, komórka elementarna i skalowanie obrazu

Dalsze informacje: grupa kosmiczna

Zarejestrowana seria dwuwymiarowych wzorów dyfrakcyjnych, z których każdy odpowiada innej orientacji kryształów, jest przekształcana w trójwymiarowy model gęstości elektronowej; konwersja wykorzystuje technikę matematyczną transformat Fouriera, co wyjaśniono poniżej . Każde miejsce odpowiada innemu rodzajowi zmian w gęstości elektronów; krystalograf musi określić, która odmiana odpowiada której plamce ( indeksowanie ), względne siły plamek na różnych obrazach ( łączenie i skalowanie ) i jak należy łączyć zmiany, aby uzyskać całkowitą gęstość elektronów ( fazowanie ).

Przetwarzanie danych rozpoczyna się od zindeksowania refleksji. Oznacza to określenie wymiarów komórki elementarnej i określenie, który pik obrazu odpowiada której pozycji w odwrotnej przestrzeni. Produktem ubocznym indeksowania jest określenie symetrii kryształu, tj. jego grupy przestrzennej . Niektóre grupy przestrzenne można wyeliminować na samym początku. Na przykład symetrii odbicia nie można zaobserwować w cząsteczkach chiralnych; tak więc tylko 65 grup przestrzennych z 230 możliwych jest dozwolonych dla cząsteczek białka, które prawie zawsze są chiralne. Indeksowanie jest zwykle realizowane za pomocą automatycznego indeksowania rutyna. Po przypisaniu symetrii dane są następnie integrowane . Konwertuje to setki obrazów zawierających tysiące odbić do pojedynczego pliku, składającego się przynajmniej z zapisów indeksu Millera dla każdego odbicia i intensywności każdego odbicia (w tym stanie plik często zawiera również oszacowania błędów oraz miary stronniczości (jaka część danego odbicia została zarejestrowana na tym obrazie)).

Pełny zestaw danych może składać się z setek oddzielnych zdjęć wykonanych w różnych orientacjach kryształu. Pierwszym krokiem jest scalenie i skalowanie tych różnych obrazów, to znaczy określenie, które piki pojawiają się na dwóch lub więcej obrazach ( łączenie ) i przeskalować względne obrazy, aby miały spójną skalę intensywności. Optymalizacja skali intensywności ma kluczowe znaczenie, ponieważ względna intensywność pików jest kluczową informacją, na podstawie której określana jest struktura. Powtarzalna technika zbierania danych krystalograficznych oraz często wysoka symetria materiałów krystalicznych powodują, że dyfraktometr wielokrotnie rejestruje wiele symetrii równoważnych odbić. współczynnik R związany z symetrią , wskaźnik niezawodności oparty na tym, jak podobne są zmierzone intensywności odbić równoważnych symetrii, oceniając w ten sposób jakość danych.

Wstępne fazowanie

Dalsze informacje: Problem z fazą

Dane zebrane z eksperymentu dyfrakcyjnego to odwrotna przestrzenna reprezentacja sieci krystalicznej. Położenie każdego „plamki” dyfrakcyjnej zależy od rozmiaru i kształtu komórki elementarnej oraz naturalnej symetrii w krysztale. Rejestruje się intensywność każdego „plamki” dyfrakcyjnej, a intensywność ta jest proporcjonalna do kwadratu amplitudy współczynnika struktury . Współczynnik struktury to liczba zespolona zawierająca informacje dotyczące zarówno amplitudy , jak i fazy fali . _ Aby uzyskać interpretowalną mapę gęstości elektronowej , należy znać zarówno amplitudę, jak i fazę (mapa gęstości elektronowej pozwala krystalografowi zbudować początkowy model cząsteczki). Fazy ​​nie można bezpośrednio zarejestrować podczas eksperymentu dyfrakcyjnego: jest to znane jako problem fazowy . Wstępne szacunki fazy można uzyskać na różne sposoby:

• Fazowanie ab initio lub metody bezpośrednie - jest to zwykle metoda z wyboru dla małych cząsteczek (<1000 atomów innych niż atomy wodoru) i była z powodzeniem stosowana do rozwiązywania problemów fazowych dla małych białek. Jeśli rozdzielczość danych jest lepsza niż 1,4 Å (140 pm ), bezpośrednie metody mogą być użyte do uzyskania informacji o fazie, wykorzystując znane zależności fazowe między pewnymi grupami odbić.
• Zastępowanie molekularne - jeśli znana jest powiązana struktura, można ją wykorzystać jako model wyszukiwania w zastępowaniu molekularnym w celu określenia orientacji i położenia cząsteczek w komórce elementarnej. Uzyskane w ten sposób fazy mogą być wykorzystane do generowania map gęstości elektronowej.
• Anomalne rozpraszanie promieniowania rentgenowskiego ( fazowanie MAD lub SAD ) - długość fali promieniowania rentgenowskiego może być skanowana poza krawędź absorpcji atomu, który zmienia rozpraszanie w znany sposób. Rejestrując pełne zestawy odbić przy trzech różnych długościach fal (znacznie poniżej, daleko powyżej i pośrodku krawędzi absorpcji) można znaleźć podstrukturę anomalnie dyfrakcyjnych atomów, a tym samym strukturę całej cząsteczki. Najpopularniejszą metodą włączania anomalnych atomów rozpraszających do białek jest ekspresja białka w metioninie auksotrof (gospodarz niezdolny do syntezy metioniny) w pożywce bogatej w seleno-metioninę, która zawiera atomy selenu . Eksperyment z anomalną dyspersją na wielu długościach fal (MAD) można następnie przeprowadzić wokół krawędzi absorpcji, co powinno następnie ujawnić pozycję dowolnych reszt metioniny w białku, zapewniając fazy początkowe.
• Metody ciężkich atomów ( wielokrotne zastępowanie izomorficzne ) - Jeśli do kryształu można wprowadzić atomy metali o dużej gęstości elektronów, do określenia ich położenia i uzyskania faz początkowych można zastosować metody bezpośrednie lub metody w przestrzeni Pattersona . Takie ciężkie atomy można wprowadzić albo przez zanurzenie kryształu w roztworze zawierającym ciężkie atomy, albo przez współkrystalizację (hodowanie kryształów w obecności ciężkiego atomu). Podobnie jak w przypadku fazowania anomalnej dyspersji o wielu długościach fal, zmiany amplitud rozpraszania można interpretować w celu uzyskania faz. Chociaż jest to oryginalna metoda rozwiązywania struktur krystalicznych białek, została ona w dużej mierze zastąpiona przez anomalne fazowanie dyspersji o wielu długościach fal z selenometioniną.

Budowa modelu i udoskonalanie faz

Struktura helisy alfa białka, z rysunkami wiązania kowalencyjnego w obrębie gęstości elektronowej dla struktury krystalicznej w ultrawysokiej rozdzielczości (0,91 Å). Kontury gęstości są zaznaczone na szaro, szkielet helisy na biało, łańcuchy boczne na cyjan, atomy O na czerwono, atomy N na niebiesko, a wiązania wodorowe jako zielone kropkowane linie.

Przedstawienie 3D gęstości elektronowej (niebieski) ligandu (pomarańczowy) związanego z miejscem wiązania w białku (żółty). Gęstość elektronową uzyskuje się z danych eksperymentalnych, a ligand modeluje się w tej gęstości elektronowej.

Dalsze informacje: Modelowanie molekularne

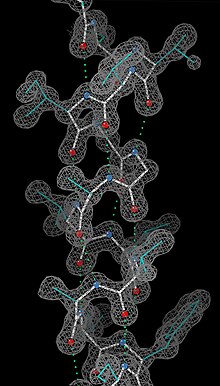
Po uzyskaniu wstępnych faz można zbudować wstępny model. Pozycje atomów w modelu i odpowiadające im współczynniki Debye'a-Wallera (lub współczynniki B , uwzględniające ruch termiczny atomu) można udoskonalić, aby pasowały do ​​​​obserwowanych danych dyfrakcyjnych, w idealnym przypadku uzyskując lepszy zestaw faz. Nowy model można następnie dopasować do nowej mapy gęstości elektronowej i przeprowadzane są kolejne rundy udoskonalania. Ten iteracyjny proces trwa do momentu maksymalizacji korelacji między danymi dyfrakcyjnymi a modelem. Zgodę mierzy się współczynnikiem R zdefiniowanym jako

$\ Displaystyle R = {\ Frac {\ suma _ {\ tekst {wszystkie odbicia}} \ lewo | F _ {\ tekst {obs}} -F _ {\ tekst {oblicz}} \ prawo |} {\ suma _ { \text{wszystkie odbicia}}\left|F_{\text{obs}}\right|}},}$

gdzie F jest współczynnikiem struktury . Podobnym kryterium jakości jest R _free , które jest obliczane z podzbioru (~10%) odbić, które nie zostały uwzględnione w udoskonalaniu struktury. Oba R zależą od rozdzielczości danych. Z reguły R _free powinno być w przybliżeniu rozdzielczością w angstremach podzieloną przez 10; w związku z tym zestaw danych o rozdzielczości 2 Å powinien dawać końcowe _wolne R ~ 0,2. Cechy wiązań chemicznych, takie jak stereochemia, wiązania wodorowe oraz rozkład długości i kątów wiązań, są uzupełniającymi miarami jakości modelu. Odchylenie fazowe jest poważnym problemem w takim iteracyjnym budowaniu modelu. Mapy pomijania są powszechną techniką stosowaną do sprawdzania tego.

Obserwacja każdego atomu w jednostce asymetrycznej może nie być możliwa. W wielu przypadkach zaburzenie krystalograficzne zamazuje mapę gęstości elektronowej. Słabo rozpraszające atomy, takie jak wodór, są rutynowo niewidoczne. Możliwe jest również wielokrotne pojawienie się pojedynczego atomu na mapie gęstości elektronowej, np. jeśli łańcuch boczny białka ma wiele (<4) dozwolonych konformacji. W jeszcze innych przypadkach krystalograf może wykryć, że wydedukowana struktura kowalencyjna cząsteczki była niepoprawna lub zmieniona. Na przykład białka mogą być rozszczepiane lub podlegać modyfikacjom potranslacyjnym, których nie wykryto przed krystalizacją.

Nieład

Główny artykuł: zaburzenie krystalograficzne

Częstym wyzwaniem w udoskonalaniu struktur krystalicznych jest nieład krystalograficzny. Zaburzenie może przybierać różne formy, ale generalnie obejmuje współistnienie dwóch lub więcej gatunków lub konformacji. Nierozpoznanie zaburzenia skutkuje błędną interpretacją. Pułapki wynikające z niewłaściwego modelowania nieporządku ilustruje zdyskontowana hipoteza izomerii rozciągania wiązań . Zaburzenie jest modelowane w odniesieniu do względnej populacji składników, często tylko dwóch, oraz ich tożsamości. W strukturach dużych cząsteczek i jonów rozpuszczalnik i przeciwjony są często nieuporządkowane.

Stosowana obliczeniowa analiza danych

Wykorzystanie metod obliczeniowych do analizy danych proszkowej dyfrakcji rentgenowskiej jest obecnie uogólnione. Zwykle porównuje dane eksperymentalne z symulowanym dyfraktogramem struktury modelu, biorąc pod uwagę parametry instrumentalne, i udoskonala parametry strukturalne lub mikrostrukturalne modelu za pomocą algorytmu minimalizacji opartego na najmniejszych kwadratach . Większość dostępnych narzędzi pozwalających na identyfikację faz i udoskonalenie struktury bazuje na metodzie Rietvelda , niektóre z nich to otwarte i darmowe oprogramowanie, takie jak FullProf Suite, Jana2006, MAUD, Rietan, GSAS itp., podczas gdy inne są dostępne na licencji komercyjnej, takie jak Diffrac.Suite TOPAS, Match! itp. Większość z tych narzędzi umożliwia również Kaucja udoskonalanie (określane również jako dopasowywanie profili), to jest udoskonalanie parametrów komórki na podstawie pozycji pików Bragga i profili pików, bez uwzględniania samej struktury krystalograficznej. Nowsze narzędzia pozwalają na udoskonalanie zarówno danych strukturalnych, jak i mikrostrukturalnych, takie jak program FAULTS zawarty w pakiecie FullProf Suite, który umożliwia udoskonalanie struktur z defektami powierzchniowymi (np. uskoki piętrowe, bliźniacze, przerosty).

Osadzanie struktury

Po sfinalizowaniu modelu struktury cząsteczki jest on często umieszczany w krystalograficznej bazie danych , takiej jak Cambridge Structural Database (dla małych cząsteczek), Inorganic Crystal Structure Database (ICSD) (dla związków nieorganicznych) lub Protein Data Bank ( dla białka i czasami kwasów nukleinowych). Wiele struktur uzyskanych w prywatnych przedsięwzięciach komercyjnych w celu krystalizacji białek o znaczeniu medycznym nie jest zdeponowanych w publicznych krystalograficznych bazach danych.

Teoria dyfrakcji

Dalsze informacje: Dynamiczna teoria dyfrakcji i dyfrakcja Bragga

Głównym celem krystalografii rentgenowskiej jest określenie gęstości elektronów f ( r ) w całym krysztale, gdzie r reprezentuje trójwymiarowy wektor położenia w krysztale. W tym celu wykorzystuje się rozpraszanie promieniowania rentgenowskiego do zebrania danych o jego transformacie Fouriera F ( q ), która jest matematycznie odwrócona w celu uzyskania gęstości określonej w przestrzeni rzeczywistej za pomocą wzoru

$\ Displaystyle f (\ mathbf {r}) = {\ Frac {1} {\ lewo (2 \ pi \ dobrze)^{3}}}\int F(\mathbf {q} )e^{\mathrm {i} \mathbf {q} \cdot \mathbf {r} }\mathrm {d} \mathbf {q} , }$

gdzie całka jest przejmowana przez wszystkie wartości q . Trójwymiarowy wektor rzeczywisty q reprezentuje punkt w przestrzeni odwrotności , to znaczy określoną oscylację gęstości elektronowej, gdy porusza się w kierunku, w którym q wskazuje. Długość q odpowiada $oscylacji$ przez długość fali Odpowiedni wzór na transformatę Fouriera zostanie użyty poniżej

${\ Displaystyle F (\ mathbf {q}) = \ int f (\ mathbf {r}) \ operatorname {e} ^ {- \ mathrm {i} \mathbf {q} \cdot \mathbf {r} }\mathrm {d} \mathbf {r} ,}$

gdzie całka jest sumowana po wszystkich możliwych wartościach wektora pozycji r w krysztale.

Transformata Fouriera F ( q ) jest na ogół liczbą zespoloną , a zatem ma wielkość | fa ( q )| oraz faza φ ( q ) powiązana równaniem

${\ Displaystyle F (\ mathbf {q}) = \ lewo | F (\ mathbf {q}) \ prawo | \ operatorname {e} ^ {\ operatorname {i} \ phi (\ mathbf {q})}.}$

Intensywności odbić obserwowane w dyfrakcji rentgenowskiej dają nam wielkości | fa ( q )| ale nie fazy φ ( q ). Aby uzyskać fazy, zbiera się pełne zestawy odbić ze znanymi zmianami rozpraszania, albo przez modulację długości fali poza określoną krawędź absorpcji, albo przez dodanie silnie rozpraszających (tj. o dużej gęstości elektronowej) atomów metali, takich jak rtęć . Połączenie wielkości i faz daje pełną transformatę Fouriera F ( q ), którą można odwrócić, aby uzyskać gęstość elektronową f ( r ).

Kryształy są często idealizowane jako doskonale okresowe. W tym idealnym przypadku atomy są rozmieszczone na idealnej siatce, gęstość elektronów jest doskonale okresowa, a transformata Fouriera F ( q ) wynosi zero, z wyjątkiem sytuacji, gdy q należy do sieci odwrotnej (tzw. szczyty Bragga ). W rzeczywistości jednak kryształy nie są idealnie okresowe; atomy wibrują wokół swojego średniego położenia i mogą występować różnego rodzaju zaburzenia, takie jak mozaikowość , dyslokacje , różne defekty punktowe oraz niejednorodność konformacji skrystalizowanych cząsteczek. Dlatego piki Bragga mają skończoną szerokość i może występować znaczne rozpraszanie rozproszone , kontinuum rozproszonych promieni rentgenowskich, które spadają między pikami Bragga.

Intuicyjne rozumienie według prawa Bragga

Intuicyjne zrozumienie dyfrakcji rentgenowskiej można uzyskać z modelu dyfrakcji Bragga . W tym modelu dane odbicie jest związane z zestawem równomiernie rozmieszczonych arkuszy przebiegających przez kryształ, zwykle przechodzących przez środki atomów sieci krystalicznej. Orientacja określonego zestawu arkuszy jest identyfikowana przez jego trzy wskaźniki Millera ( h , k , l ), ​​a ich odstępy niech będą odnotowane przez d . William Lawrence Bragg zaproponował model, w którym nadchodzące promienie rentgenowskie są rozpraszane lustrzanie (podobnie jak lustro) z każdej płaszczyzny; z tego założenia promienie rentgenowskie rozproszone z sąsiednich płaszczyzn będą się konstruktywnie łączyć ( konstruktywna interferencja ), gdy kąt θ między płaszczyzną a promieniowaniem rentgenowskim spowoduje różnicę długości dróg, która jest całkowitą wielokrotnością n długości fali promieniowania rentgenowskiego λ .

${\ Displaystyle 2d \ sin \ teta = n \ lambda.}$

Mówi się, że odbicie jest indeksowane , gdy jego wskaźniki Millera (lub dokładniej jego odwrotne składowe wektora sieci ) zostały zidentyfikowane na podstawie znanej długości fali i kąta rozpraszania 2θ. Takie indeksowanie daje parametry komórki elementarnej , długości i kąty komórki elementarnej, a także jej grupę przestrzenną . Ponieważ jednak prawo Bragga nie interpretuje względnych natężeń odbić, generalnie jest niewystarczające do rozwiązania rozmieszczenia atomów w komórce elementarnej; w tym celu należy przeprowadzić metodę transformaty Fouriera.

Rozpraszanie jako transformata Fouriera

Nadchodząca wiązka promieniowania rentgenowskiego ma polaryzację i powinna być reprezentowana jako fala wektorowa; jednakże, dla uproszczenia, przedstawmy ją tutaj jako falę skalarną. Ignorujemy również komplikację zależności fali od czasu i koncentrujemy się tylko na zależności przestrzennej fali. Fale płaskie można przedstawić za pomocą wektora falowego k _w , więc siła fali nadchodzącej w czasie t = 0 jest wyrażona wzorem

${\ Displaystyle A \ operatorname {e} ^ {\ operatorname {i} \ mathbf {k} _ {\ operatorname {w}} \ cdot \ mathbf {r}}.}$

W pozycji r w próbce niech będzie gęstość rozpraszaczy f ( r ); rozpraszacze te powinny wytwarzać rozproszoną falę sferyczną o amplitudzie proporcjonalnej do lokalnej amplitudy fali nadchodzącej pomnożonej przez liczbę rozpraszaczy w małej objętości dV około r

${\ Displaystyle {\ tekst {amplituda fali rozproszonej}} = A \ operatorname {e} ^ {\ operatorname {i} \ mathbf {k } \cdot \mathbf {r} }Sf(\mathbf {r} )\mathrm {d} V,}$

gdzie S jest stałą proporcjonalności.

Rozważ ułamek rozproszonych fal, które opuszczają wychodzący wektor falowy k _{na zewnątrz} i uderzają w ekran w punkcie r _ekran . Ponieważ energia nie jest tracona (rozpraszanie sprężyste, a nie nieelastyczne), długości fal są takie same, jak wielkości wektorów falowych | k _w |=| k _out |. Od czasu rozproszenia fotonu na r aż do pochłonięcia na _ekranie r foton przechodzi zmianę fazy

${\ Displaystyle e ^ {i \ mathbf {k} _ {\ tekst {na zewnątrz}} \ cdot \ lewo (\ mathbf {r} _ {\ tekst {ekran}} - \ mathbf {r} \ po prawej)}.}$

Promieniowanie netto docierające do _ekranu r jest sumą wszystkich fal rozproszonych w krysztale

${\ Displaystyle AS \ int \ operatorname {d} \ mathbf {r} f (\ mathbf {r}) \ operatorname {e} ^ {\ operatorname {i} \ mathbf {k} _ {\ tekst {w }}\cdot \mathbf {r} }e^{i\mathbf {k} _{\text{out}}\cdot \left(\mathbf {r} _{\text{ekran}}-\mathbf {r } \right)}=ASe^{i\mathbf {k} _{\text{out}}\cdot \mathbf {r} _{\text{screen}}}\int \mathrm {d} \mathbf {r } f(\mathbf {r} )\mathrm {e} ^{\mathrm {i} \left(\mathbf {k} _{\text{in}}-\mathbf {k} _{\text{out} }\right)\cdot \mathbf {r} },}$

co można zapisać jako transformatę Fouriera

${\ Displaystyle AS \ operatorname {e} ^ {\ operatorname {i} \ mathbf {k} _ {\ tekst {na zewnątrz}} \ cdot \ mathbf {r} _ {\ tekst {ekran}}} \ int d \ mathbf {r} f(\mathbf {r})\mathrm {e} ^{-\mathrm {i} \mathbf {q} \cdot \mathbf {r} }=AS\mathrm {e} ^{\mathrm {i } \mathbf {k} _{\text{out}}\cdot \mathbf {r} _{\text{screen}}}F(\mathbf {q}),}$

gdzie q = k _{na zewnątrz} – k _w . Zmierzona intensywność odbicia będzie kwadratem tej amplitudy

${\ Displaystyle A ^ {2} S ^ {2} \ lewo | F (\ mathbf {q}) \ prawo | ^ {2}.}$

Koleżanki Friedel i Bijvoet

Każdemu odbiciu odpowiadającemu punktowi q w przestrzeni odwrotności odpowiada inne odbicie o takim samym natężeniu w przeciwległym punkcie - q . To przeciwne odbicie jest znane jako mate Friedla pierwotnego odbicia. Ta symetria wynika z matematycznego faktu, że gęstość elektronów f ( r ) w pozycji r jest zawsze liczbą rzeczywistą . Jak wspomniano powyżej, f ( r ) jest odwrotną transformatą swojej transformaty Fouriera F ( q ); jednak taka odwrotna transformata jest ogólnie liczbą zespoloną . Aby upewnić się, że f ( r ) jest rzeczywista, transformata Fouriera F ( q ) musi być taka, że ​​wiązania Friedla F (− q ) i F ( q ) są wzajemnie złożonymi koniugatami . Zatem F (− q ) ma taką samą wielkość jak F ( q ), ale fazę przeciwną, tj. φ ( q ) = − φ ( -q )

${\ Displaystyle F (- \ mathbf {q}) = \ lewo | F (- \ mathbf {q}) \ prawo | \ operatorname {e} ^ {\ operatorname {i} \ phi (- \ mathbf {q}) }=F^{*}(\mathbf {q} )=\left|F(\mathbf {q} )\right|\mathrm {e} ^{-\mathrm {i} \phi (\mathbf {q} )}.}$

Równość ich wielkości zapewnia, że ​​mate Friedla mają taką samą intensywność | F. | ² . Ta symetria pozwala zmierzyć pełną transformatę Fouriera tylko z połowy przestrzeni odwrotności, np. obracając kryształ o nieco więcej niż 180° zamiast pełnego obrotu o 360°. W kryształach o znacznej symetrii nawet więcej odbić może mieć tę samą intensywność (maty Bijvoet); w takich przypadkach może być konieczne zmierzenie nawet mniejszej odwrotnej przestrzeni. W sprzyjających przypadkach wysokiej symetrii, czasami potrzeba tylko 90° lub nawet 45° danych, aby całkowicie zbadać odwrotność przestrzeni.

Ograniczenie Friedela-Mate'a można wyprowadzić z definicji odwrotnej transformaty Fouriera

${\ Displaystyle f (\ mathbf {r}) = \ int {\ Frac {d \ mathbf {q}}} {\ lewo (2 \ pi \ po prawej) ^ {3}}} F (\ mathbf {q}) \ mathrm {e} ^{\mathrm {i} \mathbf {q} \cdot \mathbf {r} }=\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{ 3}}}\left|F(\mathbf {q} )\right|\mathrm {e} ^{\mathrm {i} \phi (\mathbf {q} )}\mathrm {e} ^{\mathrm { i} \mathbf {q} \cdot \mathbf {r} }.}$

Ponieważ wzór Eulera stwierdza, że ​​e ^{i x} = cos( x ) + i sin( x ), odwrotną transformatę Fouriera można podzielić na sumę części czysto rzeczywistej i części czysto urojonej

${\ Displaystyle f (\ mathbf {r}) = \ int {\ Frac {d \ mathbf {q}}} {\ lewo (2 \ pi \ prawo) ^ {3}}} \ lewo | F (\ mathbf {q } )\right|\mathrm {e} ^{\mathrm {i} \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)}=\int {\frac {d\mathbf { q} }{\left(2\pi \right)^{3}}}\left|F(\mathbf {q} )\right|\cos \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)+i\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{3}}}\left|F(\mathbf {q} )\right |\sin \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)=I_{\mathrm {cos} }+iI_{\mathrm {sin} }.}$

Funkcja f ( r ) jest rzeczywista wtedy i tylko wtedy , gdy druga całka I _sin wynosi zero dla wszystkich wartości r . To z kolei jest prawdziwe wtedy i tylko wtedy, gdy powyższe ograniczenie jest spełnione

${\ Displaystyle I _ {\ sin} = \ int {\ Frac {d \ mathbf {q}}} {\ lewo (2 \ pi \ prawo) ^ {3}}} \ lewo | F (\ mathbf { q} )\right|\sin \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)=\int {\frac {d\mathbf {q}}}{\left(2\pi \right)^{3}}}\left|F(\mathbf {-q} )\right|\sin \left(-\phi -\mathbf {q} \cdot \mathbf {r} \right)=- Jest w },}$

skoro ja _grzeszę = − ja _grzech implikuje, że ja _grzeszę = 0.

Kula Ewalda

Dalsze informacje: Kula Ewalda

Reprezentacja konstrukcji Ewalda przedstawiająca incydent ( ${\ displaystyle {\ overrightarrow {k_ {b}}}}}$ , rozproszony ( ${\ displaystyle {\ overrightarrow {k_ {b} '}}}$ ) i wypadkowy wektor falowy ( ${\ displaystyle {\ overrightarrow {\ Delta k}}})$ . Ponieważ istnieje wypadkowy wektor falowy generowany między dwoma odwrotnymi punktami sieci, dyfrakcja będzie dozwolona, ​​ponieważ wynikowy wektor falowy będzie spełniał warunki „odwrotnego wektora sieci”.

Każdy obraz dyfrakcji rentgenowskiej reprezentuje tylko wycinek, sferyczny wycinek odwrotnej przestrzeni, jak widać na podstawie konstrukcji kuli Ewalda. Zarówno k _out, jak i k _in mają tę samą długość ze względu na elastyczne rozpraszanie, ponieważ długość fali nie uległa zmianie. Dlatego można je przedstawić jako dwa wektory promieniowe w kuli w przestrzeni odwrotności , która pokazuje wartości q próbkowane na danym obrazie dyfrakcyjnym. Ponieważ w przychodzących długościach fal nadchodzącej wiązki promieniowania rentgenowskiego występuje niewielka rozpiętość, wartości | F ( q )|można zmierzyć tylko dla wektorów q znajdujących się między dwiema sferami odpowiadającymi tym promieniom. Dlatego, aby uzyskać pełny zestaw danych z transformaty Fouriera, konieczne jest obrócenie kryształu o nieco więcej niż 180 °, a czasem mniej, jeśli występuje wystarczająca symetria. Pełny obrót o 360 ° nie jest potrzebny ze względu na symetrię właściwą transformatom Fouriera funkcji rzeczywistych (takich jak gęstość elektronów), ale „nieco więcej” niż 180 ° jest potrzebne do pokrycia całej odwrotnej przestrzeni w danej rozdzielczości z powodu krzywizna sfery Ewalda . W praktyce kryształ jest kołysany o niewielką wartość (0,25–1 °), aby uwzględnić odbicia w pobliżu granic kulistych powłok Ewalda.

Funkcja Pattersona

Dalsze informacje: funkcja Pattersona

Dobrze znanym wynikiem transformacji Fouriera jest twierdzenie o autokorelacji , które stwierdza, że ​​autokorelacja c ( r ) funkcji f ( r )

${\ Displaystyle c (\ mathbf {r}) = \ int d\mathbf {x} f(\mathbf {x})f(\mathbf {x} +\mathbf {r})=\int {\frac {d\mathbf {q}}}{\left(2\pi \ dobrze)^{3}}}C(\mathbf {q} )e^{i\mathbf {q} \cdot \mathbf {r} }}$

ma transformatę Fouriera C ( q ), która jest kwadratem wielkości F ( q )

${\ Displaystyle C (\ mathbf {q}) = \ lewo | F (\ mathbf {q}) \ prawo | ^ {2}.}$

Dlatego funkcję autokorelacji c ( r ) gęstości elektronowej (znaną również jako funkcja Pattersona ) można obliczyć bezpośrednio z intensywności odbicia, bez obliczania faz. Zasadniczo można to wykorzystać do bezpośredniego określenia struktury kryształu; jednak w praktyce jest to trudne do zrealizowania. Funkcja autokorelacji odpowiada rozkładowi wektorów między atomami w krysztale; zatem kryształ o N w swojej komórce elementarnej może mieć N ( N − 1) piki w swojej funkcji Pattersona. Biorąc pod uwagę nieuniknione błędy w pomiarze intensywności i matematyczne trudności w odtwarzaniu pozycji atomów z wektorów międzyatomowych, technika ta jest rzadko używana do rozwiązywania struktur, z wyjątkiem najprostszych kryształów.

Zalety kryształu

Zasadniczo strukturę atomową można określić, stosując rozpraszanie promieniowania rentgenowskiego na próbkach niekrystalicznych, nawet na pojedynczej cząsteczce. Jednak kryształy oferują znacznie silniejszy sygnał ze względu na ich okresowość. Próbka krystaliczna jest z definicji okresowa; kryształ składa się z wielu komórek elementarnych powtarzających się w nieskończoność w trzech niezależnych kierunkach. Takie układy okresowe mają transformatę Fouriera , która jest skoncentrowana w okresowo powtarzających się punktach w odwrotnej przestrzeni, znanych jako piki Bragga ; piki Bragga odpowiadają plamom odbicia obserwowanym na obrazie dyfrakcyjnym. Ponieważ amplituda przy tych odbiciach rośnie liniowo wraz z liczbą N rozpraszaczy, obserwowana intensywność tych plam powinna rosnąć kwadratowo, podobnie jak N ² . Innymi słowy, użycie kryształu skupia słabe rozproszenie poszczególnych komórek elementarnych w znacznie silniejszym, spójnym odbiciu, które można zaobserwować ponad szumem. To jest przykład konstruktywnej ingerencji .

W cieczy, proszku lub amorficznej próbce cząsteczki w tej próbce są w przypadkowych orientacjach. Takie próbki mają ciągłe widmo Fouriera, które równomiernie rozkłada swoją amplitudę, zmniejszając w ten sposób intensywność mierzonego sygnału, co obserwuje się w SAXS . Co ważniejsze, informacje orientacyjne są tracone. Chociaż teoretycznie jest to możliwe, eksperymentalnie trudno jest uzyskać struktury skomplikowanych, asymetrycznych cząsteczek o rozdzielczości atomowej z takich uśrednionych rotacyjnie danych. Przypadek pośredni to dyfrakcja włókien , w której podjednostki są ułożone okresowo w co najmniej jednym wymiarze.

Nagrody Nobla w dziedzinie krystalografii rentgenowskiej

Rok	Laureat	Nagroda	Racjonalne uzasadnienie
1914	Maxa von Laue	Fizyka	„Za odkrycie dyfrakcji promieni rentgenowskich przez kryształy”, ważny krok w rozwoju spektroskopii rentgenowskiej .
1915	Williama Henry'ego Bragga	Fizyka	„Za zasługi w analizie struktury krystalicznej za pomocą promieni rentgenowskich”
	Williama Lawrence'a Bragga
1962	Maks F. Perutz	Chemia	„za badania struktur białek globularnych ”
	Johna C. Kendrew
1962	Jamesa Deweya Watsona	Medycyna	„Za odkrycia dotyczące struktury molekularnej kwasów nukleinowych i jej znaczenia dla przekazywania informacji w żywym materiale”
	Francis Harry Compton Crick
	Maurice Hugh Frederick Wilkins
1964	Dorota Hodgkin	Chemia	„Za jej oznaczanie technikami rentgenowskimi struktur ważnych substancji biochemicznych”
1972	Stanforda Moore'a	Chemia	„Za wkład w zrozumienie związku między budową chemiczną a aktywnością katalityczną centrum aktywnego cząsteczki rybonukleazy ”
	Williama H. ​​Steina
1976	Williama N. Lipscomba	Chemia	„Za badania nad strukturą boranów , rzucające światło na problemy wiązań chemicznych”
1985	Hieronim Karol	Chemia	„Za wybitne osiągnięcia w opracowaniu bezpośrednich metod wyznaczania struktur krystalicznych”
	Herberta A. Hauptmana
1988	Johanna Deisenhofera	Chemia	„Za określenie trójwymiarowej struktury fotosyntetycznego centrum reakcji ”
	Hartmuta Michela	Chemia
	Roberta Hubera	Chemia
1997	Johna E. Walkera	Chemia	„Za ich wyjaśnienie mechanizmu enzymatycznego leżącego u podstaw syntezy trifosforanu adenozyny (ATP)”
2003	Rodericka MacKinnona	Chemia	„Za odkrycia dotyczące kanałów w błonach komórkowych [...] do badań strukturalnych i mechanistycznych kanałów jonowych ”
	Piotr Agre		„Za odkrycia dotyczące kanałów w błonach komórkowych [...] za odkrycie kanałów wodnych ”
2006	Rogera D. Kornberga	Chemia	„Za badania nad molekularnymi podstawami transkrypcji eukariotycznej ”
2009	Ada E. Yonath	Chemia	„Do badań struktury i funkcji rybosomu ”
	Thomas A. Steitz
	Venkatraman Ramakrishnan
2012	Brian Kobilka	Chemia	„Do badań receptorów sprzężonych z białkiem G ”

Aplikacje

Dyfrakcja rentgenowska ma szerokie i różnorodne zastosowanie w naukach chemicznych, biochemicznych, fizycznych, materiałowych i mineralogicznych. Laue stwierdził w 1937 r., Że technika „rozszerzyła moc obserwowania drobnych struktur dziesięć tysięcy razy poza tę, którą daje nam mikroskop”. Dyfrakcja rentgenowska jest analogiczna do mikroskopu z rozdzielczością na poziomie atomowym, który pokazuje atomy i ich rozkład elektronów.

Dyfrakcja rentgenowska, dyfrakcja elektronów i dyfrakcja neutronów dostarczają informacji o strukturze materii, krystalicznej i niekrystalicznej, na poziomie atomowym i molekularnym. Ponadto metody te mogą znaleźć zastosowanie w badaniach właściwości wszystkich materiałów, zarówno nieorganicznych, organicznych, jak i biologicznych. Ze względu na znaczenie i różnorodność zastosowań badań dyfrakcyjnych kryształów przyznano za nie wiele Nagród Nobla.

Identyfikacja narkotyków

Dyfrakcja rentgenowska została wykorzystana do identyfikacji antybiotyków, takich jak: osiem β-laktamów ( ampicylina sodowa , penicylina G prokaina , cefaleksyna , trihydrat ampicyliny , penicylina benzatynowa , benzylopenicylina sodowa , cefotaksym sodowy , ceftriakson sodowy ), trzy tetracykliny ( doksycyklina chlorowodorek , odwodniona oksytetracykliny , chlorowodorek tetracykliny ) i dwa makrolidy ( azytromycyna , estolan erytromycyny ) antybiotyki. Każdy z tych leków ma unikalny wzór dyfrakcji rentgenowskiej (XRD), który umożliwia ich identyfikację.

Charakterystyka nanomateriałów, włókien tekstylnych i polimerów

Badanie kryminalistyczne wszelkich dowodów śladowych opiera się na zasadzie wymiany Locarda . Stwierdza to, że „każdy kontakt pozostawia ślad”. W praktyce, nawet jeśli doszło do przeniesienia materiału, może to być niemożliwe do wykrycia, ponieważ przeniesiona ilość jest bardzo mała.

XRD udowodnił swoją rolę w rozwoju badań nad nanomateriałami. Jest to jedno z podstawowych narzędzi do charakteryzacji i dostarcza informacji o właściwościach strukturalnych różnych nanomateriałów zarówno w postaci proszku, jak i cienkowarstwowej.

Włókna tekstylne są mieszaniną substancji krystalicznych i amorficznych. Dlatego pomiar stopnia krystaliczności dostarcza użytecznych danych w charakterystyce włókien za pomocą dyfraktometrii rentgenowskiej. Donoszono, że dyfrakcja rentgenowska została wykorzystana do zidentyfikowania „krystalicznego” osadu znalezionego na krześle. Stwierdzono, że osad był amorficzny, ale obecny wzór dyfrakcyjny pasował do polimetakrylanu metylu. Pirolityczna spektrometria masowa zidentyfikowała później osad jako polimetylocyjanoakrylan o parametrach kryształu Boina.

Obwody scalone

Zademonstrowano dyfrakcję rentgenowską jako metodę badania złożonej struktury układów scalonych .

Zobacz też

• Pasek Beeversa-Lipsona
• Dyfrakcja Bragga
• Krystalograficzna baza danych
• Grupy punktów krystalograficznych
• Mapa gęstości różnic
• Dyfrakcja elektronów
• Dyfrakcja promieniowania rentgenowskiego z dyspersją energii
• Parametr Flacka
• granica Hendersona
• Międzynarodowy Rok Krystalografii
• Johna Desmonda Bernala
• Formalizm gęstości wielobiegunowej
• Dyfrakcja neutronów
• Dyfrakcja proszkowa
• Ptychografia
• Równanie Scherrera
• Rozpraszanie promieni rentgenowskich pod małymi kątami (SAXS)
• Określenie struktury
• Ultraszybki rentgen
• Szerokokątne rozpraszanie promieniowania rentgenowskiego (WAXS)

Dalsza lektura

Międzynarodowe Tabele Krystalografii

•   Hahn T, wyd. (2002). Międzynarodowe Tabele Krystalografii. Tom A, Symetria grupy przestrzennej (wyd. 5). Dordrecht: Kluwer Academic Publishers dla Międzynarodowej Unii Krystalografii . ISBN 0-7923-6590-9 .
•   Rossmann MG, Arnold E, wyd. (2001). Międzynarodowe Tabele Krystalografii. Tom F, Krystalografia cząsteczek biologicznych . Dordrecht: Kluwer Academic Publishers dla Międzynarodowej Unii Krystalografii. ISBN 0-7923-6857-6 .
•   Hahn T, wyd. (1996). Międzynarodowe Tabele Krystalografii. Krótkie wydanie dydaktyczne tomu A, Symetria grup przestrzennych (wyd. 4). Dordrecht: Kluwer Academic Publishers dla Międzynarodowej Unii Krystalografii. ISBN 0-7923-4252-6 .

Oprawione zbiory artykułów

•   Carter Jr CW, Sweet RM, wyd. (1997). Krystalografia makrocząsteczkowa, część A (Metody w enzymologii, w. 276) . San Diego: prasa akademicka. ISBN 0-12-182177-3 .
•   Carter Jr CW, Sweet RM, wyd. (1997). Krystalografia makrocząsteczkowa, część B (Metody w enzymologii, w. 277) . San Diego: prasa akademicka. ISBN 0-12-182178-1 .
•   Ducruix A, Giegé R, wyd. (1999). Krystalizacja kwasów nukleinowych i białek: podejście praktyczne (wyd. 2). Oksford: Oxford University Press. ISBN 0-19-963678-8 .

Podręczniki

•   Birkholz M, Fewster PF, Genzel C (2005). „Rozdział 1: Zasady_dyfrakcji_rentgenowskiej” . Analiza cienkich warstw metodą rozpraszania promieni rentgenowskich . Weinheim: Wiley-VCH. ISBN 978-3-527-31052-4 .
•   Cios D (2002). Zarys krystalografii dla biologów . Oksford: Oxford University Press. ISBN 0-19-851051-9 .
•   Burns G, Glazer AM (1990). Grupy kosmiczne dla naukowców i inżynierów (wyd. 2). Boston: Academic Press, Inc. ISBN 0-12-145761-3 .
•   Clegg W (1998). Oznaczanie struktury kryształu (Oxford Chemistry Primer) . Oksford: Oxford University Press. ISBN 0-19-855901-1 .
•   Cullity BD (1978). Elementy dyfrakcji rentgenowskiej (wyd. 2). Reading, Massachusetts: Addison-Wesley Publishing Company. ISBN 0-534-55396-6 .
•   Drenth J. (1999). Zasady krystalografii rentgenowskiej białek . Nowy Jork: Springer-Verlag. ISBN 0-387-98587-5 .
•   Giacovazzo C (1992). Podstawy krystalografii . Oksford: Oxford University Press. ISBN 0-19-855578-4 .
•   Glusker JP, Lewis M, Rossi M (1994). Analiza struktury krystalicznej dla chemików i biologów . Nowy Jork: Wydawcy VCH. ISBN 0-471-18543-4 .
•   Massa W (2004). Określenie struktury kryształu . Berlin: Springer. ISBN 3-540-20644-2 .
•   McPherson A (1999). Krystalizacja makrocząsteczek biologicznych . Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press. ISBN 0-87969-617-6 .
•   McPherson A (2003). Wprowadzenie do krystalografii makromolekularnej . John Wiley & Synowie. ISBN 0-471-25122-4 .
•   McRee DE (1993). Praktyczna krystalografia białek . San Diego: prasa akademicka. ISBN 0-12-486050-8 .
•   O'Keeffe M, Hyde BG (1996). struktury krystaliczne; I. Wzory i symetria . Waszyngton, DC: Mineralogiczne Towarzystwo Ameryki, seria monografii. ISBN 0-939950-40-5 .
•   Rodos G. (2000). Krystalografia stała się krystalicznie czysta . San Diego: prasa akademicka. ISBN 0-12-587072-8 . , kopia PDF wybranych rozdziałów
•   Rupp B (2009). Krystalografia biomolekularna: zasady, praktyka i zastosowanie w biologii strukturalnej . Nowy Jork: Garland Science. ISBN 978-0-8153-4081-2 .
•   Warren BE (1969). Dyfrakcja rentgenowska . Nowy Jork. ISBN 0-486-66317-5 .
•   Zachariasen WH (1945). Teoria dyfrakcji promieniowania rentgenowskiego w kryształach . Nowy Jork: Dover Publications. LCCN 67026967 .

Stosowana obliczeniowa analiza danych

•   Młody RA, wyd. (1993). Metoda Rietvelda . Oxford: Oxford University Press i Międzynarodowa Unia Krystalografii. ISBN 0-19-855577-6 .

Historyczny

• Bijvoet MJ , Burgers WG, Hägg G, wyd. (1969). Wczesne artykuły na temat dyfrakcji promieni rentgenowskich przez kryształy . Tom. I. Utrecht: opublikowane dla Międzynarodowej Unii Krystalografii przez A. Oosthoek's Uitgeversmaatschappij NV
• Bijvoet JM, Burgers WG, Hägg G, wyd. (1972). Wczesne artykuły na temat dyfrakcji promieni rentgenowskich przez kryształy . Tom. II. Utrecht: opublikowane dla Międzynarodowej Unii Krystalografii przez A. Oosthoek's Uitgeversmaatschappij NV
•   Bragg WL, Phillips DC, Lipson H (1992). Rozwój analizy rentgenowskiej . Nowy Jork: Dover. ISBN 0-486-67316-2 .
•   Ewald PP i in., wyd. (1962). Pięćdziesiąt lat dyfrakcji rentgenowskiej . Utrecht: opublikowane dla Międzynarodowej Unii Krystalografii przez A. Oosthoek's Uitgeversmaatschappij NV doi : 10.1007/978-1-4615-9961-6 . ISBN 978-1-4615-9963-0 .
• Ewald PP (red.). „50 lat dyfrakcji rentgenowskiej” . Międzynarodowa Unia Krystalografii. Przedruk w formacie pdf dla XVIII Kongresu IUCr, Glasgow, Szkocja
•   Friedrich W. (1922). „Die Geschichte der Auffindung der Röntgenstrahlinterferenzen” . Die Naturwissenschaften . 10 (16): 363. Bibcode : 1922NW.....10..363F . doi : 10.1007/BF01565289 . S2CID 28141506 .
• Lonsdale K. (1949). Kryształy i promieniowanie rentgenowskie . Nowy Jork: D. van Nostrand.

Linki zewnętrzne

Samouczki

• Nauka krystalografii
• Proste, nietechniczne wprowadzenie
• The Crystallography Collection , seria filmów z Royal Institution
• „Krystalizacja małych cząsteczek” ( PDF ) na stronie internetowej Illinois Institute of Technology
• Międzynarodowa Unia Krystalografii
• Krystalografia 101
• Interaktywny samouczek współczynnika struktury , demonstrujący właściwości obrazu dyfrakcyjnego kryształu 2D.
• Picturebook of Fourier Transforms , ilustrujący związek między kryształem a wzorem dyfrakcyjnym w 2D.
• Notatki z wykładów z krystalografii rentgenowskiej i wyznaczania struktury
• Wykład online na temat nowoczesnych metod rozpraszania promieniowania rentgenowskiego do analizy materiałów w nanoskali autorstwa Richarda J. Matyi
• Interaktywna oś czasu krystalografii zarchiwizowana 2021-06-30 w Wayback Machine z Royal Institution

Podstawowe bazy danych

• Otwarta baza danych krystalografii (COD)
• Bank Danych Białkowych ( PDB )
• Bank danych kwasów nukleinowych (NDB)
• Strukturalna baza danych Cambridge ( CSD )
• Baza danych nieorganicznych struktur krystalicznych ( ICSD )
• Biologiczna baza danych krystalizacji makrocząsteczek (BMCD)

Pochodne bazy danych

• Suma WPB
• Proteopedia – wspólna, trójwymiarowa encyklopedia białek i innych cząsteczek
• Baza RNA
• Baza danych HIC-Up ligandów PDB zarchiwizowana 2020-08-08 w Wayback Machine
• Klasyfikacja strukturalna bazy danych białek
• Klasyfikacja struktury białek CATH
• Lista białek transbłonowych o znanej strukturze 3D Zarchiwizowane 2011-04-11 w Wayback Machine
• Baza danych Orientacje białek w błonach

Walidacja strukturalna

• Pakiet do walidacji strukturalnej MolProbity
• Sieć ProSA
• NQ-Flipper (sprawdź niekorzystne rotamery reszt Asn i Gln)
• Serwer DALI (identyfikuje białka podobne do danego białka)