Liczba zespolona

Liczbę zespoloną można wizualnie przedstawić jako parę liczb ( a , b ) tworzących wektor na diagramie zwanym diagramem Arganda , reprezentującym płaszczyznę zespoloną . Re jest osią rzeczywistą, Im jest osią urojoną, a i jest „ jednostką urojoną ”, która spełnia i ² = −1 .

W matematyce liczba zespolona jest elementem systemu liczbowego , który rozszerza liczby rzeczywiste o określony element oznaczony ja , zwany jednostką urojoną i spełniający równanie ${\ Displaystyle i ^ {2} = -1}$ ; $b$ zespoloną można wyrazić w postaci , gdzie a i rzeczywistymi Ponieważ żadna liczba rzeczywista nie spełnia powyższego równania, René Descartes nazwał i liczbą urojoną . Dla liczby $rzeczywistą$ a nazywa się częścią , a b _ Zbiór liczb zespolonych $do$ oznaczony jednym z symboli lub . Pomimo historycznej nomenklatury „urojonej”, liczby zespolone są uważane w naukach matematycznych za równie „rzeczywiste” jak liczby rzeczywiste i mają fundamentalne znaczenie w wielu aspektach naukowego opisu świata przyrody.

Liczby zespolone umożliwiają rozwiązania wszystkich równań wielomianowych , nawet tych, które nie mają rozwiązań w liczbach rzeczywistych. Dokładniej, fundamentalne twierdzenie algebry stwierdza, że ​​każde niestałe równanie wielomianowe o rzeczywistych lub zespolonych współczynnikach ma rozwiązanie, które jest liczbą zespoloną. Na przykład równanie $dwa$ rzeczywistej nie może być ujemny, nierzeczywiste złożone rozwiązania ${\ Displaystyle -1 + 3i}$ i ${\ Displaystyle -1-3i}$ .

$w naturalny sposób$ za pomocą reguły połączonej z prawami asocjacji , przemienności i . Każda niezerowa liczba zespolona ma multiplikatywną odwrotność . To sprawia, że ​​liczby zespolone są polem , które ma liczby rzeczywiste jako pole podrzędne. Liczby zespolone tworzą również rzeczywistą przestrzeń wektorową o wymiarze dwa, z {1, i } jako standardową podstawą .

Ta standardowa podstawa sprawia, że ​​liczby zespolone są płaszczyzną kartezjańską , zwaną płaszczyzną zespoloną . Pozwala to na geometryczną interpretację liczb zespolonych i ich operacji oraz odwrotnie, wyrażając za pomocą liczb zespolonych niektóre właściwości i konstrukcje geometryczne. Na przykład liczby rzeczywiste tworzą linię rzeczywistą , która jest identyfikowana z poziomą osią płaszczyzny zespolonej. Liczby zespolone o wartości bezwzględnej jeden tworzą koło jednostkowe . Dodanie liczby zespolonej jest translacją w płaszczyźnie zespolonej, a mnożenie przez liczbę zespoloną jest podobieństwem wyśrodkowanym w początku. Złożona koniugacja to symetria odbicia względem osi rzeczywistej. Złożona wartość bezwzględna jest normą euklidesową .

Podsumowując, liczby zespolone tworzą bogatą strukturę, która jest jednocześnie algebraicznie zamkniętym ciałem , algebrą przemienną na liczbach rzeczywistych i euklidesową przestrzenią wektorową o wymiarze drugim.

Definicja

Ilustracja liczby zespolonej z = x + iy na płaszczyźnie zespolonej . Część rzeczywista to x , a część urojona to y .

zespolona to liczba postaci a + bi , gdzie aib są liczbami rzeczywistymi , a i jest nieoznaczoną spełniającą i ² = −1 . Na przykład 2 + 3 i jest liczbą zespoloną.

W ten sposób liczbę zespoloną definiuje się jako wielomian o rzeczywistych współczynnikach w jednym nieokreślonym i , dla którego narzucona jest zależność i ² + 1 = 0 . Na podstawie tej definicji można dodawać i mnożyć liczby zespolone, stosując dodawanie i mnożenie dla wielomianów. Relacja i ² + 1 = 0 indukuje równości i ^{4 k} = 1, i ^{4 k +1} = i , i ^{4 k +2} = −1 oraz i ^{4 k +3} = − i , które zachodzą dla wszystkich liczb całkowitych k ; pozwalają one na redukcję dowolnego wielomianu wynikającego z dodawania i mnożenia liczb zespolonych do wielomianu liniowego w i , ponownie postaci a + bi o rzeczywistych współczynnikach a, b.

Liczbę rzeczywistą a nazywamy częścią rzeczywistą liczby zespolonej a + bi ; liczba rzeczywista b nazywana jest jej częścią urojoną . Dla podkreślenia, część urojona nie zawiera czynnika i ; to znaczy część urojona to b , a nie bi .

Formalnie liczby zespolone definiuje się jako pierścień ilorazowy pierścienia wielomianu w nieokreślonym i , przez ideał generowany przez wielomian i ² + 1 (patrz poniżej ).

Notacja

Liczbę rzeczywistą a można uważać za liczbę zespoloną a + 0 i , której część urojona wynosi 0. Liczbę czysto urojoną bi to liczbę zespoloną 0 + bi , której część rzeczywista wynosi zero. Podobnie jak w przypadku wielomianów, często pisze się a dla a + 0 i oraz bi dla 0 + bi . Ponadto, gdy część urojona jest ujemna, to znaczy b = − |b| < 0 , często pisze się a − |b|i zamiast a + (− |b| ) i ; na przykład dla b = −4 , 3 − 4 i można zapisać zamiast 3 + (−4) i .

Ponieważ mnożenie nieokreślonego i i rzeczywistego jest przemienne w wielomianach o rzeczywistych współczynnikach, wielomian a + bi można zapisać jako a + ib . Jest to często celowe w przypadku części urojonych oznaczonych wyrażeniami, na przykład gdy b jest rodnikiem.

Część rzeczywista liczby zespolonej z jest oznaczona przez Re ( z ) , ${\ Displaystyle {\ mathcal {Re}} (z)}$ lub ${\ Displaystyle {\ mathfrak {R} }(z)}$ ; część urojona liczby zespolonej z jest oznaczona przez Im ( z ) , ${\ Displaystyle {\ mathcal {Im}} (z)}$ lub ${\ Displaystyle {\ mathfrak {I}} (z).}$ Na przykład

$${\ Displaystyle \ nazwa operatora {Re} (2 + 3i) = 2 \ quad {\ tekst {i}} \ quad \ nazwa operatora {im} (2 + 3i) = 3 ~.}$$

Zbiór wszystkich liczb zespolonych jest oznaczony przez ( pogrubiona $lub$ ) C ( pogrubiona pionowo).

W niektórych dyscyplinach, szczególnie w elektromagnetyzmie i elektrotechnice , j jest używane zamiast i , ponieważ i jest często używane do reprezentowania prądu elektrycznego . W takich przypadkach liczby zespolone są zapisywane jako a + bj lub a + jb .

Wyobrażanie sobie

Główny artykuł: Złożona płaszczyzna

Liczba zespolona z jako punkt (czarny) i jego wektor położenia (niebieski)

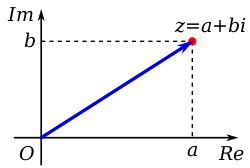
Liczbę zespoloną z można zatem utożsamić z uporządkowaną parą liczb rzeczywistych ${\ Displaystyle (\ Re (z), \ Im (z))}$ liczb rzeczywistych, które z kolei mogą być interpretowane jako współrzędne punktu w przestrzeni dwuwymiarowej. Najbardziej bezpośrednią przestrzenią jest płaszczyzna euklidesowa z odpowiednimi współrzędnymi, która jest wówczas nazywana płaszczyzną zespoloną lub diagramem Arganda , nazwanym na cześć Jeana-Roberta Arganda . Inną wyróżniającą się przestrzenią, na którą można rzutować współrzędne, jest dwuwymiarowa powierzchnia kuli, nazywana wtedy sferą Riemanna .

Kartezjańska płaszczyzna zespolona

Definicja liczb zespolonych obejmujących dwie dowolne wartości rzeczywiste natychmiast sugeruje użycie współrzędnych kartezjańskich na płaszczyźnie zespolonej. Oś pozioma ( rzeczywista ) jest zwykle używana do wyświetlania części rzeczywistej, ze wzrostem wartości po prawej stronie, a część urojona wyznacza oś pionową ( urojoną ), ze wzrostem wartości w górę.

Liczba na wykresie może być postrzegana jako punkt o współrzędnych lub jako wektor pozycji od początku do tego punktu. Wartości współrzędnych liczby zespolonej z można zatem wyrazić w jej postaci kartezjańskiej , prostokątnej lub algebraicznej .

Warto zauważyć, że operacje dodawania i mnożenia nabierają bardzo naturalnego charakteru geometrycznego, gdy liczby zespolone są postrzegane jako wektory położenia: dodawanie odpowiada dodawaniu wektorów , podczas gdy mnożenie (patrz poniżej ) odpowiada mnożeniu ich wielkości i dodawaniu kątów, które tworzą z prawdziwa oś. Patrząc w ten sposób, pomnożenie liczby zespolonej przez i odpowiada obróceniu wektora położenia w kierunku przeciwnym do ruchu wskazówek zegara o ćwierć obrotu ( 90° ) wokół początku układu współrzędnych — fakt, który można wyrazić algebraicznie w następujący sposób:

$${\ Displaystyle (a + bi) \ cdot i = ai + b (i) ^ {2} = - b + ai.}$$

Polarna płaszczyzna zespolona

Główny artykuł: biegunowy układ współrzędnych

„Postać polarna” przekierowuje tutaj. Aby zapoznać się z analogiem o wyższych wymiarach, zobacz Rozkład biegunowy .

Argument φ i moduł r wyznaczają punkt na płaszczyźnie zespolonej.

Moduł i argument

Alternatywną opcją dla współrzędnych na płaszczyźnie zespolonej jest biegunowy układ współrzędnych , który wykorzystuje odległość punktu z od początku ( O ) oraz kąt między dodatnią osią rzeczywistą a odcinkiem linii Oz w kierunku przeciwnym do ruchu wskazówek zegara. Prowadzi to do formy polarnej

${\ Displaystyle z = re ^ {i \ varphi} = r (\ cos \ varphi + i \ sin \ varphi)}$

liczby zespolonej, gdzie r jest wartością bezwzględną z , a argumentem z . $\ varphi$ displaystyle }

Wartość bezwzględna (lub moduł lub wielkość ) liczby zespolonej z = x + yi wynosi

$${\ displaystyle r = | z | = {\ sqrt {x ^ {2} + y ^ {2}}}.}$$

Jeśli z jest liczbą rzeczywistą (to znaczy, jeśli y = 0 ), to r = | x | . Oznacza to, że wartość bezwzględna liczby rzeczywistej jest równa jej wartości bezwzględnej jako liczby zespolonej.

Zgodnie z twierdzeniem Pitagorasa wartość bezwzględna liczby zespolonej jest odległością do początku punktu reprezentującego liczbę zespoloną na płaszczyźnie zespolonej .

Argument z (w wielu aplikacjach określany jako „faza” φ ) jest kątem promienia Oz z dodatnią osią rzeczywistą i jest zapisywany jako arg z . Podobnie jak w przypadku modułu, argument można znaleźć na podstawie prostokątnej postaci x + yi — stosując odwrotną styczną do ilorazu części urojonych przez rzeczywiste. Używając tożsamości półkąta, pojedyncza gałąź arctan wystarcza do pokrycia zakresu (− π , π ] funkcji arg i pozwala uniknąć bardziej subtelnej analizy poszczególnych przypadków

$${ \ Displaystyle \ varphi = \ arg (x + yi) = {\ rozpocząć {przypadki} 2 \ arctan \ lewo ({\ dfrac {y} {{\ sqrt {x ^ {2} + y ^ {2}}} + x}}\right)&{\text{if }}y\neq 0{\text{ or }}x>0,\\\pi &{\text{if }}x<0{\text{ and } }y=0,\\{\text{nieokreślony}}&{\text{if }}x=0{\text{ i }}y=0.\end{przypadki}}}$$

Zwykle, jak podano powyżej, wybierana jest wartość główna z przedziału (− π , π ) . Jeśli wartość arg jest ujemna, wartości z przedziału (− π , π ] lub [0, 2 π ) można otrzymać dodając 2 π Wartość φ jest wyrażona w tym artykule w radianach . Może wzrosnąć o dowolną całkowitą wielokrotność 2 π i nadal dawać ten sam kąt, widziany jako oparty na promieniach dodatniej osi rzeczywistej i od początku do z . Dlatego funkcja arg jest czasami uważana za wielowartościową .Kąt biegunowy dla liczby zespolonej 0 jest nieokreślony, ale powszechny jest arbitralny wybór kąta biegunowego 0.

Wartość φ jest równa wynikowi atan2 :

$${\ Displaystyle \ varphi = \ nazwa operatora {atan2} \ lewo (\ nazwa operatora {Im} (z), \ nazwa operatora {Re} (z) \ po prawej).}$$

Razem r i φ dają inny sposób reprezentacji liczb zespolonych, postać biegunową , ponieważ kombinacja modułu i argumentu w pełni określa położenie punktu na płaszczyźnie. Odzyskiwanie oryginalnych współrzędnych prostokątnych z postaci biegunowej odbywa się za pomocą wzoru zwanego formą trygonometryczną

$${\ Displaystyle z = r (\ cos \ varphi + i \ sin \ varphi).}$$

Korzystając ze wzoru Eulera można to zapisać jako

$${\ Displaystyle z = re ^ {i \ varphi} {\ tekst {lub}} z = r \ exp i \ varphi.}$$

Używając funkcji cis , jest to czasami skracane do

$${\ Displaystyle z = r \ nazwa operatora {\ operatorname {cis}} \ varphi.}$$

W zapisie kąta , często używanym w elektronice do reprezentowania wskazu o amplitudzie r i fazie φ , jest on zapisany jako

$${\ Displaystyle z = r \ kąt \ varphi.}$$

Złożone wykresy

Główny artykuł: Kolorowanie domeny

Wykres koła kolorów wyrażenia ( z ² - 1) ( z - 2 - i ) ² / z ² + 2 + 2 i

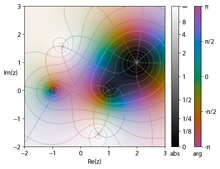
Podczas wizualizacji złożonych funkcji potrzebne są zarówno złożone dane wejściowe, jak i wyjściowe. Ponieważ każda liczba zespolona jest reprezentowana w dwóch wymiarach, wizualne przedstawienie funkcji zespolonej wymagałoby postrzegania przestrzeni czterowymiarowej , co jest możliwe tylko w projekcjach. Z tego powodu zaprojektowano inne sposoby wizualizacji złożonych funkcji.

0 W dziedzinie kolorowania wymiary wyjściowe są reprezentowane odpowiednio przez kolor i jasność. Każdy punkt na płaszczyźnie zespolonej jako dziedzina jest ozdobiony , zwykle kolorem reprezentującym argument liczby zespolonej i jasnością reprezentującą wielkość. Ciemne plamy oznaczają moduły bliskie zeru, jaśniejsze plamy są dalej od początku, gradacja może być nieciągła, ale przyjmuje się, że jest monotonna. Kolory często zmieniają się w krokach od π / 3 do 2 π od czerwonego, żółtego, zielonego, cyjanowego, niebieskiego do magenta . Wykresy te nazywane są wykresami koła kolorów . Zapewnia to prosty sposób wizualizacji funkcji bez utraty informacji. Rysunek pokazuje zera dla ±1, (2 + i ) i bieguny dla ${\ Displaystyle \ pm {\ sqrt {-2-2i}}.}$

Historia

Zobacz także: Liczba ujemna § Historia

Rozwiązanie w pierwiastkach (bez funkcji trygonometrycznych ) ogólnego równania sześciennego , gdy wszystkie trzy jego pierwiastki są liczbami rzeczywistymi, zawiera pierwiastki kwadratowe liczb ujemnych , sytuacji, której nie można naprawić za pomocą faktoryzacji wspomaganej testem pierwiastka wymiernego , jeśli sześcienny jest nieredukowalny ; jest to tak zwany casus Ireducibilis („przypadek nieredukowalny”). Ta zagadka doprowadziła włoskiego matematyka Gerolamo Cardano do wyobrażenia sobie liczb zespolonych około 1545 roku w jego Ars Magna , chociaż jego zrozumienie było szczątkowe; co więcej, później odrzucił liczby zespolone jako „subtelne, ponieważ są bezużyteczne”. Cardano używał wyimaginowanych liczb, ale opisał je jako „mentalne tortury”. Było to przed użyciem graficznej płaszczyzny zespolonej. Cardano i inni włoscy matematycy, zwłaszcza Scipione del Ferro , w XVI wieku stworzyli algorytm rozwiązywania równań sześciennych, które na ogół miały jedno rozwiązanie rzeczywiste i dwa rozwiązania zawierające liczbę urojoną. Ponieważ zignorowali odpowiedzi z wyimaginowanymi liczbami, Cardano uznał je za bezużyteczne.

Praca nad problemem wielomianów ogólnych ostatecznie doprowadziła do fundamentalnego twierdzenia algebry , które pokazuje, że w przypadku liczb zespolonych istnieje rozwiązanie każdego równania wielomianu stopnia pierwszego lub wyższego. Liczby zespolone tworzą zatem ciało algebraicznie domknięte , w którym każde równanie wielomianowe ma pierwiastek .

Wielu matematyków przyczyniło się do rozwoju liczb zespolonych. Zasady dodawania, odejmowania, mnożenia i pierwiastkowania liczb zespolonych zostały opracowane przez włoskiego matematyka Rafaela Bombellego . Bardziej abstrakcyjny formalizm liczb zespolonych został rozwinięty przez irlandzkiego matematyka Williama Rowana Hamiltona , który rozszerzył tę abstrakcję na teorię kwaternionów .

, że najwcześniejsza przelotna wzmianka o pierwiastkach kwadratowych liczb ujemnych pojawiła się w pracy greckiego matematyka Hero z Aleksandrii w I wieku naszej ery , gdzie w swoim Stereometrica rozważył, najwyraźniej błędnie, objętość niemożliwego ściętego piramidę , aby dojść do terminu w jego obliczeniach, który dziś uprościłby się do $= 3i {\ sqrt {7}}}$$-63 }$ . Ilości ujemne nie były pomyślane w hellenistycznej matematyce i Hero jedynie zastąpił je dodatnimi ${\ displaystyle {\ sqrt {144-81}} = 3 {\ sqrt {7}}.}$

Impuls do badania liczb zespolonych jako tematu samego w sobie pojawił się po raz pierwszy w XVI wieku, kiedy włoscy matematycy odkryli algebraiczne rozwiązania pierwiastków wielomianów sześciennych i kwartalnych (patrz Niccolò Fontana Tartaglia , Gerolamo Cardano ). Szybko zdano sobie sprawę (ale okazało się to znacznie później), że te wzory, nawet jeśli ktoś był zainteresowany tylko rzeczywistymi rozwiązaniami, czasami wymagały manipulacji pierwiastkami kwadratowymi liczb ujemnych. Na przykład wzór Tartaglii na równanie sześcienne postaci x ³ = px + q daje rozwiązanie równania x ³ = x jako

$${\ Displaystyle {\ tfrac {1} {\ sqrt {3}}} \ lewo (\ lewo ({\ sqrt {-1}} \ prawo) ^ {1/3} + \ lewo ({\ sqrt {-1 }}\prawo)^{-1/3}\prawo).}$$

Na pierwszy rzut oka wygląda to na nonsens. Jednak formalne obliczenia z liczbami zespolonymi pokazują, że równanie z ³ = i ma trzy rozwiązania: ${\ Displaystyle -i, {\ Frac {{\ sqrt {3}} + i} {2}}, {\ frac {- {\ sqrt {3}} + i} {2}}.} Zastępując je po$ kolei dla ${\ Displaystyle {\ sqrt {-1}} ^ {1/3}}$ we wzorze sześciennym Tartaglii i upraszczając, otrzymuje się 0, 1 i -1 jako rozwiązania x ³ - x = 0 . Oczywiście to konkretne równanie można rozwiązać na pierwszy rzut oka, ale ilustruje to, że gdy stosuje się ogólne wzory do rozwiązywania równań sześciennych z pierwiastkami rzeczywistymi, to, jak rygorystycznie wykazali późniejsi matematycy, użycie liczb zespolonych jest nieuniknione . Rafael Bombelli był pierwszym, który wyraźnie odniósł się do tych pozornie paradoksalnych rozwiązań równań sześciennych i opracował zasady złożonej arytmetyki, próbując rozwiązać te problemy.

Termin „wyimaginowany” dla tych wielkości został ukuty przez René Descartesa w 1637 r., Który starał się podkreślić ich nierealny charakter

... czasami tylko urojone, to znaczy można sobie wyobrazić tyle, ile powiedziałem w każdym równaniu, ale czasami nie istnieje żadna wielkość, która pasowałaby do tej, którą sobie wyobrażamy. [ ... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en Imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui korespondencja à celle qu'on wyobrażać sobie. ]

Kolejnym źródłem nieporozumień było to, że równanie ${\ Displaystyle {\ sqrt {-1}} ^ {2} = {\ sqrt {-1}} {\ sqrt {-1 }} = -1}$ wydawało się być kapryśnie niespójne z algebraiczną tożsamością, która jest poprawna ${\ Displaystyle {\ sqrt {a}} {\ sqrt {b}} = {\ sqrt {ab}}}$ dla nieujemnych liczb rzeczywistych a i b , który był również używany w obliczeniach liczb zespolonych z jednym z a , b dodatnim i drugim ujemnym. Niepoprawne użycie tej tożsamości (i powiązanej tożsamości ${\textstyle {\frac {1}{\sqrt {a}}}={\sqrt {\frac {1}{a}}}$ } w przypadku, gdy zarówno a, jak i b są ujemne, dokuczał nawet Leonhardowi Eulerowi . Ta trudność ostatecznie doprowadziła do konwencji używania specjalnego symbolu $aby$ zamiast , ustrzec się przed tym błędem Mimo to Euler uważał za naturalne zapoznanie studentów z liczbami zespolonymi znacznie wcześniej niż robimy to dzisiaj. W swoim podręczniku do algebry elementarnej Elements of Algebra wprowadza te liczby niemal od razu, a następnie używa ich w sposób naturalny przez cały czas.

W XVIII wieku liczby zespolone zyskały szersze zastosowanie, ponieważ zauważono, że formalne manipulacje wyrażeniami złożonymi można wykorzystać do uproszczenia obliczeń obejmujących funkcje trygonometryczne. Na przykład w 1730 roku Abraham de Moivre zauważył, że tożsamości odnoszące funkcje trygonometryczne całkowitej wielokrotności kąta do potęg funkcji trygonometrycznych tego kąta można ponownie wyrazić za pomocą następującego wzoru de Moivre'a :

$${\ Displaystyle (\ cos \ teta + i \ sin \ teta) ^ {n} = \ cos n \ teta + i \ sin n \ teta.}$$

W 1748 Euler poszedł dalej i uzyskał formułę analizy złożonej Eulera :

$${\ Displaystyle \ sałata \ teta + i \ sin \ teta = e ^ {i \ teta}}$$

przez formalne manipulowanie złożonymi szeregami potęgowymi i zauważył, że ten wzór może być użyty do zredukowania dowolnej tożsamości trygonometrycznej do znacznie prostszych tożsamości wykładniczych.

Idea liczby zespolonej jako punktu na płaszczyźnie zespolonej ( powyżej ) została po raz pierwszy opisana przez duńsko - norweskiego matematyka Caspara Wessela w 1799 r., chociaż przewidywano ją już w 1685 r. w Traktacie algebry Wallisa .

Wspomnienia Wessela ukazały się w Proceedings of the Copenhagen Academy , ale przeszły w dużej mierze niezauważone. W 1806 roku Jean-Robert Argand niezależnie wydał broszurę o liczbach zespolonych i przedstawił rygorystyczny dowód podstawowego twierdzenia algebry . Carl Friedrich Gauss opublikował wcześniej zasadniczo topologiczny dowód twierdzenia w 1797 r., Ale wyraził wówczas swoje wątpliwości co do „prawdziwej metafizyki pierwiastka kwadratowego z −1”. Dopiero w 1831 roku przezwyciężył te wątpliwości i opublikował swój traktat o liczbach zespolonych jako punktach na płaszczyźnie, w dużej mierze ustanawiając współczesną notację i terminologię:

Jeśli ktoś wcześniej rozważał ten temat z fałszywego punktu widzenia i dlatego znalazł tajemniczą ciemność, to w dużej mierze można to przypisać niezdarnej terminologii. Gdyby nie nazywano jednostek dodatnich, ujemnych lub urojonych (lub nawet niemożliwych), ale zamiast tego, powiedzmy, jednostkami bezpośrednimi, odwrotnymi $bocznymi$ wtedy trudno byłoby mówić o takiej ciemności.

Na początku XIX wieku inni matematycy niezależnie odkryli geometryczną reprezentację liczb zespolonych: Buée, Mourey , Warren, Français i jego brat Bellavitis .

Angielski matematyk GH Hardy zauważył, że Gauss był pierwszym matematykiem, który użył liczb zespolonych w „naprawdę pewny i naukowy sposób”, chociaż matematycy tacy jak Norweg Niels Henrik Abel i Carl Gustav Jacob Jacobi z konieczności używali ich rutynowo, zanim Gauss opublikował swój traktat z 1831 roku.

Augustin-Louis Cauchy i Bernhard Riemann razem doprowadzili podstawowe idee analizy złożonej do wysokiego stanu ukończenia, który rozpoczął się około 1825 roku w przypadku Cauchy'ego.

Powszechne terminy używane w teorii pochodzą głównie od założycieli. $_$ nazywa sałatę φ + ja grzech φ współczynnikiem kierunku i _ _ _ Cauchy (1821) nazwał cos φ + i sin φ formą zredukowaną ( l'expression réduite) i najwyraźniej wprowadził termin argument ; Gauss użył i dla , a ² wprowadził 2 ^liczba termin zespolona $nazwał$ a + bi i normą + . Współczynnik kierunku wyrażenia , często używany dla cos φ + i sin φ , pochodzi od Hankela (1867), a wartość bezwzględna dla modułu wynika z Weierstrassa.

Późniejsi pisarze klasyczni zajmujący się teorią ogólną to Richard Dedekind , Otto Hölder , Felix Klein , Henri Poincaré , Hermann Schwarz , Karl Weierstrass i wielu innych. Ważne prace (w tym systematyzacja) w złożonym rachunku wielowymiarowym rozpoczęto na początku XX wieku. Ważne wyniki osiągnął Wilhelm Wirtinger w 1927 roku.

Relacje i operacje

Równość

Liczby zespolone mają podobną definicję równości do liczb rzeczywistych; dwie liczby zespolone a ₁ + b ₁ i oraz a ₂ + b ₂ i są równe wtedy i tylko wtedy, gdy ich części rzeczywista i urojona są równe, to znaczy jeśli a ₁ = a ₂ i b ₁ = b ₂ . Niezerowe liczby zespolone zapisane w postaci biegunowej są równe wtedy i tylko wtedy, gdy mają tę samą wielkość, a ich argumenty różnią się o całkowitą wielokrotność 2 π .

Zamawianie

W przeciwieństwie do liczb rzeczywistych, nie ma naturalnego uporządkowania liczb zespolonych. W szczególności nie ma liniowego uporządkowania liczb zespolonych, które byłoby zgodne z dodawaniem i mnożeniem. Dlatego liczby zespolone nie mają struktury ciała uporządkowanego. Jednym z wyjaśnień jest to, że każda nietrywialna suma kwadratów w uporządkowanym polu jest różna od zera, a i ² + 1 ² = 0 jest nietrywialną sumą kwadratów. Tak więc liczby zespolone są naturalnie uważane za istniejące na płaszczyźnie dwuwymiarowej.

Sprzężony

Zobacz także: Złożony koniugat

Reprezentacja geometryczna z i jego koniugatu z na płaszczyźnie zespolonej

Zespolony koniugat liczby zespolonej z = x + yi jest dany przez x − yi . Jest oznaczony przez z lub z * . Ta jednoargumentowa operacja na liczbach zespolonych nie może być wyrażona przez zastosowanie tylko podstawowych operacji dodawania, odejmowania, mnożenia i dzielenia.

Geometrycznie z jest „odbiciem” z od rzeczywistej osi . Koniugacja dwukrotnie daje pierwotną liczbę zespoloną

$${\ Displaystyle {\ overline {\ overline {z}}} = z,}$$

co czyni tę operację inwolucją . Oznacza to , że odbicie pozostawia zarówno część rzeczywistą, jak i wielkość z niezmienioną

$${\ Displaystyle \ operatorname {Re} ({\ overline {z}}) = \ operatorname {Re} (z) \ quad}$$

i ${\ displaystyle \ quad | {\ overline {z}}|=|z|.}$

Część urojona i argument liczby zespolonej z zmieniają swój znak w koniugacji

$${\ Displaystyle \ nazwa operatora {im} ({\ overline {z}}) = - \ nazwa operatora {im} (z) \ quad {\ tekst {i}} \ quad \ nazwa operatora {arg} {\ overline {z}} \equiv -\operatorname {arg} z{\pmod {2\pi}}.}$$

Aby uzyskać szczegółowe informacje na temat argumentu i wielkości, zobacz sekcję dotyczącą formy biegunowej .

Iloczyn liczby zespolonej z = x + yi i jej koniugatu jest znany jako kwadrat bezwzględny . Jest to zawsze nieujemna liczba rzeczywista i równa kwadratowi wielkości każdego z nich:

$${\ Displaystyle z \ cdot {\ overline {z}} = x ^ {2} + y ^ {2} = | z | ^ {2} = | {\ overline {z}} | ^ {2}.}$$

Tej właściwości można użyć do przekształcenia ułamka o złożonym mianowniku na równoważny ułamek z rzeczywistym mianownikiem poprzez rozwinięcie zarówno licznika, jak i mianownika ułamka przez sprzężenie danego mianownika. Ten proces jest czasami nazywany „ racjonalizacją ” mianownika (chociaż mianownikiem w końcowym wyrażeniu może być irracjonalna liczba rzeczywista), ponieważ przypomina metodę usuwania pierwiastków z prostych wyrażeń w mianowniku.

Rzeczywiste i urojone części liczby zespolonej z można wyodrębnić za pomocą koniugacji:

$${\ Displaystyle \ nazwa operatora {Re} (z) = {\ dfrac {z + {\ overline {z}}} {2}}, \ quad {\ tekst {i}} \ quad \ nazwa operatora {im} (z) = {\dfrac {z-{\overline {z}}}{2i}}.}$$

Co więcej, liczba zespolona jest rzeczywista wtedy i tylko wtedy, gdy jest równa swojemu koniugatowi.

Koniugacja rozkłada się na podstawowe złożone operacje arytmetyczne:

$${\ Displaystyle {\ rozpocząć {wyrównane} {\ overline {z \ pm w}} & = {\ overline {z}} \ pm {\ overline {w}}, \\ {\ overline {z \ cdot w}} &={\overline {z}}\cdot {\overline {w}},\\{\overline {z/w}}&={\overline {z}}/{\overline {w}}.\end {wyrównany}}}$$

Koniugacja jest również stosowana w geometrii odwrotnej , gałęzi geometrii badającej odbicia bardziej ogólne niż te dotyczące linii. W analizie sieci obwodów elektrycznych sprzężenie zespolone jest używane do znajdowania impedancji równoważnej, gdy poszukuje się twierdzenia o maksymalnym przeniesieniu mocy .

Dodawanie i odejmowanie

Dodawanie dwóch liczb zespolonych można wykonać geometrycznie, konstruując równoległobok.

Dwie $_$$_$ dodać _ _ _ To jest do powiedzenia:

$${\ Displaystyle a + b = (x + yi) + (u + vi) = (x + u) + (y + v) i.}$$

Podobnie odejmowanie można wykonać jako

$${\ Displaystyle ab = (x + yi) - (u + vi) = (xu) + (yv) i.}$$

Mnożenie liczby zespolonej $r$ rzeczywistej można wykonać podobnie, mnożąc osobno i urojoną a :

$${\ displaystyle ra = r (x + yi) = rx + ryi.}$$

W szczególności odejmowanie można wykonać, negując odejmowanie (czyli mnożąc je przez –1 ) i dodając wynik do odejmowania :

$${\ Displaystyle ab = a + (-1) \, b.}$$

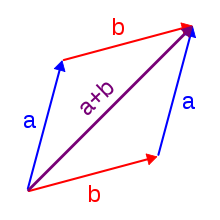
Korzystając z wizualizacji liczb zespolonych na płaszczyźnie zespolonej, dodawanie ma następującą interpretację geometryczną: suma dwóch liczb zespolonych a i b , interpretowanych jako punkty na płaszczyźnie zespolonej, jest punktem otrzymanym przez zbudowanie równoległoboku z trzech wierzchołków O , oraz punkty strzałek oznaczonych a i b (pod warunkiem, że nie leżą na jednej linii). Równoważnie nazywając te punkty A , B , odpowiednio i czwarty punkt równoległoboku X , trójkąty OAB i XBA są przystające .

Mnożenie i kwadrat

Reguły własności rozdzielności , właściwości przemienności (dodawania i mnożenia) oraz właściwości definiującej i ² = −1 mają zastosowanie do liczb zespolonych. Wynika, że

$${\ Displaystyle (x + yi) \, (u + vi) = (xu-yv) + (xv + yu) i.}$$

W szczególności,

$${\ Displaystyle (x + yi) ^ {2} = x ^ {2} -y ^ {2} + 2xyi.}$$

Wzajemność i podział

Korzystając z koniugacji, odwrotność niezerowej liczby zespolonej z = x + yi zawsze można rozłożyć na

$${\ Displaystyle {\ Frac {1} {z}} = {\ Frac {\ overline {z}} { z{\overline {z}}}}={\frac {\overline {z}}{|z|^{2}}}={\frac {\overline {z}}{x^{2}+y ^{2}}}={\frac {x}{x^{2}+y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i, }$$

ponieważ niezerowe oznacza, że ​​x ² + y ² jest większe od zera.

Można tego użyć do wyrażenia dzielenia dowolnej liczby zespolonej w = u + vi przez niezerową liczbę zespoloną z jako

$${\ Displaystyle {\ Frac {w} {z}} = w \ cdot {\ Frac {1} {z}} = (u + vi) \ cdot \ lewo ({\ Frac {x} {x ^ {2} +y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i\right)={\frac {(ux+vy)+(vx-uy)i }{x^{2}+y^{2}}}.}$$

Mnożenie i dzielenie w postaci biegunowej

Mnożenie 2 + i (niebieski trójkąt) i 3 + i (czerwony trójkąt). Czerwony trójkąt jest obracany tak, aby pasował do wierzchołka niebieskiego (dodanie obu kątów w wyrazach φ ₁ + φ ₂ w równaniu) i rozciągany o długość przeciwprostokątnej niebieskiego trójkąta (mnożenie obu promieni, zgodnie z terminem r ₁ r ₂ w równaniu).

Wzory na mnożenie, dzielenie i potęgowanie są prostsze w postaci biegunowej niż odpowiadające im wzory we współrzędnych kartezjańskich. Biorąc pod uwagę dwie liczby zespolone z ₁ = r ₁ (cos φ ₁ + i sin φ ₁ ) i z ₂ = r ₂ (cos φ ₂ + i sin φ ₂ ) , ze względu na tożsamości trygonometryczne

$${\ Displaystyle {\ rozpocząć {wyrównane dat} {4} \ cos a \ cos b & - \ sin a \ sin b & {} = {} & \ cos (a + b) \\\ cos a \ sin b & + \ sin a \cos b&{}={}&\sin(a+b).\end{wyrównanydat}}}$$

możemy czerpać

$${\ Displaystyle z_ {1} z_ {2} = r_ {1} r_ {2} (\ cos (\ varphi _ {1} + \ varphi _ {2}) + ja \ sin (\ varphi _ {1} + \varphi _{2})).}$$

Innymi słowy, wartości bezwzględne są mnożone i argumenty są dodawane w celu uzyskania postaci biegunowej iloczynu. Na przykład pomnożenie przez i odpowiada ćwierć obrotu w kierunku przeciwnym do ruchu wskazówek zegara, co daje z powrotem i ² = −1 . Obraz po prawej ilustruje mnożenie

$${\ Displaystyle (2 + ja) (3 + i) = 5 + 5i.}$$

Ponieważ część rzeczywista i urojona liczby 5 + 5 i są równe, argument tej liczby wynosi 45 stopni, czyli π /4 (w radianach ). Z drugiej strony jest to również suma kątów na początku trójkąta czerwonego i niebieskiego, arctan (1/3) i arctan (1/2). Zatem formuła

$${\ Displaystyle {\ Frac {\ pi} {4}} = \ arctan \ lewo ({\ Frac {1} {2}} \ prawej) + \arctan \left({\frac {1}{3}}\right)}$$

posiada. Ponieważ arctan można aproksymować bardzo wydajnie, takie wzory – znane jako formuły podobne do Machin – są używane do bardzo precyzyjnych przybliżeń π .

Podobnie dzielenie jest podane przez

$${\ Displaystyle {\ Frac {z_ {1}} {z_ {2}}} = {\ Frac {r_ {1}} {r_ {2}}} \ lewo (\ cos (\ varphi _ {1} - \ varphi _{2})+i\sin(\varphi _{1}-\varphi _{2})\right).}$$

Pierwiastek kwadratowy

Zobacz też: Pierwiastki kwadratowe z liczb ujemnych i zespolonych

Pierwiastki kwadratowe z a + bi (gdzie b ≠ 0 ) to ${\ Displaystyle \ pm (\ gamma + \ delta i)}$ , gdzie

$${\ Displaystyle \ gamma = {\ sqrt {\ Frac {a + {\ sqrt {a ^ {2} + b ^ {2}}}} {2}}}}$$

I

$${\ Displaystyle \ delta = (\ nazwa operatora {sgn} b) {\ sqrt {\ Frac {-a + {\ sqrt {a ^ {2} + b^{2}}}}{2}}},}$$

gdzie sgn jest funkcją signum . $przez$ zobaczyć w celu a + bi Tutaj a nazywa się modułem a + a znak $,$ kwadratowego wskazuje pierwiastek kwadratowy z część, zwana głównym pierwiastkiem kwadratowym ; także ${\ Displaystyle {\ sqrt {a ^ {2} + b ^ {2}}} = {\ sqrt {z {\ overline {z}}}},}$ gdzie z = za + bi .

Funkcja wykładnicza

Funkcja wykładnicza ${\ Displaystyle \ exp \ dwukropek \ mathbb {C} \ do \ mathbb {C} ; z \ mapsto \ exp z}$ można zdefiniować dla każdej liczby zespolonej z szeregiem potęgowym

$$\ Displaystyle \ exp z = \ suma _ {n = 0} ^ {\ infty} {\ Frac {z ^ {n}} {n!}}}$$

który ma nieskończony promień zbieżności .

Wartość 1 funkcji wykładniczej to liczba Eulera

$${\ Displaystyle e = \ exp 1 = \ suma _ {n = 0} ^ {\ infty} {\ Frac {1} {n!}} \ około 2,71828.}$$

Jeśli z jest rzeczywiste, mamy ${\ Displaystyle \ exp z = e ^ {z}.}$ Analityczna kontynuacja pozwala rozszerzyć tę równość dla każdej zespolonej wartości z , a tym samym zdefiniować złożone potęgowanie z podstawą e jako

$${\ displaystyle e ^ {z} = \ exp z.}$$

Równanie funkcjonalne

Funkcja wykładnicza spełnia równanie funkcyjne ${\ Displaystyle e ^ {z + t} = e ^ {z} e ^ {t}.}$ Można to udowodnić, porównując rozwinięcie szeregu potęg obu elementów lub stosując analityczną kontynuację od ograniczenia równania do rzeczywistego argumenty.

Wzór Eulera

Wzór Eulera stwierdza, że ​​dla dowolnej liczby rzeczywistej y ,

$${\ Displaystyle e ^ {iy} = \ cos y + i \ sin y.}$$

Z równania funkcjonalnego wynika zatem, że jeśli x i y są rzeczywiste, to tak

$${\ Displaystyle e ^ {x + iy} = e ^ {x} (\ cos y+i\sin y)=e^{x}\cos y+ie^{x}\sin y,}$$

który jest rozkładem funkcji wykładniczej na jej część rzeczywistą i urojoną.

Złożony logarytm

W rzeczywistym przypadku logarytm naturalny można zdefiniować jako odwrotność ${\ Displaystyle \ ln \ dwukropek \ mathbb {R} ^ {+} \ do \ mathbb {R} ; x \ mapsto \ ln x} funkcji$ wykładniczej. Aby rozszerzyć to na dziedzinę złożoną, można zacząć od wzoru Eulera. Oznacza to, że jeśli liczba zespolona jest zapisana w postaci biegunowej ${\ Displaystyle Z \ in \ mathbb {C} ^ {\ razy}}$

$${\ Displaystyle z = r (\ cos \ varphi + i \ sin \ varphi)}$$

z ${\ Displaystyle r, \ varphi \ in \ mathbb {R},}$ wtedy z

$${\ Displaystyle \ ln z = \ ln r + i \ varphi}$$

jako złożony logarytm ma się właściwą odwrotność:

$${\ Displaystyle \ exp \ ln z = \ exp (\ ln r + i \ varphi) = r \ exp i \ varphi = r (\ cos \ varphi + i \ sin \ varphi) = z.}$$

Jednakże, ponieważ cosinus i sinus są funkcjami okresowymi, dodanie całkowitej wielokrotności 2 π do φ nie zmienia z . Na przykład e ^iπ = e ^{3 iπ} = −1 , więc zarówno iπ , jak i 3 iπ są możliwymi wartościami logarytmu naturalnego z −1 .

Dlatego, jeśli logarytm zespolony nie ma być zdefiniowany jako funkcja wielowartościowa

$${\ Displaystyle \ ln z = \ lewo \ {\ ln r + i (\ varphi + 2 \ pi k) \ mid k\w \mathbb {Z} \right\},}$$

trzeba użyć cięcia gałęzi i ograniczyć kodomenę , co skutkuje funkcją bijektywną

$$\ Displaystyle \ ln \ dwukropek \; \ mathbb {C} ^ {\ razy} \; \ do \; \; \; \ mathbb {R} ^{+}+\;i\,\left(-\pi ,\pi \right].}$$

Jeśli ${\ Displaystyle Z \ in \ mathbb {C} \ setminus \ lewo (- \ mathbb {R} _ {\ geq 0} \ prawej)} nie jest$ dodatnią liczbą rzeczywistą (liczba dodatnia lub nierzeczywista), wynikającą z tego wartość główną logarytmu zespolonego otrzymuje się za pomocą − π < φ < π . Jest to funkcja analityczna poza ujemnymi liczbami rzeczywistymi, ale nie można jej przedłużyć do funkcji ciągłej na dowolnej ujemnej liczbie rzeczywistej $}$ } gdzie główną wartością jest ln z = ln(− z ) + iπ .

Potęgowanie

Jeśli x > 0 jest rzeczywista, a z zespolona, ​​potęgowanie definiuje się jako

$${\ Displaystyle x ^ {z} = e ^ {z \ ln x},}$$

gdzie ln oznacza logarytm naturalny.

Naturalne wydaje się rozszerzenie tego wzoru na wartości zespolone x , ale są pewne trudności wynikające z faktu, że logarytm zespolony nie jest tak naprawdę funkcją, ale funkcją wielowartościową .

Wynika z tego, że jeśli z jest jak powyżej, a t jest kolejną liczbą zespoloną, to potęgowanie jest funkcją wielowartościową

$${\ Displaystyle z ^ {t} = \ left\{e^{t\ln r}\,(\cos(\varphi t+2\pi kt)+i\sin(\varphi t+2\pi kt))\mid k\in \mathbb {Z } \Prawidłowy\}}$$

Wykładniki całkowite i ułamkowe

Reprezentacja geometryczna pierwiastków od drugiego do szóstego liczby zespolonej z , w postaci biegunowej re ^iφ   gdzie r = | z | i φ = arg z . Jeśli z jest rzeczywiste, φ = 0 lub π . Główne korzenie są pokazane na czarno.

Jeśli w poprzednim wzorze t jest liczbą całkowitą, to sinus i cosinus są niezależne od k . Tak więc, jeśli wykładnik n jest liczbą całkowitą, to z ⁿ jest dobrze zdefiniowane, a wzór na potęgowanie upraszcza się do wzoru de Moivre'a :

$${\ Displaystyle z ^ {n} = (r (\ cos \ varphi + i \ sin \ varphi)) ^ {n} = r ^ {n} \, (\ cos n \ varphi + i \ sin n \ varphi) .}$$

Pierwiastki n n- tej liczby zespolonej z są podane przez

$${\ Displaystyle z ^ {1/n} = {\ sqrt [{n}] {r}}\left(\cos \left({\frac {\varphi +2k\pi }{n}}\right)+i\sin \left({\frac {\varphi +2k\pi}}{n }}\prawo)\prawo)}$$

dla 0 ≤ k ≤ n - 1 . (Tutaj $pierwiastkiem$ (dodatnim) n -tym dodatniej liczby rzeczywistej r .) Ponieważ sinus i cosinus są okresowe, inne wartości całkowite k nie nie podawać innych wartości.

Podczas gdy n -ty pierwiastek dodatniej liczby rzeczywistej r jest wybierany jako dodatnia liczba rzeczywista c spełniająca c ⁿ = r , nie ma naturalnego sposobu na rozróżnienie jednego konkretnego zespołu n -tego pierwiastka liczby zespolonej. Dlatego n- ty pierwiastek jest n -wartościową funkcją z . Oznacza to, że w przeciwieństwie do dodatnich liczb rzeczywistych, jeden ma

$${\ Displaystyle (z ^ {n}) ^ {1/n} \ neq z}$$

ponieważ lewa strona składa się z n wartości, a prawa strona to pojedyncza wartość.

Nieruchomości

Struktura pola

Zbiór $liczb$ jest polem . W skrócie oznacza to, że zachodzą następujące fakty: po pierwsze, dowolne dwie liczby zespolone można dodać i pomnożyć, aby uzyskać inną liczbę zespoloną. Po drugie, dla dowolnej liczby zespolonej z , jej addytywna odwrotność – z jest również liczbą zespoloną; i po trzecie, każda niezerowa liczba zespolona ma odwrotną liczbę zespoloną. Ponadto operacje te spełniają szereg praw, na przykład prawo przemienności dodawania i mnożenia dla dowolnych dwóch liczb zespolonych z ₁ i z ₂ :

$${\ Displaystyle {\ rozpocząć {wyrównane} z_ {1} + z_ {2} i = z_ {2} + z_ {1}, \\ z_ {1} z_ {2} i = z_ {2} z_ {1} .\end{wyrównane}}}$$

Te dwa prawa i inne wymagania dotyczące pola można udowodnić za pomocą podanych powyżej wzorów, wykorzystując fakt, że same liczby rzeczywiste tworzą pole.

$liczb$ rzeczywistych, nie jest polem uporządkowanym , to znaczy nie jest możliwe zdefiniowanie relacji 1 _< z 2 _zgodnej z dodawaniem i mnożeniem. W rzeczywistości w każdym uporządkowanym polu kwadrat dowolnego elementu jest koniecznie dodatni, więc i ² = −1 wyklucza istnienie uporządkowania na ${\ Displaystyle \ mathbb {C}.}$

Gdy podstawowym polem tematu lub konstrukcji matematycznej jest pole liczb zespolonych, nazwa tematu jest zwykle modyfikowana, aby odzwierciedlić ten fakt. Na przykład: analiza zespolona , ​​macierz zespolona , ​​wielomian zespolony i zespolona algebra Liego .

Rozwiązania równań wielomianowych

Biorąc pod uwagę dowolne liczby zespolone (zwane współczynnikami ) ₀ a , ..., a _n , równanie

$${\ Displaystyle a_ {n} z ^ {n} + \ kropka b + a_ {1} z + a_ {0} = 0}$$

ma co najmniej jedno rozwiązanie zespolone z , pod warunkiem, że co najmniej jeden z wyższych współczynników a ₁ , ..., a _n jest niezerowy. Jest to stwierdzenie fundamentalnego twierdzenia algebry Carla Friedricha Gaussa i Jeana le Rond d'Alemberta . Z tego powodu nazywa się $zamkniętym$ algebraicznie . Ta właściwość nie obowiązuje dla ciała liczb wymiernych $x$ wielomian 2 ^- 2 nie ma pierwiastka wymiernego, ponieważ √ 2 nie jest liczbą wymierną) ani liczb rzeczywistych ${ \displaystyle \mathbb {R}}$ (wielomian x ² + a nie ma pierwiastka rzeczywistego dla a > 0 , ponieważ kwadrat x jest dodatni dla dowolnej liczby rzeczywistej x ).

Istnieją różne dowody tego twierdzenia, albo metodami analitycznymi, takimi jak twierdzenie Liouville'a , albo topologicznymi , takimi jak liczba uzwojenia , lub dowód łączący teorię Galois i fakt, że każdy rzeczywisty wielomian nieparzystego stopnia ma co najmniej jeden rzeczywisty pierwiastek.

Z tego powodu twierdzenia, które obowiązują dla dowolnego ciała algebraicznie domkniętego, mają zastosowanie do ${\ displaystyle \ mathbb {C}.}$ Na przykład każda niepusta zespolona macierz kwadratowa ma co najmniej jedną (zespoloną) wartość własną .

Charakteryzacja algebraiczna

Pole ma następujące trzy właściwości: ${\ displaystyle \ mathbb {C}}$

• Po pierwsze, ma cechę 0. Oznacza to, że 1 + 1 + ⋯ + 1 ≠ 0 dla dowolnej liczby sum (z których wszystkie są równe jeden).
• $.$ drugie , $jego$ transcendencji nad głównym polem to liczność _
• Po trzecie, jest algebraicznie domknięty (patrz wyżej).

Można wykazać, że dowolne pole mające te właściwości jest izomorficzne (jako pole) z ${\ Displaystyle \ mathbb {C}.}$ Na pola przykład algebraiczne zamknięcie pola $spełnia$ -adycznej również te trzy właściwości, więc te dwa są izomorficzne (jako pola, ale nie jako pola topologiczne). Również $jest$ z polem zespolonego szeregu Puiseux . Jednak określenie izomorfizmu wymaga aksjomatu wyboru . ${\ displaystyle \ mathbb {C}}$ konsekwencją tej algebraicznej charakterystyki jest to, że $zawiera$ wiele odpowiednich podpól, które są izomorficzne z .

Charakteryzacja jako pole topologiczne

Powyższa charakterystyka $C$${\ Displaystyle \ mathbb {C}.}$ algebraiczne aspekty Oznacza to, że nie uwzględniono właściwości bliskości i ciągłości , które mają znaczenie w obszarach takich jak analiza i topologia . Poniższy opis jako $pola$ topologicznego (to znaczy pola wyposażonego w topologię , która na pojęcie zbieżności) uwzględnia właściwości topologiczne. zawiera podzbiór P (mianowicie zbiór dodatnich liczb rzeczywistych) niezerowych elementów spełniających następujące trzy warunki: do $\ displaystyle \ mathbb {C}}$

• P jest domknięte na dodawanie, mnożenie i przyjmowanie odwrotności.
• Jeśli x i y są odrębnymi elementami P , to albo x - y albo y - x jest w P .
• Jeśli S jest dowolnym niepustym podzbiorem P , to S + P = x + P dla pewnego x w ${\ Displaystyle \ mathbb {C}.}$

Co więcej, ma nietrywialny automorfizm inwolucyjny x ↦ x * (mianowicie złożoną koniugację), taki że x x * $P$ w dla dowolnego niezerowego x w ${\ Displaystyle \ mathbb {C}.}$

Dowolne pole F o tych właściwościach można wyposażyć w topologię, biorąc zbiory B ( x , p ) = { y | p - ( y - x ) ( y - x )* ∈ P } jako podstawa , gdzie x rozciąga się na polu, a p rozciąga się na P . Przy tej topologii F jest izomorficzne jako pole topologiczne z ${\ Displaystyle \ mathbb {C}.}$

Jedynymi połączonymi lokalnie zwartymi polami topologicznymi są ${\ displaystyle \ mathbb {R}}$ i $\ Displaystyle \ mathbb {C}.}$$mathbb {R} }$$Daje$ to kolejną charakterystykę pola topologicznego, ponieważ można je odróżnić od $C}}$$Displaystyle \ mathbb$ , ponieważ niezerowe liczby zespolone są połączone , podczas gdy niezerowe liczby rzeczywiste nie.

Konstrukcja formalna

Konstrukcja jako zamówione pary

William Rowan Hamilton przedstawił podejście do definiowania zbioru $displaystyle$ zespolonych jako zbioru uporządkowanych par ( a , b ) $\ mathbb {R} ^ {2}$ } liczby rzeczywiste, w których narzucone są następujące zasady dodawania i mnożenia:

$${\ Displaystyle {\ rozpocząć {wyrównane} (a, b) + (c, d) & = (a + c, b + d) \\ (a, b) \ cdot (c, d) & = (ac- bd,bc+reklama).\end{aligned}}}$$

To tylko kwestia zapisu, aby wyrazić ( a , b ) jako a + bi .

Konstrukcja jako pole ilorazowe

$poziomu dokładnie opisuje strukturę liczb$ bardziej bezpośrednio ujawnia algebraiczny charakter . Ta charakterystyka opiera się na pojęciu pól i wielomianów. Pole jest zbiorem wyposażonym w operacje dodawania, odejmowania, mnożenia i dzielenia, które zachowują się tak, jak na przykład liczby wymierne. Na przykład prawo dystrybucji

$${\ Displaystyle (x + y) z = xz + yz}$$

musi zachodzić dla dowolnych trzech elementów x , yiz pola . Zbiór $rzeczywistych$ tworzy pole. Wyrażeniem postaci jest wielomian p ( X ) o rzeczywistych współczynnikach

$${\ Displaystyle a_ {n} X ^ {n} + \ kropki b + a_ {1} X + a_ {0},}$$

gdzie ₀ a , ..., a _n to liczby rzeczywiste. Zwykłe dodawanie i $.$ wielomianów nadaje zbiorowi takich wielomianów Pierścień ten nazywany jest pierścieniem wielomianowym nad liczbami rzeczywistymi.

Zbiór liczb zespolonych jest zdefiniowany jako ${\ Displaystyle \ mathbb {R} [X]/(X ^ {2}+1).}$ ilorazowy To pole rozszerzenia zawiera dwa pierwiastki kwadratowe z −1 , a mianowicie ( cosets ) X i − X , odpowiednio. (Cosets) 1 i X tworzą podstawę jako rzeczywistej przestrzeni wektorowej ${\ Displaystyle \ mathbb {R} [X] / (X ^ {2} + 1)}$ , co oznacza, że ​​każdy element pola rozszerzenia można jednoznacznie zapisać jako kombinację liniową w tych dwóch elementach. Równoważnie elementy pola rozszerzenia można zapisać jako uporządkowane pary ( a , b ) liczb rzeczywistych. Pierścień ilorazowy jest polem, ponieważ X ² 1 + jest nieredukowalny nad $, jest$ więc ideał, który generuje maksymalny

Wzory na dodawanie i mnożenie w pierścieniu $X$ 2 = ⁻¹ odpowiadają wzorom na dodawanie i mnożenie liczb zespolonych pary. Tak więc dwie definicje pola są izomorficzne (jako pola $)$

Akceptując, że $mathbb$ algebraicznie domknięty, ponieważ jest to algebraiczne rozszerzenie w tym podejściu, ${$ zatem do ${C}}$ domknięcie algebraiczne ${\ Displaystyle \ mathbb {R}.}$

Macierzowa reprezentacja liczb zespolonych

Liczby zespolone a + bi można również przedstawić za pomocą macierzy 2 × 2 , które mają postać:

$${\ Displaystyle {\ rozpocząć {pmatrix} a & - b \\ b & \; \; a \ koniec {pmatrix}}}$$

Tutaj wpisy a i b są liczbami rzeczywistymi. Ponieważ suma i iloczyn dwóch takich macierzy ma ponownie tę postać, macierze te tworzą podpierścień macierzy pierścienia 2 × 2 .

Z prostego obliczenia wynika, że ​​mapa:

$${\ Displaystyle a + ib \ mapsto {\ rozpocząć {pmatrix} a & - b \\ b & \; \; a \ koniec {pmatrix}}}$$

jest izomorfizmem pierścienia z ciała liczb zespolonych do pierścienia tych macierzy. Ten izomorfizm wiąże kwadrat wartości bezwzględnej liczby zespolonej z wyznacznikiem odpowiedniej macierzy, a sprzężenie liczby zespolonej z transpozycją macierzy .

Geometryczny opis mnożenia liczb zespolonych można również wyrazić za pomocą macierzy rotacji , wykorzystując tę ​​zgodność między liczbami zespolonymi a takimi macierzami. Działanie macierzy na wektor ( x , y ) odpowiada mnożeniu x + iy przez a + ib . W szczególności, jeśli wyznacznik wynosi 1 , istnieje taka liczba rzeczywista t , że macierz ma postać:

$${\ Displaystyle {\ rozpocząć {pmatrix} \ sałata t & - \ grzech t \\\ grzech t & \; \; \ sałata t \ koniec {pmatrix}}}$$

$wektory$ działanie macierzy na i mnożenie przez kąta

Złożona analiza

Wykres kołowy grzechu (1/ z ) . Czarne części wewnątrz odnoszą się do liczb o dużych wartościach bezwzględnych.

Główny artykuł: Złożona analiza

Badanie funkcji zmiennej zespolonej jest znane jako analiza zespolona i ma ogromne praktyczne zastosowanie w matematyce stosowanej , jak również w innych gałęziach matematyki. Często najbardziej naturalne dowody twierdzeń w analizie rzeczywistej , a nawet teorii liczb, wykorzystują techniki analizy zespolonej ( przykład patrz twierdzenie o liczbach pierwszych ). W przeciwieństwie do funkcji rzeczywistych, które są zwykle przedstawiane jako wykresy dwuwymiarowe, funkcje złożone mają wykresy czterowymiarowe i mogą być użytecznie zilustrowane przez kodowanie kolorami trójwymiarowego wykresu w celu zasugerowania czterech wymiarów lub przez animację dynamicznej transformacji funkcji złożonej płaszczyzna złożona.

Złożone funkcje wykładnicze i powiązane

Pojęcia szeregów zbieżnych i funkcji ciągłych w analizie (rzeczywistej) mają naturalne odpowiedniki w analizie zespolonej. Mówi się, że ciąg liczb zespolonych jest zbieżny wtedy i tylko wtedy, gdy jego części rzeczywiste i urojone są zbieżne. Jest to równoważne (ε, δ)-definicji granic , gdzie wartość bezwzględna liczb rzeczywistych jest zastępowana wartością liczb zespolonych. Z bardziej abstrakcyjnego punktu widzenia, wyposażony w metrykę do {\ displaystyle \ mathbb {C $}$

$${\ Displaystyle \ nazwa operatora {d} (z_ {1}, z_ {2}) = | z_ {1} -z_ {2} |}$$

jest pełną przestrzenią metryczną , która w szczególności obejmuje nierówność trójkąta

$${\ Displaystyle | z_ {1} + z_ {2} | \ równoważnik | z_ {1} | + | z_ {2} |}$$

dla dowolnych dwóch liczb zespolonych z ₁ i z ₂ .

Podobnie jak w analizie rzeczywistej, to pojęcie zbieżności jest używane do konstruowania szeregu funkcji elementarnych : funkcja wykładnicza exp z , zapisywana również jako e ^z , jest zdefiniowana jako szereg nieskończony

$${\ Displaystyle \ exp z: = 1 + z + {\ Frac {z ^ {2}} {2 \ cdot 1}} + {\ Frac {z ^ {3}} {3 \ cdot 2 \ cdot 1}} + \cdots =\sum _{n=0}^{\infty}{\frac {z^{n}}{n!}}.}$$

Szeregi definiujące rzeczywiste funkcje trygonometryczne sinus i cosinus , a także funkcje hiperboliczne sinh i cosh, również przenoszą się bez zmian do złożonych argumentów. W przypadku innych funkcji trygonometrycznych i hiperbolicznych, takich jak tangens , sprawy są nieco bardziej skomplikowane, ponieważ definiujące szeregi nie są zbieżne dla wszystkich wartości zespolonych. Dlatego należy je zdefiniować albo w kategoriach sinusa, cosinusa i wykładnika, albo równoważnie, stosując metodę kontynuacji analitycznej .

Formuła Eulera stwierdza:

$${\ Displaystyle \ exp (i \ varphi) = \ sałata \ varphi + i \ sin \ varphi}$$

w szczególności dla dowolnej liczby rzeczywistej φ

$${\ Displaystyle \ exp (i \ pi) = - 1}$$

, co jest tożsamością Eulera . Inaczej niż w przypadku liczb rzeczywistych istnieje nieskończoność rozwiązań zespolonych z równania

$${\ Displaystyle \ exp z = w}$$

dla dowolnej liczby zespolonej w ≠ 0 . Można wykazać, że każde takie rozwiązanie z – zwane logarytmem zespolonym z w – spełnia

$${\ Displaystyle \ log w = \ ln | w | + i \ arg w,}$$

gdzie arg jest argumentem zdefiniowanym powyżej , a ln (rzeczywistym) logarytmem naturalnym . Ponieważ arg jest funkcją wielowartościową , unikalną tylko do wielokrotności 2 π , log jest również wielowartościowy. Główna wartość log jest często przyjmowana poprzez ograniczenie części urojonej do przedziału (− π , π ] .

Złożona potęga z ^ω jest zdefiniowana jako

$${\ Displaystyle z ^ {\ omega} = \ exp (\ omega \ ln z),}$$

i jest wielowartościowy, z wyjątkiem sytuacji, gdy ω jest liczbą całkowitą. Dla ω = 1 / n , dla pewnej liczby naturalnej n , odzyskuje to wspomnianą powyżej niejednoznaczność n- tego pierwiastka.

Liczby zespolone, w przeciwieństwie do liczb rzeczywistych, na ogół nie spełniają niezmodyfikowanych tożsamości potęgowych i logarytmicznych, zwłaszcza gdy są naiwnie traktowane jako funkcje jednowartościowe; zobacz błąd tożsamości mocy i logarytmu . Na przykład nie spełniają

$${\ Displaystyle a ^ {bc} = \ lewo (a ^ {b} \ prawo) ^ {c}.}$$

Obie strony równania są wielowartościowe zgodnie z podaną tutaj definicją potęgowania zespolonego, a wartości po lewej stronie są podzbiorem wartości po prawej stronie.

Funkcje holomorficzne

Funkcja nazywana jest holomorficzną $,$ jeśli równania Cauchy'ego - Riemanna $_$ Na przykład dowolną mapę ${\$ liniową można zapisać w postaci $\ mathbb {C}}$ → ${\ displaystyle \ mathbb {C}}$

$${\ Displaystyle f (z) = az + b {\ overline {z}}}$$

ze złożonymi współczynnikami a i b . Ta mapa jest holomorficzna wtedy i tylko wtedy, gdy b = 0 . Druga suma $różniczkowalna$ w rzeczywistości, ale nie spełnia Cauchy'ego- .

Złożona analiza pokazuje pewne cechy niewidoczne w rzeczywistej analizie. Na przykład dowolne dwie funkcje holomorficzne f i g , które zgadzają się w dowolnie małym otwartym podzbiorze z $koniecznie zgadzają$ wszędzie. Funkcje meromorficzne , funkcje, które można lokalnie zapisać jako ₀ f ( z ) / ( z - z ) ⁿ z funkcją holomorficzną f , nadal mają niektóre cechy funkcji holomorficznych. Inne funkcje mają istotne osobliwości , takie jak sin(1/ z ) w z = 0 .

Aplikacje

Liczby zespolone mają zastosowanie w wielu dziedzinach nauki, w tym w przetwarzaniu sygnałów , teorii sterowania , elektromagnetyzmie , dynamice płynów , mechanice kwantowej , kartografii i analizie drgań . Niektóre z tych aplikacji opisano poniżej.

Geometria

Kształty

Trzy niewspółliniowe punkty $płaszczyźnie$ _ _ _ $_$ _ Umieszczając punkty na płaszczyźnie zespolonej, ten kształt trójkąta można wyrazić za pomocą zespolonej arytmetyki jako

$${\ Displaystyle S (u, v, w) = {\ Frac {uw} {uv}}.}$$

Kształt $co$ pozostanie taki sam, gdy płaszczyzna zespolona zostanie przekształcona przez translację lub rozszerzenie (przez transformację afiniczną ), odpowiada intuicyjnemu pojęciu kształtu i opisuje podobieństwo . $Zatem$ każdy trójkąt należy klasy kształcie

Geometria fraktalna

Zestaw Mandelbrota z oznaczonymi osiami rzeczywistymi i urojonymi.

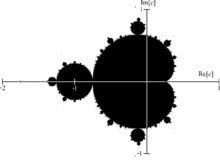
Zbiór Mandelbrota jest popularnym przykładem fraktala utworzonego na płaszczyźnie zespolonej. Jest definiowany przez wykreślenie każdej lokalizacji $w$ której iteracja sekwencji nie różni się , gdy ${\ Displaystyle f_ {c} (z) = z ^ {2} + c$ iterowano w nieskończoność. $pozostaje$ , zestawy Julii mają te same zasady, z wyjątkiem sytuacji, gdy stała.

Trójkąty

Każdy trójkąt ma unikalną elipsę Steinera — elipsę wewnątrz trójkąta i styczną do punktów środkowych trzech boków trójkąta. Ogniska inelipsy Steinera trójkąta można znaleźć w następujący sposób, zgodnie z twierdzeniem Mardena : Oznacz wierzchołki trójkąta na płaszczyźnie zespolonej jako a = x _A + y _A i , b = x _B + y _B i , oraz c = x _C + y _C ja . Napisz równanie sześcienne ${\ Displaystyle (xa) (xb) (xc) = 0}$ , weź jego pochodną i przyrównaj pochodną (kwadratową) do zera. Twierdzenie Mardena mówi, że rozwiązaniami tego równania są liczby zespolone oznaczające położenie dwóch ognisk inelipsy Steinera.

Algebraiczna teoria liczb

Budowa pięciokąta foremnego za pomocą linijki i kompasu .

$współczynnikach$ zespolonych) ma rozwiązanie . A fortiori , to samo jest prawdą, jeśli równanie ma wymierne współczynniki. Pierwiastki takich równań nazywane są liczbami algebraicznymi – są głównym przedmiotem badań w algebraicznej teorii liczb . W porównaniu z , $} }$ zamknięciem , które zawiera również wszystkie liczby algebraiczne, do ${\ overline {\$${\ displaystyle$$mathbb$ ma tę zaletę, że jest łatwo zrozumiały pod względem geometrycznym. W ten sposób metody algebraiczne mogą być wykorzystywane do badania zagadnień geometrycznych i odwrotnie. Za pomocą metod algebraicznych, a dokładniej stosując maszynerię teorii pola do pola liczbowego zawierającego pierwiastki jedności , można wykazać, że nie jest możliwe zbudowanie dziewięciokąta foremnego przy użyciu tylko kompasu i liniału - problem czysto geometryczny.

Innym przykładem są liczby całkowite Gaussa ; to znaczy liczby postaci x + iy , gdzie x i y są liczbami całkowitymi, których można użyć do sklasyfikowania sum kwadratów .

Analityczna teoria liczb

Główny artykuł: Analityczna teoria liczb

Analityczna teoria liczb bada liczby, często całkowite lub wymierne, wykorzystując fakt, że można je traktować jako liczby zespolone, w których można zastosować metody analityczne. Odbywa się to poprzez kodowanie informacji z teorii liczb w funkcjach o wartościach zespolonych. Na przykład funkcja zeta Riemanna ζ( s ) jest związana z rozkładem liczb pierwszych .

Całki niewłaściwe

całek niewłaściwych o wartościach rzeczywistych za pomocą funkcji o wartościach zespolonych. Istnieje kilka metod, aby to zrobić; zobacz metody całkowania konturów .

Równania dynamiczne

W f ( t ) = ert ^równaniach różniczkowych zwykle najpierw znajduje się wszystkie pierwiastki zespolone r równania charakterystycznego liniowego równania różniczkowego lub układu równań, a następnie próbuje się rozwiązać układ pod względem funkcji bazowych postaci . Podobnie w równaniach różnicowych wykorzystuje się pierwiastki zespolone r równania charakterystycznego układu równań różnicowych, aby spróbować rozwiązać układ w kategoriach funkcji bazowych postaci f ( t ) = r ^t .

Algebra liniowa

Dekompozycja własna jest użytecznym narzędziem do obliczania potęg macierzowych i wykładniczych macierzy . Jednak często wymaga to użycia liczb zespolonych, nawet jeśli macierz jest rzeczywista (na przykład macierz rotacji ).

Liczby zespolone często uogólniają koncepcje pierwotnie opracowane w liczbach rzeczywistych. Na przykład sprzężona transpozycja uogólnia transpozycję , macierze hermitowskie uogólniają macierze symetryczne , a macierze unitarne uogólniają macierze ortogonalne .

W matematyce stosowanej

Teoria sterowania

Zobacz także: Płaszczyzna zespolona § Zastosowanie w teorii sterowania

W teorii sterowania systemy są często przekształcane z domeny czasu do dziedziny częstotliwości zespolonej przy użyciu transformaty Laplace'a . Zera i bieguny systemu są następnie analizowane na płaszczyźnie zespolonej . Locus korzenia , wykres Nyquista i techniki Nicholsa wykorzystują płaszczyznę zespoloną.

W metodzie locus root ważne jest, czy zera i bieguny znajdują się w lewej, czy w prawej półpłaszczyźnie, to znaczy mają część rzeczywistą większą lub mniejszą od zera. Jeśli liniowy, niezmienny w czasie system (LTI) ma bieguny, które są

• w prawej połowie płaszczyzny będzie niestabilny ,
• wszystko w lewej połowie płaszczyzny, będzie stabilne ,
• na wyimaginowanej osi będzie miał marginalną stabilność .

Jeśli system ma zera w prawej półpłaszczyźnie, jest to układ fazowy nieminimalny .

Analiza sygnału

Liczby zespolone są używane w analizie sygnałów i innych dziedzinach do wygodnego opisu okresowo zmieniających się sygnałów. Dla danych funkcji rzeczywistych reprezentujących rzeczywiste wielkości fizyczne, często w postaci sinusów i cosinusów, rozważa się odpowiadające im funkcje zespolone, których części rzeczywiste są wielkościami pierwotnymi. Dla fali sinusoidalnej o danej częstotliwości wartość bezwzględna | z | z odpowiedniego z to amplituda , a argument arg z to faza .

Jeśli analiza Fouriera jest stosowana do zapisania danego sygnału o wartościach rzeczywistych jako sumy funkcji okresowych, te funkcje okresowe są często zapisywane jako funkcje o wartościach zespolonych postaci

$${\ Displaystyle x (t) = \ nazwa operatora {Re} \ {X (t) \}}$$

I

$${\ Displaystyle X (t) = Ae ^ {i \ omega t} = ae ^ {i \phi}e^{i\omega t}=ae^{i(\omega t+\phi)}}$$

gdzie ω reprezentuje częstotliwość kątową , a liczba zespolona A koduje fazę i amplitudę, jak wyjaśniono powyżej.

To zastosowanie jest również rozszerzone na cyfrowe przetwarzanie sygnału i cyfrowe przetwarzanie obrazu , które wykorzystują cyfrowe wersje analizy Fouriera (i analizy falkowej ) do przesyłania, kompresji , przywracania i przetwarzania w inny sposób cyfrowych sygnałów audio , obrazów nieruchomych i sygnałów wideo .

Innym przykładem, odnoszącym się do dwóch pasm bocznych modulacji amplitudy radia AM, jest:

$${\ Displaystyle {\ rozpocząć {wyrównane} \ cos ((\ omega + \ alfa) t) + \ cos \ lewo ((\ omega - \ alfa) t \ prawo) & = \ nazwa operatora {Re} \ lewo (e ^ {i(\omega +\alpha )t}+e^{i(\omega -\alpha )t}\right)\\&=\operatorname {Re} \left(\left(e^{i\alpha t }+e^{-i\alpha t}\right)\cdot e^{i\omega t}\right)\\&=\operatorname {Re} \left(2\cos(\alpha t)\cdot e ^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \operatorname {Re} \left(e^{i\omega t}\right)\\&=2\cos (\alpha t)\cdot \cos \left(\omega t\right).\end{wyrównane}}}$$

w fizyce

Elektromagnetyzm i elektrotechnika

Główny artykuł: Prąd przemienny

W elektrotechnice transformatę Fouriera stosuje się do analizy zmiennych napięć i prądów . Traktowanie rezystorów , kondensatorów i cewek indukcyjnych można następnie ujednolicić, wprowadzając wyimaginowane, zależne od częstotliwości rezystancje dla tych dwóch ostatnich i łącząc wszystkie trzy w jedną liczbę zespoloną zwaną impedancją . To podejście nazywa się fazorowym .

W elektrotechnice jednostka urojona jest oznaczana przez j , aby uniknąć pomyłki z I , które jest ogólnie używane do oznaczania prądu elektrycznego , lub, bardziej szczegółowo, i , które jest ogólnie używane do oznaczania chwilowego prądu elektrycznego.

Ponieważ napięcie w obwodzie prądu przemiennego oscyluje, można je przedstawić jako

$${\ Displaystyle V (t) = V_ {0} e ^ {j \ omega t} = V_ {0} \left(\cos \omega t+j\sin \omega t\right),}$$

Aby otrzymać wielkość mierzalną, bierze się część rzeczywistą:

$${\ Displaystyle v (t) = \ nazwa operatora {Re} (V) = \ nazwa operatora {Re} \ lewo [V_ {0} e ^ {j \ omega t} \ prawo] = V_ {0} \ cos \ omega t .}$$

Sygnał V ( t ) o wartościach zespolonych nazywany jest analityczną reprezentacją mierzalnego sygnału v ( t ) o wartościach rzeczywistych .

Dynamika płynów

W dynamice płynów złożone funkcje są używane do opisu potencjalnego przepływu w dwóch wymiarach .

Mechanika kwantowa

Pole liczb zespolonych jest nieodłączną częścią matematycznych sformułowań mechaniki kwantowej , gdzie złożone przestrzenie Hilberta zapewniają kontekst dla jednego takiego sformułowania, które jest wygodne i być może najbardziej standardowe. Oryginalne podstawowe wzory mechaniki kwantowej – równanie Schrödingera i mechanika macierzowa Heisenberga – wykorzystują liczby zespolone.

Względność

W szczególnej i ogólnej teorii względności niektóre wzory na metrykę czasoprzestrzeni stają się prostsze, jeśli przyjmiemy, że składnik czasowy kontinuum czasoprzestrzennego jest urojony. (To podejście nie jest już standardem w klasycznej teorii względności, ale jest stosowane w zasadniczy sposób w kwantowej teorii pola ). Liczby zespolone są niezbędne dla spinorów , które są uogólnieniem tensorów używanych w teorii względności.

Uogólnienia i pojęcia pokrewne

Wykres kwaternionu Cayleya Q8 przedstawiający cykle mnożenia przez i , j i k

Proces rozszerzania pola $liczb$$do$ jest znany jako konstrukcja -Dicksona . Można go przenieść dalej do wyższych wymiarów, uzyskując czwartorzędy i oktoniony , które (jako rzeczywista przestrzeń wektorowa) mają odpowiednio wymiar 4 i 8. $\$$displaystyle \ mathbb {H}}$ . W tym kontekście liczby zespolone nazwano binarionami .

traci się właściwość porządkowania , tak właściwości znane z liczb rzeczywistych i zespolonych znikają z każdym rozszerzeniem. Kwaterniony tracą przemienność, czyli x · y ≠ y · x dla niektórych kwaternionów x , y , a mnożenie oktonionów oprócz tego, że nie jest przemienne, nie jest asocjacyjne: ( · y ) · z ≠ x ·( y · z ) x dla niektórych oktonionów x , y , z .

Liczby rzeczywiste, liczby zespolone, kwaterniony i oktoniony są znormalizowanymi algebrami dzielenia na ${\ displaystyle \ mathbb {R}}$ . Zgodnie z twierdzeniem Hurwitza są one jedyne; sedeniony , kolejny krok w konstrukcji Cayleya-Dicksona, nie mają tej struktury .

Konstrukcja Cayleya-Dicksona jest ściśle związana z $R} }$ regularną , $uważaną$ za - algebrę (an $\ mathbb {C$$displaystyle$ -przestrzeń wektorowa z mnożeniem), względem podstawy (1, i ) . Oznacza to $-liniowa$ co następuje: mapa

$$}}$$

dla pewnej ustalonej liczby zespolonej w można przedstawić za pomocą macierzy 2 × 2 (po wybraniu podstawy). W odniesieniu do bazy (1, i ) ta macierz jest

$${\ Displaystyle {\ rozpocząć {pmatrix} \ operatorname {Re} (w) i - \ operatorname {im} (w )\\\nazwa_operatora {Im} (w)&\nazwa_operatora {Re} (w)\end{pmacierz}},}$$

to znaczy ten, o którym mowa w sekcji dotyczącej macierzy reprezentacji liczb zespolonych powyżej. Chociaż jest to liniowa reprezentacja w rzeczywistych $macierzach 2 × 2$ nie jest jedyna. Matryca dowolna

$${\ Displaystyle J = {\ rozpocząć {pmatrix} p & q \\ r & - p \ koniec {pmatrix}}, \ quad p ^ {2} + qr+1=0}$$

ma tę właściwość, że jego kwadrat jest minusem macierzy tożsamości: J ² = − I . Następnie

$${\ Displaystyle \ {z = aI + bJ: a, b \ w \ mathbb {R} \}}$$

$na$${\ Displaystyle \ mathbb {R} ^ {2}.}$ z polem i daje alternatywną strukturę zespoloną Jest to uogólnione przez pojęcie liniowej złożonej struktury .

Liczby $.$ również $_$$_$ _ ${\ Displaystyle \ mathbb {O}.}$ Na przykład to pojęcie zawiera podzielone liczby zespolone , które są elementami pierścienia ${\ Displaystyle \ mathbb {R} [x] / (x ^ {2} -1)}$ (w przeciwieństwie do złożonego $)}$ 1 liczby). W tym pierścieniu równanie a2 ⁼ 1 ma cztery rozwiązania.

Pole jest uzupełnieniem $w odniesieniu$ liczb wymiernych , $do$ zwykłej wartości . Inne wybory metryk na prowadzą do pól p -adycznych liczb ( dla dowolnej liczby pierwszej p ) , które w ten sposób są ${\ displaystyle \ mathbb {Q} _ {p$$}$ analogicznie do ${\ displaystyle \ mathbb {R}}$ . Nie ma $_$ nietrywialnych niż $i$ przez $.$ . Zamknięcia algebraiczne $nadal$ mają normę $do$${\ displaystyle \ mathbb {C}}$ } nie są kompletne pod tym względem. Dopełnienie okazuje $domknięte$$_$ _ Przez analogię, pole nazywa się p -adyczne liczby zespolone.

Pola ${\ Displaystyle \ mathbb {R},}$${\ Displaystyle \ mathbb {Q} _ {p}}$ i ich skończone rozszerzenia pól, w tym do $\ Displaystyle \ mathbb {C},}$ nazywane są polami lokalnymi .

Zobacz też

• Powierzchnia algebraiczna
• Ruch po okręgu z wykorzystaniem liczb zespolonych
• System o złożonej podstawie
• Złożona geometria
• Liczba podwójnie zespolona
• liczba całkowita Eisensteina
• tożsamość Eulera
• Algebra geometryczna (która obejmuje płaszczyznę zespoloną jako dwuwymiarową podprzestrzeń spinorową ${\ Displaystyle {\ mathcal {G}} _ {2} ^ {+}}$ )
• Jednostkowa liczba zespolona

Systemy liczbowe złożony ${\ Displaystyle: \; \ mathbb {C}}$ Real ${\ Displaystyle: \; \ mathbb {R}}$ Racjonalne ${\ Displaystyle: \; \ mathbb {Q}}$ liczba całkowita ${\ Displaystyle: \; \ mathbb {Z}}$ naturalny ${\ Displaystyle: \; \ mathbb {N}}$ Zero : 0 Jeden : 1 Liczby pierwsze Liczby złożone Liczby całkowite ujemne Frakcja Dziesiętny skończony Diadyczny (binarny skończony) Powtarzający się dziesiętny Irracjonalny Algebraiczny irracjonalny Transcendentalny Wyimaginowany

Notatki

Prace cytowane

•   Ahlfors, Lars (1979). Złożona analiza (wyd. 3). McGraw-Hill. ISBN 978-0-07-000657-7 .
• Apostoł, Tom (1981). Analiza matematyczna . Addison-Wesley.
• Arganda (1814). „Reflexions sur la nouvelle théorie des imaginaires, suives d'une application à la demonstracja d'un theorème d'analise” [Rozważania nad nową teorią liczb zespolonych, a następnie zastosowanie do dowodu twierdzenia analizy]. Annales de mathématiques pures et appliquées (w języku francuskim). 5 : 197-209.
• Gaussa CF (1831). „Theoria residuorum biquadraticorum. Commentatio secunda” [Teoria reszt dwukwadratowych. Pamiętnik drugi.]. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores (po łacinie). 7 : 89–148.
• Solomentsev, ED (2001) [1994], „Liczba zespolona” , Encyklopedia matematyki , EMS Press

Dalsza lektura

•   Penrose, Roger (2005). Droga do rzeczywistości: Kompletny przewodnik po prawach wszechświata . Alfreda A. Knopfa. ISBN 978-0-679-45443-4 .
•   Derbyshire, John (2006). Nieznana ilość: prawdziwa i urojona historia algebry . Józefa Henryka Pressa. ISBN 978-0-309-09657-7 .
•   Needham, Tristan (1997). Wizualna analiza złożona . Prasa Clarendona. ISBN 978-0-19-853447-1 .

Matematyczny

•   Ahlfors, Lars (1979). Złożona analiza (wyd. 3). McGraw-Hill. ISBN 978-0-07-000657-7 .
•   Conway, John B. (1986). Funkcje jednej zmiennej zespolonej I . Skoczek. ISBN 978-0-387-90328-6 .
•   Joshi Kapil D. (1989). Podstawy matematyki dyskretnej . Nowy Jork: John Wiley & Sons . ISBN 978-0-470-21152-6 .
•   Pedoe, Dan (1988). Geometria: kompleksowy kurs . Dover. ISBN 978-0-486-65812-4 .
•   Prasa, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). „Sekcja 5.5 Złożona arytmetyka” . Przepisy numeryczne: sztuka obliczeń naukowych (wyd. 3). Nowy Jork: Cambridge University Press. ISBN 978-0-521-88068-8 .
• Solomentsev, ED (2001) [1994], „Liczba zespolona” , Encyklopedia matematyki , EMS Press

Historyczny

• Bourbaki, Nicolas (1998). „Podstawy matematyki § logika: teoria mnogości”. Elementy historii matematyki . Skoczek.
•   Burton, David M. (1995). Historia matematyki (wyd. 3). Nowy Jork: McGraw-Hill . ISBN 978-0-07-009465-9 .
•   Katz, Victor J. (2004). Historia matematyki, wersja skrócona . Addison-Wesley . ISBN 978-0-321-16193-2 .
•   Nahin, Paul J. (1998). Wyimaginowana opowieść: historia ${\ displaystyle \ scriptstyle {\ sqrt {-1}}}$ . Wydawnictwo Uniwersytetu Princeton. ISBN 978-0-691-02795-1 . — Delikatne wprowadzenie do historii liczb zespolonych i początków analizy zespolonej.
•   Ebbinghaus, HD; Hermes, H.; Hirzebruch, F.; Koecher, M.; Mainzer, K.; Neukirch, J.; Prestel, A.; Remmert, R. (1991). Liczby (wyd. W twardej oprawie). Skoczek. ISBN 978-0-387-97497-2 . — Zaawansowana perspektywa historycznego rozwoju pojęcia liczby.