Formuła podobna do maszyny

W matematyce formuły podobne do maszyn są popularną techniką obliczania liczby π (stosunek obwodu do średnicy koła ) do dużej liczby cyfr . Są to uogólnienia Johna Machin'a z 1706 roku:

${\ Displaystyle {\ Frac {\ pi} {4}} = 4 \ arctan {\ Frac {1} {5}} - \ arctan {\ Frac {1} {239}}}$

którego używał do obliczania liczby π z dokładnością do 100 miejsc po przecinku.

Formuły podobne do maszyn mają postać

${\ Displaystyle c_ {0} {\ Frac {\ pi} {4}} = \ suma _ {n = 1} ^ {N} c_ { n}\arctan {\frac {a_{n}}{b_{n}}}}$

 

 

 

 

()

gdzie jest dodatnią liczbą całkowitą, ${n}} są$${\ displaystyle c_$ całkowitymi niezerowymi ze znakiem i ${\ displaystyle a_ {n}}$ i ${\ displaystyle b_ {n}}$ są dodatnimi liczbami całkowitymi takimi, że za $\ displaystyle a_ {n}<b_ {n}}$ .

Wzory te są używane w połączeniu z szeregiem Gregory'ego , rozszerzeniem szeregu Taylora dla arcus tangens :

${\ Displaystyle \ arctan x = \ suma _ {n =0}^{\infty}}{\frac {(-1)^{n}}{2n+1}}x^{2n+1}=x-{\frac {x^{3}}{3} }+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots }$

 

 

 

 

()

Pochodzenie

wzór na dodawanie kątów dla arcus tangens

${\ Displaystyle \ arctan {\ Frac {a_ {1}}$

 

 

 

 

()

Jeśli

$${\ Displaystyle - {\ Frac {\ pi} {2}}< \ arctan {\ Frac {a_ {1}} {b_ {1}}} + \ arctan {\ Frac {a_ {2}} {b_ {2 }}}<{\frac {\pi}}{2}}.}$$

Wszystkie wzory podobne do Machin można wyprowadzić przez wielokrotne zastosowanie równania 3 . Jako przykład pokazujemy wyprowadzenie oryginalnego wzoru Machina:

$${\ Displaystyle {\ rozpocząć {wyrównane} 2 \ arctan {\ Frac {1} {5}} & = \ arctan {\ Frac {1} {5}} + \ arctan {\ Frac {1} {5}} \ \&=\arctan {\frac {1\cdot 5+1\cdot 5}{5\cdot 5-1\cdot 1}}\\&=\arctan {\frac {10}{24}}\\& =\arctan {\frac {5}{12}},\end{wyrównane}}}$$

i konsekwentnie

$${\ Displaystyle {\ rozpocząć {wyrównane} 4 \ arctan {\ Frac {1} {5}} & = 2 \ arctan {\ Frac {1} {5}} + 2 \ arctan {\ Frac {1} {5} }\\&=\arctan {\frac {5}{12}}+\arctan {\frac {5}{12}}\\&=\arctan {\frac {5\cdot 12+5\cdot 12} {12\cdot 12-5\cdot 5}}\\&=\arctan {\frac {120}{119}}.\end{aligned}}}$$

Dlatego też

$${\ Displaystyle {\ rozpocząć {wyrównane} 4 \ arctan {\ Frac {1} {5}} - {\ Frac {\ pi }{4}}&=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{1}}\\&=4\arctan {\frac {1}{5}} +\arctan {\frac {-1}{1}}\\&=\arctan {\frac {120}{119}}+\arctan {\frac {-1}{1}}\\&=\arctan {\frac {120\cdot 1+(-1)\cdot 119}{119\cdot 1-120\cdot (-1)}}\\&=\arctan {\frac {1}{239}},\ koniec {wyrównany}}}$$

i tak ostatecznie

$${\ Displaystyle {\ Frac {\ pi} {4}} = 4 \ arctan {\ Frac {1} {5}} - \ arctan {\ Frac {1} {239}}.}$$

Wnikliwym sposobem wizualizacji równania 3 jest zobrazowanie, co się stanie, gdy dwie liczby zespolone zostaną pomnożone przez siebie:

${\ Displaystyle (b_ {1} + a_ {1} \ operatorname {i}) \ cdot (b_ {2} + a_ {2} \ operatorname {i} )}$

${\ Displaystyle = b_ {1} b_ {2} + a_ {2} b_ {1} \ operatorname {i} +a_{1}b_{2}\mathrm {i} -a_{1}a_{2}}$

${\ Displaystyle = (b_ {1} b_ {2} -a_ {1} a_ {2}) + (a_{1}b_{2}+a_{2}b_{1})\cdot \mathrm {i} }$

 

 

 

 

()

Kąt związany z liczbą zespoloną jest określony przez: ${\ Displaystyle (b_ {n} + a_ {n} \ operatorname {i})}$

${\ Displaystyle \ arctan {\ Frac {a_ {n}}} {b_ {n}}}}$

Zatem w równaniu 4 kąt związany z iloczynem wynosi:

${\ Displaystyle \ arctan {\ Frac {a_ {1} b_ {2} + a_ {2} b_ {1}} {b_ { 1}b_{2}-a_{1}a_{2}}}}$

Zauważ, że jest to to samo wyrażenie, które występuje w równaniu 3 . Zatem równanie 3 można zinterpretować jako mówiące, że mnożenie dwóch liczb zespolonych oznacza dodanie związanych z nimi kątów (patrz mnożenie liczb zespolonych ).

Ekspresja:

${\ Displaystyle c_ {n} \ arctan {\ Frac {a_ {n}} {b_ {n}}}}$

jest kątem związanym z:

${\ Displaystyle (b_ {n} + a_ {n} \ operatorname {i}) ^ {c_ {n}}}$

Równanie 1 można przepisać jako:

${\ Displaystyle k \ cdot (1 + \ operatorname {i}) ^ {c_ {0}} = \ prod _ {n=1}^{N}(b_{n}+a_{n}\mathrm {i} )^{c_{n}}}$

Tutaj jest $,$ która odpowiada za różnicę wielkości między wektorami po obu stronach równania. Wielkości można zignorować, istotne są tylko kąty.

Używanie liczb zespolonych

Inne formuły mogą być generowane przy użyciu liczb zespolonych. Na przykład kąt liczby zespolonej $b za$ przez $}}$$\ textstyle \ arctan {\ frac {$ a gdy mnoży się liczby zespolone, dodaje się ich kąty. Jeśli za $= b},$ to ${\ textstyle \ arctan {\ Frac {b} {a}}}$ wynosi 45 stopni lub ${\ textstyle {\ frac {\ pi} {4}}}$ radianów. Oznacza to, że jeśli część rzeczywista i część zespolona są równe, to arcus tangens będzie równy ${\ textstyle {\ frac {\ pi} {4}}}$ . Ponieważ arcus tangens jedynki ma bardzo wolne tempo zbieżności, jeśli znajdziemy dwie liczby zespolone, które po pomnożeniu dadzą tę samą część rzeczywistą i urojoną, otrzymamy formułę podobną do Machin. Przykładem jest ${\ textstyle (2+ \ operatorname {i} )}$ i ${\ textstyle (3+ \ operatorname {i})}$ . Jeśli je pomnożymy, otrzymamy ${\textstyle (5+5\mathrm {i} )}$ . Dlatego ${\ textstyle \ arctan {\ Frac {1} {2}} + \ arctan {\ Frac {1} {3}} = {\ Frac {\ pi} {4}}}$ .

Jeśli chcesz użyć liczb zespolonych, aby pokazać, że ${\ textstyle {\ Frac {\ pi} {4}} = 4 \ arctan {\ frac {1} {5} }-\arctan {\frac {1}{239}}}$ musisz najpierw wiedzieć, że mnożąc kąty, liczbę zespoloną podwyższasz do potęgi liczby, przez którą mnożysz. Więc ${\ textstyle (5+ \ operatorname {i}) ^ {4} (239- \ operatorname {i}) = (1+ \ operatorname {i}) \ cdot 2 ^ {2} \ cdot 13^{4}}$ a ponieważ część rzeczywista i część urojona są sobie równe, to ${\ textstyle 4 \ arctan {\ frac {1} {5}} - \ arctan {\ frac {1} {239}} = {\ frac {\ pi} {4}} ~.}$

miarę Lehmera

Jednym z najważniejszych parametrów charakteryzujących wydajność obliczeniową formuły typu Machin jest miara Lehmera, zdefiniowana jako

${\ Displaystyle {\ to {\ lambda}} = \ suma _ {n = 1} ^ {N} {\ Frac {1} {\ dziennik _{10}(b_{n}/a_{n})}}}$ .

Aby uzyskać miarę Lehmera jak najmniejszą, konieczne jest zmniejszenie stosunku dodatnich liczb całkowitych $w$ liczby warunki w formule podobnej do Machin. W dzisiejszych czasach $miarą$ Lehmera jest $\ około 1,51244}$ ze względu na H. Chien-Lih (1997), którego wzór podobny jest pokazany poniżej . We wzorach podobnych do Machin bardzo często zdarza się, że wszystkie liczniki ${\ displaystyle a_ {n} = 1 ~.}$

Formuły dwuczłonowe

W szczególnym przypadku, w którym licznik ma dokładnie cztery rozwiązania mające tylko dwa wyrazy. za ${\ displaystyle a_ {n} = 1}$ Wszystkie cztery zostały znalezione przez Johna Machin w latach 1705-1706, ale tylko jeden z nich stał się szeroko znany, gdy został opublikowany w książce Williama Jonesa Synopsis Palmariorum Matheseos , więc pozostałe trzy są często przypisywane innym matematykom. To są

Eulera 1737 (znany Machinowi 1706):

${\ Displaystyle {\ Frac {\ pi}} {4}} = \ arctan {\ Frac {1} {2}} + \ arctan {\ Frac {1} {3} }}}$

Hermann 's 1706 (znany Machinowi 1706):

${\ Displaystyle {\ Frac {\ pi}} {4}} = 2 \ arctan {\ Frac {1} {2}} - \ arctan {\ Frac {1} {7}}}$

Hutton's lub Vega's (znany Machinowi 1706):

${\ Displaystyle {\ Frac {\ pi}} {4}} = 2 \ arctan {\ Frac {1} {3}} + \ arctan {\ Frac {1} {7}}}$

i Machin's 1706:

${\ Displaystyle {\ Frac {\ pi}} {4}} = 4 \ arctan {\ Frac {1} {5}} - \ arctan {\ Frac {1} {239}}}$ .

W ogólnym przypadku, gdy wartość licznika $.$ jest ograniczona, istnieje nieskończenie wiele innych Na przykład:

${\ Displaystyle {\ Frac {\ pi}}} = 22 \ arctan {\ Frac {1} {28} }} + \ arctan {\ frac {1744507482180328366854565127} {98646395734210062276153190241239}}}$

Lub

${\ Displaystyle {\ Frac {\ pi} {4}} = 22 \ arctan {\ Frac {24478} {873121}} + 17 \ arctan {\ Frac { 685601}{69049993}}}$

 

 

 

 

()

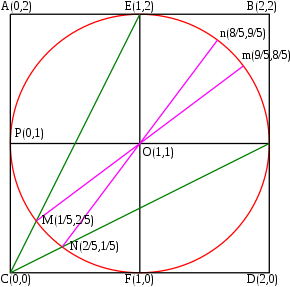
Przykład

Na sąsiednim diagramie przedstawiono zależność między arcus tangensami a ich polami. Z diagramu mamy:

${\ Displaystyle {\ rozpocząć {tablica}} {ll} {\ rm {obszar}} (PON) & = {\ rm {obszar}} (MOF) = \ pi \ razy {\ frac {\angle MOF}{2\pi}}=\angle MEF=\arctan {1 \over 2}\\{\rm {obszar}}(POM)&={\rm {obszar}}(NOF)= \arctan {1 \over 3}\\{\rm {obszar}}(POF)&={\pi \over 4}=\arctan {1 \over 2}+\arctan {1 \over 3}\\{ \rm {obszar}}(MON)&=\arctan {1 \over 7}\\\arctan {1 \over 2}&=\arctan {1 \over 3}+\arctan {1 \over 7},\ koniec {tablica}}}$

związek, który można znaleźć również za pomocą następującego obliczenia w obrębie liczb zespolonych

${\ Displaystyle (3+ \ operatorname {i}) (7+ \ operatorname {i}) = 21-1 + (3 + 7) \ operatorname {i} = 10 \ cdot (2+ \ operatorname {i}). }$

Więcej warunków

Rekord liczby π z 2002 r. , 1 241 100 000 000, uzyskał Yasumasa Kanada z Uniwersytetu Tokijskiego . Obliczenia przeprowadzono na 64-węzłowym superkomputerze Hitachi z 1 terabajtem pamięci głównej, wykonującym 2 biliony operacji na sekundę. Zastosowano dwa następujące równania:

${\ Displaystyle {\ Frac {\ pi} {4}} = 12 \ arctan {\ Frac {1} {49}}+32\arctan {\frac {1}{57}}-5\arctan {\frac {1}{239}}+12\arctan {\frac {1}{110443}}}$

Kikuo Takano ( 1982).

${\ Displaystyle {\ Frac {\ pi} {4}} = 44 \ arctan {\ Frac {1} {57}} + 7 \ arctan { \frac {1}{239}}-12\arctan {\frac {1}{682}}+24\arctan {\frac {1}{12943}}}$

FCM Störmer (1896).

Stosuje się dwa równania, aby można było sprawdzić, czy oba dają ten sam wynik; pomocne jest ponowne wykorzystanie w równaniach niektórych, ale nie wszystkich arcus tangensów, ponieważ trzeba je obliczyć tylko raz - zwróć uwagę na ponowne wykorzystanie 57 i 239 powyżej.

Podobne do maszyny wzory na π można skonstruować, znajdując zbiór liczb, w których rozkłady na czynniki pierwsze b ² + 1 razem używają nie bardziej odrębnych liczb pierwszych niż liczba elementów w zbiorze, a następnie używając albo algebry liniowej, albo podstawy LLL- algorytm redukcji do konstruowania liniowych kombinacji arcus tangensów ${\ Displaystyle \ arctan {\ Frac {1} {b_ {n}}}}$ odwrotności mianowników liczb całkowitych ${\ Displaystyle b_ {n}}$ . Na przykład dla powyższego wzoru Størmer mamy

${\ Displaystyle 57 ^ {2} + 1 = 2 \ cdot 5 ^ {3} \ cdot 13}$

${\ Displaystyle 239 ^ {2 } + 1 = 2 \ cdot 13 ^ {4}}$

${\ Displaystyle 682 ^ {2} +1 = 5 ^ {3} \ cdot 61 ^ {2}}$

${\ Displaystyle 12943 ^ {2} + 1 = 2 \ cdot 5 ^ {4} \ cdot 13 ^ {3} \ cdot 61}$

więc cztery wyrażenia używające między sobą tylko liczb pierwszych 2, 5, 13 i 61.

W 1993 roku Jörg Uwe Arndt znalazł formułę 11-członową:

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {\ pi} {4}} = &\; 36462 \ arctan {\ Frac {1} {390112}} + 135908 \ arctan {\ Frac {1} {485298} }+274509\arctan {\frac {1}{683982}}\\&-39581\arctan {\frac {1}{1984933}}+178477\arctan {\frac {1}{2478328}}-114569\arctan {\frac {1}{3449051}}\\&-146571\arctan {\frac {1}{18975991}}+61914\arctan {\frac {1}{22709274}}-69044\arctan {\frac {1 }{24208144}}\\&-89431\arctan {\frac {1}{201229582}}-43938\arctan {\frac {1}{2189376182}}\\\koniec {wyrównane}}}$

używając zestawu 11 liczb pierwszych ${\ Displaystyle \ {2,5,13,17,29,37,53,61,89,97,101 \}.}$

Inną formułę, w której 10 argumentów $:$ jest takich samych jak powyżej, odkrył Hwang Chien-Lih (黃 見 利) (2004), więc łatwiej jest sprawdzić, czy oba dają ten sam wynik

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {\ pi} {4}} = &\; 36462 \ arctan {\ Frac {1} {51387}} + 26522 \ arctan {\ Frac {1} {485298} }+19275\arctan {\frac {1}{683982}}\\&-3119\arctan {\frac {1}{1984933}}-3833\arctan {\frac {1}{2478328}}-5183\arctan {\frac {1}{3449051}}\\&-37185\arctan {\frac {1}{18975991}}-11010\arctan {\frac {1}{22709274}}+3880\arctan {\frac {1 }{24208144}}\\&-16507\arctan {\frac {1}{201229582}}-7476\arctan {\frac {1}{2189376182}}\\\koniec {wyrównane}}}$

Zauważysz, że te wzory ponownie wykorzystują wszystkie te same arcus tangensy po pierwszym. Konstruuje się je, szukając liczb, w których b ² + 1 jest podzielne tylko przez liczby pierwsze mniejsze niż 102.

Najbardziej wydajna obecnie znana formuła podobna do Machin do obliczania π to:

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {\ pi} {4}} = &\; 183 \ arctan {\ Frac {1} {239}} + 32 \ arctan {\ Frac {1} {1023} }-68\arctan {\frac {1}{5832}}\\&+12\arctan {\frac {1}{110443}}-12\arctan {\frac {1}{4841182}}-100\arctan {\frac {1}{6826318}}\\\end {wyrównane}}}$

(Hwang Chien-Lih, 1997)

gdzie zbiór liczb pierwszych to ${\ Displaystyle \ {2,5,13,229,457,1201 \}.}$

Dalszym udoskonaleniem jest użycie „Procesu Todda”, jak opisano w; prowadzi to do wyników takich jak

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {\ pi} {4}} = &\; 183 \ arctan {\ Frac {1} {239}} + 32 \ arctan {\ Frac {1} {1023} }-68\arctan {\frac {1}{5832}}\\&+12\arctan {\frac {1}{113021}}-100\arctan {\frac {1}{6826318}}\\&- 12 \ arctan {\ frac {1}{33366019650}} + 12 \ arctan {\ frac {1}{43599522992503626068}} \\\ koniec {wyrównane}}}$

(Hwang Chien-Lih, 2003)

gdzie duża liczba pierwsza 834312889110521 dzieli b _n ² + 1 ostatnich dwóch indeksów. M. Wetherfield znaleziony w 2004 roku

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {\ pi} {4}} = &\; 83 \ arctan {\ Frac {1} {107}} + 17 \ arctan {\ Frac {1} {1710} }-22\arctan {\frac {1}{103697}}\\&-24\arctan {\frac {1}{2513489}}-44\arctan {\frac {1}{18280007883}}\\&+ 12\arctan {\frac {1}{7939642926390344818}}\\&+22\arctan {\frac {1}{3054211727257704725384731479018}}.\\\end {wyrównane}}}$

Więcej metod

Istnieją dalsze metody wyprowadzania wzorów podobnych do Machin $odwrotnością$ liczb całkowitych. Jeden jest określony przez następujący wzór:

${\ Displaystyle {\ Frac {\ pi} {4}} = 2 ^ {k-1} \ cdot \ arctan {\ Frac {1} {A_ {k}}} + \ suma \ limity _ {m = 1} ^{M}\arctan {\frac {1}{\left\lfloor B_{k,m}\right\rfloor}}+\arctan {\frac {1}{B_{k,M+1}}}, }$

Gdzie

${\ displaystyle a_ {0}: = 0}$

i rekurencyjnie

${\ Displaystyle a_ {k}: = {\ sqrt {2 + a_ {k-1}}}, \ ;A_{k}:=\left\lfloor {\frac {a_{k}}{\sqrt {2-a_{k-1}}}}\right\rfloor}$

I

${\ Displaystyle B_ {k, 1}: = {\ Frac {2} {\ lewo ({\ dfrac { A_{k}+\mathrm {i}}{A_{k}-\mathrm {i} }}\right)^{2^{k-1}}-\namehrm {i} }}-\namehrm {i } }$

i rekurencyjnie

${\ Displaystyle B_ {k, m}: = {\ Frac {1+ \ lewo \ lfloor B_ {k, m-1} \ prawo \ rfloor B_ {k, m-1}}} {\ lewo \ lfloor B_ {k ,m-1}\prawa\rpodłoga -B_{k,m-1}}}~.}$

Np. dla ${\ displaystyle k = 4}$ i ${\ displaystyle M = 5}$ otrzymujemy: k = 4 {\ displaystyle k = 4}

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {\ pi} {4}} = & \; 8 \ arctan {\ Frac {1} {10}} - \ arctan {\ Frac {1} {84}} -\arctan {\frac {1}{21342}}\\&-\arctan {\frac {1}{991268848}}-\arctan {\frac {1}{193018008592515208050}}\\&-\arctan {\ frac {1}{197967899896401851763240424238758988350338}}\\&-\arctan {\frac {1}{1175738681681753529302777528441941267679919150085370188369 32014293678271636885792397}}\end{wyrównane}}}$

Potwierdza to następujący kod MuPAD:

  
   z  :=  (  10  +  ja  )  ^  8  *  (  84  -  ja  )  *  (  21342  -  ja  )  *  (  991268848  -  ja  )  *  (  193018008592515208050  -  ja  )  \  *  (  19796789989640185176324042423875898835 0338   -  ja  )  \  *  ( 
 117573868168175352930277752844194126767991915008537018836932014293678271636885792397  -  I  )  :  Re  (  z  )  -  Im  (  z  ) 
0

oznaczający

${\ Displaystyle {\ rozpocząć {wyrównane} z: = & \, (10+ \ operatorname {i}) ^ {8} \ cdot (84- \ operatorname {i}) \ cdot (21342- \ operatorname {i}) \cdot (991268848-\mathrm {i} )\cdot (193018008592515208050-\mathrm {i})\\&\cdot (197967899896401851763240424238758988350338-\mathrm {i})\\ &\cdot (117573868168175352930277752844194126767991915008537018836932014293678271636885792397-\mathrm {i} ) \\\;=&\,(1+\mathrm {i} )\cdot \Re (z)~.\end{wyrównane}}}$

Efektywność

W przypadku dużych obliczeń algorytm podziału binarnego $szybciej$ niż przez naiwne dodawanie wyrazów z szeregu Taylora pojedynczo. W praktycznych implementacjach, takich jak y-cruncher, istnieje stosunkowo duży stały narzut na semestr plus czas proporcjonalny do ${\ Displaystyle 1/\ log b_ {n}}$ , a punkt malejących zwrotów pojawia się poza trzema lub czterema arcus tangensami w sumie; dlatego powyższe obliczenia superkomputera wykorzystywały tylko wersję czteroczłonową.

Celem tej sekcji nie jest oszacowanie rzeczywistego czasu działania danego algorytmu. Zamiast tego intencją jest jedynie opracowanie względnej miary, za pomocą której można porównać ze sobą dwa algorytmy.

Niech $będzie$ liczbą cyfr, do których należy obliczyć. $\ pi}$

Niech $($ liczbą wyrazów w Taylora patrz równanie 2 ).

Niech będzie ilością czasu spędzonego na każdej cyfrze (dla każdego wyrazu w szeregu $Taylora$

Szereg Taylora będzie zbieżny, gdy:

${\ Displaystyle \ lewo (\ lewo ({\ Frac {b_ {n}}} {a_ {n}}} \ prawo) ^ {2} \ prawo) ^{N_{t}}=10^{N_{d}}}$

Zatem:

${\ Displaystyle N_ {t} = N_ {d} \ quad {\ Frac {\ ln 10} {2 \ ln {\ Frac {b_ {n}} {jakiś}}}}}}$

$W$ przypadku pierwszego wyrazu w szeregu Taylora wszystkie muszą zostać przetworzone Jednak w ostatnim wyrazie szeregu Taylora do przetworzenia pozostała tylko jedna cyfra. We wszystkich pośrednich terminach liczbę cyfr do przetworzenia można przybliżyć za pomocą interpolacji liniowej. Zatem suma jest dana przez:

${\ Displaystyle {\ Frac {N_ {d} N_ {t}} {2}}}$

Czas pracy jest określony przez:

${\ Displaystyle {\ mathit {czas}} = {\ Frac {u_ {n} N_ {d} N_ {t}} {2}}}$

Łącząc równania, czas działania jest określony wzorem:

${\ Displaystyle {\ mathit {czas}} = {\ Frac {u_ {n} N_{d}}^{2}\ln 10}{4\ln {\frac {b_{n}}{a_{n}}}}}={\frac {k\,u_{n}}{\ ln {\frac {b_{n}}{a_{n}}}}}}$

Gdzie jest $,$ która łączy wszystkie inne stałe. Ponieważ jest to $.$ względna, wartość można zignorować

Całkowity czas, we wszystkich wyrazach równania 1 , jest określony wzorem:

${\ Displaystyle {\ mathit {czas}} = \ suma _ {n = 1} ^ {N} {\ Frac {u_ {n}} {\ln {\frac {b_{n}}{a_{n}}}}}}$

${\ displaystyle u_ {n}}$ nie można dokładnie modelować bez szczegółowej znajomości konkretnego oprogramowania. Niezależnie od tego, przedstawiamy jeden z możliwych modeli.

Oprogramowanie spędza większość czasu na obliczaniu szeregu Taylora na podstawie równania 2 . Podstawową pętlę można podsumować w następującym pseudokodzie:

${\ Displaystyle 1: \ quad {\ mathit {termin}} \ quad * = \ quad {a_ {n}} ^ {2}}$

${\ Displaystyle 2: \ quad {\ mathit {termin}} \ quad / = \ quad - {b_ {n}} ^ {2}}$

${\ Displaystyle 3: \ quad {\ mathit {tmp}} \ quad = \ quad {\ mathit {termin}} \ quad / \ quad (2 * n + 1)}$

${ \ Displaystyle 4: \ quad {\ mathit {sum}} \ quad + = \ quad {\ mathit {tmp}}}$

W tym konkretnym modelu zakłada się, że każdy z tych kroków zajmuje mniej więcej tyle samo czasu. W zależności od używanego oprogramowania może to być bardzo dobre przybliżenie lub słabe.

Jednostka czasu jest zdefiniowana w taki sposób, że jeden krok pseudokodu odpowiada jednej jednostce. Wykonanie pętli w całości wymaga czterech jednostek czasu. ${\ displaystyle u_ {n}}$ jest zdefiniowany jako cztery.

Należy jednak pamiętać, że jeśli jest równe jeden, to pierwszy krok $można$ Pętla zajmuje tylko trzy jednostki czasu. ${\ displaystyle u_ {n}}$ jest zdefiniowany jako trzy.

Jako przykład rozważ równanie:

${\ Displaystyle {\ Frac {\ pi} {4}} = 44 \ arctan {\ Frac {74684} {14967113}} + 139 \arctan {\frac {1}{239}}-12\arctan {\frac {20138}{15351991}}}$

 

 

 

 

()

W poniższej tabeli przedstawiono szacowany czas dla każdego z terminów:

${\ displaystyle a_ {n}}$	${\ displaystyle b_ {n}}$	${\ Displaystyle {\ Frac {b_ {n}} {a_ {n}}}}$	${\ Displaystyle \ ln {\ Frac {b_ {n}}} {a_ {n}}}}$	${\ displaystyle u_ {n}}$	${\ Displaystyle {\ mathit {czas}}}$
74684	14967113	200,41	5.3003	4	0,75467
1	239	239,00	5,4765	3	0,54780
20138	15351991	762,34	6,6364	4	0,60274

Całkowity czas to 0,75467 + 0,54780 + 0,60274 = 1,9052

Porównaj to z równaniem 5 . W poniższej tabeli przedstawiono szacowany czas dla każdego z terminów:

${\ displaystyle a_ {n}}$	${\ displaystyle b_ {n}}$	${\ Displaystyle {\ Frac {b_ {n}} {a_ {n}}}}$	${\ Displaystyle \ ln {\ Frac {b_ {n}}} {a_ {n}}}}$	${\ displaystyle u_ {n}}$	${\ Displaystyle {\ mathit {czas}}}$
24478	873121	35.670	3,5743	4	1.1191
685601	69049993	100,71	4,6123	4	0,8672

Całkowity czas to 1,1191 + 0,8672 = 1,9863

Wniosek, oparty na tym konkretnym modelu, jest taki, że równanie 6 jest nieco szybsze niż równanie 5 , niezależnie od tego, że równanie 6 ma więcej wyrazów. Wynik ten jest typowy dla ogólnego trendu. Dominującym czynnikiem jest stosunek między ${\ displaystyle a_ {n}}$ i ${\ displaystyle b_ {n}}$ . W celu uzyskania wysokiego wskaźnika konieczne jest dodanie dodatkowych terminów. Często jest to oszczędność czasu netto.

Linki zewnętrzne

• Weisstein, Eric W. „Formuły podobne do maszyn” . MathWorld .
• Stała π
• Zasługi Machin na MathPages