Koło

Koło
Koło
	Koło obwód C średnica D promień R centrum lub początek O
Typ	Sekcja stożkowa
Grupa symetrii	O(2)
Obszar	πR 2
Obwód	C = 2πR

Okrąg jest kształtem składającym się ze wszystkich punktów na płaszczyźnie , które znajdują się w danej odległości od danego punktu, środka . Równoważnie jest to krzywa wytyczona przez punkt, który porusza się w płaszczyźnie tak, że jego odległość od danego punktu jest stała . Odległość między dowolnym punktem okręgu a środkiem nazywa się promieniem . Zwykle promień musi być liczbą dodatnią. Okrąg z $punktem$ ) jest przypadkiem zdegenerowanym . Ten artykuł dotyczy okręgów w geometrii euklidesowej , aw szczególności płaszczyzny euklidesowej , chyba że zaznaczono inaczej.

W szczególności okrąg jest prostą zamkniętą krzywą , która dzieli płaszczyznę na dwa obszary : wewnętrzny i zewnętrzny. W codziennym użyciu termin „okrąg” może być używany zamiennie w odniesieniu do granicy figury lub całej figury łącznie z jej wnętrzem; w ściśle technicznym użyciu okrąg jest tylko granicą, a cała figura nazywana jest dyskiem .

Okrąg można również zdefiniować jako specjalny rodzaj elipsy , w której dwa ogniska pokrywają się, mimośrodowość wynosi 0, a półosie duże i półosie są równe; lub dwuwymiarowy kształt obejmujący największą powierzchnię na jednostkę obwodu do kwadratu, przy użyciu rachunku wariacyjnego .

Definicja Euklidesa

Okrąg to figura płaska ograniczona jedną linią krzywą i taka, że wszystkie linie proste poprowadzone od określonego punktu w jej obrębie do linii ograniczającej są równe. Linię ograniczającą nazywamy jej obwodem, a punkt środkiem.

— Euklides , Elementy , Księga I

Definicja topologiczna

W dziedzinie topologii okrąg nie ogranicza się do koncepcji geometrycznej, ale do wszystkich jego homeomorfizmów . Dwa okręgi topologiczne są równoważne R3 ^, jeśli jeden z nich może zostać przekształcony w drugi poprzez odkształcenie względem siebie (znane jako izotop otoczenia ).

Terminologia

Pierścień : obiekt w kształcie pierścienia, obszar ograniczony dwoma koncentrycznymi okręgami.
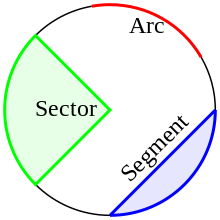
Łuk : dowolna połączona część okręgu. Określenie dwóch punktów końcowych łuku i środka pozwala na utworzenie dwóch łuków, które razem tworzą pełny okrąg.
Środek: punkt w równej odległości od wszystkich punktów na okręgu.
Cięciwa : odcinek linii, którego punkty końcowe leżą na okręgu, dzieląc w ten sposób okrąg na dwa odcinki.
Obwód : długość jednego obwodu wzdłuż okręgu lub odległość wokół okręgu.
Średnica : odcinek linii, którego punkty końcowe leżą na okręgu i który przechodzi przez środek; lub długość takiego odcinka linii. Jest to największa odległość między dowolnymi dwoma punktami na okręgu. Jest to szczególny przypadek cięciwy, a mianowicie najdłuższej cięciwy dla danego okręgu, a jej długość jest dwukrotnie większa od długości promienia.
Dysk: obszar płaszczyzny ograniczony okręgiem.
Soczewka : obszar wspólny dla (przecięcia) dwóch nakładających się dysków.
Passant: współpłaszczyznowa linia prosta, która nie ma punktu wspólnego z kołem.
Promień: odcinek linii łączący środek okręgu z dowolnym pojedynczym punktem na samym okręgu; lub długość takiego odcinka, która jest połową (długości) średnicy.
Sektor : obszar ograniczony dwoma promieniami o równej długości ze wspólnym środkiem i jednym z dwóch możliwych łuków, określonym przez ten środek i punkty końcowe promieni.
Segment : region ograniczony cięciwą i jednym z łuków łączących punkty końcowe cięciwy. Długość cięciwy narzuca dolną granicę średnicy możliwych łuków. Czasami termin segment jest używany tylko w odniesieniu do regionów niezawierających środka koła, do którego należy ich łuk.
Sieczna : przedłużona cięciwa, współpłaszczyznowa linia prosta, przecinająca okrąg w dwóch punktach.
Półkole : jeden z dwóch możliwych łuków określonych przez punkty końcowe średnicy, przyjmując punkt środkowy jako środek. W nietechnicznym użyciu potocznym może to oznaczać wnętrze dwuwymiarowego obszaru ograniczonego średnicą i jednym z jego łuków, czyli fachowo zwanym półdyskiem. Półtarcza to szczególny przypadek segmentu, czyli największego.
Styczna : współpłaszczyznowa linia prosta, która ma jeden punkt wspólny z okręgiem („dotyka okręgu w tym punkcie”).

Wszystkie określone regiony można uznać za otwarte , to znaczy niezawierające swoich granic, lub za zamknięte , łącznie z ich odpowiednimi granicami.

Cięciwa, sieczna, styczna, promień i średnica

Łuk, sektor i segment

Historia

Kompas w tym XIII-wiecznym rękopisie jest symbolem Bożego aktu stworzenia . Zwróć też uwagę na okrągły kształt aureoli .

Słowo krąg pochodzi od greckiego κίρκος/κύκλος ( kirkos/kuklos ), które samo w sobie jest metatezą homeryckiego greckiego κρίκος ( krikos ), oznaczającego „obręcz” lub „pierścień”. Pochodzenie słów cyrk i obwód jest ze sobą ściśle powiązane.

Okrągły kawałek jedwabiu z mongolskimi obrazami

Okręgi na starym arabskim rysunku astronomicznym .

Krąg był znany od początku pisanej historii. Zaobserwowano by naturalne kręgi, takie jak Księżyc, Słońce i krótką łodygę rośliny wiejącą na wietrze na piasku, która tworzy na piasku kształt koła. Koło jest podstawą koła , które wraz z powiązanymi wynalazkami, takimi jak koła zębate , umożliwia wiele nowoczesnych maszyn. W matematyce badanie koła pomogło zainspirować rozwój geometrii, astronomii i rachunku różniczkowego .

Wczesna nauka , zwłaszcza geometria , astrologia i astronomia , była dla większości uczonych średniowiecznych powiązana z boskością i wielu wierzyło, że istnieje coś z natury „boskiego” lub „doskonałego”, co można znaleźć w kręgach.

Niektóre ważne wydarzenia w historii koła to:

1700 p.n.e. – Papirus Rhinda podaje metodę wyznaczania pola koła. Wynik odpowiada 256 / 81 (3,16049...) jako przybliżonej wartości $π$ .

Wieża Tughrul od środka

300 pne - Księga 3 Elementów Euklidesa dotyczy właściwości kół.
W Siódmym Liście Platona znajduje się szczegółowa definicja i wyjaśnienie koła. Platon wyjaśnia idealne koło i czym różni się od jakiegokolwiek rysunku, słów, definicji lub wyjaśnienia.
1880 n.e. – Lindemann udowadnia, że $π$ jest transcendentalne , skutecznie rozwiązując tysiącletni problem kwadratury koła.

Wyniki analityczne

Obwód

Stosunek obwodu koła do jego średnicy wynosi $π$ (pi), niewymierna stała w przybliżeniu równa 3,141592654. Zatem obwód C jest powiązany z promieniem r i średnicą d przez:

{\ Displaystyle C = 2 \ pi r = \ pi d. \,}

Teren ogrodzony

Obszar otoczony okręgiem =

π

× obszar zacienionego kwadratu

Jak udowodnił Archimedes w swoim Pomiarze koła , pole ograniczone kołem jest równe polu trójkąta, którego podstawa ma długość obwodu koła, a wysokość jest równa promieniowi koła, co daje $π$ pomnożone przez promień do kwadratu:

{\ Displaystyle \ operatorname {obszar} = \ pi r ^ {2}. \,}

Równoważnie, oznaczając średnicę przez d ,

{\ Displaystyle \ operatorname {obszar} = {\ Frac {\ pi d ^ {2}} {4}} \ około 0 {.} 7854d ^ {2},}

czyli około 79% opisanego kwadratu (którego bok ma długość d ).

Okrąg jest płaską krzywą obejmującą maksymalny obszar dla danej długości łuku. Wiąże to koło z problemem w rachunku wariacyjnym, a mianowicie z nierównością izoperymetryczną .

równania

współrzędne kartezjańskie

Okrąg o promieniu r = 1, środek ( a , b ) = (1,2, −0,5)

Równanie koła

W kartezjańskim układzie współrzędnych x – y okrąg o współrzędnych środka ( a , b ) i promieniu r jest zbiorem wszystkich punktów ( x , y ) takich, że

{\ Displaystyle (xa) ^ {2} + (yb) ^ {2} = r ^ {2}.}

To równanie , znane jako równanie koła , wynika z twierdzenia Pitagorasa zastosowanego do dowolnego punktu na okręgu: jak pokazano na sąsiednim diagramie, promień jest przeciwprostokątną trójkąta prostokątnego, którego pozostałe boki mają długość | x − za | i | y − b |. Jeśli okrąg jest wyśrodkowany w początku (0, 0), równanie upraszcza się do

{\ Displaystyle x ^ {2} + y ^ {2} = r ^ {2}.}

Forma parametryczna

Równanie można zapisać w postaci parametrycznej za pomocą funkcji trygonometrycznych sinus i cosinus as

{\ Displaystyle x = a + r \ \ cos t}

{\ Displaystyle y = b + r \, \ sin t}

gdzie t jest zmienną parametryczną z zakresu od 0 do 2 $π$ , interpretowaną geometrycznie jako kąt , jaki tworzy promień od ( a , b ) do ( x , y ) z dodatnią osią x .

Alternatywną parametryzacją okręgu jest

{\ Displaystyle x = a + r {\ Frac {1-t ^ {2}} {1 + t ^ {2}}},}

{\ Displaystyle y = b + r {\ Frac {2t} {1 + t ^ {2}}}.}

W tej parametryzacji stosunek t do r można interpretować geometrycznie jako rzut stereograficzny linii przechodzącej przez środek równolegle do osi x (patrz podstawienie półkąta stycznego ). Jednak ta parametryzacja działa tylko wtedy, gdy t ma zakres nie tylko przez wszystkie liczby rzeczywiste, ale także do punktu w nieskończoności; w przeciwnym razie skrajny lewy punkt okręgu zostałby pominięty.

Forma za 3 punkty

Równanie koła określone przez trzy punkty ${\ Displaystyle (x_ {1}, y_ {1}), (x_ { 2},y_{2}),(x_{3},y_{3})}$ nie leżące na prostej otrzymujemy przez przekształcenie 3-punktowej postaci równania okręgu :

{\ Displaystyle {\ Frac {({\ kolor {zielony} x} -x_ {1}) ({\ kolor {zielony} x} -x_ {2}) + ({\ kolor {czerwony} y} -y_ { 1})({\kolor {czerwony}y}-y_{2})}{({\kolor {czerwony}y}-y_{1})({\kolor {zielony}x}-x_{2}) -({\kolor {czerwony}y}-y_{2})({\kolor {zielony}x}-x_{1})}}={\frac {(x_{3}-x_{1})( x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3 }-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.}

Postać jednorodna

We współrzędnych jednorodnych każdy przekrój stożkowy z równaniem koła ma postać

{\ Displaystyle x ^ {2} + y ^ {2} -2axz-2byz + cz ^ {2} = 0.}

Można udowodnić, że przekrój stożkowy jest kołem dokładnie wtedy, gdy zawiera (po rozciągnięciu na zespoloną płaszczyznę rzutową ) punkty I (1: i : 0) i J (1: - i : 0). Punkty te nazywane są okrągłymi punktami w nieskończoności .

Współrzędne biegunowe

We współrzędnych biegunowych równanie koła jest ^{[ niejasne ]}

{\ Displaystyle r ^ {2} -2rr_ {0} \ cos (\ teta - \ phi) + r_ {0} ^ {2 }=a^{2},}

₀ gdzie a jest promieniem okręgu, to współrzędne biegunowe ogólnego punktu na okręgu $r$ ${0} ,\phi )}$ to współrzędne biegunowe środka okręgu (tj. r to odległość od początku do środka okręgu, a φ to kąt skierowany w kierunku przeciwnym do ruchu wskazówek zegara między dodatnią osią x a linią łączącą początek z środek okręgu). Dla okręgu wyśrodkowanego na początku, tj. ₀ r = 0 , to sprowadza się do r = a . Gdy ₀ r = a , lub gdy początek leży na okręgu, równanie staje się

{\ displaystyle r = 2a \ cos (\ teta - \ phi).}

W ogólnym przypadku równanie można rozwiązać dla r , dając

{\ Displaystyle r = r_ {0} \ cos (\ teta - \ fi) \ pm {\ sqrt {a ^ {2} -r_ {0} ^ {2} \ sin ^ {2} (\ teta - \ fi )}}.}

Zauważ, że bez znaku ± równanie w niektórych przypadkach opisywałoby tylko połowę koła.

Skomplikowany samolot

Na płaszczyźnie zespolonej , koło o środku w punkcie c i promieniu r ma równanie

{\ displaystyle | zc | = r.}

W postaci parametrycznej można to zapisać jako

{\ displaystyle z = re ^ {to} + do.}

Nieco uogólnione równanie

{\ Displaystyle pz {\ overline {z}} + gz + {\ overline {gz}} = q}

dla rzeczywistego p , q i zespolonego g jest czasami nazywany kołem uogólnionym . Staje się to powyższym równaniem dla okręgu z ${\ Displaystyle p = 1, \ g = - {\ overline {c}}, \ q = r ^ {2} - | c | ^ {2}},$ ponieważ $\ Displaystyle | zc | ^ {2} = Z {\ overline {z}} - {\ overline {c}} zc {\ overline {z }}+c{\overline {c}}}$ . Nie wszystkie uogólnione okręgi są w rzeczywistości okręgami: uogólniony okrąg jest albo (prawdziwym) okręgiem, albo linią .

Linie styczne

Linia styczna przechodząca przez punkt P na okręgu jest prostopadła do średnicy przechodzącej przez P . Jeśli P = ( x ₁ , y ₁ ) i okrąg ma środek ( a , b ) i promień r , to styczna jest prostopadła do prostej od ( a , b ) do ( x ₁ , y ₁ ), więc ma postać ( x ₁ - za ) x + ( y ₁ - b ) y = do . Obliczanie w ( x ₁ , y ₁ ) określa wartość c , a wynikiem jest to, że równanie tangensa to

{\ Displaystyle (x_ {1} -a) x + (y_ {1 }-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1},}

Lub

{\ Displaystyle (x_ {1} -a) (xa) + (y_ {1} -b) (yb) = r ^ {2}.}

Jeśli y ₁ ≠ b , to nachylenie tej prostej wynosi

{\ Displaystyle {\ Frac {dy} {dx}} = - {\ Frac {x_ {1} -a} {y_ {1} -b}}.}

Można to również znaleźć za pomocą niejawnego różnicowania .

Gdy środek okręgu znajduje się w początku układu współrzędnych, równanie stycznej staje się równe

{\ Displaystyle x_ {1} x + y_ {1} y = r ^ {2},}

a jego nachylenie wynosi

{\ Displaystyle {\ Frac {dy} {dx}} = - {\ Frac {x_ {1}} {y_ {1}}}.}

Nieruchomości

Koło to kształt o największym polu dla danej długości obwodu (patrz nierówność izoperymetryczna ).
Koło ma wysoce symetryczny kształt: każda linia przechodząca przez środek tworzy linię symetrii odbicia i ma symetrię obrotową wokół środka pod każdym kątem. Jego grupą symetrii jest grupa ortogonalna O(2, R ). Sama grupa obrotów to grupa kołowa T .
Wszystkie kręgi są podobne .
- Obwód i promień koła są proporcjonalne .
- nim obszar i kwadrat jego promienia są proporcjonalne.
- Stałe proporcjonalności wynoszą odpowiednio 2 $π$ i $π$ .
Okrąg wyśrodkowany w początku układu współrzędnych o promieniu 1 nazywamy okręgiem jednostkowym .
- Pomyślany jako wielki okrąg sfery jednostkowej , staje się kołem riemannowskim .
Przez dowolne trzy punkty, nie wszystkie na tej samej linii, leży unikalny okrąg. We współrzędnych kartezjańskich można podać jednoznaczne wzory na współrzędne środka koła i promień w postaci współrzędnych trzech podanych punktów. Zobacz okrąg .

Akord

Akordy są jednakowo oddalone od środka koła wtedy i tylko wtedy, gdy są równej długości.
Dwusieczna cięciwy przechodzi przez środek koła; równoważnymi stwierdzeniami wynikającymi z wyjątkowości dwusiecznej prostopadłej są:
- Linia prostopadła ze środka koła przecina cięciwę na pół.
- Odcinek linii przechodzący przez środek cięciwy na pół jest prostopadły do cięciwy.
Jeżeli kąt środkowy i kąt wpisany w okrąg opierają się na tej samej cięciwie i po tej samej stronie cięciwy, to kąt środkowy jest dwa razy większy od kąta wpisanego.
Jeżeli dwa kąty są wpisane w tę samą cięciwę i po tej samej stronie cięciwy, to są równe.
Jeżeli dwa kąty są wpisane w tę samą cięciwę i po przeciwnych stronach cięciwy, to są one komplementarne .
- W czworokącie cyklicznym kąt zewnętrzny jest równy przeciwległemu kątowi wewnętrznemu.
Kąt wpisany oparty na średnicy jest kątem prostym (patrz twierdzenie Talesa ).
Średnica to najdłuższa cięciwa koła.
- Spośród wszystkich kół o wspólnej cięciwie AB, koło o najmniejszym promieniu jest tym o średnicy AB.
Jeśli przecięcie dowolnych dwóch cięciw dzieli jeden cięciwę na długości a i b , a drugi na długości c i d , to ab = cd .
Jeśli przecięcie dowolnych dwóch cięciw prostopadłych dzieli jedną cięciwę na długości a i b , a drugą na długości c i d , to a ² + b ² + c ² + d ² równa się kwadratowi średnicy.
Suma kwadratów długości dowolnych dwóch cięciw przecinających się pod kątem prostym w danym punkcie jest taka sama jak suma dowolnych dwóch prostopadłych cięciw przecinających się w tym samym punkcie i wyraża się wzorem 8 r 2 − ⁴ p 2 ^, gdzie r jest promień okręgu, a p to odległość od punktu środkowego do punktu przecięcia.
Odległość od punktu na okręgu do danej cięciwy pomnożona przez średnicę okręgu jest równa iloczynowi odległości od punktu do końców cięciwy.

Tangens

Linia poprowadzona prostopadle do promienia przechodząca przez punkt końcowy promienia leżącego na okręgu jest styczną do tego okręgu.
Linia poprowadzona prostopadle do stycznej przechodzącej przez punkt styku z okręgiem przechodzi przez środek okręgu.
Zawsze można poprowadzić dwie styczne do okręgu z dowolnego punktu poza okręgiem, a te styczne są równej długości.
Jeśli styczna w A i styczna w B przecinają się w zewnętrznym punkcie P , to oznaczając środek jako O , kąty ∠ BOA i ∠ BPA są uzupełniające.
Jeśli AD jest styczna do okręgu w punkcie ∠ DAQ = 1/2 . A łuku ( AQ ) i jeśli AQ jest cięciwą okręgu, to

Twierdzenia

Twierdzenie sieczne-sieczne

Twierdzenie o akordach mówi, że jeśli dwie akordy, CD i EB , przecinają się w A , to AC × AD = AB × AE .
Jeśli dwie sieczne, AE i AD , również przecinają okrąg odpowiednio w punktach B i C , to AC × AD = AB × AE (następstwo twierdzenia o cięciwie).
Styczną można uznać za graniczny przypadek siecznej, której końce są zbieżne. Jeśli styczna z punktu zewnętrznego A styka się z okręgiem w F , a sieczna z punktu zewnętrznego A styka się z okręgiem odpowiednio w C i D , to AF ² = AC × AD (twierdzenie styczna-sieczna).
Kąt między cięciwą a styczną w jednym z jej punktów końcowych jest równy połowie kąta opartego na środku okręgu po przeciwnej stronie cięciwy (kąt cięciwy stycznej).
Jeśli kąt oparty na cięciwie w środku wynosi 90 ° , to ℓ = r √2 , gdzie ℓ jest długością cięciwy, a r jest promieniem okręgu.
Jeśli dwie sieczne są wpisane w okrąg, jak pokazano po prawej, to pomiar kąta A jest równy połowie różnicy pomiarów zamkniętych łuków ( ${\ displaystyle {\ overset {\ marszczyć brwi} {DE} }}$ i ${\ Displaystyle {\ overset {\ marszczyć brwi} {BC}}})$ . Oznacza to, że $\ Displaystyle 2 \ kąt {CAB} = \ kąt {DOE} - \ kąt {BOC}}$ , gdzie O jest środkiem koła ( twierdzenie sieczne-sieczne).

Kąty wpisane

Twierdzenie o kącie wpisanym

Kąt wpisany (przykładami są niebieski i zielony kąt na rysunku) jest dokładnie połową odpowiedniego kąta środkowego (czerwony). Stąd wszystkie kąty wpisane oparte na tym samym łuku (różowym) są równe. Kąty wpisane na łuk (brązowy) są uzupełniające. W szczególności każdy kąt wpisany oparty na średnicy jest kątem prostym (ponieważ kąt środkowy ma 180 °).

Sagitta

Sagitta jest segmentem pionowym.

Sagitta (znana również jako werset ) to odcinek linii narysowany prostopadle do cięciwy, między środkiem tej cięciwy a łukiem koła .

Biorąc pod uwagę długość y cięciwy i długość x strzałki, twierdzenie Pitagorasa może być użyte do obliczenia promienia unikalnego okręgu, który zmieści się wokół dwóch prostych:

{\ Displaystyle r = {\ Frac {y ^ {2}} {8x}} + {\ Frac {x} {2}}.}

Kolejny dowód tego wyniku, który opiera się tylko na dwóch podanych powyżej właściwościach akordu, jest następujący. Mając cięciwę o długości y i strzałkę o długości x , skoro strzała przecina środek cięciwy, wiemy, że jest ona częścią średnicy koła. Ponieważ średnica jest dwa razy większa od promienia, „brakująca” część średnicy ma długość ( 2 r − x ). Korzystając z faktu, że jedna część jednego akordu pomnożona przez drugą część jest równa temu samemu iloczynowi wzdłuż cięciwy przecinającej pierwszy akord, stwierdzamy, że ( 2 r − x ) x = ( y / 2) ² . Rozwiązując dla r , znajdujemy wymagany wynik.

Konstrukcje kompasu i liniału

Istnieje wiele konstrukcji kompasu i linii prostej, których wynikiem są koła.

Najprostszą i najbardziej podstawową jest konstrukcja mająca środek okręgu i punkt na okręgu. Umieść stałą nóżkę kompasu w punkcie środkowym, a ruchomą nóżkę w punkcie na okręgu i obróć kompas.

Konstrukcja o podanej średnicy

Skonstruuj środek $M$ średnicy.
Skonstruuj okrąg, którego środek $M$ przechodzi przez jeden z końców średnicy (będzie też przechodził przez drugi koniec).

Skonstruuj okrąg przechodzący przez punkty A, B i C, znajdując dwusieczne (kolor czerwony) boków trójkąta (kolor niebieski). Do znalezienia środka potrzebne są tylko dwie z trzech dwusiecznych.

Konstrukcja przez trzy punkty niewspółliniowe

Nazwij punkty $P$ , $Q$ i $R$ ,
Skonstruuj dwusieczną prostopadłą odcinka $PQ$ .
Skonstruuj dwusieczną prostopadłą odcinka $PR$ .
Oznacz punkt przecięcia tych dwóch dwusiecznych prostopadłych $M$ . (Spotykają się, ponieważ punkty nie są współliniowe ).
Skonstruuj okrąg o środku $M$ przechodzącym przez jeden z punktów $P$ , $Q$ lub $R$ (przejdzie też przez dwa pozostałe punkty).

Krąg Apoloniusza

Definicja koła Apoloniusza: d ₁ / d ₂ stała

Apoloniusz z Perge wykazał, że okrąg można również zdefiniować jako zbiór punktów na płaszczyźnie o stałym stosunku (innym niż 1) odległości do dwóch stałych ognisk, A i B . (Zbiór punktów, w których odległości są równe, to dwusieczna prostopadła odcinka AB , prosta). Czasami mówi się, że ten okrąg jest narysowany wokół dwóch punktów.

Dowód składa się z dwóch części. Najpierw trzeba udowodnić, że przy danych dwóch ogniskach A i B oraz stosunku odległości każdy punkt P spełniający stosunek odległości musi leżeć na określonym okręgu. Niech C będzie kolejnym punktem, również spełniającym ten stosunek i leżącym na odcinku AB . Zgodnie z twierdzeniem o dwusiecznej kąta odcinek PC przecina na pół kąt wewnętrzny APB , ponieważ odcinki są podobne:

{\ Displaystyle {\ Frac {AP} {BP}} = {\ Frac {AC} {BC}}.}

Analogicznie, odcinek linii PD przechodzący przez pewien punkt D na przedłużeniu AB przecina odpowiedni kąt zewnętrzny BPQ , gdzie Q leży na przedłużeniu AP . Ponieważ suma kątów wewnętrznych i zewnętrznych wynosi 180 stopni, kąt CPD wynosi dokładnie 90 stopni; czyli kąt prosty. Zbiór punktów P takich, że kąt CPD jest kątem prostym tworzy okrąg, którego średnicą jest CD .

Po drugie, zobacz dowód, że każdy punkt na wskazanym okręgu spełnia podany stosunek.

Współczynniki krzyżowe

Ściśle powiązana właściwość okręgów obejmuje geometrię wzajemnego stosunku punktów na płaszczyźnie zespolonej. Jeśli A , B i C są takie jak powyżej, to okrąg Apoloniusza dla tych trzech punktów jest zbiorem punktów P , dla których bezwzględna wartość ilorazu krzyżowego jest równa jeden:

{\ Displaystyle {\ duży |} [A, B; C, P] {\ duży |} = 1.}

Innymi słowy, P jest punktem na okręgu Apoloniusza wtedy i tylko wtedy, gdy stosunek krzyżowy [ A , B ; C , P ] leży na okręgu jednostkowym na płaszczyźnie zespolonej.

Uogólnione kręgi

Jeżeli C jest środkiem odcinka AB , to zbiór punktów P spełnia warunek Apoloniusza

{\ Displaystyle {\ Frac {|AP|}{|BP|}} = {\ Frac {|AC|}{|BC|}}}

nie jest okręgiem, lecz linią.

Tak więc, jeśli A , B i C mają różne punkty na płaszczyźnie, to zbiór punktów P spełniający powyższe równanie nazywany jest „okręgiem uogólnionym”. Może to być prawdziwe koło lub linia. W tym sensie linia jest uogólnionym kołem o nieskończonym promieniu.

Inskrypcja lub opis innych postaci

W każdy trójkąt można wpisać unikalny okrąg, zwany okręgiem , tak aby był styczny do każdego z trzech boków trójkąta.

wierzchołków trójkąta .

Styczny wielokąt , taki jak styczny czworobok , to dowolny wypukły wielokąt , w który można wpisać okrąg , który jest styczny do każdej strony wielokąta. Każdy wielokąt foremny i każdy trójkąt jest wielokątem stycznym.

Cykliczny wielokąt to dowolny wielokąt wypukły, wokół którego można opisać okrąg przechodzący przez każdy wierzchołek. Dobrze zbadanym przykładem jest cykliczny czworobok. Każdy wielokąt foremny i każdy trójkąt jest wielokątem cyklicznym. Wielokąt, który jest zarówno cykliczny, jak i styczny, nazywany jest wielokątem bicentrycznym .

Hipocykloida to krzywa wpisana w dany okrąg poprzez śledzenie stałego punktu na mniejszym okręgu, który toczy się wewnątrz i jest styczny do danego okręgu .

Przypadek graniczny innych figur

Okrąg można postrzegać jako ograniczający przypadek każdej z różnych innych figur:

Owal kartezjański to taki zbiór punktów, że ważona suma odległości od dowolnego z jego punktów do dwóch stałych punktów (ognisk) jest stałą. Elipsa to przypadek, w którym wagi są równe. Okrąg jest elipsą o mimośrodowości równej zero, co oznacza, że dwa ogniska pokrywają się ze sobą jako środek koła. Okrąg jest także innym szczególnym przypadkiem owalu kartezjańskiego, w którym jedna z wag wynosi zero.
Superelipsa ${\ Displaystyle \ lewo | {\ Frac {x} {a}} \ prawo | ^ {n} \! + \ lewo | {\ Frac {y} {b}} \ prawo | ^ {n} \ !=1}$ równanie postaci | dla dodatnich a , b i n . Superkoło ma b = a . Okrąg jest szczególnym przypadkiem superkoła, w którym n = 2 .
Owal Cassiniego to taki zbiór punktów, że iloczyn odległości od któregokolwiek z jego punktów do dwóch stałych punktów jest stały. Kiedy dwa stałe punkty pokrywają się, powstaje okrąg.
Krzywa o stałej szerokości to figura, której szerokość, zdefiniowana jako prostopadła odległość między dwiema odrębnymi równoległymi liniami, z których każda przecina swoją granicę w jednym punkcie, jest taka sama niezależnie od kierunku tych dwóch równoległych linii. Koło jest najprostszym przykładem tego typu figury.

W innych p -normach

Ilustracje okręgów jednostkowych (patrz także superellipsa ) w różnych

p

-normach (każdy wektor od początku do okręgu jednostkowego ma długość jeden, przy czym długość jest obliczana ze wzoru na długość odpowiadającego

p

).

Definiując okrąg jako zbiór punktów o stałej odległości od punktu, różne kształty można uznać za okręgi przy różnych definicjach odległości. W p -norma , odległość jest określona przez

{\ Displaystyle \ lewo \ | x \ prawo \ |_ {p} = \ lewo (| x_ {1} | ^ {p} + | x_ {2} | ^ {p} + \ kropki + | x_ {n} |^{p}\prawo)^{1/p}.}

W geometrii euklidesowej p = 2, co daje chowaniec

{\ Displaystyle \ lewo \ | x \ prawo \ |_ {2} = {\ sqrt {| x_ {1} | ^ {2} + | x_ {2} | ^ {2} + \ kropki b + | x_ {n }|^{2}}}.}

W geometrii taksówki p = 1. Okręgi taksówki to kwadraty o bokach zorientowanych pod kątem 45° do osi współrzędnych. Chociaż $,$ bok miałby długość przy użyciu metryki euklidesowej gdzie r jest promieniem koła, jego długość w geometrii taksówki wynosi r . Zatem obwód koła wynosi 8 r . Zatem wartość geometrycznego analogu do $4$ w tej geometrii. Wzór na okrąg jednostkowy w geometrii taksówki to ${\ Displaystyle | x|+|y|=1}$ we współrzędnych kartezjańskich i

{\ Displaystyle R = {\ Frac {1} {1} {| \ sin \ teta | + | \ cos \ teta |}}}

we współrzędnych biegunowych.

Okrąg o promieniu 1 (wykorzystujący tę odległość) to sąsiedztwo von Neumanna jego środka.

Okrąg o promieniu r dla odległości Czebyszewa ( L _∞ metryczny ) na płaszczyźnie jest również kwadratem o boku 2 r równoległym do osi współrzędnych, więc planarną odległość Czebyszewa można postrzegać jako równoważną przez obrót i skalowanie do płaskiej odległości taksówki. Jednak ta równoważność między metrykami L ₁ i L _∞ nie uogólnia się na wyższe wymiary.

Miejsce stałej sumy

$.$ zbiór punktów na płaszczyźnie Zbiorem punktów, w którym suma kwadratów odległości do danych punktów jest stała, jest okrąg, którego środek znajduje się w środku ciężkości danych punktów. Uogólnienie dla wyższych potęg odległości uzyskuje się, jeśli pod $punktami$ $zostaną$ wzięte wierzchołki Miejsce punktów takie, że suma -tej potęgi odległości $}$ wierzchołków danego wielokąta foremnego o promieniu okręgu ( $2m$ $R}$ $Displaystyle ($ jest stałą jest okręgiem, jeśli

\ Displaystyle \ suma _ {i = 1} ^ {n} d_ {i} ^ {2 m}> n R ^ {2 m}} ,

gdzie

{\ Displaystyle m}

= 1,2,…,

{\ displaystyle n}

-1;

którego środkiem jest środek ciężkości . ${\ displaystyle P_ {n}}$ .

W przypadku trójkąta równobocznego loci stałych sum drugiej i czwartej potęgi są okręgami, podczas gdy dla kwadratu loci są okręgami dla stałych sum drugiej, czwartej i szóstej potęgi. Dla pięciokąta foremnego zostanie dodana stała suma ósmych potęg odległości i tak dalej.

Kwadratura koła

starożytnych geometrów problem konstruowania kwadratu o takim samym polu jak dany okrąg przy użyciu tylko skończonej liczby kroków za pomocą kompasu i liniału .

W 1882 r. zadanie okazało się niemożliwe w wyniku twierdzenia Lindemanna-Weierstrassa , które dowodzi, że pi ( $π$ ) jest liczbą przestępną , a nie algebraiczną liczbą niewymierną ; to znaczy nie jest pierwiastkiem żadnego wielomianu o wymiernych współczynnikach. Pomimo niemożliwości, temat ten nadal jest interesujący dla pseudomatematyki .

Znaczenie w sztuce i symbolizmie

Od czasów najwcześniejszych znanych cywilizacji – takich jak Asyryjczycy i starożytni Egipcjanie, te w dolinie Indusu i wzdłuż Żółtej Rzeki w Chinach oraz zachodnie cywilizacje starożytnej Grecji i Rzymu w klasycznej starożytności – koło było używane bezpośrednio lub pośrednio w sztukach wizualnych, aby przekazać przesłanie artysty i wyrazić pewne idee. Jednak różnice w światopoglądzie (wierzeniach i kulturze) miały ogromny wpływ na postrzeganie artystów. Podczas gdy niektórzy podkreślali obwód koła, aby zademonstrować swoją demokratyczną manifestację, inni skupiali się na jego środku, aby symbolizować koncepcję kosmicznej jedności. W doktrynach mistycznych krąg symbolizuje głównie nieskończoną i cykliczną naturę istnienia, ale w tradycjach religijnych reprezentuje ciała niebieskie i boskie duchy. Koło oznacza wiele świętych i duchowych koncepcji, w tym między innymi jedność, nieskończoność, całość, wszechświat, boskość, równowagę, stabilność i doskonałość. Takie koncepcje zostały przekazane w kulturach na całym świecie za pomocą symboli, na przykład kompasu, aureoli, vesica piscis i jego pochodnych (ryba, oko, aureola, mandorla itp.), Uroborosa, koła Dharmy , tęcza, mandale, rozety i tak dalej.

Zobacz też

Specjalnie nazwane kręgi

Z trójkąta

Z niektórych czworoboków

Ośmiopunktowy okrąg ortodiagonalnego czworoboku

O przekroju stożkowym

Z torusa

Kręgi Villarceau

Dalsza lektura

Pedoe, Dan (1988). Geometria: kompleksowy kurs . Dover. ISBN 9780486658124 .
„Koło” w archiwum The MacTutor History of Mathematics

Linki zewnętrzne

„Koło” , Encyklopedia matematyki , EMS Press , 2001 [1994]
Krąg w PlanetMath .
Weisstein, Eric W. „Koło” . MathWorld .
„Interaktywne aplety Java” . dla właściwości i elementarnych konstrukcji z udziałem okręgów
„Interaktywne równanie koła w postaci standardowej” . Kliknij i przeciągnij punkty, aby zobaczyć równanie w postaci standardowej w akcji
„Grupa na kółkach” . przeciąć węzeł

Koło
Koło obwód C średnica D promień R centrum lub początek O
Typ	Sekcja stożkowa
Grupa symetrii	$O(2)$
Obszar	$πR 2$
Obwód	$C = 2πR$