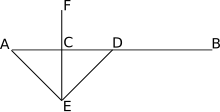
Przepołowienie

Prosta DE przecina prostą AB w punkcie D, prosta EF jest dwusieczną prostopadłą odcinka AD w punkcie C, a prosta EF jest wewnętrzną dwusieczną kąta prostego AED

W geometrii bisekcja to podział czegoś na dwie równe lub przystające części, zwykle za pomocą linii , która jest wtedy nazywana dwusieczną . Najczęściej rozważanymi typami dwusiecznych są dwusieczna odcinka (linia przechodząca przez środek danego odcinka ) i dwusieczna kąta (linia przechodząca przez wierzchołek kąta , dzieląca go na dwa równe kąty).

W przestrzeni trójwymiarowej przepołowienie odbywa się zwykle za pomocą płaszczyzny i nazywane jest dwusieczną lub dwusieczną .

Dwusieczna segmentu linii prostopadłej

Definicja

Dwusieczna prostopadła odcinka

Dwusieczna prostopadła odcinka to prosta, która prostopadle przecina odcinek w jego środku .

$AB$ przecięcie segmentu ${\ displaystyle$ również tę właściwość, że każdy z jego punktów w równej odległości od punktów końcowych odcinka: ZA b ${\ displaystyle \ quad | XA | = | XB |}$ .

Dowód wynika z ${\ displaystyle}$ i twierdzenia Pitagorasa :

{\ Displaystyle | XA | ^ {2} = | XM | ^ {2} + | MA | ^ {2} = | XM | ^ {2} + | MB | ^ {2} = | XB | ^ {2} \;.}

Właściwość (D) jest zwykle używana do budowy dwusiecznej prostopadłej:

Budowa przez prostą krawędź i kompas

W geometrii klasycznej dwusekcja jest prostą konstrukcją cyrkla i liniału , której możliwość zależy od umiejętności rysowania łuków o równych promieniach i różnych środkach:

Segment jest podzielony $na pół$ narysowanie przecinających się okręgów o równym ${\ displaystyle r> {\ tfrac {1}{2}}|AB|}$ , których centra są punktami końcowymi odcinka. Linia wyznaczona przez punkty przecięcia dwóch okręgów jest dwusieczną prostopadłą odcinka. Ponieważ konstrukcja dwusiecznej odbywa się bez znajomości punktu środkowego odcinka $konstrukcja$ służy do określenia jako $przecięcia$ i odcinka.

Ta konstrukcja jest w rzeczywistości używana podczas konstruowania $P}$ prostopadłej do danej linii w danym punkcie $:$ rysowanie okręgu, którego środek jest , że przecina linię $displaystyle$ ${\ displaystyle g}$ w dwóch punktach ${\ displaystyle A, B}$ , a prostopadła do zbudowania to jeden przecinający odcinek ${\ displaystyle AB}$ .

równania

Jeśli $,$ wektorami ${\ Displaystyle M: {\ vec {m}} = {\ tfrac {{\ vec {a}} + {\ vec {b}}} {2}}} i$ $_$ _ wektor ${\ Displaystyle {\ vec {a}} - {\ vec {b}}}$ jest wektorem normalnym dwusiecznej segmentu linii prostopadłej. Stąd jego równanie wektorowe to ${\ Displaystyle ({\ vec {x}} - {\ vec {m}}) \ cdot ({\ vec {a} }-{\vec {b}})=0}$ . Wstawianie i rozwinięcie równania prowadzi do równania wektorowego ${\ Displaystyle {\ vec {m}} = \ cdots}$

(V) ${\ Displaystyle \ quad {\ vec {x}} \ cdot ({\ vec {a}} - {\ vec {b}}) = {\ tfrac {1} {2}} ({\ vec {a}} ^{2}-{\vec {b}}^{2}).}$

ZA $(a_ {1}, a_ {2}), B = (b_ {1}, b_ {2}) }$ otrzymujemy równanie w postaci współrzędnych:

( do ) ${\ Displaystyle \ quad (a_ {1}-b_ {1}) x + (a_ {2} -b_ {2}) y = {\ tfrac {1} {2}} (a_ {1} ^ {2} - b_{1}^{2}+a_{2}^{2}-b_{2}^{2})\;.}$

Lub wyraźnie: (E) ${\ Displaystyle \ quad y = m (xx_ {0}) + y_ {0}}$ , gdzie ${\ Displaystyle \; m = - {\ tfrac {b_ {1} -a_ {1}} {b_ {2} -a_ {2}}}}$ , ${\ Displaystyle \; x_ {0} = {\ tfrac {1}{2}} (a_ {1} + b_ {1}) \;} i$ y $\ Displaystyle \;y_{0}={\tfrac {1}{2}}(a_{2}+b_{2})\;}$ .

Aplikacje

Zastosowano dwusieczne segmentów linii prostopadłych do rozwiązania różnych problemów geometrycznych:

Budowa środka koła Talesa ,
Budowa środka Excircle trójkąta,
diagramu Woronoja składają się z odcinków takich linii lub płaszczyzn.

Płaszczyzna dwusieczna

Dwusieczne segmentów linii prostopadłych w przestrzeni

Dwusieczna prostopadła odcinka jest płaszczyzną , która prostopadle przecina odcinek w jego środku .

Jego równanie wektorowe jest dosłownie takie samo jak w przypadku płaszczyzny:

(V) ${\ Displaystyle \ quad {\ vec {x}} \ cdot ({\ vec {a}} - {\ vec {b}}) = {\ tfrac {1} {2}} ({\ vec {a}} ^{2}-{\vec {b}}^{2}).}$

ZA $Displaystyle A = (a_ {1}, a_ {2}, a_ {3}), B = (b_{1},b_{2},b_{3})}$ otrzymujemy równanie w postaci współrzędnych:

(C3) ${\ Displaystyle \ quad (a_ {1}-b_ {1}) x + (a_ {2} -b_ {2}) y + (a_ {3} -b_ {3}) z = {\ tfrac {1} {2} }}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2}+a_{3}^{2}-b_{ 3}^{2})\;.}$

Właściwość (D) (patrz wyżej) jest $AB$ prawdziwa również w przestrzeni: (D) Prostopadła płaszczyzna dwusiecznej odcinka ma dla dowolnego punktu ${\ Displaystyle \;| XA | = | XB |}$ : $}$ .

Dwusieczna kąta

Dwusieczne kąta za pomocą kompasu i liniału

Dwusieczna kąta dzieli kąt na dwa kąty o równych środkach. Kąt ma tylko jedną dwusieczną. Każdy punkt dwusiecznej kąta jest jednakowo oddalony od boków kąta.

Wewnętrzna lub wewnętrzna dwusieczna kąta to prosta, półprosta lub odcinek dzielący kąt mniejszy niż 180° na dwa równe kąty . Zewnętrzna lub zewnętrzna dwusieczna to linia, która dzieli kąt dodatkowy (180° minus kąt pierwotny), utworzony przez jeden bok tworzący kąt pierwotny i przedłużenie drugiego boku, na dwa równe kąty.

Aby podzielić kąt na pół za pomocą liniału i kompasu , rysujemy okrąg, którego środkiem jest wierzchołek. Okrąg styka się z kątem w dwóch punktach: po jednym na każdej nodze. Używając każdego z tych punktów jako środka, narysuj dwa koła tego samego rozmiaru. Przecięcie okręgów (dwa punkty) wyznacza prostą będącą dwusieczną kąta.

Dowód poprawności tej konstrukcji jest dość intuicyjny, polegający na symetrii problemu. Trisekcji kąta (podziału go na trzy równe części) nie da się osiągnąć za pomocą samego kompasu i linijki (po raz pierwszy udowodnił to Pierre Wantzel ).

Dwusieczne wewnętrzne i zewnętrzne kąta są prostopadłe . Jeśli kąt jest utworzony przez dwie linie podane algebraicznie jako ${\ Displaystyle l_ {1} x + m_ {1} y + n_ {1} = 0}$ i ${\ Displaystyle l_ {2} x + m_ {2} y + n_ {2} = 0,}$ wtedy dwusieczne wewnętrzne i zewnętrzne są określone przez dwa równania

{\ Displaystyle {\ Frac {l_ {1} x + m_ {1} y + n_ {1}} {\ sqrt {l_ {1} ^ {2} + m_ {1} ^ {2}}}} = \ pm {\frac {l_{2}x+m_{2}y+n_{2}}{\sqrt {l_{2}^{2}+m_{2}^{2}}}}.}

Trójkąt

Współbieżności i współliniowości

The interior angle bisectors of a triangle are concurrent in a point called the incenter of the triangle, as seen in the diagram.

Dwusieczne dwóch kątów zewnętrznych i dwusieczna drugiego kąta wewnętrznego są sobie równe.

Trzy punkty przecięcia, każdy dwusiecznej kąta zewnętrznego z przeciwległym przedłużonym bokiem , są współliniowe (leżą na tej samej linii).

Trzy punkty przecięcia, dwa z nich między wewnętrzną dwusieczną kąta a przeciwległym bokiem, a trzeci między drugą dwusieczną kąta zewnętrznego a przeciwległym przedłużonym bokiem, są współliniowe.

Twierdzenie o dwusiecznej kąta

Na tym schemacie BD:DC = AB:AC.

Twierdzenie o dwusiecznej kąta dotyczy względnych długości dwóch odcinków, na które bok trójkąta jest podzielony linią przecinającą przeciwny kąt. Przyrównuje ich względne długości do względnych długości pozostałych dwóch boków trójkąta.

Długości

Jeśli długości boków trójkąta wynoszą $do {\ Displaystyle a, b, c}$ ${\ Displaystyle s = (a + b + c) / 2,}$ półobwód i A jest kątem przeciwnej strony ${\ displaystyle a}$ wtedy długość wewnętrznej dwusiecznej kąta A wynosi za

{\ Displaystyle {\ Frac {2 {\ sqrt {bcs (sa)}}} {b + c}}}

lub w kategoriach trygonometrycznych,

{\ Displaystyle {\ Frac {2bc} {b + c}} \ cos {\ Frac {A} {2}}.}

Jeśli wewnętrzna dwusieczna kąta A w trójkącie ABC ma długość $m$ ta dwusieczna dzieli bok przeciwległy A na odcinki o długości i n , to

{\ Displaystyle t_ {a} ^ {2} + mn = pne}

gdzie b i c to długości boków przeciwległych wierzchołków B i C; a bok przeciwległy do A jest podzielony w proporcji b : c .

Jeśli wewnętrzne dwusieczne kątów A, B i C mają długości ${\ Displaystyle t_ {a}, t_ {b}}$ i ${\ displaystyle t_ {c}}$ , to

{\ Displaystyle {\ Frac {(b + c) ^ {2}} {bc}} t_ {a} ^ {2} + {\ Frac {(c + a) ^ {2}} {ca}} t_ { b}^{2}+{\frac {(a+b)^{2}}{ab}}t_{c}^{2}=(a+b+c)^{2}.}

Żadne dwa nieprzystające trójkąty nie mają tego samego zestawu trzech długości dwusiecznych kątów wewnętrznych.

Trójkąty całkowite

Istnieją trójkąty całkowite z wymierną dwusieczną kąta .

Czworoboczny

Wewnętrzne dwusieczne kąta wypukłego czworoboku albo tworzą cykliczny czworobok (to znaczy cztery punkty przecięcia sąsiednich dwusiecznych kątów są koncykliczne ), albo są współbieżne . W tym drugim przypadku czworobok jest czworobokiem stycznym .

Romb

Każda przekątna rombu dzieli na pół przeciwne kąty.

Ex-styczny czworobok

Mimośród ex-stycznego czworoboku leży na przecięciu sześciu dwusiecznych kątów. Są to dwusieczne kątów wewnętrznych przy dwóch przeciwległych kątach wierzchołków, dwusieczne kątów zewnętrznych (dodatkowe dwusieczne kątów) przy pozostałych dwóch kątach wierzchołków oraz dwusieczne kątów zewnętrznych przy kątach utworzonych w miejscu przecięcia się przedłużeń przeciwległych boków .

Parabola

Styczna do paraboli w dowolnym punkcie przecina kąt między linią łączącą punkt z ogniskiem a linią biegnącą od punktu i prostopadłą do kierownicy.

Dwusieczne boków wielokąta

Trójkąt

Mediany

Każda z trzech środkowych trójkąta jest odcinkiem linii przechodzącym przez jeden wierzchołek i środek przeciwległego boku, więc przecina ten bok na pół (choć generalnie nie prostopadle). Trzy środkowe przecinają się w punkcie zwanym środkiem ciężkości trójkąta, który jest jego środkiem masy, jeśli ma on jednakową gęstość; zatem każda linia przechodząca przez środek ciężkości trójkąta i jeden z jego wierzchołków przecina przeciwną stronę na pół. Środek ciężkości znajduje się dwa razy bliżej środka dowolnego boku niż przeciwległego wierzchołka.

Dwusieczne prostopadłe

Wewnętrzna dwusieczna prostopadła boku trójkąta to odcinek, który całkowicie spada na trójkąt i wewnątrz niego, linii, która przecina ten bok prostopadle na pół. Trzy prostopadłe dwusieczne trzech boków trójkąta przecinają się w środku okręgu opisanego (środek okręgu przechodzący przez trzy wierzchołki). Zatem każda linia przechodząca przez środek okręgu opisanego na trójkącie i prostopadła do boku przecina ten bok na pół.

W trójkącie ostrym środek okręgu opisanego dzieli w równych proporcjach wewnętrzne dwusieczne prostopadłe dwóch najkrótszych boków. W rozwartokątnym trójkącie prostopadłe dwusieczne dwóch najkrótszych boków (rozciągnięte poza ich przeciwległe boki trójkąta do środka okręgu opisanego) są podzielone przez odpowiednie przecinające się boki trójkąta w równych proporcjach.

Dla dowolnego trójkąta wewnętrzne dwusieczne prostopadłe są podane przez ${\ Displaystyle p_ {a} = {\ tfrac {2aT} {a ^ {2} + b ^ {2 } -c ^ {2}}},}$ ${\ Displaystyle p_ {b} = {\ tfrac {2bT} {a ^ {2} + b ^ { 2} -c ^ {2}}},}$ i ${\ Displaystyle p_ {c} = {\ tfrac {2cT} {a ^ {2} -b ^ {2} + c ^ {2}}},}$ gdzie boki to ${\ Displaystyle a \ geq b \ geq c},$ a obszar to ${\ Displaystyle T.}$

Czworoboczny

Dwie bimediany wypukłego czworoboku to odcinki linii łączące punkty środkowe przeciwległych boków, stąd każdy przecinający dwa boki . Dwie bimediany i odcinek linii łączący punkty środkowe przekątnych są współbieżne w punkcie zwanym „środkiem ciężkości wierzchołków” i wszystkie są podzielone przez ten punkt.

Cztery „maltitudes” wypukłego czworoboku to prostopadłe do boku przechodzące przez środek przeciwległego boku, a więc przecinające ten drugi bok na pół. Jeśli czworobok jest cykliczny (wpisany w okrąg), te maltitudes są zbieżne w (wszystkie spotykają się) we wspólnym punkcie zwanym „antycentrum”.

Twierdzenie Brahmagupty głosi, że jeśli cykliczny czworobok jest ortodiagonalny (to znaczy ma prostopadłe przekątne ), to prostopadła do boku od punktu przecięcia przekątnych zawsze przecina przeciwną stronę.

Konstrukcja dwusiecznej prostopadłej tworzy czworobok z prostopadłych dwusiecznych boków innego czworoboku.

Dwusieczne obszaru i dwusieczne obwodu

Trójkąt

nieskończona liczba linii przecinających obszar trójkąta . Trzy z nich to mediany trójkąta (które łączą punkty środkowe boków z przeciwległymi wierzchołkami) i są one zbieżne w środku ciężkości trójkąta ; w rzeczywistości są to jedyne dwusieczne obszaru, które przechodzą przez środek ciężkości. Trzy inne dwusieczne obszaru są równoległe do boków trójkąta; każdy z nich przecina pozostałe dwa boki, tak aby podzielić je na segmenty o proporcjach ${\ Displaystyle {\ sqrt {2}} + 1: 1}$ . Te sześć linii jest równoległych po trzy na raz: oprócz tego, że trzy środkowe są współbieżne, każda jedna środkowa jest zbieżna z dwiema równoległymi do boków dwusiecznymi.

Obwiednią nieskończoności dwusiecznych obszaru jest naramiennik ( szeroko definiowany jako figura z trzema wierzchołkami połączonymi krzywymi wklęsłymi na zewnątrz naramiennika, dzięki czemu punkty wewnętrzne są zbiorem niewypukłym). Wierzchołki mięśnia naramiennego znajdują się w punktach środkowych środkowych; wszystkie punkty wewnątrz mięśnia naramiennego znajdują się na trzech różnych dwusiecznych obszaru, podczas gdy wszystkie punkty na zewnątrz znajdują się tylko na jednym. [1] Boki mięśnia naramiennego to łuki hiperbol , które są asymptotyczne względem przedłużonych boków trójkąta. Stosunek pola obwiedni dwusiecznych obszaru do pola trójkąta jest niezmienny dla wszystkich trójkątów i wynosi ${\ Displaystyle {\ tfrac {3} {4}} \log _{e}(2)-{\tfrac {1}{2}},}$ czyli 0,019860... lub mniej niż 2%.

Tasak trójkąta to odcinek linii, który przecina obwód trójkąta na pół i ma jeden koniec w punkcie środkowym jednego z trzech boków . Trzy tasaki zbiegają się (wszystkie przechodzą przez) środek okręgu Spiekera , który jest okręgiem przyśrodkowego trójkąta . Tasaki są równoległe do dwusiecznych kątów.

Dzielnik trójkąta to odcinek linii mający jeden koniec w jednym z trzech wierzchołków trójkąta i przecinający obwód na pół. Trzy rozdzielacze zbiegają się w punkcie Nagela trójkąta.

Każda linia przechodząca przez trójkąt, która dzieli zarówno pole trójkąta, jak i jego obwód na pół, przechodzi przez środek trójkąta (środek jego okręgu ). Istnieje jeden, dwa lub trzy z nich dla danego trójkąta. Linia przechodząca przez incenter przecina na pół jeden obszar lub obwód wtedy i tylko wtedy, gdy przecina również drugi.

Równoległobok

Każda linia przechodząca przez środek równoległoboku przecina pole i obwód na pół.

Koło i elipsa

Wszystkie dwusieczne obszaru i dwusieczne obwodu koła lub innej elipsy przechodzą przez środek , a wszelkie cięciwy przechodzące przez środek przecinają obszar i obwód na pół. W przypadku koła są to średnice koła.

Dwusieczne przekątnych

Równoległobok

Przekątne równoległoboku przecinają się w połowie.

Czworoboczny

Jeśli odcinek linii łączący przekątne czworoboku przecina obie przekątne na pół, to ten odcinek linii ( linia Newtona ) jest sam podzielony na pół przez środek ciężkości wierzchołka.

Dwusieczne objętości

Płaszczyzna, która dzieli dwie przeciwległe krawędzie czworościanu w danym stosunku, dzieli również objętość czworościanu w tym samym stosunku. Zatem każda płaszczyzna zawierająca bimedianę (łącznik punktów środkowych przeciwległych krawędzi) czworościanu dzieli objętość czworościanu na pół

^ Weisstein, Eric W. „Dwusieczna kąta zewnętrznego”. Z MathWorld — zasób internetowy firmy Wolfram.
^ Hiszpania, Barry. Stożki analityczne , Dover Publications, 2007 (oryg. 1957).
^ ^a ^b ^c ^d ^e Johnson, Roger A., Advanced Euclidean Geometry , Dover Publ., 2007 (oryg. 1929).
Bibliografia _ „O istnieniu trójkątów o danych długościach jednego boku i dwóch sąsiednich dwusiecznych kątów”, Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
Bibliografia _ Mathematical Gazette 93, marzec 2009, 115-116.
^ Mironescu, P. i Panaitopol, L., „Istnienie trójkąta o określonych długościach dwusiecznych kątów”, American Mathematical Monthly 101 (1994): 58–60.
^ Oxman, Victor, „Czysto geometryczny dowód wyjątkowości trójkąta z zadanymi dwusiecznymi kątów”, Forum Geometricorum 8 (2008): 197–200.
^ Weisstein, Eric W. „Czworokąt”. Z MathWorld — zasób internetowy firmy Wolfram. http://mathworld.wolfram.com/Quadrilateral.html
^ ^a ^b Mitchell, Douglas W. (2013), „Prostopadłe dwusieczne boków trójkąta”, Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
^ Altshiller-Court, Nathan, College Geometry , Dover Publ., 2007.
^ ^a ^b ^c ^d Dunn, Jas. A.; Ładnie, Jasiu. E. (maj 1972). „Połówka trójkąta”. Gazeta Matematyczna . 56 (396): 105–108. doi : 10.2307/3615256 . JSTOR 3615256 .
^ Kodokostas, Dimitrios, „Triangle Equalizers”, Mathematics Magazine 83, kwiecień 2010, s. 141-146.
^ Weisstein, Eric W. „Czworościan”. Z MathWorld — zasób internetowy firmy Wolfram. http://mathworld.wolfram.com/Tetrahedron.html
^ Altshiller-Court, N. „Czworościan”. Ch. 4 w Modern Pure Solid Geometry : Chelsea, 1979.

Linki zewnętrzne

Dwusieczna kąta przy przecięciu węzła
Definicja dwusiecznej kąta. Math Open Reference Z interaktywnym apletem
Definicja dwusiecznej linii. Math Open Reference Z interaktywnym apletem
Dwusieczna linii prostopadłej. Z interaktywnym apletem
Animowane instrukcje dzielenia na pół kąta i linii przy użyciu kompasu i liniału
Weisstein, Eric W. „Linia dwusieczna” . MathWorld .

Ten artykuł zawiera materiał z dwusiecznej kąta w serwisie PlanetMath , który jest objęty licencją Creative Commons Attribution/Share-Alike License .

[1] Weisstein, Eric W. „Dwusieczna kąta zewnętrznego”. Z MathWorld — zasób internetowy firmy Wolfram.

[2] Hiszpania, Barry. Stożki analityczne , Dover Publications, 2007 (oryg. 1957).

[Johnson-3] Johnson, Roger A., Advanced Euclidean Geometry , Dover Publ., 2007 (oryg. 1929).

[4] Bibliografia _ „O istnieniu trójkątów o danych długościach jednego boku i dwóch sąsiednich dwusiecznych kątów”, Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf

[5] Bibliografia _ Mathematical Gazette 93, marzec 2009, 115-116.

[6] Mironescu, P. i Panaitopol, L., „Istnienie trójkąta o określonych długościach dwusiecznych kątów”, American Mathematical Monthly 101 (1994): 58–60.

[7] Oxman, Victor, „Czysto geometryczny dowód wyjątkowości trójkąta z zadanymi dwusiecznymi kątów”, Forum Geometricorum 8 (2008): 197–200.

[8] Weisstein, Eric W. „Czworokąt”. Z MathWorld — zasób internetowy firmy Wolfram. http://mathworld.wolfram.com/Quadrilateral.html

[Mitchell-9] Mitchell, Douglas W. (2013), „Prostopadłe dwusieczne boków trójkąta”, Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf

[Altshiller-Court-10] Altshiller-Court, Nathan, College Geometry , Dover Publ., 2007.

[Dunn-11] Dunn, Jas. A.; Ładnie, Jasiu. E. (maj 1972). „Połówka trójkąta”. Gazeta Matematyczna . 56 (396): 105–108. doi : 10.2307/3615256 . JSTOR 3615256 .

[12] Kodokostas, Dimitrios, „Triangle Equalizers”, Mathematics Magazine 83, kwiecień 2010, s. 141-146.

[13] Weisstein, Eric W. „Czworościan”. Z MathWorld — zasób internetowy firmy Wolfram. http://mathworld.wolfram.com/Tetrahedron.html

[14] Altshiller-Court, N. „Czworościan”. Ch. 4 w Modern Pure Solid Geometry : Chelsea, 1979.