Cykliczny czworobok

Przykłady cyklicznych czworoboków

W geometrii euklidesowej cykliczny czworobok lub wpisany czworobok to czworobok , którego wszystkie wierzchołki leżą na jednym okręgu . Okrąg ten nazywany jest okręgiem opisanym lub okręgiem opisanym , a wierzchołki nazywamy koncyklicznymi . Środek okręgu i jego promień nazywane są środkiem okręgu i promieniem okręgu . Inne nazwy tych czworoboków to czworobok koncykliczny i czworobok akordowy , ten ostatni, ponieważ boki czworoboku są akordami okręgu opisanego. Zwykle zakłada się, że czworobok jest wypukły , ale istnieją również skrzyżowane cykliczne czworoboki. Podane poniżej wzory i właściwości obowiązują w przypadku wypukłym.

Słowo cykliczny pochodzi od starożytnego greckiego κύκλος ( kuklos ), co oznacza „koło” lub „koło”.

Wszystkie trójkąty mają okrąg opisany , ale nie wszystkie czworoboki. Przykładem czworokąta, który nie może być cykliczny, jest romb niekwadratowy . Poniższe charakterystyki sekcji określają, jakie warunki konieczne i wystarczające musi spełniać czworobok, aby mieć okrąg opisany.

Przypadki specjalne

Każdy kwadrat , prostokąt , trapez równoramienny lub antyrównoległobok jest cykliczny. Latawiec jest cykliczny wtedy i tylko wtedy, gdy ma dwa kąty proste. Bicentryczny czworobok to cykliczny czworobok, który jest również styczny , a ex-bicentryczny czworobok to cykliczny czworobok, który jest również eks-styczny . Czworokąt harmoniczny to czworokąt cykliczny, w którym iloczyn długości przeciwległych boków jest równy.

Charakteryzacje

Cykliczny czworokąt ABCD

środek okręgu

Wypukły czworobok jest cykliczny wtedy i tylko wtedy, gdy cztery dwusieczne prostopadłe do boków są współbieżne . Ten wspólny punkt to środek okręgu opisanego .

Kąty dodatkowe

Wypukły czworokąt ABCD jest cykliczny wtedy i tylko wtedy, gdy jego przeciwległe kąty są komplementarne , to znaczy

${\ Displaystyle \ alfa + \ gamma = \ beta + \ delta = \ pi \ {\ tekst {radiany}} \ (= 180 ^ {\ circ}).}$

Bezpośrednim twierdzeniem było Twierdzenie 22 w Księdze 3 Elementów Euklidesa . Równoważnie wypukły czworobok jest cykliczny wtedy i tylko wtedy, gdy każdy kąt zewnętrzny jest równy przeciwległemu kątowi wewnętrznemu .

W 1836 roku Duncan Gregory uogólnił ten wynik w następujący sposób: Biorąc pod uwagę dowolny wypukły cykliczny 2 n -gon, to każda z dwóch sum alternatywnych kątów wewnętrznych jest równa ( n -1) ${\ Displaystyle \ pi}$ .

Biorąc rzut stereograficzny (styczna do połowy kąta) każdego kąta, można to ponownie wyrazić,

${\ Displaystyle {\ Frac {\ tan {\ Frac {\ alfa} {2}} + \ tan {\ Frac {\ gamma} {2}}} {1- \ tan {\ Frac {\ alfa} {2} } \ tan {\ frac {\ gamma }{2}}}} = {\ frac {\ tan {\ frac {\ beta }{2}} + \ tan {\ frac {\ delta }{2}}} 1-\ tan {\ frac {\ beta }{2}} \ tan {\ frac {\ delta }{2}}}} = \ infty .}$

Co implikuje, że

${\ Displaystyle \ dębnik {\ Frac {\ alfa} {2}} \ dębnik {\ Frac {\ gamma} {2}} = \ tan {\frac {\beta}}{2}}{\tan {\frac {\delta}}{2}}}=1}$

Kąty między bokami i przekątnymi

Wypukły czworokąt ABCD jest cykliczny wtedy i tylko wtedy, gdy kąt między bokiem a przekątną jest równy kątowi między przeciwległym bokiem a drugą przekątną. czyli np.

${\ Displaystyle \ kąt ACB = \ kąt ADB.}$

Punkty Pascala

ABCD jest cyklicznym czworobokiem. E jest punktem przecięcia przekątnych, a F jest punktem przecięcia przedłużeń boków BC i AD . ${\ Displaystyle \ omega}$ to okrąg, którego średnicą jest odcinek EF . P i Q to punkty Pascala utworzone przez okrąg . ${\ displaystyle \ omega}$ . Trójkąty FAB i FCD są podobne.

Inne konieczne i wystarczające warunki, aby wypukły czworobok ABCD był cykliczny, to: niech E będzie punktem przecięcia przekątnych, niech F będzie punktem przecięcia przedłużeń boków AD i BC , niech ${\ displaystyle \ omega} niech będzie okręgiem$$,$ którego średnica jest odcinkiem EF , i niech P i Q będą punktami Pascala na bokach AB i CD utworzonymi przez . (1) $P$ jest czworobokiem cyklicznym wtedy i tylko wtedy, gdy punkty i Q są współliniowe ze środkiem okręgu O . (2) ABCD jest czworokątem cyklicznym wtedy i tylko wtedy, gdy punkty P i Q są środkami boków AB i CD .

Przecięcie przekątnych

Jeśli dwie linie, jedna zawierająca odcinek AC , a druga zawierająca odcinek BD , przecinają się w E , to cztery punkty A , B , C , D są koncykliczne wtedy i tylko wtedy, gdy

${\ Displaystyle \ Displaystyle AE \ cdot EC = BE \ cdot ED.}$

Przecięcie E może być wewnętrzne lub zewnętrzne względem okręgu. W pierwszym przypadku cyklicznym czworobokiem jest ABCD , aw drugim przypadku cyklicznym czworobokiem jest ABDC . Gdy przecięcie jest wewnętrzne, równość stwierdza, że ​​iloczyn długości segmentów, na które E dzieli jedną przekątną, jest równy iloczynowi długości drugiej przekątnej. Jest to znane jako twierdzenie o przecinających się cięciwach , ponieważ przekątne cyklicznego czworoboku są cięciwami okręgu opisanego.

Twierdzenie Ptolemeusza

Twierdzenie Ptolemeusza wyraża iloczyn długości dwóch przekątnych e i f cyklicznego czworoboku jako równy sumie iloczynów przeciwległych boków:

${\ Displaystyle \ Displaystyle ef = ac + bd,}$

gdzie a , b , c , d to długości boków w kolejności. Odwrotność jest również prawdziwa . Oznacza to, że jeśli to równanie jest spełnione w wypukłym czworoboku, powstaje cykliczny czworobok.

Trójkąt ukośny

ABCD jest cyklicznym czworobokiem. EFG to przekątna trójkąta ABCD . Punkt T przecięcia dwuśrodkowych ABCD należy do dziewięciopunktowego koła EFG .

W wypukłym czworoboku ABCD niech EFG $będzie$ ukośnym trójkątem ABCD i niech dziewięciopunktowym kołem EFG . ABCD jest cykliczny wtedy i tylko wtedy, gdy punkt przecięcia dwuśrodkowych ABCD należy do dziewięciopunktowego koła ${\ displaystyle \ omega}$ .

Obszar

Pole K cyklicznego czworoboku o bokach a , b , c , d jest określone wzorem Brahmagupty

${\ Displaystyle K = {\ sqrt {(sa) (sb) (sc) (sd)}} \,}$

gdzie s , półobwód , wynosi s = 1 / 2 ( a + b + c + re ) . Jest to następstwo wzoru Bretschneidera na ogólny czworobok, ponieważ przeciwne kąty są uzupełniające w przypadku cyklicznym. Jeśli również d = 0 , cykliczny czworobok staje się trójkątem, a wzór sprowadza się do wzoru Herona .

Cykliczny czworobok ma maksymalne pole spośród wszystkich czworoboków o tej samej długości boków (niezależnie od kolejności). To kolejny wniosek z formuły Bretschneidera. Można to również udowodnić za pomocą rachunku różniczkowego .

Cztery nierówne długości, z których każda jest mniejsza niż suma pozostałych trzech, to boki każdego z trzech nieprzystających cyklicznych czworoboków, które zgodnie ze wzorem Brahmagupty mają tę samą powierzchnię. W szczególności dla boków a , b , c i d , bok a może znajdować się naprzeciwko dowolnego boku b , boku c lub boku d .

Pole cyklicznego czworoboku z kolejnymi bokami a , b , c , d , kątem A między bokami a i d oraz kątem B między bokami a i b można wyrazić jako

${\ Displaystyle K = {\ tfrac {1} {2}} (ab + cd) \ sin {B}}$

Lub

${\ Displaystyle K = {\ tfrac {1} {2}} (reklama + bc) \ sin {A}}$

Lub

$\ Displaystyle K = {\ tfrac {1} {2}} (ac + bd) \ sin {\ teta}}$

gdzie θ jest dowolnym kątem między przekątnymi. Pod warunkiem, że A nie jest kątem prostym, obszar można również wyrazić jako

${\ Displaystyle K = {\ tfrac {1} {4}} (a ^ {2} -b ^ {2} -c ^ {2} + d ^ {2}) \ tan {A}.}$

Inna formuła to

${\ Displaystyle \ Displaystyle K = 2R ^ {2} \ sin {A} \ sin {B} \ sin {\ theta}}$

gdzie R jest promieniem okręgu opisanego . Bezpośrednią konsekwencją

${\ Displaystyle K \ równoważnik 2R ^ {2}}$

gdzie istnieje równość wtedy i tylko wtedy, gdy czworokąt jest kwadratem.

przekątne

W cyklicznym czworoboku z kolejnymi wierzchołkami A , B , C , D i bokami a = AB , b = BC , c = CD i d = DA , długości przekątnych p = AC i q = BD można wyrazić jako boków jako

${\ Displaystyle p = {\ sqrt {\ Frac {(ac + bd) (reklama + bc)} {ab + cd}} }}$ i ${\ Displaystyle q = {\ sqrt {\ Frac {(ac + bd) (ab + cd)} {reklama + pne}}}}$

więc pokazując twierdzenie Ptolemeusza

${\ displaystyle pq = ac + bd.}$

Zgodnie z drugim twierdzeniem Ptolemeusza ,

${\ Displaystyle {\ Frac {p} {q}} = {\ Frac {reklama + bc} {ab + cd}}$

używając tych samych oznaczeń jak powyżej.

Dla sumy przekątnych mamy nierówność

${\ displaystyle p + q \ geq 2 {\ sqrt {ac + bd}}.}$

Równość zachodzi wtedy i tylko wtedy, gdy przekątne mają równe długości, co można udowodnić za pomocą nierówności AM-GM .

Ponadto,

${\ Displaystyle (p + q) ^ {2} \ równoważnik (a + c) ^ {2} + (b + d) ^ {2}.}$

W każdym wypukłym czworoboku dwie przekątne razem dzielą czworobok na cztery trójkąty; w cyklicznym czworoboku przeciwległe pary tych czterech trójkątów są do siebie podobne .

Jeśli M i N są środkami przekątnych AC i BD , to

${\ Displaystyle {\ Frac {MN} {EF}} = {\ Frac {1} {2}} \ lewo | {\ Frac {AC} {BD}} - {\ Frac {BD} {AC}} \ prawo |}$

gdzie E i F są punktami przecięcia przedłużeń przeciwległych boków.

Jeśli ABCD jest cyklicznym czworobokiem, w którym AC spotyka się z BD w E , to

${\ Displaystyle {\ Frac {AE} {CE}} = {\ Frac {AB} {CB}} \ cdot {\ Frac {AD} {CD}}.}$

Zestaw boków, które mogą tworzyć cykliczny czworobok, można ułożyć w dowolną z trzech różnych sekwencji, z których każda może tworzyć cykliczny czworobok o tym samym obszarze w tym samym okręgu opisanym (obszary są takie same zgodnie ze wzorem Brahmagupty na pola). Każde dwa z tych cyklicznych czworoboków mają jedną wspólną długość przekątnej.

Formuły kątowe

Dla cyklicznego czworoboku z kolejnymi bokami a , b , c , d , półobwodem s i kątem A między bokami a i d , funkcje trygonometryczne A są określone wzorem

${\ Displaystyle \ sałata A = {\ Frac {a ^ {2} -b ^ {2} -c ^ { 2}+d^{2}}{2(ad+bc)}},}$

$\ Displaystyle \ sin A = {\ Frac {2 {\ sqrt {(sa) (sb) (sc) (sd)}}} {(reklama + bc)}}}$

${\ Displaystyle \ tan {\ Frac {A} {2}} = {\ sqrt {\ Frac {(sa) (sd)} {(sb) (sc)}}}.}$

Kąt θ między przekątnymi przeciwległymi bokami a i c jest spełniony

${\ Displaystyle \ tan {\ Frac {\ theta} {2}} = {\ sqrt {\ Frac {(sb) (sd)} {(sa) (sc)}}}.}$

Jeżeli przedłużenia przeciwległych boków a i c przecinają się pod kątem φ , to

$\ Displaystyle \ sałata {\ Frac {\ varphi} {2} }={\sqrt {\frac {(sb)(sd)(b+d)^{2}}{(ab+cd)(ad+bc)}}}}$

gdzie s jest półobwodem .

Formuła okręgu Parameśwary

Cykliczny czworobok z kolejnymi bokami a , b , c , d i półobwodem s ma promień okręgu opisanego przez

${\ Displaystyle R = {\ Frac {1} {4}}} {\ sqrt {\ Frac {(ab + cd) (ac + bd) (ad + bc)} {(sa) (sb) (sc) (sd )}}}.}$

Zostało to wyprowadzone przez indyjskiego matematyka Vatasseri Parameśvara w XV wieku.

Używając formuły Brahmagupty , formuła Parameśwary może zostać przekształcona jako

${\ Displaystyle 4KR = {\ sqrt {(ab + cd) (ac + bd) (reklama + pne)} }}$

gdzie K jest polem cyklicznego czworoboku.

Antycentrum i współliniowość

Cztery odcinki linii, każdy prostopadły do ​​jednego boku cyklicznego czworoboku i przechodzący przez środek przeciwległego boku , są współbieżne . Te odcinki linii nazywane są maltitudes , co jest skrótem od wysokości punktu środkowego. Ich wspólny punkt nazywa się antycentrum . Ma właściwość bycia odbiciem środka okręgu opisanego w „środku wierzchołka” . Tak więc w cyklicznym czworoboku środek okręgu opisanego, środek ciężkości wierzchołka i antycentrum są współliniowe .

Jeśli przekątne cyklicznego czworoboku przecinają się w P , a środki przekątnych to M i N , to antycentrum czworoboku jest ortocentrum trójkąta MNP .

Antycentrum cyklicznego czworoboku to punkt Ponceleta jego wierzchołków.

Inne właściwości

Twierdzenie japońskie

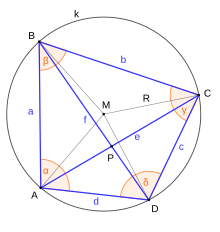
• _W cyklicznym czworoboku ABCD wierzchołki M1 , M2 , _M3 , _M4 ( patrz rysunek po prawej) w trójkątach DAB _, ABC , BCD i CDA są wierzchołkami prostokąta . Jest to jedno z twierdzeń znanych jako twierdzenie japońskie . Ortocentra tych samych czterech trójkątów są wierzchołkami czworoboku przystającego do ABCD , a środki ciężkości w tych czterech trójkątach są wierzchołkami innego czworoboku cyklicznego .
• W cyklicznym czworokącie ABCD ze środkiem okręgu opisanego na O , niech P będzie punktem przecięcia się przekątnych AC i BD . Wtedy kąt APB jest średnią arytmetyczną kątów AOB i COD . Jest to bezpośrednią konsekwencją twierdzenia o kącie wpisanym i twierdzenia o kącie zewnętrznym .
• Nie ma cyklicznych czworoboków o wymiernym polu i nierównych wymiernych bokach w postępie arytmetycznym lub geometrycznym .

• Jeśli cykliczny czworobok ma długości boków, które tworzą postęp arytmetyczny, czworobok jest również ex-bicentryczny .
• Jeśli przeciwległe boki cyklicznego czworoboku są rozciągnięte tak, że spotykają się w E i F , to dwusieczne kątów wewnętrznych w E i F są prostopadłe.

Czworokąty Brahmagupty

Czworokąt Brahmagupty to cykliczny czworobok z całkowitymi bokami, całkowitymi przekątnymi i całkowitym obszarem. Wszystkie czworoboki Brahmagupty o bokach a , b , c , d , przekątnych e , f , polu K i promieniu okręgu R można uzyskać usuwając mianowniki z następujących wyrażeń zawierających parametry wymierne t , u i v :

${\ Displaystyle a = [t (u + v) + (1-uv)][ u + vt (1-uv)]}$

${\ Displaystyle b = (1 + u ^ {2}) (vt) (1 + telewizor )}$

${\ Displaystyle c = t (1 + u ^ {2}) (1 + v ^ {2})}$

${\ Displaystyle d = (1 + v ^ {2}) (ut) (1 + tu)}$

${ \ Displaystyle e = u (1 + t ^ {2}) (1 + v ^ {2})}$

${\ Displaystyle f = v (1 + t ^ {2})(1+u^{2})}$

${\ Displaystyle K = uv [2t (1-uv) - (u + v) (1-t ^ {2})] [2 (u + v) t + ( 1-uv)(1-t^{2})]}$

${\ Displaystyle 4R = (1 + u ^ {2}) (1 + v ^ {2}) (1 + t ^ {2}).}$

Przypadek ortodiagonalny

Promień okręgu i pole

Dla cyklicznego czworoboku, który jest również ortodiagonalny (ma prostopadłe przekątne), załóżmy, że przecięcie przekątnych dzieli jedną przekątną na odcinki o długości p ₁ i p ₂ , a drugą przekątną na odcinki o długości q ₁ i q ₂ . Wtedy (pierwsza równość to Twierdzenie 11 w Księdze Lematów Archimedesa )

${\ Displaystyle D ^ {2} = p_ {1} ^ {2} + p_ { 2}^{2}+q_{1}^{2}+q_{2}^{2}=a^{2}+c^{2}=b^{2}+d^{2}}$

gdzie D jest średnicą okręgu opisanego . Dzieje się tak, ponieważ przekątne są prostopadłymi cięciwami koła . Z równań tych wynika, że ​​promień okręgu R można wyrazić jako

${\ Displaystyle R = {\ tfrac {1} {2}} {\ sqrt {p_ {1} ^ {2} + p_ {2} }^{2}+q_{1}^{2}+q_{2}^{2}}}}$

lub, jeśli chodzi o boki czworoboku, as

${\ Displaystyle R = {\ tfrac {1} {2}}} {\ sqrt {a ^ {2} + c ^ {2}}} = {\ tfrac {1} {2}} {\ sqrt {b ^ { 2}+d^{2}}}.}$

Z tego też wynika

${\ Displaystyle a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2} = 8R ^ {2}.}$

Tak więc, zgodnie z twierdzeniem Eulera o czworoboku , promień okręgu można wyrazić za pomocą przekątnych p i q , a odległość x między środkami przekątnych jako

${\ Displaystyle R = {\ sqrt {\ Frac {p ^ {2} + q ^ {2} + 4x ^ {2} {8}}}.}$

Wzór na pole K cyklicznego czworoboku ortodiagonalnego pod względem czterech boków otrzymuje się bezpośrednio, łącząc twierdzenie Ptolemeusza i wzór na pole czworoboku ortodiagonalnego . Wynik to

${\ Displaystyle K = {\ tfrac {1} {2}} (ac + bd).}$

Inne właściwości

• W cyklicznym czworoboku ortodiagonalnym antycentrum pokrywa się z punktem, w którym przecinają się przekątne.
• Twierdzenie Brahmagupty stwierdza, że ​​​​dla cyklicznego czworoboku, który jest również ortodiagonalny , prostopadła z dowolnej strony przechodząca przez punkt przecięcia przekątnych przecina przeciwną stronę na pół.
• Jeśli cykliczny czworobok jest również ortodiagonalny, odległość od środka okręgu opisanego do dowolnego boku jest równa połowie długości przeciwległego boku.
• W cyklicznym prostopadłościennym czworoboku odległość między środkami przekątnych jest równa odległości między środkiem okręgu opisanego a punktem, w którym przecinają się przekątne.

Cykliczne sferyczne czworoboki

W geometrii sferycznej sferyczny czworobok utworzony z czterech przecinających się większych okręgów jest cykliczny wtedy i tylko wtedy, gdy sumy przeciwległych kątów są równe, tj. α + γ = β + δ dla kolejnych kątów α, β, γ, δ czworoboku . Jeden kierunek tego twierdzenia udowodnił IA Lexell w 1786 r. Lexell wykazał, że w sferycznym czworokącie wpisanym w mały okrąg kuli sumy przeciwległych kątów są równe, aw opisanym czworoboku sumy przeciwległych boków są równe. Pierwsze z tych twierdzeń jest sferycznym odpowiednikiem twierdzenia o płaszczyźnie, a drugie twierdzenie jest jego dualnością, czyli wynikiem zamiany kół wielkich i ich biegunów. Kiper i in. udowodnił odwrotność twierdzenia: Jeśli sumy przeciwległych boków są równe w kulistym czworokącie, to istnieje okrąg wpisujący się w ten czworokąt.

Zobacz też

• Twierdzenie motyla
• Cykliczny wielokąt
• Moc punktu
• Tabela akordów Ptolemeusza
• Pięciokąt Robbinsa

Dalsza lektura

• D. Fraivert: Czworokąty w punktach Pascala wpisane w czworobok cykliczny

Linki zewnętrzne

• Wyprowadzenie wzoru na pole czworoboku cyklicznego
• Incenters w cyklicznym czworoboku na przecięciu węzła
• Cztery współbieżne linie w cyklicznym czworoboku na przecięciu węzła
• Weisstein, Eric W. „Cykliczny czworobok” . MathWorld .