Geometria euklidesowa

„Geometria płaszczyzny” przekierowuje tutaj. W przypadku innych zastosowań zobacz Geometria płaszczyzny (ujednoznacznienie) .

Fragment ze Szkoły ateńskiej Rafaela przedstawiający greckiego matematyka - być może reprezentującego Euklidesa lub Archimedesa - używającego kompasu do narysowania konstrukcji geometrycznej.

Geometria euklidesowa to system matematyczny przypisywany starożytnemu greckiemu matematykowi Euklidesowi , który opisał w swoim podręczniku geometrii : Elementy . Podejście Euklidesa polega na przyjęciu małego zestawu intuicyjnie atrakcyjnych aksjomatów (postulatów) i wyprowadzeniu z nich wielu innych twierdzeń ( twierdzeń ). Chociaż wiele wyników Euklidesa zostało podanych wcześniej, Euclid był pierwszym, który zorganizował te twierdzenia w logiczny system , w którym każdy wynik jest udowodnione z aksjomatów i wcześniej udowodnionych twierdzeń.

Elementy zaczyna się od geometrii płaskiej , nauczanej jeszcze w szkole średniej jako pierwszy system aksjomatyczny i pierwsze przykłady dowodów matematycznych . Przechodzi do bryłowej geometrii trzech wymiarów . Wiele Elementów zawiera wyniki tego, co obecnie nazywa się algebrą i teorią liczb , wyjaśnione w języku geometrycznym.

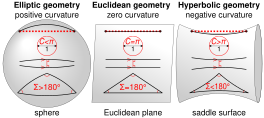
Przez ponad dwa tysiące lat przymiotnik „euklidesowy” był zbędny, ponieważ nie wymyślono żadnego innego rodzaju geometrii. Aksjomaty Euklidesa wydawały się tak intuicyjnie oczywiste (z możliwym wyjątkiem postulatu równoległości ) , że każde twierdzenie z nich udowodnione uznano za prawdziwe w sensie absolutnym, często metafizycznym. Jednak obecnie znanych jest wiele innych samospójnych geometrii nieeuklidesowych , z których pierwsze odkryto na początku XIX wieku. Implikacja ogólnej teorii względności Alberta Einsteina jest to, że sama przestrzeń fizyczna nie jest euklidesowa, a przestrzeń euklidesowa jest jej dobrym przybliżeniem tylko na krótkich odległościach (w stosunku do siły pola grawitacyjnego ).

Geometria euklidesowa jest przykładem geometrii syntetycznej , ponieważ logicznie przechodzi od aksjomatów opisujących podstawowe właściwości obiektów geometrycznych, takich jak punkty i linie, do twierdzeń dotyczących tych obiektów. Kontrastuje to z geometrią analityczną , wprowadzoną prawie 2000 lat później przez René Descartesa , która wykorzystuje współrzędne do wyrażania właściwości geometrycznych jako wzory algebraiczne .

Elementy _

Główny artykuł: Elementy Euklidesa

Elementy to przede wszystkim usystematyzowanie wcześniejszej wiedzy o geometrii . Szybko zauważono jego poprawę w stosunku do wcześniejszych metod leczenia, w wyniku czego zainteresowanie zachowaniem wcześniejszych metod leczenia było niewielkie i obecnie prawie wszystkie zostały utracone.

Elementach jest 13 ksiąg :

Książki I – IV i VI omawiają geometrię płaszczyzny. Udowodniono wiele wyników dotyczących figur płaskich, na przykład: „W dowolnym trójkącie dwa kąty wzięte razem w dowolny sposób są mniejsze niż dwa kąty proste”. (Księga I propozycja 17) i twierdzenie Pitagorasa „W trójkątach prostokątnych kwadrat na boku leżącym naprzeciw kąta prostego jest równy kwadratom na bokach zawierających kąt prosty”. (Księga I, propozycja 47)

Księgi V i VII – X zajmują się teorią liczb , gdzie liczby są traktowane geometrycznie jako długości odcinków linii lub obszary obszarów powierzchni. Wprowadzane są takie pojęcia, jak liczby pierwsze oraz liczby wymierne i niewymierne. Udowodniono, że istnieje nieskończenie wiele liczb pierwszych.

Księgi XI – XIII dotyczą geometrii brył . Typowym wynikiem jest stosunek 1:3 między objętością stożka i walca o tej samej wysokości i podstawie. Bryły platońskie są zbudowane.

Aksjomaty

Postulat równoległy (postulat 5): Jeśli dwie linie przecinają trzecią w taki sposób, że suma kątów wewnętrznych z jednej strony jest mniejsza niż dwa kąty proste, to te dwie linie nieuchronnie muszą przecinać się po tej stronie, jeśli są daleko rozciągnięte wystarczająco.

Geometria euklidesowa jest systemem aksjomatycznym , w którym wszystkie twierdzenia („twierdzenia prawdziwe”) wywodzą się z niewielkiej liczby prostych aksjomatów. Aż do pojawienia się geometrii nieeuklidesowej aksjomaty te uważano za oczywiście prawdziwe w świecie fizycznym, tak więc wszystkie twierdzenia były równie prawdziwe. Jednak rozumowanie Euklidesa od założeń do wniosków pozostaje ważne niezależnie od ich fizycznej rzeczywistości.

Na początku pierwszej księgi Elementów Euklides podaje pięć postulatów (aksjomatów) dotyczących geometrii płaszczyzny, określonych w kategoriach konstrukcji (w tłumaczeniu Thomasa Heatha):

Postulujmy, co następuje:

1. Aby narysować linię prostą z dowolnego punktu do dowolnego punktu.
2. Aby utworzyć (przedłużyć) skończoną linię prostą w sposób ciągły w linii prostej.
3. Aby opisać okrąg o dowolnym środku i odległości (promieniu).
4. Że wszystkie kąty proste są sobie równe.
5. [Pulat równoległości ]: Jeśli prosta leżąca na dwóch prostych sprawia, że ​​kąty wewnętrzne po tej samej stronie są mniejsze niż dwa kąty proste, to dwie proste, jeśli są tworzone w nieskończoność, spotykają się po tej stronie, po której kąty są mniejsze niż dwa kąty proste.

Chociaż Euclid wyraźnie stwierdza jedynie istnienie skonstruowanych przedmiotów, w swoim rozumowaniu zakłada również implicite, że są one unikalne.

Elementy obejmują również pięć następujących „powszechnych pojęć” :

1. Rzeczy, które są równe tej samej rzeczy, są również sobie równe ( właściwość przechodnia relacji euklidesowej ) .
2. Jeśli równe są dodawane do równych, to całości są równe (właściwość dodawania równości).
3. Jeśli równe są odejmowane od równych, to różnice są równe (właściwość odejmowania równości).
4. Rzeczy, które pokrywają się ze sobą, są sobie równe (właściwość refleksyjna).
5. Całość jest większa niż część.

Współcześni uczeni zgadzają się, że postulaty Euklidesa nie zapewniają pełnej logicznej podstawy, której Euklides wymagał do swojej prezentacji. Nowoczesne metody leczenia wykorzystują bardziej rozbudowane i kompletne zestawy aksjomatów.

Postulat równoległy

Główny artykuł: postulat równoległy

Starożytnym postulat równoległy wydawał się mniej oczywisty niż inne. Dążyli do stworzenia systemu absolutnie pewnych twierdzeń i wydawało im się, że postulat linii równoległej wymaga dowodu z prostszych zdań. Obecnie wiadomo, że taki dowód jest niemożliwy, ponieważ można konstruować spójne układy geometrii (przestrzegając innych aksjomatów), w których postulat równoległości jest prawdziwy, i takie, w których jest on fałszywy. Wydaje się, że sam Euklides uważał ją za jakościowo różną od innych, o czym świadczy organizacja elementów : jego pierwszych 28 twierdzeń to te, które można udowodnić bez niej.

Można sformułować wiele alternatywnych aksjomatów, które są logicznie równoważne postulatowi równoległemu (w kontekście innych aksjomatów). Na przykład aksjomat Playfair stwierdza:

Na płaszczyźnie przez punkt nie leżący na danej prostej można poprowadzić co najwyżej jedną linię, która nigdy nie przecina się z daną prostą.

Klauzula „co najwyżej” jest wszystkim, czego potrzeba, ponieważ z pozostałych aksjomatów można udowodnić, że istnieje co najmniej jedna prosta równoległa.

Dowód z Elementów Euklidesa, że ​​mając dany odcinek linii, można skonstruować trójkąt równoboczny, który zawiera odcinek jako jeden z jego boków: trójkąt równoboczny ΑΒΓ jest tworzony przez narysowanie okręgów Δ i Ε wyśrodkowanych w punktach Α i Β oraz biorąc jedno przecięcie okręgów jako trzeci wierzchołek trójkąta.

Metody dowodu

Geometria euklidesowa jest konstruktywna . Postulaty 1, 2, 3 i 5 stwierdzają istnienie i niepowtarzalność pewnych figur geometrycznych, a twierdzenia te mają charakter konstruktywny, to znaczy nie tylko mówi się nam, że pewne rzeczy istnieją, ale także podaje się metody ich tworzenia za pomocą nie więcej niż kompas i nieoznakowana liniał . W tym sensie geometria euklidesowa jest bardziej konkretna niż wiele współczesnych systemów aksjomatycznych, takich jak teoria mnogości , które często stwierdzają istnienie obiektów, nie mówiąc, jak je konstruować, lub nawet twierdzą istnienie obiektów, których nie można skonstruować w ramach teorii. Ściśle mówiąc, linie na papierze są modelami obiektów zdefiniowanych w systemie formalnym, a nie instancjami tych obiektów. Na przykład prosta euklidesowa nie ma szerokości, ale ma ją każda rzeczywista narysowana linia. Chociaż prawie wszyscy współcześni matematycy rozważają metody niekonstruktywne równie solidne jak konstruktywne, konstruktywne dowody Euklidesa często wypierały błędne, niekonstruktywne - np. niektóre dowody Pitagorejczyków, które dotyczyły liczb niewymiernych, co zwykle wymagało stwierdzenia takiego jak „Znajdź największą wspólną miarę…”

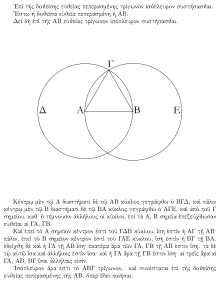
Euklides często stosował dowód przez zaprzeczenie . Geometria euklidesowa pozwala również na metodę superpozycji, w której figura jest przenoszona do innego punktu w przestrzeni. Na przykład twierdzenie I.4, przystawanie trójkątów bok-kąt-bok, jest udowodnione przez przesunięcie jednego z dwóch trójkątów tak, że jeden z jego boków pokrywa się z równym bokiem drugiego trójkąta, a następnie udowodnienie, że pozostałe boki również się pokrywają . Niektóre nowoczesne zabiegi dodają szósty postulat, sztywność trójkąta, który może być użyty jako alternatywa dla superpozycji.

Notacja i terminologia

Nazywanie punktów i figur

Punkty są zwyczajowo nazywane wielkimi literami alfabetu. Inne figury, takie jak linie, trójkąty lub okręgi, są nazywane poprzez podanie wystarczającej liczby punktów, aby jednoznacznie wyodrębnić je z odpowiedniej figury, np. trójkąt ABC byłby zwykle trójkątem z wierzchołkami w punktach A, B i C .

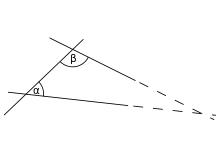
Kąty dopełniające i dopełniające

Kąty, których suma jest kątem prostym, nazywamy kątami komplementarnymi . Kąty dopełniające powstają, gdy promień ma ten sam wierzchołek i jest skierowany w kierunku leżącym pomiędzy dwoma pierwotnymi promieniami tworzącymi kąt prosty. Liczba promieni pomiędzy dwoma pierwotnymi promieniami jest nieskończona.

Kąty, których suma jest kątem prostym, są kątami dodatkowymi . Kąty dodatkowe powstają, gdy promień ma ten sam wierzchołek i jest skierowany w kierunku leżącym pomiędzy dwoma pierwotnymi promieniami tworzącymi kąt prosty (kąt 180 stopni). Liczba promieni pomiędzy dwoma pierwotnymi promieniami jest nieskończona.

Współczesne wersje notacji Euklidesa

We współczesnej terminologii kąty byłyby zwykle mierzone w stopniach lub radianach .

Współczesne podręczniki szkolne często definiują oddzielne figury zwane liniami (nieskończonymi), półprostymi (półnieskończonymi) i odcinkami linii (o skończonej długości). Euclid, zamiast omawiać promień jako obiekt, który rozciąga się w nieskończoność w jednym kierunku, zwykle używałby określeń, takich jak „jeśli linia jest rozciągnięta na wystarczającą długość”, chociaż czasami odnosił się do „nieskończonych linii”. „Linia” u Euclida może być prosta lub zakrzywiona, aw razie potrzeby użył bardziej szczegółowego terminu „linia prosta”.

Niektóre ważne lub dobrze znane wyniki

• 

  pons asinorum lub most osłów mówi, że w trójkącie równoramiennym α = β i γ = δ.

• 

  Twierdzenie o sumie kątów trójkąta stwierdza , że ​​suma trzech kątów dowolnego trójkąta, w tym przypadku kątów α, β i γ, będzie zawsze równa 180 stopni.

• 

  Twierdzenie Pitagorasa mówi , że suma pól dwóch kwadratów na bokach ( a i b ) trójkąta prostokątnego jest równa polu kwadratu na przeciwprostokątnej ( c ).

• 

  Twierdzenie Talesa stwierdza, że ​​jeśli AC jest średnicą, to kąt w punkcie B jest kątem prostym.

Pons asinorum

Pons asinorum ( most osłów ) stwierdza, że ​​w trójkątach równoramiennych kąty u podstawy są sobie równe, a jeśli równe linie proste są dalej tworzone, to kąty pod podstawą są sobie równe . Jego nazwę można przypisać jego częstej roli jako pierwszego prawdziwego testu w Elementach inteligencji czytelnika i jako pomost do trudniejszych twierdzeń, które nastąpiły później. Może być również tak nazwany ze względu na podobieństwo figury geometrycznej do stromego mostu, który może przejść tylko pewny osioł.

Kongruencja trójkątów

Przystawanie trójkątów określa się przez podanie dwóch boków i kąta między nimi (SAS), dwóch kątów i boku między nimi (ASA) lub dwóch kątów i odpowiadającego im boku przyległego (AAS). Określenie dwóch boków i sąsiedniego kąta (SSA) może jednak dać dwa różne możliwe trójkąty, chyba że określony kąt jest kątem prostym.

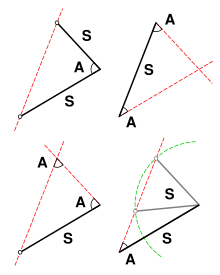
Trójkąty są przystające, jeśli mają wszystkie trzy boki równe (SSS), dwa boki i kąt między nimi równy (SAS) lub dwa kąty i jeden bok równy (ASA) (Księga I, twierdzenia 4, 8 i 26). Trójkąty z trzema równymi kątami (AAA) są podobne, ale niekoniecznie przystające. Ponadto trójkąty o dwóch równych bokach i sąsiednim kącie niekoniecznie są równe lub przystające.

Suma kątów trójkąta

Suma kątów trójkąta jest równa kątowi prostemu (180 stopni). Powoduje to, że trójkąt równoboczny ma trzy kąty wewnętrzne po 60 stopni. Ponadto powoduje, że każdy trójkąt ma co najmniej dwa kąty ostre i maksymalnie jeden rozwarty lub prosty .

twierdzenie Pitagorasa

Słynne twierdzenie Pitagorasa (księga I, twierdzenie 47) mówi, że w dowolnym trójkącie prostokątnym pole kwadratu, którego bok jest przeciwprostokątną (bokiem przeciwległym do kąta prostego), jest równe sumie pól kwadratów, których boki są dwie nogi (dwie strony, które spotykają się pod kątem prostym).

Twierdzenie Talesa

Twierdzenie Talesa , nazwane na cześć Talesa z Miletu, stwierdza, że ​​jeśli A, B i C są punktami na okręgu, gdzie prosta AC jest średnicą okręgu, to kąt ABC jest kątem prostym. Cantor przypuszczał, że Tales dowiódł swego twierdzenia za pomocą Księgi Euklidesa I, Tw. 32, na sposób opisany w Księdze III Euklidesa, Tw. 31.

Skalowanie powierzchni i objętości

$bryły$ z jej wymiarów liniowych, a do ​​sześcianu ${\ Displaystyle V \ propto L ^ {3}}$ . Euclid udowodnił te wyniki w różnych szczególnych przypadkach, takich jak pole koła i objętość bryły równoległościanu. Euclid określił niektóre, ale nie wszystkie, odpowiednie stałe proporcjonalności. Np. był to jego następca Archimedes który udowodnił, że kula ma 2/3 objętości opisanego walca.

System miar i arytmetyka

Geometria euklidesowa ma dwa podstawowe typy pomiarów: kąt i odległość . Skala kątów jest bezwzględna, a Euclid używa kąta prostego jako swojej podstawowej jednostki, tak że na przykład kąt 45 stopni byłby określany jako połowa kąta prostego. Skala odległości jest względna; arbitralnie wybiera się jako jednostkę odcinek linii o pewnej niezerowej długości, a inne odległości wyraża się w stosunku do niego. Dodawanie odległości jest reprezentowane przez konstrukcję, w której jeden odcinek linii jest kopiowany na koniec innego odcinka linii w celu wydłużenia jego długości i podobnie w przypadku odejmowania.

Pomiary powierzchni i objętości pochodzą z odległości. Na przykład prostokąt o szerokości 3 i długości 4 ma pole reprezentujące iloczyn 12. Ponieważ ta geometryczna interpretacja mnożenia była ograniczona do trzech wymiarów, nie było bezpośredniego sposobu interpretacji iloczynu czterech lub więcej liczby, a Euklides unikał takich produktów, chociaż są one sugerowane, na przykład w dowodzie księgi IX, twierdzenie 20.

Przykład kongruencji. Dwie figury po lewej stronie są przystające, a trzecia jest podobna . Ostatnia cyfra też nie. Kongruencje zmieniają niektóre właściwości, takie jak położenie i orientacja, ale pozostawiają inne niezmienione, takie jak odległość i kąty . Te ostatnie właściwości nazywane są niezmiennikami i badanie ich jest istotą geometrii.

Euklides odnosi się do pary linii lub pary płaskich lub bryłowych figur jako „równych” (ἴσος), jeśli ich długości, pola lub objętości są odpowiednio równe i podobnie w przypadku kątów. Silniejszy termin „ przystający ”. ” odnosi się do idei, że cała figura ma taki sam rozmiar i kształt jak inna figura. Alternatywnie, dwie figury są przystające, jeśli można je przesunąć na drugą, tak aby dokładnie do niej pasowały. (Odwracanie jest dozwolone .) Tak więc na przykład prostokąt 2x6 i prostokąt 3x4 są równe, ale nie przystające, a litera R jest przystająca do swojego lustrzanego odbicia. Figury, które byłyby przystające, gdyby nie ich różne rozmiary , są określane jako podobne . para podobnych kształtów jest przystająca, a odpowiednie boki są do siebie proporcjonalne.

Aplikacje

Ze względu na fundamentalny status geometrii euklidesowej w matematyce podawanie tutaj więcej niż reprezentatywnej próbki zastosowań jest niepraktyczne.

• 

  Geodeta używa poziomu

• 

  Pakowanie sfer dotyczy stosu pomarańczy .

• 

  Zwierciadło paraboliczne skupia równoległe promienie światła.

Jak sugeruje etymologia tego słowa, jednym z najwcześniejszych powodów zainteresowania geometrią, a także jednym z najczęstszych obecnych zastosowań geometrii, jest geodezja i pewne praktyczne wyniki geometrii euklidesowej, takie jak właściwość kąta prostego 3- Trójkąty 4-5 były używane na długo przed ich formalnym udowodnieniem. Podstawowymi typami pomiarów w geometrii euklidesowej są odległości i kąty, z których oba mogą być mierzone bezpośrednio przez geodetę. W przeszłości odległości często mierzono za pomocą łańcuchów, takich jak łańcuch Guntera , a kąty za pomocą stopniowanych okręgów, a później teodolitu .

Zastosowanie euklidesowej geometrii bryłowej polega na określaniu układów upakowania , na przykład problem znalezienia najbardziej wydajnego upakowania kul w n wymiarach. Ten problem ma zastosowanie w wykrywaniu i korygowaniu błędów .

Optyka geometryczna wykorzystuje geometrię euklidesową do analizy skupiania światła przez soczewki i lustra.

• 

  Geometria jest wykorzystywana w sztuce i architekturze.

• 

  Wieża ciśnień składa się ze stożka, cylindra i półkuli. Jego objętość można obliczyć za pomocą geometrii bryłowej.

• 

  Geometria może być wykorzystana do projektowania origami.

Geometria jest szeroko stosowana w architekturze .

Geometria może być wykorzystana do projektowania origami . Niektórych klasycznych problemów konstrukcyjnych geometrii nie da się rozwiązać za pomocą kompasu i liniału , ale można je rozwiązać za pomocą origami .

Wiele programów CAD (projektowanie wspomagane komputerowo) i CAM (produkcja wspomagana komputerowo) opiera się na geometrii euklidesowej. Geometria projektowa zazwyczaj składa się z kształtów ograniczonych płaszczyznami, walcami, stożkami, torusami i innymi podobnymi kształtami. W dzisiejszych czasach CAD/CAM jest niezbędny w projektowaniu prawie wszystkiego, w tym samochodów, samolotów, statków i smartfonów. Kilka dekad temu wyrafinowani kreślarze nauczyliby się dość zaawansowanej geometrii euklidesowej, w tym takich rzeczy jak twierdzenie Pascala i twierdzenie Brianchona , ale w dzisiejszych czasach nie jest to już potrzebne.

• 

Późniejsza praca

Archimedes i Apoloniusz

Kula ma 2/3 objętości i pola powierzchni opisującego ją walca. Kula i cylinder zostały umieszczone na grobie Archimedesa na jego prośbę.

Archimedes (ok. 287 pne - ok. 212 pne), barwna postać, o której odnotowano wiele anegdot historycznych, jest pamiętany wraz z Euklidesem jako jeden z największych starożytnych matematyków. Chociaż podstawy jego pracy położył Euclid, uważa się, że jego praca, w przeciwieństwie do Euclida, była całkowicie oryginalna. Udowodnił równania objętości i powierzchni różnych figur w dwóch i trzech wymiarach oraz ogłosił własność Archimedesa liczb skończonych.

Apoloniusz z Perge (ok. 262 p.n.e. – ok. 190 p.n.e.) znany jest głównie z badań przekrojów stożkowych.

René Descartes. Portret według Fransa Halsa , 1648.

XVII wiek: Kartezjusz

René Descartes (1596-1650) opracował geometrię analityczną , alternatywną metodę formalizacji geometrii, która skupiała się na przekształceniu geometrii w algebrę.

W tym podejściu punkt na płaszczyźnie jest reprezentowany przez jego współrzędne kartezjańskie ( x , y ), linia jest reprezentowana przez jej równanie i tak dalej.

W oryginalnym podejściu Euklidesa twierdzenie Pitagorasa wynika z aksjomatów Euklidesa. W podejściu kartezjańskim aksjomaty są aksjomatami algebry, a równanie wyrażające twierdzenie Pitagorasa jest wówczas definicją jednego z terminów w aksjomatach Euklidesa, które obecnie są uważane za twierdzenia.

Równanie

${\ Displaystyle | PQ | = {\ sqrt {(p_ {x} -q_ {x}) ^ {2} + (p_ {y} -q_{y})^{2}}}\,}$

definiowanie odległości między dwoma punktami P = ( p _x , p _y ) i Q = ( q _x , q _y ) jest wtedy znane jako metryka euklidesowa , a inne metryki definiują geometrie nieeuklidesowe .

Jeśli chodzi o geometrię analityczną, ograniczenie geometrii klasycznej do konstrukcji kompasu i liniału oznacza ograniczenie do równań pierwszego i drugiego rzędu, np. y = 2 x + 1 (linia) lub x ² + y ² = 7 ( koło).

Również w XVII wieku Girard Desargues , motywowany teorią perspektywy , wprowadził koncepcję wyidealizowanych punktów, linii i płaszczyzn w nieskończoności. Wynik można uznać za rodzaj geometrii uogólnionej, geometrii rzutowej , ale można go również wykorzystać do uzyskania dowodów w zwykłej geometrii euklidesowej, w której zmniejszono liczbę przypadków specjalnych.

Kwadrat koła: pola tego kwadratu i tego koła są równe. W 1882 roku udowodniono, że tej figury nie można zbudować w skończonej liczbie kroków za pomocą wyidealizowanego kompasu i liniału .

18 wiek

Geometry XVIII wieku zmagali się z określeniem granic systemu euklidesowego. Wielu bezskutecznie próbowało udowodnić piąty postulat z pierwszych czterech. Do 1763 roku opublikowano co najmniej 28 różnych dowodów, ale wszystkie okazały się błędne.

Przed tym okresem geometrzy próbowali również określić, jakie konstrukcje można wykonać w geometrii euklidesowej. Na przykład problem podzielenia kąta na trzy części za pomocą kompasu i linijki to problem, który naturalnie występuje w teorii, ponieważ aksjomaty odnoszą się do konstruktywnych operacji, które można przeprowadzić za pomocą tych narzędzi. Jednak stulecia wysiłków nie przyniosły rozwiązania tego problemu, dopóki Pierre Wantzel nie opublikował w 1837 roku dowodu, że taka konstrukcja jest niemożliwa. Inne konstrukcje, które okazały się niemożliwe, to podwojenie sześcianu i kwadratura koła . W przypadku podwojenia sześcianu niemożność konstrukcji wynika z faktu, że metoda kompasu i liniału obejmuje równania, których rząd jest całkowitą potęgą dwójki, podczas gdy podwojenie sześcianu wymaga rozwiązania równania trzeciego rzędu.

Euler omówił uogólnienie geometrii euklidesowej zwane geometrią afiniczną , które zachowuje piąty postulat niezmodyfikowany, osłabiając postulaty trzeci i czwarty w sposób, który eliminuje pojęcia kąta (dla którego trójkąty prostokątne stają się bez znaczenia) i ogólnie równości długości odcinków linii ( stąd okręgi stają się bez znaczenia), zachowując pojęcia równoległości jako relacji równoważności między liniami i równości długości równoległych odcinków linii (a więc odcinki linii nadal mają punkt środkowy).

19 wiek

Porównanie geometrii eliptycznej, euklidesowej i hiperbolicznej w dwóch wymiarach

Na początku XIX wieku Carnot i Möbius systematycznie rozwijali wykorzystanie oznaczonych kątów i odcinków linii jako sposobu na uproszczenie i ujednolicenie wyników.

Wyższe wymiary

W latach czterdziestych XIX wieku kwaterniony opracował William Rowan Hamilton , a oktoniony John T. Graves i Arthur Cayley . Są to algebry znormalizowane , które rozszerzają liczby zespolone . Później zrozumiano, że kwaterniony są również euklidesowym układem geometrycznym z czterema rzeczywistymi współrzędnymi kartezjańskimi. Cayley użył kwaternionów do badania obrotów w 4-wymiarowej przestrzeni euklidesowej .

W połowie stulecia Ludwig Schläfli rozwinął ogólną koncepcję przestrzeni euklidesowej , rozszerzając geometrię euklidesową na wyższe wymiary . Zdefiniował polischemy , zwane później polytopami , które są wielowymiarowymi odpowiednikami wielokątów i wielościanów . Rozwinął ich teorię i odkrył wszystkie regularne polytopy, tj. $analogi$ regularnych wielokątów i brył platońskich . Odkrył, że jest ich sześć regularne wypukłe polytopy w wymiarze czwartym i trzy we wszystkich wyższych wymiarach.

Regularne wypukłe 4-politopy
Grupa symetrii	4 _	4 _		F 4	4 _
Nazwa	5-ogniwowy Hiper- czworościan 5-punktowy	16-ogniwowy Hiperośmiościan 8- punktowy	8-ogniwowy Hipersześcian 16- punktowy	24-ogniwowy 24-punktowy	600 ogniw Hiper- dwudziestościan 120-punktowy	120 ogniw Hiperdwunastościan 600- punktowy
Symbol Schläfliego	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
lusterka Coxetera
Lustrzane dwuściany	𝝅 / 3 𝝅 / 3 𝝅 / 3 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 3 𝝅 / 3 𝝅 / 4 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 4 𝝅 / 3 𝝅 / 3 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 3 𝝅 / 4 𝝅 / 3 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 3 𝝅 / 3 𝝅 / 5 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 5 𝝅 / 3 𝝅 / 3 𝝅 / 2 𝝅 / 2 𝝅 / 2
Wykres
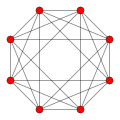
Wierzchołki	5 czworościennych	8 ośmiościenny	16 czworościennych	24 sześcienne	120 dwudziestościennych	600 czworościennych
Krawędzie	10 trójkątnych	24 kwadraty	32 trójkątne	96 trójkątny	720 pięciokątny	1200 trójkątny
Twarze	10 trójkątów	32 trójkąty	24 kwadraty	96 trójkątów	1200 trójkątów	720 pięciokątów
Komórki	5 czworościanów	16 czworościanów	8 kostek	24 ośmiościany	600 czworościanów	120 dwunastościanów
Tori	1 5-czworościan	2 8-czworościan	2 4-sześcian	4 6-ośmiościan	20 30-czworościan	12 10-dwunastościan
Wpisany	120 w 120 komórkach	675 w 120 komórkach	2 16-komorowe	3 8-ogniw	25 24-ogniw	10 600 ogniw
Świetne wielokąty		2 𝅅 / 2 kwadraty x 3	4 / 2 3 prostokąty x	4 / 3 sześciokąty x 4	12 / 5 dziesięciokątów x 6	50 / 15 dwunastokątów x 4
Wielokąty Petriego	1 pięciokąt	1 ośmiokąt	2 ośmiokąty	2 dwunastokąty	4 30-gonów	20 30-gonów
Długi promień	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$
Długość krawędzi	${\ Displaystyle {\ sqrt {\ tfrac {5} {2}}} \ około 1,581}$	${\ Displaystyle {\ sqrt {2}} \ około 1,414}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle {\ tfrac {1} {\ fi}} \ około 0,618}$	${\ Displaystyle {\ tfrac {1} {\ fi ^ {2} {\ sqrt {2}}}} \ około 0,270}$
Krótki promień	${\ Displaystyle {\ tfrac {1} {4}}}$	${\ Displaystyle {\ tfrac {1} {2}}}$	${\ Displaystyle {\ tfrac {1} {2}}}$	${\ Displaystyle {\ sqrt {\ tfrac {1} {2}}} \ około 0,707}$	${\ Displaystyle {\ sqrt {\ tfrac {\ fi ^ {4}} {8}}} \ około 0,926}$	${\ Displaystyle {\ sqrt {\ tfrac {\ fi ^ {4}} {8}}} \ około 0,926}$
Obszar	${\ Displaystyle 10 \ lewo ({\ tfrac {5 {\ sqrt {3}}} {8}} \ prawej) \ około 10,825}$	${\ Displaystyle 32 \ lewo ({\ sqrt {\ tfrac {3} {4}}} \ prawej) \ około 27,713}$	${\ Displaystyle 24}$	${\ Displaystyle 96 \ lewo ({\ sqrt {\ tfrac {3} {16}}} \ prawej) \ około 41,569}$	${\ Displaystyle 1200 \ lewo ({\ tfrac {\ sqrt {3}} {4 \ phi ^ {2}}} \ prawej) \ około 198,48}$	${\ Displaystyle 720 \ lewo ({\ tfrac {\ sqrt {25 + 10 {\ sqrt {5}}}} {8 \ phi ^ {4}}} \ prawo )\około 90,366}$
Tom	${\ Displaystyle 5 \ lewo ({\ tfrac {5 {\ sqrt {5}}} {24}} \ prawej) \ około 2,329}$	${\ Displaystyle 16 \ lewo ({\ tfrac {1} {3}} \ prawej) \ około 5,333}$	${\ Displaystyle 8}$	${\ Displaystyle 24 \ lewo ({\ tfrac {\ sqrt {2}} {3}} \ prawej) \ około 11,314}$	${\ Displaystyle 600 \ lewo ({\ tfrac {\ sqrt {2}} {12 \ phi ^ {3}}} \ prawej) \ około 16,693}$	${\ Displaystyle 120 \ lewo ({\ tfrac {15 + 7 {\ sqrt {5}}} {4 \ phi ^ {6} {\ sqrt {8}} }}\prawo)\około 18,118}$
4-Zawartość	${\ Displaystyle {\ tfrac {\ sqrt {5}} {24}} \ lewo ({\ tfrac {\ sqrt {5}}} {2}} \ prawej) ^ {4} \około 0,146}$	${\ Displaystyle {\ tfrac {2} {3}} \ około 0,667}$	${\ Displaystyle 1}$	${\ Displaystyle 2}$	${\ Displaystyle {\ tfrac {{\ tekst {krótki}} \ razy {\ tekst {tom}}} {4}} \ około 3,863}$	${\ Displaystyle {\ tfrac {{\ tekst {krótki}} \ razy {\ tekst {tom}}} {4}} \ około 4,193}$

Schläfli wykonał tę pracę we względnym zapomnieniu i została opublikowana w całości dopiero pośmiertnie w 1901 roku. Miała niewielki wpływ, dopóki nie została ponownie odkryta iw pełni udokumentowana w 1948 roku przez HSM Coxetera .

W 1878 roku William Kingdon Clifford wprowadził tak zwaną algebrę geometryczną , ujednolicając kwaterniony Hamiltona z algebrą Hermanna Grassmanna i ujawniając geometryczną naturę tych układów, zwłaszcza w czterech wymiarach. Operacje algebry geometrycznej skutkują odbiciem lustrzanym, obracaniem, translacją i mapowaniem obiektów geometrycznych, które są modelowane w nowych pozycjach. Torus Clifforda na powierzchni 3-kuli jest najprostszym i najbardziej symetrycznym płaskim osadzeniem iloczynu kartezjańskiego dwóch kół (w tym samym sensie, w jakim powierzchnia walca jest „płaska”).

Geometria nieeuklidesowa

Najbardziej wpływowy rozwój geometrii stulecia nastąpił, gdy około 1830 r. János Bolyai i Nikolai Ivanovich Lobachevsky osobno opublikowali pracę na temat geometrii nieeuklidesowej , w której postulat równoległości nie jest ważny. Ponieważ geometria nieeuklidesowa jest względnie zgodna z geometrią euklidesową, której można dowieść, postulatu równoległego nie można udowodnić na podstawie innych postulatów.

W XIX wieku zdano sobie również sprawę, że dziesięć aksjomatów i powszechnych pojęć Euklidesa nie wystarcza do udowodnienia wszystkich twierdzeń zawartych w Elementach . Na przykład Euklides założył implicite, że każda linia zawiera co najmniej dwa punkty, ale tego założenia nie można udowodnić na podstawie innych aksjomatów, a zatem samo w sobie musi być aksjomatem. Pierwszym geometrycznym dowodem w Elementach, pokazanym na powyższym rysunku, jest to, że każdy odcinek linii jest częścią trójkąta; Euclid konstruuje to w zwykły sposób, rysując okręgi wokół obu punktów końcowych i przyjmując ich przecięcie jako trzeci wierzchołek . Jego aksjomaty nie gwarantują jednak, że okręgi faktycznie się przecinają, ponieważ nie potwierdzają geometrycznej właściwości ciągłości, która w kategoriach kartezjańskich jest równoważna właściwości kompletności liczb rzeczywistych. Począwszy od Moritza Pascha w 1882 roku, zaproponowano wiele ulepszonych systemów aksjomatycznych dla geometrii, z których najbardziej znane to systemy Hilberta , George'a Birkhoffa i Tarskiego .

XX wiek i teoria względności

Obalenie geometrii euklidesowej jako opisu przestrzeni fizycznej. W teście ogólnej teorii względności z 1919 r. sfotografowano gwiazdy (oznaczone krótkimi poziomymi liniami) podczas zaćmienia Słońca . Promienie światła gwiazd zostały zagięte przez grawitację Słońca w drodze na Ziemię. Jest to interpretowane jako dowód na korzyść przewidywań Einsteina, że ​​grawitacja spowoduje odchylenia od geometrii euklidesowej.

Teoria szczególnej teorii względności Einsteina obejmuje czterowymiarową czasoprzestrzeń , przestrzeń Minkowskiego , która nie jest euklidesowa . Pokazuje to, że geometrie nieeuklidesowe, które zostały wprowadzone kilka lat wcześniej w celu wykazania, że postulatu równoległości , są również przydatne do opisu świata fizycznego.

Jednak trójwymiarowa „część przestrzenna” przestrzeni Minkowskiego pozostaje przestrzenią geometrii euklidesowej. Inaczej jest w przypadku ogólnej teorii względności , dla której geometria przestrzennej części czasoprzestrzeni nie jest geometrią euklidesową. Na przykład, jeśli trójkąt jest zbudowany z trzech promieni światła, to na ogół kąty wewnętrzne nie sumują się do 180 stopni z powodu grawitacji. Stosunkowo słabe pole grawitacyjne, takie jak ziemskie lub słoneczne, jest reprezentowane przez metrykę, która jest w przybliżeniu euklidesowa, ale nie do końca. Aż do XX wieku nie było technologii zdolnej wykryć te odchylenia w promieniach światła od geometrii euklidesowej, ale Einstein przewidział, że takie odchylenia będą istnieć. Zostały one później zweryfikowane przez obserwacje, takie jak lekkie zakrzywienie światła gwiazd przez Słońce podczas zaćmienia Słońca w 1919 r., i takie rozważania są obecnie integralną częścią oprogramowania obsługującego System GPS .

Jako opis struktury przestrzeni

Euclid uważał, że jego aksjomaty są oczywistymi stwierdzeniami dotyczącymi rzeczywistości fizycznej. Dowody Euklidesa opierają się na założeniach być może nieoczywistych w podstawowych aksjomatach Euklidesa, w szczególności na tym, że pewne ruchy figur nie zmieniają ich właściwości geometrycznych, takich jak długości boków i kątów wewnętrznych, tak zwane ruchy euklidesowe , które obejmują translacje, odbicia i obroty figur. Wzięty jako fizyczny opis przestrzeni, postulat 2 (przedłużenie linii) stwierdza, że ​​przestrzeń nie ma dziur ani granic; postulat 4 (równość kątów prostych) mówi, że przestrzeń jest izotropowa a figurki można przenosić w dowolne miejsce, zachowując spójność ; i postulat 5 ( postulat równoległy ), że przestrzeń jest płaska (nie ma wewnętrznej krzywizny ).

Jak omówiono powyżej, teoria względności Alberta Einsteina znacznie modyfikuje ten pogląd.

Niejednoznaczny charakter aksjomatów pierwotnie sformułowanych przez Euklidesa sprawia, że ​​różni komentatorzy mogą nie zgadzać się co do niektórych innych ich implikacji dla struktury przestrzeni, takich jak to, czy jest ona nieskończona (patrz poniżej) i jaka jest jej topologia . Nowoczesne, bardziej rygorystyczne przeformułowania systemu zazwyczaj mają na celu czystsze oddzielenie tych kwestii. Interpretując aksjomaty Euklidesa w duchu tego bardziej nowoczesnego podejścia, aksjomaty 1–4 są zgodne z przestrzenią nieskończoną lub skończoną (jak w geometrii eliptycznej ), a wszystkie pięć aksjomatów jest zgodnych z różnymi topologiami (np. płaszczyzna, walec lub torus dla dwuwymiarowej geometrii euklidesowej).

Leczenie nieskończoności

Nieskończone obiekty

Euklides czasami wyraźnie rozróżniał „linie skończone” (np. Postulat 2) i „ linie nieskończone ” (księga I, twierdzenie 12). Jednak zazwyczaj nie dokonywał takich rozróżnień, chyba że były one konieczne. Postulaty nie odnoszą się wprost do linii nieskończonych, chociaż na przykład niektórzy komentatorzy interpretują postulat 3, istnienie koła o dowolnym promieniu, jako sugerujący, że przestrzeń jest nieskończona.

Pojęcie nieskończenie małych wielkości było wcześniej szeroko dyskutowane przez szkołę eleacką , ale nikt nie był w stanie postawić ich na solidnej logicznej podstawie, z paradoksami takimi jak paradoks Zenona , które nie zostały rozwiązane w sposób powszechny. Euclid zastosował metodę wyczerpania niż nieskończenie małych.

Późniejsi komentatorzy starożytni, tacy jak Proklos (410–485 n.e.), traktowali wiele pytań dotyczących nieskończoności jako kwestie wymagające dowodu i np. Proklos twierdził, że udowodnił nieskończoną podzielność linii, opierając się na dowodzie przez sprzeczność, w którym rozważał przypadki parzystej i nieparzystej liczby składających się na nią punktów.

Na przełomie XIX i XX wieku Otto Stolz , Paul du Bois-Reymond , Giuseppe Veronese i inni stworzyli kontrowersyjne prace nad niearchimedesowymi modelami geometrii euklidesowej, w których odległość między dwoma punktami może być nieskończona lub nieskończenie mała, w modelu Newtona – zmysł Leibniza . Pięćdziesiąt lat później Abraham Robinson dostarczył rygorystycznej logicznej podstawy pracy Veronese'a.

Nieskończone procesy

Starożytni geometrzy mogli uważać postulat równoległości – że dwie równoległe linie nigdy się nie przecinają – za mniej pewny niż inne, ponieważ dotyczy on nieskończenie odległych obszarów przestrzeni, a zatem nie można go fizycznie zweryfikować.

Nowoczesna formuła dowodu przez indukcję została opracowana dopiero w XVII wieku, ale niektórzy późniejsi komentatorzy uważają ją za domyślną w niektórych dowodach Euklidesa, np. w dowodzie nieskończoności liczb pierwszych.

Domniemane paradoksy obejmujące nieskończone serie, takie jak paradoks Zenona , były starsze niż Euklides. Euklides unikał takich dyskusji, podając na przykład wyrażenie na sumy cząstkowe szeregu geometrycznego w IX.35, nie komentując możliwości dopuszczenia liczby wyrazów do nieskończoności.

Podstawa logiczna

Zobacz też: aksjomaty Hilberta , system aksjomatyczny i rzeczywiste pole zamknięte

Logika klasyczna

Euklides często stosował metodę dowodu przez sprzeczność , dlatego tradycyjne przedstawienie geometrii euklidesowej zakłada klasyczną logikę , w której każde zdanie jest albo prawdziwe, albo fałszywe, tj. dla dowolnego zdania P, zdanie „P albo nie P” jest automatycznie prawdziwe .

Nowoczesne standardy rygoru

Umieszczenie geometrii euklidesowej na solidnej podstawie aksjomatycznej było przedmiotem troski matematyków przez wieki. Rola pojęć pierwotnych , czyli pojęć niezdefiniowanych, została wyraźnie przedstawiona przez Alessandro Padoa z delegacji Peano na konferencji paryskiej w 1900 roku:

... kiedy zaczynamy formułować teorię, możemy sobie wyobrazić, że niezdefiniowane symbole są całkowicie pozbawione znaczenia , a niesprawdzone twierdzenia są po prostu warunkami nałożonymi na niezdefiniowane symbole.

Zatem system idei , który wybraliśmy na początku, jest po prostu jedną z interpretacji niezdefiniowanych symboli; ale… ta interpretacja może zostać zignorowana przez czytelnika, który może ją zastąpić w swoim umyśle inną interpretacją … spełniającą warunki…

W ten sposób pytania logiczne stają się całkowicie niezależne od pytań empirycznych lub psychologicznych …

System niezdefiniowanych symboli można zatem uznać za abstrakcję uzyskaną z wyspecjalizowanych teorii , która powstaje, gdy… system niezdefiniowanych symboli jest sukcesywnie zastępowany przez każdą z interpretacji…

— Padoa, Essai d'une théorie algébrique des nombre entiers, avec une Introduction logique à une théorie déductive quelconque

Oznacza to, że matematyka jest wiedzą niezależną od kontekstu w ramach hierarchicznych. Jak powiedział Bertrand Russell :

Jeśli nasza hipoteza dotyczy czegokolwiek , a nie jakiejś konkretnej rzeczy, to nasze dedukcje stanowią matematykę. Tak więc matematykę można zdefiniować jako przedmiot, w którym nigdy nie wiemy, o czym mówimy, ani czy to, co mówimy, jest prawdą.

— Bertrand Russell, Matematyka i metafizycy

Takie fundamentalne podejścia wahają się między fundamentalizmem a formalizmem .

Sformułowania aksjomatyczne

Geometria jest nauką o prawidłowym rozumowaniu na podstawie błędnych figur.

— George Pólya , Jak to rozwiązać , s. 208

• Aksjomaty Euklidesa: W swojej rozprawie wygłoszonej w Trinity College w Cambridge Bertrand Russell podsumował zmieniającą się rolę geometrii Euklidesa w umysłach filozofów do tego czasu. Był to konflikt między pewną wiedzą, niezależną od eksperymentu, a empiryzmem, wymagającym wkładu eksperymentalnego. Kwestia ta stała się jasna, gdy odkryto, że postulat równoległości niekoniecznie był ważny, a jego zastosowanie było kwestią empiryczną, decydującą, czy stosowna geometria była euklidesowa, czy nieeuklidesowa .
• Aksjomaty Hilberta : Aksjomaty Hilberta miały na celu zidentyfikowanie prostego i kompletnego zestawu niezależnych aksjomatów, z których można było wywnioskować najważniejsze twierdzenia geometryczne. Nadrzędnymi celami było uczynienie geometrii euklidesowej rygorystyczną (unikając ukrytych założeń) i wyjaśnienie konsekwencji postulatu równoległości.
• Aksjomaty Birkhoffa : Birkhoff zaproponował cztery postulaty geometrii euklidesowej, które można potwierdzić eksperymentalnie za pomocą skali i kątomierza. System ten w dużym stopniu opiera się na właściwościach liczb rzeczywistych . Pojęcia kąta i odległości stają się pojęciami prymitywnymi.
• Aksjomaty Tarskiego : Alfred Tarski (1902–1983) i jego uczniowie zdefiniowali elementarną geometrię euklidesową jako geometrię, którą można wyrazić w logice pierwszego rzędu i której podstawa logiczna nie zależy od teorii mnogości , w przeciwieństwie do aksjomatów Hilberta, które obejmują punkt zestawy. Tarski udowodnił, że jego aksjomatyczne sformułowanie elementarnej geometrii euklidesowej jest w pewnym sensie spójne i kompletne : istnieje algorytm, który dla każdego twierdzenia można wykazać albo jako prawdziwe, albo jako fałszywe. (To nie narusza twierdzenia Gödla , ponieważ geometria euklidesowa nie może opisać wystarczającej ilości arytmetyki , aby twierdzenie mogło zostać zastosowane.) Jest to równoważne rozstrzygalności rzeczywistych ciał zamkniętych , których modelem jest elementarna geometria euklidesowa.

Zobacz też

• Absolutna geometria
• Geometria analityczna
• Aksjomaty Birkhoffa
• Kartezjański układ współrzędnych
• Aksjomaty Hilberta
• Geometria padania
• Lista interaktywnego oprogramowania do geometrii
• Przestrzeń metryczna
• Geometria nieeuklidesowa
• Geometria zamówiona
• Postulat równoległy
• Teoria typów

Twierdzenia klasyczne

• Twierdzenie o dwusiecznej kąta
• Twierdzenie motyla
• Twierdzenie Cevy
• Formuła Herona
• Twierdzenie Menelaosa
• Dziewięciopunktowe koło
• twierdzenie Pitagorasa

Notatki

•   Piłka, WW Rouse (1960). A Short Account of the History of Mathematics (wyd. 4. [Przedruk. Publikacja oryginalna: Londyn: Macmillan & Co., 1908] wyd.). Nowy Jork: Dover Publications. s. 50–62 . ISBN 0-486-20630-0 .
• Coxeter, HSM (1961). Wprowadzenie do geometrii . Nowy Jork: Wiley.
• Ewy, Howard (1963). Przegląd geometrii (tom pierwszy) . Allyn i Bacon.
•       Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (wyd. 2. [Faks. Publikacja oryginalna: Cambridge University Press, 1925] wyd.). Nowy Jork: Dover Publications. W 3 tomach: obj. 1 ISBN 0-486-60088-2 , tom. 2 ISBN 0-486-60089-0 , tom. 3 ISBN 0-486-60090-4 . Autorytatywne tłumaczenie Elementów Euklidesa autorstwa Heatha, a także jego obszerne badania historyczne i szczegółowe komentarze w całym tekście.
• Misner, Charles W .; Thorne, Kip S .; Wheeler, John Archibald (1973). Grawitacja . WH Freemana.
•   Młodinow (2001). Okno Euklidesa . Wolna prasa. ISBN 9780684865232 .
• Nagel, E.; Newmana, JR (1958). Dowód Gödla . Wydawnictwo Uniwersytetu Nowojorskiego.
• Tarski, Alfred (1951). Metoda decyzyjna dla elementarnej algebry i geometrii . Uniw. prasy kalifornijskiej.
• Stillwell, John (styczeń 2001). „Historia 120-ogniw” (PDF) . Zawiadomienia AMS . 48 (1): 17–25.

Linki zewnętrzne

• „Geometria euklidesowa” , Encyklopedia matematyki , EMS Press , 2001 [1994]
• „Trygonometria płaszczyzny” , Encyklopedia matematyki , EMS Press , 2001 [1994]
• Kiran Kedlaya, Geometry Unbound (leczenie z wykorzystaniem geometrii analitycznej; format PDF, na licencji GFDL)