Złoty podział

W przypadku innych zastosowań zobacz Złoty podział (ujednoznacznienie) i Złota liczba (ujednoznacznienie) .

Złoty podział ( φ )

Segmenty linii w złotej proporcji
Reprezentacje
Dziesiętny	1.618 033 988 749 894 ...
Forma algebraiczna	${\ Displaystyle {\ Frac {1 + {\ sqrt {5}}} {2}}}$
Ciąg dalszy ułamka	${\ Displaystyle 1 + {\ cfrac {1} {1 + {\ cfrac {1} {1 + {\ cfrac {1} {1 + {\ cfrac {1}{1+\ddots }}}}}}}}}$
Dwójkowy	1.1001 1110 0011 0111 0111 ...
Szesnastkowy	1.9E37 79B9 7F4A 7C15 ...

Złoty prostokąt o długim boku a i krótkim boku b (zacieniowany na czerwono, po prawej) oraz kwadrat o bokach długości a (zacieniony na niebiesko, po lewej) łączą się, tworząc podobny złoty prostokąt o długim boku a + b i krótszym boku a . Ilustruje to zależność ${\ Displaystyle {\ Frac {a + b} {a}} = {\ Frac {a} {b}} \ równoważnik \ varphi.}$

W matematyce dwie wielkości są w złotym stosunku , jeśli ich stosunek jest taki sam, jak stosunek ich sumy do większej z dwóch wielkości. ${\ Displaystyle a> b> 0$ algebraicznie, dla ilości i $Displaystyle$$b}$ z za ,

$Frac {a + b} {a}} = {\ Frac {a} {b}} = \ varphi}$

$podział$ grecka litera phi ( $lub$ ) oznacza złoty Stała spełnia równanie kwadratowe $varphi$ jest o wartości $Displaystyle$

${\ Displaystyle \ varphi = {\ Frac {1 + {\ sqrt {5}}} {2}} =}$ 1,618 033 988 749 ....

Złota proporcja została nazwana przez Euklidesa skrajną i średnią proporcją , a boska proporcja przez Luca Pacioli , a także nosi kilka innych nazw.

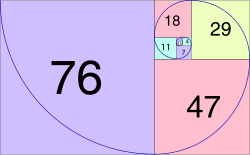
Matematycy badali właściwości złotego podziału od starożytności. Jest to stosunek przekątnej pięciokąta foremnego do jego boku i dlatego pojawia się w konstrukcji dwunastościanu i dwudziestościanu . Złoty prostokąt - to znaczy prostokąt o współczynniku proporcji $-$ można pociąć na kwadrat i mniejszy prostokąt o tym samym współczynniku proporcji . Złota proporcja została wykorzystana do analizy proporcji obiektów naturalnych i sztucznych układów, takich jak np rynków finansowych , w niektórych przypadkach w oparciu o wątpliwe dopasowanie danych. Złota proporcja pojawia się w niektórych wzorach w przyrodzie , w tym w spiralnym układzie liści i innych części roślinności.

Niektórzy XX-wieczni artyści i architekci , w tym Le Corbusier i Salvador Dalí , dostosowali swoje prace do proporcji zbliżonej do złotego podziału, wierząc, że jest to estetyczne . Zastosowania te często pojawiają się w postaci złotego prostokąta.

Obliczenie

Dwie wielkości ${$ b $\ displaystyle b}$ są w złotym stosunku jeśli $varphi}$

${\ Displaystyle {\ Frac {a + b} {a}} = {\ Frac {a} {b}} = \ varphi.}$

Jedna metoda znajdowania $się$ od lewej frakcji. Upraszczając ułamek i podstawiając odwrotność , ${\ Displaystyle b/a = 1/\ varphi$ }

${\ Displaystyle {\ Frac {a + b} {a}} = {\ Frac {a} {a}} + {\ Frac {b} {a}} = 1 + {\ Frac {b} {a}} =1+{\frac {1}{\varphi}}.}$

Dlatego,

${\ Displaystyle 1 + {\ Frac {1} {\ varphi}} = \ varphi.}$

Mnożenie przez daje ${\ displaystyle \ varphi}$

${\ Displaystyle \ varphi + 1 = \ varphi ^ {2}}$

które można przeorganizować

${\ Displaystyle {\ varphi} ^ {2} - \ varphi -1 = 0.}$

Wzór kwadratowy daje dwa rozwiązania:

${\ Displaystyle {\ Frac {1 + {\ sqrt {5}}} {2}} = 1,618033 \ kropki}$ i ${\ Displaystyle {\ Frac {1- {\ sqrt {5}}} {2}} = -0,618033 \ kropki.}$

Ponieważ jest $}$ stosunek między wielkościami dodatnimi, $varphi$ jest z konieczności dodatnim pierwiastkiem. Ujemny pierwiastek jest w $.$ ujemną odwrotnością ze złotym podziałem

Historia

Zobacz także: Matematyka i sztuka oraz liczba Fibonacciego § Historia

Według Mario Livio ,

Niektóre z największych umysłów matematycznych wszystkich epok, od Pitagorasa i Euklidesa w starożytnej Grecji , przez średniowiecznego włoskiego matematyka Leonarda z Pizy i renesansowego astronoma Johannesa Keplera , po współczesne postacie naukowe, takie jak fizyk z Oksfordu Roger Penrose , spędziłem niekończące się godziny nad tym prostym stosunkiem i jego właściwościami. ... Biolodzy, artyści, muzycy, historycy, architekci, psychologowie, a nawet mistycy zastanawiali się i debatowali nad podstawami jego wszechobecności i atrakcyjności. W rzeczywistości można chyba śmiało powiedzieć, że Złoty Podział zainspirował myślicieli wszystkich dyscyplin, jak żadna inna liczba w historii matematyki.

— The Golden Ratio: The Story of Phi, najbardziej zdumiewająca liczba na świecie

Starożytni greccy matematycy najpierw badali złoty podział ze względu na jego częste występowanie w geometrii ; podział linii na „stosunek ekstremalny i średni” (złoty podział) jest ważny w geometrii pentagramów foremnych i pięciokątów . Według jednej z historii, matematyk Hippasus z V wieku p.n.e. odkrył, że złoty podział nie jest ani liczbą całkowitą, ani ułamkiem (jest irracjonalny ), co zaskakuje pitagorejczyków . Elementy Euklidesa ( _ C. 300 pne ) zawiera kilka twierdzeń i ich dowodów wykorzystujących złoty podział i zawiera pierwszą znaną definicję, która brzmi następująco:

Mówi się, że linia prosta została przecięta w skrajnym i średnim stosunku, gdy cała linia ma się tak, jak cała linia do większego odcinka, tak jest większa do mniejszego.

Michael Maestlin jako pierwszy napisał dziesiętne przybliżenie współczynnika

Złoty podział był badany peryferyjnie przez następne tysiąclecie. Abu Kamil (ok. 850–930) zastosował go w swoich geometrycznych obliczeniach pięciokątów i dziesięciokątów; jego pisma wywarły wpływ na pisma Fibonacciego (Leonardo z Pizy) (ok. 1170–1250), który stosował współczynnik w powiązanych problemach z geometrią, ale nie zauważył, że jest on powiązany z liczbami Fibonacciego .

Luca Pacioli nazwał swoją książkę Divina ratione ( 1509 ) na cześć ratio; książka, w dużej mierze splagiatowana przez Piero della Francesca , badała jej właściwości, w tym jej pojawienie się w niektórych bryłach platońskich . Leonardo da Vinci , który zilustrował książkę Pacioli, nazwał ratio sectio aurea ('Złota sekcja'). Chociaż często mówi się, że Pacioli opowiadał się za zastosowaniem złotego podziału w celu uzyskania przyjemnych, harmonijnych proporcji, Livio zwraca uwagę, że interpretacja została przypisana błędowi w 1799 r. I że Pacioli faktycznie opowiadał się za witruwiańskim systemem racjonalnych proporcji . Pacioli dostrzegł także katolickie znaczenie religijne w proporcji, co doprowadziło do tytułu jego pracy. XVI-wieczni matematycy, tacy jak Rafael Bombelli, rozwiązywali problemy geometryczne za pomocą współczynnika.

Niemiecki matematyk Simon Jacob (zm. 1564) zauważył, że kolejne liczby Fibonacciego zbiegają się do złotego podziału ; zostało to ponownie odkryte przez Johannesa Keplera w 1608 r. Pierwsze znane przybliżenie dziesiętne (odwrotnego) złotego podziału zostało określone jako „około $w$ 1597 r. przez Michaela Maestlina z Uniwersytetu w Tybindze w liście do Keplera, jego były student. W tym samym roku Kepler napisał do Maestlina o trójkącie Keplera , który łączy złoty podział z tzw Twierdzenie Pitagorasa . Kepler powiedział o nich:

Geometria ma dwa wielkie skarby: jednym jest twierdzenie Pitagorasa, drugim podział prostej na iloraz skrajny i średni. Pierwszą możemy porównać do masy złota, drugą możemy nazwać cennym klejnotem.

XVIII-wieczni matematycy Abraham de Moivre , Nicolaus I Bernoulli i Leonhard Euler zastosowali formułę opartą na złotym współczynniku, która określa wartość liczby Fibonacciego na podstawie jej umieszczenia w sekwencji; w 1843 roku został ponownie odkryty przez Jacquesa Philippe'a Marie Bineta , dla którego nazwano go „formułą Bineta”. Martin Ohm po raz pierwszy użył niemieckiego terminu goldener Schnitt („złota sekcja”) do opisania tego stosunku w 1835 r. James Sully użył równoważnego terminu angielskiego w 1875 r.

W 1910 roku wynalazca Mark Barr zaczął używać greckiej litery phi $podziału$ ( ) jako symbolu złotego Jest również reprezentowany przez tau ( $)$ , pierwszą literę starożytnej Grecji τομή („cięcie” lub „sekcja”)

Dan Shechtman demonstruje kwazikryształy w NIST w 1985 roku, używając modelu Zometoy .

System konstrukcyjny zome , opracowany przez Steve'a Baera pod koniec lat 60. XX wieku, oparty jest na systemie symetrii dwudziestościanu / dwunastościanu i wszechobecnie wykorzystuje złoty podział. W latach 1973-1974 Roger Penrose opracował kafelki Penrose'a , wzór związany ze złotym podziałem zarówno pod względem stosunku powierzchni dwóch rombowych płytek, jak i ich względnej częstotliwości we wzorze. Zainteresowanie to zyskało po kwazikryształów przez Dana Shechtmana, zdobywcę Nagrody Nobla w 1982 roku z dwudziestościenną symetrią, którą wkrótce potem wyjaśniono przez analogie do płytek Penrose'a.

Matematyka

Irracjonalność

Złoty podział to liczba niewymierna . Poniżej znajdują się dwa krótkie dowody irracjonalności:

Sprzeczność z wyrażenia w najniższych terminach

Gdyby φ było wymierne , to byłby to stosunek boków prostokąta do boków całkowitych (prostokąt składający się na cały diagram). Ale byłby to również stosunek całkowitych boków mniejszego prostokąta (skrajna prawa część diagramu) uzyskany przez usunięcie kwadratu. Sekwencja malejących długości boków liczb całkowitych utworzona przez usuwanie kwadratów nie może być kontynuowana w nieskończoność, ponieważ dodatnie liczby całkowite mają dolną granicę, więc φ nie może być wymierne.

Odwołaj to:

całość to dłuższa część plus krótsza; całość ma się do dłuższej części, tak jak dłuższa część do krótszej.

Jeśli nazwiemy całość $m$ dłuższą część ${\ displaystyle m,},$ to drugie stwierdzenie powyżej stanie się n {\ displaystyle n

${\ displaystyle n}$ ma się do ${\ displaystyle m}$ jak ${\ displaystyle m}$ do ${\ displaystyle nm.}$

Powiedzieć, że złoty podział $racjonalny,$$displaystyle n/m} i$ , że ​​jest to ułamek gdzie $\$${\ displaystyle n}$ i ${\ displaystyle m }$ są liczbami całkowitymi. Możemy przyjąć ${\ displaystyle n/m}$ w najniższych kategoriach i ${\ displaystyle n}$ i ${\ displaystyle m}$ być pozytywnym. $niższych$ jeśli $najniższych kategoriach$ to równie Jest to sprzeczność wynikająca z założenia, że $racjonalny$ .

Przez irracjonalność √ 5

Inny krótki dowód – być może bardziej znany – na irracjonalność złotego podziału wykorzystuje domknięcie liczb wymiernych przez dodawanie i mnożenie. Jeśli ${\ Displaystyle \ varphi = {\ tfrac {1} {2}} (1 + {\ sqrt {5}})}$ jest wymierne, to ${\ displaystyle 2\varphi -1={\sqrt {5}}}$ jest również wymierne, co jest sprzecznością, jeśli już wiadomo, że pierwiastek kwadratowy ze wszystkich nie- kwadratowych liczby naturalne są niewymierne.

Minimalny wielomian

Złoty podział φ i jego ujemna odwrotność − φ ⁻¹ to dwa pierwiastki wielomianu kwadratowego x ² − x − 1 . Negatywny złoty podział − φ i odwrotność φ ⁻¹ to dwa pierwiastki wielomianu kwadratowego x ² + x − 1 .

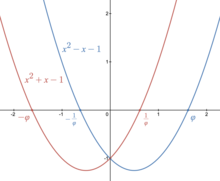
Złoty podział jest także liczbą algebraiczną , a nawet algebraiczną liczbą całkowitą . Ma minimalny wielomian

${\ Displaystyle x ^ {2} -x-1.}$

Ten ${\ Displaystyle - \ varphi ^ {- 1}.}$ kwadratowy ma dwa pierwiastki i $_$

Złoty podział jest również ściśle powiązany z wielomianem

${\ Displaystyle x ^ {2} + x-1,}$

który ma korzenie ${\ displaystyle - \ varphi}$ i ${\ Displaystyle \ varphi ^ {-1}.}$ Jako pierwiastek wielomianu kwadratowego, złoty podział jest liczbą konstrukcyjną .

Koniugat złotego podziału i potęgi

Koniugat pierwiastek do minimalnego wielomianu to ${\ Displaystyle x ^ {2} -x-1$ }

${\ Displaystyle - {\ Frac {1} {\ varphi}} = 1- \ varphi = {\ Frac {1- {\ sqrt {5}}} {2}} = -0,618033 \ kropki.}$

Wartość bezwzględna tej wielkości ${$ ( ) odpowiada stosunkowi długości przyjętemu w odwrotnej kolejności (krótsza długość segmentu w stosunku do dłuższej długości segmentu, $displaystyle b/a}$ .

Ilustruje to wyjątkową właściwość złotego podziału między liczbami dodatnimi, tj

${\ Displaystyle {\ Frac {1} {\ varphi}} = \ varphi -1,}$

lub jego odwrotność:

${\ Displaystyle {\ Frac {1} {1 / \ varphi}} = {\ Frac {1} {\ varphi}} + 1.}$

Koniugat i definiujący kwadratowy związek wielomianowy prowadzą do wartości dziesiętnych, których część ułamkowa jest wspólna z: ${\ displaystyle \ varphi}: φ {\ displaystyle \ varphi$ }

${\ Displaystyle {\ rozpocząć {wyrównane} \ varphi ^ {2} & = \ varphi + 1 = 2,618033 \ kropki, \\ [5mu] {\ Frac {1} {\ varphi}} & = \ varphi -1 = 0,618033 \dots .\end{wyrównane}}}$

Sekwencja $te$$_$ wartości $_$$_$${\ Displaystyle 2.618033 \ ldots;}$ bardziej ogólnie, każda potęga jest równa sumie dwóch bezpośrednio poprzedzających potęg: ${\ displaystyle \ varphi}$

${\ Displaystyle \ varphi ^ {n} = \ varphi ^ {n-1} + \ varphi ^ {n-2} = \ varphi \ cdot \ nazwa operatora {F} _ {n} + \ nazwa operatora {F} _ {n -1}.}$

$na$ można łatwo rozłożyć dowolną potęgę $.$ i stałą Wielokrotność i stała są zawsze sąsiadującymi liczbami Fibonacciego. Prowadzi to do innej właściwości dodatnich potęg: φ $\ displaystyle \ varphi}: φ {\ displaystyle \ varphi}$

Jeśli ${\ Displaystyle \ lfloor n/2-1 \ rfloor = m},$ to:

${\ Displaystyle {\ rozpocząć {wyrównane} \ varphi ^ {n} & = \ varphi ^ {n-1} + \ varphi ^ {n-3} + \ cdots + \ varphi ^ {n-1-2m} + \ varphi ^{n-2-2m}\\[5mu]\varphi ^{n}-\varphi ^{n-1}&=\varphi ^{n-2}.\end{wyrównane}}}$

Ciąg dalszy ułamka i pierwiastek kwadratowy

Zobacz także: liczba Lucasa § Ułamki ciągłe dla potęg złotego podziału

Przybliżenia do odwrotności złotego podziału przez skończone ułamki ciągłe lub stosunki liczb Fibonacciego

Wzór można rozwinąć rekurencyjnie, aby uzyskać ułamek ciągły dla złotego podziału: ${\ Displaystyle \ varphi = 1 + 1/\ varphi}$

${\ Displaystyle \ varphi = [1; 1,1,1, \ kropki] = 1 + {\ cfrac {1} {1} +{\cfrac {1}{1+{\cfrac {1}{1+\ddots}}}}}}}$

W rzeczywistości jest to najprostsza forma ułamka ciągłego, obok jego postaci odwrotnej:

${\ Displaystyle \ varphi ^ {- 1} = [0; 1,1,1, \ kropki] = 0 + {\ cfrac { 1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots}}}}}}}$

Zbieżności tych ułamków ciągłych ( ${\ Displaystyle 1/1,}$${\ Displaystyle 2/1,}$${\ Displaystyle 2/1,}$ 3 $\ Displaystyle 3/2,}$${\ Displaystyle 5/3,}$${\ Displaystyle 8/5,}$${\ Displaystyle 13/8,}$ ... lub ${\ Displaystyle 1/1,}$${\ Displaystyle 1/2,}$${\ Displaystyle 2/3,}$${\ Displaystyle 3/5 ,}$${\ Displaystyle 5/8,}$${\ Displaystyle 8/13,}$ ...) to stosunki kolejnych liczb Fibonacciego . Konsekwentnie małe wyrazy w jej ułamku ciągłym wyjaśniają, dlaczego przybliżenia zbiegają się tak wolno. To sprawia, że ​​​​złoty podział jest skrajnym przypadkiem nierówności Hurwitza dla przybliżeń diofantycznych , który stwierdza, że ​​dla każdego irracjonalnego $p$ nieskończenie wiele różnych ułamków takich, że: $\ displaystyle p/q}$

${\ Displaystyle \ lewo | \ xi - {\ Frac {p} {q}} \ prawo | < {\ Frac {1} {{\ sqrt {5}} q ^ {2}}}.}$

$,$ że stałej można poprawić bez wykluczenia złotego podziału. W rzeczywistości jest to najmniejsza liczba, którą należy wykluczyć, aby wygenerować bliższe przybliżenia takich liczb Lagrange'a .

Ciągłą postać $varphi$ kwadratowego dla można uzyskać z , $}$ φ

${\ Displaystyle \ varphi = {\ sqrt {1+ {\ sqrt {1+ {\ sqrt {1+ \ cdots}}}}}}.}$

Związek z liczbami Fibonacciego i Lucasa

Dalsze informacje: Liczba Fibonacciego § Związek ze złotym podziałem

Zobacz też: liczba Lucasa § Związek z liczbami Fibonacciego

Spirala Fibonacciego (u góry), która jest zbliżona do złotej spirali , przy użyciu kwadratów sekwencji Fibonacciego o rozmiarach do 21 . Złota spirala jest również generowana (na dole) z układania kwadratów, których długości boków są liczbami należącymi do ciągu liczb Lucasa , tutaj do 76 .

Liczby Fibonacciego i liczby Lucasa mają skomplikowany związek ze złotym podziałem. W ciągu Fibonacciego każda liczba jest równa sumie dwóch poprzednich, zaczynając od ciągu podstawowego ${\ Displaystyle 0,1}$ :

${\ Displaystyle 0,}$${\ Displaystyle 1,}$${\ Displaystyle 1,}$${\ Displaystyle 2,}$${\ Displaystyle 3,}$${\ Displaystyle 5,}$${ \ Displaystyle 8,}$${\ Displaystyle 13,}$${\ Displaystyle 21,}$${\ Displaystyle 34,}$${\ Displaystyle 55,}$${\ Displaystyle 89,}$${\ Displaystyle \ ldots}$ ( OEIS : A000045 ).

Sekwencja liczb Lucasa (nie mylić z uogólnionymi sekwencjami Lucasa , których ta część jest częścią) jest podobna do sekwencji Fibonacciego, w której każdy wyraz jest sumą dwóch poprzednich, ale zamiast tego zaczyna się od ${\ styl wyświetlania 2,1}$ :

${\ Displaystyle 2,}$${\ Displaystyle 1,}$${\ Displaystyle 3,}$${\ Displaystyle 4,}$${\ Displaystyle 7,}$${\ Displaystyle 11,}$${\ Displaystyle 18,}$${\ Displaystyle 29,}$${\ Displaystyle 47,}$${\ Displaystyle 76,}$${\ Displaystyle 123,}$${\ Displaystyle 199,}$ ${\ Displaystyle \ ldots}$ ( OEIS : A000032 ).

Wyjątkowo złoty podział jest równy granicy stosunków kolejnych wyrazów ciągu Fibonacciego i ciągu liczb Lucasa:

${\ Displaystyle \ lim _ {n \ do \ infty} {\ Frac {F_ {n + 1}}} {F_ {n}}} = \ lim _ {n \ do \ infty} } {\ frac {L_ {n + 1}}{L_{n}}}=\varphi.}$

Innymi słowy, jeśli liczba Fibonacciego i Lucasa jest podzielona przez jej bezpośredniego poprzednika w sekwencji, iloraz $przybliżony$ .

Na przykład ${\ Displaystyle {\ Frac {F_ {16}} {F_ {15}}} = {\ Frac {987} {610}} = 1,6180327 \ ldots,}$ i ${\ Displaystyle {\ Frac {L_ {16}} {L_ {15}}} = {\ Frac {2207} {1364}} = 1,6180351 \ ldots.}$

Te przybliżenia są na przemian niższe i wyższe niż i zbiegają się do $\ displaystyle$$\ varphi}$ wraz ze wzrostem liczb Fibonacciego i

Wyrażenia w postaci zamkniętej dla sekwencji Fibonacciego i Lucasa, które obejmują złoty podział, to:

${\ Displaystyle F \ lewo (n \ prawo) = {{\ varphi ^ {n} - (1 -\varphi )^{n}} \over {\sqrt {5}}}={{\varphi ^{n}-(-\varphi)^{-n}} \over {\sqrt {5}}} ,}$

${\ Displaystyle L \ lewo (n \ prawo) = \ varphi ^ {n} + (- \ varphi) ^ {- n} = \ lewo ({1 + {\ sqrt {5}} \ ponad 2} \ prawo) ^{n}+\lewo({1-{\sqrt {5}} \ponad 2}\prawo)^{n}\,.}$

Łącząc oba powyższe wzory, otrzymuje się wzór na ${\ displaystyle \ varphi ^ {n}}$ , który obejmuje zarówno liczby Fibonacciego, jak i Lucasa: φ n {\ displaystyle \ varphi ^ {n}}

${\ Displaystyle \ varphi ^ {n} = {{L_ {n} + F_ {n} {\ sqrt {5}}} \ ponad 2} \,.}$

$5F_ {n} ^ {2 }+2(-1)^{n}=L_{n}^{2}-2(-1)^{n},} co$ ( upraszcza wyrażenie granicy ilorazu liczb Lucasa przez liczby Fibonacciego jako równej pierwiastek kwadratowy z pięciu :

${\ Displaystyle \ lim _ {n \ do \ infty} {\ Frac {L_ {n}} {F_ {n}}} = {\ sqrt {5}}.}$

Rzeczywiście, znacznie silniejsze stwierdzenia są prawdziwe:

${\ Displaystyle \ vert L_ {n} - {\ sqrt {5}} F_ {n} \ vert = {\ Frac {2} {\ varphi ^ {n}}} \ do 0}$ ,

${\ Displaystyle (L_ {3n}/2) ^ {2} = 5 (F_ {3n}/2) ^ { 2}+(-1)^{n}}$ .

$}$ te opisują jako podstawową jednostkę algebraicznego pola liczbowego. ${\ Displaystyle \ mathbb {Q} ({\ sqrt {5}})$ .

Kolejne potęgi złotego podziału podlegają rekurencji Fibonacciego , tj. ${\ Displaystyle \ varphi ^ {n + 1} = \ varphi ^ {n} + \ varphi ^ {n-1}.}$

Redukcję do wyrażenia liniowego można przeprowadzić w jednym kroku, stosując:

${\ Displaystyle \ varphi ^ {n} = F_ {n} \ varphi + F_ {n-1}.}$

na zredukowanie dowolnego wielomianu do wyrażenia liniowego, jak w: ${\ displaystyle \ varphi}$

${\ Displaystyle {\ rozpocząć {wyrównane} 3 \ varphi ^ {3} -5 \ varphi ^ {2} + 4 i = 3 (\ varphi ^ {2} + \ varphi) -5 \ varphi ^ {2} + 4 \ \[5mu]&=3[(\varphi +1)+\varphi ]-5(\varphi +1)+4\\[5mu]&=\varphi +2\około 3,618033.\end{wyrównane}}}$

Kolejne liczby Fibonacciego można również wykorzystać do uzyskania podobnego wzoru na złoty podział, tutaj przez nieskończone sumowanie :

${\ Displaystyle \ suma _ {n = 1} ^ {\ infty} | F_ {n} \ varphi -F_ {n + 1} | = \ varphi.}$

W szczególności same potęgi zaokrąglają się do liczb $φ$ (w kolejności, z wyjątkiem dwóch pierwszych potęg, i $\ displaystyle \ varphi ^ {0}}$ , to ${\ displaystyle \ varphi}$ w odwrotnej kolejności):

${\ Displaystyle {\ rozpocząć {wyrównane} \ varphi ^ {0} i = 1, \\ [5mu] \ varphi ^ {1} i = 1,618033989 ... \ około 2, \\ [5mu] \ varphi ^ {2 }&=2,618033989...\około 3,\\[5mu]\varphi ^{3}&=4,236067978...\około 4,\\[5mu]\varphi ^{4}&=6,854101967...\ około 7,\end{wyrównane}}}$

i tak dalej. Liczby Lucasa również bezpośrednio generują moce złotego podziału; dla ${\ displaystyle n \ geq 2}$ :

${\ Displaystyle \ varphi ^ {n} = L_ {n} - (- \ varphi) ^ {- n}.}$

Zakorzeniony w ich wzajemnym związku ze złotym podziałem jest pogląd, że suma trzecich kolejnych liczb Fibonacciego jest równa liczbie Lucasa, czyli ${\ Displaystyle L_ {n} = F_ {n -1}+F_{n+1}}$ ; i, co ważne, ${\ Displaystyle {L_ {n}} = {\ Frac {F_ {2n}}} {F_ {n}}}}$ .

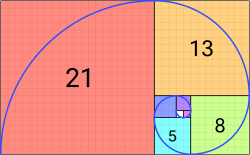
Zarówno ciąg Fibonacciego, jak i ciąg liczb Lucasa można wykorzystać do wygenerowania przybliżonych kształtów złotej spirali ( która jest specjalną formą spirali logarytmicznej ) za pomocą ćwierćokręgów o promieniach z tych ciągów, różniących się tylko nieznacznie od prawdziwego złotego logarytmu spirala. Spirala Fibonacciego jest ogólnie terminem używanym w odniesieniu do spiral, które przybliżają złote spirale za pomocą kwadratów i ćwierćokręgów z sekwencjami liczbowymi Fibonacciego.

Geometria

Złota proporcja jest widoczna w geometrii. Na przykład jest nierozerwalnie związany z wewnętrzną symetrią pięciokąta i rozciąga się, tworząc część współrzędnych wierzchołków dwunastościanu foremnego , jak również wierzchołków 5-komórkowego . Występuje również w trójkącie Keplera i nachyleniach Penrose'a , a także w różnych innych polytopach .

Budowa

Podział odcinka linii przez podział wewnętrzny (góra) i podział zewnętrzny (dół) zgodnie ze złotym podziałem.

Podział według podziału wewnętrznego

1. $B$ odcinek $,$$AB$ prostopadłą ${$ punkcie ${\ Displaystyle AB.}$ z długości Narysuj przeciwprostokątną ${\ Displaystyle AC.}$
2. Narysuj łuk o $promieniu$ i $BC.}$${\ Displaystyle D.}$$Displaystyle$ Ten łuk przecina przeciwprostokątną punkcie
3. Narysuj łuk o środku i promieniu ${\ Displaystyle AD.}$$}$ Ten łuk przecina oryginalny odcinek linii w punkcie ${\ displaystyle S.}$${\ displaystyle AB}$ Punkt $displaystyle S}$$\ displaystyle AS}$ dzieli oryginalny odcinek linii na odcinki linii ${$ i $SB}$ z długościami w złotej proporcji.

Podział przez podział zewnętrzny

1. ${\ Displaystyle AS.}$ odcinek linii $skonstruuj$ punktem odcinek $prostopadły$ do ​​i o tej samej długości $co$$AS$
2. Przetnij segment linii $M$ za ${\ Displaystyle M.}$
3. Okrągły łuk wokół promienia przecina w punkcie prostą przechodzącą przez punkty i M $}$${$$\ Displaystyle$$S$$($ również jako rozszerzenie ZA $\ displaystyle AS}$ ). Stosunek do $skonstruowanego$$_$ złoty

Przykłady zastosowań można zobaczyć w artykułach Pentagon o podanej długości boku , Dekagon o zadanym okręgu opisanym oraz Dekagon o podanej długości boku .

Oba powyższe różne algorytmy tworzą konstrukcje geometryczne , które określają dwa wyrównane odcinki linii , gdzie stosunek dłuższego do krótszego jest złotym podziałem.

Złoty kąt

Główny artykuł: Złoty kąt

g ≈ 137,508°

Kiedy dwa kąty tworzące pełny okrąg mają miary w złotym stosunku, mniejszy nazywa się złotym kątem , którego miara jest ${\ textstyle g \ okrężnica}$

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {2 \ pi -g} {g}} & = {\ Frac {2 \ pi} {2 \ pi -g}} = \ varphi, \\ [8mu] 2\pi -g&={\frac {2\pi }{\varphi}}\około 222,5^{\circ},\\[8mu]g&={\frac {2\pi}}{\varphi ^{2} }}\około 137,5^{\circ}.\end{wyrównane}}}$

Kąt ten występuje we wzorcach wzrostu roślin jako optymalne rozmieszczenie pędów liściowych wokół łodyg roślin, tak aby kolejne liście nie blokowały światła słonecznego z liści znajdujących się pod nimi.

System symetrii pięciokątnej

Pentagon i pentagram

Pentagram kolorowy, aby odróżnić odcinki linii o różnej długości. Cztery długości są względem siebie w złotym stosunku.

W pięciokącie foremnym stosunek przekątnej do boku to złoty podział, podczas gdy przecinające się przekątne przecinają się w złotym stosunku. Właściwości złotego podziału pięciokąta foremnego można potwierdzić, stosując twierdzenie Ptolemeusza do czworoboku utworzonego przez usunięcie jednego z jego wierzchołków. Jeśli długa krawędź i przekątne czworoboku to $displaystyle$ krótsze krawędzie to $b,} to twierdzenie$ daje $= b ^ {2} + ab.}$${\ displaystyle ab}$ Dzielenie obu stron przez plony (patrz § Obliczenia powyżej), za

${\ Displaystyle {\ Frac {a} {b}} = {\ Frac {a + b} {a}} = \ varphi.}$

Ukośne segmenty pięciokąta tworzą pentagram lub wielokąt pięcioramiennej gwiazdy , którego geometria jest kwintesencją opisaną przez ${\ displaystyle \ varphi}$ . Przede wszystkim każde przecięcie krawędzi dzieli inne krawędzie w złotej proporcji. Stosunek długości krótszego odcinka do odcinka ograniczonego przez dwie przecinające się krawędzie (czyli bok odwróconego pięciokąta w środku pentagramu) wynosi φ , {\ displaystyle \ varphi}, $czterokolorowa$ ilustracja .

Geometria pięciokątna i pentagramowa pozwala nam obliczyć następujące wartości dla: ${\ displaystyle \ varphi}$ :

${\ Displaystyle {\ rozpocząć {wyrównane} \ varphi & = 1 + 2 \ sin (\ pi / 10) = 1 + 2 \ sin 18 ^ {\ circ}, \\ [5mu] \ varphi & = {\ tfrac { 1}{2}}\csc(\pi /10)={\tfrac {1}{2}}\csc 18^{\circ},\\[5mu]\varphi &=2\cos(\pi / 5)=2\cos 36^{\circ },\\[5mu]\varphi &=2\sin(3\pi /10)=2\sin 54^{\circ }.\end{wyrównane}}}$

Złoty trójkąt i złoty gnomon

Główny artykuł: Złoty trójkąt (matematyka)

Złoty trójkąt ABC można podzielić przez dwusieczną kąta na mniejszy złoty trójkąt CXB i złoty gnomon XAC .

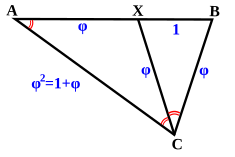
Trójkąt utworzony przez dwie przekątne i bok pięciokąta foremnego nazywany jest złotym trójkątem lub wzniosłym trójkątem . Jest to trójkąt równoramienny ostry o kącie wierzchołkowym 36° i kącie przy podstawie 72°. Jego dwa równe boki są w złotym stosunku do podstawy. Trójkąt utworzony przez dwa boki i przekątną pięciokąta foremnego nazywany jest złotym gnomonem . Jest to trójkąt równoramienny rozwartokątny o kącie wierzchołkowym 108° i kącie podstawy 36°. Jego podstawa jest w złotej proporcji do dwóch równych boków. Pięciokąt można zatem podzielić na dwa złote gnomony i środkowy złoty trójkąt. Pięć punktów A regularny pentagram to złote trójkąty, podobnie jak dziesięć trójkątów utworzonych przez połączenie wierzchołków dziesięciokąta foremnego z jego środkiem.

Przepołowienie jednego z kątów podstawowych złotego trójkąta dzieli go na mniejszy złoty trójkąt i złoty gnomon. Analogicznie, każdy ostry trójkąt równoramienny można podzielić na podobny trójkąt i rozwarty trójkąt równoramienny, ale złoty trójkąt jest jedynym, dla którego ten podział jest dokonywany przez dwusieczną kąta, ponieważ jest to jedyny trójkąt równoramienny, którego kąt podstawy jest dwa razy jego kąt wierzchołkowy. Dwusieczna kąta złotego trójkąta dzieli bok, który styka się w złotym stosunku, a obszary dwóch podzielonych kawałków są również w złotym stosunku.

Jeśli kąt wierzchołkowy złotego gnomona jest podzielony na trzy części , trójsektor ponownie dzieli go na mniejszego złotego gnomonu i złotego trójkąta. Trójsektor dzieli podstawę w złotym stosunku, a dwie części mają obszary w złotym stosunku. Analogicznie, każdy trójkąt rozwarty można podzielić na podobny trójkąt i ostry trójkąt równoramienny, ale złoty gnomon jest jedynym, dla którego ten podział jest dokonywany przez trisektor kąta, ponieważ jest to jedyny trójkąt równoramienny, którego kąt wierzchołkowy jest trzykrotnie jego kąt bazowy.

Płytki Penrose'a

Główny artykuł: płytki Penrose'a

Płytki z latawcem i rzutkami z płytek Penrose. Kolorowe łuki dzielą każdą krawędź w złotej proporcji; kiedy dwie płytki mają wspólną krawędź, ich łuki muszą się zgadzać.

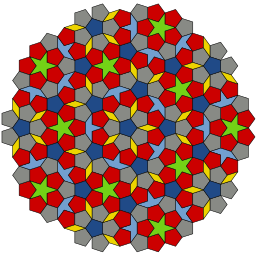
Złoty podział pojawia się wyraźnie w kafelkach Penrose'a , rodzinie aperiodycznych nachyleń płaszczyzny opracowanych przez Rogera Penrose'a , zainspirowanych uwagą Johannesa Keplera , że ​​pentagramy, dziesięciokąty i inne kształty mogą wypełnić luki, które same kształty pięciokątne pozostawiają po ułożeniu razem. Zbadano kilka odmian tego układania płytek, z których wszystkie wykazują złoty podział:

• Oryginalna wersja tej płytki Penrose'a wykorzystywała cztery kształty: regularne pięciokąty i pentagramy, figury „łódek” z trzema wierzchołkami pentagramu oraz romby w kształcie „diamentów”.
• Latawiec i rzutki Płytki Penrose'a wykorzystują latawce z trzema wewnętrznymi kątami 72 ° i jednym wewnętrznym kątem 144 ° oraz rzutki, wklęsłe czworoboki z dwoma wewnętrznymi kątami 36 °, jednym 72 ° i jednym niewypukłym kątem 216 ° . Specjalne zasady dopasowywania ograniczają sposób, w jaki płytki mogą się łączyć na dowolnej krawędzi, co daje siedem kombinacji płytek w dowolnym wierzchołku. Zarówno latawce, jak i rzutki mają boki o dwóch długościach, w złotym stosunku do siebie. Obszary tych dwóch kształtów płytek są również w stosunku do siebie w złotym stosunku.
• Latawiec i rzutka można pociąć na ich osiach symetrii odpowiednio na parę złotych trójkątów i złotych gnomonów. Przy odpowiednich regułach dopasowywania, te trójkąty, zwane w tym kontekście trójkątami Robinsona , mogą być użyte jako prototile dla formy kafelkowania Penrose'a.
• Rombowa płytka Penrose zawiera dwa rodzaje rombów, cienki romb o kątach 36° i 144° oraz gruby romb o kątach 72° i 108°. Wszystkie długości boków są równe, ale stosunek długości boków do krótkiej przekątnej w cienkim rombie jest równy ${\ Displaystyle 1: \ varphi}$ , podobnie jak stosunek boków do długiej przekątnej grubego rombu romb. Podobnie jak w przypadku układania latawca i rzutki, obszary dwóch rombów są względem siebie w złotym stosunku. Ponownie, te romby można rozłożyć na pary trójkątów Robinsona.

Oryginalna czteropłytkowa płytka Penrose

Płytka rombowa Penrose

W trójkątach i czworobokach

Konstrukcja Odoma

Konstrukcja Odoma: AB : BC = AC : AB = φ : 1

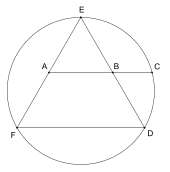
George Odom znalazł konstrukcję dla trójkąta $:$ jeśli odcinek łączący środki dwóch boków zostanie przedłużony do przecięcia okręgu opisanego , to dwa punkty środkowe i punkt przecięcia z okręgiem są w kolorze złotym proporcja.

Trójkąt Keplera

Główny artykuł: trójkąt Keplera

Postęp geometryczny obszarów kwadratów po bokach trójkąta Keplera

Trójkąt równoramienny utworzony z dwóch trójkątów Keplera maksymalizuje stosunek jego promienia do długości boku

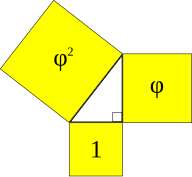
Trójkąt Keplera , nazwany na cześć Johannesa Keplera , jest unikalnym trójkątem prostokątnym o bokach w postępie geometrycznym :

${\ Displaystyle 1 \ mathbin {:} {\ sqrt {\ varphi}} \ mathbin {:} \ varphi}$ .

Te długości boków to trzy pitagorejskie średnie z dwóch liczb . ${\ Displaystyle \ varphi \ pm 1}$ . Trzy kwadraty po bokach mają obszary w złotym ciągu geometrycznym . ${\ Displaystyle 1 \ mathbin {:} \ varphi \ mathbin {:} \ varphi ^ {2}}$ .

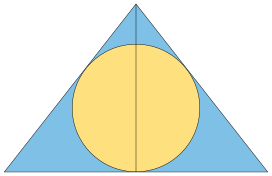
Wśród trójkątów równoramiennych stosunek promienia do długości boku jest zmaksymalizowany dla trójkąta utworzonego przez dwie odbite kopie trójkąta Keplera, dzielące dłuższą z dwóch nóg. Ten sam trójkąt równoramienny maksymalizuje stosunek promienia półkola u podstawy do jego obwodu .

Dla trójkąta Keplera o najmniejszej długości boku ${\ displaystyle s}$ powierzchni i ostre kąty wewnętrzne wynoszą: s

${\ Displaystyle {\ rozpocząć {wyrównane} A & = {\ tfrac {s ^ {2}} {2}} {\ sqrt {\ varphi}}, \\ [5mu] \ theta & = \ sin ^ {-1} {\frac {1}{\varphi}}\około 38,1727^{\circ},\\[5mu]\theta &=\cos ^{-1}{\frac {1}{\varphi}}\około 51,8273 ^{\circ}.\end{wyrównane}}}$

Złoty prostokąt

Główny artykuł: Złoty prostokąt

Aby zbudować złoty prostokąt tylko z liniałem i kompasem w czterech prostych krokach:

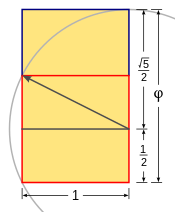
Narysuj kwadrat.

Narysuj linię od środka jednego boku kwadratu do przeciwległego rogu.

Użyj tej linii jako promienia, aby narysować łuk, który określa wysokość prostokąta.

Uzupełnij złoty prostokąt.

Złoty podział określa proporcje sąsiednich długości boków złotego prostokąta w stosunku ${\ Displaystyle 1: \ varphi} . Układanie złotych prostokątów tworzy nowe złote prostokąty, a$$usuwanie$ lub dodawanie kwadratów ze złotych prostokątów pozostawia prostokąty nadal proporcjonalne w . Mogą być generowane przez złote spirale , poprzez kolejne kwadraty i ćwierćokręgi wielkości liczb Fibonacciego i Lucasa. Występują one w widocznym miejscu w dwudziestościanie , jak również w dwunastościanie (więcej informacji znajduje się w sekcji poniżej).

Złoty romb

Główny artykuł: Złoty romb

Złoty romb to romb $są$ przekątne proporcjonalne do złotego podziału, najczęściej Dla rombu o takich proporcjach jego kąt ostry i rozwarty to:

${\ Displaystyle {\ rozpocząć {wyrównane} \ alfa & = 2 \ arctan {1 \ ponad \ varphi} \ około 63,43495 ^ {\ circ}, \\ [5mu] \ beta & = 2 \ arctan \ varphi = \ pi - \arctan 2=\arctan 1+\arctan 3\około 116,56505^{\circ}.\end{wyrównane}}}$

Długości jego krótkich i długich przekątnych $pod$ względem długości boku $a}$ : $displaystyle$

${\ Displaystyle {\ rozpocząć {wyrównane} d & = {2a \ ponad {\ sqrt {2+ \ varphi}}} = 2 {\ sqrt {{3- \ varphi} \ ponad 5}} a \ około 1,05146a, \ \[5mu]D&=2{\sqrt {{2+\varphi} \ponad 5}}a\około 1,70130a.\end{wyrównane}}}$

Jego powierzchnia pod względem za $\ displaystyle a}$ i ${\ displaystyle d}$ : za {\ displaystyle a}

${\ Displaystyle {\ rozpocząć {wyrównane} A & = (\ sin (\ arctan 2)) ~ a ^ {2} = {2 \ ponad {\ sqrt {5}}} ~ a ^ {2} \ około 0,89443a ^ {2},\\[5mu]A&={{\varphi } \ponad 2}d^{2}\około 0,80902d^{2}.\end{wyrównane}}}$

Jego promień , jeśli chodzi o bok: za $\ displaystyle a}$ :

${\ displaystyle r = {\ frac {a} {\ sqrt {5}}}.}$

Złoty romb w trójścianie rombowym (patrz sekcja poniżej). Można je również znaleźć w złotym romboedrze , dwunastościanie Bilińskiego i sześciokątie rombowym .

Złota spirala

Główny artykuł: Złota spirala

Złota spirala logarytmiczna wiruje wokół złotego trójkąta , dotykając jego trzech wierzchołków, poruszając się do wewnątrz podobnych fraktalnych złotych trójkątów.

Spirale logarytmiczne to spirale samopodobne , w których odległości pokonywane na obrót są postępem geometrycznym . Co ważne, równoramienne złote trójkąty mogą być otoczone złotą spiralą logarytmiczną, tak że kolejne zwoje spirali generują wewnątrz nowe złote trójkąty. Ten szczególny przypadek spiral logarytmicznych nazywany jest złotą spiralą i wykazuje ciągły wzrost złotego podziału. Oznacza to, że na każdy obrót przypada współczynnik wzrostu równy $}$$\ Displaystyle 90 ^ {\ circ}$ . Te spirale można przybliżyć za pomocą ćwierćokręgów utworzonych z kwadratów wielkości liczb Fibonacciego i Lucasa, które są ułożone razem. W ich dokładnej postaci można je opisać równaniem biegunowym z : ${\ Displaystyle (r, \ theta)}$ :

${\ displaystyle r = \ varphi ^ {2 \ teta / \ pi}.}$

${right} }}=\varphi }$ w przypadku każdej spirali logarytmicznej, dla mi $t$ = $^ {b \ theta _$ pod kątem prostym :

${\ Displaystyle | b | = {\ ln {\ varphi} \ ponad \ theta _ {\ operatorname {po prawej}}} \ doteq 0,0053468 ^ {\ circ} \ doteq 0,3063489 {\ tekst {rad.}}}$

Jego nachylenie biegunowe można obliczyć za pomocą tan $\ tan \ alpha = b}$$Displaystyle$${\ Displaystyle | b |}$ z góry,

${\ Displaystyle \ alfa = \ arctan (| b |) = \ arctan \ lewo ({\ ln {\ varphi} \ nad \ pi / 2} \ prawej) \ doteq 17,03239113 ^ {\ circ} \ doteq 0,2972713047 {\ tekst {rad.}}}$

Ma kąt dopełniający, ${\ displaystyle \ beta}: β {\ displaystyle \ beta$ }

${\ Displaystyle \ beta = \ pi / 2- \ alfa \ doteq 72,96760887 ^ {\ circ} \ doteq 1,273525022 {\ tekst {rad.}}}$

Złote spirale można również umieszczać symetrycznie wewnątrz pięciokątów i pentagramów, tak że fraktalne kopie podstawowej geometrii są odtwarzane we wszystkich skalach.

W dwunastościanie i dwudziestościanie

(0, ± φ , ± 1 Współrzędne φ )
/ kartezjańskie dwunastościanu :
(±1, ±1, ±1)
(± 1 / φ , 0, ± φ )
(± φ , ± 1 / φ , 0)
A zagnieżdżony sześcian wewnątrz dwunastościanu jest reprezentowany przez kropkowane linie.

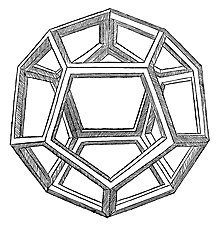
Dwunastościan foremny i jego podwójny wielościan dwudziestościan to bryły platońskie , których wymiary są związane ze złotym podziałem. $pięciokątnych ścian, podczas gdy$ składa się z regularnych $równobocznych$ składa się z trójkątów ; oba z $_$ .

Dla dwunastościanu o boku $r$ promień opisanej i wpisanej kuli oraz środek to ( ${u}}$${\ displaystyle r_ {i}}$ , i $\displaystyle r_{m}} ):$${$ odpowiednio

${\ Displaystyle r_ {u} = a \, {\ Frac {{\ sqrt {3}} \ varphi} {2}}}$ , ${\ displaystyle r_ {i} = a \, {\ Frac {\ varphi ^ {2}} {2 {\ sqrt {3- \ varphi}}}}} i r m = za$ φ $m }=a\,{\frac {\varphi ^{2}}{2}}}$ .

Podczas gdy dla dwudziestościanu o boku ${\ displaystyle a}$ opisanej i wpisanej kuli oraz środek to: za

${\ Displaystyle r_ {u} = a {\ Frac {\ sqrt {\ varphi {\ sqrt {5}}}} {2}}}$ , ${\ displaystyle r_ {i} = a {\ Frac {\ varphi ^ {2}} {2 {\ sqrt {3}}}}} i r m$ = $r_ {m} = a {\ frac {\ varphi} {2}}}$ .

Objętość i pole powierzchni dwunastościanu można wyrazić za pomocą: ${\ displaystyle \ varphi$ }

${\ Displaystyle A_ {d} = {\ Frac {15 \ varphi} {\ sqrt {3- \ varphi}}}}$ i ${\ Displaystyle V_{d}={\frac {5\varphi ^{3}}{6-2\varphi}}}$ .

Jak również dla dwudziestościanu:

${\ Displaystyle A_ {i} = 20 {\ Frac {\ varphi ^ {2}} {2}}}$ i ${\ Displaystyle V_ {i} = {\ Frac {5} {6}} (1+ \ varphi).}$

Trzy złote prostokąty dotykają wszystkich 12 wierzchołków dwudziestościanu foremnego .

Te wartości geometryczne można obliczyć na podstawie ich współrzędnych kartezjańskich , które można również podać za pomocą wzorów obejmujących ${\ displaystyle \ varphi}$ . Współrzędne dwunastościanu pokazano na powyższym rysunku, podczas gdy współrzędne dwudziestościanu to cykliczne permutacje :

${\ Displaystyle (0, \ pm 1, \ pm \ varphi)}$ , ${\ Displaystyle (\ pm 1, \ pm \ varphi, 0)}$ , ${\ Displaystyle (\ pm \ varphi, 0, \ pm 1).}$

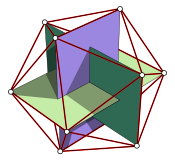
Zestawy trzech złotych prostokątów przecinają się prostopadle wewnątrz dwunastościanów i dwudziestościanów, tworząc pierścienie boromejskie . W dwunastościanach pary przeciwległych wierzchołków w złotych prostokątach stykają się ze środkami pięciokątnych ścian, aw dwudziestościanach spotykają się w wierzchołkach. W sumie trzy złote prostokąty zawierają $wierzchołki$$lub$ równoważnie przecinają środki ścian dwunastościanu

Sześcian można wpisać w dwunastościan foremny, przy czym niektóre przekątne pięciokątnych ścian dwunastościanu służą jako krawędzie sześcianu ; dlatego długości krawędzi są w złotym stosunku. Objętość sześcianu jest ${\ Displaystyle {\ tfrac {2} {2+ \ varphi}}}$ razy większa niż dwunastościanu. W rzeczywistości złote prostokąty wewnątrz dwunastościanu są w złotych proporcjach do wpisanego sześcianu, tak że krawędzie sześcianu i długie krawędzie złotego prostokąta są same w ${\ displaystyle \ varphi: \ varphi ^ {2}}$ stosunek. Z drugiej strony ośmiościan , który jest podwójnym wielościanem sześcianu, może wpisać dwudziestościan tak, że wierzchołki dwudziestościanu dotykają krawędzi ośmiościanu w punktach, które dzielą jego $12}$$\ displaystyle$ krawędzie w złotej proporcji.

Inne wielościany są powiązane z dwunastościanem i dwudziestościanem lub ich symetriami, a zatem mają odpowiednie relacje ze złotym podziałem. Należą do nich związek pięciu kostek , związek pięciu ośmiościanów , związek pięciu czworościanów , związek dziesięciu czworościanów , triacontahedron rombowy , dwudziestościan rombowy , dwudziestościan ścięty , dwunastościan ścięty i dziesięciościan rombowy , enneacontahedron rombowy i Wielościany Keplera-Poinsota i sześcian rombowy . W czterech wymiarach dwunastościan i dwudziestościan pojawiają się jako ściany komórek 120-ogniwowych i 600-ogniwowych , które ponownie mają wymiary związane ze złotym podziałem.

Inne właściwości

Rozwinięcie dziesiętne złotego podziału można obliczyć za pomocą metod znajdowania pierwiastków, takich jak metoda Newtona lub metoda Halleya , na podstawie równania ${\ Displaystyle x ^ {2} -x-1 = 0}$ lub na ${\ Displaystyle x ^ {2} -5 = 0}$$.$ aby najpierw obliczyć) Czas potrzebny do obliczenia ${\ displaystyle n}$ cyfry złotego podziału przy użyciu metody Newtona to zasadniczo $)$ ) $n$${\ displaystyle n}$ to czasowa n -cyfrowe liczby. Jest to znacznie szybsze niż znane algorytmy dla i ${$$\ displaystyle e$ . Łatwą do zaprogramowania alternatywą wykorzystującą tylko arytmetykę liczb całkowitych jest obliczenie dwóch dużych kolejnych liczb Fibonacciego i podzielenie ich. Stosunek liczb Fibonacciego i $Displaystyle F_ {25000}$$każda$ ponad ${\ Displaystyle 5000}$ cyfr, daje ponad ${\ Displaystyle 10 {,} 000}$ znaczące cyfry złotego podziału. Dziesiętne rozwinięcie złotego podziału ${\ displaystyle \ varphi}$ został obliczony z dokładnością do dziesięciu bilionów ( $000 {\ Displaystyle 1 \ razy 10 ^ {13} = 10 {,} 000 {,} 000 {,} 000 {,} 000} )$ cyfr .

Na płaszczyźnie zespolonej piąte pierwiastki jedności (dla liczby całkowitej $textstyle k}$${\ Displaystyle z = e ^ {2 \ pi ki/5}$ ) spełniające ${\ Displaystyle z ^ {5} = 1}$ to wierzchołki pięciokąta. Nie tworzą one pierścienia liczb całkowitych kwadratowych , jednak suma dowolnego piątego pierwiastka jedności i jego sprzężenia zespolonego , ${\ Displaystyle z + {\ bar {z}},}$ jest kwadratową liczbą całkowitą, elementem ${\textstyle \mathbb {Z} [\varphi].}$ Konkretnie,

${\ Displaystyle {\ rozpocząć {wyrównane} e ^ {0} + e ^ {- 0} i = 2, \\ [5mu] e ^ {2 \ pi i/5} + e ^ {- 2 \ pi i / 5}&=\varphi ^{-1}=-1+\varphi ,\\[5mu]e^{4\pi i/5}+e^{-4\pi i/5}&=-\varphi .\end{wyrównane}}}$

Dotyczy to również pozostałych dziesiątych pierwiastków jedności spełniających ${\ Displaystyle Z ^ {10} = 1,}$

${\ Displaystyle {\ rozpocząć {wyrównane} e ^ {\ pi i} + e ^ {- \ pi i} & = - 2, \\ [5mu] e ^ {\ pi i/5} + e ^ {- \ pi i/5}&=\varphi ,\\[5mu]e^{3\pi i/5}+e^{-3\pi i/5}&=-\varphi ^{-1}=1- \varphi .\end{wyrównane}}}$

Dla funkcji gamma $jedyne$ rozwiązania równania ${\ Displaystyle \ Gamma (z-1) = \ Gamma (z + 1)$ są ${\ Displaystyle z = \ varphi}$ i ${\ Displaystyle z = - \ varphi ^ {- 1}}$ .

Kiedy złoty podział jest używany jako podstawa systemu liczbowego (patrz podstawa złotego podziału , czasami nazywana finarnym lub $kwadratowe$ ), liczby całkowite w pierścieniu $\ Displaystyle \ mathbb {Z } [\ varphi ]}$ { - czyli liczby postaci za ${\ Displaystyle a + b \ varphi}$ dla $mathbb {Z}}$ – mają reprezentacje kończące , ale ułamki wymierne mają reprezentacje niekończące się.

Złoty podział pojawia się również w geometrii hiperbolicznej , jako maksymalna odległość od punktu po jednej stronie idealnego trójkąta do bliższego z pozostałych dwóch boków: ta odległość, długość boku trójkąta równobocznego utworzonego przez punkty styczności a okrąg wpisany w idealny trójkąt to ${\ Displaystyle 4 \ log (\ varphi).}$

również w teorii funkcji modularnych . dla ${\ Displaystyle \ lewo | q \ prawo | <1}$ niech

${\ Displaystyle R (q) = {\ cfrac {q ^ {1/5}} {1 + {\ cfrac {q} {1 + {\ cfrac {q ^ {2}} {1 + {\ cfrac {q ^{3}}{1+\ddots }}}}}}}}.}$

Następnie

${\ Displaystyle R (e ^ {- 2 \ pi}) = {\ sqrt {\ varphi {\sqrt {5}}}}-\varphi ,\quad R(-e^{-\pi})=\varphi ^{-1}-{\sqrt {2-\varphi ^{-1}} }}$

I

${\ Displaystyle R (e ^ {- 2 \ pi ja / \ tau}) ={\frac {1-\varphi R(e^{2\pi i\tau})}{\varphi +R(e^{2\pii\tau})}}}$

gdzie należy ocenić ${\ Displaystyle \ operatorname {Im} \ tau > 0}$ i ${\ Displaystyle (e ^ {z}) ^ {1/5}}$ jak ${\ displaystyle e ^ {z / 5}}$ . τ ${\ Displaystyle \ tau \ mapsto R (e ^ {2 \ pi i \ tau})}$ niezmiennikiem pod ${\ Displaystyle \ Gamma (5)}$ , podgrupa kongruencji grupy modułowej . Również dla dodatnich liczb rzeczywistych ${\ Displaystyle a, b \ in \ mathbb {R} ^ {+}}$ i ${\ Displaystyle ab = \ pi ^ {2},}$

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Bigl (} \ varphi + R {{\ bigl (} e ^ {-2a} {\ bigr)}} {\ Bigr)}} {\ Bigl (} \ varphi + R {{\bigl (}e^{-2b}{\bigr )}}{\Bigr )}&=\varphi {\sqrt {5}},\\[5mu]{\Bigl (}\varphi ^{- 1}-R{{\bigl (}{-e^{-a}}{\bigr )}}{\Bigr )}{\Bigl (}\varphi ^{-1}-R{{\bigl (} {-e^{-b}}{\bigr )}}{\Bigr )}&=\varphi ^{-1}{\sqrt {5}}.\end{aligned}}}$

${\ Displaystyle \ varphi}$ to liczba Pisota-Vijayaraghavana .

Zastosowania i obserwacje

Architektura

Dalsze informacje: Matematyka i architektura

Szwajcarski architekt Le Corbusier , znany ze swojego wkładu w nowoczesny styl międzynarodowy , skupił swoją filozofię projektowania na systemach harmonii i proporcji. Wiara Le Corbusiera w matematyczny porządek wszechświata była ściśle związana ze złotym podziałem i szeregiem Fibonacciego, które opisał jako „rytmy widoczne dla oka i jasne w ich wzajemnych relacjach. Rytmy te leżą u samych podstaw ludzkie działania. Rozbrzmiewają w człowieku przez organiczną nieuchronność, tę samą subtelną nieuchronność, która powoduje śledzenie Złotego Podziału przez dzieci, starców, dzikusów i uczonych.

Le Corbusier wyraźnie użył złotego podziału w swoim systemie Modulor dla skali proporcji architektonicznych . Postrzegał ten system jako kontynuację długiej tradycji Witruwiusza , „ Człowieka witruwiańskiego ” Leonarda da Vinci , dzieła Leona Battisty Albertiego i innych, którzy wykorzystali proporcje ludzkiego ciała do poprawy wyglądu i funkcji architektury .

Oprócz złotego podziału, Le Corbusier oparł system na pomiarach człowieka , liczbach Fibonacciego i podwójnej jednostce. Sugestię złotego podziału w ludzkich proporcjach doprowadził do skrajności: podzielił wysokość swojego modelowego ludzkiego ciała w pępku na dwie sekcje w złotym stosunku, a następnie podzielił te sekcje w złotym stosunku na kolanach i gardle; zastosował te proporcje złotego podziału w Modulor . Willa Stein Le Corbusiera z 1927 r. W Garches zilustrował zastosowanie systemu Modulor. Prostokątny plan terenu, elewacja i struktura wewnętrzna willi są bardzo zbliżone do złotych prostokątów.

Inny szwajcarski architekt, Mario Botta , opiera wiele swoich projektów na figurach geometrycznych. Kilka prywatnych domów, które zaprojektował w Szwajcarii, składa się z kwadratów i kół, sześcianów i cylindrów. W domu, który zaprojektował w Origlio , złoty podział to proporcja między częścią środkową a bocznymi częściami domu.

Sztuka

Dalsze informacje: Matematyka i sztuka oraz Historia estetyki

Da Vinci przedstawiająca dwunastościan z Divina ratione Pacioli (1509)

Ilustracje Leonarda da Vinci przedstawiające wielościany w Divina ratione Pacioli doprowadziły niektórych do spekulacji, że włączył on złoty podział do swoich obrazów. Ale sugestia, że ​​na przykład jego Mona Lisa stosuje złote proporcje, nie znajduje poparcia w pismach samego Leonarda. Podobnie, chociaż Człowiek witruwiański Leonarda jest często przedstawiany w połączeniu ze złotym podziałem, proporcje postaci w rzeczywistości mu nie odpowiadają, a tekst wspomina tylko o stosunkach liczb całkowitych.

Salvador Dalí , pod wpływem twórczości Matili Ghyki , wyraźnie zastosował złoty podział w swoim arcydziele Sakrament Ostatniej Wieczerzy . Wymiary płótna to złoty prostokąt. Ogromny dwunastościan, w perspektywie tak, że krawędzie pojawiają się w stosunku do siebie w złotych proporcjach, zawieszony jest nad i za Jezusem i dominuje w kompozycji.

Badanie statystyczne przeprowadzone w 1999 roku na 565 dziełach różnych wielkich malarzy wykazało, że artyści ci nie stosowali złotego podziału w wielkości swoich płócien. Badanie wykazało, że średni stosunek obu stron badanych obrazów wynosi $displaystyle$ przy czym średnie dla poszczególnych artystów wahają się od $1,04}$ (Goya) do ${\ displaystyle 1,46}$ (Bellini) . Z kolei Pablo Tosto wymienił ponad 350 dzieł znanych artystów, w tym ponad 100 z płótnami ze złotym prostokątem i $}}$$\$$Displaystyle$ { $\$ proporcje i inne o proporcjach ${\ Displaystyle 6.}$

Przedstawienie proporcji w średniowiecznym rękopisie. Według Jana Tschicholda : „Proporcje strony 2:3. Proporcje marginesów 1:1:2:3. Obszar tekstu proporcjonalny do złotego podziału”.

Książki i projektowanie

Główny artykuł: Kanony budowy strony

Zdaniem Jana Tschicholda ,

Był czas, kiedy odchylenia od naprawdę pięknych proporcji strony ${\ Displaystyle 2 \ mathbin {:} 3,}$${\ Displaystyle 1 \ mathbin {:} {\ sqrt {3}},}$ i Złoty Podział były rzadkie. Wiele książek wyprodukowanych między 1550 a 1770 rokiem pokazuje te proporcje dokładnie z dokładnością do pół milimetra.

Według niektórych źródeł złoty podział jest stosowany w codziennym projektowaniu, na przykład w proporcjach kart do gry, pocztówek, plakatów, tabliczek włączników światła i szerokoekranowych telewizorów.

Flagi

Flaga Togo , której współczynnik proporcji wykorzystuje złoty podział

współczynnik kształtu (stosunek szerokości do wysokości) flagi Togo miał być złotym podziałem.

Muzyka

Ernő Lendvai analizuje utwory Béli Bartóka jako oparte na dwóch przeciwstawnych systemach, złotym podziale i skali akustycznej , choć inni muzycy odrzucają tę analizę. Francuski kompozytor Erik Satie zastosował złoty podział w kilku swoich utworach, w tym w Sonneries de la Rose+Croix . Złota proporcja jest również widoczna w organizacji sekcji w muzyce Debussy'ego Reflets dans l'eau (Refleksje w wodzie) , z obrazów (1. seria, 1905), w której „sekwencja klawiszy jest wyznaczona interwałami 34, 21, 13 i 8, a główny punkt kulminacyjny znajduje się w pozycji phi”.

Muzykolog Roy Howat zauważył, że formalne granice La Mer Debussy'ego odpowiadają dokładnie złotemu podziałowi. Trezise uważa wewnętrzne dowody za „niezwykłe”, ale ostrzega, że ​​​​żadne pisemne ani zgłoszone dowody nie sugerują, że Debussy świadomie poszukiwał takich proporcji.

Teoretycy muzyki, w tym Hans Zender i Heinz Bohlen , eksperymentowali ze skalą 833 centów , skalą muzyczną opartą na wykorzystaniu złotego podziału jako podstawowego interwału muzycznego . Mierzony w centach , skali logarytmicznej dla interwałów muzycznych, złoty podział wynosi około 833,09 centów.

Natura

Fragment rośliny spodka, Aeonium tabuliforme , przedstawiający układ wielu spirali ( parastichy )

Główny artykuł: Wzory w przyrodzie

Zobacz też: Liczba Fibonacciego § Natura

Johannes Kepler napisał, że „obraz mężczyzny i kobiety wynika z boskiej proporcji. Moim zdaniem rozmnażanie roślin i akty prokreacyjne zwierząt są w tym samym stosunku”.

Psycholog Adolf Zeising zauważył, że złoty podział pojawił się w filotaksji i argumentował na podstawie tych wzorców w naturze , że złoty podział jest prawem uniwersalnym. Zeising napisał w 1854 r. O uniwersalnym ortogenetycznym „dążenia do piękna i kompletności zarówno w dziedzinie natury, jak i sztuki”.

Jednak niektórzy argumentowali, że wiele pozornych przejawów złotego podziału w przyrodzie, zwłaszcza w odniesieniu do wymiarów zwierząt, jest fikcyjnych.

Fizyka

Quasi-jednowymiarowy ferromagnes Ising CoNb ₂ O ₆ (niobian kobaltu) ma 8 przewidywanych stanów wzbudzenia (z symetrią E ₈ ), które po zbadaniu za pomocą rozpraszania neutronów wykazały, że jego najniższe dwa były w złotym stosunku. Konkretnie, te kwantowe przejścia fazowe podczas wzbudzenia spinowego, które występują w temperaturze bliskiej zera bezwzględnego, wykazały pary załamań w fazie uporządkowanej do przewrotów spinowych w fazie paramagnetycznej ; odsłaniając, tuż poniżej jego pola krytycznego , dynamika wirowania z ostrymi modami przy niskich energiach zbliżających się do złotego środka.

Optymalizacja

Nie jest znany ogólny algorytm równomiernego rozmieszczania danej liczby węzłów na kuli dla dowolnej z kilku definicji parzystego rozkładu (patrz na przykład problem Thomsona lub problem Tammesa ). Jednak użyteczne przybliżenie wynika z podzielenia kuli na równoległe pasma o równej powierzchni i umieszczenia po jednym węźle w każdym z pasm na długościach rozdzielonych złotym odcinkiem koła, tj. ${\ Displaystyle 360 ​​^ {\ circ} / \ varphi \ około 222,5 ^ {\ circ}.}$ Metodę tę wykorzystano do ułożenia 1500 luster studenckiego satelity Starshine-3 .

również krytycznym elementem wyszukiwania złotego podziału .

Kwestionowane obserwacje

Przykłady spornych obserwacji złotego podziału obejmują:

Nautilusa mają złote proporcje.

• Często twierdzi się, że określone proporcje w ciałach kręgowców (w tym ludzi) odpowiadają złotemu podziałowi; na przykład mówi się, że stosunek kolejnych kości paliczków i śródręcza (kości palców) jest zbliżony do złotego podziału. Istnieje jednak duże zróżnicowanie rzeczywistych miar tych pierwiastków u poszczególnych osób, a omawiana proporcja często znacznie różni się od złotego podziału.
• , że muszle mięczaków, takich jak nautilus , są w złotej proporcji. Wzrost muszli łodzików następuje po spirali logarytmicznej i czasami błędnie twierdzi się, że jakakolwiek spirala logarytmiczna jest związana ze złotym podziałem, lub czasami twierdzi się, że każda nowa komora ma złote proporcje w stosunku do poprzedniej. Jednak pomiary muszli łodzików nie potwierdzają tego twierdzenia.
• Historyk John Man twierdzi, że zarówno strony, jak i obszar tekstowy Biblii Gutenberga były „oparte na kształcie złotego podziału”. Jednak według jego własnych pomiarów stosunek wysokości do szerokości stron wynosi ${\ Displaystyle 1.45.}$
• Badania psychologów, poczynając od Gustava Fechnera c. 1876, zostały opracowane w celu sprawdzenia idei, że złoty podział odgrywa rolę w ludzkim postrzeganiu piękna . Podczas gdy Fechner preferował proporcje prostokątów wyśrodkowane na złotym podziale, późniejsze próby dokładnego przetestowania takiej hipotezy były w najlepszym razie niejednoznaczne.
• W inwestowaniu niektórzy praktycy analizy technicznej używają złotego podziału, aby wskazać wsparcie poziomu cen lub opór wobec wzrostu cen akcji lub towaru; po znacznych zmianach cen w górę lub w dół, nowe poziomy wsparcia i oporu są rzekomo znajdowane w cenach zbliżonych do ceny początkowej za pomocą złotego podziału. Stosowanie złotego podziału w inwestowaniu wiąże się również z bardziej skomplikowanymi wzorcami opisanymi liczbami Fibonacciego (np. zasada fal Elliotta i zniesienie Fibonacciego ). Jednak inni analitycy rynkowi opublikowali analizy sugerujące, że te wartości procentowe i wzorce nie są poparte danymi.

Piramidy egipskie

Wielka Piramida w Gizie

Wielka Piramida w Gizie (znana również jako Piramida Cheopsa lub Cheopsa) została przeanalizowana przez piramidologów jako posiadająca podwójny trójkąt Keplera jako przekrój poprzeczny. Gdyby ta teoria była prawdziwa, złoty podział opisywałby stosunek odległości od środka jednego z boków piramidy do jej wierzchołka oraz od tego samego punktu środkowego do środka podstawy piramidy. Jednak niedokładność pomiaru spowodowana częściowo usunięciem zewnętrznej powierzchni piramidy uniemożliwia odróżnienie tej teorii od innych numerycznych teorii proporcji piramidy, opartych na pi lub na stosunkach liczb całkowitych. Współcześni uczeni są zgodni co do tego, że proporcje tej piramidy nie opierają się na złotej proporcji, gdyż taka podstawa byłaby niespójna zarówno z tym, co wiadomo o egipskiej matematyce od czasów budowy piramidy, jak i z egipskimi teoriami architektury i proporcji wykorzystane w innych pracach.

Partenon

, że wiele proporcji Partenonu wykazuje złoty podział, ale zostało to w dużej mierze zdyskredytowane.

Partenonu (ok. 432 pne), a także elementy jego elewacji i innych miejsc są otoczone złotymi prostokątami. Inni uczeni zaprzeczają, jakoby Grecy mieli jakiekolwiek estetyczne skojarzenia ze złotym podziałem. Na przykład Keith Devlin mówi: „Z pewnością często powtarzane twierdzenie, że Partenon w Atenach jest oparty na złotym podziale, nie jest poparte rzeczywistymi pomiarami. W rzeczywistości cała historia o Grekach i złotym podziale wydaje się być bezpodstawna. " Midhat J. Gazale potwierdza, że ​​„Dopiero przed Euclidem… zbadano matematyczne właściwości złotego podziału”.

Na podstawie pomiarów 15 świątyń, 18 monumentalnych grobowców, 8 sarkofagów i 58 stel nagrobnych od V w. p.n.e. do II w. n.e. jeden z badaczy doszedł do wniosku, że złoty podział był całkowicie nieobecny w greckiej architekturze klasycznego V w. p.n.e. i prawie nieobecny w ciągu następnych sześciu stuleci. Późniejsze źródła, takie jak Witruwiusz (I wiek pne), omawiają wyłącznie proporcje, które można wyrazić w liczbach całkowitych, tj. współmierne, w przeciwieństwie do proporcji niewymiernych.

Sztuka współczesna

Albert Gleizes , Les Baigneuses (1912)

Sekcja d'Or („Złota Sekcja”) była kolektywem malarzy , rzeźbiarzy, poetów i krytyków związanych z kubizmem i orfizmem . Aktywni od 1911 do około 1914 roku, przyjęli tę nazwę zarówno po to, aby podkreślić, że kubizm reprezentował kontynuację wielkiej tradycji, a nie izolowany ruch, oraz w hołdzie matematycznej harmonii związanej z Georgesem Seuratem . (Kilku autorów twierdziło, że Seurat stosował złoty podział w swoich obrazach, ale pisma i obrazy Seurata sugerują, że stosował on proste proporcje liczb całkowitych, a wszelkie przybliżenie złotego podziału było przypadkowe.) Kubiści obserwowali w swoich harmoniach geometryczną strukturę ruch i forma, „prymat idei nad naturą”, „absolutna naukowa jasność koncepcji”. Jednak pomimo tego ogólnego zainteresowania harmonią matematyczną, czy obrazy prezentowane w słynnym Salon de la Section d'Or z 1912 r. wystawa zastosowała złoty podział w jakichkolwiek kompozycjach jest trudniejsza do określenia. Na przykład Livio twierdzi, że nie, a Marcel Duchamp powiedział to samo w wywiadzie. Z drugiej strony analiza sugeruje, że Juan Gris wykorzystywał złoty podział przy komponowaniu dzieł, które prawdopodobnie, ale nie definitywnie, były pokazywane na wystawie. Historyk sztuki Daniel Robbins argumentował, że oprócz odniesienia do terminu matematycznego, nazwa wystawy nawiązuje również do wcześniejszej grupy Bandeaux d'Or , z którą Albert Gleizes i inni byli członkowie Abbaye de Créteil byli zaangażowani.

Piet Mondrian szeroko wykorzystywał złoty podział w swoich geometrycznych obrazach, chociaż inni eksperci (w tym krytyk Yve-Alain Bois ) zdyskredytowali te twierdzenia.

Zobacz też

• Lista prac zaprojektowanych zgodnie ze złotym podziałem
• Metaliczny średni
• Plastikowy numer
• Święta geometria
• Superzłoty stosunek

Prace cytowane

•   Herz-Fischler, Roger (1998) [1987]. Matematyczna historia złotej liczby . Dover. ISBN 9780486400075 . (Pierwotnie zatytułowany A Mathematical History of Division in Extreme and Mean Ratio ).
•   Livio, Mario (2002). The Golden Ratio: The Story of Phi, najbardziej zdumiewająca liczba na świecie . Nowy Jork: Broadway Books. ISBN 9780767908153 .
•   Posamentier, Alfred S. ; Lehmann, Ingmar (2011). Chwalebna złota proporcja . Książki Prometeusz. ISBN 9-781-61614-424-1 .

Dalsza lektura

• Doczi, György (1981). Potęga granic: proporcjonalne harmonie w przyrodzie, sztuce i architekturze . Boston: Szambala.
•   Hargittai, István, wyd. (1992). Pięciokrotna symetria . Świat naukowy. ISBN 9789810206000 .
•   Huntley, ON (1970). Boska proporcja: studium matematycznego piękna . Nowy Jork: Dover. ISBN 978-0-486-22254-7 .
• Schaaf, William L., wyd. (1967). Złota miara (PDF) . Seria przedruków California School Mathematics Study Group. Uniwersytet Stanford. Zarchiwizowane (PDF) od oryginału w dniu 2015-04-25.
•   Szimone, Aldo (1997). Sezione Aurea. Historia kultury di un leitmotiv della Matematica . Palermo: Sigma Edizioni. ISBN 978-88-7231-025-0 .
•   Walser, Hans (2001) [ Der Goldene Schnitt 1993]. Złota Sekcja . Przekład Petera Hiltona. Waszyngton, DC: Amerykańskie Stowarzyszenie Matematyczne. ISBN 978-0-88385-534-8 .

Linki zewnętrzne

• Weisstein, Eric W. „Złoty podział” . MathWorld .
• Bogomolny, Aleksander (2018). „Złoty podział w geometrii” . Przeciąć węzeł .
• Knot, Ron. „Współczynnik złotego przekroju: Phi” . Informacje i działania profesora matematyki.
• Mit, który nie zniknie , Keith Devlin , odnosząc się do wielu zarzutów dotyczących stosowania złotego podziału w kulturze.
• Fałszywe złote spirale zebrane przez Randalla Munroe
• Wykład na YouTube o problemie myszy Zenona i spiralach logarytmicznych