Związek pięciu czworościanów
| Związek pięciu czworościanów | |
|---|---|

|
|
| Typ | Regularny związek |
| Symbol Coxetera | {5,3}[5{3,3}] {3,5} |
| Indeks | UC 5 , W 24 |
|
Pierwiastki (jako związek) |
5 czworościanów : F = 20, E = 30, V = 20 |
| Podwójny związek | Samopodwójny |
| Grupa symetrii | chiralny dwudziestościan ( I ) |
| Podgrupa ograniczająca się do jednego składnika | chiralny czworościenny ( T ) |
Związek pięciu czworościanów jest jednym z pięciu regularnych związków wielościennych. Ten złożony wielościan jest również gwiazdą regularnego dwudziestościanu . Po raz pierwszy został opisany przez Edmunda Hessa w 1876 roku.
Można to postrzegać jako fasetowanie dwunastościanu foremnego .
Jako związek
Można go skonstruować, układając pięć czworościanów w obrotowej dwudziestościennej symetrii ( I ), jak pokazano w prawym górnym modelu. Jest to jeden z pięciu związków regularnych , które można zbudować z identycznych brył platońskich .
Ma taki sam układ wierzchołków jak dwunastościan zwykły .
Istnieją dwie formy enancjomorficzne (ta sama figura, ale o przeciwnej chiralności) tego złożonego wielościanu. Obie formy razem tworzą refleksyjny symetryczny związek dziesięciu czworościanów .
Ma gęstość większą niż 1.
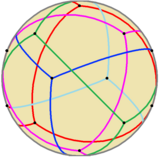 Jako dachówka sferyczna |
 Przezroczyste modele (animacja) |
 Pięć połączonych czworościanów |
Jako gwiazda
Można go również uzyskać przez stellację dwudziestościanu i jest podawany jako indeks modelu Wenningera 24 .
| Diagram stellacyjny | Rdzeń stellacyjny | Wypukły kadłub |
|---|---|---|

|
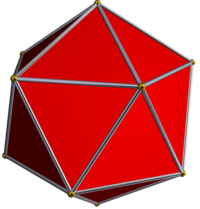 dwudziestościan |
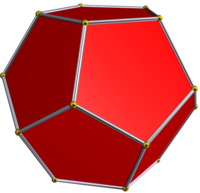 Dwunastościan |
Jako fasetowanie
Jest to fasetowanie dwunastościanu, jak pokazano po lewej stronie.
Teoria grup
Związek pięciu czworościanów jest geometryczną ilustracją pojęcia orbit i stabilizatorów w następujący sposób.
Grupą symetrii związku jest (rotacyjna) dwudziestościenna grupa I rzędu 60, natomiast stabilizatorem pojedynczego wybranego czworościanu jest (rotacyjna) tetraedryczna grupa T rzędu 12, a przestrzeń orbity I / T (rzędu 60/ 12 = 5) jest naturalnie utożsamiany z 5 czworościanami – odpowiada coset gT , któremu czworościan g wysyła wybrany czworościan.
Niezwykła podwójna właściwość
Ten związek jest niezwykły, ponieważ postać podwójna jest enancjomorfem oryginału. Jeśli twarze są skręcone w prawo, wierzchołki są skręcone w lewo. Kiedy dualizujemy , twarze ulegają dualizacji do wierzchołków skręconych w prawo, a wierzchołki do ścian skręconych w lewo, dając chiralny bliźniak. Figury z tą właściwością są niezwykle rzadkie.
Zobacz też
- Wenninger, Magnus (1974). Modele wielościanów . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-09859-9 .
- HSM Coxeter , Regularne Polytopes , (wydanie 3, 1973), wydanie Dover, ISBN 0-486-61480-8 , 3.6 Pięć regularnych związków , pp.47-50, 6.2 Stellating the Platonic solids , pp.96-104
- Coxetera, Harolda Scotta MacDonalda ; Du Val, P.; Flather, HT; Petrie, JF (1999). Pięćdziesiąt dziewięć dwudziestościanów (wyd. 3). Tarquin. ISBN 978-1-899618-32-3 . MR 0676126 . (1st Edn University of Toronto (1938))
Linki zewnętrzne
- Weisstein, Eric W. „5-związek czworościanu” . MathWorld .
- Metalowa rzeźba złożonego z pięciu czworościanów
- VRML : [1]
- Związki 5 i 10 czworościanów autorstwa Sándora Kabai, The Wolfram Demonstrations Project .
- Klitzing, Richard. „mieszanka 3D” .
| Godne uwagi stellacje dwudziestościanu | |||||||||
| Regularny | Jednolite dublety | Regularne związki | Zwykła gwiazda | Inni | |||||
| (Wypukły) dwudziestościan | Mały dwudziestościan triambiczny | Przyśrodkowy dwudziestościan triambiczny | Wielki dwudziestościan triambiczny | Związek pięciu ośmiościanów | Związek pięciu czworościanów | Związek dziesięciu czworościanów | Wielki dwudziestościan | Wykopany dwunastościan | Ostateczna stelacja |
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|
|

|

|

|

|

|

|

|

|

|
|
| Proces stellacji na dwudziestościanie tworzy szereg pokrewnych wielościanów i związków o symetrii dwudziestościanu . | |||||||||


