Charakterystyka Eulera
W matematyce , a dokładniej w topologii algebraicznej i kombinatoryce wielościennej , charakterystyka Eulera (lub liczba Eulera lub charakterystyka Eulera-Poincarégo ) jest niezmiennikiem topologicznym , liczbą opisującą kształt lub strukturę przestrzeni topologicznej niezależnie od sposobu, w jaki jest zgięty. Jest powszechnie oznaczany przez ( grecka litera ).
Charakterystyka Eulera została pierwotnie zdefiniowana dla wielościanów i używana do udowodnienia różnych twierdzeń na ich temat, w tym klasyfikacji brył platońskich . Zostało to stwierdzone dla brył platońskich w 1537 roku w niepublikowanym rękopisie Francesco Maurolico . Leonhard Euler , od którego nazwano to pojęcie, wprowadził je bardziej ogólnie dla wypukłych wielościanów, ale nie udało mu się rygorystycznie udowodnić, że jest to niezmiennik. We współczesnej matematyce charakterystyka Eulera wynika z homologii i, bardziej abstrakcyjnie, z algebry homologicznej .
Wielościany
Charakterystyka Eulera została klasycznie zdefiniowana dla powierzchni wielościanów według wzoru
gdzie V , E i F to odpowiednio liczby wierzchołków (rogów), krawędzi i ścian danego wielościanu. Każda wypukła powierzchnia wielościanu ma charakterystykę Eulera
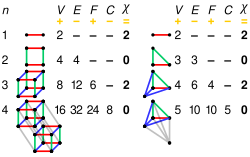
To równanie, podane przez Leonharda Eulera w 1758 roku, jest znane jako wzór wielościanu Eulera . Odpowiada charakterystyce Eulera kuli ( tj. χ = 2) i stosuje się identycznie do sferycznych wielościanów . Poniżej podano ilustrację wzoru na wszystkich wielościanach platońskich.
| Nazwa | Obraz |
Wierzchołki V |
Krawędzie E |
Twarze F |
Charakterystyka Eulera: V - E + F |
|---|---|---|---|---|---|
| Czworościan |

|
4 | 6 | 4 | 2 |
| Sześcian lub sześcian |

|
8 | 12 | 6 | 2 |
| Oktaedr |

|
6 | 12 | 8 | 2 |
| Dwunastościan |
|
20 | 30 | 12 | 2 |
| dwudziestościan |

|
12 | 30 | 20 | 2 |
Powierzchnie niewypukłych wielościanów mogą mieć różne cechy Eulera:
| Nazwa | Obraz |
Wierzchołki V |
Krawędzie E |
Twarze F |
Charakterystyka Eulera: V - E + F |
|---|---|---|---|---|---|
| czworościan |

|
6 | 12 | 7 | 1 |
| ośmiościan |

|
12 | 24 | 12 | 0 |
| Sześcian hemiośmiościan |

|
12 | 24 | 10 | −2 |
| Mały dwunastościan gwiaździsty |

|
12 | 30 | 12 | −6 |
| Wielki gwiaździsty dwunastościan |

|
20 | 30 | 12 | 2 |
W przypadku regularnych wielościanów Arthur Cayley wyprowadził zmodyfikowaną postać wzoru Eulera, używając gęstości D , gęstości figur wierzchołków d v i gęstości ścian: :
Ta wersja dotyczy zarówno wielościanów wypukłych (gdzie wszystkie gęstości wynoszą 1), jak i niewypukłych wielościanów Keplera – Poinsota .
wielościany rzutowe mają charakterystykę Eulera 1, podobnie jak rzeczywista płaszczyzna rzutowa , podczas gdy wszystkie powierzchnie wielościanów toroidalnych mają charakterystykę Eulera 0, podobnie jak torus .
Wykresy płaskie
Charakterystykę Eulera można zdefiniować dla grafów płaskich za pomocą tego samego co dla powierzchni wielościennych, gdzie to ścian na wykresie, w tym ściana
Charakterystyka Eulera dowolnego wykresu G połączonego z płaszczyzną wynosi 2. Można to łatwo udowodnić przez indukcję liczby ścian określonej przez G, zaczynając od drzewa jako przypadku podstawowego. W przypadku drzew mi i . Jeśli G ma składowe C (rozłączone wykresy), ten sam argument przez indukcję na F pokazuje, że . Jedna z nielicznych prac Cauchy'ego z teorii grafów również potwierdza ten wynik.
Za pomocą rzutu stereograficznego płaszczyzna odwzorowuje 2-kulę, tak że połączony wykres odwzorowuje wielokątny rozkład kuli, który ma charakterystykę Eulera 2. Ten punkt widzenia jest ukryty w dowodzie Cauchy'ego dotyczącym wzoru Eulera podanym poniżej.
Dowód wzoru Eulera
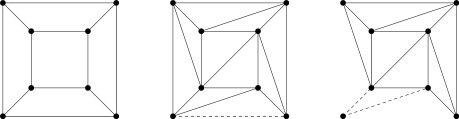
Istnieje wiele dowodów formuły Eulera. Jeden został podany przez Cauchy'ego w 1811 roku w następujący sposób. Ma zastosowanie do dowolnego wypukłego wielościanu, a bardziej ogólnie do dowolnego wielościanu, którego granica jest topologicznie równoważna kuli i którego ściany są topologicznie równoważne dyskom.
Usuń jedną ścianę powierzchni wielościennej. Odciągając krawędzie brakującej ściany od siebie, zdeformuj całą resztę w planarny wykres punktów i krzywych w taki sposób, aby obwód brakującej ściany znajdował się na zewnątrz, otaczając uzyskany wykres, jak ilustruje to pierwszy z trzech wykresów dla szczególnego przypadku sześcianu. (Umożliwia to założenie, że powierzchnia wielościenna jest na początku homeomorficzna z kulą). Po tej deformacji regularne ściany na ogół nie są już regularne. Liczba wierzchołków i krawędzi pozostała taka sama, ale liczba ścian została zmniejszona o 1. Dlatego udowodnienie wzoru Eulera dla wielościanu sprowadza się do udowodnienia V - E + F = 1 dla tego zdeformowanego, płaskiego obiektu.
Jeśli ściana ma więcej niż trzy boki, narysuj przekątną — to znaczy krzywą przechodzącą przez ścianę łączącą dwa wierzchołki, które nie są jeszcze połączone. Każda nowa przekątna dodaje jedną krawędź i jedną ścianę i nie zmienia liczby wierzchołków, więc nie zmienia wielkości V − E + F . (Tutaj potrzebne jest założenie, że wszystkie ściany są dyskami, aby pokazać za pomocą twierdzenia Jordana o krzywej , że ta operacja zwiększa liczbę ścian o jeden). Kontynuuj dodawanie krawędzi w ten sposób, aż wszystkie ściany będą trójkątne.
Zastosuj wielokrotnie jedną z następujących dwóch transformacji, zachowując niezmiennik, że granica zewnętrzna jest zawsze prostym cyklem :
- Usuń trójkąt, którego tylko jedna krawędź przylega do zewnątrz, jak pokazano na drugim wykresie. Zmniejsza to liczbę krawędzi i ścian o jedną i nie zmienia liczby wierzchołków, więc zachowuje V - E + F .
- Usuń trójkąt z dwiema krawędziami wspólnymi dla zewnętrznej części sieci, jak pokazano na trzecim wykresie. Każde usunięcie trójkąta usuwa wierzchołek, dwie krawędzie i jedną ścianę, więc zachowuje V − E + F .
Te przekształcenia ostatecznie redukują graf planarny do pojedynczego trójkąta. (Bez niezmiennika cyklu prostego usunięcie trójkąta może rozłączyć pozostałe trójkąty, unieważniając resztę argumentu. Poprawna kolejność usuwania jest podstawowym przykładem łuskania ) .
W tym momencie samotny trójkąt ma V = 3, E = 3 i F = 1, więc V - E + F = 1. Ponieważ każdy z dwóch powyższych etapów transformacji zachował tę wielkość, pokazaliśmy V - E + F = 1 dla zdeformowanego, płaskiego obiektu, co pokazuje V - E + F = 2 dla wielościanu. To dowodzi twierdzenia.
Dodatkowe dowody można znaleźć w artykule Dwadzieścia jeden dowodów formuły Eulera autorstwa Davida Eppsteina . Wiele dowodów, w tym ich wady i ograniczenia, zostało użytych jako przykłady w Dowodach i obaleniach autorstwa Imre Lakatosa .
Definicja topologiczna
Omówione powyżej powierzchnie wielościenne są, we współczesnym języku, dwuwymiarowymi skończonymi zespołami CW . (Gdy używane są tylko trójkątne ściany, są to dwuwymiarowe skończone uproszczone kompleksy ). Ogólnie rzecz biorąc, dla dowolnego skończonego zespołu CW, charakterystykę Eulera można zdefiniować jako sumę naprzemienną
gdzie k n oznacza liczbę komórek o wymiarze n w kompleksie.
Podobnie w przypadku kompleksu uproszczonego charakterystyka Eulera jest równa sumie przemiennej
gdzie k n oznacza liczbę n -simpleksów w kompleksie.
Alternatywa liczby Bettiego
Jeszcze bardziej ogólnie, dla dowolnej przestrzeni topologicznej , możemy zdefiniować n- tą liczbę Bettiego bn jako stopień n - tej osobliwej grupy homologii. Charakterystykę Eulera można zatem zdefiniować jako sumę naprzemienną
0 Ta wielkość jest dobrze zdefiniowana, jeśli wszystkie liczby Bettiego są skończone i jeśli są równe zeru poza pewnym indeksem n . W przypadku kompleksów uproszczonych nie jest to ta sama definicja, co w poprzednim akapicie, ale obliczenia homologii pokazują, że te dwie definicje dadzą tę samą wartość dla .
Nieruchomości
Charakterystyka Eulera zachowuje się dobrze w odniesieniu do wielu podstawowych operacji na przestrzeniach topologicznych, jak następuje.
Niezmienność homotopii
Homologia jest niezmiennikiem topologicznym, a ponadto niezmiennikiem homotopii : Dwie przestrzenie topologiczne, które są równoważne homotopii, mają izomorficzne grupy homologii. Wynika z tego, że charakterystyka Eulera jest również niezmiennikiem homotopii.
Na przykład każda kurczliwa przestrzeń (to znaczy jedna homotopia równoważna punktowi) ma trywialną homologię, co oznacza, że 0-ta liczba Bettiego wynosi 1, a pozostałe 0. Dlatego jej charakterystyka Eulera wynosi 1. Ten przypadek obejmuje przestrzeń euklidesową dowolnego wymiaru, a także solidna kula jednostkowa w dowolnej przestrzeni euklidesowej - jednowymiarowy przedział, dwuwymiarowy dysk, trójwymiarowa kula itp.
Dla innego przykładu, każdy wypukły wielościan jest homeomorficzny z trójwymiarową kulą , więc jego powierzchnia jest homeomorficzna (stąd homotopia równoważna) z dwuwymiarową kulą , która ma charakterystykę Eulera 2. To wyjaśnia, dlaczego wypukłe wielościany mają charakterystykę Eulera 2.
Zasada włączenia-wyłączenia
Jeśli M i N są dowolnymi dwiema przestrzeniami topologicznymi, to charakterystyka Eulera ich rozłącznego związku jest sumą ich charakterystyk Eulera, ponieważ homologia jest addytywna w przypadku związku rozłącznego:
Bardziej ogólnie, jeśli M i N są podprzestrzeniami większej przestrzeni X , to tak samo jest z ich sumą i przecięciem. W niektórych przypadkach charakterystyka Eulera jest zgodna z wersją zasady włączenia-wyłączenia :
Jest to prawdą w następujących przypadkach:
- jeśli M i N są parą wycinającą. W szczególności, jeśli wnętrza M i N wewnątrz związku nadal obejmują związek.
- jeśli X jest lokalnie zwartą przestrzenią i używa się charakterystyki Eulera ze zwartymi podporami , nie są potrzebne żadne założenia dotyczące M lub N.
- jeśli X jest przestrzenią warstwową , której wszystkie warstwy są parzyste, zasada włączenia-wyłączenia obowiązuje, jeśli M i N są sumą warstw. Dotyczy to w szczególności sytuacji, gdy M i N są podrozmaitymi złożonej rozmaitości algebraicznej .
Ogólnie rzecz biorąc, zasada włączania i wyłączania jest fałszywa. Kontrprzykład się przyjmując, że X jest linią rzeczywistą , M podzbiorem składającym się z jednego punktu, a N dopełnieniem M.
Łączna suma
połączonych zamkniętych n-rozmaitości nową połączoną pomocą połączonej operacji Charakterystyka Eulera jest powiązana wzorem
Właściwość produktu
Również charakterystyka Eulera dla dowolnej przestrzeni produktowej M × N jest
Z tych właściwości dodawania i mnożenia korzysta również liczność zbiorów . W ten sposób charakterystykę Eulera można postrzegać jako uogólnienie liczności; patrz [1] .
Zakrywanie przestrzeni
Podobnie, dla k -arkuszowej przestrzeni pokrywającej ma się }
Mówiąc bardziej ogólnie, dla rozgałęzionej przestrzeni pokrycia , charakterystykę Eulera pokrycia można obliczyć na podstawie powyższego, ze współczynnikiem korygującym dla punktów rozgałęzienia, co daje wzór Riemanna – Hurwitza .
Właściwość fibracji
Właściwość produktu odnosi się znacznie bardziej ogólnie do włókien z pewnymi warunkami.
Jeśli jest fibracją z włóknem F, z połączoną ścieżką podstawy B i fibracja jest zorientowana na polu K, to charakterystyka Eulera ze współczynnikami w pole K spełnia właściwość produktu:
Obejmuje to przestrzenie produktów i przestrzenie pokrywające jako przypadki szczególne i można to udowodnić za pomocą sekwencji widmowej Serre'a dotyczącej homologii fibracji.
w transferu - zauważ, że jest to podnoszenie i idzie „w złą stronę” - którego kompozycja z mapą projekcji to pomnożenie włókna przez klasę Eulera :
Przykłady
Powierzchnie
Charakterystykę Eulera można łatwo obliczyć dla ogólnych powierzchni, znajdując poligonizację powierzchni (to znaczy opis jako kompleks CW ) i stosując powyższe definicje.
| Nazwa | Obraz | χ |
|---|---|---|
| Interwał |

|
1 |
| Koło |

|
0 |
| Dysk |

|
1 |
| Kula |

|
2 |
|
Torus (Iloczyn dwóch kół) |

|
0 |
| Podwójny torus |

|
−2 |
| Potrójny torus |

|
−4 |
|
Prawdziwa płaszczyzna rzutowa |

|
1 |
| Butelka Kleina |
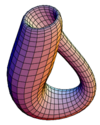
|
0 |
| z paskiem Möbiusa |
|
0 |
|
Dwie sfery (niepołączone) (Rozłączne połączenie dwóch sfer) |

|
2 + 2 = 4 |
|
Trzy sfery (niepołączone) (Rozłączne połączenie trzech sfer) |
  
|
2 + 2 + 2 = 6 |
|
kule (niepołączone) (Rozłączny związek kul n ) |
 . . . . . .
|
2 + ... + 2 = 2n |
Piłka nożna
Powszechne jest konstruowanie piłek nożnych przez zszywanie ze sobą pięciokątnych i sześciokątnych elementów, przy czym trzy elementy spotykają się w każdym wierzchołku (patrz na przykład Adidas Telstar ). Jeśli pięciokąty P i sześciokąty H , to mamy ściany F = P + H , V = (5 P + 6 H ) / 3 wierzchołki i E = (5 P + 6 H ) / 2 krawędzie. Charakterystyka Eulera jest taka
Ponieważ kula ma charakterystykę Eulera 2, wynika z tego, że P = 12. Oznacza to, że piłka nożna skonstruowana w ten sposób ma zawsze 12 pięciokątów. W zasadzie liczba sześciokątów jest nieograniczona. Wynik ten dotyczy fulerenów i wielościanów Goldberga .
Dowolne wymiary
|
Zwykły 4-politop |
0 V ( k ) |
mi ( k 1 ) |
fa ( k 2 ) |
do ( k 3 ) |
= V - mi + fa - do |
|---|---|---|---|---|---|
| 5-ogniwowy | 5 | 10 | 10 | 5 | 0 |
| 8-ogniwowy | 16 | 32 | 24 | 8 | 0 |
| 16-ogniwowy | 8 | 24 | 32 | 16 | 0 |
| 24-ogniwowy | 24 | 96 | 96 | 24 | 0 |
| 120 ogniw | 600 | 1200 | 720 | 120 | 0 |
| 600 ogniw | 120 | 720 | 1200 | 600 | 0 |
N - wymiarowa kula ma osobliwe grupy homologii równe
stąd ma liczbę Bettiego 1 w wymiarach 0 i n , a wszystkie inne liczby Bettiego to 0. Jego charakterystyka Eulera to wtedy 1 + (-1) n - to znaczy 0 lub 2.
N - wymiarowa rzeczywista przestrzeń rzutowa jest ilorazem n -sfery przez mapę antypodów . Wynika z tego, że jego charakterystyka Eulera jest dokładnie o połowę mniejsza od odpowiadającej jej kuli — albo 0, albo 1.
N - wymiarowy torus to przestrzeń iloczynu n okręgów. Jego charakterystyka Eulera wynosi 0, zgodnie z właściwością iloczynu. Mówiąc bardziej ogólnie, każda zwarta rozmaitość równoległa , w tym dowolna zwarta grupa Liego , ma charakterystykę Eulera 0.
Charakterystyka Eulera dowolnej zamkniętej rozmaitości nieparzystej również wynosi 0. Przypadek przykładów orientowalnych jest następstwem dualizmu Poincarégo . Właściwość ta odnosi się bardziej ogólnie do dowolnej zwartej przestrzeni warstwowej, której wszystkie warstwy mają nieparzysty wymiar. Dotyczy to również zamkniętych rozmaitości nieorientowalnych o nieparzystych wymiarach, poprzez orientowalną podwójną pokrywę dwa do jednego .
Relacje z innymi niezmiennikami
Charakterystykę Eulera zamkniętej powierzchni orientowanej można obliczyć z jej rodzaju g (liczba torusów w połączonym rozkładzie sumy powierzchni; intuicyjnie liczba „uchwytów”) jako
Charakterystykę Eulera zamkniętej nieorientowalnej powierzchni można obliczyć na podstawie jej nieorientowalnego rodzaju k (liczba rzeczywistych płaszczyzn rzutowych w połączonym rozkładzie sumy powierzchni) jako
Dla rozmaitości gładkich zamkniętych charakterystyka Eulera pokrywa się z liczbą Eulera , tj. klasą Eulera jej wiązki stycznej ocenianej na podstawowej klasie rozmaitości. Z kolei klasa Eulera odnosi się do wszystkich innych charakterystycznych klas wiązek wektorowych .
W przypadku zamkniętych rozmaitości riemannowskich charakterystykę Eulera można również znaleźć, całkując krzywiznę; patrz twierdzenie Gaussa – Bonneta dla przypadku dwuwymiarowego i uogólnione twierdzenie Gaussa – Bonneta dla przypadku ogólnego.
Dyskretnym analogiem twierdzenia Gaussa-Bonneta jest twierdzenie Kartezjusza , że „całkowity defekt” wielościanu mierzony w pełnych kołach jest cechą charakterystyczną wielościanu Eulera; patrz wada (geometria) .
Twierdzenie Hadwigera charakteryzuje charakterystykę Eulera jako unikalną ( aż do mnożenia przez skalar ) niezmienną translację, skończenie addytywną, niekoniecznie nieujemną funkcję zbioru zdefiniowaną na skończonych sumach zwartych zbiorów wypukłych w R n , która jest „jednorodna stopnia 0”.
Uogólnienia
Dla każdego kombinatorycznego kompleksu komórek definiuje się charakterystykę Eulera jako liczbę komórek 0 minus liczbę komórek 1 plus liczbę komórek 2 itd., jeśli ta naprzemienna suma jest skończona. W szczególności cechą Eulera zbioru skończonego jest po prostu jego liczność, a cechą Eulera grafu jest liczba wierzchołków minus liczba krawędzi.
Mówiąc bardziej ogólnie, można zdefiniować charakterystykę Eulera dowolnego kompleksu łańcuchowego jako naprzemienną sumę rzędów grup homologii kompleksu łańcuchowego, zakładając, że wszystkie te rzędy są skończone.
Wersja charakterystyki Eulera używana w geometrii algebraicznej jest następująca. Dla każdego spójnego snopka na odpowiednim schemacie definiuje się jego charakterystykę Eulera jako fa {
gdzie jest wymiarem i -tej grupy kohomologii snopów z . W tym przypadku wszystkie wymiary są skończone na mocy twierdzenia Grothendiecka o skończoności . Jest przykład charakterystyki Eulera dla kompleksu łańcuchowego, gdzie kompleks łańcuchowy jest skończoną rozdzielczością acykliczne snopy.
Inne uogólnienie koncepcji charakterystyki Eulera na rozmaitościach pochodzi z orbifoldów (patrz charakterystyka orbifoldu Eulera ). Podczas gdy każda rozmaitość ma całkowitą charakterystykę Eulera, orbifold może mieć ułamkową charakterystykę Eulera. Na przykład orbifold łezka ma charakterystykę Eulera 1 + 1/ p , gdzie p jest liczbą pierwszą odpowiadającą kątowi stożka 2 π / p .
Pojęcie Eulera charakterystyczne dla zredukowanej homologii ograniczonego skończonego zbioru jest kolejnym uogólnieniem, ważnym w kombinatoryce . Poset jest „ograniczony”, jeśli ma najmniejsze i największe elementy; nazwijmy je 0 i 1. Charakterystyka Eulera takiego posetu jest zdefiniowana jako liczba całkowita μ (0,1), gdzie μ jest funkcją Möbiusa w algebrze występowania tego posetu .
Można to dalej uogólnić, definiując charakterystykę Eulera o wartości Q dla pewnych skończonych kategorii , pojęcie zgodne z charakterystykami Eulera grafów, orbifoldów i pozycji wspomnianych powyżej. W tym ustawieniu charakterystyka Eulera skończonej grupy lub monoidu G wynosi 1/| G |, a charakterystyka Eulera skończonej grupoidy jest sumą 1/| G i |, gdzie wybraliśmy jedną reprezentatywną grupę G i dla każdego połączonego składnika groupoidy.
Zobacz też
- rachunek Eulera
- klasa Eulera
- Lista tematów nazwanych imieniem Leonharda Eulera
- Lista jednolitych wielościanów
Notatki
Bibliografia
- Richeson, David S .; Klejnot Eulera: formuła wielościanu i narodziny topologii . Princeton University Press 2008.
Dalsza lektura
- Flegg, H. Graham; Od geometrii do topologii , Dover 2001, s. 40.