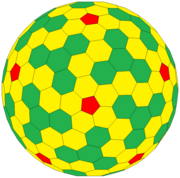
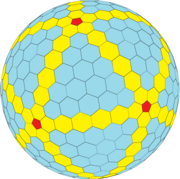
Wielościan Goldberga
W matematyce , a dokładniej w kombinatoryce wielościennej , wielościan Goldberga jest wypukłym wielościanem złożonym z sześciokątów i pięciokątów . Zostały one po raz pierwszy opisane w 1937 roku przez Michaela Goldberga (1902–1990). Są one zdefiniowane przez trzy właściwości: każda ściana jest albo pięciokątem, albo sześciokątem, dokładnie trzy ściany spotykają się w każdym wierzchołku i mają obrotową symetrię dwudziestościanu . Niekoniecznie są lustrzanie symetryczne ; np GP(5,3) i GP(3,5) są swoimi enancjomorfami . Wielościan Goldberga to podwójny wielościan sfery geodezyjnej .
Konsekwencją wzoru wielościanu Eulera jest to, że wielościan Goldberga ma zawsze dokładnie dwanaście pięciokątnych ścian. Dwudziestościan zapewnia, że pięciokąty są zawsze regularne i zawsze jest ich 12. Jeśli wierzchołki nie są ograniczone do kuli, wielościan można zbudować z płaskimi równobocznymi (ale nie na ogół równokątnymi) ścianami.
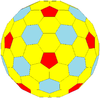
Proste przykłady wielościanów Goldberga obejmują dwunastościan i dwudziestościan ścięty . Inne formy można opisać, wykonując skoczka szachowego od jednego pięciokąta do drugiego: najpierw wykonaj m kroków w jednym kierunku, następnie skręć o 60° w lewo i wykonaj n kroków. Taki wielościan jest oznaczany jako GP( m , n ). Dwunastościan to GP(1,0) , a dwudziestościan ścięty to GP(1,1).
Podobną technikę można zastosować do konstruowania wielościanów o symetrii czworościennej i symetrii ośmiościennej . Te wielościany będą miały raczej trójkąty lub kwadraty niż pięciokąty. Odmianom tym podano rzymskie indeksy dolne oznaczające liczbę boków na niesześciokątnych ścianach: GP III ( n , m ), GP IV ( n , m ) i GP V ( n , m ).
Elementy
Liczbę wierzchołków, krawędzi i ścian GP ( m , n ) można obliczyć z m i n , gdzie T = m 2 + mn + n 2 = ( m + n ) 2 − mn , w zależności od jednej z trzech symetrii systemy: Liczbę niesześciokątnych ścian można określić za pomocą charakterystyki Eulera, jak pokazano tutaj .
| Symetria | dwudziestościenny | ośmiościenny | czworościenny |
|---|---|---|---|
| Baza |
Dwunastościan GP V (1,0) = {5+,3} 1,0 |
Sześcian GP IV (1,0) = {4+,3} 1,0 |
Czworościan GP III (1,0) = {3+,3} 1,0 |
| Obraz |

|

|

|
| Symbol | GP V ( m , n ) = {5+,3} m , n | GP IV ( m , n ) = {4+,3} m , n | GP III ( m , n ) = {3+,3} m , n |
| Wierzchołki | |||
| Krawędzie | |||
| Twarze | |||
| Twarze według typu | 12 {5} i 10 ( T - 1) {6} | 6 {4} i 4 ( T - 1) {6} | 4 {3} i 2 ( T - 1) {6} |
Budowa
Większość wielościanów Goldberga można skonstruować przy użyciu notacji wielościanów Conwaya, zaczynając od nasion (T) etraedru, (C) ube i (D) dwudziestościanu. Operator fazowania , c , zastępuje wszystkie krawędzie sześciokątami, przekształcając GP ( m , n ) w GP (2 m ,2 n ), z mnożnikiem T równym 4. Obcięty operator kis , y = tk , generuje GP (3, 0), transformacja GP ( m , n ) do GP (3 m ,3 n ), z mnożnikiem T równym 9.
W przypadku formularzy klasy 2 podwójny operator kis , z = dk , przekształca GP ( a , 0) w GP ( a , a ), z mnożnikiem T równym 3. W przypadku formularzy klasy 3 operator wirowania w generuje GP ( 2,1), z mnożnikiem T równym 7. Generator wiru zgodny z ruchem wskazówek zegara i przeciwnie do ruchu wskazówek zegara, w w = wrw generuje GP (7,0) w klasie 1. Generalnie wir może przekształcić GP( a , b ) w GP( a + 3 b ,2 ab ) dla a > b i tego samego kierunku chiralności. Jeśli kierunki chiralne są odwrócone, GP( a , b ) staje się GP(2 a + 3 b , a - 2 b ) jeśli a ≥ 2 b , a GP(3 a + b ,2 b - a ) jeśli za < 2 b .
Przykłady
| Częstotliwość | (1,0) | (2,0) | (3,0) | (4,0) | (5,0) | (6,0) | (7,0) | (8,0) | ( m , 0) |
|---|---|---|---|---|---|---|---|---|---|
| T | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | m 2 |
| Dwudziestościan (Goldberg) |
 regularny dwunastościan |
 dwunastościan ścięty |
|

|
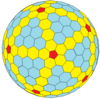
|
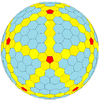
|
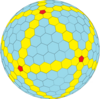
|
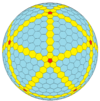
|
więcej |
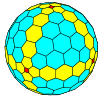
| ośmiościenny |
 sześcian |
 sfazowany sześcian |

|
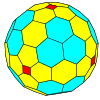
|

|
|

|

|
więcej |
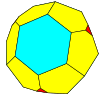
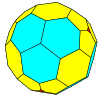
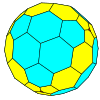
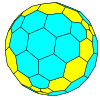
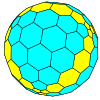
| czworościenny |
 czworościan |
 sfazowany czworościan |
|
|
|
|
|

|
więcej |
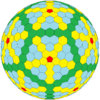
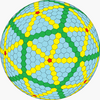
| Częstotliwość | (1,1) | (2,2) | (3,3) | (4,4) | (5,5) | (6,6) | (7,7) | (8,8) | ( m , m ) |
|---|---|---|---|---|---|---|---|---|---|
| T | 3 | 12 | 27 | 48 | 75 | 108 | 147 | 192 | 3m2 _ _ |
| Dwudziestościan (Goldberg) |
 dwudziestościan ścięty |

|

|
|

|
|

|

|
więcej |
| ośmiościenny |
 ścięty ośmiościan |

|

|
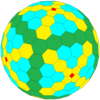
|

|
więcej | |||
| czworościenny |
 ścięty czworościan |
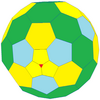
|
więcej |
| Częstotliwość | (1,2) | (1,3) | (2,3) | (1,4) | (2,4) | (3,4) | (5,1) | ( m , n ) |
|---|---|---|---|---|---|---|---|---|
| T | 7 | 13 | 19 | 21 | 28 | 37 | 31 | m 2 + mn + n 2 |
| Dwudziestościan (Goldberg) |
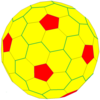
|
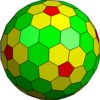
|

|

|
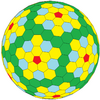
|

|

|
więcej |
| ośmiościenny |
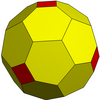
|
więcej | ||||||
| czworościenny |
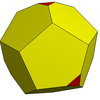
|
więcej |
Zobacz też
- Kapsyd
- Sfera geodezyjna
- Fullerene#Inne buckyballs
- Notacja wielościanów Conwaya
- Konstrukcja Goldberga-Coxetera
Notatki
- Goldberg, Michael (1937). „Klasa multi-symetrycznych wielościanów” . Dziennik matematyczny Tohoku . 43 : 104–108.
- Joseph D. Clinton, Hipoteza Clintona o równym kącie środkowym
- Hart, George (2012). „Wielościany Goldberga”. W Senechal, Marjorie (red.). Kształtowanie przestrzeni (wyd. 2). Skoczek. s. 125–138. doi : 10.1007/978-0-387-92714-5_9 . ISBN 978-0-387-92713-8 . [1]
- Hart, George (18 czerwca 2013). „Impresje matematyczne: wielościany Goldberga” . Wiadomości naukowe Simonsa.
- Schein, S.; Wesoły, JM (2014-02-25). „Czwarta klasa wypukłych wielościanów równobocznych o symetrii wielościanów związanych z fulerenami i wirusami” . Obrady Narodowej Akademii Nauk . 111 (8): 2920–2925. Bibcode : 2014PNAS..111.2920S . doi : 10.1073/pnas.1310939111 . ISSN 0027-8424 . PMC 3939887 . PMID 24516137 .
Linki zewnętrzne
- Podwójny dwudziestościan geodezyjny
- Wariacje Goldberga: Nowe kształty klatek molekularnych Płaskie sześciokąty i pięciokąty łączą się w nowej odsłonie starego wielościanu, autor: Dana Mackenzie, 14 lutego 2014 r.