Symetria ośmiościenna

Wybrane grupy punktów w trzech wymiarach
Grupa wielościenna , [n,3], (*n32)
Symetria inwolucyjna C _s , (*) [ ] =	Symetria cykliczna C _nv , (*nn) [n] =	Symetria dwuścienna D _nh , (*n22) [n,2] =
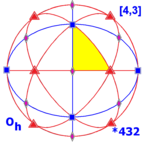
Symetria czworościenna T _d , (*332) [3,3] =	Symetria ośmiościenna O _h , (*432) [4,3] =	Symetria dwudziestościenna I _h , (*532) [5,3] =

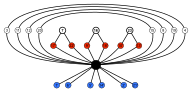
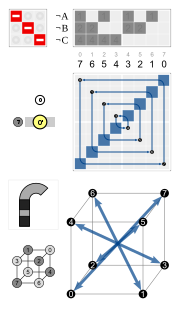
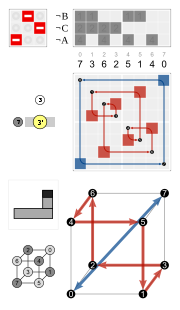
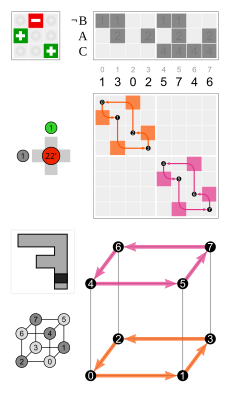
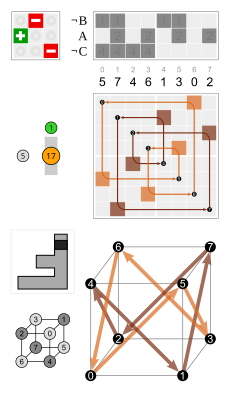
Wykres cyklu Cztery sześciokątne cykle mają wspólną inwersję (czarny węzeł na górze). Sześciokąty są symetryczne, więc np. 3 i 4 są w tym samym cyklu.

Regularny ośmiościan ma 24 symetrie obrotowe (lub zachowujące orientację) i łącznie 48 symetrii. Należą do nich przekształcenia łączące odbicie i obrót. Sześcian ma ten sam zestaw symetrii, ponieważ to wielościan jest podwójny z ośmiościanem.

Grupą symetrii zachowujących orientację jest S ₄ , grupa symetryczna lub grupa permutacji czterech obiektów, ponieważ istnieje dokładnie jedna taka symetria dla każdej permutacji czterech przekątnych sześcianu.

Detale

Chiralna i pełna (lub achiralna ) symetria oktaedryczna to dyskretne symetrie punktowe (lub równoważnie symetrie na kuli ) z największymi grupami symetrii zgodnymi z symetrią translacyjną . Należą do krystalograficznych grup punktowych sześciennego układu kryształów .

Klasy koniugacji
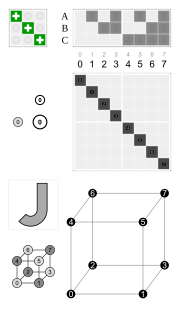
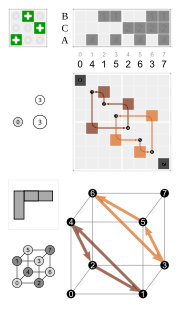
Elementy O		Inwersje elementów O
tożsamość	0	inwersja	0'
3 × obrót o 180° wokół 4-krotnej osi	7, 16, 23	3 × odbicie w płaszczyźnie prostopadłej do 4-krotnej osi	7', 16', 23'
8 × obrót o 120° wokół 3-krotnej osi	3, 4, 8, 11, 12, 15, 19, 20	8 × odbicie obrotowe o 60°	3', 4', 8', 11', 12', 15', 19', 20'
6 × obrót o 180° wokół dwukrotnej osi	1', 2', 5', 6', 14', 21'	6 × odbicie w płaszczyźnie prostopadłej do dwukrotnej osi	1, 2, 5, 6, 14, 21
6 × obrót o 90° wokół 4-krotnej osi	9', 10', 13', 17', 18', 22'	6 × odbicie obrotowe o 90°	9, 10, 13, 17, 18, 22

Przykłady
${\ Displaystyle (0,0) = 0}$	${\ Displaystyle (3,0) = 7}$	${\ Displaystyle (0,3) = 3}$	${\ Displaystyle (7,1) = 1'}$	${\ Displaystyle (4,5) = 9'}$
${\ Displaystyle (7,0) = 0'}$	${\ Displaystyle (4,0) = 7'}$	${\ Displaystyle (7,3) = 3'}$	${\ Displaystyle (0,1) = 1}$	${\ Displaystyle (3,5) = 9}$
Pełną listę można znaleźć w artykule na Wikiwersytecie .

Jako grupa $_ \rtimes S_ {3}}$ pełna produktem , a naturalnym sposobem identyfikacji jego elementów jest tworzenie par ${\ Displaystyle (m, n)}$ z ${\ Displaystyle m \ in [0, 2^{3})}$
i ${\ Displaystyle n \ w [0,3!)}$ . $4$ ponieważ jest to również można prostu zidentyfikować elementy podgrupy ${\ Displaystyle a \ in [0,4!)}$ T _d jako i ich inwersje jako ${\ displaystyle a'}$ .

$,$ tożsamość jest reprezentowana jako ${\ Displaystyle 0}$ inwersja ${\ Displaystyle (7,0)}$ ′ $\ Displaystyle 0'}$ . ${\ Displaystyle (3,1)}$ jest reprezentowany jako ${\ Displaystyle 6}$ i ${\ Displaystyle (4,1)}$ jako ${\ Displaystyle 6 '}$ .

Rotorodbicie to połączenie obrotu i odbicia .

Ilustracja odbicia obrotowego
odbicie ${\ Displaystyle 7'}$ zastosowany przy obrocie o 120 ° ${\ displaystyle 4}$ daje 60 ° rotoreflection ${\ displaystyle 8'}$ . ${\ Displaystyle 7 '\ cyrk 4 = 8'}$
odbicie ${\ Displaystyle 7'}$ zastosowany przy obrocie o 90 ° ${\ Displaystyle 22'}$ daje 90 ° rotoreflection ${\ displaystyle 17}$ . ${\ Displaystyle 7 '\ circ 22' = 17}$

Chiralna symetria oktaedryczna

Osie obrotu
C ₄	C ₃	C ₂
3	4	6

O , 432 lub [4,3] ⁺ rzędu 24 jest chiralną symetrią oktaedryczną lub rotacyjną symetrią oktaedryczną . Ta grupa jest podobna do chiralnej symetrii czworościennej T , ale osie C ₂ są teraz osiami C ₄ , a dodatkowo jest 6 osi C ₂ przechodzących przez środki krawędzi sześcianu. Td _grupie i O _są izomorficzne jako grupy abstrakcyjne: obie odpowiadają S4 , symetrycznej na 4 obiektach. T _d jest sumą T i zbioru otrzymanego przez połączenie każdego elementu O \ T z inwersją. O jest grupą rotacji sześcianu i ośmiościanu foremnego .

Chiralna symetria oktaedryczna
Projekcja ortogonalna	Projekcja stereograficzna
2-krotnie	4-krotnie	3-krotnie	2-krotnie

Pełna symetria oktaedryczna

O _h , *432 , [4,3] lub m3m rzędu 48 - achiralna symetria oktaedryczna lub pełna symetria oktaedryczna . Ta Td _grupa Th _ma takie same osie obrotu jak O , ale z płaszczyznami lustrzanymi, obejmującymi obie płaszczyzny lustrzane i . Ta grupa jest izomorficzna _z S4 . C ₂ , i jest pełną grupą symetrii sześcianu i ośmiościanu . Jest to grupa hiperoktaedryczna dla n = 3. Zobacz także izometrie sześcianu .

Związek sześcianu i ośmiościanu

Każda ściana dwunastościanu disdyakis jest podstawową domeną.

Grupa oktaedryczna O _h z domeną podstawową

Przy 4-krotnych osiach jako osiach współrzędnych podstawowa dziedzina O _h jest dana przez 0 ≤ x ≤ y ≤ z . Obiekt o tej symetrii charakteryzuje się częścią przedmiotu w dziedzinie podstawowej, na przykład sześcian jest dany przez z = 1, a ośmiościan przez x + y + z = 1 (lub odpowiednie nierówności, aby uzyskać bryłę zamiast powierzchni). topór + przez + cz = 1 daje wielościan o 48 ścianach, np. dwunastościan disdyakis.

0 Ściany są 8 na 8 połączone w większe ściany dla a = b = (sześcian) i 6 na 6 dla a = b = c (ośmiościan).

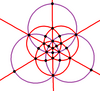
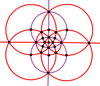
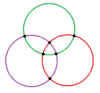
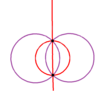
9 lustrzanych linii pełnej symetrii ośmiościennej można podzielić na dwie podgrupy 3 i 6 (narysowane na fioletowo i czerwono), reprezentujące dwie ortogonalne podsymetrie: D _2h i T _d . Symetrię D _2h można podwoić do D _4h , przywracając 2 zwierciadła z jednej z trzech orientacji.

Symetria ośmiościenna i podgrupy refleksyjne

Projekcja ortograficzna	Projekcja stereograficzna
Projekcja ortograficzna	4-krotnie	3-krotnie	2-krotnie


O _h , [4,3], , pełna symetria oktaedryczna (3+6 zwierciadeł)
T _d , [3,3]=[1 ⁺ ,4,3], = , podgrupa tetraedryczna (6 zwierciadeł)
C _3v , [3 ], , podgrupa dwuścienna (3 lustra)

Projekcja ortograficzna	Projekcja stereograficzna
Projekcja ortograficzna	4-krotnie	3-krotnie	2-krotnie


D _4h , [4,2], podgrupa dwuścienna (1+2+2 zwierciadła)
D _2h , [2,2]=[4,3*], = podgrupa dwuścienna (1+1+1 zwierciadła)
C _4v , [ 4], , podgrupa dwuścienna (2+2 lustra)

Macierze rotacji

Weź zestaw wszystkich macierzy permutacji 3 × 3 i przypisz znak + lub − do każdej z trzech jedynek. Jest $}$ $oktaedryczną$ permutacje i kombinacje znaków dla łącznie 48 macierzy, co daje pełną grupę 24 z tych macierzy ma wyznacznik +1; są to macierze rotacji chiralnej grupy oktaedrycznej. Pozostałe 24 macierze mają wyznacznik -1 i odpowiadają odbiciu lub odwróceniu.

Do symetrii oktaedrycznej potrzebne są trzy refleksyjne matryce generatora, które reprezentują trzy lustra diagramu Coxetera-Dynkina . Produkt odbić wytwarza 3 generatory rotacyjne.

[4,3],
	Refleksje			Rotacje			Rotorefleksja
Generatory	R₀	R ₁	R2 _{_}	₀ R R ₁	R ₁ R ₂	₀ R R ₂	₀ R R ₁ R ₂
Grupa
Zamówienie	2	2	2	4	3	2	6
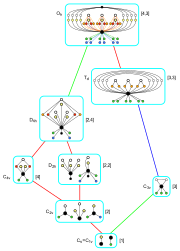
Matryca	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 1 i 0 i 0 \\ 0 i 1 i 0 \\ 0 i 0 i -1 \\\ koniec {mała macierz}} \ prawo]}$	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 1 i 0 i 0 \\ 0 i 0 i 1 \\ 0 i 1 i 0 \\\ koniec {mała macierz}} \ w prawo]}$	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 0 i 1 i 0 \\ 1 i 0 i 0 \\ 0 i 0 i 1 \\\ koniec {mała macierz}} \ prawo]}$	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 1 i 0 i 0 \\ 0 i 0 i 1 \\ 0 i -1 i 0 \\\ koniec {mała macierz}} \ w prawo]}$	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 0 i 1 i 0 \\ 0 i 0 i 1 \\ 1 i 0 i 0 \\\ koniec {mała macierz}} \ prawo]}$	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 0 i 1 i 0 \\ 1 i 0 i 0 \\ 0 i 0 i -1 \\\ koniec {mała macierz}} \ prawo]}$	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 0 i 1 i 0 \\ 0 i 0 i 1 \\ -1 i 0 i 0 \\\ koniec {mała macierz}} \ prawo]}$

Podgrupy o pełnej symetrii oktaedrycznej

O

T _d

T _godz

Wykresy cykli podgrup rzędu 24

Podgrupy uporządkowane na diagramie Hassego

Podgrupy rotacyjne

Podgrupy refleksyjne

Podgrupy zawierające inwersję

Schoe.	Coxeter	Kula.	HM	Struktura	Zamówienie	Indeks
O _godz	[4,3]	*432	m 3 m	S ₄ × S ₂	48	1
T _d	[3,3]	*332	4 3m	S ₄	24	2
D _{4 godz}	[2,4]	*224	4/mm	re ₂ × re ₈	16	3
D _{2 godz}	[2,2]	*222	mmm	re ₂³ = re ₂ × re ₄	8	6
C _4v	[4]	*44	4 mm	8 _{_}	8	6
C _3v	[3]	*33	3m	re ₆ = S ₃	6	8
C _2v	[2]	*22	mm2	re ₂² = re ₄	4	12
C _s = C _{1 v}	[ ]	*	2 lub m	D2 _{_}	2	24
T _godz	[3 ⁺ ,4]	3*2	m 3	A ₄ × S ₂	24	2
C _{4 godz}	[4 ⁺ ,2]	4*	4/m	Z ₄ × D ₂	8	6
D _3d	[2 ⁺ ,6]	2*3	3 m	re ₁₂ = Z ₂ × re ₆	12	4
D _2d	[2 ⁺ ,4]	2*2	4 2m	8 _{_}	8	6
do _2h = re _1d	[2 ⁺ ,2]	2*	2/m	Z ₂ × D ₂	4	12
S ₆	[2 ⁺ ,6 ⁺ ]	3×	3	Z ₆ = Z ₂ × Z ₃	6	8
S ₄	[2 ⁺ ,4 ⁺ ]	2×	4	Z ₄	4	12
S ₂	[2 ⁺ ,2 ⁺ ]	×	1	S ₂	2	24
O	[4,3] ⁺	432	432	S ₄	24	2
T	[3,3] ⁺	332	23	4 _{_}	12	4
D ₄	[2,4] ⁺	224	422	8 _{_}	8	6
D3 _{_}	[2,3] ⁺	223	322	re ₆ = S ₃	6	8
D2 _{_}	[2,2] ⁺	222	222	re ₄ = Z ₂²	4	12
C ₄	[4] ⁺	44	4	Z ₄	4	12
C ₃	[3] ⁺	33	3	Z ₃ = A ₃	3	16
C ₂	[2] ⁺	22	2	Z ₂	2	24
C ₁	[ ] ⁺	11	1	Z ₁	1	48

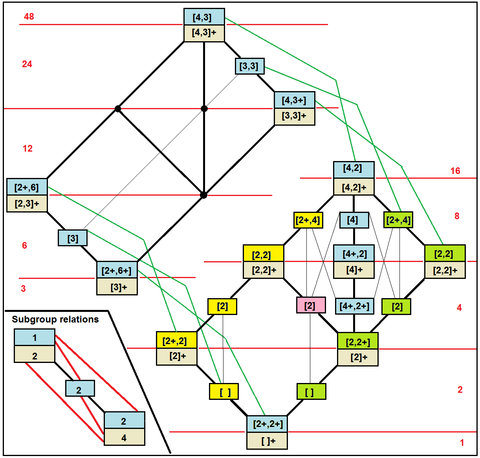
Podgrupy oktaedryczne w notacji Coxetera

Izometrie sześcianu

48 elementów symetrii sześcianu

Sześcian ma 48 izometrii (elementów symetrii), tworzących grupę symetrii O _h , izomorficzną z S ₄ × Z ₂ . Można je sklasyfikować w następujący sposób:

O (tożsamość i 23 właściwe obroty) z następującymi klasami koniugacji (w nawiasach podano permutacje przekątnych ciała i reprezentację kwaternionów jednostkowych ):
- tożsamość (tożsamość; 1)
- obrót wokół osi od środka ściany do środka przeciwległej ściany o kąt 90°: 3 osie, po 2 na oś, razem 6 ((1 2 3 4) itd.; ((1 ± i ) / √ 2 , itd.)
- j.w. o kąt 180°: 3 osie, po 1 na oś, razem 3 ((1 2) (3 4) itd.; i , j , k )
- obrót wokół osi od środka krawędzi do środka przeciwległej krawędzi o kąt 180°: 6 osi, po 1 na oś, razem 6 ((1 2) itd.; (( i ± j ) / √ 2 itd.)
- obrót wokół ciała po przekątnej o kąt 120°: 4 osie, po 2 na oś, razem 8 ((1 2 3) itd.; (1 ± i ± j ± k )/2)
To samo z inwersją ( x jest odwzorowane na − x ) (również 24 izometrie). Zauważ, że obrót o kąt 180° wokół osi połączony z odwróceniem jest po prostu odbiciem w płaszczyźnie prostopadłej. Połączenie odwrócenia i obrotu wokół przekątnej ciała o kąt 120° to obrót wokół przekątnej ciała o kąt 60° połączony z odbiciem w płaszczyźnie prostopadłej (sam obrót nie odwzorowuje sześcianu na siebie; przecięcie płaszczyzny odbicia z sześcianem to sześciokąt foremny ) .

Izometrię sześcianu można zidentyfikować na różne sposoby:

przez ściany odwzorowywane są trzy podane sąsiednie ściany (powiedzmy 1, 2 i 3 na kostce).
przez obraz sześcianu z niesymetrycznym oznaczeniem na jednej ścianie: ściana z oznaczeniem, czy jest to normalna, czy lustrzane odbicie, oraz orientacja
przez permutację czterech przekątnych ciała (każda z 24 permutacji jest możliwa), połączoną z przełącznikiem do odwrócenia sześcianu lub nie

W przypadku kostek z kolorami lub oznaczeniami (jak kostka do gry), grupa symetrii jest podgrupą O _h .

Przykłady:

C _{4 v} , [4], (*422): jeśli jedna ściana ma inny kolor (lub dwie przeciwległe ściany mają kolory różne od siebie i od pozostałych czterech), sześcian ma 8 izometrii, tak jak kwadrat ma w 2D .
D _{2 h} , [2,2], (*222): jeśli przeciwległe ściany mają te same kolory, różne dla każdego zestawu dwóch, sześcian ma 8 izometrii, podobnie jak prostopadłościan .
D _{4 h} , [4,2], (*422): jeśli dwie przeciwległe ściany mają ten sam kolor, a wszystkie pozostałe ściany mają inny kolor, sześcian ma 16 izometrii, podobnie jak graniastosłup kwadratowy .
C _{2 v} , [2], (*22):
- jeśli dwie sąsiednie ściany mają ten sam kolor, a wszystkie pozostałe ściany mają inny kolor, sześcian ma 4 izometrie.
- jeśli trzy ściany, z których dwie przeciwne do siebie, mają jeden kolor, a pozostałe trzy inny kolor, to sześcian ma 4 izometrie.
- jeśli dwie przeciwległe ściany mają ten sam kolor i dwie inne przeciwległe ściany również, a dwie ostatnie mają różne kolory, sześcian ma 4 izometrie, jak kartka czystego papieru o kształcie o lustrzanej symetrii.
Cs , [ _] , (*):
- jeśli dwie sąsiednie ściany mają różne kolory, a pozostałe cztery mają trzeci kolor, sześcian ma 2 izometrie.
- jeśli dwie przeciwległe ściany mają ten sam kolor, a wszystkie pozostałe ściany mają różne kolory, sześcian ma 2 izometrie, jak asymetryczna kartka czystego papieru.
C _{3 v} , [3], (*33): jeśli trzy ściany, z których żadna nie jest naprzeciwko siebie, mają jeden kolor, a pozostałe trzy inny kolor, to sześcian ma 6 izometrii.

W przypadku niektórych większych podgrup sześcian z tą grupą jako grupą symetrii nie jest możliwy, wystarczy pokolorować całe ściany. Trzeba narysować jakiś wzór na twarzach.

Przykłady:

D _{2 d} , [2 ⁺ ,4], (2*2): jeśli jedna ściana ma odcinek dzielący ścianę na dwa równe prostokąty, a przeciwna ma taki sam odcinek w kierunku prostopadłym, to sześcian ma 8 izometrii; istnieje płaszczyzna symetrii i 2-krotna symetria obrotowa z osią leżącą pod kątem 45° do tej płaszczyzny, w wyniku czego jest jeszcze jedna płaszczyzna symetrii prostopadła do pierwszej i kolejna oś 2-krotnej symetrii obrotowej prostopadle do pierwszego.
T _h , [3 ⁺ ,4], (3*2): jeśli każda ściana ma odcinek dzielący ścianę na dwa równe prostokąty, tak że odcinki sąsiednich ścian nie stykają się na krawędzi, sześcian ma 24 izometrie: parzyste permutacje przekątnych ciała i to samo w połączeniu z inwersją ( x jest odwzorowane na − x ).
T _d , [3,3], (*332): jeśli sześcian składa się z ośmiu mniejszych sześcianów, czterech białych i czterech czarnych, ułożonych naprzemiennie we wszystkich trzech standardowych kierunkach, sześcian ma ponownie 24 izometrie: tym razem parzyste permutacje przekątnych ciała i odwrotności innych obrotów właściwych.
T , [3,3] ⁺ , (332): jeśli każda ściana ma ten sam wzór z 2-krotną symetrią obrotową, powiedzmy literę S, tak że na wszystkich krawędziach wierzchołek jednej S styka się z bokiem drugiej S, sześcian ma 12 izometrii: parzyste permutacje przekątnych ciała.

Pełna symetria sześcianu, O _h , [4,3], (*432), jest zachowana wtedy i tylko wtedy, gdy wszystkie ściany mają taki sam wzór, że zachowana jest pełna symetria kwadratu , przy czym dla kwadratu symetria grupa, Dih ₄ , [4], rzędu 8.

Pełna symetria sześcianu przy odpowiednich obrotach O , [4,3] ⁺ , (432) jest zachowana wtedy i tylko wtedy, gdy wszystkie ściany mają ten sam wzór z 4-krotną symetrią obrotową Z ₄ , [4] ⁺ .

Symetria ośmiościenna powierzchni Bolza

W teorii powierzchni Riemanna powierzchnia Bolza , czasami nazywana krzywą Bolzy, jest otrzymywana jako rozgałęzione podwójne pokrycie sfery Riemanna, z locus rozgałęzienia w zbiorze wierzchołków ośmiościanu foremnego wpisanego. Jej grupa automorfizmów obejmuje hipereliptyczną inwolucję, która odwraca dwie strony okładki. Iloraz podgrupy rzędu 2 wygenerowany przez inwolucję hipereliptyczną daje dokładnie grupę symetrii ośmiościanu. Wśród wielu niezwykłych właściwości powierzchni Bolza jest fakt, że maksymalizuje skurcz wśród wszystkich powierzchni hiperbolicznych rodzaju 2.

Ciała stałe o symetrii chiralnej oktaedrycznej

Klasa	Nazwa	Zdjęcie	Twarze	Krawędzie	Wierzchołki	Podwójna nazwa	Zdjęcie
Bryła Archimedesa ( bryła katalońska )	sześcian zadarty		38	60	24	pięciokątny icositetrahedron

Ciała stałe o pełnej symetrii oktaedrycznej

Klasa	Nazwa	Twarze	Krawędzie	Wierzchołki	Podwójna nazwa
Bryła platońska	Sześcian	6	12	8	Oktaedr
Bryła Archimedesa (podwójna bryła katalońska )	sześcienny ośmiościan	14	24	12	dwunastościan rombowy
	Ścięty sześcian	14	36	24	Ośmiościan triakisa
	Ścięty ośmiościan	14	36	24	Sześcian Tetrakisa
	ośmiościan rombowy	26	48	24	Icositetrahedron naramienny
	Ścięty ośmiościan sześcienny	26	72	48	Disdyakis dwunastościan
Regularny wielościan złożony	Stella ośmiornica	8	12	8	Samopodwójny
Regularny wielościan złożony	Sześcian i ośmiościan	14	24	14	Samopodwójny

Zobacz też

Symetria czworościenna
Dwudziestościenna symetria
Binarna grupa oktaedryczna
Grupa hiperoktaedryczna
Materiały do nauki związane z pełną grupą oktaedryczną na Wikiwersytecie

Peter R. Cromwell, Wielościany (1997), s. 295
Symetrie rzeczy 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5
Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
NW Johnson : Geometries and Transformations , (2018) ISBN 978-1-107-10340-5 Rozdział 11: Skończone grupy symetrii , 11,5 Sferyczne grupy Coxetera

Linki zewnętrzne

Weisstein, Eric W. „Grupa oktaedryczna” . MathWorld .
Groupprops: Bezpośredni produkt S4 i Z2