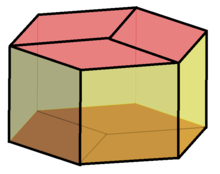
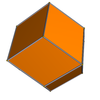
dwunastościan rombowy
| Rombowy dwunastościan | |
|---|---|
 (kliknij tutaj, aby zobaczyć obrotowy model) |
|
| Typ | solidny kataloński |
| Diagram Coxetera |
   
|
| Notacja Conwaya | jC |
| Typ twarzy | Romb V3.4.3.4  |
| Twarze | 12 |
| Krawędzie | 24 |
| Wierzchołki | 14 |
| Wierzchołki według typu | 8{3}+6{4} |
| Grupa symetrii | O h , B3 , [4,3], (*432) |
| Grupa rotacyjna | O, [4,3] + , (432) |
| Kąt dwuścienny | 120° |
| Nieruchomości | wypukły, przechodni izoedryczny , izotoksalny , równoległoboczny |
 Sześcienny ośmiościan ( podwójny wielościan ) |
 Internet |
W geometrii rombowy dwunastościan jest wypukłym wielościanem z 12 przystającymi rombowymi ścianami . Ma 24 krawędzie i 14 wierzchołków 2 typów. Jest to katalońska bryła i podwójny wielościan ośmiościanu sześciennego .
Nieruchomości
Dwunastościan rombowy to zonohedron . Jego wielościan dualny to ośmiościan sześcienny . Długa przekątna ściany jest dokładnie √ 2 razy większa od długości przekątnej krótszej ściany; tak więc ostre na każdej ścianie mierzą arccos ( 1 / 3 ), czyli około 70,53 °.
będący dwoistym wielościanem Archimedesa , jest przechodni względem ścian , co oznacza, że grupa symetrii bryły działa przechodnie na jej zbiór ścian. W kategoriach elementarnych oznacza to, że dla dowolnych dwóch ścian A i B istnieje obrót lub odbicie bryły, które pozostawia ją zajmującą ten sam obszar przestrzeni podczas przesuwania ściany A do ściany B.
Dwunastościan rombowy można postrzegać jako wypukły kadłub połączenia wierzchołków sześcianu i ośmiościanu. 6 wierzchołków, w których spotykają się 4 romby, odpowiada wierzchołkom ośmiościanu , podczas gdy 8 wierzchołków, w których stykają się 3 romby, odpowiada wierzchołkom sześcianu .
Dwunastościan rombowy jest jednym z dziewięciu wypukłych wielościanów przechodnich przechodnich , pozostałe to pięć brył platońskich , ośmiościan sześcienny , dwudziestościan rombowy i triakontaedr rombowy .
Rombowy dwunastościan może być użyty do teselacji trójwymiarowej przestrzeni: można go układać w stosy, aby wypełnić przestrzeń, podobnie jak sześciokąty wypełniają płaszczyznę.
Ten wielościan w teselacji wypełniającej przestrzeń można postrzegać jako teselację Woronoja sieci sześciennej centrowanej na twarzy . Jest to strefa Brillouina skupionych na ciele kryształów sześciennych (bcc). Niektóre minerały, takie jak granat, tworzą rombowy dwunastościenny pokrój kryształów . Jak Johannes Kepler w swojej książce o płatkach śniegu z 1611 r. ( Strena seu de Nive Sexangula ), pszczoły miodne wykorzystują geometrię rombowych dwunastościanów do tworzenia plastrów miodu z mozaiki komórek, z których każda jest graniastosłup sześciokątny zwieńczony połową dwunastościanu rombowego. Rombowy dwunastościan pojawia się również w komórkach elementarnych diamentu i diamentoidów . W tych przypadkach nie ma czterech wierzchołków (naprzemiennie potrójnych), ale wiązania chemiczne leżą na pozostałych krawędziach.
Wykres dwunastościanu rombowego jest niehamiltonowski .
Rombowy dwunastościan można podzielić na 4 rozwarte trójkątne trapezy wokół jego środka. Te romboedry to komórki trygonalnego trapezu o strukturze plastra miodu . Analogia: regularny sześciokąt można podzielić na 3 romby wokół jego środka. Te romby to płytki rombu .
W zbiorach Luwru znajduje się kostka w kształcie rombowego dwunastościanu pochodząca z Egiptu ptolemejskiego . Twarze są wyryte greckimi literami reprezentującymi cyfry od 1 do 12: Α Β Γ Δ Ε Ϛ Z Η Θ Ι ΙΑ ΙΒ. Funkcja matrycy jest nieznana.
Rombowy dwunastościan podzielony na 4 romboedry
Sześciokąt podzielony na 3 romby
Kryształ granatu _
Ta animacja przedstawia konstrukcję dwunastościanu rombowego z sześcianu poprzez odwrócenie piramid o środkowej powierzchni sześcianu.
Wymiary
Oznaczone przez długość krawędzi dwunastościanu rombowego,
- = promień jego wpisanej kuli ( styczny do każdej ze ścian dwunastościanu rombowego) wynosi
- promień środkowej kuli wynosi
- promień kuli przechodzącej przez sześć wierzchołków rzędu 4, ale nie przez wierzchołki ośmiu rzędu 3, wynosi
- promień kuli przechodzącej przez osiem wierzchołków rzędu 3 jest dokładnie równy długości boków
Powierzchnia i objętość
Pole powierzchni A i objętość V dwunastościanu rombowego o długości krawędzi a wynoszą:
Projekcje ortogonalne
Rombowy dwunastościan ma cztery specjalne ortogonalne rzuty wzdłuż osi symetrii , wyśrodkowane na ścianie, krawędzi i dwóch typach wierzchołków, trzykrotnym i czterokrotnym. Dwa ostatnie odpowiadają B2 i A2 Coxetera .
| Symetria projekcyjna |
[4] | [6] | [2] | [2] |
|---|---|---|---|---|
|
Dwunastościan rombowy |
|
|
|
|
|
Sześcian ośmiościan (podwójny) |
|
|
|
|
współrzędne kartezjańskie
 pirytościanu między sześcianem a dwunastościanem rombowym |
 Rozbudowa dwunastościanu rombowego |
Osiem wierzchołków, w których trzy ściany stykają się pod kątem rozwartym, ma współrzędne kartezjańskie :
- (±1, ±1, ±1)
Współrzędne sześciu wierzchołków, w których cztery ściany stykają się pod kątem ostrym, to:
- (±2, 0, 0), (0, ±2, 0) i (0, 0, ±2)
Dwunastościan rombowy można postrzegać jako zdegenerowany przypadek graniczny pirytościanu , z permutacją współrzędnych (±1, ±1, ±1) i (0, 1 + h , 1 − h 2 ) z parametrem h = 1.
Topologicznie równoważne formy
równoległobok
Dwunastościan rombowy jest równoległobokiem , wypełniającym przestrzeń wielościanem , dwunastościanem , który jest podwójny do tetroctahedrylu lub półsześciennego plastra miodu i opisany dwoma diagramami Coxetera : i . Przy symetrii D 3d można go postrzegać jako wydłużony trójkątny trapez .
 Dwunastościan rombowy może teselować przestrzeń przez translacyjne kopie samego siebie , podobnie jak dwunastościan gwiaździsty rombowy . |
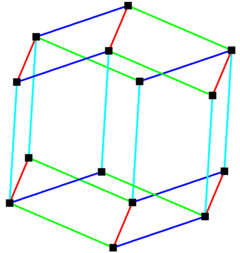 Dwunastościan rombowy można zbudować z 4 zestawów po 6 równoległych krawędzi. |
Dwuścienny dwunastościan rombowy
Inne konstrukcje symetrii dwunastościanu rombowego również wypełniają przestrzeń i jako równoległoboki są podobne do odmian wypełniających przestrzeń ośmiościanów ściętych .
Na przykład z 4 kwadratowymi ścianami i 60-stopniowymi rombowymi ścianami i dwuścienną symetrią D 4h , rząd 16. Można to postrzegać jako ośmiościan sześcienny z kwadratowymi piramidami powiększonymi na górze i na dole.
|
 Internet |
Współrzędne
|
dwunastościan Bilińskiego
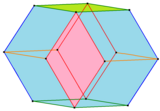 Dwunastościan Bilińskiego z krawędziami i przednimi ścianami pokolorowanymi według ich pozycji symetrii. |
 Dwunastościan Bilińskiego pokolorowany równoległymi krawędziami |
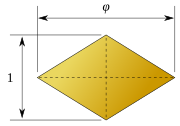
W 1960 roku Stanko Biliński odkrył drugi dwunastościan rombowy z 12 przystającymi ścianami rombów, dwunastościan Bilińskiego . Ma tę samą topologię, ale inną geometrię. Rombowe twarze w tej formie mają złoty podział .
| Pierwsza forma | Druga forma |
|---|---|
|
|
|
| √ 2 :1 | √ 5 + 1 / 2 : 1 |
Dwunastościan naramienny
.jpg)
Inna topologicznie równoważna odmiana, czasami nazywana dwunastościanem naramiennym lub dwunastościanem trapezowym , jest izoedryczna z czworościennym rzędem symetrii 24, zniekształcając rombowe ściany w latawce (naramienniki). Ma 8 wierzchołków dostosowanych do wewnątrz lub na zewnątrz w naprzemiennych zestawach po 4, z granicznym przypadkiem czworościennej obwiedni. Wariacje można sparametryzować za pomocą ( a , b ), gdzie b i a zależą od siebie w taki sposób, że czworościan zdefiniowany przez cztery wierzchołki ściany ma objętość zero, tj. jest ścianą płaską. (1,1) jest rozwiązaniem rombowym. Gdy a zbliża się do 1/2 do , b zbliża się nieskończoności. Zawsze utrzymuje, że 1 / a + 1 / b = 2, gdzie a , b > 1 / 2 .
- (±2, 0, 0), (0, ±2, 0), (0, 0, ±2) ( za , za , za )
- , ( − za , − za , za ) , ( − za , za , - za ), ( za , - za , - za )
- ( - b , - b , - b ), ( - b , b , b ), ( b , - b , b ), ( b , b , − b )
| (1,1) | ( 7 / 8 , 7 / 6 ) | ( 3 / 4 , 3 / 2 ) | ( 2 / 3 ,2) | ( 5 / 8 , 5 / 2 ) | ( 9 / 16 , 9 / 2 ) |
|---|---|---|---|---|---|
|
|
|
|
|
|
Powiązane wielościany
| Jednolite wielościany ośmiościenne | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symetria : [4,3], (*432) |
[4,3] + (432) |
[1 + ,4,3] = [3,3] (*332) |
[3 + ,4] (3*2) |
|||||||
| {4,3} | t{4,3} |
r{4,3} r{3 1,1 } |
t{3,4} t{3 1,1 } |
{3,4} {3 1,1 } |
rr{4,3} s 2 {3,4} |
tr{4,3} | sr{4,3} |
h{4,3} {3,3} |
h 2 {4,3} t{3,3} |
s{3,4} s{3 1,1 } |
|
|
|
|
|
|
|
|
|
||
 = 
|
=
|
=
|
|
  = lub 
|
= lub
|
=
|
||||
|
|
 
|
 
|
 
|
 
|
|
|
 
|
 
|
 
|
| Podwójne do jednolitych wielościanów | ||||||||||
| V4 3 | Wersja 3.8 2 | V(3.4) 2 | V4.6 2 | V3 4 | wersja 3.4 3 | V4.6.8 | V3 4 .4 | V3 3 | Wersja 3.6 2 | V3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Po rzucie na kulę (patrz po prawej) widać, że krawędzie tworzą krawędzie dwóch czworościanów ułożonych w ich podwójnych pozycjach (stella octangula). Trend ten jest kontynuowany w przypadku dwudziestościanu naramiennego i sześciokąta naramiennego dla podwójnych par innych regularnych wielościanów (obok trójkątnej dwupiramidy , jeśli należy wziąć pod uwagę niewłaściwe nachylenie), nadając temu kształtowi alternatywną systematyczną nazwę dwunastościan naramienny .
|
Symetria * n 32 [n,3] |
Kulisty | Euklides. | Kompaktowy hiperb. | Parako. | ||||
|---|---|---|---|---|---|---|---|---|
|
*232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
|
|
rysunku . |
 V3.4.2.4 |
 V3.4.3.4 |
 V3.4.4.4 |
 V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
 V3.4.∞.4 |
Wielościan ten jest częścią ciągu wielościanów rombowych i ukośników o symetrii grupowej [ n ,3] Coxetera . Sześcian można postrzegać jako sześcian rombowy, w którym romby są kwadratami.
| Mutacje symetrii podwójnych quasiregularnych nachyleń: V(3.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| *n32 | Kulisty | euklidesowy | Hiperboliczny | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Dekarstwo |
|
|
|
|
|
|
|
||||
| konf. | V(3.3) 2 | V(3.4) 2 | V(3.5) 2 | V(3.6) 2 | V(3.7) 2 | V(3.8) 2 | V(3.∞) 2 | ||||
| * n 42 mutacje symetrii quasiregularnych podwójnych nachyleń: V (4.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Symetria *4n2 [n,4] |
Kulisty | euklidesowy | Kompaktowy hiperboliczny | Parakompaktowy | Niekompaktowy | ||||||
|
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
[iπ/λ,4] |
||||
|
Konf . |
V4.3.4.3 |
 V4.4.4.4 |
 V4.5.4.5 |
 V4.6.4.6 |
 V4.7.4.7 |
 V4.8.4.8 |
 V4.∞.4.∞ |
V4.∞.4.∞ | |||
Podobnie odnosi się to do nieskończonej serii nachyleń o konfiguracjach ścian V3.2 n .3.2 n , pierwsza na płaszczyźnie euklidesowej, a pozostałe na płaszczyźnie hiperbolicznej.
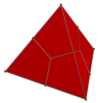
 V3.4.3.4 (Narysowany jako sieć ) |
 V3.6.3.6 Dachówka płaszczyzny euklidesowej Dachówka rombowa |
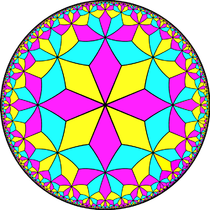 V3.8.3.8 Układanie płaszczyzny hiperbolicznej (narysowane w modelu dysku Poincarégo ) |
Stellacje
Podobnie jak wiele wypukłych wielościanów, dwunastościan rombowy można ułożyć w gwiazdki, wydłużając ściany lub krawędzie, aż spotkają się, tworząc nowy wielościan. Dorman Luke opisał kilka takich gwiazd.
Pierwsza gwiazda, często nazywana po prostu gwiaździstym dwunastościanem rombowym , jest dobrze znana. Można go postrzegać jako rombowy dwunastościan z każdą ścianą powiększoną przez przymocowanie do niego piramidy rombowej, o wysokości piramidy takiej, że boki leżą w płaszczyznach ścian sąsiednich ścian:
Pierwsza gwiazda dwunastościanu rombowego
Model 3D rozkładu na 12 piramid i 4 półsześciany
Łukasz opisuje jeszcze cztery gwiazdy: drugą i trzecią gwiazdę (rozszerzającą się na zewnątrz), jedną utworzoną przez usunięcie drugiej z trzeciej, a drugą przez dodanie pierwotnego dwunastościanu rombowego z powrotem do poprzedniego.
| Drugi | Trzeci |
|---|---|
 Dwunastościan rombowy gwiaździsty |
 Wielki rombowy dwunastościan gwiaździsty |
Powiązane polytopy
Rombowy dwunastościan tworzy kadłub pierwszego wierzchołka rzutu tesseraktu na trzy wymiary. Istnieją dokładnie dwa sposoby rozkładu dwunastościanu rombowego na cztery przystające romboedry , dające osiem możliwych romboedrów jako rzuty tesseraktów na 8 komórek sześciennych. Jeden zestaw wektorów rzutowych to: u = (1,1,−1,−1), v = (−1,1,−1,1), w = (1,−1,−1,1).
Dwunastościan rombowy tworzy maksymalny przekrój 24-komorowy , a także tworzy kadłub jego równoległego rzutu pierwszego wierzchołka w trzech wymiarach. Rombowy dwunastościan można rozłożyć na sześć przystających (ale nieregularnych) kwadratowych dwupiramid spotykających się w jednym wierzchołku w środku; tworzą one obrazy sześciu par ośmiościennych komórek 24 komórek. Pozostałe 12 komórek ośmiościennych wystaje na powierzchnie dwunastościanu rombowego. Nieregularność tych obrazów jest spowodowana zniekształceniem projekcyjnym; fasetki 24-komórek są regularnymi ośmiościanami w 4-przestrzeni.
Ten rozkład daje interesującą metodę konstruowania dwunastościanu rombowego: pociąć sześcian na sześć przystających kwadratowych piramid i przymocować je do ścian drugiego sześcianu. Trójkątne ściany każdej pary sąsiednich piramid leżą na tej samej płaszczyźnie i w ten sposób łączą się w romby. 24-komorę można również zbudować w analogiczny sposób, używając dwóch tesseraktów .
Praktyczne zastosowanie
W układzie koła reakcyjnego statku kosmicznego powszechnie stosuje się czworościenną konfigurację czterech kół. W przypadku kół, które działają jednakowo (z punktu widzenia szczytowego momentu obrotowego i maksymalnego momentu pędu) w obu kierunkach obrotu i na wszystkich czterech kołach, obwiednie maksymalnego momentu obrotowego i maksymalnego pędu dla 3-osiowego systemu kontroli położenia (biorąc pod uwagę wyidealizowane siłowniki) są określone przez rzutowanie tesserakt _ reprezentujące granice momentu obrotowego lub pędu każdego koła w przestrzeni 3D za pomocą macierzy osi kół 3 × 4; powstały wielościan 3D jest rombowym dwunastościanem. Taki układ kół reakcyjnych nie jest jedyną możliwą konfiguracją (prostszy układ składa się z trzech kół zamontowanych w celu obracania się wokół ortogonalnych osi), ale jest korzystny w zapewnieniu redundancji w celu złagodzenia awarii jednego z czterech kół (przy pogorszeniu ogólnej wydajności dostępnych z pozostałych trzech aktywnych kół) oraz w zapewnieniu bardziej wypukłej obwiedni niż sześcian, co prowadzi do mniejszej zależności zwinności od kierunku osi (z punktu widzenia siłownika/instalacji). Właściwości masy statku kosmicznego wpływają na ogólny pęd i zwinność systemu, więc zmniejszona zmienność granic obwiedni niekoniecznie prowadzi do zwiększonej jednorodności preferowanych odchyleń osi (to znaczy, nawet przy idealnie rozłożonym limicie wydajności w podsystemie siłownika, preferowane osie obrotu niekoniecznie są arbitralne na poziomie systemu).
Zobacz też
- Dwunastościan
- Rombowy triacontahedron
- Ścięty dwunastościan rombowy
- 24-ogniwowy - analog 4D dwunastościanu rombowego
- Systemy konstrukcyjne Archimede'a
- W pełni ścięty dwunastościan rombowy
Dalsza lektura
- Williams, Robert (1979). Geometryczne podstawy naturalnej struktury: źródłowa księga projektowania . Dover Publications, Inc. ISBN 0-486-23729-X . (Sekcja 3-9)
- Wenninger, Magnus (1983). Modele dualne . Wydawnictwo Uniwersytetu Cambridge. doi : 10.1017/CBO9780511569371 . ISBN 978-0-521-54325-5 . MR 0730208 . (Trzynaście półregularnych wypukłych wielościanów i ich liczby podwójne, strona 19, dwunastościan rombowy)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Rozdział 21, Nazewnictwo wielościanów archimedesowych i katalońskich oraz nachyleń, s. 285, dwunastościan rombowy)
Linki zewnętrzne
- Eric W. Weisstein , dwunastościan rombowy ( bryła katalońska ) w MathWorld .
- Wielościany wirtualnej rzeczywistości - Encyklopedia wielościanów
Modele komputerowe
- Odnoszący rombowy triacontahedron i rombowy dwunastościan , rombowy dwunastościan 5-złożony i rombowy dwunastościan 5-złożony przez Sándora Kabai, The Wolfram Demonstrations Project .
Projekty papierowe
- Kalendarz rombowy dwunastościan – wykonaj rombowy kalendarz dwunastościan bez kleju
- Kolejny dwunastościan rombowy – wykonany przez splatanie pasków papieru
Praktyczne zastosowania
- Archimede Institute Przykłady rzeczywistych projektów budownictwa mieszkaniowego wykorzystujących tę geometrię
