Disdyakis triacontahedron

Disdyakis triacontahedron
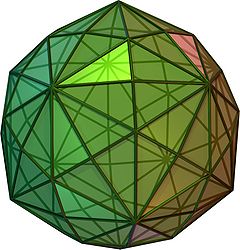( obrotowy i model 3D )
Typ	kataloński
Notacja Conwaya	mD lub dbD
Diagram Coxetera
Wielokąt twarzy	trójkąt pochyły
Twarze	120
Krawędzie	180
Wierzchołki	62 = 12 + 20 + 30
Konfiguracja twarzy	V4.6.10
Grupa symetrii	I _h , H ₃ , [5,3], (*532)
Grupa rotacyjna	ja, [5,3] ⁺ , (532)
Kąt dwuścienny	164° 53' 17'' arccos( -179-24 √ 5 / 241 )
Podwójny wielościan	dwudziestościan ścięty
Nieruchomości	wypukła, przechodnia twarzy
internet

W geometrii disdyakis triacontahedron , hexakis dwudziestościan , decakis dwunastościan lub kisrombowy triacontahedron jest bryłą katalońską ze 120 ścianami i podwójną do dwudziestościanu ściętego Archimedesa . Jako taka jest jednolita twarzą , ale z nieregularnymi wielokątami twarzy . To trochę przypomina napompowany rombowy triacontahedr : jeśli zastąpimy każdą ścianę rombowego triacontahedru pojedynczym wierzchołkiem i czterema trójkątami w regularny sposób, otrzymamy triacontahedron disdyakis. Oznacza to, że triacontahedron disdyakis jest Kleetopem rombowego triacontahedru. Jest to również podział barycentryczny dwunastościanu regularnego i dwudziestościanu regularnego . Ma najwięcej ścian wśród brył archimedesowych i katalońskich, z zadartym dwunastościanem z 92 ścianami na drugim miejscu.

Jeśli wykluczymy bipiramidy , dwupiramidy wydłużone żyroskopowo i trapezoedry , triacontahedron disdyakis ma najwięcej ścian ze wszystkich innych ściśle wypukłych wielościanów , w których każda ściana wielościanu ma ten sam kształt.

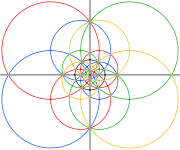
Rzutowane na kulę krawędzie triacontahedru disdyakis wyznaczają 15 kół wielkich . Buckminster Fuller użył tych 15 wielkich kręgów, wraz z 10 i 6 innymi w dwóch innych wielościanach, aby zdefiniować swoje 31 wielkich kręgów sferycznego dwudziestościanu .

współrzędne kartezjańskie

62 wierzchołki trójkąta disdyakis dzielą się na trzy zestawy:

Dwanaście $wierzchołków$ ma postać jej cykliczne permutacje
Dwadzieścia wierzchołków ma postać ${\ Displaystyle \ lewo (\ pm 1, \ pm 1, \ pm 1 \ prawej)}$ lub ${\ displaystyle \left(0,\pm \phi ,\pm \phi ^{-1}\right)}$ i jego cykliczne permutacje, które razem tworzą dwunastościan foremny .
Kiedy powyższe 32 wierzchołki są razem wzięte, tworzą wierzchołki trójkąta rombowego , którego 30 środków ścian tworzy dwudziestościan o współrzędnych ${\ Displaystyle \ lewo (0,0, \ pm \ phi \ prawej) }$ i ${\ Displaystyle \ lewo (\ pm {\ Frac {\ fi ^ {2}} {2}}, \ pm {\ Frac {\ fi}} 2}},\pm {\frac {1}{2}}\right)}$ i ich cykliczne permutacje. Jeśli ${\ Displaystyle \ lewo (0,0, \ pm R \ phi \ prawej)}$ $otrzymując$ zewnątrz początku o i ${\ Displaystyle \ lewo (\ pm {\ frac {R\phi ^{2}}{2}},\pm {\frac {R\phi }{2}},\pm {\frac {R}{2}}\right)} wtedy oni i ich$ cykliczne permutacje tworzą ostatnie 30 wierzchołków triacontahedru disdyakis.

Kadłuby te są zwizualizowane na poniższym rysunku w skali, więc dwudziestościan ma jednostkowy promień obwodu :

Twarze

Twarze triacontahedru disdyakis to trójkąty skalenowe. Jeśli ${\ Displaystyle \ phi}$ jest złotym podziałem , to ich kąty są równe ${\ Displaystyle \ arccos ({\ Frac {-4 \ phi +7 {30}}) \ około 88,991 \ 801 \, 907 \, 82 ^ {\ circ}}$ , ${\ Displaystyle \ arccos ({\ frac {-4 \ phi + 17} {20}}) \ około 58,237 \ 919 \, 620 \, 89 ^ {\ circ}}$ i ${\ Displaystyle \arccos({\frac {5\phi +2}{12}})\około 32,770\,278\,471\,29^{\circ}}$ .

Symetria

Krawędzie wielościanu rzutowane na kulę tworzą 15 wielkich kół i reprezentują wszystkie 15 płaszczyzn lustrzanych odbijającej symetrii 1 _- hikosaedrycznej . Łączenie par jasnych i ciemnych trójkątów definiuje podstawowe domeny nieodblaskowej ( I ) dwudziestościennej symetrii. Krawędzie złożonego z pięciu ośmiościanów reprezentują również 10 lustrzanych płaszczyzn symetrii dwudziestościennej.

Disdyakis triacontahedron	Sześciokąt naramienny	Rombowy triacontahedron	Dwunastościan	dwudziestościan	Pirytoedr

Sferyczny wielościan

(patrz obracający się model )	Projekcje ortograficzne z osi 2-, 3- i 5-krotnych

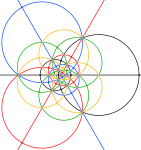
Projekcje stereograficzne

	2-krotnie	3-krotnie	5-krotny


Pokolorowane jako złożenie pięciu ośmiościanów , z 3 kołami wielkimi dla każdego ośmiościanu. Obszar w czarnych kółkach poniżej odpowiada przedniej półkuli kulistego wielościanu.

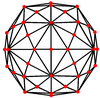
Projekcje ortogonalne

Disdyakis triacontahedron ma trzy rodzaje wierzchołków, które mogą być wyśrodkowane w rzucie ortogonalnym:

Projekcje ortogonalne
Symetria projekcyjna	[2]	[6]	[10]
Obraz
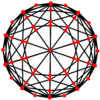
Podwójny obraz

Używa

Układanka Big Chop

Disdyakis triacontahedron , jako regularny dwunastościan z pięciokątami podzielonymi na 10 trójkątów, jest uważany za „świętego Graala” dla łamigłówek, takich jak kostka Rubika . Ten nierozwiązany problem, często nazywany problemem „dużego kotleta”, obecnie nie ma zadowalającego mechanizmu. Jest to najważniejszy nierozwiązany problem w układankach mechanicznych. Ten kształt został wykorzystany do wykonania kości d120 za pomocą druku 3D. Od 2016 roku Dice Lab używa triacontahedronu disdyakis do masowego wprowadzania na rynek formowanej wtryskowo 120-stronnej matrycy . Uważa się, że k120 to największa możliwa liczba ścian na zwykłej kości, poza nieskończonymi rodzinami (takimi jak graniastosłupy proste , dwupiramidy i trapezościany ), które w rzeczywistości byłyby niepraktyczne ze względu na tendencję do toczenia przez długi czas .

Disdyakis tricontahedron rzutowany na kulę jest używany jako logo Brilliant , strony internetowej zawierającej serię lekcji na tematy związane z STEM .

Powiązane wielościany i tilings


Wielościany podobne do triacontahedronu disdyakis są podwójnie do dwudziestościanu Bowtie i dwunastościanu Bowtie, zawierające dodatkowe pary trójkątnych ścian.

Rodzina jednolitych dwudziestościanów wielościanów
Symetria : [5,3] , (*532)							[5,3] ⁺ , (532)


{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rrr{5,3}	tr{5,3}	sr{5,3}
Podwójne do jednolitych wielościanów

V5.5.5	Wersja 3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Jest topologicznie powiązany z sekwencją wielościanów zdefiniowaną przez konfigurację ścian V4.6.2n . Ta grupa jest wyjątkowa, ponieważ ma wszystkie parzyste krawędzie na wierzchołek i tworzy płaszczyzny przecinające się przez wielościany i nieskończone linie na płaszczyźnie oraz przechodzące do płaszczyzny hiperbolicznej dla dowolnego n ≥ 7 .

Przy parzystej liczbie ścian w każdym wierzchołku te wielościany i kafelki można pokazać naprzemiennie dwoma kolorami, tak aby wszystkie sąsiednie ściany miały różne kolory.

Każda ściana w tych domenach odpowiada również podstawowej domenie grupy symetrii o rzędzie 2,3, n luster w każdym wierzchołku ściany trójkąta. To jest * n 32 w notacji orbifold i [ n , 3] w notacji Coxetera .

* n 32 mutacja symetrii omnitruncated tilings: 4.6.2n
Sym. * n 32 [ n ,3]	Kulisty				Euklides.	Kompaktowy hiperb.		Parako.	Niezwarty hiperboliczny
Sym. * n 32 [ n ,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figurki
Konfig.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Podwójne
Konfig.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Williams, Robert (1979). Geometryczne podstawy naturalnej struktury: źródłowa księga projektowania . Dover Publications, Inc. ISBN 0-486-23729-X . (Sekcja 3-9)
Wenninger, Magnus (1983), Dual Models , Cambridge University Press , doi : 10.1017 / CBO9780511569371 , ISBN 978-0-521-54325-5 , MR 0730208 (Trzynaście półregularnych wypukłych wielościanów i ich liczby podwójne, strona 25, Disdyakistriacontahedron)
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 [1] (Rozdział 21, Nazywanie wielościanów Archimedesa i katalońskiego oraz nachyleń, strona 285, kisRhombic triacontahedron )

Linki zewnętrzne

Eric W. Weisstein , Disdyakis triacontahedron ( bryła katalońska ) w MathWorld .
Disdyakis triacontahedron (Hexakis Icosahedron) – Interaktywny model wielościanu