Diagram Coxetera-Dynkina

Diagramy Coxetera-Dynkina dla podstawowych skończonych grup Coxetera

Diagramy Coxetera-Dynkina dla podstawowych afinicznych grup Coxetera

W geometrii diagram Coxetera-Dynkina (lub diagram Coxetera , wykres Coxetera ) to wykres z numerycznie oznaczonymi krawędziami (zwanymi gałęziami ) reprezentującymi relacje przestrzenne między zbiorem luster (lub odbijającymi hiperpłaszczyznami ). Opisuje kalejdoskopową konstrukcję: każdy „węzeł” wykresu reprezentuje lustro ( aspekt domeny ), a etykieta dołączona do gałęzi koduje dwuścienny porządek kątowy między dwoma lustrami (na grzbiecie domeny ), to znaczy wielkość, o którą kąt między odbijające płaszczyzny można pomnożyć, aby uzyskać 180 stopni. Nieoznakowana gałąź domyślnie reprezentuje rząd-3 (60 stopni), a każda para węzłów, która w ogóle nie jest połączona gałęzią (na przykład węzły niesąsiadujące), reprezentuje parę luster w porządku-2 (90 stopni).

Każdy diagram reprezentuje grupę Coxetera , a grupy Coxetera są klasyfikowane według powiązanych z nimi diagramów.

Diagramy Dynkina są blisko spokrewnionymi obiektami, które różnią się od diagramów Coxetera pod dwoma względami: po pierwsze, gałęzie oznaczone jako „4” lub większe są skierowane , podczas gdy diagramy Coxetera są niekierowane ; po drugie, diagramy Dynkina muszą spełniać dodatkowe ( krystalograficzne ) ograniczenie, a mianowicie, że jedynymi dozwolonymi etykietami gałęzi są 2, 3, 4 i 6. Diagramy Dynkina odpowiadają i są używane do klasyfikowania systemów korzeni , a zatem półprostych algebr Liego .

Opis

Gałęzie diagramu Coxetera-Dynkina są oznaczone liczbą wymierną p , reprezentującą kąt dwuścienny 180 ° / p . Gdy $p = 2$ kąt wynosi 90°, a zwierciadła nie oddziałują, więc gałąź można pominąć na schemacie. Jeśli gałąź nie jest oznaczona, zakłada się, że ma $p = 3$ , reprezentujące kąt 60°. Dwa równoległe lustra mają odgałęzienie oznaczone „∞”. W zasadzie n luster można przedstawić za pomocą pełnego wykresu , w którym narysowane są wszystkie n ( $n - 1) / 2 gałęzie.$ W praktyce prawie wszystkie interesujące konfiguracje zwierciadeł zawierają pewną liczbę kątów prostych, więc odpowiadające im gałęzie są pomijane.

Diagramy można oznaczyć według ich struktury grafu. Pierwsze formy badane przez Ludwiga Schläfliego to ortoschemy , które mają grafy liniowe generujące regularne polytopy i regularne plastry miodu . Plagioschemy to uproszczenia reprezentowane przez grafy rozgałęzione, a cykloschematy to uproszczenia reprezentowane przez grafy cykliczne.

Macierz Schläfliego

Każdy diagram Coxetera ma odpowiednią macierz Schläfliego (nazwaną tak na cześć Ludwiga Schläfliego ), z elementami macierzy $a i,j = aj,i = -2 cos(π / p)$ , gdzie p jest kolejnością rozgałęzień między parami luster. Jako macierz cosinusów nazywana jest również macierzą Gramiana od nazwiska Jørgena Pedersena Grama . Wszystkie grupy Coxetera są symetryczne, ponieważ ich wektory pierwiastków są znormalizowane. Jest ściśle powiązana z macierzą Cartana , używaną w podobnych, ale skierowanych diagramach Dynkina w ograniczonych przypadkach p = 2,3,4 i 6, które na ogół nie są symetryczne.

Wyznacznik macierzy Schläfliego, zwany Schläflianem , oraz jego znak określają, czy grupa jest skończona (dodatnia), afiniczna (zero), nieokreślona (ujemna). Reguła ta nosi nazwę Kryterium Schläfliego . ^{[ nieudana weryfikacja ]}

Wartości własne macierzy Schläfliego określają, czy grupa Coxetera jest typu skończonego (wszystkie dodatnie), typu afinicznego (wszystkie nieujemne, co najmniej jeden to zero), czy typu nieokreślonego (w przeciwnym razie). Typ nieokreślony jest czasami dalej dzielony, np. na grupy hiperboliczne i inne grupy Coxetera. Istnieje jednak wiele nierównoważnych definicji hiperbolicznych grup Coxetera. Stosujemy następującą definicję: Grupa Coxetera z diagramem spójnym jest hiperboliczna , jeśli nie jest typu skończonego ani afinicznego, ale każdy odpowiednio spójny poddiagram jest typu skończonego lub afinicznego. Hiperboliczna grupa Coxetera jest zwarta , jeśli wszystkie podgrupy są skończone (tj. mają wyznaczniki dodatnie), a parazwarta , jeśli wszystkie jej podgrupy są skończone lub afiniczne (tj. mają wyznaczniki nieujemne).

Grupy skończone i afiniczne są również nazywane odpowiednio eliptycznymi i parabolicznymi . Grupy hiperboliczne są również nazywane Lannér, po F. Lannér, który wyliczył zwarte grupy hiperboliczne w 1950 r., Oraz Koszul (lub quasi-Lannér) dla grup parazwartych.

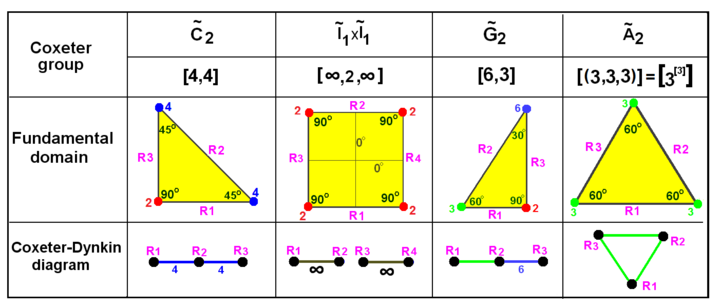
Grupy Coxeter rangi 2

Dla rangi 2 typ grupy Coxetera jest w pełni określony przez wyznacznik macierzy Schläfliego, ponieważ jest to po prostu iloczyn wartości własnych: typ skończony (wyznacznik dodatni), typ afiniczny (wyznacznik zerowy) lub hiperboliczny (wyznacznik ujemny) . Coxeter używa równoważnej notacji nawiasów , która wymienia sekwencje rzędów rozgałęzień jako substytut diagramów graficznych węzeł-rozgałęzienie. Istnieją również racjonalne rozwiązania [p/q], , gdzie gcd (p,q)=1, które definiują nakładające się domeny podstawowe. Na przykład 3/2, 4/3, 5/2, 5/3, 5/4 i 6/5.

Typ	Skończone					afiniczny	Hiperboliczny
Geometria					...
Coxeter	[ ]	[2]	[3]	[4]	[P]	[∞]	[∞]	[iπ/λ]
Zamówienie	2	4	6	8	2 str	∞
Linie lustrzane są kolorowe, aby odpowiadały węzłom diagramu Coxetera. Domeny podstawowe są naprzemiennie kolorowe.

Diagramy grupy Coxetera rangi 2
zamów str	Grupa	Diagram Coxetera		Macierz Schläfliego
zamów str	Grupa	Diagram Coxetera		${\ Displaystyle \ lewo [{\ rozpocząć {macierz} 2 i a_ {12} \\ a_ {21} i 2 \ koniec {macierz}} \ prawo]}$	Wyznacznik (4-a ₂₁ *a ₁₂ )
skończony (wyznacznik>0)
2	Ja ₂ (2) = ZA ₁ x ZA ₁		[2]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i 0 \\ 0 i 2 \ koniec {mała macierz}} \ prawo]}$	4
3	Ja ₂ (3) = A ₂		[3]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i -1 \\ -1 i 2 \ koniec {mała macierz}} \ prawo]}$	3
3/2			[3/2]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i 1 \\ 1 i 2 \ koniec {mała macierz}} \ prawo]}$	3
4	Ja ₂ (4) = B ₂		[4]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i - {\ sqrt {2}} \\ - {\ sqrt {2}} i 2 \ koniec {mała macierz}} \ prawo]}$	2
4/3			[4/3]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i {\ sqrt {2}} \\ {\ sqrt {2}} i 2 \ koniec {mała macierz}} \ prawo]}$	2
5	ja ₂ (5) = H ₂		[5]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i - \ phi \\ - \ phi & 2 \ koniec {mała macierz}} \ prawo]}$	${\ Displaystyle (5- {\ sqrt {5}}) / 2}$ ~ 1,38196601125
5/4			[5/4]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i \ phi \\\ phi & 2 \ koniec {mała macierz}} \ prawo]}$	${\ Displaystyle (5- {\ sqrt {5}}) / 2}$ ~ 1,38196601125
5/2			[5/2]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i 1 - \ phi \\ 1- \ phi & 2 \ koniec {mała macierz}} \ prawo]}$	${\ Displaystyle (5 + {\ sqrt {5}}) / 2}$ ~ 3,61803398875
5/3			[5/3]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i \ phi -1 \\\ phi -1 i 2 \ koniec {mała macierz}} \ prawo]}$	${\ Displaystyle (5 + {\ sqrt {5}}) / 2}$ ~ 3,61803398875
6	Ja ₂ (6) = G ₂		[6]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i - {\ sqrt {3}} \\ - {\ sqrt {3}} i 2 \ koniec {mała macierz}} \ prawo]}$	1
6/5			[6/5]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i {\ sqrt {3}} \\ {\ sqrt {3}} i 2 \ koniec {mała macierz}} \ prawo]}$	1
8	ja ₂ (8)		[8]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i - {\ sqrt {2 + {\ sqrt {2}}}} \\ - {\ sqrt {2+ {\sqrt {2}}}}&2\end{mała macierz}}\right]}$	${\ Displaystyle 2- {\ sqrt {2}}}$ ~ 0,58578643763
10	I ₂ (10)		[10]	${\ Displaystyle \ lewo [{\ rozpocząć {smallmatrix} 2 & - {\ sqrt {(5 + {\ sqrt {5}}) / 2}}\\-{\sqrt {(5+{\sqrt {5}})/2}}&2\end{małamacierz}}\right]}$	${\ Displaystyle (3- {\ sqrt {5}}) / 2}$ ~0,38196601125
12	ja ₂ (12)		[12]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i - {\ sqrt {2 + {\ sqrt {3}}}} \\ - {\ sqrt {2+ {\sqrt {3}}}}&2\end{mała macierz}}\right]}$	${\ Displaystyle 2- {\ sqrt {3}}}$ ~0,26794919243
P	ja ₂ (p)		[P]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i -2 \ sałata (\ pi / p) \\ - 2 \ cos(\pi /p)&2\end{małamacierz}}\right]}$	${\ Displaystyle 4 \ grzech ^ {2} (\ pi / p)}$
Afiniczny (wyznacznik=0)
∞	ja ₂ (∞) = ${\ Displaystyle {\ tylda {I}} _ {1}}$ = ${\ Displaystyle {\ tylda {A}} _ {1}}$		[∞]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i - 2 \\ - 2 i 2 \ koniec {mała macierz}} \ prawo]}$	0
Hiperboliczny (wyznacznik ≤0)
∞			[∞]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i - 2 \\ - 2 i 2 \ koniec {mała macierz}} \ prawo]}$	0
∞			[iπ/λ]	${\ Displaystyle \ lewo [{\ rozpocząć {mała macierz} 2 i -2 \ kosz (2 \ lambda) \\ - 2 \ kosz (2 \lambda )&2\end{małamacierz}}\right]}$	${\ Displaystyle -4 \ sinh ^ {2} (2 \ lambda) \ równoważnik 0}$

Wizualizacje geometryczne

Diagram Coxetera-Dynkina można postrzegać jako graficzny opis podstawowej dziedziny luster. Lustro reprezentuje hiperpłaszczyznę w danej wymiarowej przestrzeni sferycznej, euklidesowej lub hiperbolicznej. (W przestrzeniach 2D zwierciadło jest linią, aw przestrzeniach 3D zwierciadło jest płaszczyzną).

Wizualizacje te przedstawiają podstawowe domeny dla grup euklidesowych 2D i 3D oraz grup sferycznych 2D. Dla każdego diagramu Coxetera można wywnioskować, identyfikując zwierciadła hiperpłaszczyznowe i oznaczając ich łączność, ignorując kąty dwuścienne 90 stopni (kolejność 2).

Grupy Coxetera na płaszczyźnie euklidesowej z równoważnymi diagramami. Odbicia są oznaczone jako węzły wykresu R 1, R 2 itd. i są pokolorowane zgodnie z kolejnością odbić. Odbicia pod kątem 90 stopni są nieaktywne i dlatego są pomijane na diagramie. Zwierciadła równoległe są połączone gałęzią oznaczoną ∞. Grupa $_$ jest $_$ C $}} _ {2}} , ale$ $podwojenie$ je również tworzyć jako domeny prostokątne przez . $.$ trójkąta _ $_$ _
Wiele grup Coxetera na płaszczyźnie hiperbolicznej można rozszerzyć z przypadków euklidesowych jako serię rozwiązań hiperbolicznych.
Grupy Coxetera w przestrzeni 3 z diagramami. Lustra (powierzchnie trójkątów) są oznaczone przeciwległym wierzchołkiem 0..3. Gałęzie są pokolorowane według kolejności ich odbicia. ${\ Displaystyle {\ tylda {C}} _ {3}}$ wypełnia 1/48 sześcianu. ${\ Displaystyle {\ tylda {B}} _ {3}}$ wypełnia 1/24 sześcianu. ${\ Displaystyle {\ tylda {A}} _ {3}}$ wypełnia 1/12 sześcianu.	Grupy Coxetera w sferze z równoważnymi diagramami. Jedna podstawowa domena jest zaznaczona na żółto. Wierzchołki domeny (i gałęzie grafu) są kolorowane według kolejności ich odbicia.

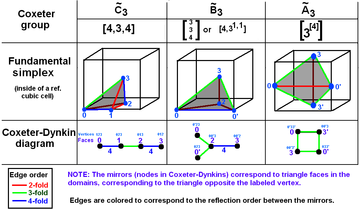
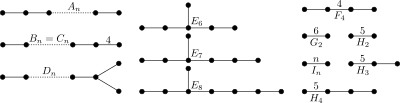
Skończone grupy Coxetera

Zobacz także rodziny polytope , aby zapoznać się z tabelą jednolitych polytopów węzłów końcowych powiązanych z tymi grupami.

Dla tych samych grup podane są trzy różne symbole - jako litera/cyfra, jako zestaw liczb w nawiasach i jako diagram Coxetera.
Rozwidlona grupa Dn _jest pół lub naprzemienną wersją grupy _Cn .
Rozwidlone grupy Dn _i En _są również oznaczone indeksem górnym [3 ^{a , b , c} ], gdzie a , b , c to numery segmentów w każdej z trzech gałęzi.

Połączone skończone diagramy Coxetera-Dynkina (rangi od 1 do 9)
Ranga	Proste grupy kłamstw			Wyjątkowe grupy kłamstw
Ranga	${\ Displaystyle {A} _ {1+}}$	${\ Displaystyle {B} _ {2+}}$	${\ Displaystyle {D} _ {2+}}$	${\ Displaystyle {E} _ {3-8}}$	${\ Displaystyle {F} _ {3-4}}$	${\ Displaystyle {G} _ {2}}$	${\ Displaystyle {H} _ {2-4}}$	${\ Displaystyle {I} _ {2} (p)}$
1	1 ₌ [ ]
2	2 ₌ [3]	B ₂ = [4]	re ₂ = ZA ₁ ZA ₁			G ₂ = [6]	H2 ₌ [5]	ja ₂ [p]
3	ZA ₃ = [3 ² ]	B ₃ = [3,4]	re ₃ = ZA ₃	mi ₃ = ZA ₂ ZA ₁	fa ₃ = B ₃		H ₃
4	ZA ₄ = [3 ³ ]	B ₄ = [3 ² ,4]	re ₄ = [3 ^1,1,1 ]	mi ₄ = A ₄	F ₄		4 _{_}
5	ZA ₅ = [3 ⁴ ]	B ₅ = [3 ³ ,4]	re ₅ = [3 ^2,1,1 ]	mi ₅ = re ₅
6	ZA ₆ = [3 ⁵ ]	B ₆ = [3 ⁴ ,4]	re ₆ = [3 ^3,1,1 ]	mi ₆ = [3 ^2,2,1 ]
7	ZA ₇ = [3 ⁶ ]	B ₇ = [3 ⁵ ,4]	re ₇ = [3 ^4,1,1 ]	mi ₇ = [3 ^3,2,1 ]
8	ZA ₈ = [3 ⁷ ]	B ₈ = [3 ⁶ ,4]	re ₈ = [3 ^5,1,1 ]	mi ₈ = [3 ^4,2,1 ]
9	ZA ₉ = [3 ⁸ ]	B ₉ = [3 ⁷ ,4]	re ₉ = [3 ^6,1,1 ]
10+	..	..	..	..

Aplikacja z jednolitymi polytopami

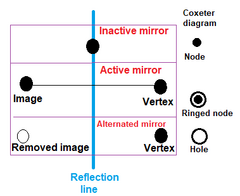Podczas konstruowania jednolitych polytopów węzły są oznaczane jako aktywne pierścieniem, jeśli punkt generatora znajduje się poza lustrem, tworząc nową krawędź między punktem generatora a jego lustrzanym odbiciem. Węzeł bez pierścienia reprezentuje nieaktywne lustro, które nie generuje nowych punktów. Pierścień bez węzła nazywany jest otworem .	Dwa ortogonalne lustra mogą być użyte do wygenerowania kwadratu, , widocznego tutaj z czerwonym punktem generatora i 3 wirtualnymi kopiami w poprzek luster. Generator musi być wyłączony z obu zwierciadeł w tym ortogonalnym przypadku, aby wygenerować wnętrze. Znacznik pierścienia zakłada, że aktywne pierścienie mają generatory w równej odległości od wszystkich luster, podczas gdy prostokąt może również reprezentować niejednorodne rozwiązanie.

Diagramy Coxetera-Dynkina mogą wyraźnie wyliczyć prawie wszystkie klasy jednolitych polytopów i jednolitych teselacji . Każdy jednolity polytope z czystą symetrią refleksyjną (wszystkie przypadki specjalne z wyjątkiem kilku mają czystą symetrię refleksyjną) można przedstawić za pomocą diagramu Coxetera-Dynkina z permutacjami znaczników . Każdy jednolity polytope można wygenerować za pomocą takich luster i pojedynczego punktu generatora: lustrzane odbicia tworzą nowe punkty jako odbicia, następnie krawędzie polytope między punktami a punktem lustrzanego odbicia. Twarze są generowane przez powtarzające się odbicie krawędzi, która ostatecznie zawija się wokół oryginalnego generatora; ostateczny kształt, jak również wszelkie fasetki o wyższych wymiarach, są również tworzone przez odbicie twarzy w celu zamknięcia obszaru.

Aby określić generujący wierzchołek, jeden lub więcej węzłów jest oznaczonych pierścieniami, co oznacza, że wierzchołek nie znajduje się na lustrach reprezentowanych przez węzły otoczone pierścieniami. (Jeśli zaznaczono dwa lub więcej zwierciadeł, wierzchołek znajduje się w równej odległości od nich.) Zwierciadło jest aktywne (tworzy odbicia) tylko w odniesieniu do punktów, które na nim nie leżą. Diagram wymaga co najmniej jednego aktywnego węzła do reprezentowania polytope. Niepowiązany diagram (podgrupy oddzielone gałęziami rzędu 2 lub ortogonalnymi zwierciadłami) wymaga co najmniej jednego aktywnego węzła w każdym podgrafie.

Wszystkie regularne polytopy , reprezentowane przez symbol Schläfliego { $p, q, r, ...$ }, mogą mieć swoje podstawowe domeny reprezentowane przez zestaw n luster z powiązanym diagramem Coxetera-Dynkina linii węzłów i gałęzi oznaczonych przez $p, q, r, ...,$ z pierwszym węzłem otoczonym pierścieniami.

Jednolite polytopy z jednym pierścieniem odpowiadają punktom generatora w rogach simpleksu domeny podstawowej. Dwa pierścienie odpowiadają krawędziom simpleksu i mają pewien stopień swobody, przy czym tylko punkt środkowy jest jednolitym rozwiązaniem dla równych długości krawędzi. Generalnie k -pierścieni znajdują się na (k-1) -powierzchniach simpleksu, a jeśli wszystkie węzły są otoczone pierścieniami, punkt generatora znajduje się we wnętrzu simpleksu.

Szczególny przypadek jednolitych polytopów z nieodblaskową symetrią jest reprezentowany przez drugorzędny znacznik, w którym usunięto środkową kropkę węzła otoczonego pierścieniami (nazywanego dziurą ) . Te kształty są naprzemiennymi polytopami z odblaskową symetrią, co oznacza, że każdy inny wierzchołek jest usunięty. Powstały polytope będzie miał subsymetrię oryginalnej grupy Coxetera . Skrócona przemiana nazywana jest afrontem .

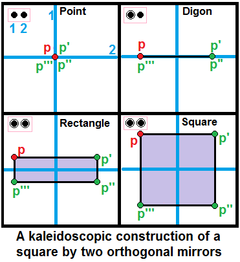
Pojedynczy węzeł reprezentuje pojedyncze lustro. Nazywa się to grupą A ₁ . W przypadku pierścienia tworzy to odcinek prostopadły do lustra, reprezentowany jako {}.
Dwa nieprzyłączone węzły reprezentują dwa prostopadłe zwierciadła. Jeśli oba węzły są otoczone pierścieniami, można utworzyć prostokąt lub kwadrat , jeśli punkt znajduje się w równej odległości od obu luster.
Dwa węzły połączone gałęzią rzędu n mogą utworzyć n -gon , jeśli punkt znajduje się na jednym zwierciadle, i 2 n -gon, jeśli punkt znajduje się poza obydwoma zwierciadłami. Tworzy to grupę I ₁ (n).
Dwa równoległe zwierciadła mogą reprezentować nieskończoną grupę wielokątów I ₁ (∞), zwaną także Ĩ ₁ .
Trzy lustra w trójkącie tworzą obrazy widziane w tradycyjnym kalejdoskopie i mogą być reprezentowane przez trzy węzły połączone w trójkąt. Powtarzające się przykłady będą miały rozgałęzienia oznaczone jako (3 3 3), (2 4 4), (2 3 6), chociaż ostatnie dwa można narysować jako linię (z pominięciem 2 rozgałęzień ) . Spowodują one wygenerowanie jednolitych nachyleń .
Trzy lustra mogą generować jednolite wielościany ; włączając liczby wymierne daje zbiór trójkątów Schwarza .
Trzy zwierciadła, z których jedno jest prostopadłe do dwóch pozostałych, mogą tworzyć jednolite graniastosłupy .

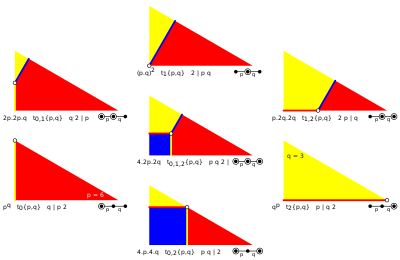Istnieje 7 odblaskowych jednolitych konstrukcji w obrębie ogólnego trójkąta, opartych na 7 pozycjach generatora topologicznego w domenie podstawowej. Każde aktywne lustro generuje krawędź, przy czym dwa aktywne lustra mają generatory po bokach domeny, a trzy aktywne lustra mają generator we wnętrzu. Można rozwiązać jeden lub dwa stopnie swobody dla unikalnej pozycji dla równych długości krawędzi powstałego wielościanu lub płytki.	Przykład 7 generatorów na symetrii oktaedrycznej , trójkąt domeny podstawowej (4 3 2), z 8. generacją snub jako naprzemienną

Podwójne jednorodne polytopy są czasami oznaczane prostopadłym ukośnikiem zastępującym węzły z pierścieniami oraz ukośnym otworem na węzły otworów w zadartych. Na przykład reprezentuje prostokąt (jako dwa aktywne lustra ortogonalne) i reprezentuje jego podwójny wielokąt , romb .

Przykładowe wielościany i tilingi

Na przykład grupa B ₃ Coxeter ma diagram: . Nazywa się to również symetrią oktaedryczną .

Istnieje 7 wypukłych jednorodnych wielościanów , które można zbudować z tej grupy symetrii i 3 z jej podsymetrii naprzemiennych , z których każdy ma jednoznacznie zaznaczony diagram Coxetera-Dynkina. Symbol Wythoffa reprezentuje szczególny przypadek diagramu Coxetera dla wykresów rangi 3, z nazwanymi wszystkimi 3 rzędami rozgałęzień, zamiast pomijania rozgałęzień rzędu 2. Symbol Wythoffa jest w stanie obsłużyć awersu , ale nie ogólne zmiany bez obramowania wszystkich węzłów.

Jednolite wielościany ośmiościenne
Symetria : [4,3], (*432)							[4,3] ⁺ (432)	[1 ⁺ ,4,3] = [3,3] (*332)		[3 ⁺ ,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3 ^1,1 }	t{3,4} t{3 ^1,1 }	{3,4} {3 ^1,1 }	rr{4,3} s ₂ {3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h ₂ {4,3} t{3,3}	s{3,4} s{3 ^1,1 }

		=	=	=				= lub	= lub	=

Podwójne do jednolitych wielościanów
V4 ³	Wersja 3.8 ²	V(3.4) ²	V4.6 ²	V3 ⁴	wersja 3.4 ³	V4.6.8	V3 ⁴ .4	V3 ³	Wersja 3.6 ²	V3 ⁵

Te same konstrukcje można wykonać na rozłącznych (ortogonalnych) grupach Coxetera, takich jak jednolite graniastosłupy , i można je wyraźniej zobaczyć jako nachylenie dwuścianów i hosohedrów na kuli, jak ta rodzina [6] × [] lub [6,2]:

Jednolite sześciokątne dwuścienne sferyczne wielościany
Symetria : [6,2] , (*622)							[6,2] ⁺ , (622)	[6,2 ⁺ ], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rrr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Podwójne do mundurów

V6 ²	V12 ²	V6 ²	V4.4.6	V2 ⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Dla porównania, rodzina [6,3] tworzy równoległy zestaw 7 jednolitych nachyleń płaszczyzny euklidesowej i ich podwójnych nachyleń. Są znowu 3 alternatywy i jakaś wersja półsymetryczna.

Jednolite płytki sześciokątne / trójkątne
Symetria : [6,3], (*632)							[6,3] ⁺ (632)	[6,3 ⁺ ] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rrr{6,3}	tr{6,3}	sr{6,3}	s{3,6}


6 ³	3.12 ²	(3.6) ²	6.6.6	3 ⁶	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Jednolite dublety

V6 ³	V3.12 ²	V(3.6) ²	V6 ³	V3 ⁶	V3.4.6.4	V.4.6.12	V3 ⁴ .6	V3 ⁶

W płaszczyźnie hiperbolicznej [7,3] rodzina tworzy równoległy zbiór jednolitych nachyleń i ich podwójnych nachyleń. Istnieje tylko 1 zmiana ( snub ), ponieważ wszystkie rzędy gałęzi są nieparzyste. Wiele innych hiperbolicznych rodzin jednolitych nachyleń można zobaczyć na jednolitych nachyleniach w płaszczyźnie hiperbolicznej .

Jednolite nachylenie siedmiokątne / trójkątne
Symetria: $[7,3], (*732)$							$[7,3] +, (732)$


${7,3}$	$t{7,3}$	$r{7,3}$	$t{3,7}$	${3,7}$	$rrr{7,3}$	$tr{7,3}$	$sr{7,3}$
Jednolite dublety


$V7 3$	$Wersja 3.14.14$	$V3.7.3.7$	$Wersja 6.6.7$	$V3 7$	$V3.4.7.4$	$V4.6.14$	$V3.3.3.3.7$

Afiniczne grupy Coxetera

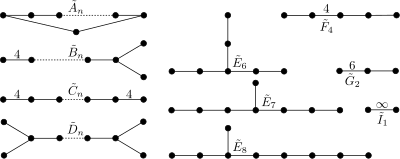
Rodziny wypukłych jednorodnych teselacji euklidesowych są definiowane przez afiniczne grupy Coxetera . Grupy te są identyczne z grupami skończonymi z włączeniem jednego dodanego węzła. W nazwach literowych otrzymują tę samą literę z „~” nad literą. Indeks odnosi się do grupy skończonej, więc ranga to indeks plus 1. ( Ernsta Witta dla grup afinicznych są również podane jako )

${\ Displaystyle {\ tylda {A}} _ {n-1}}$ : diagramy tego typu to cykle. (Również P _n )
$jest$ powiązany z rodziną regularnej teselacji hipersześcianu , $4$ (Również R _n )
${\ Displaystyle {\ tylda {B}} _ {n-1}}$ związane z C przez jedno usunięte lustro. ( Również Sn ₎
${\ Displaystyle {\ tylda {D}} _ {n-1}}$ związane z C przez dwa usunięte lustra. ( Również Qn ₎
${\ Displaystyle {\ tylda {E}} _ {6}}$ , ${\ Displaystyle {\ tylda {E}} _ {7}}$ , ${\ Displaystyle {\ tylda {E} }_{8}}$ . (Również T ₇ , T ₈ , T ₉ )
${\ Displaystyle {\ tylda {F}} _ {4}}$ tworzy regularną teselację {3,4,3,3}. (Również U ₅ )
${\ Displaystyle {\ tylda {G}} _ {2}}$ tworzy 30-60-90 trójkątów podstawowych domen. (Również V ₃ )
${\ displaystyle {\ tylda {I}} _ {1}}$ to dwa równoległe lustra. ( ${\ Displaystyle {} = {\ tylda {A}} _ {1} = {\ tylda {C}} _ {1}})$ (Również W ₂ )

Grupy złożone można również zdefiniować jako projekty ortogonalne. Najczęstsze zastosowanie , ${1}}$ jak , kwadrat ZA $\ Displaystyle {\$ lub prostokątne domeny szachownicy na płaszczyźnie euklidesowej. I $reprezentuje podstawowe$ trójkątnego 3 .

Wykresy afiniczne Coxetera do (od 2 do 10 węzłów)
Ranga	${\ Displaystyle {\ tylda {A}} _ {1+}}$ ( P ₂₊ )	${\ Displaystyle {\ tylda {B}} _ {3+}}$ ( S ₄₊ )	${\ Displaystyle {\ tylda {C}} _ {1+}}$ ( R ₂₊ )	${\ Displaystyle {\ tylda {D}} _ {4+}}$ ( P ₅₊ )	${\ Displaystyle {\ tylda {E}} _ {n} (T_ {n + 1}) / {\ tylda {F}}_{4}(U_{5})/{\tylda {G}}_{2}\,(V_{3})}$
2	${\ Displaystyle {\ tylda {A}} _ {1}}$ = [∞]		${\ Displaystyle {\ tylda {C}} _ {1}}$ = [∞]
3	${\ Displaystyle {\ tylda {A}} _ {2}}$ = [3 ^[3] ] *		${\ Displaystyle {\ tylda {C}} _ {2}}$ = [4,4] *		${\ Displaystyle {\ tylda {G}} _ {2}}$ = [6,3] *
4	${\ Displaystyle {\ tylda {A}} _ {3}}$ = [3 ^[4] ] *	${\ Displaystyle {\ tylda {B}} _ {3}}$ = [4,3 ^1,1 ] *	${\ Displaystyle {\ tylda {C}} _ {3}}$ = [4,3,4] *	${\ Displaystyle {\ tylda {D}} _ {3}}$ = [3 ^1,1 , 3 ^-1 , 3 ^1,1 ] = ${\ Displaystyle {\ tylda {A}} _ { 3}}$
5	${\ Displaystyle {\ tylda {A}} _ {4}}$ = [3 ^[5] ] *	${\ Displaystyle {\ tylda {B}} _ {4}}$ = [4,3,3 ^1,1 ] *	${\ Displaystyle {\ tylda {C}} _ {4}}$ = [4,3 ^2,4 ] *	${\ Displaystyle {\ tylda {D}} _ {4}}$ = [3 ^1,1,1,1 ] *	${\ Displaystyle {\ tylda {F}} _ {4}}$ = [3,4,3,3] *
6	${\ Displaystyle {\ tylda {A}} _ {5}}$ = [3 ^[6] ] *	${\ Displaystyle {\ tylda {B}} _ {5}}$ = [4,3 ² , 3 ^1,1 ] *	${\ Displaystyle {\ tylda {C}} _ {5}}$ = [4,3 ^3,4 ] *	${\ Displaystyle {\ tylda {D}} _ {5}}$ = [3 ^1,1 , 3,3 ^1,1 ] *
7	${\ Displaystyle {\ tylda {A}} _ {6}}$ = [3 ^[7] ] *	${\ Displaystyle {\ tylda {B}} _ {6}}$ = [4,3 ³ , 3 ^1,1 ]	${\ Displaystyle {\ tylda {C}} _ {6}}$ = [4,3 ^4,4 ]	${\ Displaystyle {\ tylda {D}} _ {6}}$ = [3 ^1,1 , 3 ² , 3 ^1,1 ]	${\ Displaystyle {\ tylda {E}} _ {6}}$ = [3 ^2,2,2 ]
8	${\ Displaystyle {\ tylda {A}} _ {7}}$ = [3 ^[8] ] *	${\ Displaystyle {\ tylda {B}} _ {7}}$ = [4,3 ⁴ , 3 ^1,1 ] *	${\ Displaystyle {\ tylda {C}} _ {7}}$ = [4,3 ^5,4 ]	${\ Displaystyle {\ tylda {D}} _ {7}}$ = [3 ^1,1 , 3 ³ , 3 ^1,1 ] *	${\ Displaystyle {\ tylda {E}} _ {7}}$ = [3 ^3,3,1 ] *
9	${\ Displaystyle {\ tylda {A}} _ {8}}$ = [3 ^[9] ] *	${\ Displaystyle {\ tylda {B}} _ {8}}$ = [4,3 ⁵ , 3 ^1,1 ]	${\ Displaystyle {\ tylda {C}} _ {8}}$ = [4,3 ^6,4 ]	${\ Displaystyle {\ tylda {D}} _ {8}}$ = [3 ^1,1 , 3 ⁴ , 3 ^1,1 ]	${\ Displaystyle {\ tylda {E}} _ {8}}$ = [3 ^5,2,1 ] *
10	${\ Displaystyle {\ tylda {A}} _ {9}}$ = [3 ^[10] ] *	${\ Displaystyle {\ tylda {B}} _ {9}}$ = [4,3 ⁶ , 3 ^1,1 ]	${\ Displaystyle {\ tylda {C}} _ {9}}$ = [4,3 ^7,4 ]	${\ Displaystyle {\ tylda {D}} _ {9}}$ = [3 ^1,1 , 3 ⁵ , 3 ^1,1 ]
11	...	...	...	...

Hiperboliczne grupy Coxetera

Istnieje wiele nieskończonych hiperbolicznych grup Coxetera . Grupy hiperboliczne są klasyfikowane jako zwarte lub nie, przy czym grupy zwarte mają ograniczone domeny podstawowe. Zwarte simpleksowe grupy hiperboliczne ( Lannér simplices ) istnieją na poziomie od 3 do 5. Parazwarte grupy simpleksowe ( Koszul simplices ) istnieją do rangi 10. Grupy hiperzwarte ( Vinberg polytopes ) zostały zbadane, ale nie zostały w pełni określone. W 2006 roku Allcock udowodnił, że istnieje nieskończenie wiele zwartych polytopów Vinberga dla wymiaru do 6 i nieskończenie wiele polytopów Vinberga o skończonej objętości dla wymiaru do 19, więc pełne wyliczenie nie jest możliwe. Wszystkie te podstawowe domeny refleksyjne, zarówno proste, jak i nieproste, są często nazywane wielościanami Coxetera lub czasami mniej dokładnie wielościanami Coxetera .

Grupy hiperboliczne w H ²

Model dysku Poincarégo podstawowych trójkątów domeny
Przykładowe trójkąty prostokątne [p,q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞,∞]
Przykładowe trójkąty ogólne [(p,q,r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3,∞)]
[(3,4,4)]	[(3,6,6)]	[(3,∞,∞)]	[(6,6,6)]	[(∞,∞,∞)]

Dwuwymiarowe grupy trójkątów hiperbolicznych istnieją jako diagramy Coxetera stopnia 3, zdefiniowane przez trójkąt (pqr) dla:

{\ Displaystyle {\ Frac {1} {p}} + {\ Frac {1} {q}} + {\ Frac {1} {r} <1.}

Istnieje nieskończenie wiele zwartych trójkątnych hiperbolicznych grup Coxetera, w tym grafów liniowych i trójkątnych. Wykresy liniowe istnieją dla trójkątów prostokątnych (z r=2).

Zwarte hiperboliczne grupy Coxetera

Liniowy

Cykliczny

∞ [p,q], : 2(p+q)<pq

... ... ...

∞ [(p,q,r)], : p+q+r>9

			...

Grupy Paracompact Coxeter rzędu 3 istnieją jako ograniczenia dla grup zwartych.

Wykresy liniowe	Wykresy cykliczne
[p,∞] [∞,∞]	[(p,q,∞)] [(p,∞,∞)] [(∞,∞,∞)]

Grupa trójkątów arytmetycznych

Hiperboliczne grupy trójkątów , które są również grupami arytmetycznymi, tworzą skończony podzbiór. Pełną listę ustalił za pomocą wyszukiwania komputerowego Kisao Takeuchi w swoim artykule z 1977 r. „Arytmetyczne grupy trójkątów” . Jest ich łącznie 85, 76 kompaktowych i 9 parakompaktowych.

Trójkąty prostokątne (pq 2)	Trójkąty ogólne (pqr)
) , , , , , , , , , , , , , , , , , , , Grupy , , , , , zwarte : , , , , (76 Parazwarte trójkąty prostokątne: (4) , , ,	, , Trójkąty : , , , , ogólne , , , , , , , , , , , , , , , , , , , , , , , , , (39) Parazwarte trójkąty ogólne: (5) , , , ,
(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30) (2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12) , (2 4 18), (2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30) (2 6 6), ( 2 6 8), (2 6 12) (2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18) (2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18) (2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)	(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15) (3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30) , (3 12 12) (4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16) (5 5 5), (5 5 10), (5 5 15), (5 10 10) (6 6 6), (6 12 12), (6 24 24) ( 7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15) (3,3 ∞) (3 ∞ ∞) (4,4 ∞) ( 6 6 ∞) (∞ ∞ ∞)

Hiperboliczne wielokąty Coxetera nad trójkątami

Dziedziny podstawowe grup czworobocznych
Dziedziny z idealnymi wierzchołkami
lub [∞,3,∞] [iπ/λ ₁ ,3,iπ/λ ₂ ] (*3222)	lub [((3,∞,3)),∞] [(3,iπ/λ ₁ ,3)),iπ/λ ₂ ] (*3322)	lub [(3,∞) ^[2] ] [(3,iπ/λ ₁ ,3,iπ/λ ₂ )] (*3232)	lub [(4,∞) ^[2] ] [(4,iπ/λ ₁ ,4,iπ/λ ₂ )] (*4242)	(*3333)
[iπ/λ ₁ ,∞,iπ/λ ₂ ] (*∞222)	(*∞∞22)	[(iπ/λ ₁ ,∞,iπ/λ ₂ ,∞)] (*2∞2∞)	(*∞∞∞∞)	(*4444)

Inne hiperboliczne kalejdoskopy H ² można zbudować z wielokątów wyższego rzędu. Podobnie jak grupy trójkątów , te kalejdoskopy można zidentyfikować na podstawie cyklicznej sekwencji lustrzanych rzędów przecięć wokół domeny podstawowej, as (abcd…) lub równoważnie w notacji orbifold jako * abcd … Diagramy Coxetera-Dynkina dla tych wielokątnych kalejdoskopów może być postrzegane jako zdegenerowane (n-1)- simpleksowe domeny fundamentalne, z cyklicznym rzędem rozgałęzień a,b,c... a pozostałe gałęzie n*(n-3)/2 są oznaczone jako nieskończone (∞) reprezentujące nieprzecinające się lustra. Jedynym niehiperbolicznym przykładem jest symetria euklidesowa z czterema lustrami w kwadracie lub prostokącie jako , [∞,2,∞] (orbifold *2222). Inna reprezentacja gałęzi dla nieprzecinających się zwierciadeł autorstwa Vinberga daje nieskończone gałęzie jako linie kropkowane lub przerywane, więc ten diagram można przedstawić jako , z czterema gałęziami rzędu 2 stłumionymi na obwodzie.

Na przykład czworoboczna domena (abcd) będzie miała dwie nieskończone gałęzie porządku łączące ultrarównoległe lustra. Najmniejszym przykładem hiperbolicznym jest , [∞,3,∞] lub [iπ/λ ₁ ,3,iπ/λ ₂ ] (orbifold *3222), gdzie (λ ₁ ,λ ₂ ) to odległość między ultrarównoległymi zwierciadłami. Alternatywnym wyrażeniem jest , z trzema gałęziami rzędu 2 stłumionymi na obwodzie. Podobnie (2 3 2 3) (orbifold *3232) można przedstawić jako i (3 3 3 3), (orbifold *3333) można przedstawić jako pełny graf .

Najwyższą domeną czworoboku (∞ ∞ ∞ ∞) jest nieskończony kwadrat, reprezentowany przez pełny graf czworościenny z 4 gałęziami obwodowymi jako wierzchołkami idealnymi i dwiema gałęziami ukośnymi jako nieskończonością (pokazanymi jako linie przerywane) dla zwierciadeł ultrarównoległych : .

Kompaktowe (grupy Lannér simplex)

Zwarte grupy hiperboliczne nazywane są grupami Lannéra na cześć Folke Lannéra, który jako pierwszy badał je w 1950 roku. Istnieją tylko jako wykresy rangi 4 i 5. Coxeter badał liniowe hiperboliczne grupy Coxetera w swoim artykule z 1954 r. Regular Honeycombs in hyperbolic space , który zawierał dwa racjonalne rozwiązania w hiperbolicznej 4-przestrzeni : [5/2,5,3,3] = i [5,5/2,5, 3] = .

Rangi 4–5

Dziedzina podstawowa jednej z dwóch grup bifurkacyjnych, [5,3 ^1,1 ] i [5,3,3 ^1,1 ], jest dwukrotnie większa niż w przypadku odpowiedniej grupy liniowej [5,3,4] i [5 ,3,3,4] odpowiednio. Nazwy liter są podane przez Johnsona jako rozszerzone symbole Witta .

Zwarte hiperboliczne grupy Coxetera
Wymiar wys ^{. śr}	Ranga	Całkowita liczba	Liniowy	rozwidlające się	Cykliczny
H ³	4	9	3: ${\ Displaystyle {\ overline {BH}} _ {3}}$ = [4,3,5]: ${\ Displaystyle {\ overline {K}} _ {3}}$ = [5, 3,5]: ${\ Displaystyle {\ overline {J}} _ {3}}$ = [3,5,3]:	${\ Displaystyle {\ overline {DH}} _ {3}}$ = [5,3 ^1,1 ]:	${\ Displaystyle {\ widehat {AB}} _ {3}}$ = [(3 ^3,4 )]: ${\ Displaystyle {\ widehat {AH}} _ {3}}$ = [ (3 ^3,5 )]: ${\ Displaystyle {\ widehat {BB}} _ {3}}$ = [(3,4) ^[2] ]: ${\ Displaystyle {\ widehat { BH}} _ {3}}$ = [(3,4,3,5)]: ${\ Displaystyle {\ widehat {HH}} _ {3}}$ = [(3,5) ^[2] ]:
4 ^_	5	5	3: ${\ Displaystyle {\ overline {H}} _ {4}}$ = [3 ^3,5 ]: ${\ Displaystyle {\ overline {BH}} _ {4}}$ = [4,3 3,5]: ${\ Displaystyle {\ overline {K}} _ {4}}$ = [5,3,3,5]:	${\ Displaystyle {\ overline {DH}} _ {4}}$ = [5,3,3 ^1,1 ]:	${\ Displaystyle {\ widehat {AF}} _ {4}}$ = [(3 ^4,4 )]:

Paracompact (koszulskie grupy simplex)

Przykładowe ułożenie apeirogonalne rzędu 3 , {∞,3} z jednym zielonym apeirogonem i jego opisanym horocyklem

Parazwarte (zwane także niezwartymi) hiperboliczne grupy Coxetera zawierają podgrupy afiniczne i mają asymptotyczne domeny podstawowe simplex. Najwyższa parazwarta hiperboliczna grupa Coxetera ma rangę 10. Grupy te zostały nazwane na cześć francuskiego matematyka Jean-Louisa Koszula . Są one również nazywane grupami quasi-Lannéra rozszerzającymi zwarte grupy Lannéra. Lista została uznana za kompletną na podstawie wyszukiwania komputerowego przez M. Cheina i opublikowana w 1969 roku.

Według Vinberga, wszystkie oprócz ośmiu z tych 72 zwartych i parazwartych uproszczeń są arytmetyczne. Dwie grupy niearytmetyczne są zwarte: i . Pozostałe sześć grup niearytmetycznych jest parazwartych, z pięcioma grupami trójwymiarowymi , , , , i oraz jedną grupą 5-wymiarową .

Idealne uproszczenia

Idealne podstawowe domeny , [(∞, ∞, ∞)] widoczne w modelu dysku Poincarego

Istnieje 5 hiperbolicznych grup Coxetera wyrażających idealne uproszczenia , wykresy, w których usunięcie dowolnego węzła daje afiniczną grupę Coxetera. Zatem wszystkie wierzchołki tego idealnego simpleksu są w nieskończoności.

Ranga	Idealna grupa	Podgrupy afiniczne
3	[(∞,∞,∞)]	[∞]
4	[4 ^[4] ]	[4,4]
4	[3 ^[3,3] ]	[3 ^[3] ]
4	[(3,6) ^[2] ]	[3,6]
6	[(3,3,4) ^[2] ]	[4,3,3,4], [3,4,3,3]	,

Rangi 4–10

Nieskończone komórki euklidesowe, takie jak sześciokątne kafelki , odpowiednio wyskalowane, zbiegają się w jednym idealnym punkcie w nieskończoności, jak sześciokątny kafelkowy plaster miodu , {6,3,3}, jak pokazano z tą pojedynczą komórką w projekcji modelu dysku Poincarégo .

Istnieje łącznie 58 parakompaktowych hiperbolicznych grup Coxetera od rangi 4 do 10. Wszystkie 58 są pogrupowane poniżej w pięciu kategoriach. Symbole literowe są podane przez Johnsona jako rozszerzone symbole Witta , używając PQRSTWUV z afinicznych symboli Witta i dodając LMNOXYZ. Te grupy hiperboliczne mają nadkreślenie lub czapkę dla cykloschematów. Notacja nawiasów z Coxetera jest linearyzowaną reprezentacją grupy Coxetera.

Hiperboliczne grupy parazwarte
Ranga	Całkowita liczba	Grupy
4	23	${\ Displaystyle {\ widehat {BR}} _ {3}}$ = [(3,3,4,4)]: ${\ Displaystyle {\ widehat {CR}} _ {3} }$ = [(3,4 ³ )]: ${\ Displaystyle {\ widehat {RR}} _ {3}}$ = [4 ^[4] ]: ${\ Displaystyle {\ widehat {AV }} _ {3}}$ = [(3 ^3,6 )]: ${\ Displaystyle {\ widehat {BV}} _ {3}}$ = [(3,4,3,6)]: ${\ Displaystyle {\ widehat {HV}} _ {3}}$ = [(3,5,3,6)]: ${\ Displaystyle {\ widehat {VV}} _ {3}}$ = [(3,6) ^[2] ]:	${\ Displaystyle {\ overline {P}} _ {3}}$ = [3,3 ^[3] ]: ${\ Displaystyle {\ overline {BP}} _ {3}}$ = [4 3 ^[3] ]: ${\ Displaystyle {\ overline {HP}} _ {3}}$ = [5,3 ^[3] ]: ${\ Displaystyle {\ overline {VP}} _ {3}}$ = [6,3 ^[3] ]: ${\ Displaystyle {\ overline {DV}} _ {3}}$ = [6,3 ^1,1 ]: ${\ Displaystyle {\ overline {O}} _ {3}}$ = [3,4 ^1,1 ]: ${\ Displaystyle {\ overline {M}} _ {3}}$ = [4 ^1,1,1 ]:	${\ Displaystyle {\ overline {R}} _ {3}}$ = [3,4,4]: ${\ Displaystyle {\ overline {N}} _ {3}}$ = [4 ³ ] : ${\ Displaystyle {\ overline {V}} _ {3}}$ = [3,3,6]: ${\ Displaystyle {\ overline {BV}} _ {3}}$ = [4 ,3,6]: ${\ Displaystyle {\ overline {HV}} _ {3}}$ = [5,3,6]: ${\ Displaystyle {\ overline {Y}} _ {3 }}$ = [3,6,3]: ${\ Displaystyle {\ overline {Z}} _ {3}}$ = [6,3,6]:	${\ Displaystyle {\ overline {DP}} _ {3}}$ = [3 ^{[] x []} ]: ${\ Displaystyle {\ overline {PP}} _ {3}}$ = [ 3 ^[3,3] ]:
5	9	${\ Displaystyle {\ overline {P}} _ {4}}$ = [3,3 ^[4] ]: ${\ Displaystyle {\ overline {BP}} _ {4}}$ = [4 3 ^[4] ]: ${\ Displaystyle {\ widehat {FR}} _ {4}}$ = [(3 ² , 4,3,4)]: $\ Displaystyle {\ overline {DP}}_{4}}$ = [3 ^[3]x[] ]:	${\ Displaystyle {\ overline {N}} _ {4}}$ = [4,3, ((4,2,3))]: ${\ Displaystyle {\ overline {O}} _ { 4}}$ = [3,4,3 ^1,1 ]: ${\ Displaystyle {\ overline {S}} _ {4}}$ = [4,3 ^2,1 ]:	${\ Displaystyle {\ overline {R}} _ {4}}$ = [(3,4) ² ]:	${\ Displaystyle {\ overline {M}} _ {4}}$ = [4,3 ^1,1,1 ]:
6	12	${\ Displaystyle {\ overline {P}} _ {5}}$ = [3,3 ^[5] ]: ${\ Displaystyle {\ widehat {AU}} _ {5}}$ = [( 3 ⁵ , 4)]: ${\ Displaystyle {\ widehat {AR}} _ {5}}$ = [(3,3,4) ^[2] ]:	${\ Displaystyle {\ overline {S}} _ {5}}$ = [4,3,3 ^2,1 ]: ${\ Displaystyle {\ overline {O}} _ {5}}$ = [ 3,4,3 ^1,1 ]: ${\ Displaystyle {\ overline {N}} _ {5}}$ = [3, (3,4) ^1,1 ]:	${\ Displaystyle {\ overline {U}} _ {5}}$ = [3 ^3,4,3 ]: ${\ Displaystyle {\ overline {X}} _ {5}}$ = [3, 3,4,3,3]: ${\ Displaystyle {\ overline {R}} _ {5}}$ = [3,4,3,3,4]:	${\ Displaystyle {\ overline {Q}} _ {5}}$ = [3 ^2,1,1,1 ]: ${\ Displaystyle {\ overline {M}} _ {5}}$ = [4,3,3 ^1,1,1 ]: ${\ Displaystyle {\ overline {L}} _ {5}}$ = [3 ^1,1,1,1,1 ]:
7	3	${\ Displaystyle {\ overline {P}} _ {6}}$ = [3,3 ^[6] ]:	${\ Displaystyle {\ overline {Q}} _ {6}}$ = [3 ^1,1 , 3,3 ^2,1 ]:	${\ Displaystyle {\ overline {S}} _ {6}}$ = [4,3 ² , 3 ^2,1 ]:
8	4	${\ Displaystyle {\ overline {P}} _ {7}}$ = [3,3 ^[7] ]:	${\ Displaystyle {\ overline {Q}} _ {7}}$ = [3 ^1,1 , 3 ² , 3 ^2,1 ]:	${\ Displaystyle {\ overline {S}} _ {7}}$ = [4,3 ^3,3^2,1 ] :	${\ Displaystyle {\ overline {T}} _ {7}}$ = [3 ^3,2,2 ]:
9	4	${\ Displaystyle {\ overline {P}} _ {8}}$ = [3,3 ^[8] ]:	${\ Displaystyle {\ overline {Q}} _ {8}}$ = [3 ^1,1 , 3 ³ , 3 ^2,1 ]:	${\ Displaystyle {\ overline {S}} _ {8}}$ = [4,3 ^4,3^2,1 ] :	${\ Displaystyle {\ overline {T}} _ {8}}$ = [3 ^4,3,1 ]:
10	3		${\ Displaystyle {\ overline {Q}} _ {9}}$ = [3 ^1,1 , 3 ⁴ , 3 ^2,1 ]:	${\ Displaystyle {\ overline {S}} _ {9}}$ = [4,3 ^5,3^2,1 ] :	${\ Displaystyle {\ overline {T}} _ {9}}$ = [3 ^6,2,1 ]:

Relacje podgrup parazwartych grup hiperbolicznych

Drzewa te reprezentują relacje podgrup parazwartych grup hiperbolicznych. Indeksy podgrup na każdym połączeniu są podane na czerwono. Podgrupy indeksu 2 reprezentują usunięcie lustra i podwojenie domeny podstawowej. Inne można wywnioskować na podstawie współmierności (całkowitego stosunku objętości) dla domen czworościennych.

Drzewa podgrup
H ³
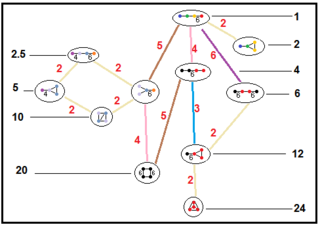
H ⁴
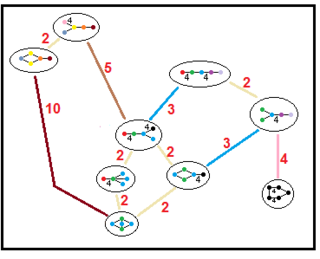
H ⁵

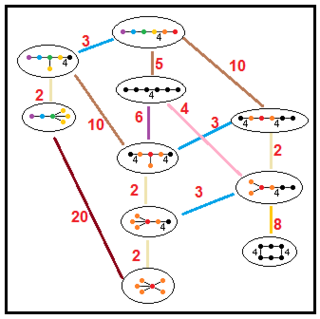
Hiperkompaktowe grupy Coxetera (Vinberg polytopes)

Tak jak płaszczyzna hiperboliczna $H 2$ ma nietrójkątne domeny wielokątne, podobnie domeny niesimpleksowe istnieją w wielowymiarowych przestrzeniach hiperbolicznych. Te domeny nieproste można uznać za zdegenerowane uproszczenia z nieprzecinającymi się lustrami o nieskończonym porządku; na diagramie Coxetera takie gałęzie są oznaczone liniami przerywanymi lub przerywanymi. Te niesimpleksowe nazywane są Vinberg polytopes , na cześć Ernesta Vinberga , który opracował algorytm znajdowania niesimpleksowej domeny podstawowej hiperbolicznej grupy refleksyjnej. Geometrycznie te podstawowe domeny można sklasyfikować jako czworoboczne $kątach$ lub graniastosłupy lub inne polytopy z krawędziami jako przecięcie dwóch luster dwuściennych dla ${\ displaystyle n = 2,3,4...}$

W domenie opartej na simpleksie istnieje $n+1$ luster dla przestrzeni $n$ -wymiarowej. W domenach innych niż simplex istnieje więcej niż $n+1$ serwerów lustrzanych. Lista jest skończona, ale nie do końca znana. Zamiast tego listy częściowe zostały wyliczone jako $n + k$ luster dla $k$ jako 2, 3 i 4.

Hiperkompaktowe grupy Coxetera w przestrzeni trójwymiarowej lub wyższej różnią się od grup dwuwymiarowych pod jednym zasadniczym względem. Dwa $n$ -kąty hiperboliczne mające te same kąty w tym samym porządku cyklicznym mogą mieć różne długości krawędzi i generalnie nie są przystające . Natomiast politopy Vinberga w 3 wymiarach lub wyższych są całkowicie określone przez kąty dwuścienne. Fakt $definiują$ opiera się na twierdzeniu Mostowa o sztywności , że dwie grupy izomorficzne generowane przez odbicia w $przystające domeny$ polytopy Vinberga ).

Politopy Vinberga o randze $n+2$ dla przestrzeni $n -wymiarowej$

Pełną listę zwartych hiperbolicznych polytopów Vinberga ze zwierciadłami rangi $n + 2$ dla $n$ wymiarów wyliczył F. Esselmann w 1996 r. Częściowa lista została opublikowana w 1974 r. Przez IM Kaplinskaya.

Pełną listę rozwiązań parakompaktowych opublikował P. Tumarkin w 2003 roku, o wymiarach od 3 do 17.

Najmniejsza forma parazwarta w $H 3$ może być reprezentowana przez , lub [∞,3,3,∞], które można skonstruować przez lustrzane usunięcie parazwartej grupy hiperbolicznej [3,4,4] jako [3,4,1 ⁺ , 4]. Podwojona domena podstawowa zmienia się z czworościanu w czworoboczną piramidę. Inne piramidy to [4,4,1 ⁺ ,4] = [∞,4,4,∞], = . Usunięcie lustra z niektórych cyklicznych hiperbolicznych grafów Coxetera staje się grafami muszkowymi: [(3,3,4,1 ⁺ ,4)] = [((3,∞,3)),((3,∞,3 ))] lub , [(3,4,4,1 ⁺ ,4)] = [((4,∞,3)),((3,∞,4))] lub , [(4,4,4 ,1 ⁺ ,4)] = [((4,∞,4)),((4,∞,4))] lub .

Inne ważne grafy parazwarte z podstawowymi domenami piramidy czworobocznej obejmują:

Wymiar	Ranga	Wykresy
H ³	5	, , , , , , , , , , , , , , , , , , , , , , , , _ _ _

Kolejna podgrupa [1 ⁺ ,4 ^1,1,1 ] = [∞,4,1 ⁺ ,4,∞] = [∞ ^[6] ]. = = .

Politopy Vinberga o randze $n+3$ dla przestrzeni $n -wymiarowej$

Istnieje skończona liczba zdegenerowanych podstawowych uproszczeń aż do wymiaru 8. Grupy te są oznaczone liniami przerywanymi/kropkowanymi dla gałęzi ultrarównoległych.

Pełna lista zwartych polytopów Vinberga ze zwierciadłami rangi $n + 3$ dla $n$ wymiarów została po raz pierwszy wyliczona przez P. Tumarkina w 2004 r., A następnie opublikowana w całości w 2007 r. Z pewnymi poprawkami. Najwyższą liczbę odkrył Bugaenko w 1984 roku w wymiarze 8, ranga 11. W wymiarze 7 nie ma rozwiązań.

Pomiędzy wymiarami 4 a 8, rangi od 7 do 11 grup Coxetera są liczone odpowiednio jako 40, 16, 3, 0 i 1:

Wymiary	Ranga	Sprawy	Wykresy
4 ^_	7	40	...
5 ^_	8	16	..
H ⁶	9	3
H ⁷	10	0
H ⁸	11	1

Z drugiej strony, pełną listę niezwartych polytopów Vinberga ze zwierciadłami rangi $n + 3$ i jednym nieprostym wierzchołkiem dla $n$ wymiarów wyliczył Mike Roberts.

Politopy Vinberga o randze $n+4$ dla przestrzeni $n -wymiarowej$

Istnieje skończona liczba zdegenerowanych podstawowych uproszczeń, które istnieją aż do wymiaru 7. Zwarte politopy Vinberga ze zwierciadłami rangi $n + 4$ dla $n$ wymiarów zostały zbadane przez A. Feliksona i P. Tumarkina po raz pierwszy w 2005 r., A wyniki zostały formalnie opublikowane w 2008 r. Oni zgłosił znalezienie jednego unikalnego rozwiązania w wymiarze 7 z 11 lustrzanymi ścianami i udowodnił, że nie istnieją żadne inne rozwiązania w wyższych wymiarach.

grupy lorentzowskie

Regularne plastry miodu z grupami Lorentza
{3,3,7} oglądane poza modelem kuli Poincarego	{7,3,3} oglądane poza modelem kuli Poincarego

To pokazuje grupy lorentzowskie rangi 5 ułożone jako podgrupy z [6,3,3,3] i [6,3,6,3]. Wysoce symetryczna grupa [3 ^[3,3,3] ] jest podgrupą o indeksie 120 [6,3,3,3].

Grupy Lorentza dla domen simplex można zdefiniować jako wykresy wykraczające poza parazwarte formy hiperboliczne. Są one czasami nazywane superidealnymi uproszczeniami i są również związane z geometrią Lorentza , nazwaną na cześć Hendrika Lorentza w dziedzinie czasoprzestrzeni szczególnej i ogólnej teorii względności , zawierającej jeden (lub więcej) podobnych do czasu komponentów wymiarowych, których iloczyny własne są ujemne . Danny Calegari nazywa te wypukłe współzwarte grupy Coxetera w n-wymiarowej przestrzeni hiperbolicznej.

Poziom 2

Artykuł George'a Maxwella z 1982 r., Sphere Packings and Hyperbolic Reflection Groups , wylicza skończoną listę lorentzowskich grup refleksyjnych o randze od 5 do 11. Nazywa je poziomem 2 , co oznacza, że usunięcie dowolnej permutacji 2 węzłów pozostawia graf skończony lub euklidesowy.

Wszystkie grupy gałęzi Coxetera wyższego rzędu rangi 4 są lorentzowskie i kończą się w granicy jako pełny wykres 3- simpleksowy diagram Coxetera-Dynkina z 6 gałęziami nieskończonego rzędu, co można wyrazić jako [∞ ^[3,3] ). Rangi 5-11 mają skończoną liczbę grup odpowiednio 186, 66, 36, 13, 10, 8 i 4 grup Lorentza.

Artykuł z 2013 r. autorstwa H. Chena i J.-P. Labbé, Lorentzian Coxeter groups i Boyd--Maxwell ball Packagings przeliczyli i opublikowali pełną listę, dodając 3 nowe grupy o randze 5, w sumie 189.

To jest pełna lista, w tym grafiki dla rang od 5 do 7.

grupy Lorentza Coxetera
Ranga	Wykresy	Opakowania	Grupy
4	∞	∞	[3,3,7] ... [∞,∞,∞]: ... [4,3 ^[3] ] ... [∞,∞ ^[3] ]: ... [5,4 ^1,1 ] ... [∞ ^1,1,1 ]: ... ... [ (5,4,3,3)] ... [∞ ^[4] ]: ... ... ... [4 ^[]×[] ] ... [∞ ^[]×[] ]: . .. ... [4 ^[3,3] ] ... [∞ ^[3,3] ]
5	186+3	95+	...[3 ^[3,3,3] ]: ...
6	66	30	...[4,3 ^1,1,1,1 ]:
7	36	13	...[3 ^1,1,1,1,1,1 ]:
8	13	9	[3,3,3 ^[6] ]: [3,3 ^[6] ,3]: [3,3 ^[2+4] ,3]: [3,3 ^[1+5] ,3]: [3 ^{[ ]e×[3]} ]:	[4,3,3,3 ^3,1 ]: [3 ^1,1 ,3,3 ^3,1 ]: [3,(3,3,4) ^1,1 ]: [3 ^2,1 ,3, 3 ^2,1 ]:		[4,3,3,3 ^2,2 ]: [3 ^1,1 ,3,3 ^2,2 ]:
9	10	8	[3,3 ^[3+4] ,3]: [3,3 ^[9] ]: [3,3 ^[2+5] ,3]:	[3 ^2,1 ,3 ² ,3 ^2,1 ]:	[3 ^3,1 ,3 ³ ,4]: [3 ^3,1 ,3,3,3 ^1,1 ]:	[3 ^3,3,2 ]: [3 ^2,2,4 ]: [3 ^2,2 ,3 ³ ,4]: [3 ^2,2 ,3,3,3 ^1,1 ]:
10	8	7	[3,3 ^[8] ,3]: [3,3 ^[3+5] ,3]: [3,3 ^[9] ]:	[3 ^2,1 ,3 ³ ,3 ^2,1 ]:	[3 ^5,3,1 ]: [3 ^3,1 ,3 ⁴ ,4]: [3 ^3,1 ,3 ³ ,3 ^1,1 ]:	[3 ^4,4,1 ]:
11	4	3		[3 ^2,1 ,3 ⁴ ,3 ^2,1 ]:	[3 ^2,1 ,3 ⁶ ,4]: [3 ^2,1 ,3 ⁵ ,3 ^1,1 ]:	[3 ^7,2,1 ]:

Bardzo rozbudowane diagramy Coxetera

Jedno użycie obejmuje bardzo rozszerzoną definicję z bezpośredniego użycia diagramu Dynkina , która traktuje grupy afiniczne jako rozszerzone , hiperboliczne grupy nadmiernie rozszerzone , a trzeci węzeł jako bardzo rozszerzone grupy proste. Te rozszerzenia są zwykle oznaczone wykładnikiem 1, 2 lub 3 + symbole liczby rozszerzonych węzłów. Ta rozszerzająca się seria może zostać przedłużona wstecz, poprzez sekwencyjne usuwanie węzłów z tej samej pozycji na wykresie, chociaż proces zatrzymuje się po usunięciu rozgałęzionego węzła. E i ₈ jest najczęściej pokazywanym przykładem rozciągającym się wstecz od E ₃ dalej do E ₁₁ .

Proces rozszerzania może definiować ograniczoną serię grafów Coxetera, które przechodzą od skończonych do afinicznych, hiperbolicznych do lorentzowskich. Wyznacznik macierzy Cartana określa, gdzie szereg zmienia się od skończonego (dodatniego) do afinicznego (zero) do hiperbolicznego (ujemnego) i kończącego się jako grupa Lorentza, zawierająca co najmniej jedną podgrupę hiperboliczną. Niekrystalograficzne grupy Hn _tworzą rozszerzony szereg, w którym H4 _jest rozszerzony jako zwarta hiperbola i nadmiernie rozciągnięty do grupy lorentzowskiej.

Wyznacznikami macierzy Schläfli według rangi są:

det(A ₁ⁿ = [2 ^n-1 ]) = 2 ⁿ (skończony dla wszystkich n)
det(A _n =[3 ^n-1 ]) = n+1 (skończony dla wszystkich n)
det(B _n = [4,3 ^n-2 ]) = 2 (skończony dla wszystkich n)
det(D _n = [3 ^n-3,1,1 ]) = 4 (skończony dla wszystkich n)

Wyznacznikami macierzy Schläfliego w szeregach wyjątkowych są:

det( E _n =[3 ^n-3,2,1 ]) = 9-n (Skończony dla E ₃ (=A ₂ A ₁ ), E ₄ (=A ₄ ), E ₅ (=D ₅ ), E ₆ , mi ₇ i mi ₈ , afinicznie na mi ₉ ( ${\ Displaystyle {\ tylda {E}} _ {8}}$ ), hiperboliczny na mi ₁₀ )
det ([3 ^n-4,3,1 ]) = 2 (8-n) (skończony dla n = 4 do 7, afiniczny ( ${\ Displaystyle {\ tylda {E}} _ {7}}$ ) i hiperboliczny przy n=8.)
det ([3 ^n-4,2,2 ]) = 3 (7-n) (skończony dla n = 4 do 6, afiniczny ( ${\ Displaystyle {\ tylda {E}} _ {6}}$ ) i hiperboliczny przy n=7.)
det (fa _n = [3,4,3 ^n-3 ]) = 5-n (skończony dla fa ₃ (= b ₃ ) do fa ₄ , afiniczny w fa ₅ ( ${\ Displaystyle {\ tylda {f. }}_{4}}$ ), hiperboliczny w F ₆ )
det (G _n = [6,3 ^n-2 ]) = 3-n (skończony dla G ₂ , afiniczny w sol ₃ ( ${\ Displaystyle {\ tylda {G}} _ {2}}$ ), hiperboliczny w _G4 )

Mniejsza rozszerzona seria
Skończone	${\ Displaystyle A_ {2}}$	${\ displaystyle C_ {2}}$	${\ Displaystyle G_ {2}}$	${\ Displaystyle A_ {3}}$	${\ Displaystyle B_ {3}}$	${\ displaystyle C_ {3}}$	${\ Displaystyle H_ {4}}$
Ranga nr	[3 ^[3] ,3 ^n-3 ]	[4,4,3 ^n-3 ]	G _n = [6,3 ^n-2 ]	[3 ^[4] ,3 ^n-4 ]	[4,3 ^1,n-3 ]	[4,3,4,3 ^n-4 ]	H _n = [5,3 ^n-2 ]
2	[3 _] 2	[4] C ₂	[6] G ₂		[2] A ₁²	[4] C ₂	[5 _] H2
3	[3 ^[3] ] ZA ₂⁺ = ${\ Displaystyle {\ tylda {A}} _ {2}}$	[4,4] do ₂⁺ = ${\ Displaystyle {\ tylda {C}} _ {2}}$	[6,3] sol ₂⁺ = ${\ Displaystyle {\ tylda {G}} _ {2}}$	[3,3]=A ₃	[4,3] B ₃	[4,3] C ₃	[5,3] H ₃
4	[3 ^[3] , 3] ZA ₂⁺⁺ = ${\ Displaystyle {\ overline {P}} _ {3}}$	[4,4,3] do ₂⁺⁺ = ${\ Displaystyle {\ overline {R}} _ {3}}$	[6,3,3] sol ₂⁺⁺ = ${\ Displaystyle {\ overline {V}} _ {3}}$	[3 ^[4] ] ZA ₃⁺ = ${\ Displaystyle {\ tylda {A}} _ {3}}$	[4,3 ^1,1 ] b ₃⁺ = ${\ Displaystyle {\ tylda {B}} _ {3}}$	[4,3,4] do ₃⁺ = ${\ Displaystyle {\ tylda {C}} _ {3}}$	[5,3,3] H ₄
5	[3 ^[3] ,3,3] A ₂⁺⁺⁺	[4,4,3,3] C ₂⁺⁺⁺	[6,3,3,3] G ₂⁺⁺⁺	[3 ^[4] , 3] ZA ₃⁺⁺ = ${\ Displaystyle {\ overline {P}} _ {4}}$	[4,3 ^2,1 ] b ₃⁺⁺ = ${\ Displaystyle {\ overline {S}} _ {4}}$	[4,3,4,3] do ₃⁺⁺ = ${\ Displaystyle {\ overline {R}} _ {4}}$	[5,3 ³ ] H. ₅ = ${\ Displaystyle {\ overline {H}} _ {4}}$
6				[3 ^[4] ,3,3] A ₃⁺⁺⁺	[4,3 ^3,1 ] B ₃⁺⁺⁺	[4,3,4,3,3] do ₃⁺⁺⁺	[5,3 ⁴ ] H ₆
Det(M _n )	3(3- n )	2(3- n )	3- przyp	4(4- n )	2(4- n )

Seria średnio rozszerzona
Skończone	${\ Displaystyle A_ {4}}$	${\ Displaystyle B_ {4}}$	${\ Displaystyle C_ {4}}$	${\ Displaystyle D_ {4}}$	${\ Displaystyle F_ {4}}$	${\ Displaystyle A_ {5}}$	${\ Displaystyle B_ {5}}$	${\ Displaystyle D_ {5}}$
Ranga nr	[3 ^[5] ,3 ^n-5 ]	[4,3,3 ^n-4,1 ]	[4,3,3,4,3 ^n-5 ]	[3 ^n-4,1,1,1 ]	[3,4,3 ^n-3 ]	[3 ^[6] ,3 ^n-6 ]	[4,3,3,3 ^n-5,1 ]	[3 ^1,1 ,3,3 ^n-5,1 ]
3		[4,3 ^−1,1 ] B ₂ ZA ₁	[4,3] B ₃	[3 ^−1,1,1,1 ] ZA ₁³	[3,4] B ₃		[4,3,3] C ₃
4	[3 ³ ] A ₄	[4,3,3] B ₄	[4,3,3] C ₄	[3 ^0,1,1,1 ] D ₄	[3,4,3] F ₄		[4,3,3,3 ^−1,1 ] B ₃ ZA ₁	[3 ^1,1 ,3,3 ^−1,1 ] ZA ₃ ZA ₁
5	[3 ^[5] ] ZA ₄⁺ = ${\ Displaystyle {\ tylda {A}} _ {4}}$	[4,3,3 ^1,1 ] b ₄⁺ = ${\ Displaystyle {\ tylda {B}} _ {4}}$	[4,3,3,4] do ₄⁺ = ${\ Displaystyle {\ tylda {C}} _ {4}}$	[3 ^1,1,1,1 ] re ₄⁺ = ${\ Displaystyle {\ tylda {D}} _ {4}}$	[3,4,3,3] fa ₄⁺ = ${\ Displaystyle {\ tylda {F}} _ {4}}$	[3 ⁴ ] A ₅	[4,3,3,3,3] B ₅	[3 ^1,1 ,3,3] D ₅
6	[3 ^[5] , 3] ZA ₄⁺⁺ = ${\ Displaystyle {\ overline {P}} _ {5}}$	[4,3,3 ^2,1 ] b ₄⁺⁺ = ${\ Displaystyle {\ overline {S}} _ {5}}$	[4,3,3,4,3] do ₄⁺⁺ = ${\ Displaystyle {\ overline {R}} _ {5}}$	[3 ^2,1,1,1 ] re ₄⁺⁺ = ${\ Displaystyle {\ overline {Q}} _ {5}}$	[3,4,3 ³ ] fa ₄⁺⁺ = ${\ Displaystyle {\ overline {U}} _ {5}}$	[3 ^[6] ] ZA ₅⁺ = ${\ Displaystyle {\ tylda {A}} _ {5}}$	[4,3,3,3 ^1,1 ] b ₅⁺ = ${\ Displaystyle {\ tylda {B}} _ {5}}$	[3 ^1,1 ,3,3 ^1,1 ] re ₅⁺ = ${\ Displaystyle {\ tylda {D}} _ {5}}$
7	[3 ^[5] ,3,3] A ₄⁺⁺⁺	[4,3,3 ^3,1 ] B ₄⁺⁺⁺	[4,3,3,4,3,3] do ₄⁺⁺⁺	[3 ^3,1,1,1 ] D ₄⁺⁺⁺	[3,4,3 ⁴ ] F ₄⁺⁺⁺	[3 ^[6] , 3] ZA ₅⁺⁺ = ${\ Displaystyle {\ overline {P}} _ {6}}$	[4,3,3,3 ^2,1 ] b ₅⁺⁺ = ${\ Displaystyle {\ overline {S}} _ {6}}$	[3 ^1,1 ,3,3 ^2,1 ] re ₅⁺⁺ = ${\ Displaystyle {\ overline {Q}} _ {6}}$
8						[3 ^[6] ,3,3] A ₅⁺⁺⁺	[4,3,3,3 ^3,1 ] B ₅⁺⁺⁺	[3 ^1,1 ,3,3 ^3,1 ] D ₅⁺⁺⁺
Det(M _n )	5(5- n )	2(5- n )		4(5- n )	5- przyp	6(6- n )	4(6- n )

Niektóre wyższe rozszerzone serie
Skończone	${\ Displaystyle A_ {6}}$	${\ Displaystyle B_ {6}}$	${\ Displaystyle D_ {6}}$	${\ Displaystyle E_ {6}}$	${\ Displaystyle A_ {7}}$	${\ Displaystyle B_ {7}}$	${\ Displaystyle D_ {7}}$	${\ Displaystyle E_ {7}}$	${8}}$
Ranga nr	[3 ^[7] ,3 ^n-7 ]	[4,3 ³ ,3 ^n-6,1 ]	[3 ^1,1 ,3,3,3 ^n-6,1 ]	[3 ^n-5,2,2 ]	[3 ^[8] ,3 ^n-8 ]	[4,3 ⁴ ,3 ^n-7,1 ]	[3 ^1,1 ,3,3,3,3 ^n-7,1 ]	[3 ^n-5,3,1 ]	mi _n = [3 ^n-4,2,1 ]
3									[3 ^−1,2,1 ] mi ₃ = ZA ₂ ZA ₁
4				[3 ^−1,2,2 ] ZA ₂²				[3 ^−1,3,1 ] ZA ₃ ZA ₁	[3 ^0,2,1 ] mi ₄ = ZA ₄
5		[4,3,3,3,3 ^−1,1 ] B ₄ ZA ₁	[3 ^1,1 ,3,3,3 ^−1,1 ] re ₄ ZA ₁	[3 ^0,2,2 ] A ₅				[3 ^0,3,1 ] A ₅	[3 ^1,2,1 ] mi ₅ = re ₅
6	[3 ⁵ ] A ₆	[4,3 ⁴ ] B ₆	[3 ^1,1 ,3,3,3] D ₆	[3 ^1,2,2 ] E ₆		[4,3,3,3,3,3 ^−1,1 ] B ₅ ZA ₁	[3 ^1,1 ,3,3,3,3 ^−1,1 ] re ₅ ZA ₁	[3 ^1,3,1 ] D ₆	[3 ^2,2,1 ] E ₆ *
7	[3 ^[7] ] ZA ₆⁺ = ${\ Displaystyle {\ tylda {A}} _ {6}}$	[4,3 ^3,3 1,1 ] b ₆⁺ = $B}} _ {6}}$ ^{	[3 ^1,1 ,3,3,3 ^1,1 ] re ₆⁺ = ${\ Displaystyle {\ tylda {D}} _ {6}}$	[3 ^2,2,2 ] mi ₆⁺ = ${\ Displaystyle {\ tylda {E}} _ {6}}$	[3 ⁶ ] A ₇	[4,3 ⁵ ] B ₇	[3 ^1,1 ,3,3,3,3 ^0,1 ] D ₇	[3 ^2,3,1 ] E ₇ *	[3 ^3,2,1 ] E ₇ *
8	[3 ^[7] , 3] ZA ₆⁺⁺ = ${\ Displaystyle {\ overline {P}} _ {7}}$	[4,3 ^3,3 2,1 ] b ₆⁺⁺ = ${S}} _ {7}}$ ^overline	[3 ^1,1 ,3,3,3 ^2,1 ] re ₆⁺⁺ = ${\ Displaystyle {\ overline {Q}} _ {7}}$	[3 ^3,2,2 ] mi ₆⁺⁺ = ${\ Displaystyle {\ overline {T}} _ {7}}$	[3 ^[8] ] ZA ₇⁺ = ${\ Displaystyle {\ tylda {A}} _ {7}}$ *	[4,3 ^4,3 1,1 ] b ₇⁺ = ${B}} _ {7}}$ ^tylda *	[3 ^1,1 ,3,3,3,3 ^1,1 ] re ₇⁺ = ${\ Displaystyle {\ tylda {D}} _ {7}}$ *	[3 ^3,3,1 ] mi ₇⁺ = ${\ Displaystyle {\ tylda {E}} _ {7}}$ *	[3 ^4,2,1 ] E ₈ *
9	[3 ^[7] ,3,3] A ₆⁺⁺⁺	[4,3 ³ ,3 ^3,1 ] B ₆⁺⁺⁺	[3 ^1,1 ,3,3,3 ^3,1 ] D ₆⁺⁺⁺	[3 ^4,2,2 ] E ₆⁺⁺⁺	[3 ^[8] , 3] ZA ₇⁺⁺ = ${\ Displaystyle {\ overline {P}} _ {8}}$ *	[4,3 ^4,3^2,1 ] b ₇⁺⁺ = ${\ Displaystyle {\ overline {S}} _ {8}$ } *	[3 ^1,1 ,3,3,3,3 ^2,1 ] re ₇⁺⁺ = ${\ Displaystyle {\ overline {Q}} _ {8}}$ *	[3 ^4,3,1 ] mi ₇⁺⁺ = ${\ Displaystyle {\ overline {T}} _ {8}}$ *	[3 ^5,2,1 ] mi ₉ = mi ₈⁺ = ${\ Displaystyle {\ tylda {E}} _ {8}}$ *
10					[3 ^[8] ,3,3] A ₇⁺⁺⁺ *	[4,3 ⁴ ,3 ^3,1 ] B ₇⁺⁺⁺ *	[3 ^1,1 ,3,3,3,3 ^3,1 ] D ₇⁺⁺⁺ *	[3 ^5,3,1 ] E ₇⁺⁺⁺ *	[3 ^6,2,1 ] mi ₁₀ = mi ₈⁺⁺ = ${\ Displaystyle {\ overline {T}} _ {9}}$ *
11									[3 ^7,2,1 ] E ₁₁ = E ₈⁺⁺⁺ *
Det(M _n )	7(7- n )	2(7- n )	4(7- n )	3(7- n )	8(8- n )	2(8- n )	4(8- n )	2(8- n )	9- przyp

Składanie geometryczne

Fałdowania skończone i afiniczne
φ _A : A _Γ --> A _Γ' dla typów skończonych
Γ	Γ'	Składany opis	Diagramy Coxetera-Dynkina
ja ₂ ( godz )	Γ(h)	Składanie dwuścienne
B _n	2n _{_}	(ja, s _n )
B _n	Re _n+1 , ZA _2n-1	(A ₃ ,+/-ε)
F ₄	E6 _{_}	( _A3 ,±ε)
4 _{_}	E ₈	( _A4 ,±ε)
H ₃	D ₆
H2 _{_}	4 _{_}
G ₂	5 _{_}	( _A5 ,±ε)
G ₂	D ₄	(D ₄ ,±ε)
φ: A _Γ⁺ --> A _Γ'⁺ dla typów afinicznych
${\ Displaystyle {\ tylda {A}} _ {n-1}}$	${\ Displaystyle {\ tylda {A}} _ {kn-1}}$	Lokalnie banalne
${\ Displaystyle {\ tylda {B}} _ {n}}$	${\ Displaystyle {\ tylda {D}} _ {2n + 1}}$	(ja, s _n )
${\ Displaystyle {\ tylda {B}} _ {n}}$	${\ Displaystyle {\ tylda {D}} _ {n + 1}}$ , ${\ Displaystyle {\ tylda {D}} _ {2n}}$	( _A3 ,±ε)
${\ Displaystyle {\ tylda {C}} _ {n}}$	${\ Displaystyle {\ tylda {B}} _ {n + 1}}$ , ${\ Displaystyle {\ tylda {C}} _ {2n}}$	( _A3 ,±ε)
${\ Displaystyle {\ tylda {C}} _ {n}}$	${\ Displaystyle {\ tylda {C}} _ {2n + 1}}$	(ja, s _n )
${\ Displaystyle {\ tylda {C}} _ {n}}$	${\ Displaystyle {\ tylda {A}} _ {2n + 1}}$	₀ (ja,s _n ) & (ja,s )
	${\ Displaystyle {\ tylda {A}} _ {2n}}$	₀ (A ₃ ,ε) & (I, s )
	${\ Displaystyle {\ tylda {A}} _ {2n-1}}$	(A ₃ ,ε) & (A ₃ ,ε')
${\ Displaystyle {\ tylda {C}} _ {n}}$	${\ Displaystyle {\ tylda {D}} _ {n + 2}}$	(A ₃ ,-ε) & (A ₃ ,-ε')
${\ Displaystyle {\ tylda {C}} _ {2}}$	${\ Displaystyle {\ tylda {D}} _ {5}}$	(ja, s ₁ )
${\ Displaystyle {\ tylda {F}} _ {4}}$	${\ Displaystyle {\ tylda {E}} _ {6}}$ , ${\ Displaystyle {\ tylda {E}} _ {7}}$	( _A3 ,±ε)
${\ Displaystyle {\ tylda {G}} _ {2}}$	${\ Displaystyle {\ tylda {D}} _ {6}}$ , ${\ Displaystyle {\ tylda {E}} _ {7}}$	( _A5 ,±ε)
	${\ Displaystyle {\ tylda {B}} _ {3}}$ , ${\ Displaystyle {\ tylda {F}} _ {4}}$	(B3 _, ±ε)
	${\ Displaystyle {\ tylda {D}} _ {4}}$ , ${\ Displaystyle {\ tylda {E}} _ {6}}$	(D4 _, ±ε)

(Po prostu spleciony) diagram Coxetera-Dynkina (skończony, afiniczny lub hiperboliczny), który ma symetrię (spełniający jeden warunek poniżej), można podzielić przez symetrię, uzyskując nowy, generalnie wielokrotnie spleciony diagram, z procesem o nazwie „ składanie".

Na przykład, w D ₄ składanym do G ₂ , krawędź w G ₂ wskazuje od klasy 3 węzłów zewnętrznych (wartościowość 1) do klasy węzła środkowego (wartościowość 3). A E ₈ składa się na 2 kopie H ₄ , druga kopia przeskalowana przez τ .

Geometrycznie odpowiada to ortogonalnym rzutom jednolitych polytopów i teselacji. Warto zauważyć, że każdy skończony prosty diagram Coxetera-Dynkina można złożyć do I ₂ ( h ), gdzie h jest liczbą Coxetera , która odpowiada geometrycznie rzutowi na płaszczyznę Coxetera .

Kilka hiperbolicznych fałd

Złożone refleksje

Diagramy Coxetera-Dynkina zostały rozszerzone na przestrzeń zespoloną , C ⁿ , gdzie węzły są jednostkowymi odbiciami o okresie większym niż 2. Węzły są oznaczone indeksem, który przyjmuje się za 2 dla zwykłego rzeczywistego odbicia, jeśli jest stłumiony. Coxeter zapisuje grupę zespoloną p[q]r jako diagram .

Jednowymiarowy regularny polytope złożony w jest $reprezentowany$ jako p wierzchołków. Jego rzeczywistą reprezentacją jest wielokąt foremny { p }. Jego symetria to _p [] lub rząd p . Generator operatora unitarnego dla jest postrzegany jako obrót o $ruchu wskazówek zegara$ π/ p radianów w kierunku przeciwnym do , a jest tworzona przez kolejne zastosowania pojedynczego jednostkowego odbicia. Generatorem jednostkowego odbicia dla 1-polytopu z p wierzchołkami jest $e 2π i / p = cos(2π/ p) + i sin(2π/ p)$ . Gdy p = 2, generatorem jest e ^{π i} = –1, to samo co odbicie punktowe w płaszczyźnie rzeczywistej.

W wyższym polytope, _p {} lub reprezentuje element p -krawędziowy, z 2-krawędziami, {} lub , reprezentującymi zwykłą rzeczywistą krawędź między dwoma wierzchołkami.

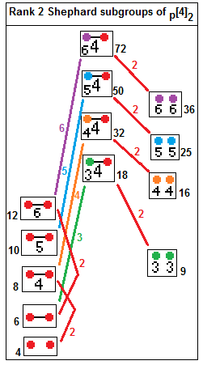
Regularne złożone 1-polytopy
Złożone 1-polytopy, , reprezentowane na płaszczyźnie Arganda jako wielokąty foremne dla p = 2, 3, 4, 5 i 6, z czarnymi wierzchołkami. Środek ciężkości p jest pokazany na czerwono. Boki wielokątów reprezentują jedno zastosowanie generatora symetrii, odwzorowując każdy wierzchołek na następną kopię w kierunku przeciwnym do ruchu wskazówek zegara. Te wieloboczne boki nie są elementami krawędziowymi polytope, ponieważ złożony 1-polytope może nie mieć krawędzi (często jest to krawędź złożona) i zawiera tylko elementy wierzchołków.

12 nieredukowalnych grup Shepharda z ich relacjami indeksów podgrup. Podgrupy o indeksie 2 odnoszą się poprzez usunięcie rzeczywistego odbicia: _p [2 q ] ₂ --> _p [ q ] _p , indeks 2. _p [4] _q --> _p [ q ] _p , indeks q .	_p [4] ₂ podgrupy: p=2,3,4... _p [4] ₂ --> [ p ], indeks p _p [4] ₂ --> _p []× _p [], indeks 2

Regularne złożone wielokąty w , ma postać _diagramu ${\ displaystyle \ mathbb {C} ^ {2}$ lub _do } } . Grupa symetrii wielokąta foremnego zespolonego nie jest nazywana grupą Coxetera , ale grupą Shepharda , rodzajem złożonej grupy refleksyjnej . Kolejność _p [ q ] _r to ${\ Displaystyle 8/q \ cdot (1/p + 2/q + 1/r -1)^{-2}}$ .

Grupy pasterzy rangi 2 to: ₂ [ q ] ₂ , _p [4] ₂ , ₃ [3] ₃ , ₃ [6] ₂ , ₃ [4] ₃ , ₄ [3] ₄ , ₃ [8] ₂ , ₄ [6] ₂ , ₄ [4] ₃ , ₃ [5] ₃ , ₅ [3] ₅ , ₃ [10] ₂ , ₅ [6] ₂ i ₅ [4] 3 _lub , , , , , , , , , , , , , rzędu 2 q , 2 p ² , 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 i 1800 odpowiednio.

Grupa symetrii _{p ₁} [ q ] _{p ₂} jest reprezentowana przez 2 generatory R ₁ , R ₂ , gdzie: R ₁^{p ₁} = R ₂^{p ₂} = I. Jeśli q jest parzyste, (R ₂ R ₁ ) ^{q /2} = (R ₁ R ₂ ) ^{q / 2} . Jeśli q jest nieparzyste, (R ₂ R ₁ ) ^(q-1)/2 R ₂ = (R ₁ R ₂ ) ^{( q -1)/2} R ₁ . Gdy q jest nieparzyste, p ₁ = p ₂ .

Grupa lub [1 1 1] $p$ ^{jest zdefiniowana przez 3} 2 jednostkowych odbić {R _, R ₂ , R ₃ }: R ₁² = R ₁² = R ₃² = (R ₁ R ₂ ) ³ = (R ₂ R ₃ ) ³ = (R ₃ R ₁ ) ³ = (R ₁ R ₂ R ₃ R ₁ ) ^p = 1. Okres p można postrzegać jako podwójny obrót w rzeczywistości ${\ Displaystyle \ mathbb {R} ^ {4}}$ .

Podobna grupa lub [1 1 1] $($ ^p) jest zdefiniowana przez 3 okresy 2 jednostkowych odbić {R _, 2 _, R ₃ }: R ₁² = R ₁² = R ₃² = (R ₁ R ₂ ) ³ = (R ₂ R ₃ ) ³ = (R ₃ R ₁ ) ³ = (R ₁ R ₂ R ₃ R ₂ ) ^p = 1.

Zobacz też

Dalsza lektura

James E. Humphreys , Reflection Groups and Coxeter Groups , Cambridge studies in Advanced Math, 29 (1990)
Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [8] , Googlebooks [ 9]
- (Papier 17) Coxeter , The Evolution of Coxeter-Dynkin diagrams , [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
Coxeter , The Beauty of Geometry: Twelve Essays , Dover Publications, 1999, ISBN 978-0-486-40919-1 (Rozdział 3: Konstrukcja Wythoffa dla jednolitych polytopów)
Coxeter , Regular Polytopes (1963), Macmillan Company
- Regular Polytopes , wydanie trzecie, (1973), wydanie Dover, ISBN 0-486-61480-8 (rozdział 5: Kalejdoskop i sekcja 11.3 Reprezentacja za pomocą wykresów)
HSM Coxeter i WOJ Moser. Generatory i relacje dla grup dyskretnych, wydanie 4, Springer-Verlag. Nowy Jork. 1980
Norman Johnson , Geometrie i transformacje , rozdziały 11,12,13, przedruk 2011
NW Johnson , R. Kellerhals , JG Ratcliffe, ST Tschantz, Rozmiar hiperbolicznego Coxeter simplex , Transformation Groups 1999, tom 4, wydanie 4, s. 329–353 [10] [11]
Norman W. Johnson i Asia Ivic Weiss Kwadratowe liczby całkowite i grupy Coxetera PDF Can. J. Matematyka. Tom. 51 (6), 1999 s. 1307–1336

Linki zewnętrzne

Weisstein, Eric W. „Diagram Coxetera-Dynkina” . MathWorld .
Październik 1978 dyskusja na temat historii diagramów Coxetera autorstwa Coxetera i Dynkina w Toronto , Kanada ; Eugene Dynkin Collection of Mathematics Interviews, Cornell University Library .