Wypukły jednolity plaster miodu

Naprzemienny sześcienny plaster miodu jest jedną z 28 wypełniających przestrzeń jednolitych teselacji w euklidesowej 3-przestrzeni, składających się z naprzemiennych żółtych czworościanów i czerwonych ośmiościanów .

W geometrii wypukły jednolity plaster miodu jest jednolitą teselacją , która wypełnia trójwymiarową przestrzeń euklidesową nienakładającymi się wypukłymi jednolitymi komórkami wielościennymi .

Znanych jest dwadzieścia osiem takich plastrów miodu:

• znajomy sześcienny plaster miodu i 7 jego obciętych części;
• sześcienny plaster miodu i 4 jego obcięcia;
• 10 form graniastosłupowych opartych na równomiernych pokryciach płaskich (11, jeśli zawiera sześcienny plaster miodu);
• 5 modyfikacji niektórych z powyższych przez wydłużenie i/lub bezwładność.

Można je uznać za trójwymiarowy odpowiednik jednolitych nachyleń płaszczyzny .

Diagram Woronoja dowolnej sieci tworzy wypukły jednolity plaster miodu, w którym komórki są zonohedrami .

Historia

• 1900 : Thorold Gosset wyliczył listę półregularnych wypukłych polytopów z regularnymi komórkami ( bryły platońskie ) w swojej publikacji O regularnych i półregularnych figurach w przestrzeni n wymiarów , w tym jeden regularny sześcienny plaster miodu i dwie formy półregularne z czworościanami i ośmiościanami.
• 1905 : Alfredo Andreini wyliczył 25 z tych teselacji.
• 1991 : Manuskrypt Normana Johnsona Uniform Polytopes zidentyfikował listę 28.
• 1994 : Branko Grünbaum w swoim artykule Uniform tilings of 3-space , również niezależnie wyliczył wszystkie 28, po odkryciu błędów w publikacji Andreiniego. Odkrył, że artykuł z 1905 roku, który zawierał 25, zawierał 1 błąd, a 4 brakowało . Grünbaum stwierdza w tym artykule, że Norman Johnson zasługuje na pierwszeństwo w osiągnięciu tego samego wyliczenia w 1991 r. Wspomina również, że I. Aleksiejew z Rosji skontaktował się z nim w sprawie domniemanego wyliczenia tych formularzy, ale Grünbaum nie był wówczas w stanie tego zweryfikować.
• 2006 : George Olshevsky w swoim rękopisie Uniform Panoploid Tetracombs , wraz z powtórzeniem wyprowadzonej listy 11 wypukłych jednolitych nachyleń i 28 wypukłych jednolitych plastrów miodu, rozszerza dalszą pochodną listę 143 wypukłych jednolitych tetracombs ( plastry miodu jednolitych 4- politopów w 4- przestrzeń).

Tylko 14 wypukłych jednorodnych wielościanów pojawia się w tych wzorach:

• trzy z pięciu brył platońskich ( czworościan , sześcian i ośmiościan ),
• sześć z trzynastu brył Archimedesa (tych o odblaskowej symetrii czworościennej lub ośmiościennej) oraz
• pięć z nieskończonej rodziny graniastosłupów (3-, 4-, 6-, 8- i 12-kątne; pryzmat 4-kątny powiela sześcian).

Dwudziestościan , sześcian zadarty i kwadratowy antygraniastosłup pojawiają się w niektórych odmianach, ale te plastry miodu nie mogą być zrealizowane ze wszystkimi krawędziami o jednostkowej długości .

Nazwy

Zestaw ten można nazwać regularnymi i półregularnymi plastrami miodu . Został nazwany plastrami miodu Archimedesa przez analogię do wypukłych jednolitych (nieregularnych) wielościanów, powszechnie nazywanych bryłami Archimedesa . Ostatnio Conway zasugerował nazwanie zestawu teselacjami Architectonic , a podwójnych plastrów miodu teselacjami Catoptric .

Poszczególne plastry miodu są wymienione wraz z nazwami nadanymi im przez Normana Johnsona . (Niektóre z terminów użytych poniżej są zdefiniowane w Uniform 4-polytope # Derivations geometryczne dla 46 niepryzmatycznych uniformów Wythoffian 4-polytopes )

Dla porównania podano je wraz z indeksami z list Andreini (1-22), Williams (1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49) , 51-52, 61-65) i Grünbaum (1-28). Coxeter używa δ ₄ dla sześciennego plastra miodu , hδ ₄ dla naprzemiennego sześciennego plastra miodu , qδ ₄ dla ćwiartki sześciennego plastra miodu , z indeksami dolnymi dla innych form opartych na wzorach pierścieni na diagramie Coxetera.

Kompaktowe jednolite teselacje euklidesowe (według ich nieskończonych rodzin grup Coxetera)

Dziedziny podstawowe w elemencie sześciennym trzech grup.

Korespondencja rodzinna

Podstawowe nieskończone grupy Coxetera dla 3-przestrzeni to:

1. C ${\ Displaystyle {\ tylda {C}} _ ​​{3}}$ , [4,3,4] sześcienny 8 unikalnych form plus jedna odmiana)
2. B ${\ Displaystyle {\ tylda {B}} _ {3}}$ , [4,3 ^1,1 ], naprzemiennie sześcienny ( formularzy, 3 nowe)
3. Grupa cykliczna, [(3,3,3,3)] lub [3 ^[4] ], (5 form, jedna nowa) ZA ~ 3 $Displaystyle {\ tylda {A}} _ {3}$

Istnieje korespondencja między wszystkimi trzema rodzinami. Usunięcie jednego lustra z ${\ Displaystyle {\ tylda {B}} _ {3}}$ i $B}}$ jednego lustra z $\ Displaystyle {\ tylda$ produkuje ${\ Displaystyle {\ tylda {A}} _ {3}}$ . Pozwala to na wiele konstrukcji tych samych plastrów miodu. Jeśli komórki są pokolorowane na podstawie unikalnych pozycji w każdej konstrukcji Wythoffa, można pokazać te różne symetrie.

Ponadto istnieje 5 specjalnych plastrów miodu, które nie mają czystej symetrii odbicia i są zbudowane z form odbicia z operacjami wydłużenia i bezwładności .

Łączna liczba unikalnych plastrów miodu powyżej to 18.

Pryzmatyczne stosy z nieskończonych grup Coxetera dla 3-przestrzeni to:

1. Grupa pryzmatyczna do $\ Displaystyle {\ tylda {C}} _ ​​{2}}$ × ${\ Displaystyle {\ tylda {I}} _ {1}}$ , (2 nowe formy)
2. Grupa ${\ Displaystyle {\ tylda {I}} _ {1}$${\ Displaystyle {\ tylda {G}} _ {2}}$ × } , (7 unikalnych form)
3. ZA ${\ tylda {A}} _ {2}}$${\ Displaystyle {\ tylda {I}} _ {1}}$ × , [(3,3,3), 2, ∞] grupa pryzmatyczna, (Brak nowych form)
4. ja ${\ Displaystyle {\ tylda {I}} _ {1}}$ × ${\ Displaystyle {\ tylda {I}} _ {1}}$ ja $\ Displaystyle {\ tylda {ja }}_{1}}$ , [∞,2,∞,2,∞] grupa pryzmatyczna, (wszystkie stają się sześciennym plastrem miodu )

Ponadto istnieje jeden specjalny wydłużony kształt trójkątnego pryzmatycznego plastra miodu.

Łączna liczba unikalnych pryzmatycznych plastrów miodu powyżej (z wyłączeniem wcześniej zliczonych sześciennych) to 10.

Łącząc te liczby, 18 i 10 daje nam w sumie 28 jednolitych plastrów miodu.

C̃ ₃ , [4,3,4] (sześcienna)

Regularny sześcienny plaster miodu, reprezentowany przez symbol Schläfliego {4,3,4}, oferuje siedem unikalnych wyprowadzonych jednolitych plastrów miodu za pomocą operacji obcinania. (Jedna zbędna forma, sześcienny plaster miodu , jest uwzględniony dla kompletności, chociaż jest identyczny z sześciennym plastrem miodu.) Symetria odbicia to afiniczna grupa Coxetera [4,3,4]. Istnieją cztery podgrupy indeksu 2, które generują alternatywy: [1 ⁺ ,4,3,4], [(4,3,4,2 ⁺ )], [4,3 ⁺ ,4] i [4,3,4 ] ⁺ , przy czym pierwsze dwie wygenerowały powtarzające się formy, a dwie ostatnie są niejednorodne.

plastry miodu C3
Grupa kosmiczna	fibryfold	Rozszerzona symetria	Rozszerzony schemat	Zamówienie	plastry miodu
Pm 3 m (221)	4 − :2	[4,3,4]		×1	1 , 2 , 3 , 4 , 5 , 6
Fm 3 m (225)	2 − : 2	[1 + ,4,3,4] ↔ [4,3 1,1 ]	↔	Połowa	7 , 11 , 12 , 13
I 4 3m (217)	4 o :2	[[(4,3,4,2 + )]]		Połowa × 2	(7) ,
Fd 3 m (227)	2 + :2	[[1 + ,4,3,4,1 + ]] ↔ [[3 [4] ]]	↔	Ćwiartka × 2	10 ,
Im 3 m (229)	8 o :2	[[4,3,4]]		×2	(1) , 8 , 9

[4,3,4], grupa przestrzenna Pm 3 m (221)

Indeksy referencyjne	Nazwa plastra miodu Diagram Coxetera i symbol Schläfliego	Liczba komórek / wierzchołek i pozycje w sześciennym plastrze miodu						Ramki (Perspektywa)	figura wierzchołka	Podwójna komórka
		(0)	(1)	(2)	(3)	Alt	Bryły (częściowe)
J 11,15 A 1 W 1 G 22 δ 4	0 sześcienny (chon) t {4,3,4} {4,3,4}				(8) (4.4.4)				oktaedr	sześcian ,
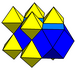
J 12,32 A 15 W 14 G 7 O 1	rektyfikowany sześcienny (bogaty) t 1 {4,3,4} r{4,3,4}	(2) (3.3.3.3)			(4) (3.4.3.4)				prostopadłościan	Kwadratowa bipiramida
J 13 A 14 W 15 G 8 t 1 δ 4 O 15	ścięty sześcienny (tich) t 0,1 {4,3,4} t{4,3,4}	(1) (3.3.3.3)			(4) (3.8.8)				kwadratowa Piramida	Kwadratowa piramida równoramienna
J 14 A 17 W 12 G 9 t 0,2 δ 4 O 14	kantelowany sześcienny (srich) t 0,2 {4,3,4} rr{4,3,4}	(1) (3.4.3.4)	(2) (4.4.4)		(2) (3.4.4.4)				ukośny trójkątny pryzmat	Trójkątna bipiramida
J 17 A 18 W 13 G 25 t 0,1,2 δ 4 O 17	kantitruncated sześcienny (grich) t 0,1,2 {4,3,4} tr{4,3,4}	(1) (4.6.6)	(1) (4.4.4)		(2) (4.6.8)				nieregularny czworościan	Piramida trójkątna
J 18 A 19 W 19 G 20 t 0,1,3 δ 4 O 19	sześcienny ze ściętym cytrynem (prich) t 0,1,3 {4,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.8)	(1) (3.8.8)				ukośna piramida trapezowa	Kwadratowa ćwiartka piramidy
J 21,31,51 A 2 W 9 G 1 hδ 4 O 21	naprzemiennie sześcienny (oktet) h{4,3,4}				(8) (3.3.3)	(6) (3.3.3.3)			sześcienny ośmiościan	dwunastościan
J 22,34 A 21 W 17 G 10 h 2 δ 4 O 25	Kantyk sześcienny (tatoh) ↔	(1) (3.4.3.4)			(2) (3.6.6)	(2) (4.6.6)			ostrosłup prostokątny	Półspłaszczony ośmiościan
J 23 A 16 W 11 G 5 h 3 δ 4 O 26	Runcic sześcienny (sratoh) ↔	(1) (4.4.4)			(1) (3.3.3)	(3) (3.4.4.4)			zwężający się trójkątny pryzmat	Ćwiartka kubika
J 24 A 20 W 16 G 21 h 2,3 δ 4 O 28	Runcicantic sześcienny (gratoh) ↔	(1) (3.8.8)			(1) (3.6.6)	(2) (4.6.8)			Nieregularny czworościan	Pół piramidy
niejednolity b	zadarty rektyfikowany sześcienny (serch) sr{4,3,4}	(1) (3.3.3.3.3)	(1) (3.3.3)		(2) (3.3.3.3.4)	(4) (3.3.3)			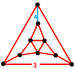Irr. dwudziestościan trójwymiarowy
Niejednolity	0 Cantic snub sześcienny (casch) 2s {4,3,4}	(1) (3.3.3.3.3)			(2) (3.4.4.4)	(3) (3.4.4)
Niejednolity	Runcicantic snub sześcienny (rusch)	(1) (3.4.3.4)	(2) (4.4.4)	(1) (3.3.3)	(1) (3.6.6)	(3) Tricup
Niejednolity	Runcic kantitruncated sześcienny (esch) sr 3 {4,3,4}	(1) (3.3.3.3.4)	(1) (4.4.4)	(1) (4.4.4)	(1) (3.4.4.4)	(3) (3.4.4)

[[4,3,4]] plastry miodu, grupa przestrzenna Im 3 m (229)

Indeksy referencyjne	Nazwa plastra miodu Diagram Coxetera i symbol Schläfliego	Liczba komórek / wierzchołek i pozycje w sześciennym plastrze miodu			Bryły (częściowe)	Ramki (Perspektywa)	figura wierzchołka	Podwójna komórka
		(0,3)	(1,2)	Alt
J 11,15 A 1 W 1 G 22 δ 4 O 1	sześcienny runcinated (tak samo jak zwykły sześcienny ) ( chon ) t 0,3 {4,3,4}	(2) (4.4.4)	(6) (4.4.4)				oktaedr	Sześcian
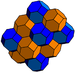
J 16 A 3 W 2 G 28 t 1,2 δ 4 O 16	bitruncated sześcienny (partia) t 1,2 {4,3,4} 2t{4,3,4}	(4) (4.6.6)					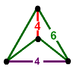( dwufenoidalny )	Oblat czworościan
J 19 A 22 W 18 G 27 t 0,1,2,3 δ 4 O 20	wielościenny sześcienny (gippich) t 0,1,2,3 {4,3,4}	(2) (4.6.8)	(2) (4.4.8)				nieregularny czworościan	Ósma piramida
J 21,31,51 A 2 W 9 G 1 hδ 4 O 27	0 Ćwiartka sześciennego plastra miodu ( batatoh ) ht ht 3 {4,3,4}	(2) (3.3.3)	(6) (3.6.6)				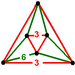wydłużony trójkątny antygraniastosłup	Kabina oblata
J 21,31,51 A 2 W 9 G 1 hδ 4 O 21	Naprzemienny biegnący sześcienny (oktet) (taki sam jak naprzemienny sześcienny) ht 0,3 {4,3,4}	(2) (3.3.3)	(6) (3.3.3)	(6) (3.3.3.3)			sześcienny ośmiościan
Niejednolity	Bioorthosnub sześcienny plaster miodu (gabreth) 2s 0,3 {(4,2,4,3)}	(2) (4.6.6)	(2) (4.4.4)	(2) (4.4.6)
Niejednolity _	Naprzemiennie sześcienny bitruncated (bisch) h2t {4,3,4}	(4) (3.3.3.3.3)		(4) (3.3.3)
Niejednolity	Cantic bisnub sześcienny (cabisch) 2s 0,3 {4,3,4}	(2) (3.4.4.4)	(2) (4.4.4)	(2) (4.4.4)
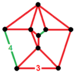
niejednolity c	Naprzemiennie omnitruncated sześcienny (snich) ht 0,1,2,3 {4,3,4}	(2) (3.3.3.3.4)	(2) (3.3.3.4)	(4) (3.3.3)

B̃ ₃ , [4,3 ^1,1 ] grupa

Grupa oferuje 11 form pochodnych za pomocą operacji obcinania, z których cztery to unikalne $miodu$ Istnieją 3 podgrupy indeksu 2, które generują alternatywy: [1 ⁺ ,4,3 ^1,1 ], [4,(3 ^1,1 ) ⁺ ] i [4,3 ^1,1 ] ⁺ . Pierwszy generuje powtarzający się plaster miodu, a dwa ostatnie są niejednorodne, ale uwzględnione dla kompletności.

Plastry miodu z tej grupy nazywane są naprzemiennymi sześciennymi , ponieważ pierwszą formę można postrzegać jako sześcienny plaster miodu z usuniętymi naprzemiennymi wierzchołkami, redukując komórki sześcienne do czworościanów i tworząc komórki ośmiościanu w szczelinach.

0 Węzły są indeksowane od lewej do prawej jako 0,1,0',3, przy czym 0' znajduje się poniżej i jest wymienne z . Podane alternatywne sześcienne są oparte na tej kolejności.

plastry miodu B3
Grupa kosmiczna	fibryfold	Rozszerzona symetria	Rozszerzony schemat	Zamówienie	plastry miodu
Fm 3 m (225)	2 − : 2	[4,3 1,1 ] ↔ [4,3,4,1 + ]	↔	×1	1 , 2 , 3 , 4
Fm 3 m (225)	2 - :2	<[1 + ,4,3 1,1 ]> ↔ <[3 [4] ]>	↔	×2	(1) , (3)
Pm 3 m (221)	4 − :2	<[4,3 1,1 ]>		×2	5 , 6 , 7 , (6) , 9 , 10 , 11

[4,3 ^1,1 ] jednolite plastry miodu, grupa przestrzenna Fm 3 m (225)

Indeksy referencyjne	Diagramy Coxetera o strukturze plastra miodu	Komórki według lokalizacji (i licz wokół każdego wierzchołka)				Bryły (częściowe)	Ramki (Perspektywa)	figura wierzchołka
		(0)	(1)	(0')	(3)
J 21,31,51 A 2 W 9 G 1 hδ 4 O 21	Naprzemiennie sześcienny (oktet) ↔			(6) (3.3.3.3)	(8) (3.3.3)			sześcienny ośmiościan
J 22,34 A 21 W 17 G 10 h 2 δ 4 O 25	Kantyk sześcienny (tatoh) ↔	(1) (3.4.3.4)		(2) (4.6.6)	(2) (3.6.6)			ostrosłup prostokątny
J 23 A 16 W 11 G 5 h 3 δ 4 O 26	Runcic sześcienny (sratoh) ↔	(1) sześcian		(3) (3.4.4.4)	(1) (3.3.3)			zwężający się trójkątny pryzmat
J 24 A 20 W 16 G 21 h 2,3 δ 4 O 28	Runcicantic sześcienny (gratoh) ↔	(1) (3.8.8)		(2) (4.6.8)	(1) (3.6.6)			Nieregularny czworościan

<[4,3 ^1,1 ]> jednolite plastry miodu, grupa przestrzenna Pm 3 m (221)

Indeksy referencyjne	Nazwa plastra miodu Diagramy Coxetera ↔	Komórki według lokalizacji (i licz wokół każdego wierzchołka)				Bryły (częściowe)	Ramki (Perspektywa)	figura wierzchołka
		(0,0')	(1)	(3)	Alt
J 11,15 A 1 W 1 G 22 δ 4 O 1	Sześcienny (chon) ↔	(8) (4.4.4)						oktaedr
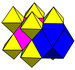
J 12,32 A 15 W 14 G 7 t 1 δ 4 O 15	Rektyfikowany sześcienny (bogaty) ↔	(4) (3.4.3.4)		(2) (3.3.3.3)				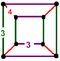prostopadłościan
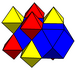
	Rektyfikowany sześcienny (bogaty) ↔	(2) (3.3.3.3)		(4) (3.4.3.4)				prostopadłościan
J 13 A 14 W 15 G 8 t 0,1 δ 4 O 14	Obcięty sześcienny ( tich ) ↔	(4) (3.8.8)		(1) (3.3.3.3)				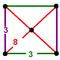kwadratowa Piramida
J 14 A 17 W 12 G 9 t 0,2 δ 4 O 17	Kantelowany sześcienny (srich) ↔	(2) (3.4.4.4)	(2) (4.4.4)	(1) (3.4.3.4)				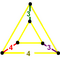ukośny trójkątny pryzmat
J 16 A 3 W 2 G 28 t 0,2 δ 4 O 16	Bitruncated sześcienny (partia) ↔	(2) (4.6.6)		(2) (4.6.6)				czworościan równoramienny
J 17 A 18 W 13 G 25 t 0,1,2 δ 4 O 18	Ścięty sześcienny (grich) ↔	(2) (4.6.8)	(1) (4.4.4)	(1) (4.6.6)				nieregularny czworościan
J 21,31,51 A 2 W 9 G 1 hδ 4 O 21	Naprzemiennie sześcienny (oktet) ↔	(8) (3.3.3)			(6) (3.3.3.3)			sześcienny ośmiościan
J 22,34 A 21 W 17 G 10 h 2 δ 4 O 25	Kantyk sześcienny (tatoh) ↔	(2) (3.6.6)		(1) (3.4.3.4)	(2) (4.6.6)			ostrosłup prostokątny
Niejednolity _	Naprzemiennie sześcienny bitruncated (bisch) ↔	(2) (3.3.3.3.3)		(2) (3.3.3.3.3)	(4) (3.3.3)
niejednolity b	Naprzemiennie sześcienny ścięty ścięty (serch) ↔	(2) (3.3.3.3.4)	(1) (3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)			Irr. dwudziestościan trójwymiarowy

Ă ₃ , [3 ^[4] ] grupa

Istnieje 5 form zbudowanych z ^grupy Coxetera , z $jest$ sześciennego plastra miodu wyjątkowa. Istnieje jedna podgrupa indeksu 2 [3 ^[4] ] ⁺ , która generuje formę lekceważenia, która nie jest jednolita, ale uwzględniona dla kompletności.

plastry miodu A3
Grupa kosmiczna	fibryfold	Symetria kwadratowa	Rozszerzona symetria	Rozszerzony schemat	Rozszerzona grupa	Diagramy o strukturze plastra miodu
F4 3m (216 )	1 o :2	a1	[3 [4] ]		${\ Displaystyle {\ tylda {A}} _ {3}}$	(Nic)
Fm 3 m (225)	2 − : 2	d2	<[3 [4] ]> ↔ [4,3 1,1 ]	↔	${\ Displaystyle {\ tylda {A}} _ {3}}$ × 2 1 ↔ ${\ Displaystyle {\ tylda {B}} _ {3}}$	1 , 2
Fd 3 m (227)	2 + :2	g2	[[3 [4] ]] lub [2 + [3 [4] ]]	↔	${\ Displaystyle {\ tylda {A}} _ {3}}$ × 2 2	3
Pm 3 m (221)	4 − :2	d4	<2[3 [4] ]> ↔ [4,3,4]	↔	${\ Displaystyle {\ tylda {A}} _ {3}}$ × 4 1 ​​↔ ${\ Displaystyle {\ tylda {C}} _ ​​{3}}$	4
ja 3 (204)	8 −o	r8	[4[3 [4] ]] + ↔ [[4,3 + ,4]]	↔	½ ${\ Displaystyle {\ tylda {A}} _ {3}}$ × 8 ↔ ½ ${\ Displaystyle {\ tylda {C}} _ ​​{3}}$ × 2	(*)
Im 3 m (229)	8 o :2		[4[3 [4] ]] ↔ [[4,3,4]]		${\ Displaystyle {\ tylda {A}} _ {3}}$ × 8 ↔ ${\ Displaystyle {\ tylda {C}} _ ​​{3}}$ × 2	5

[[3 ^[4] ]] jednolite plastry miodu, grupa przestrzenna Fd 3 m (227)

Indeksy referencyjne	Diagramy Coxetera o strukturze plastra miodu	Komórki według lokalizacji (i licz wokół każdego wierzchołka)		Bryły (częściowe)	Ramki (Perspektywa)	figura wierzchołka
		(0,1)	(2,3)
J 25,33 A 13 W 10 G 6 qδ 4 O 27	ćwiartka sześcienna (batatoh) ↔ q{4,3,4}	(2) (3.3.3)	(6) (3.6.6)			trójkątny antygraniastosłup

<[3 ^[4] ]> ↔ [4,3 ^1,1 ] jednolite plastry miodu, grupa przestrzenna Fm 3 m (225)

Indeksy referencyjne	Nazwa plastra miodu Diagramy Coxetera ↔	Komórki według lokalizacji (i licz wokół każdego wierzchołka)			Bryły (częściowe)	Ramki (Perspektywa)	figura wierzchołka
		0	(1,3)	2
J 21,31,51 A 2 W 9 G 1 hδ 4 O 21	naprzemiennie sześcienny (oktet) ↔ ↔ h{4,3,4}		(8) (3.3.3)	(6) (3.3.3.3)			sześcienny ośmiościan
J 22,34 A 21 W 17 G 10 h 2 δ 4 O 25	kantyk sześcienny (tatuaż) ↔ ↔ h 2 {4,3,4}	(2) (3.6.6)	(1) (3.4.3.4)	(2) (4.6.6)			Prostokątna piramida

[2[3 ^[4] ]] ↔ [4,3,4] jednolite plastry miodu, grupa przestrzenna Pm 3 m (221)

Indeksy referencyjne	Nazwa plastra miodu Diagramy Coxetera ↔	Komórki według lokalizacji (i licz wokół każdego wierzchołka)		Bryły (częściowe)	Ramki (Perspektywa)	figura wierzchołka
		(0,2)	(1,3)
J 12,32 A 15 W 14 G 7 t 1 δ 4 O 1	rektyfikowany sześcienny (bogaty) ↔ ↔ ↔ r{4,3,4}	(2) (3.4.3.4)	(1) (3.3.3.3)			prostopadłościan

[4[3 ^[4] ]] ↔ [[4,3,4]] jednolite plastry miodu, grupa przestrzenna Im 3 m (229)

Indeksy referencyjne	Nazwa plastra miodu Diagramy Coxetera ↔ ↔	Komórki według lokalizacji (i licz wokół każdego wierzchołka)		Bryły (częściowe)	Ramki (Perspektywa)	figura wierzchołka
		(0,1,2,3)	Alt
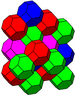
J 16 A 3 W 2 G 28 t 1,2 δ 4 O 16	bitruncated sześcienny (partia) ↔ ↔ 2t{4,3,4}	(4) (4.6.6)				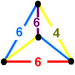czworościan równoramienny
Niejednolity _	Naprzemienny ścięty sześcienny (bisch) ↔ ↔ h2t{4,3,4}	(4) (3.3.3.3.3)	(4) (3.3.3)

Formy nonwythoffiańskie (zawirowane i wydłużone)

Trzy bardziej jednolite plastry miodu są generowane przez rozbicie jednego lub drugiego z powyższych plastrów miodu, gdzie ich powierzchnie tworzą ciągłą płaszczyznę, a następnie obracanie naprzemiennych warstw o ​​60 lub 90 stopni ( bezwładność ) i/lub wstawienie warstwy pryzmatów ( wydłużenie ).

Wydłużone i wydłużone żyroskopowo naprzemienne nachylenia sześcienne mają tę samą figurę wierzchołków, ale nie są do siebie podobne. W wydłużonej formie każdy pryzmat styka się z czworościanem na jednym trójkątnym końcu i ośmiościanem na drugim. W wydłużonej żyroskopowo pryzmaty stykające się z czworościanami na obu końcach występują na przemian z pryzmatami stykającymi się z ośmiościanami na obu końcach.

Wydłużony żyroskopowo trójkątny pryzmatyczny dach ma taki sam kształt wierzchołka, jak jeden ze zwykłych pryzmatycznych dachówek; te dwa można wyprowadzić odpowiednio z wirujących i prostych trójkątnych pryzmatycznych nachyleń, poprzez wstawienie warstw kostek.

Indeksy referencyjne	symbol	Nazwa plastra miodu	typy komórek (# w każdym wierzchołku)	Bryły (częściowe)	Ramki (Perspektywa)	figura wierzchołka
J 52 A 2' G 2 O 22	h{4,3,4}:g	wirujący naprzemiennie sześcienny ( gytoh )	czworościan (8) ośmiościan (6)			trójkątna ortobicupola
J 61A ? _ G 3 O 24	h{4,3,4}:ge	gyroelongated naprzemiennie sześcienny (gyetoh)	graniastosłup trójkątny (6) czworościan (4) ośmiościan (3)
J 62A ? _ G 4 O 23	h{4,3,4}:e	wydłużony naprzemienny sześcienny ( etoh )	graniastosłup trójkątny (6) czworościan (4) ośmiościan (3)
J 63A ? _ G 12 O 12	{3,6}:g × {∞}	zawirowany trójkątny pryzmatyczny ( gytoph )	pryzmat trójkątny (12)
J 64A ? _ G 15 O 13	{3,6}:ge × {∞}	żyroskopowo wydłużony trójkątny pryzmatyczny (gyetaph)	graniastosłup trójkątny (6) sześcian (4)

Stosy pryzmatyczne

Jedenaście pryzmatycznych płytek uzyskuje się przez ułożenie jedenastu jednorodnych płytek płaskich , pokazanych poniżej, w równoległych warstwach. (Jednym z tych plastrów miodu jest sześcienny, pokazany powyżej). Wierzchołek każdego z nich to nieregularna bipiramida , której ściany są trójkątami równoramiennymi .

C̃ ₂ × Ĩ ₁ (∞), [4,4,2,∞], grupa pryzmatyczna

Istnieją tylko 3 unikalne plastry miodu z kwadratowej płytki, ale wszystkie 6 obciętych płytek jest wymienionych poniżej dla kompletności, a obrazy płytek są pokazane kolorami odpowiadającymi każdej formie.

Indeksy	Symbole Coxetera-Dynkina i Schläfliego	Nazwa plastra miodu	Dachówka samolotu	Bryły (częściowe)	Dekarstwo
J 11,15 A 1 G 22	{4,4}×{∞}	Sześcienny (pryzmatyczny kwadratowy) ( chon )	(4.4.4.4)
	r{4,4}×{∞}
	rr{4,4}×{∞}
J 45 A 6 G 24	t{4,4}×{∞}	Pryzmatyczny kwadratowy ścięty / ubity (tassiph)	(4.8.8)
	tr{4,4}×{∞}
J 44 A 11 G 14	sr{4,4}×{∞}	Snub kwadratowy pryzmatyczny (sassiph)	(3.3.4.3.4)
Niejednolity	godz. 0,1,2,3 {4,4,2,∞}

G̃ ₂ xĨ ₁ (∞), [6,3,2,∞]

Indeksy	Symbole Coxetera-Dynkina i Schläfliego	Nazwa plastra miodu	Dachówka samolotu	Bryły (częściowe)	Dekarstwo
J 41 A 4 G 11	{3,6} × {∞}	Trójkątny pryzmatyczny (końcówka)	(3 6 )
J 42 A 5 G 26	{6,3} × {∞}	Sześciokątny pryzmatyczny (biodrowy)	(6 3 )
	t{3,6} × {∞}
J 43 A 8 G 18	r{6,3} × {∞}	Triheksagonalny pryzmatyczny (thiph)	(3.6.3.6)
J 46 A 7 G 19	t{6,3} × {∞}	Ścięty sześciokątny pryzmatyczny ( thaph )	(3.12.12)
J 47 A 9 G 16	rr{6,3} × {∞}	Romb-trójsześciokątny pryzmatyczny (srotaph)	(3.4.6.4)
J 48 A 12 G 17	sr{6,3} × {∞}	Snub sześciokątny pryzmatyczny (snathaph)	(3.3.3.3.6)
J 49 A 10 G 23	tr{6,3} × {∞}	ścięty trójkątny graniastosłup (grothaph)	(4.6.12)
J 65 A 11' G 13	{3,6}: e × {∞}	wydłużony trójkątny pryzmatyczny (etoph)	(3.3.3.4.4)
J 52 A 2' G 2	h3t{3,6,2,∞}	wirujący czworościenny-oktaedryczny ( gytoh )	(3 6 )
	s2r{3,6,2,∞}
Niejednolity	godz. 0,1,2,3 {3,6,2,∞}

Wyliczanie form Wythoffa

Wszystkie niepryzmatyczne konstrukcje Wythoffa według grup Coxetera podano poniżej wraz z ich odmianami . Jednolite rozwiązania indeksowane są zestawieniem Branko Grünbauma . Zielone tła są pokazane na powtarzających się plastrach miodu, a relacje wyrażone są na rozszerzonych diagramach symetrii.

zespół Coxetera	Rozszerzona symetria	plastry miodu		Chiralna rozszerzona symetria	Naprzemienne plastry miodu
[4,3,4]	[4,3,4]	6	22 | 7 | 8 9 | 25 | 20	[1 + ,4,3 + ,4,1 + ]	(2)	1 | B
	[2 + [4,3,4]] =	(1)	22	[2 + [(4,3 + ,4,2 + )]]	(1)	1 | 6
	[2 + [4,3,4]]	1	28	[2 + [(4,3 + ,4,2 + )]]	(1)	A
	[2 + [4,3,4]]	2	27	[2 + [4,3,4]] +	(1)	C
[4,3 1,1 ]	[4,3 1,1 ]	4	1 | 7 | 10 | 28
	[1[4,3 1,1 ]]=[4,3,4] =	(7)	22 | 7 | 22 | 7 | 9 | 28 | 25	[1[1 + ,4,3 1,1 ]] +	(2)	1 | 6 | A
				[1[4,3 1,1 ]] + =[4,3,4] +	(1)	B
[3 [4] ]	[3 [4] ]	(nic)
	[2 + [3 [4] ]]	1	6
	[1[3 [4] ]]=[4,3 1,1 ] =	(2)	1 | 10
	[2[3 [4] ]]=[4,3,4] =	(1)	7
	[(2 + ,4)[3 [4] ]]=[2 + [4,3,4]] =	(1)	28	[(2 + ,4)[3 [4] ]] + = [2 + [4,3,4]] +	(1)	A

Przykłady

Wszystkie 28 z tych teselacji znajduje się w układach kryształów .

Naprzemienny sześcienny plaster miodu ma szczególne znaczenie, ponieważ jego wierzchołki tworzą sześcienne ścisłe upakowanie kul. Wypełniająca przestrzeń kratownica upakowanych ośmiościanów i czworościanów została najwyraźniej po raz pierwszy odkryta przez Alexandra Grahama Bella i niezależnie ponownie odkryta przez Buckminstera Fullera (który nazwał ją kratownicą oktetu i opatentował ją w latach czterdziestych XX wieku). [3] [4] [5] [6] . Kratownice oktetowe należą obecnie do najpowszechniejszych typów kratownic stosowanych w budownictwie.

Formy fryzowe

Jeśli komórki mogą być jednolitymi płytkami , można zdefiniować bardziej jednolite plastry miodu:

Rodziny:

• ${\ Displaystyle {\ tylda {C}} _ ​​{2}}$ × ${\ Displaystyle A_ {1}}$ : [4,4,2] Sześcienne plastry miodu (3 formy)
• ${\ Displaystyle {\ tylda {G}} _ {2}}$ × ${\ Displaystyle A_ {1}}$ : [6,3,2] Trójsześciokątne plastry miodu (8 form)
• ${\ Displaystyle {\ tylda {A}} _ {2}}$ × ${\ Displaystyle A_ {1}}$ : [(3,3,3), 2] Trójkątne plastry miodu (brak nowych form)
• ${\ Displaystyle {\ tylda {I}} _ {1}}$ × ${\ Displaystyle A_ {1}}$ × ${\ Displaystyle A_ {1}}$ : [∞, 2,2] = sześcienny plastry miodu w kolumnie (1 forma)
• ${\ Displaystyle I_ {2} (p)}$ × ${\ Displaystyle {\ tylda {I}} _ {1}}$ : [p, 2, ∞] Wielokątne plastry miodu w kolumnach (analogicznie do duopryzmatów : wyglądają jak pojedyncza nieskończona wieża z pryzmatów p-gonalnych, z pozostałą przestrzenią wypełnioną graniastosłupami apeirogonalnymi )
• ${\ Displaystyle {\ tylda {I}} _ {1}}$ × ${\ Displaystyle {\ tylda {I}} _ {1}}$ × ${\ Displaystyle A_ {1}}$ : [ ∞,2,∞,2] = [4,4,2] - = (Tak samo jak rodzina sześciennych płyt o strukturze plastra miodu)

Przykłady (częściowo narysowane)

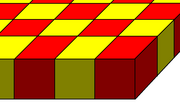
Sześcienny plaster miodu	Naprzemiennie sześciokątna płyta o strukturze plastra miodu	Trójsześciokątna płyta o strukturze plastra miodu
(4) 4 3 : sześcian (1) 4 4 : kwadratowe płytki	(4) 3 3 : czworościan (3) 3 4 : ośmiościan (1) 3 6 : dachówka trójkątna	(2) 3.4.4: Graniastosłup trójkątny (2) 4.4.6: Graniastosłup sześciokątny (1) (3.6) 2 : Dachówka triheksagonalna

Pierwsze dwie formy pokazane powyżej są półregularne (jednolite tylko z regularnymi ściankami) i zostały wymienione przez Thorolda Gosseta w 1900 r. Odpowiednio jako 3-ic semi-check i tetroctahedric semi-check .

Plaster miodu łuskowatego

Skalowaty elementy plaster miodu jest przechodni przez wierzchołki , podobnie jak jednolity plaster miodu , z regularnymi wielokątami, podczas gdy komórki i wyższe muszą być tylko orbiformami , równobocznymi, z wierzchołkami leżącymi na hipersferach. W przypadku trójwymiarowych plastrów miodu pozwala to na podzbiór brył Johnsona wraz z jednolitymi wielościanami. Niektóre łuskowate mogą być generowane w procesie naprzemiennym, pozostawiając na przykład w piramidach i kopułach .

Euklidesowe łuskowate plastry miodu

Płyty fryzowe			Stosy pryzmatyczne
s 3 {2,6,3},	s 3 {2,4,4},	s{2,4,4},	3s 4 {4,4,2,∞},
(1) 3.4.3.4: trójkątna kopuła (2) 3.4.6: trójkątna kopuła (1) 3.3.3.3: ośmiościan (1) 3.6.3.6: triheksagonalna dachówka	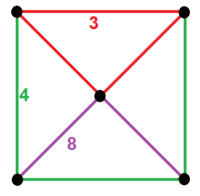(1) 3.4.4.4: kwadratowa kopuła (2) 3.4.8: kwadratowa kopuła (1) 3.3.3: czworościan (1) 4.8.8: ścięta kwadratowa dachówka	(1) 3.3.3.3: ostrosłup kwadratowy (4) 3.3.4: ostrosłup kwadratowy (4) 3.3.3: czworościan (1) 4.4.4.4: dachówka kwadratowa	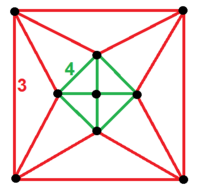(1) 3.3.3.3: ostrosłup kwadratowy (4) 3.3.4: ostrosłup kwadratowy (4) 3.3.3: czworościan (4) 4.4.4: sześcian

Formy hiperboliczne

plaster miodu rzędu 4 , {5,3,4} w perspektywie

Parakompaktowy sześciokątny plaster miodu , {6,3,3}, w perspektywie

Główny artykuł: Jednolite plastry miodu w przestrzeni hiperbolicznej

Istnieje 9 rodzin grup Coxetera zwartych jednolitych plastrów miodu w hiperbolicznej 3-przestrzeni , generowanych jako konstrukcje Wythoffa i reprezentowanych przez permutacje pierścieniowe diagramów Coxetera-Dynkina dla każdej rodziny.

Z tych 9 rodzin wygenerowano łącznie 76 unikalnych plastrów miodu:

• [3,5,3] : - 9 form
• [5,3,4] : - 15 formularzy
• [5,3,5] : - 9 form
• [5,3 ^1,1 ] : - 11 form (7 pokrywa się z rodziną [5,3,4], 4 są unikalne)
• [(4,3,3,3)] : - 9 form
• [(4,3,4,3)] : - 6 form
• [(5,3,3,3)] : - 9 form
• [(5,3,4,3)] : - 9 form
• [(5,3,5,3)] : - 6 form

kilka form innych niż Wythoffian spoza listy 76; nie wiadomo, ile ich jest.

Parazwarte formy hiperboliczne

Główny artykuł: jednolite plastry miodu Paracompact

Istnieją również 23 parakompaktowe grupy Coxetera o randze 4. Rodziny te mogą tworzyć jednolite plastry miodu z nieograniczonymi ścianami lub figurą wierzchołków, w tym idealne wierzchołki w nieskończoności:

Podsumowanie grupy simplectic hiperbolic paracompact

Typ	grupy Coxetera	Unikalna liczba plastrów miodu
Wykresy liniowe	| | | | | |	4×15+6+8+8 = 82
Grafy trójzębne	| |	4+4+0 = 8
Wykresy cykliczne	| | | | | | | |	4×9+5+1+4+1+0 = 47
Wykresy pętli i ogona	| | |	4+4+4+2 = 14

•   John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss , (2008) The Symmetries of Things , ISBN 978-1-56881-220-5 (Rozdział 21, Nazewnictwo wielościanów Archimedesa i katalońskiego oraz tilings, Teselacje architektoniczne i katoptryczne, s. 292–298, obejmuje wszystkie formy niepryzmatyczne)
• Branko Grünbaum , (1994) Jednolite nachylenie 3-przestrzeni. Geombinatoryka 4, 49 - 56.
• Norman Johnson (1991) Uniform Polytopes , Rękopis
•   Williams, Robert (1979). Geometryczne podstawy naturalnej struktury: źródłowa księga projektowania . Dover Publications, Inc. ISBN 0-486-23729-X . (Rozdział 5: Pakowanie wielościanów i wypełnianie przestrzeni)
•   Critchlow, Keith (1970). Porządek w kosmosie: książka źródłowa do projektowania . Prasa Wikingów. ISBN 0-500-34033-1 .
•   Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [7]
  • (Papier 22 ) HSM Coxeter, Regularne i półregularne Polytopy I , [Math. Zeit. 46 (1940) 380–407, MR 2,10] (1.9 Jednolite wypełnienia przestrzeni)
• A. Andreini , (1905) Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (O regularnych i półregularnych sieciach wielościanów i odpowiednich sieciach korelacyjnych), Mem. Società Italiana della Scienze, Ser.3, 14 75–129. PDF [8]
• DMY Sommerville , (1930) Wprowadzenie do geometrii n wymiarów. Nowy Jork, EP Dutton, . 196 s. (wydanie Dover Publications, 1958) Rozdział X: The Regular Polytopes
•   Anthony'ego Pugha (1976). Wielościany: podejście wizualne . Kalifornia: University of California Press Berkeley. ISBN 0-520-03056-7 . Rozdział 5. Łączenie wielościanów
• Krystalografia kwazikryształów: koncepcje, metody i struktury, Walter Steurer, Sofia Deloudi (2009), s. 54-55. 12 opakowań 2 lub więcej jednolitych wielościanów o symetrii sześciennej

Linki zewnętrzne

• Weisstein, Eric W. „Plaster miodu” . MathWorld .
• Jednolite plastry miodu w 3-przestrzennych modelach VRML
• Elementarne plastry miodu Przestrzeń przechodnia wierzchołków wypełniająca plastry miodu niejednorodnymi komórkami.
• Jednolite partycje 3-przestrzeni, ich krewni i osadzanie , 1999
• Jednolite wielościany
• Wielościany wirtualnej rzeczywistości Encyklopedia wielościanów
• animacja kratownicy oktetu
• Recenzja: AF Wells, Trójwymiarowe sieci i wielościany, HSM Coxeter (Źródło: Bull. Amer. Math. Soc. Tom 84, Numer 3 (1978), 466-470.)
• Klitzing, Richard. „Teselacje euklidesowe 3D” .
• (sekwencja A242941 w OEIS )

Podstawowe wypukłe regularne i jednolite plastry miodu w wymiarach 2–9
Przestrzeń	Rodzina	${\ Displaystyle {\ tylda {A}} _ {n-1}}$	${\ Displaystyle {\ tylda {C}} _ ​​{n-1}}$	${\ Displaystyle {\ tylda {B}} _ {n-1}}$	${\ Displaystyle {\ tylda {D}} _ {n-1}}$	${\ Displaystyle {\ tylda {G}} _ {2}}$ / ${\ Displaystyle {\ tylda {F}} _ {4}}$ / ${\ Displaystyle {\ tylda { E}}_{n-1}}$
E 2	Jednolita płytka	{3 [3] }	δ 3	hδ 3	qδ 3	Sześciokątny
E 3	Jednolity wypukły plaster miodu	{3 [4] }	δ 4	hδ 4	qδ 4
E 4	Jednolity 4-plaster miodu	{3 [5] }	δ 5	hδ 5	qδ 5	24-komorowy plaster miodu
E5 _	Jednolity 5-plaster miodu	{3 [6] }	δ 6	hδ 6	qδ 6
E6 _	Jednolity 6-plaster miodu	{3 [7] }	δ 7	hδ 7	qδ 7	2 22
E7 _	Jednolity 7-plaster miodu	{3 [8] }	δ 8	hδ 8	qδ 8	1 33 • 3 31
E 8	Jednolity 8-plaster miodu	{3 [9] }	δ 9	hδ 9	qδ 9	1 52 • 2 51 • 5 21
E 9	Jednolity 9-plaster miodu	{3 [10] }	δ 10	hδ 10	qδ 10
E 10	Mundur 10-plaster miodu	{3 [11] }	δ 11	hδ 11	qδ 11
E n -1	Mundur ( n -1)- plaster miodu	{3 [n] }	δ rz	hδ rz	qδ rz	1 k2 • 2 k1 • k 21