Simplectic plaster miodu

${\ Displaystyle {\ tylda {A}} _ {2}}$	${\ Displaystyle {\ tylda {A}} _ {3}}$
Płytki trójkątne	Czworościenno-ośmiościenny plaster miodu
Z czerwonymi i żółtymi trójkątami równobocznymi	Z cyjanowymi i żółtymi czworościanami oraz czerwonymi rektyfikowanymi czworościanami ( ośmiościanami )

W geometrii simplektyczny plaster miodu ( lub $n$ -simpleksowy plaster miodu ) $jest$ wymiarową nieskończoną serią plastrów miodu opartą na grupy Coxetera . Jest to reprezentowane przez diagram Coxetera-Dynkina jako cykliczny wykres $n + 1$ węzłów z jednym węzłem otoczonym pierścieniami. Składa się z $n$ - ścianek simpleksowych wraz ze wszystkimi rektyfikowanymi $n$ -uproszczenia. Można $który$ traktować jako $-$ wymiarowy hipersześcienny plaster miodu został podzielony wzdłuż wszystkich hiperpłaszczyzn głównej przekątnej aż uproszczenia na końcach hipersześcianów stają się regularne. Figura wierzchołka plastra miodu typu $n$ - simplex jest rozszerzonym $n$ - simplexem .

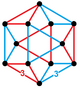
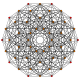
W dwóch wymiarach plaster miodu przedstawia trójkątne płytki , z wykresem Coxetera wypełniającym płaszczyznę naprzemiennie kolorowymi trójkątami. W 3 wymiarach przedstawia czworościenny-ośmiościenny plaster miodu , z grafem Coxetera wypełniającym przestrzeń naprzemiennie czworościennymi i ośmiościennymi komórkami. W 4 wymiarach nazywa się to 5-komorowym plastrem miodu , z wykresem Coxetera , z 5-komorowymi i rektyfikowanymi 5-komorowymi ściankami. W 5 wymiarach nazywa się to plastrem miodu 5-simplex , z wykresem Coxetera , wypełniającym przestrzeń przez 5-simplex , rektyfikowany 5-simplex i birectified 5-simplex fasetami. W 6 wymiarach nazywa się to plastrem miodu 6-simplex , z wykresem Coxetera , wypełniającym przestrzeń przez 6-simplex , rektyfikowany 6-simplex i birectified 6-simplex fasetami.

Według wymiaru

N	${\ Displaystyle {\ tylda {A}} _ {2+}}$	Teselacja	figura wierzchołka	Fasetki na figurę wierzchołka	Wierzchołki na figurę wierzchołka	Rysunek krawędzi
1	${\ Displaystyle {\ tylda {A}} _ {1}}$	Apeirogon	Odcinek	2	2	Punkt
2	${\ Displaystyle {\ tylda {A}} _ {2}}$	Płytki trójkątne 2-simplex o strukturze plastra miodu	Sześciokąt (trójkąt ścięty)	3+3 trójkąty	6	Odcinek
3	${\ Displaystyle {\ tylda {A}} _ {3}}$	Czworościenno-oktaedryczny plaster miodu 3-simplex plaster miodu	Cuboctahedron (Czworościan kantelowany)	4+4 czworościan 6 czworościanów rektyfikowanych	12	Prostokąt
4	${\ Displaystyle {\ tylda {A}} _ {4}}$	4-prosty plaster miodu	Runcynowany 5-komorowy	5+5 5-ogniwowe 10+10 rektyfikowane 5-ogniwowe	20	Antygraniastosłup trójkątny
5	${\ Displaystyle {\ tylda {A}} _ {5}}$	5-prosty plaster miodu	Sterylizowany 5-simplex	6+6 5-simplex 15+15 rektyfikowany 5-simplex 20 birektyfikowany 5-simplex	30	Antygraniastosłup czworościenny
6	${\ Displaystyle {\ tylda {A}} _ {6}}$	6-prosty plaster miodu	Pentellatowany 6-simplex	7+7 6-simplex 21+21 rektyfikowany 6-simplex 35+35 birektyfikowany 6-simplex	42	Antypryzmat 4-simplex
7	${\ Displaystyle {\ tylda {A}} _ {7}}$	7-prosty plaster miodu	Hexicated 7-simplex	8+8 7-simplex 28+28 rektyfikowany 7-simplex 56+56 birektyfikowany 7-simplex 70 trirektyfikowany 7-simplex	56	Antypryzmat 5-simplex
8	${\ Displaystyle {\ tylda {A}} _ {8}}$	8-prosty plaster miodu	Heptelated 8-simplex	9+9 8-simplex 36+36 rektyfikowany 8-simplex 84+84 birektyfikowany 8-simplex 126+126 trirektyfikowany 8-simplex	72	6-prostokątny antypryzmat
9	${\ Displaystyle {\ tylda {A}} _ {9}}$	9-prosty plaster miodu	Octellated 9-simplex	10+10 9-simplex 45+45 rektyfikowany 9-simplex 120+120 birektyfikowany 9-simplex 210+210 trirektyfikowany 9-simplex 252 quadrectified 9-simplex	90	7-prostokątny antypryzmat
10	${\ Displaystyle {\ tylda {A}} _ {10}}$	10-prosty plaster miodu	Ennecated 10-simplex	11+11 10-simplex 55+55 rektyfikowany 10-simplex 165+165 birektyfikowany 10-simplex 330+330 trirektyfikowany 10-simplex 462+462 quadrectified 10-simplex	110	8-prostokątny antypryzmat
11	${\ Displaystyle {\ tylda {A}} _ {11}}$	11-prosty plaster miodu	...	...	...	...

Projekcja przez złożenie

Plastry miodu (2n-1)-simplex i plastry miodu 2n-simplex można rzutować na n-wymiarowy hipersześcienny plaster miodu za pomocą geometrycznej operacji składania , która odwzorowuje dwie pary luster na siebie, dzieląc ten sam układ wierzchołków :

${\ Displaystyle {\ tylda {A}} _ {2}}$	${\ Displaystyle {\ tylda {A}} _ {4}}$	${\ Displaystyle {\ tylda {A}} _ {6}}$	${\ Displaystyle {\ tylda {A}} _ {8}}$	${\ Displaystyle {\ tylda {A}} _ {10}}$	...
${\ Displaystyle {\ tylda {A}} _ {3}}$	${\ Displaystyle {\ tylda {A}} _ {3}}$	${\ Displaystyle {\ tylda {A}} _ {5}}$	${\ Displaystyle {\ tylda {A}} _ {7}}$	${\ Displaystyle {\ tylda {A}} _ {9}}$	...
${\ Displaystyle {\ tylda {C}} _ {1}}$	${\ Displaystyle {\ tylda {C}} _ {2}}$	${\ Displaystyle {\ tylda {C}} _ {3}}$	${\ Displaystyle {\ tylda {C}} _ {4}}$	${\ Displaystyle {\ tylda {C}} _ {5}}$	...

Całowanie numeru

Te plastry miodu, postrzegane jako styczne n-sfery znajdujące się w środku każdego wierzchołka plastra miodu, mają stałą liczbę stykających się sfer i odpowiadają liczbie wierzchołków na figurze wierzchołków . Stanowi to najwyższą liczbę pocałunków dla wymiarów 2 i 3, ale jest niewystarczająca dla wyższych wymiarów. W 2 wymiarach trójkątne płytki definiują okrągłe opakowanie 6 stycznych kul ułożonych w regularny sześciokąt, aw 3 wymiarach jest 12 stycznych kul ułożonych w konfiguracji sześcienno- oktaedrycznej . Dla wymiarów od 4 do 8 całujące się liczby to 20 , 30 , 42 , 56 , i 72 kul, podczas gdy największe rozwiązania to odpowiednio 24, 40, 72, 126 i 240 kul.

Zobacz też

George Olshevsky, Uniform Panoploid Tetracombs , Manuscript (2006) (Pełna lista 11 wypukłych jednolitych nachyleń, 28 wypukłych jednolitych plastrów miodu i 143 wypukłych jednolitych tetracombs)
Branko Grünbaum , Jednolite nachylenie 3-przestrzeni. Geombinatoryka 4(1994), 49 - 56.
Norman Johnson Uniform Polytopes , Rękopis (1991)
Coxeter, HSM Regularne Polytopes , (wydanie trzecie, 1973), wydanie Dover, ISBN 0-486-61480-8
Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Jednolite wypełnienie przestrzeni)
- (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]

Podstawowe wypukłe regularne i jednolite plastry miodu w wymiarach 2–9
Przestrzeń	Rodzina	${\ Displaystyle {\ tylda {A}} _ {n-1}}$	${\ Displaystyle {\ tylda {C}} _ {n-1}}$	${\ Displaystyle {\ tylda {B}} _ {n-1}}$	${\ Displaystyle {\ tylda {D}} _ {n-1}}$	${\ Displaystyle {\ tylda {G}} _ {2}}$ / ${\ Displaystyle {\ tylda {F}} _ {4}}$ / ${\ Displaystyle {\ tylda { E}}_{n-1}}$
E ²	Jednolita płytka	{3 ^[3] }	δ ₃	hδ ₃	qδ ₃	Sześciokątny
E ³	Jednolity wypukły plaster miodu	{3 ^[4] }	δ ₄	hδ ₄	qδ ₄
E ⁴	Jednolity 4-plaster miodu	{3 ^[5] }	δ ₅	hδ ₅	qδ ₅	24-komorowy plaster miodu
E5 ^_	Jednolity 5-plaster miodu	{3 ^[6] }	δ ₆	hδ ₆	qδ ₆
E6 ^_	Jednolity 6-plaster miodu	{3 ^[7] }	δ ₇	hδ ₇	qδ ₇	2 ₂₂
E7 ^_	Jednolity 7-plaster miodu	{3 ^[8] }	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
E ⁸	Jednolity 8-plaster miodu	{3 ^[9] }	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E ⁹	Jednolity 9-plaster miodu	{3 ^[10] }	δ ₁₀	hδ ₁₀	qδ ₁₀
E ¹⁰	Mundur 10-plaster miodu	{3 ^[11] }	δ ₁₁	hδ ₁₁	qδ ₁₁
E ^{n -1}	Mundur ( n -1)- plaster miodu	{3 ^[n] }	δ _rz	hδ _rz	qδ _rz	1 _k2 • 2 _k1 • k ₂₁