Układ wierzchołków

W geometrii układ wierzchołków to zbiór punktów w przestrzeni opisany przez ich względne położenie. Można je opisać za pomocą ich zastosowania w polytopes .

Na przykład, kwadratowy układ wierzchołków jest rozumiany jako oznaczający cztery punkty na płaszczyźnie, równe odległości i kąty od punktu środkowego.

Dwa polytopy mają ten sam układ wierzchołków , jeśli mają ten sam szkielet 0 .

Grupa polytopów, która ma wspólny układ wierzchołków, nazywana jest armią .

Układ wierzchołków

Ten sam zestaw wierzchołków może być połączony krawędziami na różne sposoby. Na przykład pięciokąt i pentagram mają ten sam układ wierzchołków , podczas gdy drugi łączy naprzemienne wierzchołki.

Dwa wielokąty z tym samym *układem wierzchołków* .
pięciokąt	pentagram

Układ wierzchołków jest często opisywany przez wypukły politop kadłuba , który go zawiera. Na przykład można powiedzieć, że regularny pentagram ma (regularny) pięciokątny układ wierzchołków .

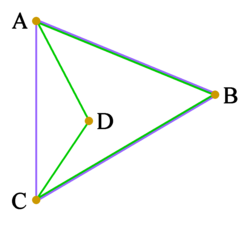
	ABCD to czworokąt wklęsły (zielony). Jego układ wierzchołków to zbiór {A, B, C, D}. Jego wypukła powłoka to trójkąt ABC (niebieski). Układ otoczki wypukłej to zbiór {A, B, C}, który nie jest taki sam jak układ czworoboku; więc tutaj wypukła powłoka nie jest sposobem na opisanie układu wierzchołków.

Nieskończone nachylenia mogą również mieć wspólne układy wierzchołków .

Na przykład tę trójkątną siatkę punktów można połączyć, tworząc trójkąty równoramienne lub rombowe ściany.

Cztery kafelki z tym samym *układem wierzchołków* .
Punkty kratowe	Płytki trójkątne	płytki rombowe	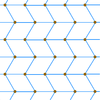Płytka rombowa zygzakowata	Płytki Rombille

Układ krawędzi

Wielościany mogą również dzielić układ krawędzi , różniąc się twarzami.

Na przykład samoprzecinający się dwunastościan wielki dzieli swój układ krawędzi z wypukłym dwudziestościanem :

Dwa wielościany o tym samym *układzie krawędzi* .
dwudziestościan (20 trójkątów)	wielki dwunastościan (12 przecinających się pięciokątów)

Grupa polytopów, które dzielą zarówno układ wierzchołków , jak i układ krawędzi , nazywana jest pułkiem .

Układ twarzy

4-polytopy mogą również mieć ten sam układ ścian , co oznacza, że mają podobne układy wierzchołków, krawędzi i ścian, ale mogą różnić się komórkami.

Na przykład z dziesięciu niewypukłych regularnych polichor Schläfli-Hess istnieje tylko 7 unikalnych układów twarzy.

Na przykład wielkie gwiaździste 120 komórek i wielkie gwiaździste 120 komórek , oba z pentagramowymi twarzami, wydają się wizualnie nie do odróżnienia bez reprezentacji ich komórek :

Dwie (rzutowane) polichory z takim samym *ułożeniem twarzy*
Wielkie gwiaździste 120 komórek (120 małych dwunastościanów gwiaździstych )	Wielkie gwiaździste 120 komórek (120 wielkich dwunastościanów gwiaździstych )

Klasy podobnych polytopów

George Olshevsky opowiada się za terminem pułk dla zbioru polytopów, które mają wspólny układ krawędzi, a bardziej ogólnie n-pułk dla zbioru polytopów, które mają wspólne elementy do wymiaru n . Synonimy przypadków specjalnych obejmują kompanię dla 2-pułku (wspólne twarze) i armię dla 0-pułku (wspólne wierzchołki).

Zobacz też

n-szkielet - zbiór elementów o wymiarze n i niższym w wyższym polytopie.
Figura wierzchołka - Lokalny układ ścian w wielościanie (lub układ komórek w polichoronii) wokół pojedynczego wierzchołka.

Linki zewnętrzne

Olszewski, Jerzy. „Armia” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r. (Ten sam układ wierzchołków)
Olszewski, Jerzy. „pułk” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r. (Ten sam układ wierzchołków i krawędzi)
Olszewski, Jerzy. „Firma” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r. (Ten sam układ wierzchołków, krawędzi i ścian)