Pięciornikowe 6-proste

6-jednostronny	Pentellatowany 6-simplex	Pentitruncated 6-simplex	Pentykantelowany 6-simplex
Penticantitruncated 6-simplex	Pentiruncitruncated 6-simplex	Pentiruncicantelated 6-simplex	Pentiruncicantitruncated 6-simplex
6-sympleks pentesterobcięty	Pentistericantitruncated 6-simplex	Pentisteriruncicantitruncated 6-simplex (Omnitruncated 6-simplex)
Rzuty ortogonalne w płaszczyźnie A 6 Coxetera

geometrii sześciowymiarowej pentelated 6-simplex jest wypukłym jednolitym 6-polytopem z obcięciami piątego rzędu zwykłego 6-simplex .

Istnieje unikalnych 10 stopni pentelacji 6-simpleksu z permutacjami obcięć, kantelacji, przebiegów i sterykcji. Prosty pentelowany 6-simplex jest również nazywany rozszerzonym 6-simplexem , zbudowanym przez operację rozszerzania zastosowaną do zwykłego 6-simplexu . Najwyższa forma, pentisteriruncicantitruncated 6-simplex , nazywana jest omnitruncated 6-simplex ze wszystkimi węzłami otoczonymi pierścieniami.

Pentellatowany 6-simplex

Pentellatowany 6-simplex
Typ	Jednolity 6-politop
Symbol Schläfliego	t 0,5 {3,3,3,3,3}
Diagram Coxetera-Dynkina
5 twarzy	126: 7+7 {3 4 } 21+21 {}×{3,3,3} 35+35 {3}×{3,3}
4 twarze	434
Komórki	630
Twarze	490
Krawędzie	210
Wierzchołki	42
figura wierzchołka	5-ogniwowy antypryzmat
zespół Coxetera	A 6 × 2, [[3,3,3,3,3]], rząd 10080
Nieruchomości	wypukły

Alternatywne nazwy

• Rozszerzony 6-simplex
• Mały tetradekapeton (skrót: staf) (Jonathan Bowers)

Wierzchołki pentelowanego 6-simpleksu można umieścić w przestrzeni 7 jako permutacje (0,1,1,1,1,1,2). Ta konstrukcja jest oparta na aspektach pentelowanego 7-ortopleksu .

Druga konstrukcja w przestrzeni 7, ze środka rektyfikowanego 7-ortopleksu, jest dana przez permutacje współrzędnych:

(1,-1,0,0,0,0,0)

Wektory korzeniowe

Jego 42 wierzchołki reprezentują wektory korzeniowe prostej grupy Liego A ₆ . Jest to figura wierzchołka 6-prostego plastra miodu .

Obrazy

rzuty ortograficzne

Samolot A k Coxeter	6 _	5 _	4 _
Wykres
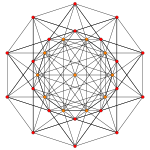
Symetria	[[7]] (*) =[14]	[6]	[[5]] (*) =[10]
Samolot A k Coxeter	3 _	2 _
Wykres
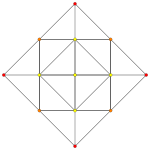
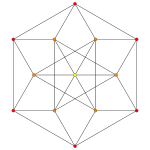
Symetria	[4]	[[3]] (*) =[6]

Uwaga: (*) Symetria podwoiła się dla grafów Ak o parzystym _k dzięki symetrycznie pierścieniowemu diagramowi Coxetera-Dynkina.

Pentitruncated 6-simplex

Pentitruncated 6-simplex
Typ	jednolity 6-politop
Symbol Schläfliego	t 0,1,5 {3,3,3,3,3}
Diagramy Coxetera-Dynkina
5 twarzy	126
4 twarze	826
Komórki	1785
Twarze	1820
Krawędzie	945
Wierzchołki	210
figura wierzchołka
zespół Coxetera	A 6 , [3,3,3,3,3], zamówienie 5040
Nieruchomości	wypukły

Alternatywne nazwy

• Heptapeton z teracellu (akronim: tocal) (Jonathan Bowers)

Współrzędne

Wierzchołki runcitruncated 6-simplex można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,1,1,1,2,3). Ta konstrukcja jest oparta na aspektach 7-ortopleksów runcitruncated .

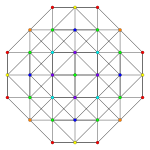
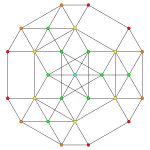
Obrazy

rzuty ortograficzne

Samolot A k Coxeter	6 _	5 _	4 _
Wykres
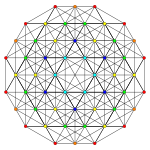
Symetria dwuścienna	[7]	[6]	[5]
Samolot A k Coxeter	3 _	2 _
Wykres
Symetria dwuścienna	[4]	[3]

Pentykantelowany 6-simplex

Pentykantelowany 6-simplex
Typ	jednolity 6-politop
Symbol Schläfliego	t 0,2,5 {3,3,3,3,3}
Diagramy Coxetera-Dynkina
5 twarzy	126
4 twarze	1246
Komórki	3570
Twarze	4340
Krawędzie	2310
Wierzchołki	420
figura wierzchołka
zespół Coxetera	A 6 , [3,3,3,3,3], zamówienie 5040
Nieruchomości	wypukły

Alternatywne nazwy

• Heptapeton teripryzowy (akronim: topal) (Jonathan Bowers)

Współrzędne

Wierzchołki runcicantelated 6-simplex można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,1,1,1,2,3). Ta konstrukcja jest oparta na fasetach pentykantelowanego 7-ortopleksu .

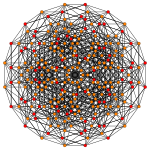
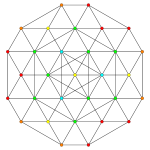
Obrazy

rzuty ortograficzne

Samolot A k Coxeter	6 _	5 _	4 _
Wykres
Symetria dwuścienna	[7]	[6]	[5]
Samolot A k Coxeter	3 _	2 _
Wykres
Symetria dwuścienna	[4]	[3]

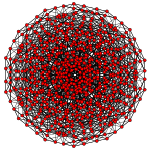
Penticantitruncated 6-simplex

pentykantitruncated 6-simplex
Typ	jednolity 6-politop
Symbol Schläfliego	t 0,1,2,5 {3,3,3,3,3}
Diagramy Coxetera-Dynkina
5 twarzy	126
4 twarze	1351
Komórki	4095
Twarze	5390
Krawędzie	3360
Wierzchołki	840
figura wierzchołka
zespół Coxetera	A 6 , [3,3,3,3,3], zamówienie 5040
Nieruchomości	wypukły

Alternatywne nazwy

• Heptapeton terigreatorhombated (akronim: togral) (Jonathan Bowers)

Współrzędne

Wierzchołki 6-simpleksu z pentykantą imitacją można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,1,1,2,3,4). Ta konstrukcja jest oparta na fasetach 7-ortopleksów pentykantytrowanych .

Obrazy

rzuty ortograficzne

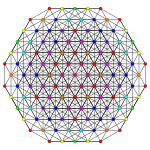
Samolot Ak Coxeter	6 _	5 _	4 _
Wykres
Symetria dwuścienna	[7]	[6]	[5]
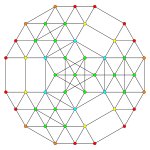
Samolot Ak Coxeter	3 _	2 _
Wykres
Symetria dwuścienna	[4]	[3]

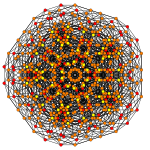
Pentiruncitruncated 6-simplex

pentiruncitruncated 6-simplex
Typ	jednolity 6-politop
Symbol Schläfliego	t 0,1,3,5 {3,3,3,3,3}
Diagramy Coxetera-Dynkina
5 twarzy	126
4 twarze	1491
Komórki	5565
Twarze	8610
Krawędzie	5670
Wierzchołki	1260
figura wierzchołka
zespół Coxetera	A 6 , [3,3,3,3,3], zamówienie 5040
Nieruchomości	wypukły

Alternatywne nazwy

• Tericellirhombated heptapeton (akronim: tocral) (Jonathan Bowers)

Współrzędne

Wierzchołki pentiruncitruncated 6-simplex można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,1,1,2,3,4). Ta konstrukcja jest oparta na fasetach 7-ortopleksu pięciorurowego .

Obrazy

rzuty ortograficzne

Samolot A k Coxeter	6 _	5 _	4 _
Wykres
Symetria dwuścienna	[7]	[6]	[5]
Samolot A k Coxeter	3 _	2 _
Wykres
Symetria dwuścienna	[4]	[3]

Pentiruncicantelated 6-simplex

Pentiruncicantelated 6-simplex
Typ	jednolity 6-politop
Symbol Schläfliego	t 0,2,3,5 {3,3,3,3,3}
Diagramy Coxetera-Dynkina
5 twarzy	126
4 twarze	1596
Komórki	5250
Twarze	7560
Krawędzie	5040
Wierzchołki	1260
figura wierzchołka
zespół Coxetera	A 6 , [[3,3,3,3,3]], rząd 10080
Nieruchomości	wypukły

Alternatywne nazwy

• Teriprismatorhombated tetradecapeton (akronim: taporf) (Jonathan Bowers)

Współrzędne

Wierzchołki 6-simpleksu pięcioramiennego można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,1,2,3,3,4). Ta konstrukcja jest oparta na fasetach 7-ortopleksu pięcioramiennego .

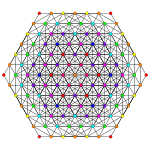
Obrazy

rzuty ortograficzne

Samolot A k Coxeter	6 _	5 _	4 _
Wykres
Symetria	[[7]] (*) =[14]	[6]	[[5]] (*) =[10]
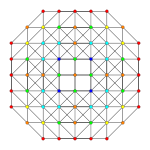
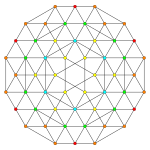
Samolot A k Coxeter	3 _	2 _
Wykres
Symetria	[4]	[[3]] (*) =[6]

Uwaga: (*) Symetria podwoiła się dla grafów Ak _z parzystym k dzięki symetrycznie pierścieniowemu diagramowi Coxetera-Dynkina.

Pentiruncicantitruncated 6-simplex

Pentiruncicantitruncated 6-simplex
Typ	jednolity 6-politop
Symbol Schläfliego	t 0,1,2,3,5 {3,3,3,3,3}
Diagramy Coxetera-Dynkina
5 twarzy	126
4 twarze	1701
Komórki	6825
Twarze	11550
Krawędzie	8820
Wierzchołki	2520
figura wierzchołka
zespół Coxetera	A 6 , [3,3,3,3,3], zamówienie 5040
Nieruchomości	wypukły

Alternatywne nazwy

• Heptapeton terigreatopryzmatyczny (akronim: tagopal) (Jonathan Bowers)

Współrzędne

Wierzchołki 6-simpleksu pięciorunkowego skróconego można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,1,2,3,4,5). Ta konstrukcja jest oparta na aspektach pięciorunkowego 7-ortopleksu .

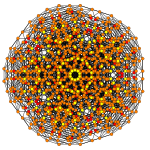
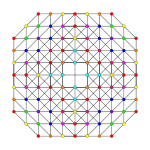
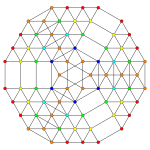
Obrazy

rzuty ortograficzne

Samolot A k Coxeter	6 _	5 _	4 _
Wykres
Symetria dwuścienna	[7]	[6]	[5]
Samolot A k Coxeter	3 _	2 _
Wykres
Symetria dwuścienna	[4]	[3]

6-sympleks pentesterobcięty

6-sympleks pentesterobcięty
Typ	jednolity 6-politop
Symbol Schläfliego	t 0,1,4,5 {3,3,3,3,3}
Diagramy Coxetera-Dynkina
5 twarzy	126
4 twarze	1176
Komórki	3780
Twarze	5250
Krawędzie	3360
Wierzchołki	840
figura wierzchołka
zespół Coxetera	A 6 , [[3,3,3,3,3]], rząd 10080
Nieruchomości	wypukły

Alternatywne nazwy

• Tericellitruncated tetradecapeton (akronim: taktaf) (Jonathan Bowers)

Współrzędne

Wierzchołki pentisteritruncated 6-simplex można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,2,2,2,3,4). Ta konstrukcja jest oparta na aspektach 7-ortopleksów z penisteritruncated .

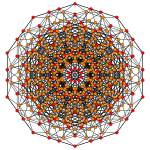
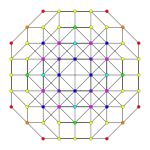
Obrazy

rzuty ortograficzne

Samolot A k Coxeter	6 _	5 _	4 _
Wykres
Symetria	[[7]] (*) =[14]	[6]	[[5]] (*) =[10]
Samolot A k Coxeter	3 _	2 _
Wykres
Symetria	[4]	[[3]] (*) =[6]

Uwaga: (*) Symetria podwoiła się dla grafów Ak _z parzystym k dzięki symetrycznie pierścieniowemu diagramowi Coxetera-Dynkina.

Pentistericantitruncated 6-simplex

pentistericantitruncated 6-simplex
Typ	jednolity 6-politop
Symbol Schläfliego	t 0,1,2,4,5 {3,3,3,3,3}
Diagramy Coxetera-Dynkina
5 twarzy	126
4 twarze	1596
Komórki	6510
Twarze	11340
Krawędzie	8820
Wierzchołki	2520
figura wierzchołka
zespół Coxetera	A 6 , [3,3,3,3,3], zamówienie 5040
Nieruchomości	wypukły

Alternatywne nazwy

• Wielki teracellirhombated heptapeton (akronim: gatokral) (Jonathan Bowers)

Współrzędne

Wierzchołki pentistericantittruncated 6-simplex można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,2,2,3,4,5). Ta konstrukcja jest oparta na aspektach pentistericantitruncated 7-orthoplex .

Obrazy

rzuty ortograficzne

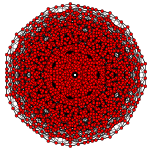
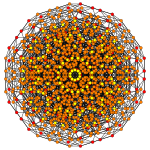
Samolot A k Coxeter	6 _	5 _	4 _
Wykres
Symetria dwuścienna	[7]	[6]	[5]
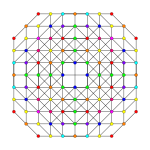
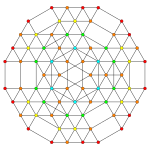
Samolot A k Coxeter	3 _	2 _
Wykres
Symetria dwuścienna	[4]	[3]

Omnitruncated 6-simplex

Omnitruncated 6-simplex
Typ	Jednolity 6-politop
Symbol Schläfliego	t 0,1,2,3,4,5 {3 5 }
Diagramy Coxetera-Dynkina
5 twarzy	126: 14 t 0,1,2,3,4 {3 4 } 42 {}×t 0,1,2,3 {3 3 } × 70 {6}×t 0,1,2 {3,3} ×
4 twarze	1806
Komórki	8400
Twarze	16800: 4200 {6} 1260 {4}
Krawędzie	15120
Wierzchołki	5040
figura wierzchołka	nieregularny 5-simplex
zespół Coxetera	A 6 , [[3 5 ]], rząd 10080
Nieruchomości	wypukłe , izogonalne , zonotopowe

Wielościenny 6-simplex ma 5040 wierzchołków , 15120 krawędzi , 16800 ścian (4200 sześciokątów i 1260 kwadratów ), 8400 komórek , 1806 4-ścian i 126 5-ścian. Z 5040 wierzchołkami jest największym z 35 jednolitych 6-polytopów wygenerowanych z regularnego 6-simpleksu .

Alternatywne nazwy

• omnitruncation Johnsona dla 6-polytopes)
• Heptapeton wielościenny
• Wielki tetradekapeton (akronim: gotaf) (Jonathan Bowers)

Permutoedr i pokrewna teselacja

Omnitruncated 6-simplex jest permutoedrem rzędu 7. Omnitruncated 6-simplex jest zonotopem , sumą Minkowskiego siedmiu odcinków równoległych do siedmiu linii przechodzących przez początek i siedem wierzchołków 6-simplex.

Podobnie jak wszystkie jednorodne omnitruncated n-simplices, omnitruncated 6-simplex może samodzielnie teselować przestrzeń, w tym przypadku 6-wymiarową przestrzeń z trzema ściankami wokół każdej hiperkomórki. Posiada diagram Coxetera-Dynkina .

Współrzędne

Wierzchołki omnitruncated 6-simplex można najprościej umieścić w przestrzeni 7 jako permutacje (0,1,2,3,4,5,6). Ta konstrukcja jest oparta na fasetach 7-ortopleksów pięciorunkowych , t _0,1,2,3,4,5 {3 ⁵ ,4}, .

Obrazy

rzuty ortograficzne

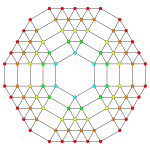
Samolot A k Coxeter	6 _	5 _	4 _
Wykres
Symetria	[[7]] (*) =[14]	[6]	[[5]] (*) =[10]
Samolot A k Coxeter	3 _	2 _
Wykres
Symetria	[4]	[[3]] (*) =[6]

Uwaga: (*) Symetria podwoiła się dla grafów Ak _z parzystym k dzięki symetrycznie pierścieniowemu diagramowi Coxetera-Dynkina.

Pełny afront 6-simplex

Pełny snub 6-simplex lub omnisnub 6-simplex , zdefiniowany jako przemiana omnitruncated 6-simplex nie jest jednorodny, ale można mu nadać diagram Coxetera i symetrię [[3,3,3,3,3]] ⁺ , i zbudowany z 14 snub 5-simplexes , 42 snub 5-komorowych antypryzmatów, 70 3-s {3,4} du oantypryzmaty i 2520 nieregularnych 5-simpleksów wypełniających luki w usuniętych wierzchołkach.

Powiązane jednolite 6-polytopy

Pentellatowany 6-simplex jest jednym z 35 jednolitych 6-polytopów opartych na [3,3,3,3,3] grupie Coxetera , wszystkie pokazane tutaj w rzutach ortograficznych płaszczyzny A ₆ Coxetera .

Notatki

• HSM Coxeter :
  • HSM Coxeter, Regularne Polytopes , wydanie 3, Dover, Nowy Jork, 1973
  •   Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papier 23) HSM Coxeter, Regularne i półregularne Polytopy II , [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Rękopis (1991)
  • NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
• Klitzing, Richard. „Jednolite polytopy 6D (polipeta)” . x3o3o3o3o3x - laska, x3x3o3o3o3x - tokal, x3o3x3o3o3x - topal, x3x3x3o3o3x - togral, x3x3o3x3o3x - tokral, x3x3x3x3o3x - tagopal, x3x3o3o3x3x - taktaf, x3x3x3o3x3x - ta cogral, x3x3x3x3x3x - gotaf

Linki zewnętrzne

• Glosariusz hiperprzestrzeni , George Olshevsky.
• Polytopy o różnych wymiarach
• Glosariusz wielowymiarowy