Rektyfikowane 6-proste

Rzuty ortogonalne w płaszczyźnie A ₆ Coxetera
6-jednostronny	Rektyfikowany 6-simplex	Birektyfikowany 6-simplex

W sześciowymiarowej geometrii rektyfikowany 6-simplex jest wypukłym jednolitym 6-polytopem , będącym rektyfikacją regularnego 6-simplexu .

Istnieją trzy unikalne stopnie rektyfikacji, w tym zero, sam 6-simplex. Wierzchołki rektyfikowanego 6-simpleksu znajdują się w środkach krawędzi 6-simpleksu . Wierzchołki birectified 6-simplex znajdują się w trójkątnych środkach twarzy 6-simplex .

Rektyfikowany 6-simplex

Rektyfikowany 6-simplex
Typ	jednolity polipeton
Symbol Schläfliego	t ₁ {3 ⁵ } r {3 ⁵ } = {3 ^4,1 } lub ${\ Displaystyle \ lewo \ {{\ rozpocząć {tablica} {l} 3,3,3 ,3\\3\koniec{tablica}}\prawo\}}$
Diagramy Coxetera
Elementy	fa ₅ = 14, fa ₄ = 63, C = 140, F = 175, E = 105, V = 21 (χ=0)
zespół Coxetera	A ₆ , [3 ⁵ ], zamówienie 5040
Bowers nazwa i (akronim)	Heptapeton rektyfikowany (ril)
figura wierzchołka	Pryzmat 5-ogniwowy
promień okręgu	0,845154
Nieruchomości	wypukły , izogonalny

EL Elte zidentyfikował go w 1912 jako półregularny polytop, oznaczając go jako S
¹₆ . Jest również nazywany 0_4,1 ze względu na rozgałęziony diagram Coxetera-Dynkina, pokazany jako .

Alternatywne nazwy

Heptapeton rektyfikowany (akronim: ril) (Jonathan Bowers)

Współrzędne

Wierzchołki rektyfikowanego 6-simpleksu można najprościej umieścić w przestrzeni 7 jako permutacje (0,0,0,0,0,1,1). Ta konstrukcja oparta jest na fasetach rektyfikowanego 7-ortopleksu .

Obrazy

rzuty ortograficzne
Samolot A _{k Coxeter}	6 _{_}	5 _{_}	4 _{_}
Wykres
Symetria dwuścienna	[7]	[6]	[5]
Samolot A _{k Coxeter}	3 _{_}	2 _{_}
Wykres
Symetria dwuścienna	[4]	[3]

Birektyfikowany 6-simplex

Birektyfikowany 6-simplex
Typ	jednolity 6-politop
Klasa	Politop A6
Symbol Schläfliego	t ₂ {3,3,3,3,3} 2r {3 ⁵ } = {3 ^3,2 } lub ${\ Displaystyle \ lewo \ {{\ rozpocząć {tablica} l}3,3,3\\3,3\koniec{tablica}}\prawo\}}$
Symbol Coxetera	0₃₂
Diagramy Coxetera
5 twarzy	14 łącznie: 7 t ₁ {3,3,3,3} 7 t ₂ {3,3,3,3}
4 twarze	84
Komórki	245
Twarze	350
Krawędzie	210
Wierzchołki	35
figura wierzchołka	{3}x{3,3}
wielokąt Petriego	Siedmiokąt
grupy Coxetera	A ₆ , [3,3,3,3,3]
Nieruchomości	wypukły

EL Elte zidentyfikował go w 1912 jako półregularny polytop, oznaczając go jako S
²₆ . Jest również nazywany 0_3,2 ze względu na rozgałęziony diagram Coxetera-Dynkina, pokazany jako .

Alternatywne nazwy

Heptapeton z birektyfikacją (akronim: bril) (Jonathan Bowers)

Współrzędne

Wierzchołki birektyfikowanego 6-simpleksu można najprościej umieścić w przestrzeni 7 jako permutacje (0,0,0,0,1,1,1). Ta konstrukcja jest oparta na aspektach birektyfikowanego 7-ortopleksu .

Obrazy

rzuty ortograficzne
Samolot A _{k Coxeter}	6 _{_}	5 _{_}	4 _{_}
Wykres
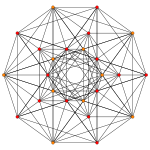
Symetria dwuścienna	[7]	[6]	[5]
Samolot A _{k Coxeter}	3 _{_}	2 _{_}
Wykres
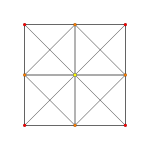
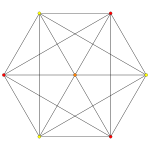
Symetria dwuścienna	[4]	[3]

Powiązane jednolite 6-polytopy

Rektyfikowany polytop 6-simplex jest figurą wierzchołka 7 -półsześcianu i figurą krawędzi jednolitego polytopu 2 ₄₁ .

Te polytopy są częścią 35 jednolitych 6-polytopów opartych na [3,3,3,3,3] grupie Coxetera , wszystkie pokazane tutaj w rzutach ortograficznych płaszczyzny A ₆ Coxetera .

Notatki

HSM Coxeter :
- HSM Coxeter, Regularne Polytopes , wydanie 3, Dover, Nowy Jork, 1973
- Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Papier 23) HSM Coxeter, Regularne i półregularne Polytopes II , [Math. Zeit. 188 (1985) 559-591]
  - (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
Norman Johnson Uniform Polytopes , Rękopis (1991)
- NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
Klitzing, Richard. „Jednolite polytopy 6D (polipeta)” . o3x3o3o3o3o - ril, o3x3o3o3o3o - bril

Linki zewnętrzne

Podstawowe wypukłe regularne i jednolite polytopy w wymiarach 2–10
Rodzina	rz _{_}	B _n	I ₂ (p) / D _n	mi ₆ / mi ₇ / mi ₈ / fa ₄ / sol ₂	H _n
Regularny wielokąt	Trójkąt	Kwadrat	p-gon	Sześciokąt	Pięciokąt
Jednolity wielościan	Czworościan	Ośmiościan • Sześcian	Demisześcian		Dwunastościan • Dwudziestościan
Jednolity polichoron	pentachoron	16-ogniwowy • Tesserakt	Demitesseract	24-ogniwowy	120-ogniwowy • 600-ogniwowy
Jednolity 5-politop	5-jednostronny	5-ortopleks • 5-sześcian	5-sześcian
Jednolity 6-politop	6-jednostronny	6-ortopleks • 6-sześcian	6-sześcian	1 ₂₂ • 2 ₂₁
Jednolity 7-politop	7-jednostronny	7-ortopleks • 7-sześcian	7-sześcian	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Jednolity 8-politop	8-jednostronny	8-ortopleks • 8-sześcian	8-sześcian	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Jednolity 9-politop	9-jednostronny	9-ortopleks • 9-sześcian	9-sześcian
Jednolity 10-politop	10-jednostronny	10-ortopleks • 10-sześcian	10-sześcian
Jednolity n - polytope	n - simpleks	n - ortopleks • n - sześcian	n - półsześcian	1 _k2 • 2 _k1 • k ₂₁	n - pięciokątny politop
Tematy: Rodziny polytopów • Regularne polytopy • Lista regularnych polytopów i związków

politopy A6
T₀	t ₁	t ₂	t _0,1	t _0,2	t _1,2	t _0,3	t _1,3	t _2,3
t _0,4	t _1,4	t _0,5	t _0,1,2	t _0,1,3	t _0,2,3	t _1,2,3	t _0,1,4	t _0,2,4
t _1,2,4	t _0,3,4	t _0,1,5	t _0,2,5	t _0,1,2,3	t _0,1,2,4	t _0,1,3,4	t _0,2,3,4	t _1,2,3,4
t _0,1,2,5	t _0,1,3,5	t _0,2,3,5	t _0,1,4,5	t _0,1,2,3,4	t _0,1,2,3,5	t _0,1,2,4,5	t _0,1,2,3,4,5