5-sześcian

Demipenteract (5-demicube)
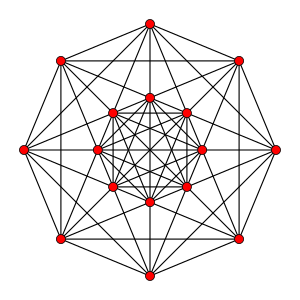projekcja wielokąta Petriego
Typ	Jednolity 5-politop
Rodzina ( _Dn )	5- półsześcian
Rodziny (E _n )	k ₂₁ polytope 1 _k2 polytope
Symbol Coxetera	1 ₂₁
symbole Schläfliego	{3,3 ^2,1 } = h{4,3 ³ } s{2,4,3,3} lub h{2}h{4,3,3} sr{2,2,4,3} lub h{2}h{2}h{4,3} h{2}h{2}h{2}h{4} s{2 ^1,1,1,1 } lub h{2}h{2} h{2}s{2}
Diagramy Coxetera	=
4 twarze	26	10 {3 ^1,1,1 } 16 {3,3,3}
Komórki	120	40 {3 ^1,0,1 } 80 {3,3}
Twarze	160	{3}
Krawędzie	80
Wierzchołki	16
figura wierzchołka	rektyfikowany 5-ogniwowy
wielokąt Petriego	Ośmiokąt
Symetria	re ₅ , [3 ^2,1,1 ] = [1 ⁺ ,4,3 ³ ] [2 ⁴ ] ⁺
Nieruchomości	wypukły

W geometrii pięciowymiarowej , półpenterakt lub 5-sześcian to półregularny 5-polytop , zbudowany z 5-hipersześcianu ( penterakt ) z usuniętymi naprzemiennymi wierzchołkami.

Został odkryty przez Thorolda Gosseta . Ponieważ był to jedyny półregularny 5-politop (złożony z więcej niż jednego rodzaju regularnych faset ), nazwał go 5-ic półregularnym . EL Elte zidentyfikował go w 1912 roku jako półregularny polytop, oznaczając go jako HM ₅ dla 5-wymiarowego polytopu półwymiarowego .

Coxeter nazwał ten polytop jako 1 ₂₁ ze swojego diagramu Coxetera , który ma gałęzie o długości 2, 1 i 1 z obrączkowanym węzłem na jednej z krótkich gałęzi, oraz symbol Schläfliego ${\ Displaystyle \ lewo \ { 3{\begin{array}{l}3,3\\3\end{array}}\right\}}$ lub {3,3 ^2,1 }.

Występuje w rodzinie k ₂₁ polytope jako 1 ₂₁ z polytopes Gosset: 2 ₂₁ , 3 ₂₁ i 4 ₂₁ .

Wykres utworzony przez wierzchołki i krawędzie demipenterakty jest czasami nazywany wykresem Clebscha , chociaż nazwa ta czasami odnosi się zamiast tego do złożonego wykresu sześciennego rzędu piątego.

współrzędne kartezjańskie

Współrzędne kartezjańskie dla wierzchołków półpiętrakty wyśrodkowanej w początku i długości krawędzi 2 √ 2 to naprzemienne połówki pięcioraczki :

(±1,±1,±1,±1,±1)

z nieparzystą liczbą znaków plus.

Jako konfiguracja

Ta macierz konfiguracji reprezentuje 5-sześcian. Wiersze i kolumny odpowiadają wierzchołkom, krawędziom, ścianom, komórkom i 4-ścianom. Liczby po przekątnej mówią, ile każdego elementu występuje w całym 5-sześcianie. Liczby niediagonalne mówią, ile elementów kolumny występuje w elemencie wiersza lub na nim.

Ukośne liczby f-wektorów są uzyskiwane za pomocą konstrukcji Wythoffa , dzieląc pełny porządek grupowy rzędu podgrup poprzez usuwanie jednego lustra na raz.

D5 _{_}	k-twarz	f _k	F₀	f ₁	f ₂	fa ₃		f ₄		k -figura	notatki
4 _{_}	( )	F₀	16	10	30	10	20	5	5	rektyfikowany 5-ogniwowy	R ₅ /A ₄ = 16*5!/5! = 16
ZA ₂ ZA ₁ ZA ₁	{}	f ₁	2	80	6	3	6	3	2	trójkątny pryzmat	re ₅ /za ₂ za ₁ za ₁ = 16*5!/3!/2/2 = 80
2 A ₁_{_}	{3}	f ₂	3	3	160	1	2	2	1	Trójkąt równoramienny	re ₅ /za ₂ za ₁ = 16*5!/3!/2 = 160
A ₃ A ₁	h{4,3}	fa ₃	4	6	4	40	*	2	0	{}	re ₅ /za ₃ za ₁ = 16*5!/4!/2 = 40
3 _{_}	{3,3}	fa ₃	4	6	4	*	80	1	1	{}	R ₅ /A ₃ = 16*5!/4! = 80
D ₄	h{4,3,3}	f ₄	8	24	32	8	8	10	*	( )	R5 /R4 _{= 16*5!/}₈ /4! = 10
4 _{_}	{3,3,3}	f ₄	5	10	10	0	5	*	16	( )	R ₅ /A ₄ = 16*5!/5! = 16

* = ^{[ wymagane wyjaśnienie ]}

Wyświetlane obrazy

Projekcja perspektywiczna .

Obrazy

rzuty ortograficzne
Samolot Coxetera	B5 _{_}
Wykres
Symetria dwuścienna	[10/2]
Samolot Coxetera	D5 _{_}	D ₄
Wykres
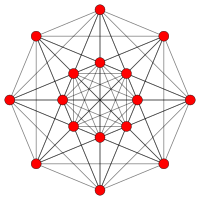
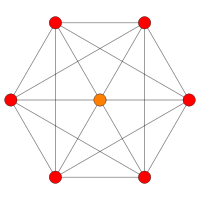
Symetria dwuścienna	[8]	[6]
Samolot Coxetera	D3 _{_}	3 _{_}
Wykres
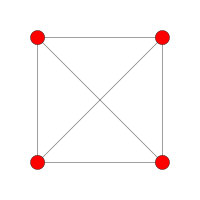
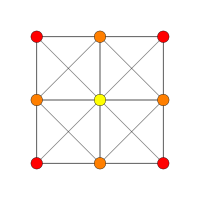
Symetria dwuścienna	[4]	[4]

Powiązane polytopy

Jest częścią wymiarowej rodziny jednolitych polytopów zwanych półhipersześcianami , ponieważ jest naprzemiennością rodziny hipersześcianów .

Istnieje 23 jednolitych 5-polytopów (jednolitych 5-polytopów), które można zbudować z symetrii D5 _{półpiętraktu} , z których 8 jest unikalnych dla tej rodziny, a 15 jest wspólnych dla rodziny penterataktycznej .

politopy D5
h{4,3,3,3}	godz. ₂ {4,3,3,3}	h ₃ {4,3,3,3}	h ₄ {4,3,3,3}	h _2,3 {4,3,3,3}	h _2,4 {4,3,3,3}	h _3,4 {4,3,3,3}	h _2,3,4 {4,3,3,3}

5-półsześcian jest trzecim wymiarowym szeregiem półregularnych polytopów . Każdy progresywny jednorodny polytop jest konstruowaną figurą wierzchołka poprzedniego polytopu. Thorold Gosset zidentyfikował tę serię w 1900 roku jako zawierającą wszystkie regularne ścianki polytope, zawierające wszystkie simplexy i ortopleksy ( 5-simplice i 5-ortopleksy w przypadku 5-półsześcianu). W Coxetera półsześcian 5 ma symbol 1 ₂₁ .

k ₂₁ cyfr w n-wymiarowych
Przestrzeń	Skończone						euklidesowy	Hiperboliczny
E _n	3	4	5	6	7	8	9	10
zespół Coxetera	mi ₃ = ZA ₂ ZA ₁	mi ₄ = A ₄	mi ₅ = re ₅	E6 _{_}	E7 _{_}	E ₈	mi ₉ = ${\ Displaystyle {\ tylda {E}} _ {8}}$ = mi ₈⁺	mi ₁₀ = ${\ Displaystyle {\ bar {T}} _ {8}}$ = mi ₈⁺⁺
Diagram Coxetera
Symetria	[3 ^−1,2,1 ]	[3 ^0,2,1 ]	[3 ^1,2,1 ]	[3 ^2,2,1 ]	[3 ^3,2,1 ]	[3 ^4,2,1 ]	[3 ^5,2,1 ]	[3 ^6,2,1 ]
Zamówienie	12	120	1920	51840	2.903.040	696 729 600	∞
Wykres							-	-
Nazwa	−1 ₂₁	0₂₁	1 ₂₁	2 ₂₁	3 ₂₁	4 ₂₁	5 ₂₁	6 ₂₁

1 _k2 figur w n wymiarach
Przestrzeń	Skończone						euklidesowy	Hiperboliczny
N	3	4	5	6	7	8	9	10
zespół Coxetera	mi ₃ = ZA ₂ ZA ₁	mi ₄ = A ₄	mi ₅ = re ₅	E6 _{_}	E7 _{_}	E ₈	mi ₉ = ${\ Displaystyle {\ tylda {E}} _ {8}}$ = mi ₈⁺	mi ₁₀ = ${\ Displaystyle {\ bar {T}} _ {8}}$ = mi ₈⁺⁺
Diagram Coxetera
Symetria (kolejność)	[3 ^−1,2,1 ]	[3 ^0,2,1 ]	[3 ^1,2,1 ]	[[3 ^2,2,1 ]]	[3 ^3,2,1 ]	[3 ^4,2,1 ]	[3 ^5,2,1 ]	[3 ^6,2,1 ]
Zamówienie	12	120	1920	103680	2.903.040	696 729 600	∞
Wykres							-	-
Nazwa	1-1,2 _{_}	1 ₀₂	1 ₁₂	1 ₂₂	1 ₃₂	1 ₄₂	1 ₅₂	1 ₆₂

^ Coxeter, Regularne Polytopes, sek. 1.8 Konfiguracje
^ Coxeter, Złożone regularne politopy, s. 117
Bibliografia _ "x3o3o *b3o3o - hin" .

T. Gosset : O figurach regularnych i półregularnych w przestrzeni n wymiarów , Messenger of Mathematics , Macmillan, 1900
HSM Coxeter :
- Coxeter, Regular Polytopes , (3. wydanie, 1973), wydanie Dover, ISBN 0-486-61480-8 , s. 296, Tabela I (iii): Regularne polytopy, trzy regularne polytopy w n-wymiarach (n≥5)
- HSM Coxeter, Regular Polytopes , 3. wydanie, Dover, Nowy Jork, 1973, s. 296, Tabela I (iii): Regularne polytopy, trzy regularne polytopy w n-wymiarach (n≥5)
- Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Papier 23) HSM Coxeter, Regularne i półregularne Polytopy II , [Math. Zeit. 188 (1985) 559-591]
  - (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetry of Things 2008, ISBN 978-1-56881-220-5 (Rozdział 26. s. 409: Hemicubes: 1 _n1 )
Klitzing, Richard. „Jednolite politopy 5D (polytera) x3o3o * b3o3o - hin” .

Linki zewnętrzne

Olszewski, Jerzy. „Demipenterakt” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r.
Słowniczek wielowymiarowy

Podstawowe wypukłe regularne i jednolite polytopy w wymiarach 2–10
Rodzina	rz _{_}	B _n	I ₂ (p) / D _n	mi ₆ / mi ₇ / mi ₈ / fa ₄ / sol ₂	H _n
Regularny wielokąt	Trójkąt	Kwadrat	p-gon	Sześciokąt	Pięciokąt
Jednolity wielościan	Czworościan	Ośmiościan • Sześcian	Demisześcian		Dwunastościan • Dwudziestościan
Jednolity polichoron	pentachoron	16-ogniwowy • Tesserakt	Demitesseract	24-ogniwowy	120-ogniwowy • 600-ogniwowy
Jednolity 5-politop	5-jednostronny	5-ortopleks • 5-sześcian	5-sześcian
Jednolity 6-politop	6-jednostronny	6-ortopleks • 6-sześcian	6-sześcian	1 ₂₂ • 2 ₂₁
Jednolity 7-politop	7-jednostronny	7-ortopleks • 7-sześcian	7-sześcian	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Jednolity 8-politop	8-jednostronny	8-ortopleks • 8-sześcian	8-sześcian	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Jednolity 9-politop	9-jednostronny	9-ortopleks • 9-sześcian	9-sześcian
Jednolity 10-politop	10-jednostronny	10-ortopleks • 10-sześcian	10-sześcian
Jednolity n - polytope	n - simpleks	n - ortopleks • n - sześcian	n - półsześcian	1 _k2 • 2 _k1 • k ₂₁	n - pięciokątny politop
Tematy: Rodziny polytopów • Regularne polytopy • Lista regularnych polytopów i związków

[1] Coxeter, Regularne Polytopes, sek. 1.8 Konfiguracje

[2] Coxeter, Złożone regularne politopy, s. 117

[3] Bibliografia _ "x3o3o *b3o3o - hin" .