Runcic 5 kostek

5-sześcian	Runcic 5 kostek =
5-sześcian =	Runcicantic 5-sześcian =
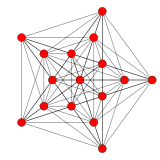
Rzuty ortogonalne w płaszczyźnie B 5 Coxetera

W sześciowymiarowej geometrii , runcic 5-cube lub ( runcic 5-demicube , runcihalf 5-cube ) jest wypukłym jednolitym 5-polytopem . Istnieją 2 formy runcic dla kostki 5. Runcic 5-cubes ma połowę wierzchołków runcinated 5-cubes .

Runcic 5-kostka

Runcic 5-kostka
Typ	jednolity 5-polytop
Symbol Schläfliego	h 3 {4,3,3,3}
Diagram Coxetera-Dynkina
4 twarze	42
Komórki	360
Twarze	880
Krawędzie	720
Wierzchołki	160
figura wierzchołka
grupy Coxetera	re 5 , [3 2,1,1 ]
Nieruchomości	wypukły

Alternatywne nazwy

• Cantelated 5-demicube / demienteract
• Mały rombowy hemipenterakta (sirhin) (Jonathan Bowers)

współrzędne kartezjańskie

Współrzędne kartezjańskie dla 960 wierzchołków Runcic 5-sześcianów wyśrodkowanych na początku to permutacje współrzędnych:

(±1,±1,±1,±3,±3)

z nieparzystą liczbą znaków plus.

Obrazy

rzuty ortograficzne

Samolot Coxetera	B5 _
Wykres
Symetria dwuścienna	[10/2]
Samolot Coxetera	D5 _	D 4
Wykres
Symetria dwuścienna	[8]	[6]
Samolot Coxetera	D3 _	3 _
Wykres
Symetria dwuścienna	[4]	[4]

Powiązane polytopy

Ma połowę wierzchołków runcinated 5-cube , w porównaniu tutaj w projekcjach płaszczyzny B5 Coxetera:

Runcic 5-kostka

Runcinated 5-cube

Runcic n -kostki
N	4	5	6	7	8
[1 + ,4,3 n-2 ] = [3,3 n-3,1 ]	[1 + ,4,3 2 ] = [3,3 1,1 ]	[1 + ,4,3 3 ] = [3,3 2,1 ]	[1 + ,4,3 4 ] = [3,3 3,1 ]	[1 + ,4,3 5 ] = [3,3 4,1 ]	[1 + ,4,3 6 ] = [3,3 5,1 ]
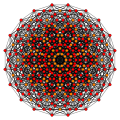
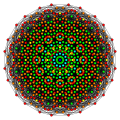
Runcic postać
Coxeter	=	=	=	=	=
Schläfli	h 3 {4,3 2 }	h 3 {4,3 3 }	h 3 {4,3 4 }	h 3 {4,3 5 }	h 3 {4,3 6 }

Runcicantic 5-sześcian

Runcicantic 5-sześcian
Typ	jednolity 5-polytop
Symbol Schläfliego	t 0,1,2 {3,3 2,1 } godz 3 {4,3 3 }
Diagram Coxetera-Dynkina
4 twarze	42
Komórki	360
Twarze	1040
Krawędzie	1200
Wierzchołki	480
figura wierzchołka
grupy Coxetera	re 5 , [3 2,1,1 ]
Nieruchomości	wypukły

Alternatywne nazwy

• Kantitruncated 5-demicube/demienteract
• Hemipenteract rombowy (girhin) (Jonathan Bowers)

współrzędne kartezjańskie

Współrzędne kartezjańskie dla 480 wierzchołków runcicantic 5-sześcianu wyśrodkowanego na początku to permutacje współrzędnych:

(±1,±1,±3,±5,±5)

z nieparzystą liczbą znaków plus.

Obrazy

rzuty ortograficzne

Samolot Coxetera	B5 _
Wykres
Symetria dwuścienna	[10/2]
Samolot Coxetera	D5 _	D 4
Wykres
Symetria dwuścienna	[8]	[6]
Samolot Coxetera	D3 _	3 _
Wykres
Symetria dwuścienna	[4]	[4]

Powiązane polytopy

Ma połowę wierzchołków runcicantelated 5-cube , w porównaniu tutaj w projekcjach płaszczyzny B5 Coxetera:

Runcicantic 5-sześcian

Runcicantelated 5-sześcian

Powiązane polytopy

Ten polytope jest oparty na 5-demisześcianie , części wymiarowej rodziny jednolitych polytopów zwanych półhipersześcianami , ponieważ jest to odmiana rodziny hipersześcianów .

Istnieje 23 jednolitych 5-politopów , które można zbudować z symetrii D ₅ półsześcianu 5, z których są unikalne dla tej rodziny, a 15 jest wspólnych w rodzinie 5 sześcianów .

Notatki

• HSM Coxeter :
  • HSM Coxeter, Regularne Polytopes , wydanie 3, Dover, Nowy Jork, 1973
  •   Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena , Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papier 23) HSM Coxeter, Regularne i półregularne Polytopes II , [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Rękopis (1991)
  • NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
• Klitzing, Richard. „Jednolite polytopy 5D (polytera)” . x3o3o *b3x3o - syrhin, x3x3o *b3x3o - girhin

Linki zewnętrzne

• Weisstein, Eric W. „Hypercube” . MathWorld .
• Polytopy o różnych wymiarach
• Słowniczek wielowymiarowy