8-ortopleks

8-ortoplex Octacross
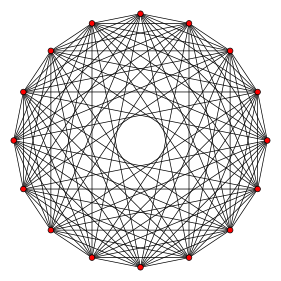Projekcja ortogonalna wewnątrz wielokąta Petriego
Typ	Zwykły 8-politop
Rodzina	ortopleks
Symbol Schläfliego	{3 6 ,4} {3,3,3,3,3,3 1,1 }
Diagramy Coxetera-Dynkina
7 twarzy	256 {3 6 }
6-twarzy	1024 {3 5 }
5 twarzy	1792 {3 4 }
4 twarze	1792 {3 3 }
Komórki	1120 {3,3}
Twarze	448 {3}
Krawędzie	112
Wierzchołki	16
figura wierzchołka	7-ortopleks
wielokąt Petriego	sześciokąt
grupy Coxetera	do 8 , [3 6 ,4] re 8 , [3 5,1,1 ]
Podwójny	8-sześcian
Nieruchomości	wypukły , polytope Hannera

W geometrii 8 -ortoplex lub 8- cross polytope jest regularnym 8-polytopem z 16 wierzchołkami , 112 krawędziami , 448 trójkątnymi ścianami , 1120 czworościennymi komórkami , 1792 5 komórkami 4 ścianami , 1792 5 ścianami , 1024 6 ścianami i 256 7 twarzy .

Ma dwie konstruktywne formy, pierwsza jest regularna z symbolem Schläfliego {3 ⁶ ,4}, a druga z naprzemiennie oznaczonymi (szachownicowymi) fasetami, z symbolem Schläfliego {3,3,3,3,3,3 ^1,1 } lub symbol Coxetera 5 ₁₁ .

Jest częścią nieskończonej rodziny polytopów, zwanych cross-polytopami lub ortopleksami . Podwójny polytope to 8- hipersześcian lub ośmiokąt .

Alternatywne nazwy

• Octacross , wywodzący się z połączenia nazwy rodziny cross polytope z oct dla ośmiu (wymiarów) w języku greckim
• Diacosipentacontahexazetton jako 256- fasetowany 8-polytop (polyzetton)

Jako konfiguracja

Ta macierz konfiguracji reprezentuje 8-ortopleks. Wiersze i kolumny odpowiadają wierzchołkom, krawędziom, ścianom, komórkom, 4-ścian, 5-ścian, 6-ścian i 7-ścian. Liczby po przekątnej mówią, ile każdego elementu występuje w całym 8-ortopleksie. Liczby niediagonalne mówią, ile elementów kolumny występuje w elemencie wiersza lub na nim.

${\ Displaystyle {\ rozpocząć {bmatrix} {\ rozpocząć {macierz} 16 i 14 i 84 i 280 i 560 i 672 i 448 i 128 \\ 2 i 112 i 12 i 60 i 160 i 240 i 192 i 64 \\ 3 i 3 i 448 i 10 i 40 i 80 i 80 i 32 \\ 4 i 6 i 4 i 1120 i 8 i 24 i 32 i 16\\5&10&10&5&1792&6&12&8\\6&15&20&15&6&1792&4&4\\7&21&35&35&21&7&1024&2\\8&28&56&70&56&28&8&256\end{macierz}}\end{bmatrix}}}$

Ukośne numery wektorów f są uzyskiwane za pomocą konstrukcji Wythoffa , dzieląc pełny porządek grupowy rzędu podgrup przez usunięcie poszczególnych luster.

B8 _		k-twarz	f k	F0	f 1	f 2	fa 3	f 4	f 5	f 6	f 7	k -figura	notatki
B7 _		( )	F0	16	14	84	280	560	672	448	128	{3,3,3,3,3,4}	B 8 / B 7 = 2^8*8!/2^7/7! = 16
A 1 B 6		{}	f 1	2	112	12	60	160	240	192	64	{3,3,3,3,4}	B 8 /A 1 B 6 = 2^8*8!/2/2^6/6! = 112
2 B 5 _		{3}	f 2	3	3	448	10	40	80	80	32	{3,3,3,4}	B 8 /A 2 B 5 = 2^8*8!/3!/2^5/5! = 448
A 3 B 4		{3,3}	fa 3	4	6	4	1120	8	24	32	16	{3,3,4}	B 8 /A 3 B 4 = 2^8*8!/4!/2^4/4! = 1120
4 B 3 _		{3,3,3}	f 4	5	10	10	5	1792	6	12	8	{3,4}	B 8 / A 4 B 3 = 2^8*8!/5!/8/3! = 1792
5 B 2 _		{3,3,3,3}	f 5	6	15	20	15	6	1792	4	4	{4}	B 8 /A 5 B 2 = 2^8*8!/6!/4/2 = 1792
6 A 1 _		{3,3,3,3,3}	f 6	7	21	35	35	21	7	1024	2	{}	B 8 /A 6 ZA 1 = 2^8*8!/7!/2 = 1024
7 _		{3,3,3,3,3,3}	f 7	8	28	56	70	56	28	8	256	( )	B 8 /A 7 = 2^8*8!/8! = 256

Budowa

Istnieją dwie grupy Coxetera związane z sześcianem 8, jedna regularna , podwójna ośmiornicy z grupą symetrii C ₈ lub [4,3,3,3,3,3,3] i półsymetria z dwiema kopiami 7-proste ścianki, naprzemiennie, z grupą symetrii D ₈ lub [3 ^5,1,1 ]. Konstrukcja o najniższej symetrii oparta jest na dualnym 8- ortotopie , zwanym 8-fusilem .

Nazwa	Diagram Coxetera	Symbol Schläfliego	Symetria	Zamówienie	figura wierzchołka
regularny 8-ortopleks		{3,3,3,3,3,3,4}	[3,3,3,3,3,3,4]	10321920
Quasiregularny 8-ortopleks		{3,3,3,3,3,3 1,1 }	[3,3,3,3,3,3 1,1 ]	5160960
8-fusil		8{}	[2 7 ]	256

współrzędne kartezjańskie

Współrzędne kartezjańskie wierzchołków sześcianu 8, wyśrodkowane w początku, to

(±1,0,0,0,0,0,0,0), (0,±1,0,0,0,0,0,0), (0,0,±1,0,0, 0,0,0), (0,0,0,±1,0,0,0,0),

(0,0,0,0,±1,0,0,0), (0,0, 0,0,0,±1,0,0), (0,0,0,0,0,0,0,±1), (0,0,0,0,0,0,0,±1 )

Każda para wierzchołków jest połączona krawędzią , z wyjątkiem przeciwieństw.

Obrazy

rzuty ortograficzne

B8 _			B7 _
[16]			[14]
6 _			B5 _
[12]			[10]
4 _		B3 _		B2 _
[8]		[6]		[4]
7 _		5 _		3 _
[8]		[6]		[4]

Jest używany w swojej naprzemiennej postaci 5 ₁₁ z 8-simplexem, aby utworzyć plaster miodu 5 ₂₁ .

• HSM Coxeter :
  • HSM Coxeter, Regularne Polytopes , wydanie 3, Dover, Nowy Jork, 1973
  •   Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papier 23) HSM Coxeter, Regularne i półregularne Polytopes II , [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Rękopis (1991)
  • NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
• Klitzing, Richard. „Jednolite polytopy 8D (polyzetta) x3o3o3o3o3o3o4o - ek” .

Linki zewnętrzne

• Olszewski, Jerzy. „Krzyż polytope” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r.
• Polytopy o różnych wymiarach
• Słowniczek wielowymiarowy