9-sześcian

9-sześcian Enneract
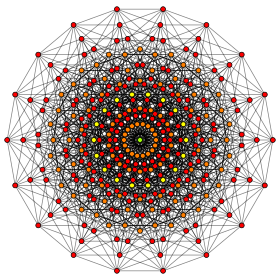Rzut ortogonalny wewnątrz wielokąta Petriego Pomarańczowe wierzchołki są podwojone, żółty ma 4, a zielony środek ma 8
Typ	Zwykły 9-politop
Rodzina	hipersześcian
Symbol Schläfliego	{4,3 7 }
Diagram Coxetera-Dynkina
8-twarzy	18 {4,3 6 }
7 twarzy	144 {4,3 5 }
6-twarzy	672 {4,3 4 }
5 twarzy	2016 {4,3 3 }
4 twarze	4032 {4,3,3}
Komórki	5376 {4,3}
Twarze	4608 {4}
Krawędzie	2304
Wierzchołki	512
figura wierzchołka	8-jednostronny
wielokąt Petriego	ośmiokąt
zespół Coxetera	C9 , [3 7 , 4]
Podwójny	9-ortopleks
Nieruchomości	wypukły , polytope Hannera

W geometrii 9 -sześcian to dziewięciowymiarowy hipersześcian z 512 wierzchołkami , 2304 krawędziami , 4608 kwadratowymi ścianami , 5376 komórkami sześciennymi , 4032 tesseract 4-ściany , 2016 5-sześcian 5-ściany , 672 6-sześcian 6-ściany , 144 7-sześcianów 7-ścian i 18 8-kostek 8-ścian .

Można go nazwać po symbolu Schläfliego {4,3 ⁷ }, składającym się z trzech 8-kostek wokół każdej 7-ściany. Jest również nazywany enneract , połączenie tesseract ( 4-sześcian ) i enne dla dziewięciu (wymiary) w języku greckim . Można go również nazwać regularnym octadeca-9-tope lub octadecayotton , jako dziewięciowymiarowy polytop zbudowany z 18 regularnych faset .

Należy do nieskończonej rodziny polytopów, zwanych hipersześcianami. Podwójny sześcian 9 można nazwać 9-ortopleksem i jest częścią nieskończonej rodziny cross - politopów .

współrzędne kartezjańskie

Współrzędne kartezjańskie wierzchołków 9-sześcianu wyśrodkowanego w początku i długości krawędzi 2 to

(±1,±1,±1,±1,±1,±1,±1,±1,±1)

₀ podczas gdy wnętrze tego samego składa się ze wszystkich punktów ( x , x ₁ , x ₂ , x ₃ , x ₄ , x ₅ , x ₆ , x ₇ , x ₈ ) z −1 < x _i < 1.

projekcje

Ten 9-sześcienny wykres jest rzutem ortogonalnym . Ta orientacja pokazuje kolumny wierzchołków rozmieszczonych w odległości wierzchołek-krawędź-wierzchołek od jednego wierzchołka po lewej do jednego wierzchołka po prawej oraz krawędzie łączące sąsiednie kolumny wierzchołków. Liczba wierzchołków w każdej kolumnie odpowiada wierszom trójkąta Pascala i wynosi 1:9:36:84:126:126:84:36:9:1.

Obrazy

rzuty ortograficzne

B 9		B8 _		7 _
[18]		[16]		[14]
6 _			B5 _
[12]			[10]
4 _		B3 _		B2 _
[8]		[6]		[4]
7 _		5 _		3 _
[8]		[6]		[4]

Pochodne polytopy

Zastosowanie operacji naprzemiennej , usunięcie naprzemiennych wierzchołków 9-sześcianu , tworzy kolejny jednolity polytope , zwany 9-demicube (część nieskończonej rodziny zwanej demihypercubes ), który ma 18 8-demicube i 256 8-simplex faset.

Notatki

• HSM Coxeter :
  •   Coxeter, Regular Polytopes , (3. wydanie, 1973), wydanie Dover, ISBN 0-486-61480-8 , s. 296, Tabela I (iii): Regularne polytopy, trzy regularne polytopy w n-wymiarach (n≥5)
  • HSM Coxeter, Regular Polytopes , 3. wydanie, Dover, Nowy Jork, 1973, s. 296, Tabela I (iii): Regularne polytopy, trzy regularne polytopy w n-wymiarach (n≥5)
  •   Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papier 23) HSM Coxeter, Regularne i półregularne Polytopy II , [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Rękopis (1991)
  • NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966)
• Klitzing, Richard. „9D jednolite politopy (poliyotta) o3o3o3o3o3o3o3o4x - enne” .

Linki zewnętrzne

• Weisstein, Eric W. „Hypercube” . MathWorld .
• Olszewski, Jerzy. „Zmierz polytope” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r.
• Glosariusz wielowymiarowy: hipersześcian Garrett Jones