120 ogniw

120-komorowy
diagram Schlegla (wierzchołki i krawędzie)
Typ	Wypukły regularny 4-politop
Symbol Schläfliego	{5,3,3}
Diagram Coxetera
Komórki	120 {5,3}
Twarze	720 {5}
Krawędzie	1200
Wierzchołki	600
figura wierzchołka	czworościan
wielokąt Petriego	30-gon
zespół Coxetera	H4 , [3,3,5]
Podwójny	600 ogniw
Nieruchomości	wypukłe , izogonalne , izotoksalne , izoedryczne
Jednolity indeks	32

Internet

W geometrii 120 komórek jest wypukłym regularnym 4-polytopem (czterowymiarowym odpowiednikiem bryły platońskiej) z symbolem Schläfliego {5,3,3}. Jest również nazywany C ₁₂₀ , dodecaplex (skrót od „kompleks dwunastościenny”), hiperdodecahedron , polydodecahedron , hecatonicosachoron , dodecacontachoron i hecatonicosahedroid .

Granica 120 komórek składa się ze 120 dwunastościennych komórek z 4 spotkaniami w każdym wierzchołku. Razem tworzą 720 pięciokątnych ścian, 1200 krawędzi i 600 wierzchołków. Jest to 4- wymiarowy odpowiednik dwunastościanu foremnego , ponieważ tak jak dwunastościan ma 12 pięciokątnych ścianek, z trzema wokół każdego wierzchołka, dwunastościan ma 120 dwunastościanów, po trzy wokół każdej krawędzi. Jego podwójny polytope to 600-komórkowy .

Geometria

Komórka 120 zawiera geometrie każdego wypukłego regularnego polytopu w pierwszych czterech wymiarach (z wyjątkiem wielokątów {7} i wyższych). Jako szósty i największy regularny wypukły 4-politop, zawiera wpisane instancje swoich czterech poprzedników (rekurencyjnie). Zawiera również 120 wpisanych wystąpień pierwszego w sekwencji, komórki 5 , której nie ma w żadnej z pozostałych. 120-komorowy to czterowymiarowy szwajcarski scyzoryk : zawiera wszystko po jednym.

Studiowanie 120 komórek jest zniechęcające, ale pouczające, ponieważ zawiera przykłady każdego związku między wszystkimi wypukłymi regularnymi polytopami znalezionymi w pierwszych czterech wymiarach. I odwrotnie, można to zrozumieć tylko poprzez uprzednie zrozumienie każdego z jego poprzedników i sekwencji coraz bardziej złożonych symetrii, które wykazują. Dlatego Stillwell zatytułował swój artykuł na temat 4-polytopów i historii matematyki więcej niż 3 wymiarów The Story of the 120-cell .

Regularne wypukłe 4-politopy
Grupa symetrii	4 _	4 _		F 4	4 _
Nazwa	5-ogniwowy Hiper- czworościan 5-punktowy	16-ogniwowy Hiperośmiościan 8- punktowy	8-ogniwowy Hipersześcian 16- punktowy	24-ogniwowy 24-punktowy	600 ogniw Hiper- dwudziestościan 120-punktowy	120 ogniw Hiperdwunastościan 600- punktowy
Symbol Schläfliego	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
lusterka Coxetera
Lustrzane dwuściany	𝝅 / 3 𝝅 / 3 𝝅 / 3 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 3 𝝅 / 3 𝝅 / 4 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 4 𝝅 / 3 𝝅 / 3 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 3 𝝅 / 4 𝝅 / 3 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 3 𝝅 / 3 𝝅 / 5 𝝅 / 2 𝝅 / 2 𝝅 / 2	𝝅 / 5 𝝅 / 3 𝝅 / 3 𝝅 / 2 𝝅 / 2 𝝅 / 2
Wykres
Wierzchołki	5 czworościennych	8 ośmiościenny	16 czworościennych	24 sześcienne	120 dwudziestościennych	600 czworościennych
Krawędzie	10 trójkątnych	24 kwadraty	32 trójkątne	96 trójkątny	720 pięciokątny	1200 trójkątny
Twarze	10 trójkątów	32 trójkąty	24 kwadraty	96 trójkątów	1200 trójkątów	720 pięciokątów
Komórki	5 czworościanów	16 czworościanów	8 kostek	24 ośmiościany	600 czworościanów	120 dwunastościanów
Tori	1 5-czworościan	2 8-czworościan	2 4-sześcian	4 6-ośmiościan	20 30-czworościan	12 10-dwunastościan
Wpisany	120 w 120 komórkach	675 w 120 komórkach	2 16-komorowe	3 8-ogniw	25 24-ogniw	10 600 ogniw
Świetne wielokąty		2 𝅅 / 2 kwadraty x 3	4 / 2 3 prostokąty x	4 / 3 sześciokąty x 4	12 / 5 dziesięciokątów x 6	50 / 15 dwunastokątów x 4
Wielokąty Petriego	1 pięciokąt	1 ośmiokąt	2 ośmiokąty	2 dwunastokąty	4 30-gonów	20 30-gonów
Długi promień	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$
Długość krawędzi	${\ Displaystyle {\ sqrt {\ tfrac {5} {2}}} \ około 1,581}$	${\ Displaystyle {\ sqrt {2}} \ około 1,414}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle {\ tfrac {1} {\ fi}} \ około 0,618}$	${\ Displaystyle {\ tfrac {1} {\ fi ^ {2} {\ sqrt {2}}}} \ około 0,270}$
Krótki promień	${\ Displaystyle {\ tfrac {1} {4}}}$	${\ Displaystyle {\ tfrac {1} {2}}}$	${\ Displaystyle {\ tfrac {1} {2}}}$	${\ Displaystyle {\ sqrt {\ tfrac {1} {2}}} \ około 0,707}$	${\ Displaystyle {\ sqrt {\ tfrac {\ fi ^ {4}} {8}}} \ około 0,926}$	${\ Displaystyle {\ sqrt {\ tfrac {\ fi ^ {4}} {8}}} \ około 0,926}$
Obszar	${\ Displaystyle 10 \ lewo ({\ tfrac {5 {\ sqrt {3}}} {8}} \ prawej) \ około 10,825}$	${\ Displaystyle 32 \ lewo ({\ sqrt {\ tfrac {3} {4}}} \ prawej) \ około 27,713}$	${\ Displaystyle 24}$	${\ Displaystyle 96 \ lewo ({\ sqrt {\ tfrac {3} {16}}} \ prawej) \ około 41,569}$	${\ Displaystyle 1200 \ lewo ({\ tfrac {\ sqrt {3}} {4 \ phi ^ {2}}} \ prawej) \ około 198,48}$	${\ Displaystyle 720 \ lewo ({\ tfrac {\ sqrt {25 + 10 {\ sqrt {5}}}} {8 \ phi ^ {4}}} \ prawo )\około 90,366}$
Tom	${\ Displaystyle 5 \ lewo ({\ tfrac {5 {\ sqrt {5}}} {24}} \ prawej) \ około 2,329}$	${\ Displaystyle 16 \ lewo ({\ tfrac {1} {3}} \ prawej) \ około 5,333}$	${\ Displaystyle 8}$	${\ Displaystyle 24 \ lewo ({\ tfrac {\ sqrt {2}} {3}} \ prawej) \ około 11,314}$	${\ Displaystyle 600 \ lewo ({\ tfrac {\ sqrt {2}} {12 \ phi ^ {3}}} \ prawej) \ około 16,693}$	${\ Displaystyle 120 \ lewo ({\ tfrac {15 + 7 {\ sqrt {5}}} {4 \ phi ^ {6} {\ sqrt {8}} }}\prawo)\około 18,118}$
4-Zawartość	${\ Displaystyle {\ tfrac {\ sqrt {5}} {24}} \ lewo ({\ tfrac {\ sqrt {5}}} {2}} \ prawej) ^ {4} \około 0,146}$	${\ Displaystyle {\ tfrac {2} {3}} \ około 0,667}$	${\ Displaystyle 1}$	${\ Displaystyle 2}$	${\ Displaystyle {\ tfrac {{\ tekst {krótki}} \ razy {\ tekst {tom}}} {4}} \ około 3,863}$	${\ Displaystyle {\ tfrac {{\ tekst {krótki}} \ razy {\ tekst {tom}}} {4}} \ około 4,193}$

współrzędne kartezjańskie

Naturalne współrzędne kartezjańskie dla 4-polytopu wyśrodkowanego na początku przestrzeni 4 występują w różnych układach odniesienia, w zależności od wybranego długiego promienia (od środka do wierzchołka).

√ 8 współrzędnych promienia

120 komórek o długim promieniu √ 8 = 2 √ 2 ≈ 2,828 ma długość krawędzi 2 / φ ² = 3− √ 5 ≈ 0,764.

W tym układzie odniesienia jego 600 współrzędnych wierzchołków to { permutacje } i [ parzyste permutacje ] następujących elementów:

24	({0, 0, ±2, ±2})	24-ogniwowy	600-punktowy 120-komorowy
96	([0, ±φ −1 , ±φ, ± √ 5 ])	afront 24-ogniwowy
120	({±φ, ±φ, ±φ, ±φ −2 })	24 5-ogniw
120	({±1, ±1, ±1, ± √ 5 })	24 5-ogniw
120	({±φ −1 , ±φ −1 , ±φ −1 , ±φ 2 })	24 5-ogniw
96	([0, ±φ −2 , ±1, ±φ 2 ])	afront 24-ogniwowy
24	([±φ −1 , ±1, ±φ, ±2])	24-ogniwowy

1 + √ 5/2 także . τ) jest złotym podziałem , ≈ 1,618

Współrzędne promienia jednostki

Komórka o promieniu jednostkowym 120 ma długość krawędzi 1 / φ ² √ 2 ≈ 0,270.

W tym układzie odniesienia komórka 120 leży wierzchołkiem do góry, a jej współrzędne to {permutacje} i [permutacje parzyste] w lewej kolumnie poniżej:

			24	120	600
8	({±1, 0, 0, 0})	16-ogniwowy	24-ogniwowy	600 ogniw	120 ogniw
16	({± 1 / 2 , ± 1 / 2 , ± 1 / 2 , ± 1 / 2 })	tesserakt
96	([0, ± φ -1 / 2 , ± 1 / 2 , ± φ / 2 ])	afront 24-ogniwowy
480	podwójne, 24-ogniwowe środkowe krawędzie: 120 (±..., ±..., ±..., ±...) 120 (±..., ±..., ±..., ±...) 120 (±... , ±..., ±..., ±...) 96 (0, ±..., ±..., ±...) 24 ({± √ 1/2 , ± √ 1/2 , 0, 0})	5-punktowy 5-ogniwowy : (1, 0, 0, 0) (− 1 / 4 , √ 5/2 , √ 5/2 , √ 5/2 ) (− 1 / 4 , − √ 5/2 , − √ 5/2 , √ 5 /2 ) (− 1 / 4 , − √ 5/2 , √ 5/2 , − √ 5/2 ) (− 1 / 4 , √ 5/2 , − √ 5/2 , − √ 5/2 )	24-ogniwowy : ({± √ 1/2 , ± √ 1/2 , 0, 0})	600 ogniw : ({±1, 0, 0, 0}) ({± 1 / 2 , ± 1 / 2 , ± 1 / 2 , ± 1 / 2 }) ([0, ± φ −1 / 2 , ± 1 / 2 , ± φ / 2 ])
	Współrzędne promienia jednostkowego jednolitych wypukłych 4-polytopów są powiązane przez mnożenie kwaternionów . Ponieważ zwykłe 4-polytopy są wzajemnymi związkami, ich zestawy 4-współrzędnych kartezjańskich ( kwaternionów ) są wzajemnymi iloczynami. Współrzędne promienia jednostkowego 600 wierzchołków komórki 120 (w lewej kolumnie powyżej) to wszystkie możliwe iloczyny kwaternionów 5 wierzchołków komórki 5, 24 wierzchołków komórki 24 i 120 wierzchołków komórki 600 (w środku trzy kolumny powyżej).

Tabela podaje współrzędne dwóch instancji każdego z wpisanych 4-polytopów, ale komórka 120 zawiera wielokrotności pięciu wpisanych instancji każdego z jej prekursorów 4-polytopów, zajmujących różne podzbiory jej wierzchołków. (600-punktowa) 120-ogniwowa jest wypukłą otoczką 5 rozłącznych (120-punktowych) 600-ogniwowych. Każda (120-punktowa) 600-komorowa jest wypukłą otoczką 5 rozłącznych (24-punktowych) 24-komórek, więc 120-komorowa jest wypukłą otoczką 25 rozłącznych 24-komórek. Każda 24 komórka to wypukła otoczka 3 rozłącznych (8-punktowych) 16 komórek, więc komórka 120 to wypukła otoczka 75 rozłącznych 16 komórek. Wyjątkowo (600-punktowa) 120-ogniwowa jest wypukłą otoczką 120 rozłącznych (5-punktowych) 5-ogniwowych.

Wykres wielościenny

Biorąc pod uwagę macierz sąsiedztwa wierzchołków reprezentujących jej wykres wielościenny, średnica wykresu wynosi 15, łącząc każdy wierzchołek z jego negacją współrzędnych, w odległości euklidesowej 4 √ 2 daleko (jego obwód), a istnieją 24 różne ścieżki łączące je wzdłuż krawędzi polytopu. Z każdego wierzchołka są 4 wierzchołki w odległości 1, 12 w odległości 2, 24 w odległości 3, 36 w odległości 4, 52 w odległości 5, 68 w odległości 6, 76 w odległości 7, 78 w odległości 8, 72 w odległości 9, 64 w odległości 10, 56 w odległości 11, 40 w odległości 12, 12 w odległości 13, 4 w odległości 14 i 1 w odległości 15. Macierz sąsiedztwa ma 27 różnych wartości własnych w zakresie od 2 / φ 2 , ^z krotnością od 4 do 4, z krotnością 1. Wielokrotność wartości własnej 0 wynosi 18, a rząd macierzy sąsiedztwa wynosi 582.

Wierzchołki grafu wielościennego złożonego ze 120 komórek można pokolorować 3 razy .

Nie opublikowano, czy graf jest hamiltonowski . Jest to Eulera mające stopień 4 w każdym wierzchołku.

Koncentryczne kadłuby

Rzut ortogonalny 120 komórek przy użyciu dowolnych 3 z tych wymiarów współrzędnych kartezjańskich tworzy zewnętrzną powłokę sfazowanego dwunastościanu o Norm = √ 8 . Kadłuby 1, 2 i 7 to nachodzące na siebie pary dwunastościanów . Kadłub 3 to para dwunastościanów . Kadłuby 4 i 5 to pary dwudziestościanów ściętych . Kadłuby 6 i 8 to pary ośmiościanów rombowych .

Konstrukcje

Komórka 120 jest szóstą w sekwencji 6 wypukłych regularnych 4-polytopów (w kolejności wielkości i złożoności). Można go zdekonstruować na dziesięć odrębnych instancji (lub pięć rozłącznych instancji) swojego bezpośredniego poprzednika (i podwójnego) komórki 600 , tak jak komórkę 600 można rozłożyć na dwadzieścia pięć odrębnych instancji (lub pięć rozłącznych instancji) jej bezpośredni poprzednik 24-komorowy , 24-komorowy można rozłożyć na trzy odrębne instancje swojego poprzednika tesseraktu ( 8-komorowego), a 8-komorowy można rozłożyć na dwa rozłączne instancje jego poprzednika, 16 -komorowego . Komórka 120 zawiera 675 odrębnych instancji (75 rozłącznych instancji) komórki 16-osobowej.

Odwrotna procedura konstruowania każdego z nich z instancji jego poprzednika zachowuje promień poprzednika, ale generalnie tworzy następcę o mniejszej długości krawędzi. Długość krawędzi 600 komórek jest ~ 0,618 razy większa od jej promienia (odwrotna złota proporcja ), ale długość krawędzi 120 komórek jest ~ 0,270 razy większa od jej promienia.

Podwójne ogniwa 600

Pięć czworościanów wpisanych w dwunastościan. Można również wpisać pięć przeciwstawnych czworościanów (nie pokazano).

Ponieważ komórka 120 jest podwójna komórki 600, można ją zbudować z komórki 600, umieszczając jej 600 wierzchołków w środku objętości każdej z 600 czworościennych komórek. Z 600 komórek o jednostkowym promieniu daje to 120 komórek o nieco mniejszym promieniu ( φ ² / √ 8 ≈ 0,926) i długości krawędzi dokładnie 1/4. Zatem 120-komórkowa długość krawędzi jednostkowej (o długim promieniu φ ² √ 2 ≈ 3,702) może być skonstruowana w ten sposób wewnątrz 600-komórkowej komórki o dużym promieniu 4.

Jeden z pięciu różnych sześcianów wpisanych w dwunastościan (linie przerywane). Dwa przeciwstawne czworościany (nie pokazane) leżą wpisane w każdy sześcian, więc dziesięć różnych czworościanów (po jednym z każdej 600-komórkowej w 120-komórkowej) jest wpisanych w dwunastościan.

Odwrotnie, 120 komórek, których współrzędne podano powyżej , o długim promieniu √ 8 = 2 √ 2 ≈ 2,828 i długości krawędzi 2 / φ ² = 3− √ 5 ≈ 0,764, można zbudować tuż poza 600 komórkami o nieco mniejszym długim promieniu , umieszczając środek każdej dwunastościennej komórki w jednym ze 120 600 wierzchołków komórek. Komórka 600 musi mieć długi promień φ ² , który jest mniejszy niż √ 8 w tym samym stosunku ≈ 0,926; jest w złotym stosunku do długości krawędzi komórki 600, więc musi to być φ.

Rotacje komórek wpisanych liczb podwójnych

Ponieważ komórka 120 zawiera wpisane komórki 600, zawiera własną liczbę podwójną o tym samym promieniu. Komórka 120 zawiera pięć rozłącznych komórek 600 (dziesięć nakładających się wpisanych komórek 600, z których możemy wybrać pięć rozłącznych komórek 600 na dwa różne sposoby), więc można ją postrzegać jako złożenie pięciu własnych komórek podwójnych (w dwie drogi). Wierzchołki każdej wpisanej 600-komórkowej są wierzchołkami 120-komórkowej i (podwójnie) każde dwunastościenne centrum komórki jest czworościennym centrum komórki w każdej z wpisanych 600-komórek.

Komórki dwunastościenne komórki 120 mają wpisane komórki czworościenne komórek 600. Tak jak komórka 120 jest złożeniem pięciu komórek 600 (na dwa sposoby), tak dwunastościan jest złożeniem pięciu czworościanów foremnych (na dwa sposoby). Ponieważ dwa przeciwstawne czworościany można wpisać w sześcian, a pięć sześcianów można wpisać w dwunastościan, dziesięć czworościanów w pięciu sześcianach można wpisać w dwunastościan: dwa przeciwstawne zestawy po pięć, z których każdy obejmuje wszystkie 20 wierzchołków i każdy wierzchołek w dwa czworościany (po jednym z każdego zestawu, ale oczywiście nie przeciwna para sześcianu). To pokazuje, że 120-ogniwowy zawiera wśród wielu elementów wnętrza 120 związki dziesięciu czworościanów , z których każdy jest wymiarowo analogiczny do całej 120-komórki jako związek dziesięciu 600-komórek.

Wszystkie dziesięć czworościanów można wygenerować przez dwa chiralne pięciokrotne obroty dowolnego czworościanu. W każdej komórce dwunastościennej jedna komórka czworościenna pochodzi z każdej z dziesięciu komórek 600 wpisanych w komórkę 120. Dlatego całe 120-ogniwo, ze wszystkimi dziesięcioma wpisanymi 600-ogniwami, można wygenerować z tylko jednej 600-ogniwa, obracając jego komórki.

Powiększenie

Inną konsekwencją 120-komórek zawierających wpisane 600-komórek jest to, że można je skonstruować poprzez umieszczenie pewnego rodzaju 4-piramid na komórkach 600-komórek. Te czworościenne piramidy muszą być w tym przypadku dość nieregularne (z wierzchołkiem stępionym na kilka „wierzchołków”), ale możemy rozpoznać ich kształt po sposobie, w jaki czworościan jest wpisany w dwunastościan .

Tylko 120 czworościennych komórek z każdej 600 komórek można wpisać w dwunastościany 120 komórek; jego pozostałe 480 czworościanów obejmuje komórki dwunastościenne. Każdy czworościan z wpisanym dwunastościanem jest centralną komórką skupiska pięciu czworościanów , z czterema innymi połączonymi twarzą wokół niego, leżącymi tylko częściowo w dwunastościanie. Centralny czworościan jest połączony krawędziowo z dodatkowymi 12 czworościennymi komórkami, również leżącymi tylko częściowo w dwunastościanie. Centralna komórka jest połączona wierzchołkowo z 40 innymi komórkami czworościennymi, które leżą całkowicie poza dwunastościanem.

orbity Weyla

Inna metoda konstrukcji wykorzystuje kwaterniony i dwudziestościenną symetrię orbit grup Weyla rzędu 120. ${\ Displaystyle O (\ Lambda) = W (H_ {4}) = I$ } opisz 24-komórki jako kwaterniony orbity D4 pod grupą Weyla W (D4): ${\ displaystyle T}$ i ${\ displaystyle T ' }$



O(0100) : T = {±1,±e1,±e2,±e3,(±1±e1±e2±e3)/2} O(1000) : V1 O(0010) : V2 O( 0001 ) : V3

Z czwartorzędami ${\ Displaystyle (p, q)}$ gdzie ${\ Displaystyle {\ bar {p}}}$ jest koniugatem ${\ Displaystyle p}$ i ${\ Displaystyle [p, q]: r \ rightarrow r' = prq}$ i ${\ Displaystyle [p, q] ^ {*}: r \ rightarrow r'' = p {\ bar {r}} q}$ , a następnie grupa Coxeter ${\ Displaystyle W (H_ {4}) = \ lbrace [p, {\ bar {p}}] \ oplus [p, {\ bar {p}}] ^{*}\rbrace }$ to grupa symetrii komórki 600 i komórki 120 rzędu 14400.

Biorąc pod uwagę ${\ Displaystyle p \ in T}$ tak, że ${\ Displaystyle {\ bar { p}}=\pm p^{4},{\bar {p}}^{2}=\pm p^{3},{\bar {p}}^{3}=\pm p^{2 } {\ bar {p}} ^ {4} = \ pm p}$ i ${\ Displaystyle p ^ {\ sztylet}}$ jako wymianę możemy skonstruować: ${\ Displaystyle -1 / \ varphi \ leftrightarrow \$$}$

• ${\ Displaystyle S = \ suma _ {i = 1} ^ {4} \ oplus p ^ {i}$ ∑ T
• ja ${\ Displaystyle I = T + S = \ suma _ {i = 0} ^ {4} \ oplus p ^ {i}$ }
• ${\ Displaystyle J = \ suma _ {i, j = 0} ^ {4} \ oplus p ^ {i} {\$ ∑
• alternatywny afront 24-ogniwowy ${\ Displaystyle S '= \ suma _ {i = 1} ^ {4} \ oplus p ^ {i} {\ takt {p}}^{\sztylet i}T'}$
• podwójny afront 24-ogniwowy = ${\ Displaystyle T \ oplus T'\ oplus S'}$ .

Jako konfiguracja

Ta macierz konfiguracji reprezentuje 120 komórek. Wiersze i kolumny odpowiadają wierzchołkom, krawędziom, ścianom i komórkom. Liczby po przekątnej mówią, ile każdego elementu występuje w całej 120 komórce. Liczby niediagonalne mówią, ile elementów kolumny występuje w elemencie wiersza lub na nim.

${\ displayStyle {\ begin {bmatrix} {\ begin {matrix} 600 i 4 i 4 \\ 2 i 1200 i 3 i 3 \\ 5 i 720 i 2 \\ 20 i 30 i 12 i 120 \ end {Matrix}}$

Oto konfiguracja rozszerzona o k -elementy twarzy i k -figury. Liczby elementów diagonalnych to stosunek pełnego grupy Coxetera , 14400, podzielonego przez rząd podgrupy z usunięciem lustra.

4 _		k -twarz	f k	F0	f 1	f 2	fa 3	k -rys	Notatki
3 _		( )	F0	600	4	6	4	{3,3}	H4 /A3 = 14400/24 ​​= 600
A 1 A 2		{}	f 1	2	720	3	3	{3}	H 4 /A 2 ZA 1 = 14400/6/2 = 1200
H 2 A 1		{5}	f 2	5	5	1200	2	{}	H 4 /H 2 ZA 1 = 14400/10/2 = 720
H 3		{5,3}	fa 3	20	30	12	120	( )	H4 /H3 = 14400/120 = 120

Wyobrażanie sobie

120 komórek składa się ze 120 dwunastościennych komórek. Dla celów wizualizacji wygodne jest, aby dwunastościan miał przeciwległe równoległe ściany (cecha, którą dzieli z komórkami tesseraktu i komórki 24 ). Dwunastościany można układać naprzeciw siebie w linii prostej zagiętej w czwartym kierunku w wielkie koło o obwodzie 10 pól. Zaczynając od tego początkowego konstruktu dziesięciu komórek, można użyć dwóch typowych wizualizacji: warstwowej projekcji stereograficznej i struktury przeplatających się pierścieni.

Wielowarstwowa projekcja stereograficzna

Lokalizacje komórek nadają się do hipersferycznego opisu. Wybierz dowolny dwunastościan i nazwij go „biegunem północnym”. Dwanaście południków koła wielkiego (o długości czterech komórek) rozchodzi się promieniście w 3 wymiarach, zbiegając się w piątej komórce „bieguna południowego”. Ten szkielet stanowi 50 ze 120 komórek (2 + 4 × 12).

Zaczynając od bieguna północnego, możemy zbudować 120 komórek w 9 równoleżnikowych warstwach, z aluzjami do ziemskiej topografii 2-sfer w poniższej tabeli. Z wyjątkiem biegunów, środki ciężkości komórek każdej warstwy leżą na oddzielnej 2-sferze, a środki ciężkości równika leżą na wielkiej 2-sferze. Środki ciężkości 30 komórek równikowych tworzą wierzchołki dwudziestościanu z południkami (jak opisano powyżej) przechodzącymi przez środek każdej pięciokątnej ściany. Komórki oznaczone w poniższej tabeli jako „śródmiąższowe” nie leżą na wielkich kręgach południka.

Warstwa #	Liczba komórek	Opis	Kolatitude	Region
1	1 komórka	biegun północny	0°	Półkula północna
2	12 komórek	Pierwsza warstwa komórek południkowych / „ Koło podbiegunowe ”	36°
3	20 komórek	Nie południkowe / śródmiąższowe	60°
4	12 komórek	Druga warstwa komórek południkowych / „ Zwrotnik Raka ”	72°
5	30 komórek	Nie południkowe / śródmiąższowe	90°	Równik
6	12 komórek	Trzecia warstwa komórek południkowych / „ Zwrotnik Koziorożca ”	108°	Półkula południowa
7	20 komórek	Nie południkowe / śródmiąższowe	120°
8	12 komórek	Czwarta warstwa komórek południkowych / „ Krąg podbiegunowy ”	144°
9	1 komórka	biegun południowy	180°
Całkowity	120 komórek

Komórki warstw 2, 4, 6 i 8 znajdują się na powierzchniach komórki biegunowej. Komórki warstw 3 i 7 znajdują się bezpośrednio nad wierzchołkami komórki biegunowej. Komórki warstwy 5 znajdują się nad krawędziami komórki biegunowej.

Przeplatające się pierścienie

Dwa przeplatające się pierścienie 120 ogniw.

Dwa ortogonalne pierścienie w rzucie wyśrodkowanym na komórkę

120 komórek można podzielić na 12 rozłącznych 10-komorowych pierścieni koła wielkiego, tworząc dyskretne / skwantowane włóknienie Hopfa . Zaczynając od jednego 10-ogniwowego pierścienia, obok niego można umieścić kolejny pierścień, który kręci się spiralnie wokół pierwotnego pierścienia, wykonując pełny obrót w dziesięciu ogniwach. Pięć takich pierścieni 10-ogniwowych można umieścić obok oryginalnego pierścienia 10-ogniwowego. Chociaż pierścienie zewnętrzne „kręcą się spiralnie” wokół pierścienia wewnętrznego (i siebie nawzajem), w rzeczywistości nie mają spiralnego skrętu . Wszystkie są równoważne. Spiralizacja jest wynikiem 3-sferycznej krzywizny. Pierścień wewnętrzny i pięć pierścieni zewnętrznych tworzą teraz sześciopierścieniowy, pełny torus o 60 komórkach. Można kontynuować dodawanie 10-komorowych pierścieni sąsiadujących z poprzednimi, ale bardziej pouczające jest skonstruowanie drugiego torusa, rozłącznego z powyższym, z pozostałych 60 komórek, który łączy się z pierwszym. Komórka 120, podobnie jak kula 3, jest połączeniem tych dwóch ( Clifford ) tori. Jeśli środkowy pierścień pierwszego torusa jest południkowym kołem wielkim, jak zdefiniowano powyżej, środkowy pierścień drugiego torusa jest równikowym wielkim kołem, którego środek znajduje się na okręgu południka. Należy również zauważyć, że spiralna powłoka 50 komórek wokół środkowego pierścienia może być lewoskrętna lub prawoskrętna. To tylko kwestia innego podziału komórek w powłoce, tj. wybrania innego zestawu rozłącznych ( równoległości Clifforda ) wielkich kół.

Inne konstrukcje wielkiego koła

Istnieje jeszcze jedna interesująca ścieżka koła wielkiego, która naprzemiennie przechodzi przez przeciwległe wierzchołki komórki, a następnie wzdłuż krawędzi. Ta ścieżka składa się z 6 komórek i 6 krawędzi. Obie powyższe trajektorie po ortodromie mają podwójne trajektorie po ortodromie w komórce 600 . Ścieżka z 10 komórkami twarzą w twarz powyżej odwzorowuje ścieżkę z 10 wierzchołkami przechodzącą wyłącznie wzdłuż krawędzi w komórce 600, tworząc dziesięciokąt. Powyższa naprzemienna ścieżka komórki/krawędzi odwzorowuje ścieżkę składającą się z 12 czworościanów naprzemiennie spotykających się twarzą w twarz, a następnie wierzchołek w wierzchołek (sześć trójkątnych bipiramid ) w komórce 600. Ta ostatnia ścieżka odpowiada a pierścień sześciu dwudziestościanów spotykających się twarzą w twarz w zdartej 24-komorowej (lub dwudziestościennych piramidach w 600-komorowej).

projekcje

Projekcje ortogonalne

Rzuty ortogonalne 120 komórek można wykonać w 2D, definiując dwa ortonormalne wektory bazowe dla określonego kierunku widoku. Projekcja 30-gonalna została wykonana w 1963 roku przez BL Chiltona.

dziesięciokątny H3 przedstawia płaszczyznę wielokąta van Ossa .

Projekcje ortograficzne płaszczyzn Coxetera

4 _	-	F 4
[30] (Czerwony=1)	[20] (Czerwony=1)	[12] (Czerwony=1)
H 3	ZA 2 / B 3 / R 4	A 3 / B 2
[10] (Czerwony=5, pomarańczowy=10)	[6] (Czerwony=1, pomarańczowy=3, żółty=6, limonkowy=9, zielony=12)	[4] (Czerwony=1, pomarańczowy=2, żółty=4, limonkowy=6, zielony=8)

Trójwymiarowe rzuty ortogonalne można również wykonać za pomocą trzech ortonormalnych wektorów bazowych i wyświetlić jako model 3D, a następnie rzutować określoną perspektywę w 3D dla obrazu 2D.

Projekcje ortograficzne 3D

Rzut izometryczny 3D

Animowany obrót 4D

Projekcje perspektywiczne

Projekcje te wykorzystują projekcję perspektywiczną , z określonego punktu widzenia w czterech wymiarach, rzutując model jako cień 3D. Dlatego twarze i komórki, które wyglądają na większe, są po prostu bliżej punktu widzenia 4D. Diagramy Schlegla wykorzystują perspektywę, aby pokazać czterowymiarowe figury, wybierając punkt nad określoną komórką, czyniąc w ten sposób tę komórkę obwiednią modelu 3D, a inne komórki wydają się w niej mniejsze. Projekcje stereograficzne wykorzystują to samo podejście, ale są pokazane z zakrzywionymi krawędziami, przedstawiającymi polytope jako kafelki 3-kuli .

Porównanie projekcji perspektywicznych z 3D do 2D pokazano w analogii.

Porównanie z dwunastościanem regularnym

Występ	Dwunastościan	120 ogniw
diagram Schlegla	12 pięciokątów na płaszczyźnie	120 dwunastościennych komórek w 3-przestrzeni
Projekcja stereograficzna		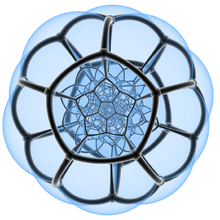Z przezroczystymi twarzami

Projekcja perspektywiczna
	Rzut perspektywiczny w pierwszej komórce w odległości 5 razy większej od środka do wierzchołka, z zastosowanymi ulepszeniami: Najbliższy dwunastościan do punktu widzenia 4D renderowany na żółto 12 dwunastościanów bezpośrednio do niego przylegających jest renderowanych w kolorze cyjan; Pozostałe dwunastościany renderowane na zielono; Komórki odwrócone od punktu widzenia 4D (te leżące po „drugiej stronie” komórki 120) zostały usunięte, aby zminimalizować bałagan na końcowym obrazie.
	Projekcja perspektywiczna wierzchołka w odległości 5 razy większej od środka do wierzchołka, z następującymi ulepszeniami: Cztery komórki otaczające najbliższy wierzchołek pokazane w 4 kolorach Najbliższy wierzchołek pokazany na biało (środek obrazu, gdzie spotykają się 4 komórki) Pozostałe komórki pokazane w przezroczystym zielonym kolorze Komórki odwrócone od punktu widzenia 4D zostały usunięte dla przejrzystości
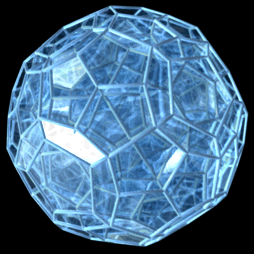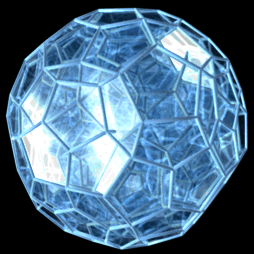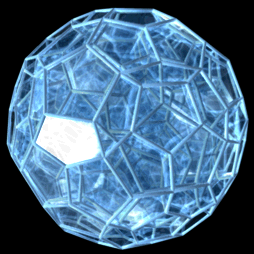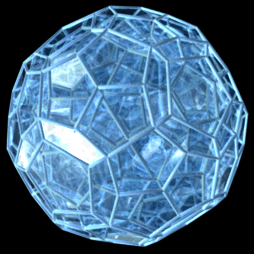
	Projekcja 3D przedstawiająca 120 komórek wykonujących prosty obrót .
	Projekcja 3D 120 komórek wykonujących prosty obrót (od wewnątrz).
	Animowany obrót 4D

Powiązane wielościany i plastry miodu

H ₄ polytopy

120-komórkowy jest jednym z 15 regularnych i jednolitych polytopów o tej samej symetrii H ₄ [3,3,5]:

Polytopy z rodziny H 4
120 ogniw	rektyfikowany 120-ogniwowy	obcięte 120 komórek	cantelated 120 komórek	runcynowany 120-komorowy	cantitruncated 120 komórek	runcytruncated 120 komórek	omnitruncated 120 komórek
{5,3,3}	r{5,3,3}	t{5,3,3}	rrr{5,3,3}	t 0,3 {5,3,3}	tr{5,3,3}	t 0,1,3 {5,3,3}	t 0,1,2,3 {5,3,3}
600 ogniw	rektyfikowane 600 ogniw	obcięte 600 komórek	cantelated 600 komórek	Bitruncated 600 komórek	cantitruncated 600 komórek	runcytruncated 600 komórek	omnitruncated 600-cell
{3,3,5}	r{3,3,5}	t{3,3,5}	rrr{3,3,5}	2t{3,3,5}	tr{3,3,5}	t 0,1,3 {3,3,5}	t 0,1,2,3 {3,3,5}

{p,3,3} polytopy

120-komórkowy jest podobny do trzech zwykłych 4-politopów : 5-komórkowego {3,3,3} i tesseraktu {4,3,3} euklidesowej 4-przestrzeni oraz sześciokątnego plastra miodu {6,3,3 } przestrzeni hiperbolicznej. Wszystkie mają czworościenny wierzchołek {3,3}:

{p,3,3} polytopy
Przestrzeń		S 3			H 3
Formularz		Skończone			Parakompaktowy	Niekompaktowy
Nazwa		{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	... {∞,3,3}
Obraz
komórki {p,3}		{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

{5,3,p} polytopy

Komórka 120 jest częścią sekwencji 4-polytopów i plastrów miodu z komórkami dwunastościennymi :

{5,3,p} polytopy
Przestrzeń	S 3	H 3
Formularz	Skończone	Kompaktowy		Parakompaktowy	Niekompaktowy
Nazwa	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	... {5,3,∞}
Obraz
figura wierzchołka	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Davis 120-ogniwowy

120-komorowa Davisa , wprowadzona przez Davisa (1985) , jest zwartą 4-wymiarową rozmaitością hiperboliczną uzyskaną przez zidentyfikowanie przeciwległych ścian 120-komórkowej, której uniwersalna osłona daje regularny plaster miodu {5,3,3,5} z 4 -wymiarowa przestrzeń hiperboliczna.

Zobacz też

• Jednolita rodzina 4-polytopów z [5,3,3] symetrią
• 57-komorowy - abstrakcyjny regularny 4-polytop zbudowany z 57 hemi-dwunaścianów.
• 600-ogniwowy - podwójny 4-politopowy do 120-ogniwowego

Cytaty

• Coxeter, HSM (1973) [1948]. Regularne Polytopes (3rd ed.). Nowy Jork: Dover.
• Coxeter, HSM (1991). Regularne złożone polytopy (wyd. 2). Cambridge: Cambridge University Press.
•   Coxeter, HSM (1995). Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic (red.). Kalejdoskopy: wybrane pisma HSM Coxeter (wyd. 2). Publikacja Wiley-Interscience. ISBN 978-0-471-01003-6 .
  • (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Papier 23) HSM Coxeter, Regularne i półregularne Polytopes II , [Math. Zeit. 188 (1985) 559-591]
  • (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
• Coxeter, HSM ; du Val, Patrick ; Flather, HT; Petrie, JF (1938). Pięćdziesiąt dziewięć dwudziestościanów . Tom. 6. University of Toronto Studies (seria matematyczna).
• Coxeter, HSM (1970), „Twisted Honeycombs”, Rada Konferencyjna Regionalnej Serii Konferencji Nauk Matematycznych z matematyki , Providence, Rhode Island: American Mathematical Society, 4
• Stillwell, John (styczeń 2001). „Historia 120-ogniw” (PDF) . Zawiadomienia AMS . 48 (1): 17–25.
• JH Conway i MJT Guy : Four-Dimensional Archimedean Polytopes , Proceedings of the Colloquium on Convexity at Copenhagen, strona 38 i 39, 1965
• NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Rozprawa, University of Toronto, 1966
• Czterowymiarowy Archimedes Polytopes (niemiecki), Marco Möller, rozprawa doktorska 2004 [1]
•     Davis, Michael W. (1985), „Hiperboliczny 4-rozmaitość”, Proceedings of the American Mathematical Society , 93 (2): 325–328, doi : 10.2307/2044771 , ISSN 0002-9939 , JSTOR 2044771 , MR 0770546
•   Denney, Tommy; Prostytutka, Da'Shay; Johnson, De'Janeke; Robinson, Tianna; Butler, Majid; Claiborne, Sandernishe (2020). „Geometria polytopów H4”. Postępy w geometrii . 20 (3): 433–444. arXiv : 1912.06156v1 . doi : 10.1515/advgeom-2020-0005 . S2CID 220367622 .
•   Steinbach, Piotr (1997). „Złote pola: sprawa dla Heptagon”. Magazyn Matematyczny . 70 (luty 1997): 22–31. doi : 10.1080/0025570X.1997.11996494 . JSTOR 2691048 .
• Copher, Jessica (2019). „Sumy i iloczyny długości cięciw kwadratowych regularnych polytopów”. arXiv : 1903.06971 [ matematyka.MG ].
•   Miyazaki, Koji (1990). „Pierwotne politopy hipergeodezyjne”. Międzynarodowy Dziennik Struktur Kosmicznych . 5 (3–4): 309–323. doi : 10.1177/026635119000500312 . S2CID 113846838 .
• van Ittersum, Clara (2020). „Grupy symetrii regularnych polytopów w trzech i czterech wymiarach” . TUDelft .
• Mamona, Salvatore; Pileio, Giuseppe; Levitt, Malcolm H. (2010). „Orientacyjne schematy próbkowania oparte na czterowymiarowych polytopach” . Symetria . 2 (3): 1423–1449. doi : 10.3390/sym2031423 .
• Sullivan, John M. (1991). „Generowanie i renderowanie czterowymiarowych politopów” . Dziennik Matematyczny . 1 (3): 76–85.
•   Waegell, Mordechaj; Aravind, PK (10 września 2014). „Dowody parzystości twierdzenia Kochena-Speckera na podstawie 120 komórek”. Podstawy fizyki . 44 (10): 1085–1095. arXiv : 1309.7530v3 . doi : 10.1007/s10701-014-9830-0 . S2CID 254504443 .
• Zamboj, Michał (8 stycznia 2021). „Syntetyczna konstrukcja włóknienia Hopfa w podwójnym ortogonalnym rzucie 4-przestrzeni”. Journal of Computational Design and Engineering . 8 (3): 836–854. arXiv : 2003.09236v2 . doi : 10.1093/jcde/qwab018 .
•   Sadoc, Jean-Francois (2001). „Helisy i wypełnienia helisy pochodzące z polytopu {3,3,5}” . Europejski Dziennik Fizyczny E. 5 : 575–582. doi : 10.1007/s101890170040 . S2CID 121229939 .
• Chilton, BL (wrzesień 1964). „O rzucie regularnego polytope {5,3,3} na regularny triacontagon” . Kanadyjski Biuletyn Matematyczny . 7 (3): 385–398. doi : 10.4153/CMB-1964-037-9 .
•   Schleimer, Saul; Segerman, Henry (2013). „Zagadka 120 komórek” . Uwagi Amer. Matematyka soc . 62 (11): 1309-1316. ar Xiv : 1310.3549 . doi : 10.1090/noti1297 . S2CID 117636740 .
•   Banchoff, Thomas F. (2013). „Dekompostacje torusów regularnych polytopów w 4-przestrzeni”. W Senechal, Marjorie (red.). Kształtowanie Przestrzeni . Springera w Nowym Jorku. s. 257 –266. doi : 10.1007/978-0-387-92714-5_20 . ISBN 978-0-387-92713-8 .
•   Koca, Mehmet; Ozdes Koca, Nazife; Al-Barwani, Muataz (2012). „Snub 24-komórkowy pochodzący z grupy Coxeter-Weyl W (D4)” . Int. J. Geom. Metody mod. fizyka . 09 (8). ar Xiv : 1106.3433 . doi : 10.1142/S0219887812500685 . S2CID 119288632 .
•    Koca, Mehmet; Al-Ajmi, Mudhahir; Ozdes Koca, Nazife (2011). „Kwaternionowa reprezentacja 24-komórkowej komórki snub i jej podwójnego polytopu wywodzącego się z systemu korzeniowego E8” . Algebra liniowa i jej zastosowania . 434 (4): 977–989. doi : 10.1016/j.laa.2010.10.005 . ISSN 0024-3795 . S2CID 18278359 .

Linki zewnętrzne

• Weisstein, Eric W. „120 komórek” . MathWorld .
• Olszewski, Jerzy. „Hecatonicosachoron” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r.
  • Wypukła jednolita polichora oparta na hecatonicosachoron (120 komórek) i heksacosichoron (600 komórek) - Model 32 , George Olshevsky.
• Klitzing, Richard. „Jednolite polytopy 4D (polichora) o3o3o5x - cześć” .
• Der 120-Zeller (120 komórek) Regularne polytopy Marco Möllera w R ⁴ (niemiecki)
• Eksplorator 120 komórek — darmowy interaktywny program, który pozwala poznać szereg symetrii 120 komórek. 120 komórek jest rzutowane na 3 wymiary, a następnie renderowane przy użyciu OpenGL.
• Budowa hiper-dwunastościanu
• Animacja YouTube przedstawiająca budowę 120-ogniwowego Gian Marco Todesco.

Polytopy z rodziny H 4
120 ogniw	rektyfikowany 120-ogniwowy	obcięte 120 komórek	cantelated 120 komórek	runcynowany 120-komorowy	cantitruncated 120 komórek	runcytruncated 120 komórek	omnitruncated 120 komórek
{5,3,3}	r{5,3,3}	t{5,3,3}	rrr{5,3,3}	t 0,3 {5,3,3}	tr{5,3,3}	t 0,1,3 {5,3,3}	t 0,1,2,3 {5,3,3}
600 ogniw	rektyfikowane 600 ogniw	obcięte 600 komórek	cantelated 600 komórek	Bitruncated 600 komórek	cantitruncated 600 komórek	runcytruncated 600 komórek	omnitruncated 600-cell
{3,3,5}	r{3,3,5}	t{3,3,5}	rrr{3,3,5}	2t{3,3,5}	tr{3,3,5}	t 0,1,3 {3,3,5}	t 0,1,2,3 {3,3,5}