Ośmiokąt

„Ośmioboczna” przekierowuje tutaj. W przypadku innych zastosowań zobacz Octagon (ujednoznacznienie) i Octagonal (ujednoznacznienie) .

Ośmiokąt foremny
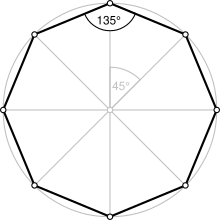Ośmiokąt foremny
Typ	Regularny wielokąt
Krawędzie i wierzchołki	8
Symbol Schläfliego	{8}, t{4}
Diagramy Coxetera-Dynkina
Grupa symetrii	Dwuścienny (D 8 ), rząd 2 × 8
Kąt wewnętrzny ( stopnie )	135°
Nieruchomości	Wypukłe , cykliczne , równoboczne , izogonalne , izotoksalne
Podwójny wielokąt	Samego siebie

W geometrii ośmiokąt (z greckiego ὀκτάγωνον oktágōnon , „osiem kątów”) to ośmioboczny wielokąt lub 8-kąt .

Ośmiokąt foremny . ma symbol Schläfliego {8} i może być również skonstruowany jako quasiregularny ścięty kwadrat t {4}, który ma na przemian dwa rodzaje krawędzi Ścięty ośmiokąt, t{8} to sześciokąt , {16}. Trójwymiarowym analogiem ośmiokąta może być rombowy ośmiościan z trójkątnymi ścianami na nim, takimi jak zastąpione krawędzie, jeśli weźmie się pod uwagę ośmiokąt jako ścięty kwadrat.

Nieruchomości

Przekątne zielonego czworoboku są równej długości i ustawione względem siebie pod kątem prostym

Suma wszystkich kątów wewnętrznych dowolnego ośmiokąta wynosi 1080°. Jak w przypadku wszystkich wielokątów, kąty zewnętrzne wynoszą łącznie 360°.

Jeśli kwadraty są zbudowane całkowicie wewnętrznie lub wszystkie na zewnątrz na bokach ośmiokąta, wówczas punkty środkowe odcinków łączących środki przeciwległych kwadratów tworzą czworokąt, który jest zarówno równoprzekątny, jak i ortodiagonalny ( to znaczy, którego przekątne są równe pod względem długości i po prawej stronie kąty względem siebie).

Ośmiokąt punktu środkowego ośmiokąta odniesienia ma osiem wierzchołków w punktach środkowych boków ośmiokąta odniesienia. Jeśli wszystkie kwadraty są zbudowane wewnętrznie lub wszystkie na zewnątrz po bokach ośmiokąta środkowego, wówczas punkty środkowe odcinków łączących środki przeciwległych kwadratów same tworzą wierzchołki kwadratu.

Prawidłowość

Ośmiokąt foremny to figura zamknięta o bokach tej samej długości i kątach wewnętrznych tej samej wielkości. Ma osiem linii symetrii refleksyjnej i symetrii obrotowej rzędu 8. Ośmiokąt foremny jest reprezentowany przez symbol Schläfliego {8}. Kąt wewnętrzny w każdym wierzchołku ośmiokąta foremnego wynosi 135 ° ( ${\ Displaystyle \ scriptstyle {\ Frac {3 \ pi} {4}}}$ radianów ). Kąt środkowy ma miarę 45° ( ${\ Displaystyle \ scriptstyle {\ Frac {\ pi} {4}}}$ radianów).

Obszar

Pole ośmiokąta foremnego o boku a jest określone wzorem

${\ Displaystyle A = 2 \ łóżeczko {\ Frac {\ pi} {8}} a ^ {2} = 2 (1 + {\ sqrt {2}}) a ^ {2} \ simeq 4,828 \, a ^ { 2}.}$

Pod względem promienia okręgu R , obszar wynosi

${\ Displaystyle A = 4 \ sin {\ Frac {\ pi} {4}} R ^ {2} = 2 {\ sqrt {2}} R ^ {2} \ simeq 2,828 \, R ^ {2}.}$

Pod względem apotemu r (patrz także wpisany rysunek ) obszar wynosi

${\ Displaystyle A = 8 \ tan {\ Frac {\ pi} {8}} r ^ {2} = 8 ({\ sqrt {2}} -1) r ^ {2} \ simeq 3,314 \, r ^ { 2}.}$

Te dwa ostatnie współczynniki stanowią nawias wartości pi , pola jednostki koła .

Pole regularnego ośmiokąta można obliczyć jako ścięty kwadrat .

Obszar można również wyrazić jako

${\ Displaystyle \, \! A = S ^ {2} -a ^ {2},}$

gdzie S jest rozpiętością ośmiokąta lub drugą najkrótszą przekątną; a a to długość jednego z boków lub podstaw. Można to łatwo udowodnić, jeśli weźmiemy ośmiokąt, narysujemy kwadrat na zewnątrz (upewniając się, że cztery z ośmiu boków pokrywają się z czterema bokami kwadratu), a następnie weźmiemy trójkąty narożne (są to trójkąty 45–45–90 ) i umieszcza je kątami prostymi skierowanymi do wewnątrz, tworząc kwadrat. Krawędzie tego kwadratu mają długość podstawy.

Biorąc pod uwagę długość boku a , rozpiętość S wynosi

${\ Displaystyle S = {\ Frac {a} {\ sqrt {2}}} + a + {\ frac {a} {\ sqrt {2}}} = (1 + {\ sqrt {2}}) a \ około 2.414a.}$

Rozpiętość jest zatem równa stosunkowi srebra pomnożonemu przez bok, a.

Obszar jest wtedy jak powyżej:

${\ Displaystyle A = ((1 + {\ sqrt {2}}) a) ^ {2} -a ^ {2} = 2 (1 + {\ sqrt {2}}) a ^ {2} \ około 4,828 a^{2}.}$

Wyrażony w kategoriach rozpiętości, obszar jest

${\ Displaystyle A = 2 ({\ sqrt {2}} -1) S ^ {2} \ około 0,828 S ^ {2}.}$

Innym prostym wzorem dla obszaru jest

${\ Displaystyle \ A = 2aS.}$

Częściej znana jest rozpiętość S i należy określić długość boków a , jak przy cięciu kwadratowego kawałka materiału na ośmiokąt foremny. Z góry,

${\ Displaystyle a \ około S / 2.414.}$

Dwie długości końcowe e z każdej strony (długości nóg trójkątów (zielony na obrazie) odcięte od kwadratu), a także mi $\ displaystyle e = a / {\ sqrt {2} },}$ można obliczyć jako

${\ Displaystyle \, \! e = (Sa) / 2.}$

Promień okręgu i promień promienia

Promień okręgu regularnego ośmiokąta pod względem długości boku a wynosi

${\ Displaystyle R = \ lewo ({\ Frac {\ sqrt {4 + 2 {\ sqrt {2}}}} {2}} \ prawej) a,}$

a promień wynosi

${\ Displaystyle r = \ lewo ({\ Frac {1 + {\ sqrt {2}}} {2}} \ prawo) a.}$

(czyli połowa stosunku srebra pomnożona przez bok, a lub połowa rozpiętości, S )

Diagonalność

Regularny ośmiokąt, pod względem długości boku a , ma trzy różne rodzaje przekątnych :

• Krótka przekątna;
• Średnia przekątna (zwana także rozpiętością lub wysokością), która jest dwukrotnie dłuższa od promienia;
• Długa przekątna, która jest dwa razy dłuższa od promienia opisanego.

Formuła każdego z nich wynika z podstawowych zasad geometrii. Oto wzory na ich długość:

• Krótka przekątna: ${\ Displaystyle a {\ sqrt {2 + {\ sqrt {2}}}}}$ ;
• Średnia przekątna: ${\ Displaystyle (1 + {\ sqrt {2}}) a}$ ; ( stosunek srebra razy a)
• Długa przekątna: $}}$ }

Budowa

zbudowanie ośmiokąta foremnego poprzez złożenie kartki papieru

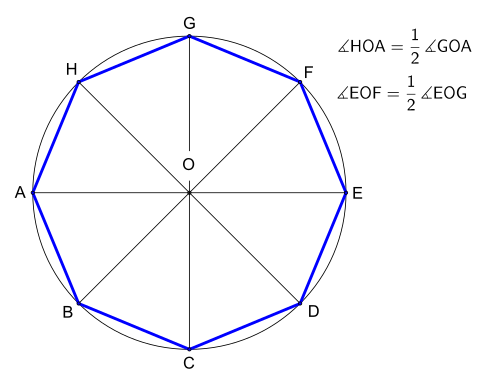
Regularny ośmiokąt na danym okręgu opisanym może być zbudowany w następujący sposób:

1. Narysuj okrąg i średnicę AOE, gdzie O to środek, a A, E to punkty na okręgu opisanym.
2. Narysuj inną średnicę GOC, prostopadłą do AOE.
3. (Zauważ mimochodem, że A,C,E,G są wierzchołkami kwadratu).
4. Narysuj dwusieczne kątów prostych GOA i EOG, tworząc kolejne dwie średnice HOD i FOB.
5. A,B,C,D,E,F,G,H to wierzchołki ośmiokąta.

Ośmiokąt na danym okręgu opisanym

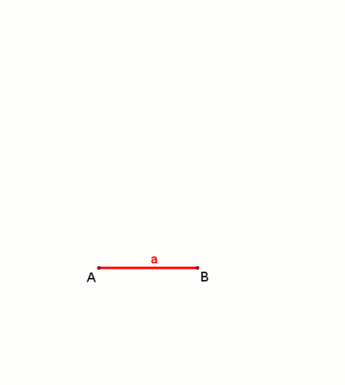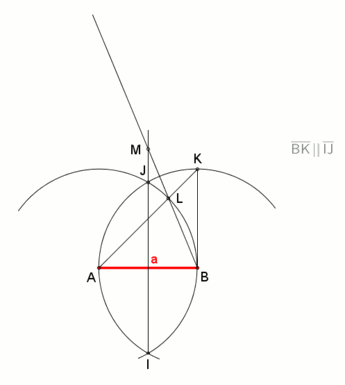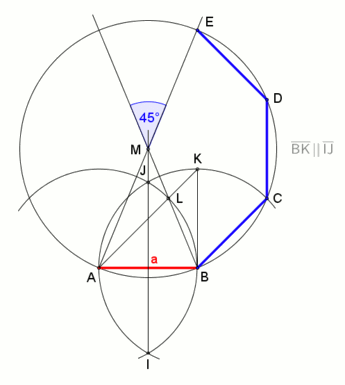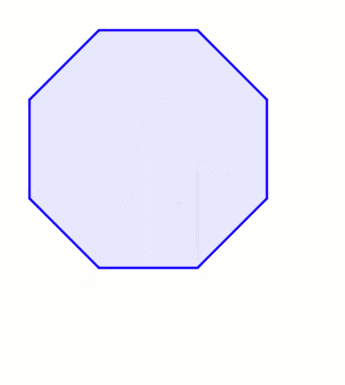
Ośmiokąt o danej długości boku, animacja (konstrukcja jest bardzo podobna do konstrukcji sześciokąta o danej długości boku ).

Ośmiokąt foremny można zbudować za pomocą liniału i kompasu , ponieważ 8 = 2 ³ , potęga dwójki :

Ośmiokątna konstrukcja Meccano.

Regularny ośmiokąt można zbudować za pomocą prętów meccano . Potrzebnych jest 12 prętów rozmiaru 4, trzy pręty rozmiaru 5 i dwa pręty rozmiaru 6.

Każdy bok regularnego ośmiokąta leży naprzeciw połowy kąta prostego w środku koła, które łączy jego wierzchołki. Jego pole można zatem obliczyć jako sumę ośmiu trójkątów równoramiennych, co daje wynik:

${\ Displaystyle {\ tekst {Obszar}} = 2a ^ {2} ({\ sqrt {2}} + 1)}$

dla ośmiokąta o boku a .

Współrzędne standardowe

Współrzędne wierzchołków ośmiokąta foremnego o środku w początku i boku długości 2 to:

• (±1, ±(1+ √ 2 ))
• (±(1+ √ 2 ), ±1).

Rozkładalność

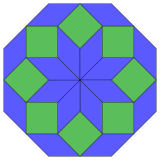
Projekcja 8-sześcienna	rozwarstwienie 24 rombów
	Regularny	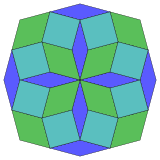izotoksal

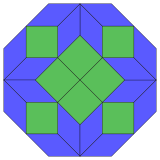
Coxeter twierdzi, że każdy zonogon (2 m -gon, którego przeciwległe boki są równoległe i równej długości) można podzielić na m ( m -1)/2 równoległoboków. W szczególności dotyczy to regularnych wielokątów o jednakowej liczbie boków, w którym to przypadku wszystkie równoległoboki są rombami. Dla ośmiokąta foremnego m = 4 i można go podzielić na 6 rombów, z jednym przykładem pokazanym poniżej . Ten rozkład można postrzegać jako 6 z 24 ścian w płaszczyźnie projekcji wielokąta Petriego tesseraktu . Lista (sekwencja A006245 w OEIS ) definiuje liczbę rozwiązań jako osiem, według ośmiu orientacji tej jednej sekcji. Te kwadraty i romby są używane w płytkach Ammanna – Beenkera .

Regularny ośmiokąt rozcięty

Tesserakt

4 romby i 2 kwadraty

Krzywy

Ośmiokąt foremny skośny widziany jako krawędzie antygraniastosłupa kwadratowego , symetria D _4d , [2 ⁺ ,8], (2*4), rząd 16.

Skośny ośmiokąt to skośny wielokąt z ośmioma wierzchołkami i krawędziami, ale nie znajdującymi się na tej samej płaszczyźnie. Wnętrze takiego ośmiokąta nie jest ogólnie określone. Skośny ośmiokąt zygzakowaty ma wierzchołki naprzemiennie między dwiema równoległymi płaszczyznami.

Regularny ośmiokąt skośny jest przechodni przez wierzchołki z równymi długościami krawędzi. W trzech wymiarach jest to zygzakowaty skośny ośmiokąt i można go zobaczyć w wierzchołkach i bocznych krawędziach kwadratowego antygraniastosłupa o tej samej symetrii D _4d , [2 ^{+ ,8], rzędu 16.}

Wielokąty Petriego

Regularny skośny ośmiokąt jest wielokątem Petriego dla tych wielowymiarowych regularnych i jednorodnych polytopów , pokazanych w tych skośnych rzutach ortogonalnych na płaszczyznach A ₇ , B ₄ i D ₅ Coxetera .

7 _	D5 _	4 _
7-jednostronny	5-sześcian	16-ogniwowy	Tesserakt

Symetria

Symetria

Jedenaście symetrii ośmiokąta foremnego. Linie odbić są niebieskie przez wierzchołki, fioletowe przez krawędzie, a rzędy wirowania są podane w środku. Wierzchołki są kolorowane według ich pozycji symetrii.

Ośmiokąt foremny ma symetrię Dih ₈ , rząd 16. Istnieją trzy podgrupy dwuścienne: Dih ₄ , Dih ₂ i Dih ₁ oraz cztery podgrupy cykliczne : Z ₈ , Z ₄ , Z ₂ i Z ₁ , ostatnia implikująca brak symetrii .

Przykładowe ośmiokąty według symetrii

r16
d8	g8	p8
d4	g4	p4
d2	g2	p2
a1

Na regularnym ośmiokącie istnieje jedenaście różnych symetrii. John Conway określa pełną symetrię jako r16 . Symetrie dwuścienne są podzielone w zależności od tego, czy przechodzą przez wierzchołki ( d dla przekątnej), czy krawędzie ( p dla prostopadłych). Symetrie cykliczne w środkowej kolumnie są oznaczone jako g dla ich centralnych rzędów wirowania. Pełna symetria postaci regularnej to r16 i żadna symetria nie jest oznaczona jako a1 .

Najpopularniejszymi ośmiokątami o wysokiej symetrii są p8 , ośmiokąt izogonalny zbudowany z czterech zwierciadeł, które mogą zmieniać długie i krótkie krawędzie, oraz d8 , ośmiokąt izotoksalny zbudowany z równymi długościami krawędzi, ale wierzchołkami na przemian z dwoma różnymi kątami wewnętrznymi. Te dwie formy są bliźniacze względem siebie i mają połowę rzędu symetrii regularnego ośmiokąta.

Każda symetria podgrupy dopuszcza jeden lub więcej stopni swobody dla nieregularnych form. Tylko g8 nie ma stopni swobody, ale można ją postrzegać jako skierowane krawędzie .

Używać

Ośmiokątny plan piętra, Kopuła na Skale.

Ośmiokątny kształt jest używany jako element projektu w architekturze. Kopuła na Skale ma charakterystyczny ośmioboczny plan. Wieża Wiatrów w Atenach to kolejny przykład ośmiokątnej konstrukcji. Ośmiokątny plan był również obecny w architekturze sakralnej, takiej jak katedra św. Jerzego w Addis Abebie , Bazylika San Vitale (w Rawennie, Włochy), Castel del Monte (Apulia, Włochy), baptysterium we Florencji , kościół Zum Friedefürsten (Niemcy) i liczba ośmiobocznych kościołów w Norwegii . Centralna przestrzeń katedry w Akwizgranie , Kaplica Karolingów na Palatynie , ma regularny ośmioboczny plan. Zastosowania ośmiokątów w kościołach obejmują również mniejsze elementy projektu, takie jak ośmioboczna absyda katedry Nidaros .

Architekci, tacy jak John Andrews, wykorzystali ośmiokątne układy pięter w budynkach do funkcjonalnego oddzielenia obszarów biurowych od usług budowlanych, takich jak siedziba Intelsat w Waszyngtonie lub Callam Offices w Canberze.

• 

  Parasole często mają ośmiokątny zarys.

• 

  Słynny dywan Buchara zawiera ośmiokątny motyw „stopy słonia”.

• 

  Układ ulic i bloków barcelońskiej dzielnicy Eixample oparty jest na nieregularnych ośmiokątach

• 

  Janggi używa ośmiokątnych kawałków.

• 

  Japońskie loterie często mają ośmiokątny kształt.

• 

  Znak stop używany w krajach anglojęzycznych , a także w większości krajów europejskich

• 

  Ikona znaku stopu z ręką na środku.

• 

  Trygramy taoistycznej bagua są często ułożone ośmiobocznie

• 

  Słynny ośmiokątny złoty puchar z wraku statku Belitung

• 

  Zajęcia w Shimer College tradycyjnie odbywają się przy ośmiokątnych stołach

• 

  Labirynt katedry w Reims o quasi-ośmiokątnym kształcie.

• 

  Ruch drążków analogowych kontrolera Nintendo 64 , kontrolera GameCube , Wii Nunchuk i kontrolera Classic jest ograniczony przez obrócony ośmiokątny obszar, dzięki czemu drążek może poruszać się tylko w ośmiu różnych kierunkach.

Dane pochodne

• 

  Ścięte kwadratowe kafelki mają 2 ośmiokąty wokół każdego wierzchołka.
  

• 

  Ośmiokątny pryzmat zawiera dwie ośmiokątne ściany.
  

• 

  Ośmiokątny antygraniastosłup zawiera dwie ośmiokątne ściany.
  

• 

  Ścięty ośmiościan sześcienny zawiera 6 ośmiokątnych ścian.
  

• 

  Wszechścięty sześcienny plaster miodu
  

Powiązane polytopy

Ośmiokąt , jako ścięty kwadrat , jest pierwszym w sekwencji ściętych hipersześcianów :

Ścięte hipersześciany

Obraz								...
Nazwa	Ośmiokąt	Ścięty sześcian	Obcięty tesserakt	Obcięta 5-kostka	Obcięty 6-sześcian	Obcięta 7-kostka	Obcięta 8-kostka
Diagram Coxetera
figura wierzchołka	( ) v ( )	( ) v { }	( )v{3}	( )v{3,3}	( )v{3,3,3}	( )v{3,3,3,3}	( )v{3,3,3,3,3}

Jako rozwinięty kwadrat jest również pierwszym w sekwencji rozszerzonych hipersześcianów:

Rozszerzone hipersześciany

							...
Ośmiokąt	ośmiościan rombowy	Przeklęty tesserakt	Sterylizowane 5 kostek	Pentelled 6-sześcian	Hexicated 7-kostka	Heptelated 8-sześcian

Zobacz też

• Basen zderzakowy
• Mały ośmiokąt Hansena
• Ośmiokątny dom
• Ośmiokątna liczba
• Oktagram
• Ośmiościan , kształt 3D z ośmioma twarzami.
• Oktogon , główne skrzyżowanie w Budapeszcie , Węgry
• Rub el Hizb (znany również jako Gwiazda Al Quds i Gwiazda Octa)
• Wygładzony ośmiokąt

Linki zewnętrzne

• Kalkulator ośmiokąta
• Definicja i właściwości ośmiokąta Z animacją interaktywną