Wielokąt równokątny
| Bezpośredni | Pośredni | Krzywy |
|---|---|---|
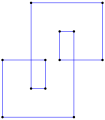
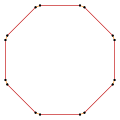
 Prostokąt , <4>, jest wypukłym prostym wielokątem równokątnym , zawierającym cztery wewnętrzne kąty 90°. |
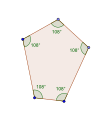
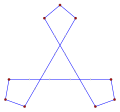
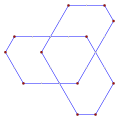
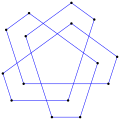
 Wklęsły pośredni wielokąt równokątny , <6-2>, taki jak ten sześciokąt, przeciwnie do ruchu wskazówek zegara, ma pięć skrętów w lewo i jeden skręt w prawo, jak to tetromino . |
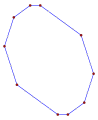
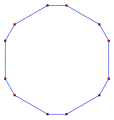
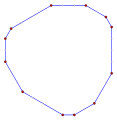
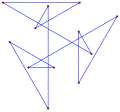
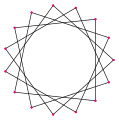
 Wielokąt skośny ma równe kąty od płaszczyzny, tak jak ten skośny ośmiokąt z naprzemiennymi czerwonymi i niebieskimi krawędziami sześcianu . |
| Bezpośredni | Pośredni | Przeciwobrócony |
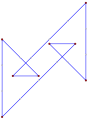
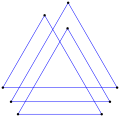
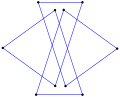
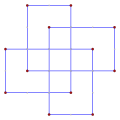
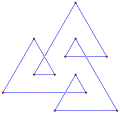
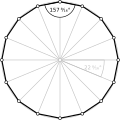
 Wielokąt równokątny z wieloma obrotami może być prosty, tak jak ten ośmiokąt <8/2> ma 8 zakrętów o 90°, co daje w sumie 720°. |
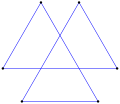
 Wklęsły pośredni wielokąt równokątny, <5-2>, w kierunku przeciwnym do ruchu wskazówek zegara, ma 4 skręty w lewo i jeden skręt w prawo. (-1.2.4.3.2) 60° |
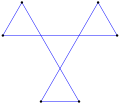
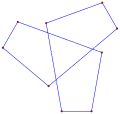
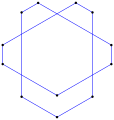
 Pośredni sześciokąt równokątny, <6-6> 90° z 3 skrętami w lewo, 3 skrętami w prawo, w sumie 0°. |
W geometrii euklidesowej wielokąt równokątny to wielokąt , którego kąty wierzchołków są równe. Jeśli długości boków są również równe (to znaczy, jeśli jest również równoboczny ), to jest to wielokąt foremny . Wielokąty izogonalne to wielokąty równokątne, które mają naprzemiennie dwie długości krawędzi.
Dla jasności płaski wielokąt równokątny można nazwać bezpośrednim lub pośrednim . Prosty wielokąt równokątny ma wszystkie kąty obracające się w tym samym kierunku w płaszczyźnie i może zawierać wiele zwojów . Wypukłe wielokąty równokątne są zawsze proste. Pośredni wielokąt równokątny może zawierać kąty obracające się w prawo lub w lewo w dowolnej kombinacji. Skośny . wielokąt równokątny może być izogonalny , ale nie można go uznać za prosty, ponieważ nie jest płaski
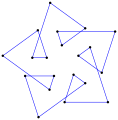
Spirolateral n θ jest szczególnym przypadkiem wielokąta równokątnego ze zbiorem n całkowitych długości krawędzi powtarzających się sekwencyjnie aż do powrotu do początku, z wewnętrznymi kątami wierzchołków θ .
Budowa
Wielokąt równokątny można zbudować z wielokąta foremnego lub wielokąta foremnego w kształcie gwiazdy, gdzie krawędzie są rozciągnięte jako nieskończone linie . Każdą krawędź można niezależnie przesuwać prostopadle do kierunku linii. Wierzchołki reprezentują punkt przecięcia między parami sąsiednich linii. Każda przesunięta linia dostosowuje długość swojej krawędzi i długości dwóch sąsiednich krawędzi. Jeśli krawędzie zostaną zredukowane do długości zerowej, wielokąt ulegnie degeneracji, a jeśli zostaną zredukowane do ujemnych , spowoduje to odwrócenie kątów wewnętrznych i zewnętrznych.
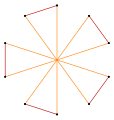
W przypadku równobocznego prostego wielokąta równokątnego, z wewnętrznymi kątami θ°, ruchome naprzemienne krawędzie mogą odwrócić wszystkie wierzchołki w dodatkowe kąty 180-θ°. Proste wielokąty równokątne o nieparzystych bokach można odwrócić tylko częściowo, pozostawiając mieszankę dodatkowych kątów.
Każdy wielokąt równokątny można dostosować w proporcjach za pomocą tej konstrukcji i nadal zachować równokątny status.
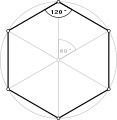
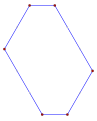
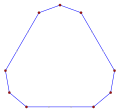
 Ten wypukły prosty sześciokąt równokątny , <6>, jest ograniczony 6 liniami z kątem 60° między nimi. Każdą linię można przesuwać prostopadle do jej kierunku. |
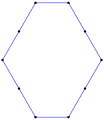
 Ten wklęsły pośredni sześciokąt równokątny , <6-2>, jest również ograniczony 6 liniami z kątem 90° między nimi, każda linia porusza się niezależnie, przesuwając wierzchołki jako nowe przecięcia. |
Twierdzenie o wielokącie równokątnym
Dla wypukłego równokątnego p -gonu każdy kąt wewnętrzny wynosi 180(1-2/ p )°; to jest twierdzenie o wielokącie równokątnym .
Dla prostego równokątnego wielokąta gwiazdy p / q , gęstości q , każdy kąt wewnętrzny wynosi 180 (1-2 q / p )°, przy czym 1 < 2 q < p . Dla w =gcd( p , q )>1, reprezentuje to wielokąt gwiazdy o ranach w ( p / w )/( q / w ), który jest zdegenerowany dla zwykłego przypadku.
Wklęsły pośredni równokątny ( p r + p l )-gon, z wierzchołkami p r skrętu w prawo i wierzchołkami p l skrętu w lewo, będzie miał kąty wewnętrzne 180(1-2/| pr - p l | ))°, niezależnie od ich sekwencji. Gwiazda pośrednia równokątna ( p r + p l )-gon, z p r wierzchołkami skrętu w prawo i p l wierzchołkami skrętu w lewo i q całkowitą liczbą zwojów , będzie miała kąty wewnętrzne 180(1-2 q /| p r - pl l | ))°, niezależnie od ich kolejności. Wielokąt równokątny z taką samą liczbą skrętów w prawo i w lewo ma zerową całkowitą liczbę obrotów i nie ma ograniczeń co do jego kątów.
Notacja
Każdemu prostemu równokątnemu p -kątowi można nadać oznaczenie < p > lub < p / q >, podobnie jak wielokąty foremne { p } i wielokąty foremne gwiazdy { p / q }, zawierające wierzchołki p i gwiazdy o gęstości q .
Wypukłe równokątne p -kąty <p> mają kąty wewnętrzne 180(1-2/ p )°, podczas gdy wielokąty równokątne gwiazd prostych < p / q > mają kąty wewnętrzne 180 (1-2 q / p )°.
Wklęsły pośredni równokątny p -gon można zapisać w notacji < p -2 c >, z c przeciwbieżnymi wierzchołkami. Na przykład <6-2> to sześciokąt z wewnętrznymi kątami różnicy 90°, <4>, 1 przeciwny wierzchołek. Wieloobrotowy pośredni równoboczny p -gon można nadać notacji < p -2 c / q > z c przeciwległymi wierzchołkami skrętu i q całkowitą liczbą zwojów . Wielokąt równokątny < p - p > to p - kąt z nieokreślonymi kątami wewnętrznymi θ , ale można go wyraźnie wyrazić jako < p - p > θ .
Inne właściwości
Twierdzenie Vivianiego dotyczy wielokątów równokątnych:
- Suma odległości od punktu wewnętrznego do boków wielokąta równokątnego nie zależy od położenia punktu i jest niezmiennikiem tego wielokąta.
Cykliczny wielokąt jest równokątny wtedy i tylko wtedy, gdy naprzemienne boki są równe (to znaczy boki 1, 3, 5, ... są równe, a boki 2, 4, ... są równe). Zatem jeśli n jest nieparzyste, cykliczny wielokąt jest równokątny wtedy i tylko wtedy, gdy jest regularny.
Dla liczby pierwszej p każdy równokątny p -gon o bokach całkowitych jest regularny. Co więcej, każdy równokątny pk - gon o bokach całkowitych ma p -krotną symetrię obrotową .
zestaw długości boków n -gon wtedy i tylko wtedy dotyczy wielomianu za równe zeru przy wartości zespolonej jest podzielna przez
Bezpośrednie wielokąty równokątne po bokach
Bezpośrednie wielokąty równokątne mogą być regularnymi, izogonalnymi lub niższymi symetriami. Przykłady dla < p / q > są pogrupowane w sekcje według p i podzielone według gęstości q .
Trójkąty równoramienne
Trójkąty równoramienne muszą być wypukłe i mieć wewnętrzne kąty 60°. Jest to trójkąt równoboczny i trójkąt foremny , <3>={3}. Jedynym stopniem swobody jest długość krawędzi.
Czworokąty równoramienne
Bezpośrednie czworoboki równokątne mają kąty wewnętrzne 90 °. Jedynymi czworokątami równokątnymi są prostokąty , <4> i kwadraty , {4}.
Równokątny czworobok o całkowitych długościach boków można układać w kwadraty jednostkowe .
Spirolateral 2 90° , s. 4
Pięciokąty równoramienne
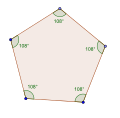
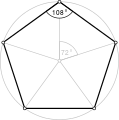
Proste pięciokąty równokątne , <5> i <5/2> mają odpowiednio kąty wewnętrzne 108° i 36°.
- Kąt wewnętrzny 108° od pięciokąta równokątnego , <5>
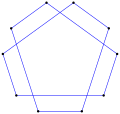
Pięciokąty równoramienne mogą być regularne , mieć symetrię dwustronną lub nie mieć symetrii.
- pentagramu równoramiennego , <5/2>
Zwykły pentagram , r 10
Sześciokąty równoramienne

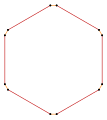
Proste sześciokąty równokątne , <6> i <6/2> mają odpowiednio kąty wewnętrzne 120° i 60°.
- Kąty wewnętrzne 120° równokątnego sześciokąta , <6>
Równokątny sześciokąt o całkowitych długościach boków może być wyłożony przez jednostkowe trójkąty równoboczne .
Spirolateral (1,2) 120° , s. 6
- Kąty wewnętrzne 60° trójkąta równoramiennego o podwójnych zwojach, <6/2>
Spirolateral (1,3) 60° , s. 6
Siedmiokąty równoramienne
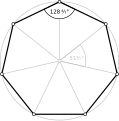
Proste równokątne siedmiokąty , <7>, <7/2> i <7/3> mają odpowiednio 128 4/7°, 77 1/7° i 25 5/7°.
- siedmiokąta równokątnego , <7>
- Kąty wewnętrzne 77,14° równokątnego heptagramu , <7/2>
- Kąty wewnętrzne 25,71° równokątnego heptagramu , <7/3>
Równokątne ośmiokąty
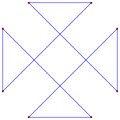
Proste ośmiokąty równokątne , <8>, <8/2> i <8/3> mają odpowiednio kąty wewnętrzne 135°, 90° i 45°.
- Kąty wewnętrzne 135° od równokątnego ośmiokąta , <8>
Spirolateral (1,2) 135° , s. 8
- Kąty wewnętrzne 90° od równokątnego kwadratu z podwójnym zwojem , <8/2>
- Kąty wewnętrzne 45° od równokątnego oktagramu , <8/3>
Spirolateral , (1,2) 45° , s. 8
Równokątne enneagony
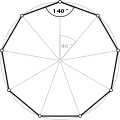
Proste przekątne równokątne , <9>, <9/2>, <9/3> i <9/4> mają odpowiednio kąty wewnętrzne 140°, 100°, 60° i 20°.
- Kąty wewnętrzne 140° od równokątnego enneagonu <9>
- Kąty wewnętrzne 100° z równokątnego enneagramu , <9/2>
- Kąty wewnętrzne 60° z trójkąta równoramiennego potrójnie zwiniętego , <9/3>
- Kąty wewnętrzne 20° od równokątnego enneagramu , <9/4>
Spirolateral 3 20° , g 3
Równokątne dziesięciokąty
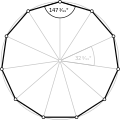
Proste równokątne dziesięciokąty , <10>, <10/2>, <10/3>, <10/4> mają odpowiednio kąty wewnętrzne 144°, 108°, 72° i 36°.
- Kąty wewnętrzne 144° od równokątnego dziesięciokąta <10>
Spirolateral (1,2) 144° , s. 10
- Kąty wewnętrzne 108° od równokątnego pięciokąta z podwójnym zwojem <10/2>
Spirolateral (1,2) 108° , s. 10
- Kąty wewnętrzne 72° od równokątnego dekagramu <10/3>
Spirolateral (1,2) 72° , s. 10
- Kąty wewnętrzne 36° od równokątnego pentagramu z podwójnym zwojem <10/4>
Spirolateral (1,2) 36° , s. 10
Sześciokąty równokątne
Proste równokątne hendecagons , <11>, <11/2>, <11/3>, <11/4> i <11/5> mają 147 3/11°, 114 6/11°, 81 9/11° , odpowiednio 49 1/11° i 16 4/11° kątów wewnętrznych.
- 147° kątów wewnętrznych od równokątnego hendekagramu , <11>
- 114° wewnętrznych kątów od równokątnego hendekagramu , <11/2>
- 81° wewnętrznych kątów od równokątnego hendekagram , <11/3>
- kąty wewnętrzne 49° od hendekagramu równokątnego , <11/4>
- 16° kąty wewnętrzne od hendekagramu równokątnego , <11 /5>
Równokątne dwunastokąty
Proste dwunastokąty równokątne , <12>, <12/2>, <12/3>, <12/4> i <12/5> mają kąty wewnętrzne 150°, 120°, 90°, 60° i 30° odpowiednio.
- Kąty wewnętrzne 150° od dwunastokąta równokątnego , <12>
Rozwiązania wypukłe o całkowitych długościach krawędzi mogą być układane w bloki wzorów , kwadraty, trójkąty równoboczne i romby 30° .
Spirolateral (1,2) 150° , s. 12
- Kąty wewnętrzne 120° z równoramiennego sześciokąta z podwójnym uzwojeniem , <12/2>
Spirolateral , (1…4) 120° , g 3
- Kąty wewnętrzne 90° z równokątnego potrójnie zwiniętego kwadratu , <12/3>
Spirolateral (1…3) 90° , g 2
- Kąty wewnętrzne 60° z trójkąta równoramiennego z poczwórnymi zwojami , <12/4>
Spirolateral (1,3,5,1) 60° , s. 6
- Kąty wewnętrzne 30° od dwunastokąta równokątnego , <12/5>
Spirolateral (1,2) 30° , s. 12
Równokątne czworokąty
Proste czworokąty równokątne , <14>, <14/2>, <14/3>, <14/4> i <14/5>, <14/6> mają 154 2/7°, 128 4/7 odpowiednio °, 102 6/7°, 77 1/7°, 51 3/7° i 25 5/7°.
- czworokąta równokątnego , <14>
- Kąty wewnętrzne 128,57° od równokątnego siedmiokąta foremnego o podwójnym uzwojeniu , <14/2>
Spirolateralny 2 128,57°
- 102,85° kątów wewnętrznych z równokątnego tetradekagramu , <14/3>
- heptagramu z podwójnym zwojem <14/4>
Spirolateralny 2 77,14°
- tetradekagramu równokątnego , <14/5>
- heptagramu z podwójnymi zwojami , <14/6>
Równokątne pięciokąty
Proste pięciokąty równokątne , <15>, <15/2>, <15/3>, <15/4>, <15/5>, <15/6> i <15/7> mają 156°, 132 Kąty wewnętrzne odpowiednio °, 108°, 84°, 60° i 12°.
- 156° kątów wewnętrznych od pięciokąta równokątnego, <15>
- 132° kątów wewnętrznych od pięciokąta równokątnego , <15/2>
- 108° kątów wewnętrznych od równokątny potrójnie zwinięty pięciokąt, <15/3>
spirolateral (1…3) 108° , g 5
- Kąty wewnętrzne 84° z pentadekagramu równokątnego, <15/4>
- trójkąta równoramiennego z 5 zwojami , <15/5>
- pentagramu z trzema zwojami , <15/6>
- 12° kątów wewnętrznych z pentadekagramu równokątnego, <15/7>
Równokątne sześciokąty
Proste sześciokąty równokątne , <16>, <16/2>, <16/3>, <16/4>, <16/5>, <16/6> i <16/7> mają 157,5°, 135 odpowiednio kąty wewnętrzne °, 112,5°, 90°, 67,5°, 45° i 22,5°.
- Kąty wewnętrzne 157,5° z równoramiennego sześciokąta , <16>
Spirolateral (1…4) 157,5° , g 4
- Kąty wewnętrzne 135° od równokątnego ośmiokąta z podwójnym zwojem, <16/2>
- 112,5° kątów wewnętrznych z heksadekagramu równokątnego , <16/3>
- Kąty wewnętrzne 90° z równoramiennego kwadratu z 4 zwojami, <16/4>
- 67,5° kątów wewnętrznych z równoramiennego heksadekagramu , <16/5>
- 45° wewnętrznych kątów z równokątnego podwójnie zwiniętego oktagramu foremnego , <16/6>
spirolateral (1…3) 45° , g 8
- Kąty wewnętrzne 22,5° od równokątnego heksadekagramu , <16/7>
Równokątne ośmiokąty
Proste ośmiokąty równokątne , <18}, <18/2>, <18/3>, <18/4>, <18/5>, <18/6>, <18/7> i <18/8> , mają kąty wewnętrzne odpowiednio 160°, 140°, 120°, 100°, 80°, 60°, 40° i 20°.
- Kąty wewnętrzne 160° od równokątnego ośmiokąta , <18>
- Kąty wewnętrzne 140° od równokątnego podwójnie uzwojonego enneagonu , <18/2>
Spirolateral 2 140° , s. 18
- Kąty wewnętrzne 120° równokątnego sześciokąta z trzema zwojami <18/3>
- Kąty wewnętrzne 100° równokątnego podwójnie zwiniętego enneagramu <18/4>
Spirolateralny 2 100° , g 3
- oktadekagramu równoramiennego {18/5}
- Kąty wewnętrzne 60° trójkąta równoramiennego z 6 zwojami <18/6>
- oktadekagramu równoramiennego <18/7>
- Kąty wewnętrzne 20° równokątnego podwójnie zwiniętego enneagramu <18/8>
Spirolateral 2 20° , s. 18
Równokątne dwudziestokąty
Bezpośredni równokątny dwudziestokąt , <20>, <20/3>, <20/4>, <20/5>, <20/6>, <20/7> i <20/9> mają 162°, 126 Kąty wewnętrzne odpowiednio °, 108°, 90°, 72°, 54° i 18°.
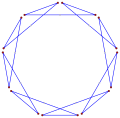
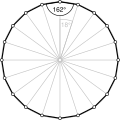
- Kąty wewnętrzne 162° od równokątnego dwudziestokąta , <20>
Spirolateral (1,3) 162° , s. 20
- dziesięciokąta o podwójnych zwojach , <20/2>
Spirolateral (1…4) 144° , g 5
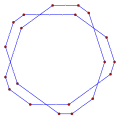
- Kąty wewnętrzne 126° z ikosagramu równokątnego , <20/3>
Spirolateral (1,3) 126° , s. 20
- pięciokąta z 4 zwojami , <20/4>
Spirolateral (1…4) 108° , g 5
- kwadratu z 5 zwojami , <20/5>
Spirolateral (1…5) 90° , g 4
Spirolateral (1,2,3,2,1) 90° , i 8
- dekagramu o podwójnym zwoju , <20/6>
Spirolateral (1,2) 72° , s. 10
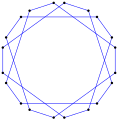
- Kąty wewnętrzne 54° od równokątnego ikosagramu , <20/7>
- Kąty wewnętrzne 36 ° od równokątnego pentagramu z poczwórnym zwojem , <20/8>
Spirolateral (1…4) 36° , g 5
- Kąty wewnętrzne 18° od równokątnego ikosagramu , <20/9>
Zobacz też
- Williams, R. Geometryczne podstawy struktury naturalnej: źródłowa księga projektowania . New York: Dover Publications , 1979. s. 32
Linki zewnętrzne
- Właściwość wielokątów równokątnych: o co w niej chodzi? omówienie twierdzenia Vivianiego w Cut-the-knot .
- Weisstein, Eric W. „Wielokąt równokątny” . MathWorld .