Tetromino
Tetromino to figura geometryczna złożona z czterech kwadratów połączonych prostopadle (tj. krawędziami, a nie rogami) . Tetromino, podobnie jak domino i pentomino , to szczególny rodzaj poliomino . Odpowiedni polisześcian , zwany tetracube , to geometryczny kształt składający się z czterech sześcianów połączonych prostopadle.
Popularnym zastosowaniem tetromino jest gra wideo Tetris stworzona przez radzieckiego projektanta gier Aleksieja Pażytnowa , który nazywa je tetrimino . Tetromino używane w grze to w szczególności jednostronne tetromino.
Tetromino
Darmowe tetromino
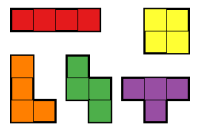
Polyominos są tworzone przez łączenie kwadratów jednostkowych wzdłuż ich krawędzi. Wolne poliomino to poliomino uznane za zgodne . Oznacza to, że dwa wolne polyominos są takie same, jeśli istnieje kombinacja translacji , obrotów i odbić , które zamieniają jedno w drugie. Darmowe tetromino to darmowe poliomino złożone z czterech kwadratów. Jest pięć darmowych tetromino.
Wolne tetromino mają następującą symetrię:
- Prosto: pionowa i pozioma symetria odbicia oraz dwa punkty symetrii obrotowej
- Kwadrat: pionowa i pozioma symetria odbicia oraz cztery punkty symetrii obrotowej
- T: tylko pionowa symetria odbicia
- L: brak symetrii
- S i Z: tylko dwa punkty symetrii obrotowej
Jednostronne tetromino
Jednostronne tetromino to tetromino, które można przesuwać i obracać, ale nie odbijać. Są używane przez Tetris i są z nim w przeważającej mierze kojarzone . Istnieje siedem różnych jednostronnych tetromino. Te tetromino są nazywane literami alfabetu, które najbardziej przypominają. Tetromino „I”, „O” i „T” mają symetrię odbicia, więc nie ma znaczenia, czy są one uważane za tetromino swobodne, czy jednostronne. Pozostałe cztery tetromino, „J”, „L”, „S” i „Z”, wykazują zjawisko zwane chiralnością . J i L są wzajemnymi odbiciami, a S i Z są wzajemnymi odbiciami.
Jako wolne tetromino, J jest równoważne L, a S jest równoważne Z. Ale w dwóch wymiarach i bez odbić nie jest możliwe przekształcenie J w L lub S w Z.
Naprawione tetromino
Stałe tetromino pozwalają tylko na translację, bez obracania lub odbicia. Istnieją dwa różne stałe I-tetromino, cztery J, cztery L, jedno O, dwa S, cztery T i dwa Z, w sumie 19 stałych tetromino:
Układanie prostokąta
Wypełnianie prostokąta jednym zestawem tetromino
Pojedynczy zestaw wolnych tetromino lub jednostronnych tetromino nie mieści się w prostokącie. Można to wykazać za pomocą dowodu podobnego do argumentu z okaleczoną szachownicą. Prostokąt 5 × 4 ze wzorem szachownicy ma 20 kwadratów, w tym 10 jasnych i 10 ciemnych kwadratów, ale pełny zestaw darmowych tetromino ma albo 11 ciemnych kwadratów i 9 jasnych kwadratów, albo 11 jasnych kwadratów i 9 ciemnych kwadratów. Wynika to z tego, że T tetromino ma albo 3 ciemne kwadraty i jeden jasny kwadrat, albo 3 jasne kwadraty i jeden ciemny kwadrat, podczas gdy wszystkie inne tetromino mają 2 ciemne kwadraty i 2 jasne kwadraty. Podobnie prostokąt 7 × 4 ma 28 kwadratów, zawierających 14 kwadratów każdego odcienia, ale zestaw jednostronnych tetromino ma albo 15 ciemnych kwadratów i 13 jasnych kwadratów, albo 15 jasnych kwadratów i 13 ciemnych kwadratów. Co za tym idzie, żadna nieparzysta liczba zestawów dla każdego typu nie może zmieścić się w prostokącie. Ponadto 19 stałych tetromino nie mieści się w prostokącie 4 × 19. Zostało to odkryte przez wyczerpanie wszystkich możliwości wyszukiwania komputerowego.
Wolne tetromino (lewa strona linii) mają 11 ciemnych kwadratów i 9 jasnych kwadratów. Jednostronne tetromino (wszystkie 7 pokazane powyżej) mają 15 ciemnych kwadratów i 13 jasnych kwadratów.
Plansza 5×4 ma po 10 pól w każdym kolorze. Plansza 7×4 ma po 14 pól w każdym kolorze.
Wypełnianie zmodyfikowanego prostokąta jednym zestawem tetromino
Jednak wszystkie trzy zestawy tetromino mogą pasować do prostokątów z otworami:
- Wszystkie 5 darmowych tetromino pasuje do prostokąta 7×3 z otworem.
- Wszystkie 7 jednostronnych tetromino pasuje do prostokąta 6 × 5 z dwoma otworami w tym samym „kolorze szachownicy”.
- Wszystkie 19 stałych tetromino pasuje do prostokąta 11 × 7 z otworem.
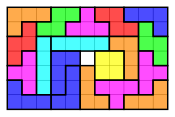
Wypełnianie prostokąta dwoma zestawami tetromino
Dwa zestawy swobodnych lub jednostronnych tetromino można zmieścić w prostokącie na różne sposoby, jak pokazano poniżej:
Etymologia
Nazwa „tetromino” jest połączeniem przedrostka tetra- „ cztery” (od starogreckiego τετρα- ) i „ domino ”. Nazwę wprowadził Solomon W. Golomb w 1953 roku wraz z inną nomenklaturą związaną z polyominos.
Wypełnianie pudełka tetracubes
Każde z pięciu wolnych tetromino ma odpowiedni tetracube, czyli tetromino wytłoczone o jedną jednostkę. J i L to ten sam czworościan, podobnie jak S i Z, ponieważ jeden można obrócić wokół osi równoległej do płaszczyzny tetromino, tworząc drugi. Możliwe są jeszcze trzy tetracuby, wszystkie utworzone przez umieszczenie sześcianu jednostkowego na wygiętym trójsześcianie :
I „prosty tetracube”
O „kwadratowy tetrasześcian”
T „T-tetracube”
L „L-tetrasześcian”
S „skośny tetrasześcian”
B. „Oddział”
D „Prawa śruba”
F „Lewa śruba”
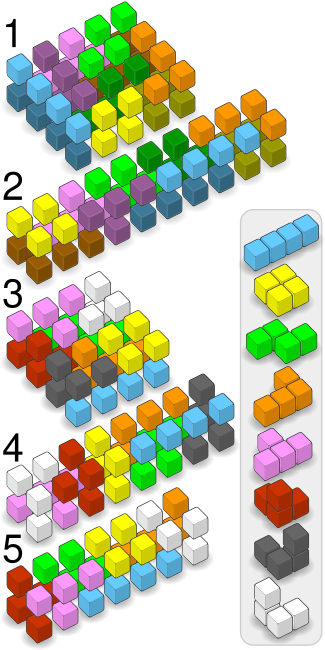
Tetracube można zapakować w dwuwarstwowe pudełka 3D na kilka różnych sposobów, w zależności od wymiarów pudełka i kryteriów włączenia. Są one pokazane zarówno na schemacie obrazkowym, jak i na diagramie tekstowym. W przypadku pudełek wykorzystujących dwa zestawy tych samych elementów schemat obrazkowy przedstawia każdy zestaw jako jaśniejszy lub ciemniejszy odcień tego samego koloru. Diagram tekstowy przedstawia każdy zestaw jako zawierający wielką lub małą literę. Na diagramie tekstowym górna warstwa znajduje się po lewej stronie, a dolna warstwa po prawej.
1.) Pudełko 2×4×5 wypełnione dwoma zestawami darmowych tetromino: ZZT t I l TTT i LZZ t I lllti L zzt I oozzi LLOOI oo OO i 2.) Pudełko 2×2×10 wypełnione dwoma zestawami darmowych tetromino tetromino: LLL zz ZZTOO oozz ZZTTT l LIIII ttt OO ooiiiitlll 3.) Pudełko 2×4×4 wypełnione jednym zestawem wszystkich tetromino: FTTTFZZB FFTBZZBB OOLDLLLD OODDIIII 4.) Pudełko 2×2×8 wypełnione jednym zestawem wszystkich tetromino: DZZLOTTTDLLLOBFF DDZZOBTFIIIIOBBF 5.) Pudełko 2×2×7 wypełnione tetromino, z usuniętymi lustrzanymi odbiciami: LLLZZBBLCOOZZB CIIIITBCCOOTTT
Zobacz też
Poprzednie i następne zamówienia
Linki zewnętrzne
- Vadim Gierasimow , „Tetris: historia”; Historia Tetrisa
- Ojciec Tetrisa ( kopia strony z archiwum internetowego tutaj )
