Spirolateralny

Proste spirolaterale

3 90° (4 cykle)	3 108° (5 cykli)	9 Spirala 90° w lewo	9 90° (4 cykle)
Spirala 100 120°		100 120° (4 cykle)

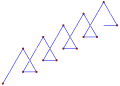
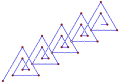
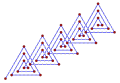
W geometrii euklidesowej spirolateral to wielokąt utworzony przez sekwencję stałych kątów wewnętrznych wierzchołków i kolejnych długości krawędzi 1,2,3,…, n , które powtarzają się, aż figura się zamknie. Liczba potrzebnych powtórzeń nazywana jest jego cyklami. Prosty spirolateral ma tylko dodatnie kąty. Prosta spirala jest zbliżona do części spirali Archimedesa . Ogólna spirolateralna dopuszcza dodatnie i ujemne kąty.

Spirolateral , który kończy się w jednym zwoju , jest prostym wielokątem , podczas gdy wymagający więcej niż 1 obrotu jest wielokątem gwiaździstym i musi się samoprzecinać. Prosty spirolateralny może być równokątnym prostym wielokątem < p > z p wierzchołkami lub równokątnym wielokątem gwiazdy < p / q > z p wierzchołkami i q zwojami.

Spirolaterale zostały wynalezione i nazwane przez Franka C. Oddsa jako nastolatka w 1962 roku jako kwadratowe spirolaterale o kątach 90 °, narysowane na papierze milimetrowym . W 1970 roku Odds odkrył, że trójkątny i sześciokątny spirolateral , o kątach 60 ° i 120 °, można narysować na izometrycznym (trójkątnym) papierze milimetrowym. Odds napisał do Martina Gardnera , który zachęcił go do opublikowania wyników w Mathematics Teacher w 1973 roku.

Proces można przedstawić na grafice żółwia , naprzemiennym kącie skrętu i instrukcjami ruchu do przodu, ale ograniczając obrót do ustalonego racjonalnego kąta.

Najmniejszym golygonem jest spirolateral, 7 _90° ⁴ , utworzony z 7 kątów prostych, a długość 4 ma wklęsłe zakręty. Golygony różnią się tym, że muszą zamykać się pojedynczą sekwencją 1,2,3,.. n , podczas gdy spirolateral będzie powtarzał tę sekwencję, aż się zamknie.

Klasyfikacje

Różne przypadki

Proste 6 90° , 2 cykle, 3 obroty	Regularne nieoczekiwane zamknięte spirolateralne, 8 90° 1,5	Niespodziewanie zamknięte spirolateralne 7 90° 4	Skrzyżowany prostokąt (1,2,-1,-2) 60°
Sześciokąt skrzyżowany (1,1,2,-1,-1,-2) 90°	(-1.2.4.3.2) 60°	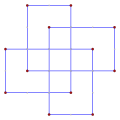(2…4) 90°	(2,1,-2,3,-4,3) 120°

Prosty spirolateral ma wszystkie zakręty w tym samym kierunku. Jest oznaczony przez n _θ , gdzie n jest liczbą kolejnych długości krawędzi całkowitych, a θ jest kątem wewnętrznym , jak każdy wymierny dzielnik 360 °. Kolejne długości krawędzi można wyrazić wprost jako (1,2,..., n ) _θ .

Uwaga: Kąt θ może być mylący, ponieważ reprezentuje kąt wewnętrzny, podczas gdy dodatkowy kąt skrętu może mieć większy sens. Te dwa kąty są takie same dla 90°.

Definiuje to wielokąt równokątny postaci < kp / kq >, gdzie kąt θ = 180 (1-2 q / p ), przy czym k = n / d i d = gcd ( n , p ). Jeśli d = n , wzór nigdy się nie zamyka. W przeciwnym razie ma kp i gęstość kq . Cykliczna symetria prostej spirolateralnej to p / d -zginać.

Wielokąt foremny { p } jest szczególnym przypadkiem wielokąta spirolateralnego 1 _{180(1−2/ p )°} . Wielokąt gwiazdy foremnej { p / q } jest szczególnym przypadkiem trójkąta spirolateralnego 1 _{180(1-2 q / p )°} . Izogonalny wielokąt jest szczególnym przypadkiem spirolateralnym, 2 _{180(1−2/ p )°} lub 2 _{180(1−2 q / p )°} .

Ogólny spirolateral może skręcić w lewo lub w prawo. Jest on oznaczony przez n _θ ^{a ₁ ,..., a _k} , gdzie a _i są indeksami o kątach ujemnych lub wklęsłych. Na przykład 2 _60° ² to skrzyżowany prostokąt z kątami wewnętrznymi ±60°, wygięty w lewo lub w prawo.

Nieoczekiwany zamknięty spiralny powrót do pierwszego wierzchołka w jednym cyklu. Tylko ogólne spirolaterale mogą się nie zamykać. Golygon to regularna nieoczekiwana zamknięta spirala , która zamyka się z oczekiwanego kierunku. Nieregularna nieoczekiwana zamknięta spirala to taka, która powraca do pierwszego punktu, ale z niewłaściwego kierunku. Na przykład 7 _90° ⁴ . Powrót na start we właściwym kierunku zajmuje 4 cykle.

Nowoczesne spirolateralne , _zwane ( i ₁ ,..., in ) _θ także przez edukatorkę Annę Weltman pętlą-de-loops _{, jest oznaczone przez} , dopuszczając dowolny ciąg liczb całkowitych jako długości krawędzi, od i ₁ do in . Na przykład (2,3,4) _90° ma długości krawędzi 2,3,4 powtarzające się. Zwojom w przeciwnym kierunku można nadać ujemną całkowitą długość krawędzi. Na przykład przekreślony prostokąt można zapisać jako (1,2,−1,−2) _θ .

Otwarty spirolateral nigdy się nie zamyka. Prosta spirolateralna n _θ nigdy się nie zamyka, jeśli n θ jest wielokrotnością 360°, gcd( p , n ) = p . Ogólny spirolateral może być również otwarty, jeśli połowa kątów jest dodatnia, a połowa ujemna.

(Częściowa) nieskończona prosta spirolateralna, 4 _90°

Zamknięcie

Liczbę cykli potrzebnych do zamknięcia spirolateralu , n θ _, przy k przeciwnych zwojach, p / q = 360/(180- θ ) można obliczyć. Skróć ułamek ( p -2 q )( n -2 k )/2 p = a / b . Rysunek powtarza się po b cyklach i wykonuje łącznie a . Jeśli b = 1, figura nigdy się nie zamyka.

Wyraźnie liczba cykli wynosi 2 p / d , gdzie d = gcd (( p -2 q ) ( n -2 k ), 2 p ). Jeśli d = 2 p , zamyka się na 1 cykl lub nigdy.

Liczbę cykli można postrzegać jako kolejność symetrii obrotowej spirolateralnej.

n _90°

• 

  1 _90° , 4 cykle, 1 obrót

• 

  2 _90° , 2 cykle, 1 obrót

• 

  3 _90° , 4 cykle, 3 obroty

• 

  4 _90° , nigdy się nie zamyka

• 

  5 _90° , 4 cykle, 5 obrotów

• 

  6 _90° , 2 cykle, 3 obroty

• 

  7 _90° , 4 cykle, 6 obrotów

• 

  8 _90° , nigdy się nie zamyka

• 

  9 _90° , 4 cykle, 9 obrotów

• 

  10 _90° , 2 cykle, 5 obrotów

n _60°

• 

  1 _60° , 3 cykle, 1 obrót

• 

  2 _60° , 3 cykle, 2 obroty

• 

  3 _60° , nigdy się nie zamyka

• 

  4 _60° , 3 cykle, 4 obroty

• 

  5 _60° , 3 cykle, 5 obrotów

• 

  6 _60° , nigdy się nie zamyka

• 

  7 _60° , 3 cykle, 7 obrotów

• 

  8 _60° , 3 cykle, 8 obrotów

• 

  9 _60° , nigdy się nie zamyka

• 

  10 _60° , 3 cykle, 10 obrotów

Małe proste spirolaterale

Spirolaterale można zbudować z dowolnego racjonalnego dzielnika 360 °. Kolumny pierwszej tabeli próbkują kąty z małych wielokątów foremnych, a druga tabela z wielokątów gwiaździstych, z przykładami do n = 6.

Wielokąt równokątny < p / q > ma p wierzchołków i gęstość q . < np / nq > można zredukować przez d = gcd( n , p ).

Małe całkowite kąty dzielnika

Proste spirolateralne (całe dzielniki p ) n _θ lub (1,2,..., n ) _θ

θ	60°	90°	108°	120°	128 4/7°	135°	140°	144°	147 3/11°	150°
180-θ Kąt skrętu	120°	90°	72°	60°	51 3/7°	45°	40°	36°	32 8/11°	30°
n θ \ s	3	4	5	6	7	8	9	10	11	12
1 θ Regularny { p. }	1 60° {3}	1 90° {4}	1 108° {5}	1 120° {6}	1 128,57° {7}	1 135° {8}	1 140° {9}	1 144° {10}	1 147,27° {11}	1 150° {12}
2 θ Izogonalny <2 p /2>	2 60° <6/2>	2 90° <8/2> → <4>	2 108° <10/2>	2 120° <12/2> → <6>	2 128,57° <14/2>	2 135° <16/2> → <8>	2 140° <18/2>	2 144° <20/2> → <10>	2 147° <22/2>	2 150° <24/2> → <12>
3 θ 2-izogonalny <3 p /3>	3 60° otwarte	3 90° <12/3>	3 108° <15/3>	3 120° <18/3> → <6>	3 128,57° <21/3>	3 135° <24/3>	3 140° <27/3> → <9>	3 144° <30/3>	3 147° <33/3>	3 150° <36/3> → <12>
4 θ 3-izogonalny <4 p /4>	4 60° <12/4>	4 90° otwarte	4 108° <20/4>	4 120° <24/4> → <12/2>	4 128,57° <28/4>	4 135° <32/4> → <8>	4 140° <36/4>	4 144° <40/4> → <20/2>	4 147° <44/4>	4 150° <48/4> → <12>
5 θ 4-izogonalny <5 p /5>	5 60° <15/5>	5 90° <20/5>	5 108° otwarte	5 120° <30/5>	5 128,57° <35/5>	5 135° <40/5>	5 140° <45/5>	5 144° <50/5> → <10>	5 147° <55/5>	5 150° <60/5>
6 θ 5-izogonalny <6 p /6>	6 60° otwarte	6 90° <24/6> → <12/3>	6 108° <30/6>	6 120° otwarte	6 128,57° <42/6>	6 135° <48/6> → <24/3>	6 140° <54/6> → <18/2>	6 144° <60/6> → <30/3>	6 147° <66/6>	6 150° <72/6> → <12>

Małe kąty dzielnika wymiernego

Proste spirolateralne (dzielniki wymierne p / q ) n _θ lub (1,2,..., n ) _θ

θ	15°	16 4/11°	20°	25 5/7°	30°	36°	45°	49 1/11°	72°	77 1/7°	81 9/11°	100°	114 6/11°
180-θ Kąt skrętu	165°	163 7/11°	160°	154 2/7°	150°	144°	135°	130 10/11°	108°	102 6/7°	98 2/11°	80°	65 5/11°
n θ \ p / q	24/11	11/5	9/4	7/3	12/5	5/2	8/3	11/4	10/3	7/2	11/3	9/2	11/2
1 θ Regularne { p / q }	1 15° {24/11}	1 16,36° {11/5}	1 20° {9/4}	1 25,71° {7/3}	1 30° {12/5}	1 36° {5/2}	1 45° {8/3}	1 49,10° {11/4}	1 72° {10/3}	1 77,14° {7/2}	1 81,82° {11/3}	1 100° {9/2}	1 114,55° {11/2}
2 θ Izogonalny <2 p /2 q >	2 15° <48/22> → <24/11>	2 16,36° <22/10>	2 20° <18/8>	2 25,71° <14/6>	2 30° <24/10> → <12/5>	2 36° <10/4>	2 45° <16/6> → <8/3>	2 49,10° <22/8>	2 72° <20/6> → <10/3>	2 77,14° <14/4>	2 81,82° <22/6>	2 100° <18/4>	2 114,55° <22/4>
3 θ 2-izogonalny <3 p /3 q >	3 15° <72/33> → <24/11>	3 16,36° <33/15>	3 20° <27/12> → <9/4>	3 25,71° <21/9>	3 30° <36/15> → <12/5>	3 36° <15/6>	3 45° <24/9>	3 49,10° <33/12>	3 72° <30/9>	3 77,14° <21/6>	3 81,82° <33/9>	3 100° <27/6> → <9/2>	3 114,55° <33/6>
4 θ 3-izogonalny <4 p /4 q >	4 15° <96/44> → <24/11>	4 16,36° <44/20>	4 20° <36/12>	4 25,71° <28/4>	4 30° <48/40> → <12/5>	4 36° <20/8>	4 45° <32/12> → <8/3>	4 49,10° <44/16>	4 72° <40/12> → <20/6>	4 77,14° <28/8>	4 81,82° <44/12>	4 100° <36/8>	4 114,55° <44/8>
5 θ 4-izogonalny <5 p /5 q >	5 15° <120/55>	5 16,36° <55/25>	5 20° <45/20>	5 25,71° <35/15>	5 30° <60/25>	5 36° otwarte	5 45° <40/15>	5 49,10° <55/20>	5 72° <50/15> → <10/3>	5 77,14° <35/10>	5 81,82° <55/15>	5 100° <45/10>	5 114,55° <55/10>
6 θ 5-izogonalny <6 p /6 q >	6 15° <144/66> → <24/11>	6 16,36° <66/30>	6 20° <54/24> → <18/8>	6 25,71° <42/18>	6 30° <72/30> → <12/5>	6 36° <30/12>	6 45° <48/18> → <24/9>	6 49,10° <66/24>	6 72° <60/18> → <30/9>	6 77,14° <42/12>	6 81,82° <66/18>	6 100° <54/12> → <18/4>	6 114,55° <66/12>

Zobacz też

• Grafika żółwia reprezentuje język komputerowy, który definiuje ścieżkę otwarcia lub zamknięcia jako długość ruchu i kąty skrętu.

• Alice Kaseberg Schwandt Spirolaterals: Zaawansowane badanie z elementarnego punktu widzenia , nauczyciel matematyki, tom 72, 1979, 166-169 [3]
• Margaret Kenney i Stanley Bezuszka, Square Spirolaterals Mathematics Teaching, tom 95, 1981, s. 22-27 [4]
• Gascoigne, Serafim Turtle Fun LOGO dla Spectrum 48K s. 42-46 | Spirolateralne 1985
• Wells, D. The Penguin Słownik ciekawej i interesującej geometrii London: Penguin, s. 239-241, 1991.
• Krawczyk, Robert, „Klocki konstrukcyjne Hilberta”, Mathematics & Design, The University of the Basque Country, s. 281-288, 1998.
• Krawczyk, Robert, Spirolaterals, Complexity from Simplicity , International Society of Arts, Mathematics and Architecture 99, The University of the Basque Country, s. 293-299, 1999. [5]
• Krawczyk, Robert J. Sztuka odwróceń spirolateralnych [6]

Linki zewnętrzne

• Aplikacja JavaScript Spirolaterals