Ikozytragon

Regularny icositetragon
Regularny icositetragon
	Regularny icositetragon
Typ	Regularny wielokąt
Krawędzie i wierzchołki	24
Symbol Schläfliego	{24}, t{12}, tt{6}, ttt{3}
Diagramy Coxetera-Dynkina	;
Grupa symetrii	Dwuścienny (D 24 ), rząd 2 × 24
Kąt wewnętrzny ( stopnie )	165°
Nieruchomości	Wypukłe , cykliczne , równoboczne , izogonalne , izotoksalne
Podwójny wielokąt	Samego siebie

W geometrii icositetragon (lub icosikaitetragon ) lub 24-gon to wielokąt o dwudziestu czterech bokach . Suma kątów wewnętrznych dowolnego icositetragonu wynosi 3960 stopni.

Zwykły icositetragon

Regularny sześciokąt icositetragon jest reprezentowany przez symbol Schläfliego {24} i może być również skonstruowany jako ścięty dwunastokąt t{12} lub dwukrotnie ścięty tt {6} lub trzykrotnie ścięty trójkąt ttt{3}.

Jeden kąt wewnętrzny w regularnym icositetragonie wynosi 165°, co oznacza, że jeden kąt zewnętrzny wynosiłby 15°.

Pole regularnego icositetragonu wynosi: (gdzie t = długość krawędzi)

{\ Displaystyle A = 6 t ^ {2} \ łóżeczko {\ Frac {\ pi} {24}} = {6} t ^ {2} (2 + {\ sqrt {2}} + {\ sqrt {3}} +{\sqrt {6}}).}

Icositetragon pojawił się w przybliżeniu pi wielokąta Archimedesa wraz z sześciokątem (6-gon), dwunastokątem (12-gon), tetracontaoctagon (48-gon) i enneacontahexagon (96-gon).

Budowa

Ponieważ 24 = 2 ³ × 3, regularny icositetragon można skonstruować za pomocą trisektora kąta . Jako ścięty dwunastokąt , można go zbudować przez przecięcie krawędzi dwunastokąta foremnego.

Symetria

Symetrie regularnego icositetragonu. Wierzchołki są kolorowane według ich pozycji symetrii. Niebieskie lustra są rysowane przez wierzchołki, a fioletowe przez krawędzie. Rozkazy wirowania są podane w środku.

Regularny ikozytragon ma symetrię Dih ₂₄ , rząd 48. Istnieje 7 symetrii dwuściennych podgrup: (Dih ₁₂ , Dih ₆ , Dih ₃ ) i (Dih ₈ , Dih ₄ , Dih ₂ Dih ₁ ) oraz 8 symetrii grup cyklicznych : ( Z ₂₄ , Z ₁₂ , Z ₆ , Z ₃ ) i (Z ₈ , Z ₄ , Z ₂ , Z ₁ ).

Te 16 symetrii można zobaczyć w 22 różnych symetriach na icositetragonie. John Conway określa je listem i zamówieniem grupowym. Pełna symetria postaci regularnej to r48 i żadna symetria nie jest oznaczona jako a1 . Symetrie dwuścienne są podzielone w zależności od tego, czy przechodzą przez wierzchołki ( d dla przekątnej), czy krawędzie ( p dla prostopadłych), oraz i , gdy linie odbicia przechodzą zarówno przez krawędzie, jak i wierzchołki. Symetrie cykliczne w środkowej kolumnie są oznaczone jako g dla ich centralnych rzędów wirowania.

Każda symetria podgrupy dopuszcza jeden lub więcej stopni swobody dla form nieregularnych. Tylko g24 nie ma stopni swobody, ale można ją postrzegać jako skierowane krawędzie .

Sekcja

24-gon z 264 rombami
regularny	izotoksal

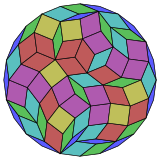
Coxeter twierdzi, że każdy zonogon (2 m -gon, którego przeciwległe boki są równoległe i równej długości) można podzielić na m ( m -1)/2 równoległoboków. W szczególności dotyczy to regularnych wielokątów o jednakowej liczbie boków, w którym to przypadku wszystkie równoległoboki są rombami. Dla icositetragonu foremnego m = 12 i można go podzielić na 66: 6 kwadratów i 5 zestawów po 12 rombów. Ten rozkład jest oparty na projekcji wielokąta Petriego 12-sześcianu .

Przykłady
12-sześcianów

Powiązane wielokąty

Regularny trójkąt, ośmiokąt i icositetragon mogą całkowicie wypełnić wierzchołek płaszczyzny.

Icositetragram to wielokąt gwiaździsty o 24 bokach . Istnieją 3 regularne formy podane przez symbole Schläfliego : {24/5}, {24/7} i {24/11}. Istnieje również 7 figur gwiazd regularnych korzystających z tego samego układu wierzchołków : 2{12}, 3{8}, 4{6}, 6{4}, 8{3}, 3{8/3} i 2{12/ 5}.

Icositetragramy jako wielokąty gwiezdne i figury gwiezdne
Formularz	Wypukły wielokąt	związki			Gwiazda wielokąta	Mieszanina
Obraz	{24/1}={24}	{24/2}=2{12}	{24/3}=3{8}	{24/4}=4{6}	{24/5}	{24/6}=6{4}
Kąt wewnętrzny	165°	150°	135°	120°	105°	90°
Formularz	Gwiazda wielokąta	związki			Gwiazda wielokąta	Mieszanina
Obraz	{24/7}	{24/8}=8{3}	{24/9}=3{8/3}	{24/10}=2{12/5}	{24/11}	{24/12}=12{2}
Kąt wewnętrzny	75°	60°	45°	30°	15°	0°

Istnieją również icositetragramy izogonalne zbudowane jako głębsze obcięcia dwunastokąta foremnego {12} i dodekagramu {12/5}. Generują one również dwa quasirunkacje: t{12/11}={24/11} i t{12/7}={24/7}.

Izogonalne obcięcia dwunastokąta foremnego i dodekagramu
Quasiregularny	izogonalny	Quasiregularny
t{12}={24}		t{12/11}={24/11}
t{12/5}={24/5}		t{12/7}={24/7}

Pochyl icositetragon

3 regularne skośne zygzaki icositetragons
{12}#{ }	{12/5}#{ }	{12/7}#{ }

Regularny skośny ikozytragon jest postrzegany jako zygzakowate krawędzie dwunastokątnego antygraniastosłupa, dodekagramowego antygraniastosłupa i dodekagramowego skrzyżowanego antygraniastosłupa.

Skośny icositetragon to skośny wielokąt z 24 wierzchołkami i krawędziami, ale nie znajdującymi się na tej samej płaszczyźnie. Wnętrze takiego icositetragonu nie jest ogólnie zdefiniowane. Skośny zygzakowaty icositetragon ma wierzchołki naprzemiennie między dwiema równoległymi płaszczyznami.

Regularny skośny icositetragon jest wierzchołkiem przechodnim z równymi długościami krawędzi. W trójwymiarze będzie to zygzakowaty skośny ikozytragon i można go zobaczyć w wierzchołkach i bocznych krawędziach dwunastokątnego antygraniastosłupa o tej samej symetrii D _12d , [2 ⁺ ,24], rząd 48. Antygraniastosłup dodekagramowy, s { 2,24/5} i dodekagramowy przekreślony antypryzmat, s{2,24/7} również mają dwunastokąty regularne skośne.

Wielokąty Petriego

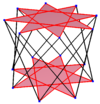
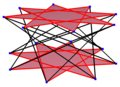
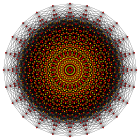
Regularny icositetragon to wielokąt Petriego dla wielu polytopów o wyższych wymiarach, postrzeganych jako rzuty ortogonalne na płaszczyznach Coxetera , w tym:

2F ₄
Bitruncated 24-komorowy	Runcinated 24-ogniwowy	Omnitruncated 24-ogniwowy

E ₈
4 ₂₁	2 ₄₁	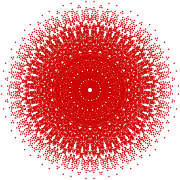1 ₄₂