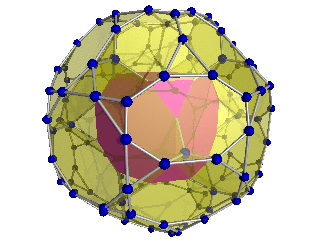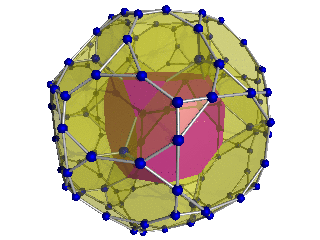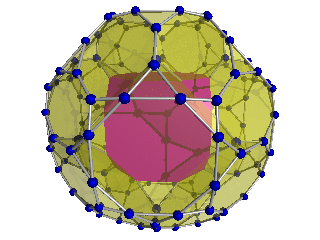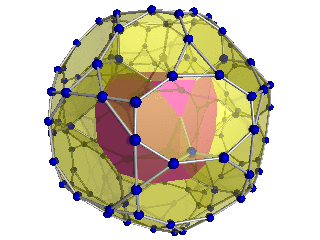
Obcięte 24 komórki

24-ogniwowy	Obcięte 24-ogniwowe	Bitruncated 24-komorowy
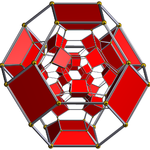
Diagramy Schlegla wyśrodkowane na jednym [3,4] (komórki po przeciwnej stronie w [4,3])

W geometrii obcięta 24 komórka to jednolity 4-polytop (4-wymiarowy jednolity polytop ) utworzony jako obcięcie zwykłego 24-komórkowego .

Istnieją dwa stopnie obcięcia, w tym bitruncation .

Obcięte 24-ogniwowe

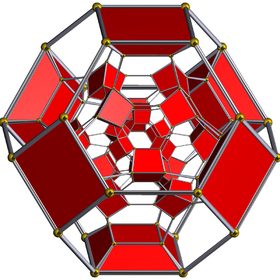Diagram Schlegla
Obcięty 24-ogniwowy
Typ	Jednolity 4-politop
symbole Schläfliego	t {3,4,3} tr {3,3,4} = ${\ Displaystyle t \ lewo \ {{\ rozpocząć {tablica} {l} 3 \\ 3,4 \ koniec { tablica}} \ prawo \}}$ t {3 ^1,1,1 } = ${\ Displaystyle t \ lewo \ {{\ początek {tablica} {l} 3 \\ 3 \\ 3 \ koniec {tablica}}\w prawo\}}$
Diagram Coxetera
Komórki	48	24 4.6.6 24 4.4.4
Twarze	240	144 {4} 96 {6}
Krawędzie	384
Wierzchołki	192
figura wierzchołka	równoboczna trójkątna piramida
Grupa symetrii	F ₄ [3,4,3], rozkaz 1152
Podgrupa rotacji	[3,4,3] ⁺ , rząd 576
Podgrupa komutatora	[3 ⁺ ,4,3 ⁺ ], rząd 288
Nieruchomości	wypukły
Jednolity indeks	23 24 25

Skrócony 24-komórkowy lub obcięty icositetrachoron jest jednolitym 4-wymiarowym politopem (lub jednolitym 4-polytopem ), który jest ograniczony przez 48 komórek : 24 sześciany i 24 ściętych ośmiościanów . Każdy wierzchołek łączy trzy ścięte ośmiościany i jeden sześcian, tworząc wierzchołek trójkąta równobocznego piramidy .

Budowa

Skrócone 24 komórki można zbudować z polytopów z trzema grupami symetrii:

F ₄ [3,4,3]: Obcięcie 24- komorowego .
B ₄ [3,3,4]: kantytruntacja 16-ogniw , z dwiema rodzinami ściętych komórek oktaedrycznych.
D ₄ [3 ^1,1,1 ]: Wielokrotność demitesseractu , z trzema rodzinami ściętych komórek ośmiościennych.

zespół Coxetera	${\ Displaystyle {F} _ {4}}$ = [3,4,3]	${\ Displaystyle {C} _ {4}}$ = [4,3,3]	${\ Displaystyle {D} _ {4}}$ = [3,3 ^1,1 ]
Symbol Schläfliego	t{3,4,3}	tr{3,3,4}	t{3 ^1,1,1 }
Zamówienie	1152	384	192
Pełna grupa symetrii	[3,4,3]	[4,3,3]	<[3,3 ^1,1 ]> = [4,3,3] [3[3 ^1,1,1 ]] = [3,4,3]
Diagram Coxetera
aspekty	3: 1:	2: 1: 1:	1,1,1: 1:
figura wierzchołka

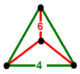
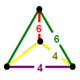
Zonotop

Jest to również zonotop : można go utworzyć jako sumę Minkowskiego sześciu odcinków linii łączących przeciwne pary spośród dwunastu permutacji wektora (+1, −1,0,0).

współrzędne kartezjańskie

Wszystkie współrzędne kartezjańskie wierzchołków obciętej 24-komórkowej komórki o długości krawędzi sqrt(2) są permutacjami współrzędnych i kombinacjami znaków:

(0,1,2,3) [4!×2 ³ = 192 wierzchołki]

Podwójna konfiguracja ma współrzędne we wszystkich permutacjach współrzędnych i znakach

(1,1,1,5) [4×2 ⁴ = 64 wierzchołków]

(1,3,3,3) [4×2 ⁴ = 64 wierzchołków]

(2,2,2,4) [4×2 ⁴ = 64 wierzchołków]

Struktura

24 komórki sześcienne są połączone kwadratowymi ścianami ze ściętymi ośmiościanami; a 24 ścięte ośmiościany są połączone ze sobą sześciokątnymi ścianami.

projekcje

Rzut równoległy obciętej 24-komórkowej komórki na trójwymiarową przestrzeń, zaczynając od ściętego ośmiościanu, ma następujący układ:

Obwiednia projekcji jest ściętym ośmiościanem sześciennym .
Dwa ze ściętych ośmiościanów wystają na ośmiościan ścięty leżący pośrodku koperty.
Sześć prostopadłościanów łączy kwadratowe ściany tego centralnego ściętego ośmiościanu ze środkiem ośmiokątnych ścian wielkiego ośmiościanu rombu. To są obrazy 12 sześciennych komórek, para komórek do każdego obrazu.
12 kwadratowych ścian wielkiego ośmiościanu rombu to obrazy pozostałych 12 sześcianów.
6 ośmiokątnych ścian wielkiego ośmiościanu rombowego to obrazy 6 ośmiościanów ściętych.
8 (niejednolitych) ściętych ośmiościanów leżących między sześciokątnymi powierzchniami obwiedni projekcyjnej a środkowym ośmiościanem ściętym to obrazy pozostałych 16 ściętych ośmiościanów, po parze komórek na każdy obraz.

Obrazy

rzuty ortograficzne
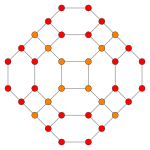
Samolot Coxetera	F ₄
Wykres
Symetria dwuścienna	[12]
Samolot Coxetera	B3 / A2 ₍_a )	B3 / A2 ₍_b )
Wykres
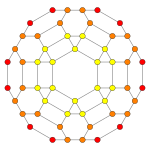
Symetria dwuścienna	[6]	[6]
Samolot Coxetera	4 _{_}	B2 / _A3_{_}
Wykres
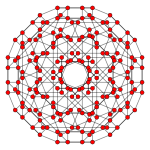
Symetria dwuścienna	[8]	[4]

Diagram Schlegla ( widoczne komórki sześcienne )	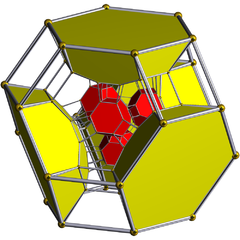Diagram Schlegla 8 z 24 widocznymi ściętymi ośmiościennymi komórkami
Rzut stereograficzny Wyśrodkowany na ściętym czworościanie

Sieci
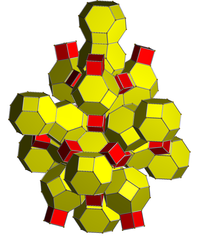Obcięte 24-ogniwowe	Podwójny do obciętego 24-ogniwowego

Powiązane polytopy

Wypukły kadłub ściętej 24-komorowej i jej podwójnej (zakładając, że są przystające) to niejednorodna polichoron złożona z 480 komórek: 48 sześcianów , 144 kwadratowych antygraniastosłupów , 288 czworościanów (jako tetragonalne dwusfenoidy) i 384 wierzchołków. Jego figura wierzchołka to trójkątna kopuła heksakisa .

figura wierzchołka

Bitruncated 24-komorowy

Bitruncated 24-cell
Schlegel diagram , wyśrodkowany na ściętym sześcianie, z ukrytymi alternatywnymi komórkami
Typ	Jednolity 4-politop
Symbol Schläfliego	2t{3,4,3}
Diagram Coxetera
Komórki	48 ( 3.8.8 )
Twarze	336	192 {3} 144 {8}
Krawędzie	576
Wierzchołki	288
Rysunek krawędzi	3.8.8
figura wierzchołka	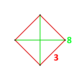tetragonalny disfenoid
podwójny politop	Dysfenoidalna 288-ogniwowa
Grupa symetrii	Aut (F ₄ ), [[3,4,3]], rząd 2304
Nieruchomości	wypukłe , izogonalne , izotoksalne , izochoryczne
Jednolity indeks	26 27 28

Internet

Bitruncated 24-komórkowy plik . 48-komórkowy lub tetracontoctachoron to 4-wymiarowy jednolity politop (lub jednolity 4-polytop ) pochodzący z 24-komórkowego .

EL Elte zidentyfikował go w 1912 roku jako półregularny polytope.

Jest konstruowany przez bitruncating 24-cell (obcięcie w połowie głębokości, która dałaby podwójną 24 -cell).

Będąc jednolitym 4-polytopem, jest przechodni przez wierzchołki . Ponadto jest to komórka przechodnia , składająca się z 48 ściętych kostek , a także przechodnia krawędzi , z 3 komórkami ściętych kostek na krawędź oraz z jednym trójkątem i dwoma ośmiokątami wokół każdej krawędzi.

48 komórek 24-komórkowej bitruncated odpowiada 24 komórkom i 24 wierzchołkom 24-komórkowej. Jako takie F4 _, centra 48 komórek tworzą system korzeniowy typu .

Jego figura wierzchołka to tetragonalny disfenoid , czworościan z 2 przeciwległymi krawędziami o długości 1 i wszystkimi 4 krawędziami bocznymi o długości √ (2 + √ 2).

Alternatywne nazwy

Bitruncated 24-ogniwowy ( Norman W. Johnson )
48-komórkowy jako 4-polytop przechodni przez komórkę
Bitruncated icositetrachoron
Bitruncated wieloośmiościan
Tetracontaoctachoron (kont.) (Jonathan Bowers)

Struktura

Ścięte sześciany są połączone ze sobą ośmiokątnymi ścianami w przeciwnej orientacji; I. e. dwa sąsiadujące ze sobą ścięte sześciany są obrócone względem siebie o 45 stopni, tak że żadne dwie trójkątne ściany nie mają wspólnej krawędzi.

Sekwencja ściętych kostek połączonych ze sobą przeciwległymi ośmiokątnymi ścianami tworzy cykl 8. Każdy ścięty sześcian należy do 3 takich cykli. Z drugiej strony sekwencja ściętych kostek połączonych ze sobą przeciwległymi trójkątnymi ścianami tworzy cykl 6. Każdy ścięty sześcian należy do 4 takich cykli.

Widziane w macierzy konfiguracji , pokazane są wszystkie zliczenia między elementami. Ukośne f-wektorów są uzyskiwane za pomocą konstrukcji Wythoffa , dzieląc pełny porządek grupowy rzędu podgrup poprzez usuwanie jednego lustra na raz. Krawędzie istnieją w 4 pozycjach symetrii. Kwadraty istnieją w 3 pozycjach, sześciokąty w 2 pozycjach, a ośmiokąty w jednej. Wreszcie 4 typy komórek istnieją skupione na 4 rogach podstawowego simpleksu.

F ₄	k -twarz	f _k	F₀	f ₁		f ₂			fa ₃		k -figura	Notatki
A ₁ A ₁	( )	F₀	288	2	2	1	4	1	2	2	s{2,4}	F ₄ / ZA ₁ ZA ₁ = 288
	{}	f ₁	2	288	*	1	2	0	2	1	{ } v( )
	{}	f ₁	2	*	288	0	2	1	1	2	{ } v( )
2 A ₁_{_}	{3}	f ₂	3	3	0	96	*	*	2	0	{}	F ₄ /A ₂ ZA ₁ = 1152/6/2 = 96
B2 _{_}	t{4}		8	4	4	*	144	*	1	1		F ₄ / B ₂ = 1152/8 = 144
2 A ₁_{_}	{3}		3	0	3	*	*	96	0	2		F ₄ /A ₂ ZA ₁ = 1152/6/2 = 96
B3 _{_}	t{4,3}	fa ₃	24	24	12	8	6	0	24	*	( )	F ₄ / B ₃ = 1152/48 = 24
B3 _{_}	t{4,3}	fa ₃	24	12	24	0	6	8	*	24	( )	F ₄ / B ₃ = 1152/48 = 24

Współrzędne

Wszystkie współrzędne kartezjańskie 24-bitowej komórki o długości krawędzi 2 są permutacjami współrzędnych i znaku:

(0, 2+√2, 2+√2, 2+2√2)

(1, 1+√2, 1+√2, 3+2√2)

projekcje

Projekcja do 2 wymiarów

rzuty ortograficzne
Samolot Coxetera	F ₄	4 _{_}
Wykres
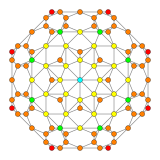
Symetria dwuścienna	[[12]] = [24]	[8]
Samolot Coxetera	B3 / _A2_{_}	B2 / _A3_{_}
Wykres
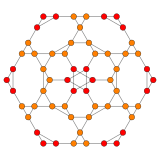
Symetria dwuścienna	[6]	[[4]] = [8]

Projekcja do 3 wymiarów

Pisowniany	Perspektywiczny
Poniższa animacja przedstawia rzut ortograficzny 24-komórkowej bitruncated w 3 wymiarach. Sama animacja jest projekcją perspektywiczną ze statycznego obrazu 3D do 2D, z dodanym obrotem, aby bardziej uwidocznić jej strukturę. Obrazy 48 ściętych kostek są ułożone w następujący sposób: Centralny obcięty sześcian to komórka znajdująca się najbliżej punktu widzenia 4D, podświetlona, aby była łatwiejsza do zobaczenia. Aby zmniejszyć wizualny bałagan, wierzchołki i krawędzie leżące na tym środkowym ściętym sześcianie zostały pominięte. Wokół tego centralnego ściętego sześcianu znajduje się 6 ściętych kostek przymocowanych przez ośmiokątne ściany i 8 ściętych kostek przymocowanych przez trójkątne ściany. Komórki te stały się przezroczyste, dzięki czemu widoczna jest komórka środkowa. 6 zewnętrznych kwadratowych ścian obwiedni projekcyjnej to obrazy kolejnych 6 ściętych sześcianów, a 12 podłużnych ośmiokątnych ścian obwiedni projekcyjnej to obrazy kolejnych 12 ściętych sześcianów. Pozostałe komórki zostały wyeliminowane, ponieważ leżą po drugiej stronie 24-komorowej bitruncated i są zasłonięte z punktu widzenia 4D. Należą do nich ścięty sześcian antypodalny, który rzutowałby do tej samej objętości, co podświetlony ścięty sześcian, z 6 innymi ściętymi sześcianami otaczającymi go za pomocą ośmiokątnych ścian i 8 innymi otaczającymi go ściętymi sześcianami przymocowanymi za pomocą trójkątnych ścian.	Poniższa animacja przedstawia projekcję perspektywiczną pierwszej komórki 24-komórkowej bitruncated w 3 wymiarach. Jego struktura jest taka sama jak poprzedniej animacji, z wyjątkiem tego, że istnieje pewne skrócenie perspektywiczne ze względu na projekcję perspektywiczną.

Projekcja stereograficzna

Powiązany regularny wielościan skośny

Regularny wielościan skośny , {8,4|3}, istnieje w 4-przestrzeni z 4 ośmiokątami wokół każdego wierzchołka, w zygzakowatej niepłaskiej figurze wierzchołków. Te ośmiokątne powierzchnie można zobaczyć na 24 komórkach bitruncated, wykorzystując wszystkie 576 krawędzi i 288 wierzchołków. 192 trójkątne powierzchnie 24-komorowej bitruncated można zobaczyć jako usunięte. Podwójny regularny wielościan skośny, {4,8|3}, jest podobnie spokrewniony z kwadratowymi ścianami 24-komorowego .

Dysfenoidalna 288-ogniwowa

Dysfenoidalna 288-ogniwowa
Typ	doskonały polichoron
Symbol	fa _1,2 fa ₄ (1,0,0,0) _{fa ₄} ⊕ (0,0,0,1) _{fa ₄}
Coxeter
Komórki	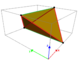288 przystających tetragonalnych disfenoidów
Twarze	576 przystających równoramiennych (2 krótkie krawędzie)
Krawędzie	336	192 długości ${\ Displaystyle \ scriptstyle 1}$ 144 długości ${\ Displaystyle \ scriptstyle {\ sqrt {2- {\ sqrt {2}}}}}$
Wierzchołki	48
figura wierzchołka	( triakis ośmiościan )
Podwójny	Bitruncated 24-komorowy
zespół Coxetera	Aut (F ₄ ), [[3,4,3]], rząd 2304
Wektor orbity	(1, 2, 1, 1)
Nieruchomości	wypukłe , izochoryczne

Dysfenoidalna 288-ogniwowa jest podwójna z bitruncated 24-ogniwową . Jest to 4-wymiarowy polytope (lub polychoron ) wywodzący się z 24 komórek . Jest skonstruowany przez podwojenie i obrócenie 24-ogniw, a następnie zbudowanie wypukłej otoczki .

Będąc podwójnym jednolitym polichoronem, jest przechodni przez komórkę i składa się z 288 przystających tetragonalnych disfenoidów . Ponadto jest przechodnia względem wierzchołków w grupie Aut(F ₄ ).

Obrazy

Projekcje ortogonalne
Samoloty Coxetera	B2 _{_}	B3 _{_}	F ₄
Disphenoidal 288-cell
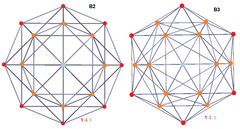
Bitruncated 24-cell

Geometria

Wierzchołki komórki 288 to dokładnie 24 czwartorzędy jednostek Hurwitza z normą do kwadratu 1, połączone z 24 wierzchołkami podwójnej 24 komórki z normą do kwadratu 2, rzutowane na jednostkę 3-sfery . Te 48 wierzchołków odpowiada binarnej grupie oktaedrycznej 2O lub <2,3,4>, rząd 48.

Zatem komórka 288 jest jedynym nieregularnym 4-polytopem, który jest wypukłą otoczką grupy czwartorzędowej, pomijając nieskończenie wiele grup dicyklicznych (takich samych jak binarne dwuścienne); zwykłe to 24-ogniwowe (≘ 2T lub <2,3,3>, kolejność 24) i 600-ogniwowe (≘ 2I lub <2,3,5>, kolejność 120). ( 16 komórek odpowiada binarnej grupie dwuściennej 2D ₂ lub <2,2,2>, rząd 16.)

Wpisana 3-sfera ma promień 1/2+ √ 2/4 ≈ 0,853553 i styka się z 288 komórkami w środkach 288 czworościanów, które są wierzchołkami 24-komórek z dwoma bitami.

Wierzchołki można pokolorować w 2 kolorach , powiedzmy czerwonym i żółtym, z 24 jednostkami Hurwitza na czerwono i 24 podwójnie na żółto, przy czym żółta 24 komórka jest zgodna z czerwoną. Zatem iloczyn 2 kwaternionów o jednakowych kolorach jest czerwony, a iloczyn 2 w mieszanych kolorach jest żółty.

Region	Warstwa	Szerokość	czerwony		żółty
Półkula północna	3	1	1	${\ Displaystyle 1}$	0
	2	√ 2 /2	0		6	${\ Displaystyle {\ tfrac {\ sqrt {2}} {2}} \ {\; \; \; 1 \ pm \ operatorname {i} \ ;\;\;1\pm \mathrm {j} ,\;\;\;1\pm \mathrm {k} \}}$
	1	1/2	8	${\ Displaystyle {\ tfrac {1} {2}} \ {1 \ pm \ operatorname {i} \ pm \ operatorname {j} \ pm \ operatorname {k} \} }$	0
Równik	0	0	6	${\ Displaystyle \ {\ pm \ operatorname {i}, \ pm \ operatorname {j}, \ pm \ operatorname {k} \}}$	12	${\ Displaystyle {\ tfrac {\ sqrt {2}} {2}} \ {\, \ pm \ operatorname {i} \ pm \ operatorname {j} ,\,\pm \mathrm {i} \pm \mathrm {k} ,\,\pm \mathrm {j} \pm \mathrm {k} \}}$
Półkula południowa	–1	–1/2	8	${\ Displaystyle - {\ tfrac {1} {2}} \ {1 \ pm \ operatorname {i} \ pm \ operatorname {j} \ pm \ operatorname {k} \}}$	0
	–2	– √ 2 /2	0		6	${\ Displaystyle {\ tfrac {\ sqrt {2}} {2}} \ {- 1 \ pm \ operatorname {i}, -1 \ pm \mathrm {j} ,-1\pm \mathrm {k} \}}$
	–3	–1	1	${\ Displaystyle -1}$	0
Całkowity			24		24

Umieszczając stały czerwony wierzchołek na biegunie północnym (1,0,0,0), na następnej głębszej „szerokości geograficznej” znajduje się 6 żółtych wierzchołków w ( √ 2 /2,x,y,z), po których następuje 8 czerwonych wierzchołków na szerokości geograficznej (1/2,x,y,z). Pełne współrzędne są podane jako liniowe kombinacje jednostek czwartorzędowych , które jednocześnie mogą być ${\ Displaystyle 1, \ operatorname {i$ } traktowane jako elementy grupy 2O . Następną głębszą szerokością geograficzną jest hiperpłaszczyzna równika przecinająca 3-sferę w 2-sferze, która jest wypełniona 6 czerwonymi i 12 żółtymi wierzchołkami.

Warstwa 2 to 2-sfera opisująca ośmiościan foremny, którego krawędzie mają długość 1. Czworościan z wierzchołkiem bieguna północnego ma 1 z tych krawędzi jako długą krawędź, której 2 wierzchołki są połączone krótkimi krawędziami z biegunem północnym. Kolejna długa krawędź biegnie od bieguna północnego do warstwy 1 i 2 krótkie krawędzie stamtąd do warstwy 2 .

Istnieją 192 długie krawędzie o długości 1 łączące równe kolory i 144 krótkie krawędzie o długości √ 2– √ 2 ≈ 0,765367 łączące mieszane kolory. 192*2/48 = 8 długości i 144*2/48 = 6 długości, czyli razem 14 krawędzi spotyka się w dowolnym wierzchołku.

576 ścian to równoramienne z 1 długą i 2 krótkimi krawędziami, wszystkie przystające. Kąty przy podstawie to arccos( √ 4+ √ 8 /4) ≈ 49,210°. 576*3/48 = 36 ścian spotyka się w wierzchołku, 576*1/192 = 3 na długiej krawędzi i 576*2/144 = 8 na krótkiej.

288 komórek to czworościany z 4 krótkimi krawędziami i 2 antypodalnymi i prostopadłymi długimi krawędziami, z których jeden łączy 2 czerwone, a pozostałe 2 żółte wierzchołki. Wszystkie komórki są przystające. 288*4/48 = 24 komórki spotykają się w wierzchołku. 288*2/192 = 3 komórki spotykają się na dłuższej krawędzi, 288*4/144 = 8 na krótkiej. 288*4/576 = 2 komórki spotykają się w trójkącie.

Powiązane polytopy

D ₄ jednolita polichora


{3,3 ^1,1 } h{4,3,3}	2r{3,3 ^1,1 } h ₃ {4,3,3}	t{3,3 ^1,1 } h ₂ {4,3,3}	2t{3,3 ^1,1 } h _2,3 {4,3,3}	r{3,3 ^1,1 } {3 ^1,1,1 }={3,4,3}	rr{3,3 ^1,1 } r{3 ^1,1,1 }=r{3,4,3}	tr{3,3 ^1,1 } t{3 ^1,1,1 }=t{3,4,3}	sr{3,3 ^1,1 } s{3 ^1,1,1 }=s{3,4,3}

B ₄ rodzina jednolitych polytopów:

Politopy symetrii B4
Nazwa	tesserakt	rektyfikowany tesserakt	obcięty tesserakt	kantelowany tesserakt	przeklęty tesserakt	bitruncated tesserakt	tesserakt kantytruncowany	tesserakt runcytruncated	omnitruncated tesserakt
Diagram Coxetera		=				=
Symbol Schläfliego	{4,3,3}	t ₁ {4,3,3} r{4,3,3}	t _0,1 {4,3,3} t{4,3,3}	t _0,2 {4,3,3} rr{4,3,3}	t _0,3 {4,3,3}	t _1,2 {4,3,3} 2t{4,3,3}	t _0,1,2 {4,3,3} tr{4,3,3}	t _0,1,3 {4,3,3}	t _0,1,2,3 {4,3,3}
Diagram Schlegla
B ₄

Nazwa	16-ogniwowy	rektyfikowany 16-ogniwowy	obcięte 16 komórek	kantelowany 16-komorowy	runcinated 16-cell	bitruncated 16-komorowy	cantitruncated 16-cell	runcytruncated 16-komorowy	omnitruncated 16-komorowy
Diagram Coxetera	=	=	=	=		=	=
Symbol Schläfliego	{3,3,4}	t ₁ {3,3,4} r{3,3,4}	t _0,1 {3,3,4} t{3,3,4}	t _0,2 {3,3,4} rr{3,3,4}	t _0,3 {3,3,4}	t _1,2 {3,3,4} 2t{3,3,4}	t _0,1,2 {3,3,4} tr{3,3,4}	t _0,1,3 {3,3,4}	t _0,1,2,3 {3,3,4}
Diagram Schlegla
B ₄

Rodzina jednolitych polytopów F _{4 :}

24-komórkowe rodziny polytopów
Nazwa	24-ogniwowy	obcięty 24-komorowy	afront 24-ogniwowy	rektyfikowane 24-ogniwowe	kantelowany 24-komorowy	bitruncated 24-komorowy	cantitruncated 24-komorowy	runcinated 24-cell	runcytruncated 24-komorowy	omnitruncated 24-komorowy
Symbol Schläfliego	{3,4,3}	t _0,1 {3,4,3} t{3,4,3}	s{3,4,3}	t ₁ {3,4,3} r{3,4,3}	t _0,2 {3,4,3} rr{3,4,3}	t _1,2 {3,4,3} 2t{3,4,3}	t _0,1,2 {3,4,3} tr{3,4,3}	t _0,3 {3,4,3}	t _0,1,3 {3,4,3}	t _0,1,2,3 {3,4,3}
Diagram Coxetera
Diagram Schlegla
F ₄
B ₄
B ₃ (a)
B ₃ (b)
B ₂

HSM Coxeter :
- Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Papier 23) HSM Coxeter, Regularne i półregularne Polytopes II , [Math. Zeit. 188 (1985) 559-591]
  - (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
Norman Johnson Uniform Polytopes , Rękopis (1991)
- NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966)
Klitzing, Richard. „Jednolite polytopy 4D (polichora)” . x3x4o3o=x3x3x4o - tiko, o3x4x3o - cd
3. Jednolita polichora wypukła oparta na icositetrachoronie (24-komorowym) - Model 24, 27 , George Olshevsky.