Regularny wielościan skośny

W geometrii regularne wielościany skośne są uogólnieniami zbioru wielościanów foremnych , które obejmują możliwość niepłaskich ścian lub figur wierzchołkowych . Coxeter przyjrzał się figurom skośnych wierzchołków, które utworzyły nowe 4-wymiarowe wielościany foremne, a znacznie później Branko Grünbaum przyjrzał się regularnym skośnym ścianom.

Nieskończone regularne wielościany skośne, które rozciągają się na 3 przestrzenie lub więcej, nazywane są regularnymi apeiroedrami skośnymi .

Historia

Według Coxetera w 1926 roku John Flinders Petrie uogólnił koncepcję regularnych wielokątów skośnych (wielokątów nieplanarnych) na regularne wielościany skośne .

Coxeter zaproponował zmodyfikowany symbol Schläfli ${l, m | n}$ dla tych figur, gdzie ${l, m}$ oznacza figurę wierzchołkową , $m$ $l$ -kąty wokół wierzchołka i $n$ -gonalne dziury. Ich figury wierzchołkowe są skośnymi wielokątami , zygzakowatymi pomiędzy dwiema płaszczyznami.

Regularne wielościany skośne, reprezentowane przez ${l, m | n}$ , postępuj zgodnie z tym równaniem:

{\ Displaystyle 2 \ cos {\ Frac {\ pi} {l}} \ cos {\ Frac {\ pi} {m}} = \ cos {\ Frac {\szpilka}}}

Pierwszy zestaw ${l, m | n}$ powtarza pięć wypukłych brył platońskich i jedną niewypukłą bryłę Keplera-Poinsota :

${l, m \| n}$	Twarze	Krawędzie	Wierzchołki	$P$	Wielościan	Porządek symetrii
{3,3\| 3} = {3,3}	4	6	4	0	Czworościan	12
{3,4\| 4} = {3,4}	8	12	6	0	Oktaedr	24
{4,3\| 4} = {4,3}	6	12	8	0	Sześcian	24
{3,5\| 5} = {3,5}	20	30	12	0	Dwudziestościan	60
{5,3\| 5} = {5,3}	12	30	20	0	Dwunastościan	60
{5,5\| 3} = {5,5/2}	12	30	12	4	Wielki dwunastościan	60

Skończone regularne wielościany skośne

Rzuty na płaszczyznę A4 Coxetera

${4, 6 \| 3}$	${6, 4 \| 3}$
Runcated 5-komórkowy (20 wierzchołków, 60 krawędzi)	Bitruncated 5-komórkowy (30 wierzchołków, 60 krawędzi)
Rzuty na płaszczyznę F4 Coxetera

${4, 8 \| 3}$	${8, 4 \| 3}$
Runcated 24-komórkowy (144 wierzchołki, 576 krawędzi)	Bitruncated 24 komórki (288 wierzchołków, 576 krawędzi)

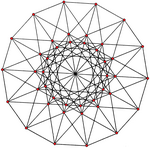
${3,8\|,4} = {3,8} 8$	${4,6\|,3} = {4,6} 6$
42 wierzchołki, 168 krawędzi	56 wierzchołków, 168 krawędzi
Niektóre z 4-wymiarowych regularnych wielościanów skośnych mieszczą się wewnątrz jednolitej polichory, jak pokazano na 4 górnych rzutach.

Coxeter wyliczył także większy zbiór skończonych regularnych wielościanów w swoim artykule „regularne wielościany skośne w trzech i czterech wymiarach oraz ich topologiczne analogi”.

Podobnie jak nieskończone wielościany skośne reprezentują różnorodne powierzchnie pomiędzy komórkami wypukłych, jednolitych plastrów miodu , wszystkie formy skończone reprezentują różnorodne powierzchnie w komórkach jednolitych 4-polytopów .

Wielościany postaci {2p, 2q | r} są powiązane z grupy Coxetera [(p,r,q,r)], która redukuje się do liniowej [r,p,r], gdy q wynosi 2. Coxeter podaje tę symetrię jako [[( p , r , q , r )] ⁺ ], który, jak twierdzi, jest izomorficzny z jego grupą abstrakcyjną (2 p ,2 q |2, r ). Powiązany plaster miodu ma rozszerzoną symetrię [[( p , r , q , r )]].

{2p,4|r} jest reprezentowane przez ściany {2p} bitruncowanego { r,p,r} jednolitego 4-polytope , a {4,2p|r} jest reprezentowane przez kwadratowe ściany runcowanego { r,p ,R}.

{4,4|n} tworzy duopryzm n - n , a konkretnie {4,4|4} pasuje do tesseraktu {4}x{4} .

{4,4\| n} rozwiązania reprezentują kwadratowe ściany duopryzmatów, z n-gonalnymi ścianami jako dziurami i reprezentują torus klifu oraz przybliżenie duocylindra	duopryzmatu 6,6 .	{4,4\|4} ma 16 kwadratowych ścian i istnieje jako podzbiór ścian w tesserakcie .

Pierścień złożony z 60 trójkątów tworzy regularny wielościan skośny w podzbiorze ścian 600-komórkowej .

Skończone wielościany w 4 wymiarach
{l, m \| N}	Twarze	Krawędzie	Wierzchołki	P	Struktura	Symetria	Zamówienie	Powiązana jednolita polichora
{4,4\| 3}	9	18	9	1	D ₃ xD ₃	[[3,2,3] ⁺ ]	9	3-3 duopryzm
{4,4\| 4}	16	32	16	1	D ₄ xD ₄	[[4,2,4] ⁺ ]	16	4-4 duopryzm lub tesserakt
{4,4\| 5}	25	50	25	1	D5 xD ₅_{_}	[[5,2,5] ⁺ ]	25	Duopryzm 5-5
{4,4\| 6}	36	72	36	1	D ₆ xD ₆	[[6,2,6] ⁺ ]	36	Duopryzm 6-6
{4,4\| N}	nr ²	2n ²	nr ²	1	D _n xD _n	[[n,2,n] ⁺ ]	nr ²	nn duopryzm
{4,6\| 3}	30	60	20	6	S5	[[3,3,3] ⁺ ]	60	Runcynowany 5-ogniwowy
{6,4\| 3}	20	60	30	6	S5	[[3,3,3] ⁺ ]	60	Bitrunkowane 5 komórek
{4,8\| 3}	288	576	144	73		[[3,4,3] ⁺ ]	576	Runcynowane 24-ogniwowe
{8,4\| 3}	144	576	288	73		[[3,4,3] ⁺ ]	576	Bitrunkowane 24-komórkowe

rozwiązania pentagramowe
{l, m \| N}	Twarze	Krawędzie	Wierzchołki	P	Struktura	Symetria	Zamówienie	Powiązana jednolita polichora
{4,5\| 5}	90	180	72	10	A6	[[5/2,5,5/2] ⁺ ]	360	Runcinate, wielkie gwiaździste 120 komórek
{5,4\| 5}	72	180	90	10	A6	[[5/2,5,5/2] ⁺ ]	360	Bitruncowane wielkie gwiaździste 120 komórek

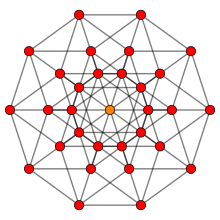
{4,5| 4} można zrealizować w 32 wierzchołkach i 80 krawędziach 5-sześcianu , co widać tutaj w rzucie na płaszczyznę B5 Coxetera pokazującym wierzchołki i krawędzie. 80 kwadratowych ścian 5-sześcianu staje się 40 kwadratowymi ścianami skośnego wielościanu i 40 kwadratowymi dziurami.

{l, m \| N}	Twarze	Krawędzie	Wierzchołki	P	Struktura	Zamówienie	Powiązane jednolite politepy
{4,5\| 4}	40	80	32	5	?	160	5 sześcianów (±1,±1,±1,±1,±1) i krawędzie
{5,4\| 4}	32	80	40	5	?	160	Rektyfikowane wierzchołki 5-ortopleksowe (±1,±1,0,0,0)
{4,7\| 3}	42	84	24	10	LF(2,7)	168
{7,4\| 3}	24	84	42	10	LF(2,7)	168
{5,5\| 4}	72	180	72	19	A6	360
{6,7\| 3}	182	546	156	105	LF(2,13)	1092
{7,6\| 3}	156	546	182	105	LF(2,13)	1092
{7,7\| 3}	156	546	156	118	LF(2,13)	1092
{4,9\| 3}	612	1224	272	171	LF(2,17)	2448
{9,4\| 3}	272	1224	612	171	LF(2,17)	2448
{7,8\| 3}	1536	5376	1344	1249	?	10752
{8,7\| 3}	1344	5376	1536	1249	?	10752

dalszej rozszerzonej formie Coxetera {q1,m|q2,q3...} lub z nieokreślonym q2: {l, m |, q}. Można je również przedstawić jako regularne skończone odwzorowanie lub { l , m } _{2 q} i grupę G ^{l , m , q} .

{ l , m \|, q } lub { l , m } _{2 q}	Twarze	Krawędzie	Wierzchołki	P	Struktura	Zamówienie	Powiązane złożone wielościany
{3,6\|, q } = {3,6} _{2 q}	2 kw. ²	3 kw ^{. 2}	q ²	1	G ^{3,6,2 q}	2 kw. ²
{3,2 q \|,3} = {3,2 q } ₆	2kw.2 ^_	3kw.2 ^_	3kw	( q -1)*( q -2)/2	G ^{3,6,2 q}	2 kw. ²
{3,7\|,4} = {3,7} ₈	56	84	24	3	LF(2,7)	168
{3,8\|,4} = {3,8} ₈	112	168	42	8	PGL(2,7)	336	(1 1 1 ₁⁴ ) ⁴ ,
{4,6\|,3} = {4,6} ₆	84	168	56	15	PGL(2,7)	336	(1 ⁴ 1 ⁴ 1 ₁ ) ⁽³⁾ ,
{3,7\|,6} = {3,7} ₁₂	364	546	156	14	LF(2,13)	1092
{3,7\|,7} = {3,7} ₁₄	364	546	156	14	LF(2,13)	1092
{3,8\|,5} = {3,8} ₁₀	720	1080	270	46	G ^3,8,10	2160	(1 1 1 ₁⁴ ) ⁵ ,
{3,10\|,4} = {3,10} ₈	720	1080	216	73	G ^3,8,10	2160	(1 1 1 ₁⁵ ) ⁴ ,
{4,6\|,2} = {4,6} ₄	12	24	8	3	S4 ×S2	48
{5,6\|,2} = {5,6} ₄	24	60	20	9	A5 ×S2	120
{3,11\|,4} = {3,11} ₈	2024	3036	552	231	LF(2,23)	6072
{3,7\|,8} = {3,7} ₁₆	3584	5376	1536	129	G ^3,7,17	10752
{3,9\|,5} = {3,9} ₁₀	12180	18270	4060	1016	LF(2,29)×A3	36540

Wyższe wymiary

Regularne wielościany skośne można również konstruować o wymiarach większych niż 4 jako osadzenia w regularnych wielościanach lub plastrach miodu. Na przykład dwudziestościan foremny można osadzić w wierzchołkach 6-półsześcianu ; został on nazwany przez HSM Coxetera dwudziestościanem regularnym skośnym . Dwunastościan można w podobny sposób osadzić w 10-demisześcianie .

Zobacz też

Notatki

Peter McMullen, Czterowymiarowe wielościany regularne , dyskretna i obliczeniowa geometria wrzesień 2007, tom 38, wydanie 2, s. 355–387
Coxeter , Regular Polytopes , wydanie trzecie (1973), wydanie Dover, ISBN 0-486-61480-8
Kalejdoskopy: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Artykuł 2) HSM Coxeter, „The Regular Sponges, or Skew Polyhedra”, Scripta Mathematica 6 (1939) 240–244.
- (Papier 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Papier 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559–591]
Coxeter , The Beauty of Geometry: Twelve Essays , Dover Publications, 1999, ISBN 0-486-40919-8 (Rozdział 5: Regularne skośne wielościany w trzech i czterech wymiarach oraz ich topologiczne analogi, Proceedings of the London Mathematics Society, Ser. 2 , tom 43, 1937.)
- Coxeter, HSM Regularne skośne wielościany w trzech i czterech wymiarach. Proc. Londyn, matematyka. Towarzystwo 43, 33-62, 1937.
Garner, CWL Regularne wielościany skośne w hiperbolicznej trójprzestrzeni. Móc. J. Matematyka. 19, 1179-1186, 1967.
E. Schulte, JM Wills O regularnych wielościanach skośnych Coxetera , Matematyka dyskretna, tom 60, czerwiec – lipiec 1986, strony 253–262