Teoria grup

W tym artykule omówiono zaawansowane pojęcia. Aby zapoznać się z podstawowymi tematami, zobacz Grupa (matematyka) .

Aby zapoznać się z teorią grup w naukach społecznych, zobacz Grupa społeczna .

Popularna łamigłówka Rubika, wynaleziona w 1974 roku przez Ernő Rubika, została wykorzystana jako ilustracja grup permutacji . Zobacz grupę Kostka Rubika .

W algebrze abstrakcyjnej teoria grup bada struktury algebraiczne znane jako grupy . Pojęcie grupy ma kluczowe znaczenie dla algebry abstrakcyjnej: inne dobrze znane struktury algebraiczne, takie jak pierścienie , pola i przestrzenie wektorowe , można postrzegać jako grupy wyposażone w dodatkowe operacje i aksjomaty . Grupy powtarzają się w całej matematyce, a metody teorii grup wpłynęły na wiele części algebry. Liniowe grupy algebraiczne i Grupy kłamstw to dwie gałęzie teorii grup, które doświadczyły postępu i stały się odrębnymi obszarami tematycznymi.

Różne układy fizyczne, takie jak kryształy i atom wodoru oraz trzy z czterech znanych podstawowych sił we wszechświecie, można modelować za pomocą grup symetrii . Tak więc teoria grup i blisko spokrewniona teoria reprezentacji mają wiele ważnych zastosowań w fizyce , chemii i materiałoznawstwie . Teoria grup jest również kluczowa dla kryptografii klucza publicznego .

Wczesna historia teorii grup sięga XIX wieku. Jednym z najważniejszych osiągnięć matematycznych XX wieku był wspólny wysiłek, obejmujący ponad 10 000 stron czasopism i opublikowany głównie w latach 1960-2004, którego kulminacją była pełna klasyfikacja skończonych grup prostych .

Historia

Osobny artykuł: Historia teorii grup

Teoria grup ma trzy główne źródła historyczne: teorię liczb , teorię równań algebraicznych i geometrię . Teoria liczb została zapoczątkowana przez Leonharda Eulera i rozwinięta przez pracę Gaussa nad arytmetyką modułową oraz grupami addytywnymi i multiplikatywnymi związanymi z polami kwadratowymi . Wczesne wyniki dotyczące grup permutacyjnych uzyskali Lagrange , Ruffini i Abel w poszukiwaniu ogólnych rozwiązań równań wielomianowych wysokiego stopnia. Évariste Galois ukuł termin „grupa” i ustanowił związek, znany obecnie jako teoria Galois , między rodzącą się teorią grup a teorią pola . W geometrii grupy najpierw stały się ważne w geometrii rzutowej , a później w geometrii nieeuklidesowej . Program Erlangen Felixa Kleina ogłosił teorię grup zasadą organizującą geometrię.

Galois w latach trzydziestych XIX wieku jako pierwszy zastosował grupy do określenia rozwiązywalności równań wielomianowych . Arthur Cayley i Augustin Louis Cauchy posunęli te badania dalej, tworząc teorię grup permutacyjnych. Drugie źródło historyczne dotyczące grup wynika z geometrycznych . Próbując uporać się z możliwymi geometriami (takimi jak geometria euklidesowa , hiperboliczna lub rzutowa ) za pomocą teorii grup, Felix Klein zainicjował programu Erlangen . Sophus Lie w 1884 roku zaczął używać grup (obecnie nazywanych grupami Liego ) związanych z problemami analitycznymi . Po trzecie, grupy były początkowo domyślnie, a później jawnie używane w algebraicznej teorii liczb .

Różny zakres tych wczesnych źródeł skutkował różnymi pojęciami grup. Teoria grup została ujednolicona począwszy od około 1880 roku. Od tego czasu wpływ teorii grup stale rośnie, dając początek algebrze abstrakcyjnej na początku XX wieku, teorii reprezentacji i wielu innym wpływowym dziedzinom spin-off. Klasyfikacja skończonych grup prostych to obszerna praca z połowy XX wieku, klasyfikująca wszystkie skończone grupy proste .

Główne klasy grup

Główny artykuł: Grupa (matematyka)

Zakres rozważanych grup stopniowo rozszerzał się od skończonych grup permutacyjnych i specjalnych przykładów grup macierzowych do grup abstrakcyjnych, które można określić poprzez prezentację za pomocą generatorów i relacji .

Grupy permutacyjne

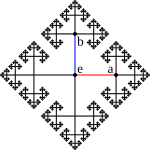
Pierwszą klasą grup, która została poddana systematycznym badaniom, były grupy permutacyjne . Biorąc pod uwagę dowolny zbiór X i zbiór G bijekcji X do samego siebie (znany jako permutacje ), który jest domknięty pod złożeniem i odwrotnością, G jest grupą działającą na X . Jeśli X składa się z n elementów, a G składa się ze wszystkich permutacji, G jest grupa symetryczna S _n ; ogólnie każda grupa permutacji G jest podgrupą grupy symetrycznej X . Wczesna konstrukcja Cayleya przedstawiała dowolną grupę jako grupę permutacyjną, działającą na siebie ( X = G ) za pomocą lewej regularnej reprezentacji .

W wielu przypadkach strukturę grupy permutacji można badać za pomocą właściwości jej działania na odpowiednim zbiorze. _Na przykład dowodzi się w ten sposób, że dla n ≥ 5 grupa przemienna An jest prosta , tj. nie dopuszcza żadnych właściwych podgrup normalnych . Fakt ten odgrywa kluczową rolę w niemożności rozwiązania ogólnego równania algebraicznego stopnia n ≥ 5 w pierwiastkach .

Grupy macierzowe

Następną ważną klasą grup są grupy macierzowe lub grupy liniowe . Tutaj G jest zbiorem składającym się z odwracalnych macierzy danego rzędu n nad polem K , które jest domknięte pod iloczynami i odwrotnościami. Taka grupa oddziałuje na n ^- wymiarową przestrzeń wektorową Kn poprzez przekształcenia liniowe . To działanie sprawia, że ​​​​grupy macierzowe są koncepcyjnie podobne do grup permutacyjnych, a geometria działania może być użytecznie wykorzystana do ustalenia właściwości grupy G .

Grupy transformacyjne

Grupy permutacyjne i grupy macierzowe są szczególnymi przypadkami grup transformacyjnych : grup, które działają na określoną przestrzeń X , zachowując jej nieodłączną strukturę. W przypadku grup permutacji X jest zbiorem; dla grup macierzowych X jest przestrzenią wektorową . Pojęcie grupy przekształceń jest ściśle związane z pojęciem grupy symetrii : grupy przekształceń często składają się ze wszystkich przekształceń, które zachowują określoną strukturę.

Teoria grup transformacji stanowi pomost łączący teorię grup z geometrią różniczkową . Długa linia badań, zapoczątkowana przez Liego i Kleina , dotyczy działań grupowych na rozmaitościach przez homeomorfizmy lub dyfeomorfizmy . Same grupy mogą być dyskretne lub ciągłe .

Grupy abstrakcyjne

Większość grup rozważanych w pierwszym etapie rozwoju teorii grup była „konkretna”, ponieważ została zrealizowana za pomocą liczb, permutacji lub macierzy. Dopiero pod koniec XIX wieku zaczęła obowiązywać idea grupy abstrakcyjnej jako zbioru z operacjami spełniającymi pewien system aksjomatów. Typowym sposobem określania grupy abstrakcyjnej jest prezentacja przez generatory i relacje ,

${\ Displaystyle G = \ langle S | R \ rangle.}$

Istotnym źródłem grup abstrakcyjnych jest konstrukcja grupy czynnikowej lub grupy ilorazowej G / H grupy G przez podgrupę normalną H. Grupy klas algebraicznych pól liczbowych były jednymi z najwcześniejszych przykładów grup czynnikowych, cieszących się dużym zainteresowaniem w teorii liczb . Jeśli grupa G jest grupą permutacji na zbiorze X , to grupa czynników G / H nie działa już na X ; ale idea abstrakcyjnej grupy pozwala nie martwić się tą rozbieżnością.

Zmiana perspektywy z grup konkretnych na abstrakcyjne sprawia, że ​​naturalne jest rozważanie własności grup niezależnych od konkretnej realizacji, czyli w języku nowożytnym niezmiennych względem izomorfizmu , a także klas grup o danej takiej własności: grupy skończone , grupy okresowe , grupy proste , grupy rozwiązywalne i tak dalej. Zamiast badać właściwości pojedynczej grupy, dąży się do ustalenia wyników, które mają zastosowanie do całej klasy grup. Nowy paradygmat miał ogromne znaczenie dla rozwoju matematyki: zapowiadał powstanie algebry abstrakcyjnej w pracach Hilberta , Emila Artina , Emmy Noether i matematyków z ich szkoły.

Grupy z dodatkową strukturą

Ważne rozwinięcie pojęcia grupy ma miejsce, gdy G ma dodatkową strukturę, w szczególności przestrzeń topologiczną , rozmaitość różniczkowalną lub rozmaitość algebraiczną . Jeśli operacje grupowe m (mnożenie) i i (inwersja),

${\ Displaystyle m: G \ razy G \ do sol, (g, h) \ mapsto gh ,\quad i:G\do G,g\mapsto g^{-1},}$

są zgodne z tą strukturą, to znaczy są ciągłymi , gładkimi lub regularnymi (w sensie geometrii algebraicznej) odwzorowaniami, to G jest grupą topologiczną , grupą Liego lub grupą algebraiczną .

Obecność dodatkowej struktury łączy tego typu grupy z innymi dyscyplinami matematycznymi i oznacza, że ​​do ich badania dostępnych jest więcej narzędzi. Grupy topologiczne tworzą naturalną dziedzinę abstrakcyjnej analizy harmonicznej , podczas gdy grupy Liego (często realizowane jako grupy transformacyjne) są podstawą geometrii różniczkowej i teorii reprezentacji unitarnej . Do pewnych pytań klasyfikacyjnych, których nie można ogólnie rozwiązać, można podejść i rozwiązać je dla specjalnych podklas grup. Zatem zwarte połączone grupy Liego zostały całkowicie sklasyfikowane. Istnieje owocny związek między nieskończonymi grupami abstrakcyjnymi a grupami topologicznymi: ilekroć grupa Γ może być zrealizowana jako krata w grupie topologicznej G , geometria i analiza dotycząca G dają ważne wyniki dotyczące Γ . Stosunkowo niedawny trend w teorii grup skończonych wykorzystuje ich powiązania ze zwartymi grupami topologicznymi ( grupami profinite ): na przykład pojedyncza p -adyczna grupa analityczna G ma rodzinę ilorazów, które są skończone p -grupy różnych rzędów, a własności G przekładają się na własności jego skończonych ilorazów.

Gałęzie teorii grup

Teoria grup skończonych

Główny artykuł: grupa skończona

W XX wieku matematycy dogłębnie badali niektóre aspekty teorii grup skończonych, zwłaszcza lokalną teorię grup skończonych oraz teorię grup rozwiązywalnych i nilpotentnych . W rezultacie uzyskano pełną klasyfikację skończonych grup prostych , co oznacza, że ​​znane są już wszystkie grupy proste , z których można zbudować wszystkie grupy skończone.

W drugiej połowie XX wieku matematycy, tacy jak Chevalley i Steinberg , również poszerzyli naszą wiedzę na temat skończonych analogów grup klasycznych i innych pokrewnych grup. Jedną z takich rodzin grup jest rodzina ogólnych grup liniowych na polach skończonych . Grupy skończone często pojawiają się przy rozważaniu symetrii obiektów matematycznych lub fizycznych, gdy obiekty te dopuszczają tylko skończoną liczbę przekształceń zachowujących strukturę. Teoria grup Liego , który można postrzegać jako zajmujący się „ ciągłą symetrią ”, jest pod silnym wpływem powiązanych grup Weyla . Są to skończone grupy generowane przez odbicia, które działają na skończoną wymiarową przestrzeń euklidesową . Właściwości grup skończonych mogą zatem odgrywać rolę w przedmiotach takich jak fizyka teoretyczna i chemia .

Reprezentacja grup

Główny artykuł: Teoria reprezentacji

Powiedzenie, że grupa G działa na zbiorze X, oznacza, że ​​każdy element G definiuje mapę bijektywną na zbiorze X w sposób zgodny ze strukturą grupy. Kiedy X ma większą strukturę, przydatne jest dalsze ograniczenie tego pojęcia: reprezentacja G w przestrzeni wektorowej V jest homomorfizmem grupowym :

${\ Displaystyle \ rho: G \ do \ nazwa operatora {GL} (V)}$

gdzie GL ( V ) składa się z odwracalnych przekształceń liniowych V . Innymi słowy, każdemu elementowi grupy g jest przypisany automorfizm ρ ( g ) taki, że ρ ( g ) ∘ ρ ( h ) = ρ ( gh ) dla dowolnego h w G .

Definicję tę można rozumieć w dwóch kierunkach, z których oba dają początek zupełnie nowym dziedzinom matematyki. Z jednej strony może to dostarczyć nowych informacji o grupie G : często operacja grupowa w G jest dana abstrakcyjnie, ale poprzez ρ odpowiada mnożeniu macierzy , co jest bardzo jednoznaczne. Z drugiej strony, biorąc pod uwagę dobrze rozumianą grupę działającą na skomplikowanym obiekcie, upraszcza to badanie danego obiektu. Na przykład, jeśli G jest skończony, wiadomo, że V powyżej rozkłada się na części nieredukowalne (patrz twierdzenie Maschkego ). Te części z kolei są znacznie łatwiejsze w zarządzaniu niż całe V (poprzez lemat Schura ).

Biorąc pod uwagę grupę G , teoria reprezentacji pyta następnie, jakie reprezentacje G istnieją. Istnieje kilka ustawień, a zastosowane metody i uzyskane wyniki są raczej różne w każdym przypadku: teoria reprezentacji grup skończonych i reprezentacje grup Liego to dwie główne poddomeny teorii. Całością przedstawień rządzą charaktery grupy . Na przykład wielomiany Fouriera można interpretować jako znaki U(1) , grupy liczby zespolone o wartości bezwzględnej 1 , działające na przestrzeni L ² funkcji okresowych.

Teoria kłamstwa

Główny artykuł: Teoria kłamstw

Grupa Liego to grupa , która jest również rozmaitością różniczkowalną , z tą właściwością, że operacje grupowe są zgodne z gładką strukturą . Grupy kłamstwa zostały nazwane na cześć Sophusa Liego , który położył podwaliny pod teorię grup ciągłej transformacji . Termin groupes de Lie pojawił się po raz pierwszy w języku francuskim w 1893 roku w tezie ucznia Lie, Arthura Tresse'a, strona 3.

Grupy Liego reprezentują najlepiej rozwiniętą teorię ciągłej symetrii obiektów i struktur matematycznych , co czyni je niezbędnymi narzędziami wielu działów współczesnej matematyki, a także współczesnej fizyki teoretycznej . Zapewniają naturalne ramy do analizy ciągłych symetrii równań różniczkowych ( teoria różniczkowa Galois ), podobnie jak grupy permutacji są używane w teorii Galois do analizy dyskretnych symetrii równań algebraicznych . Rozszerzenie teorii Galois na przypadek ciągłych grup symetrii było jedną z głównych motywacji Liego.

Kombinatoryczna i geometryczna teoria grup

Główny artykuł: Geometryczna teoria grup

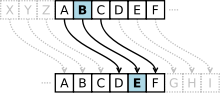
Grupy można opisywać na różne sposoby. Grupy skończone można opisać zapisując tablicę grup zawierającą wszystkie możliwe mnożenia g • h . Bardziej zwartym sposobem definiowania grupy są generatory i relacje , zwane także prezentacją grupy. Biorąc pod uwagę dowolny zestaw F generatorów ${\ Displaystyle \ {g_ {i} \} _ {i \ in I}}$ , wolna grupa generowana przez F surjektuje na grupę G . Jądro tej mapy nazywa się podgrupą relacji, generowaną przez pewien podzbiór D . Prezentacja jest zwykle oznaczana przez ${\ Displaystyle \ langle F \ mid D \ rangle.}$ Na przykład prezentacja grupowa ${\ Displaystyle \ langle a, b \ mid aba ^ {- 1} b ^{-1}\rangle }$ opisuje grupę, która jest izomorficzna ${\ Displaystyle \ mathbb {Z} \ razy \ mathbb {Z}.}$ Ciąg składający się z symboli generatora i ich odwrotności nazywany jest słowem .

Kombinatoryczna teoria grup bada grupy z perspektywy generatorów i relacji. Jest to szczególnie przydatne tam, gdzie spełnione są założenia skończoności, np. grupy skończenie generowane lub skończenie przedstawione (tj. dodatkowo relacje są skończone). Obszar ten wykorzystuje połączenie grafów poprzez ich podstawowe grupy . Na przykład można pokazać, że każda podgrupa wolnej grupy jest wolna.

Istnieje kilka naturalnych pytań wynikających z prezentowania grupy. Zadanie tekstowe polega na pytaniu, czy dwa słowa są faktycznie tym samym elementem grupy. Odnosząc problem do maszyn Turinga , można pokazać, że generalnie nie ma algorytmu rozwiązującego to zadanie. Innym, generalnie trudniejszym, algorytmicznie nierozwiązywalnym problemem jest problem izomorfizmu grupowego , który pyta, czy dwie grupy podane przez różne prezentacje są rzeczywiście izomorficzne. Na przykład grupa z prezentacją ${\ Displaystyle \ langle x, y \ mid xyxyx = e \ rangle,}$ jest izomorficzne z grupą dodatków Z liczb całkowitych, chociaż może to nie być od razu widoczne. (Pisząc ${\ displaystyle z = xy}$ , ma się ${\ Displaystyle G \ cong \ langle z, y \ mid z ^ {3} = y \ rangle \ cong \ langle z \ rangle.}$ )

Wykres Cayleya ⟨ x, y ∣ ⟩, grupa swobodna rangi 2.

Teoria grup geometrycznych atakuje te problemy z geometrycznego punktu widzenia, albo postrzegając grupy jako obiekty geometryczne, albo znajdując odpowiednie obiekty geometryczne, na które działa grupa. Pierwsza idea jest doprecyzowana za pomocą grafu Cayleya , którego wierzchołki odpowiadają elementom grupy, a krawędzie odpowiadają prawemu mnożeniu w grupie. Biorąc pod uwagę dwa elementy, konstruuje się metrykę słowną określoną przez długość minimalnej ścieżki między elementami. Twierdzenie Milnora i Svarca mówi następnie, że dana grupa G działa w rozsądny sposób w przestrzeni metrycznej X , na przykład rozmaitość zwarta , to G jest quasi-izometryczna (tj. z daleka wygląda podobnie) do przestrzeni X .

Łączenie grup i symetria

Główny artykuł: grupa Symetria

Biorąc pod uwagę obiekt strukturalny X dowolnego rodzaju, symetria to odwzorowanie obiektu na siebie, które zachowuje strukturę. Dzieje się tak w wielu przypadkach, np

• Jeśli X jest zbiorem bez dodatkowej struktury, symetria jest mapą bijektywną od zbioru do samego siebie, dającą początek grupom permutacji.
• Jeśli obiekt X jest zbiorem punktów na płaszczyźnie z jego strukturą metryczną lub inną przestrzenią metryczną , symetria jest bijekcją zbioru względem siebie, która zachowuje odległość między każdą parą punktów (izometrię ) . Odpowiednia grupa nazywana jest grupą izometrii X .
• Jeśli zamiast tego zachowane są kąty , mówi się o mapach konforemnych . Na przykład mapy konforemne dają początek grupom Kleinowskim .
• Symetrie nie ograniczają się do obiektów geometrycznych, ale obejmują również obiekty algebraiczne. Na przykład równanie ma dwa rozwiązania $i$${\ Displaystyle {\ sqrt {3}}}$ - $\ sqrt { 3}}}$ . W tym przypadku grupą, która wymienia dwa pierwiastki, jest grupa Galois należąca do równania. Każde równanie wielomianowe w jednej zmiennej ma grupę Galois, czyli pewną grupę permutacji na swoich pierwiastkach.

Aksjomaty grupy formalizują podstawowe aspekty symetrii . Symetrie tworzą grupę: są zamknięte , ponieważ jeśli weźmiesz symetrię obiektu, a następnie zastosujesz inną symetrię, wynikiem nadal będzie symetria. Tożsamość utrzymująca obiekt w stanie stałym jest zawsze symetrią obiektu. Istnienie odwrotności gwarantuje odwrócenie symetrii, a asocjatywność wynika z faktu, że symetrie są funkcjami na przestrzeni, a składanie funkcji jest asocjacyjne.

Twierdzenie Fruchta mówi, że każda grupa jest grupą symetrii jakiegoś grafu . Tak więc każda grupa abstrakcyjna jest w rzeczywistości symetriami jakiegoś wyraźnego obiektu.

Powiedzenie o „zachowaniu struktury” obiektu można uściślić, pracując w kategorii . Mapy zachowujące strukturę to wtedy morfizmy , a grupa symetrii to grupa automorfizmów danego obiektu.

Zastosowania teorii grup

Zastosowania teorii grup są liczne. Prawie wszystkie struktury w algebrze abstrakcyjnej są szczególnymi przypadkami grup. Na przykład pierścienie można postrzegać jako grupy abelowe (odpowiadające dodawaniu) wraz z drugą operacją (odpowiadającą mnożeniu). Dlatego argumenty teorii grup leżą u podstaw dużej części teorii tych bytów.

Teoria Galois

Główny artykuł: teoria Galois

Teoria Galois używa grup do opisu symetrii pierwiastków wielomianu (a dokładniej automorfizmów algebr generowanych przez te pierwiastki). Podstawowe twierdzenie teorii Galois zapewnia powiązanie między algebraicznymi rozszerzeniami pola a teorią grup. Daje skuteczne kryterium rozwiązywalności równań wielomianowych pod względem rozwiązywalności odpowiedniej grupy Galois . Na przykład S ₅ , grupa symetryczna w 5 elementach, nie jest rozwiązywalna, co oznacza, że ​​ogólne równanie kwintyczne nie mogą być rozwiązane przez pierwiastki w sposób, w jaki mogą to zrobić równania niższego stopnia. Teoria, będąca jednym z historycznych korzeni teorii grup, jest nadal owocnie stosowana w celu uzyskania nowych wyników w takich dziedzinach, jak teoria pola klas .

Topologia algebraiczna

Główny artykuł: Topologia algebraiczna

Topologia algebraiczna to kolejna dziedzina, która wyraźnie wiąże grupy z obiektami, którymi interesuje się teoria. Tam grupy są używane do opisu pewnych niezmienników przestrzeni topologicznych . Nazywa się je „niezmiennikami”, ponieważ są zdefiniowane w taki sposób, że nie zmieniają się, jeśli przestrzeń jest poddawana pewnym deformacjom . Na przykład grupa podstawowa „zlicza”, ile ścieżek w przestrzeni jest zasadniczo różnych. Hipoteza Poincarégo , udowodniona w latach 2002/2003 przez Grigorija Perelmana , jest wybitnym zastosowaniem tego pomysłu. Wpływ ten nie jest jednak jednokierunkowy. Na przykład topologia algebraiczna wykorzystuje przestrzenie Eilenberga – MacLane'a , które są przestrzeniami z określonymi grupami homotopii . Podobnie algebraiczna K-teoria opiera się w pewnym sensie na klasyfikowaniu przestrzeni grup. Wreszcie nazwa podgrupy skrętnej grupy nieskończonej pokazuje dziedzictwo topologii w teorii grup.

torus. Jego abelowa struktura grupowa jest indukowana z odwzorowania C → C /( Z + τ Z ) , gdzie τ jest parametrem znajdującym się w górnej połowie płaszczyzny .

Geometria algebraiczna

Główny artykuł: geometria algebraiczna

Geometria algebraiczna podobnie wykorzystuje teorię grup na wiele sposobów. Odmiany abelowe zostały wprowadzone powyżej. Obecność działania grupowego dostarcza dodatkowych informacji, które sprawiają, że te odmiany są szczególnie dostępne. Często służą również jako test dla nowych przypuszczeń. (Na przykład hipoteza Hodge'a (w niektórych przypadkach).) Przypadek jednowymiarowy, a mianowicie krzywe eliptyczne , jest badany szczególnie szczegółowo. Są interesujące zarówno teoretycznie, jak i praktycznie. Z drugiej strony rozmaitości toryczne są rozmaitościami algebraicznymi, na które działa a torus . Osadzenie toroidalne doprowadziło ostatnio do postępu w geometrii algebraicznej , w szczególności w rozwiązywaniu osobliwości .

Algebraiczna teoria liczb

Główny artykuł: algebraiczna teoria liczb

Algebraiczna teoria liczb wykorzystuje grupy do niektórych ważnych zastosowań. Na przykład formuła produktu Eulera ,

${\ Displaystyle {\ rozpocząć {wyrównane} \ suma _ {n \ geq 1} {\ Frac {1} {n ^ {s}}} &=\prod _{p{\text{prim}}}{\frac {1}{1-p^{-s}}},\\\end{wyrównane}}\!}$

oddaje fakt , że każda liczba całkowita rozkłada się w unikalny sposób na liczby pierwsze . Niepowodzenie tego stwierdzenia dla bardziej ogólnych pierścieni prowadzi do powstania grup klas i regularnych liczb pierwszych , które występują w traktowaniu przez Kummera Wielkiego Twierdzenia Fermata .

Analiza harmoniczna

Główny artykuł: Analiza harmoniczna

Analiza grup Liego i niektórych innych grup nazywana jest analizą harmoniczną . Miary Haara , czyli całki niezmienne pod translacją w grupie Liego, są używane do rozpoznawania wzorców i innych technik przetwarzania obrazu .

Kombinatoryka

W kombinatoryce pojęcie grupy permutacji i pojęcie działania grupowego są często używane w celu uproszczenia liczenia zbioru obiektów; patrz w szczególności lemat Burnside'a .

Krąg piątych może być wyposażony w cykliczną strukturę grupową

Muzyka

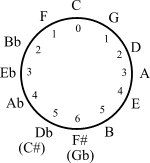
Obecność 12- okresowości w kręgu kwint daje możliwość zastosowania elementarnej teorii grup w muzycznej teorii mnogości . Teoria transformacyjna modeluje przemiany muzyczne jako elementy grupy matematycznej.

Fizyka

W fizyce grupy są ważne, ponieważ opisują symetrie, którym wydają się podlegać prawa fizyki. Zgodnie z twierdzeniem Noether , każdej ciągłej symetrii układu fizycznego odpowiada prawo zachowania tego układu. Fizycy są bardzo zainteresowani reprezentacjami grupowymi, zwłaszcza grupami Liego, ponieważ te reprezentacje często wskazują drogę do „możliwych” teorii fizycznych. Przykłady wykorzystania grup w fizyce obejmują Model Standardowy , teorię cechowania , grupę Lorentza i grupa Poincarégo .

Teorię grup można wykorzystać do rozwiązania niekompletności statystycznych interpretacji mechaniki opracowanych przez Willarda Gibbsa , odnoszących się do sumowania nieskończonej liczby prawdopodobieństw w celu uzyskania sensownego rozwiązania.

Chemia i materiałoznawstwo

Główny artykuł: Symetria molekularna

W chemii i materiałoznawstwie grupy punktowe służą do klasyfikowania regularnych wielościanów, a symetrie cząsteczek i grupy przestrzenne do klasyfikowania struktur krystalicznych . Przypisane grupy można następnie wykorzystać do określenia właściwości fizycznych (takich jak polarność chemiczna i chiralność ), właściwości spektroskopowych (szczególnie przydatnych w spektroskopii Ramana , spektroskopii w podczerwieni , spektroskopia dichroizmu kołowego, spektroskopia magnetycznego dichroizmu kołowego, spektroskopia UV/Vis i spektroskopia fluorescencyjna) oraz konstruowanie orbitali molekularnych .

Symetria molekularna odpowiada za wiele właściwości fizycznych i spektroskopowych związków oraz dostarcza istotnych informacji o przebiegu reakcji chemicznych. Aby przypisać grupę punktową dowolnej cząsteczce, należy znaleźć występujący na niej zbiór operacji symetrii. Operacja symetrii to działanie, takie jak obrót wokół osi lub odbicie przez płaszczyznę lustra. Innymi słowy, jest to operacja, która przesuwa cząsteczkę w taki sposób, że jest nie do odróżnienia od pierwotnej konfiguracji. W teorii grup osie obrotu i płaszczyzny lustrzane nazywane są „elementami symetrii”. Elementami tymi może być punkt, linia lub płaszczyzna, względem których przeprowadzana jest operacja symetrii. Operacje symetrii cząsteczki określają specyficzną grupę punktową dla tej cząsteczki.

Cząsteczka wody z osią symetrii

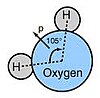
W chemii istnieje pięć ważnych operacji symetrii. Są to operacja identyczności ( E ) , operacja obrotu lub obrót właściwy ( C _n ), operacja odbicia ( σ ), inwersja ( i ) i obrót operacja odbicia lub obrót niewłaściwy ( S _n ). Operacja identyczności ( E ) polega na pozostawieniu cząsteczki bez zmian. Odpowiada to dowolnej liczbie pełnych obrotów wokół dowolnej osi. Jest to symetria wszystkich cząsteczek, natomiast grupa symetrii chiralna cząsteczka składa się tylko z operacji tożsamościowej. Operacja tożsamościowa jest cechą charakterystyczną każdej cząsteczki, nawet jeśli nie ma ona symetrii. Obrót wokół osi ( C _n ) polega na obracaniu cząsteczki wokół określonej osi o określony kąt. Jest to obrót o kąt 360°/ n , gdzie n jest liczbą całkowitą, wokół osi obrotu. Na przykład, jeśli wody obraca się o 180° wokół osi przechodzącej przez atom tlenu i pomiędzy atomami wodoru , to jest w tej samej konfiguracji, w jakiej się zaczęła. W tym przypadku, n = 2 , ponieważ dwukrotne zastosowanie go daje operację identyczności. W cząsteczkach z więcej niż jedną osią obrotu, oś Cn _mająca największą wartość n jest osią obrotu najwyższego rzędu lub osią główną. Na przykład w trifluorku boru (BF ₃ ) oś obrotu najwyższego rzędu to C ₃ , więc główną osią obrotu jest C ₃ .

W operacji odbicia ( σ ) wiele cząsteczek ma płaszczyzny lustrzane, chociaż mogą one nie być oczywiste. Operacja odbicia zamienia się w lewo i w prawo, tak jakby każdy punkt przesunął się prostopadle przez płaszczyznę do pozycji dokładnie tak oddalonej od płaszczyzny, jak na początku. Gdy płaszczyzna jest prostopadła do głównej osi obrotu, nazywa się to σ _h (poziomo). Inne płaszczyzny, które zawierają główną oś obrotu, są oznaczone jako pionowe ( σ _v ) lub dwuścienne ( σ _d ).

Inwersja (i ) jest bardziej złożoną operacją. Każdy punkt przesuwa się przez środek cząsteczki do pozycji przeciwnej do pierwotnej pozycji i tak daleko od punktu centralnego, jak punkt początkowy. Wiele cząsteczek, które na pierwszy rzut oka wydają się mieć centrum inwersji, nie ma; na przykład metan i inne czworościenne cząsteczki nie mają symetrii inwersji. Aby to zobaczyć, przytrzymaj model metanu z dwoma atomami wodoru w płaszczyźnie pionowej po prawej stronie i dwoma atomami wodoru w płaszczyźnie poziomej po lewej stronie. Inwersja powoduje powstanie dwóch atomów wodoru w płaszczyźnie poziomej po prawej stronie i dwóch atomów wodoru w płaszczyźnie pionowej po lewej stronie. Inwersja nie jest zatem operacją symetrii metanu, ponieważ orientacja cząsteczki po operacji inwersji różni się od pierwotnej orientacji. A ostatnią operacją jest niewłaściwy obrót lub operacja odbicia obrotu ( S _n ) wymaga obrotu o 360°/ n , po którym następuje odbicie przez płaszczyznę prostopadłą do osi obrotu.

Kryptografia

Grupa cykliczna Z ₂₆ leży u podstaw szyfru Cezara .

Do kryptografii z kluczem publicznym służą bardzo duże grupy pierwszego rzędu zbudowane w kryptografii krzywych eliptycznych . Metody kryptograficzne tego rodzaju korzystają z elastyczności obiektów geometrycznych, stąd ich struktury grupowe, wraz ze skomplikowaną strukturą tych grup, co sprawia, że ​​logarytm dyskretny jest bardzo trudny do obliczenia. Jeden z najwcześniejszych protokołów szyfrowania, szyfr Cezara , może być również interpretowana jako (bardzo łatwa) operacja grupowa. Większość schematów kryptograficznych w jakiś sposób wykorzystuje grupy. W szczególności wymiana kluczy Diffiego-Hellmana wykorzystuje skończone grupy cykliczne. Tak więc termin kryptografia oparta na grupach odnosi się głównie do protokołów kryptograficznych, które wykorzystują nieskończone grupy nieabelowe, takie jak grupa warkoczowa.

Zobacz też

• Lista tematów teorii grup
• Przykłady grup

Notatki

•    Borel, Armand (1991), Liniowe grupy algebraiczne , Absolwent Teksty z matematyki, tom. 126 (wyd. 2), Berlin, Nowy Jork: Springer-Verlag , doi : 10.1007/978-1-4612-0941-6 , ISBN 978-0-387-97370-8 , MR 1102012
•    Carter, Nathan C. (2009), wizualna teoria grup , Classroom Resource Materials Series , Mathematical Association of America , ISBN 978-0-88385-757-1 , MR 2504193
•    Cannon, John J. (1969), „Komputery w teorii grup: badanie”, Communications of the ACM , 12 : 3–12, doi : 10.1145/362835.362837 , MR 0290613 , S2CID 18226463
•   Frucht, R. (1939), „Herstellung von Graphen mit vorgegebener abstrakter Gruppe” , Compositio Mathematica , 6 : 239–50, ISSN 0010-437X , zarchiwizowane od oryginału w dniu 01.12.2008
•   Golubicki, Marcin ; Stewart, Ian (2006), „Nieliniowa dynamika sieci: formalizm grupowy”, Bull. Amer. Matematyka soc. ( NS ) . _ _ _ _ _ _ _ _ _
• Judson, Thomas W. (1997), Abstract Algebra: Theory and Applications Wstępny tekst licencjacki w duchu tekstów Galliana lub Hersteina, obejmujący grupy, pierścienie, domeny całkowe, pola i teorię Galois. Bezpłatny plik PDF do pobrania z licencją GFDL typu open source .
•     Kleiner, Izrael (1986), „Ewolucja teorii grup: krótkie badanie”, Mathematics Magazine , 59 (4): 195–215, doi : 10.2307/2690312 , ISSN 0025-570X , JSTOR 2690312 , MR 0863090
•   La Harpe, Pierre de (2000), Tematy z geometrycznej teorii grup , University of Chicago Press , ISBN 978-0-226-31721-2
•   Livio, M. (2005), Równanie, którego nie można rozwiązać: Jak geniusz matematyczny odkrył język symetrii , Simon & Schuster, ISBN 0-7432-5820-7 Przekazuje praktyczną wartość teorii grup, wyjaśniając, w jaki sposób wskazuje do symetrii w fizyce i innych naukach.
•    Mumford, David (1970), odmiany abelowe , Oxford University Press , ISBN 978-0-19-560528-0 , OCLC 138290
•   Ronan M. , 2006. Symetria i potwór . Oxford University Press. ISBN 0-19-280722-6 . Dla laików. Opisuje zadanie znalezienia podstawowych bloków konstrukcyjnych dla skończonych grup.
•   Rotman, Joseph (1994), Wprowadzenie do teorii grup , Nowy Jork: Springer-Verlag, ISBN 0-387-94285-8 Standardowe współczesne odniesienie.
•   Schupp, Paul E .; Lyndon, Roger C. (2001), kombinatoryczna teoria grup , Berlin, Nowy Jork: Springer-Verlag , ISBN 978-3-540-41158-1
•   Scott, WR (1987) [1964], Group Theory , New York: Dover, ISBN 0-486-65377-3 Niedrogi i dość czytelny, ale nieco przestarzały pod względem nacisku, stylu i zapisu.
•    Shatz, Stephen S. (1972), grupy określone, arytmetyka i geometria , Princeton University Press , ISBN 978-0-691-08017-8 , MR 0347778
•     Weibel, Charles A. (1994), Wprowadzenie do algebry homologicznej , Cambridge Studies in Advanced Mathematics, tom. 38, Cambridge University Press, ISBN 978-0-521-55987-4 , MR 1269324 , OCLC 36131259

Linki zewnętrzne

• Historia pojęcia grupy abstrakcyjnej
• Wyższa wymiarowa teoria grup Przedstawia pogląd na teorię grup jako pierwszy poziom teorii, która rozciąga się we wszystkich wymiarach i ma zastosowanie w teorii homotopii oraz w wielowymiarowych metodach nieabelowych dla problemów lokalnych do globalnych.
• Pakiet Plus dla nauczycieli i uczniów: Teoria grup Ten pakiet zawiera wszystkie artykuły na temat teorii grup z Plus , internetowego magazynu matematycznego opracowanego przez Millennium Mathematics Project na Uniwersytecie w Cambridge, omawiającego zastosowania i najnowsze przełomy oraz podające jasne definicje i przykłady grupy.
• Burnside, William (1911), „Grupy, teoria” , w Chisholm, Hugh (red.), Encyclopædia Britannica , tom. 12 (wyd. 11), Cambridge University Press, s. 626–636 Jest to szczegółowy opis współczesnego rozumienia teorii grup przez wczesnego badacza w tej dziedzinie.