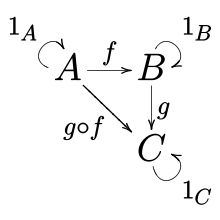Kategoria (matematyka)

Jest to kategoria ze zbiorem obiektów A, B, C i zbiorem morfizmów oznaczonych f, g, g ∘ f , a pętle są strzałkami tożsamości. Ta kategoria jest zazwyczaj oznaczona pogrubioną czcionką 3 .

W matematyce kategoria (czasami nazywana kategorią abstrakcyjną , aby odróżnić ją od kategorii konkretnej ) to zbiór „obiektów” połączonych „strzałkami”. Kategoria ma dwie podstawowe właściwości: możliwość asocjacyjnego komponowania strzałek oraz istnienie strzałki tożsamości dla każdego obiektu. Prostym przykładem jest kategoria zbiorów , których obiektami są zbiory , a strzałkami funkcje .

Teoria kategorii to gałąź matematyki, która stara się uogólnić całą matematykę pod względem kategorii, niezależnie od tego, co reprezentują ich obiekty i strzałki. Praktycznie każdą gałąź współczesnej matematyki można opisać za pomocą kategorii, a robienie tego często ujawnia głębokie spostrzeżenia i podobieństwa między pozornie różnymi dziedzinami matematyki. Jako taka, teoria kategorii zapewnia alternatywną podstawę dla matematyki dla teorii mnogości i innych proponowanych podstaw aksjomatycznych. Ogólnie rzecz biorąc, obiekty i strzałki mogą być bytami abstrakcyjnymi dowolnego rodzaju, a pojęcie kategorii zapewnia podstawowy i abstrakcyjny sposób opisywania bytów matematycznych i ich relacji.

Oprócz sformalizowania matematyki, teoria kategorii jest również wykorzystywana do sformalizowania wielu innych systemów w informatyce, takich jak semantyka języków programowania .

Dwie kategorie są takie same, jeśli mają tę samą kolekcję przedmiotów, tę samą kolekcję strzałek i tę samą asocjacyjną metodę komponowania dowolnej pary strzałek. Dwie różne kategorie można również uznać za „ równoważne ” dla celów teorii kategorii, nawet jeśli nie mają one dokładnie takiej samej struktury.

Dobrze znane kategorie są oznaczone krótkim słowem pisanym wielką literą lub skrótem pogrubionym lub kursywą: przykłady obejmują Set , kategorię zbiorów i funkcje zbioru ; Pierścień , kategoria pierścieni i homomorfizmy pierścieni ; i Top , kategoria przestrzeni topologicznych i map ciągłych . Wszystkie powyższe kategorie mają mapę tożsamości jako strzałki tożsamości i kompozycję jako operację asocjacyjną na strzałkach.

Klasycznym i wciąż często używanym tekstem na temat teorii kategorii są Kategorie dla pracującego matematyka autorstwa Saundersa Mac Lane'a . Inne odnośniki podano w odnośnikach poniżej. Podstawowe definicje w tym artykule są zawarte w kilku pierwszych rozdziałach dowolnej z tych książek.

Struktury grupowe
	Całość	Asocjatywność	Tożsamość	Odwrotność	Przemienność
Półgrupoida	Niepotrzebne	Wymagany	Niepotrzebne	Niepotrzebne	Niepotrzebne
Mała kategoria	Niepotrzebne	Wymagany	Wymagany	Niepotrzebne	Niepotrzebne
Groupoid	Niepotrzebne	Wymagany	Wymagany	Wymagany	Niepotrzebne
Magma	Wymagany	Niepotrzebne	Niepotrzebne	Niepotrzebne	Niepotrzebne
Quasigrupa	Wymagany	Niepotrzebne	Niepotrzebne	Wymagany	Niepotrzebne
Magma jednostkowa	Wymagany	Niepotrzebne	Wymagany	Niepotrzebne	Niepotrzebne
Półgrupa	Wymagany	Wymagany	Niepotrzebne	Niepotrzebne	Niepotrzebne
Pętla	Wymagany	Niepotrzebne	Wymagany	Wymagany	Niepotrzebne
monoid	Wymagany	Wymagany	Wymagany	Niepotrzebne	Niepotrzebne
Grupa	Wymagany	Wymagany	Wymagany	Wymagany	Niepotrzebne
Przemienny monoid	Wymagany	Wymagany	Wymagany	Niepotrzebne	Wymagany
grupa abelowa	Wymagany	Wymagany	Wymagany	Wymagany	Wymagany
^ α Aksjomat domknięcia , używany przez wiele źródeł i różnie definiowany , jest równoważny.

Każdy monoid może być rozumiany jako specjalny rodzaj kategorii (z pojedynczym obiektem, którego samomorfizmy są reprezentowane przez elementy monoidu), podobnie jak każdy preorder .

Definicja

Istnieje wiele równoważnych definicji kategorii. Jedna z powszechnie używanych definicji jest następująca. Kategoria C składa się z

klasa ob ( C ) obiektów ,
klasa hom( C ) morfizmów lub strzałek lub map między obiektami,
domena lub funkcja klasy obiektów źródłowych ${\ Displaystyle \ operatorname {dom} \ dwukropek \ operatorname {hom} (C) \ rightarrow \ operatorname {ob}$ ) ,
koddomena lub funkcja klasy obiektu docelowego $C)}$ $\ Displaystyle \ operatorname {cod} \ dwukropek \ operatorname {hom} (C) \ rightarrow \ operatorname {ob}$ ( ,
dla każdych trzech obiektów a , b i c operacja binarna hom( a , b ) × hom( b , c ) → hom ( a , c ) zwana złożeniem morfizmów ; złożenie f : a → b i g : b → c jest zapisane jako g ∘ f lub gf . (Niektórzy autorzy używają „kolejności schematycznej”, pisząc f;g lub fg ).

Uwaga: tutaj hom ( a , b ) oznacza podklasę morfizmów f in hom ( do ) taką, że ${\ Displaystyle \ operatorname {dom} (f) = a}$ i ${\ Displaystyle \ operatorname {cod} (f) = b}$ . Takie morfizmy są często zapisywane jako f : a → b .

takie, że zachodzą następujące aksjomaty:

( łączność ) jeśli f : a → b , g : b → c i h : c → d wtedy h ∘ ( g ∘ f ) = ( h ∘ g ) ∘ f , oraz
( tożsamość ) dla każdego obiektu x , istnieje morfizm 1 _x : x → x (niektórzy autorzy piszą id _x ) zwany morfizmem tożsamościowym dla x , taki że każdy morfizm f : a → x spełnia 1 _x ∘ f = f , oraz każdy morfizm g : x → b spełnia g ∘ 1 _x = g .

Piszemy f : a → b , i mówimy " f jest morfizmem od a do b ". Piszemy hom( a , b ) (lub hom _C ( a , b ) gdy może być niejasność co do kategorii hom ( a , b ) się odnosi), aby określić klasę hom wszystkich morfizmów od a do b . Na podstawie tych aksjomatów można udowodnić, że dla każdego obiektu istnieje dokładnie jeden morfizm tożsamościowy. Niektórzy autorzy stosują niewielką odmianę definicji, w której każdy obiekt jest identyfikowany z odpowiednim morfizmem tożsamości.

Małe i duże kategorie

Kategoria C jest nazywana małą , jeśli zarówno ob( C ), jak i hom( C ) są w rzeczywistości zbiorami , a nie klasami właściwymi , a w przeciwnym razie kategorią dużą . Kategoria lokalnie mała to taka kategoria, że dla wszystkich obiektów a i b klasa hom hom( a , b ) jest zbiorem zwanym homset . Wiele ważnych kategorii w matematyce (takich jak kategoria zbiorów), chociaż nie są małe, są przynajmniej lokalnie małe. Ponieważ w małych kategoriach obiekty tworzą zbiór, małą kategorię można postrzegać jako strukturę algebraiczną podobną do monoidu , ale bez wymagania właściwości domknięcia . Z drugiej strony duże kategorie mogą być używane do tworzenia „struktur” struktur algebraicznych.

Przykłady

Klasa wszystkich zbiorów (jako obiektów) wraz ze wszystkimi funkcjami między nimi (jako morfizmami ) , gdzie złożenie morfizmów jest zwykłym złożeniem funkcji , tworzy dużą kategorię Zbiór . Jest to najbardziej podstawowa i najczęściej używana kategoria w matematyce. Kategoria Rel składa się ze wszystkich zbiorów (jako obiektów) z relacjami binarnymi między nimi (jako morfizmy). Abstrahowanie od relacji zamiast funkcji daje alegorie , specjalną klasę kategorii.

Każdą klasę można postrzegać jako kategorię, której jedynymi morfizmami są morfizmy tożsamościowe. Takie kategorie nazywane są dyskretnymi . Dla dowolnego zbioru I dyskretna kategoria na I jest małą kategorią, która ma elementy I jako obiekty i tylko morfizmy tożsamościowe jako morfizmy. Kategorie dyskretne są najprostszym rodzajem kategorii.

Każdy wstępnie uporządkowany zestaw ( P , ≤) tworzy małą kategorię, w której obiekty są członkami P , a morfizmy są strzałkami wskazującymi od x do y , gdy x ≤ y . Ponadto, jeśli ≤ jest antysymetryczne , między dowolnymi dwoma obiektami może występować co najwyżej jeden morfizm. Istnienie morfizmów tożsamościowych i składalność morfizmów są gwarantowane przez zwrotność i przechodniość preorderu. Na podstawie tego samego argumentu każdy częściowo uporządkowany zbiór i każda relacja równoważności może być postrzegana jako mała kategoria. Każda liczba porządkowa może być postrzegana jako kategoria, gdy jest postrzegana jako uporządkowany zbiór .

Dowolna monoida (dowolna struktura algebraiczna z pojedynczą asocjacyjną operacją binarną i elementem tożsamościowym ) tworzy małą kategorię z pojedynczym obiektem x . (Tutaj x jest dowolnym ustalonym zbiorem.) Morfizmy od x do x są dokładnie elementami monoidu, morfizm tożsamościowy x jest tożsamością monoidu, a kategoryczny skład morfizmów jest określony przez operację monoidu. Kilka definicji i twierdzeń dotyczących monoidów można uogólnić dla kategorii.

Podobnie każdą grupę można postrzegać jako kategorię z pojedynczym obiektem, w której każdy morfizm jest odwracalny , to znaczy dla każdego morfizmu f istnieje morfizm g , który jest zarówno lewy, jak i prawy odwrotny do f w złożeniu. Morfizm odwracalny w tym sensie nazywamy izomorfizmem .

Grupoida to kategoria , w której każdy morfizm jest izomorfizmem. Groupoidy to uogólnienia grup, działań grupowych i relacji równoważności . Właściwie z punktu widzenia kategorii jedyna różnica między groupoidem a grupą polega na tym, że groupoid może mieć więcej niż jeden obiekt, ale grupa musi mieć tylko jeden. $displaystyle$ przestrzeń topologiczną i ustal punkt bazowy $x_$ wtedy jest x {0} $podstawowa$ grupa przestrzeni topologicznej X i punkt bazowy a jako zbiór ma strukturę grupy; jeśli następnie niech punkt bazowy biegnie przez wszystkie punkty $\$ weź sumę wszystkich $pi _ {1} (X, x_ {0} })}$ , wtedy otrzymany zbiór ma tylko strukturę groupoidy (która jest nazywana podstawową groupoidą X ) : dwie pętle (zgodnie z relacją równoważności homotopii) mogą nie mieć tego samego punktu bazowego, więc nie mogą się ze sobą mnożyć . W języku kategorii oznacza to, że tutaj dwa morfizmy mogą nie mieć tego samego obiektu źródłowego (lub obiektu docelowego, ponieważ w tym przypadku dla dowolnego morfizmu obiekt źródłowy i obiekt docelowy są takie same: punkt bazowy), więc nie mogą się komponować z nawzajem.

Graf skierowany.

Każdy graf skierowany generuje małą kategorię: obiekty to wierzchołki grafu, a morfizmy to ścieżki na grafie (w razie potrzeby powiększone o pętle ), gdzie złożenie morfizmów jest konkatenacją ścieżek. Taka kategoria nazywana jest kategorią swobodną generowaną przez graf.

Klasa wszystkich wstępnie uporządkowanych zbiorów z monotonicznymi funkcjami jako morfizmami tworzy kategorię Ord . Jest to kategoria konkretna , tj. kategoria uzyskana przez dodanie pewnego rodzaju struktury do zbioru i wymagająca, aby morfizmy były funkcjami respektującymi tę dodaną strukturę.

Klasa wszystkich grup z homomorfizmami grupowymi jako morfizmami i złożeniem funkcji jako operacją złożenia tworzy dużą kategorię, Grp . Podobnie jak Ord , Grp jest kategorią konkretną. Kategoria Ab , składająca się ze wszystkich grup abelowych i ich homomorfizmów grupowych, jest pełną podkategorią Grp i prototypem kategorii abelowej . Inne przykłady konkretnych kategorii podano w poniższej tabeli.

Kategoria	Obiekty	Morfizmy
grupa	grupy	homomorfizmy grupowe
Mag	magmy	homomorfizmy magmy
Mężczyzna ^str	gładkie rozmaitości	p -czasy mapy różniczkowalne w sposób ciągły
Spotkał	przestrzenie metryczne	krótkie mapy
R -Mod	R -moduły , gdzie R jest pierścieniem	Homomorfizmy modułu R
pon	monoidy	homomorfizmy monoidalne
Pierścień	pierścienie	homomorfizmy pierścieni
Ustawić	zestawy	Funkcje
Szczyt	przestrzenie topologiczne	funkcje ciągłe
Uni	jednolite przestrzenie	funkcje jednostajnie ciągłe
Wekt _K	przestrzenie wektorowe nad ciałem K	K - mapy liniowe

Wiązki światłowodowe z mapami wiązek między nimi tworzą konkretną kategorię.

Kategoria Kot składa się ze wszystkich małych kategorii, z funktorami między nimi w postaci morfizmów.

Budowa nowych kategorii

Podwójna kategoria

Każdą kategorię C można samą w sobie uznać za nową kategorię w inny sposób: obiekty są takie same jak w pierwotnej kategorii, ale strzałki w pierwotnej kategorii są odwrócone. Nazywa się to dualną lub przeciwstawną i oznacza się ją jako C ^op .

Kategorie produktów

Jeśli C i D są kategoriami, można utworzyć kategorię produktu C × D : obiekty są parami składającymi się z jednego przedmiotu z C i jednego z D , a morfizmy są również parami, składającymi się z jednego morfizmu w C i jednego w D . Takie pary można składać składowo .

Rodzaje morfizmów

Nazywa się morfizm f : a → b

monomorfizm (lub moniczny ), jeśli jest usuwalny z lewej strony, tj. 2 _fg 1 ₌ fg 2 _implikuje g 1 ₌ g dla wszystkich morfizmów g ₁ , g ₂ : x → a .
epimorfizm (lub epicki ), jeśli jest prawostronnie usuwalny, tj. g ₁ f = g ₂ f implikuje g ₁ = g ₂ dla wszystkich morfizmów g ₁ , g ₂ : b → x .
bimorfizm , jeśli jest zarówno monomorfizmem, jak i epimorfizmem.
retrakcja , jeśli ma prawą odwrotność, tj. jeśli istnieje morfizm g : b → a gdzie fg = 1 _b .
sekcja , jeśli ma lewą odwrotność, tj. jeśli istnieje morfizm g : b → a gdzie gf = 1 _a .
izomorfizm , jeśli ma odwrotność, tj. jeśli istnieje morfizm g : b → a gdzie fg = 1 _b i gf = 1 _a .
endomorfizm , jeśli a = b . Klasa endomorfizmów a jest oznaczona end( a ).
automorfizmem , jeśli f jest zarówno endomorfizmem, jak i izomorfizmem. Klasa automorfizmów a jest oznaczona jako aut( a ).

Każde wycofanie jest epimorfizmem. Każda sekcja jest monomorfizmem. Następujące trzy stwierdzenia są równoważne:

f jest monomorfizmem i retrakcją;
f jest epimorfizmem i sekcją;
f jest izomorfizmem.

Relacje między morfizmami (takie jak fg = h ) można najwygodniej przedstawić za pomocą diagramów przemiennych , na których obiekty są reprezentowane jako punkty, a morfizmy jako strzałki.

Rodzaje kategorii

W wielu kategoriach, np. Ab lub Vect _K , hom-sets hom( a , b ) nie są tylko zbiorami, ale właściwie grupami abelowymi , a skład morfizmów jest zgodny z tymi strukturami grupowymi; czyli jest dwuliniowy . Taka kategoria nazywana jest preaddytywną . Jeśli ponadto kategoria ma wszystkie produkty skończone i produkty uboczne , nazywa się ją kategorią addytywną . Jeżeli wszystkie morfizmy mają jądro i kojądro , a wszystkie epimorfizmy są kojądrami, a wszystkie monomorfizmy są jądrami, to mówimy o kategorii abelowej . Typowym przykładem kategorii abelowej jest kategoria grup abelowych.
Kategoria nazywana jest kompletną , jeśli istnieją w niej wszystkie małe granice . Kategorie zbiorów, grup abelowych i przestrzeni topologicznych są kompletne.
Kategoria jest nazywana kartezjańską zamkniętą, jeśli ma skończone iloczyny bezpośrednie, a morfizm zdefiniowany na iloczynie skończonym zawsze może być reprezentowany przez morfizm zdefiniowany tylko na jednym z czynników. Przykłady obejmują Set i CPO , kategorię kompletnych zamówień częściowych z funkcjami ciągłymi Scotta .
Topos to pewien typ zamkniętej kategorii kartezjańskiej, w której można sformułować całą matematykę (tak jak klasycznie cała matematyka jest sformułowana w kategorii zbiorów) . Topos może być również używany do reprezentowania teorii logicznej.

Zobacz też

Notatki

Adamek, Jiří; Herrlich, Horst; Strecker, George E. (1990), Kategorie abstrakcyjne i konkretne (PDF) , Wiley, ISBN 0-471-60922-6 (obecnie bezpłatne wydanie on-line, GNU FDL ).
Asperti, Andrea; Longo, Giuseppe (1991), kategorie, typy i struktury , MIT Press, ISBN 0-262-01125-5 .
Awodey, Steve (2006), teoria kategorii , oksfordzkie przewodniki logiczne, tom. 49, Oxford University Press, ISBN 978-0-19-856861-2 .
Barr, Michał ; Wells, Charles (2005), Toposy, trójki i teorie , Przedruki w teorii i zastosowaniach kategorii, tom. 12 (wyd. poprawione), MR 2178101 .
Borceux, Francis (1994), „Podręcznik algebry kategorycznej”, Encyklopedia matematyki i jej zastosowań , tom. 50–52, Cambridge: Cambridge University Press, ISBN 0-521-06119-9 .
„Kategoria” , Encyklopedia matematyki , EMS Press , 2001 [1994]
Herrlich, Horst; Strecker, George E. (2007), teoria kategorii , Heldermann Verlag, ISBN 978-3-88538-001-6 .
Jacobson, Nathan (2009), algebra podstawowa (wyd. 2), Dover, ISBN 978-0-486-47187-7 .
Lawvere, William ; Schanuel, Steve (1997), Matematyka pojęciowa: pierwsze wprowadzenie do kategorii , Cambridge University Press, ISBN 0-521-47249-0 .
Mac Lane, Saunders (1998), Kategorie dla pracującego matematyka , Absolwent Teksty z matematyki, tom. 5 (wyd. 2), Springer-Verlag, ISBN 0-387-98403-8 .
Marquis, Jean-Pierre (2006), „Teoria kategorii” , w: Zalta, Edward N. (red.), Stanford Encyclopedia of Philosophy .
Sica, Giandomenico (2006), Czym jest teoria kategorii? , Zaawansowane studia z matematyki i logiki, t. 3, Polimetrica, ISBN 978-88-7699-031-1 .
kategoria w n Lab