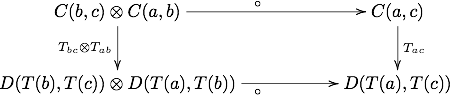Kategoria wzbogacona

W teorii kategorii , gałęzi matematyki , kategoria wzbogacona uogólnia ideę kategorii , zastępując zbiory domowe obiektami z ogólnej kategorii monoidalnej . Jest to motywowane obserwacją, że w wielu praktycznych zastosowaniach zbiór hom często ma dodatkową strukturę, której należy przestrzegać, np. jest wektorową przestrzenią morfizmów lub topologiczną przestrzenią morfizmów. W kategorii wzbogaconej zbiór morfizmów (zbiór hom) związany z każdą parą obiektów jest zastępowany przez obiekt w jakiejś ustalonej monoidalnej kategorii „obiektów domowych”. Aby naśladować (asocjacyjną) kompozycję morfizmów w zwykłej kategorii, kategoria hom musi mieć sposób na komponowanie obiektów hom w sposób asocjacyjny: to znaczy musi istnieć operacja binarna na obiektach, dająca nam co najmniej struktury kategorii monoidalnej , chociaż w niektórych kontekstach operacja może również wymagać przemienności i być może również prawego sprzężenia (tj. uczynienia kategorii odpowiednio monoidalną symetryczną lub nawet symetryczną monoidą zamkniętą ). ^{[ potrzebne źródło ]}

Wzbogacona teoria kategorii obejmuje zatem w tych samych ramach szeroką gamę struktur, w tym

zwykłe kategorie, w których zestaw domowy ma dodatkową strukturę wykraczającą poza bycie zestawem. Oznacza to, że istnieją operacje lub właściwości morfizmów, które muszą być przestrzegane przez kompozycję (np. istnienie 2-komórek między morfizmami i ich składem poziomym w 2-kategorii lub operacja dodawania na morfizmach w kategorii abelowej )
byty kategorialne, które same nie mają pojęcia o indywidualnym morfizmie, ale których obiekty domowe mają podobne aspekty kompozycyjne ( np . reguła kompozycji zapewnia nierówność trójkąta).

W przypadku, gdy kategoria hom-object jest kategorią zbiorów ze zwykłym iloczynem kartezjańskim, definicje kategorii wzbogaconej, funktora wzbogaconego itp. ... sprowadzają się do oryginalnych definicji z teorii kategorii zwyczajnych.

, że wzbogacona kategoria z hom-obiektami z kategorii monoidalnej M jest kategorią wzbogaconą nad M lub kategorią wzbogaconą w M lub po prostu kategorią M . Ze względu na preferencje Mac Lane'a dla litery V w odniesieniu do kategorii monoidalnej, kategorie wzbogacone są czasami określane ogólnie jako kategorie V.

Definicja

Niech $(M, \otimes, I, α, λ, ρ)$ będzie kategorią monoidalną . Wtedy wzbogacona kategoria C (alternatywnie, w sytuacjach gdy wybór kategorii monoidalnej musi być wyraźny, kategoria wzbogacona o M , lub M - kategoria ), składa się z

klasa ob ( C ) obiektów C , _ _
obiekt $C (za, b)$ M dla każdej pary obiektów za , b w C , używany do zdefiniowania strzałki ${\ Displaystyle f: a \ rightarrow b}$ w C jako strzałka ${\ Displaystyle f: I \ rightarrow C (a, b)}$ w M ,
strzałka $id a : I \to C (a, a)$ w M oznaczająca tożsamość dla każdego obiektu a w C , oraz
strzałka $° abc : C (b, c) \otimes C (a, b) \to C (a, c)$ w M oznaczająca skład każdej trójki przedmiotów a , b , c w C , używana do określenia składu ${\ Displaystyle f: a \ rightarrow b}$ i ${\ Displaystyle g: b \ rightarrow c}$ w C jako ${\ Displaystyle g\circ _{\textbf {C}}f={^{\circ }}_{abc}(g\otimes f)}$ wraz z trzema diagramami dojazdów, omówionymi poniżej.

Pierwszy diagram wyraża asocjatywność kompozycji:

$Math-enriched category associativity.svg$

Oznacza to, że wymóg asocjatywności jest teraz przejmowany przez asocjatora kategorii monoidalnej M .

W przypadku, gdy M jest kategorią zbiorów, a $(\otimes, I, α, λ, ρ)$ jest strukturą monoidalną $(\times, {•}, \dots)$ daną przez iloczyn kartezjański , końcowy zbiór jednopunktowy i kanoniczne izomorfizmy, które indukują, to każdy $C (a, b)$ jest zbiorem, którego elementy można traktować jako „indywidualne morfizmy” C , podczas gdy °, teraz funkcja, określa sposób, w jaki składają się kolejne morfizmy. W tym przypadku każda ścieżka prowadząca do $C (a, d)$ na pierwszym diagramie odpowiada jednemu z dwóch sposobów komponowania trzech kolejnych pojedynczych morfizmów $a \to b \to c \to d$ , czyli elementom z $C (a, b)$ , $C (b, c)$ i $C (c, d)$ . Przemienność diagramu jest zatem jedynie stwierdzeniem, że oba rzędy składu dają ten sam wynik, dokładnie taki, jaki jest wymagany dla zwykłych kategorii.

Nowością jest tutaj to, że powyższe wyraża wymaganie asocjatywności bez wyraźnego odniesienia do poszczególnych morfizmów we wzbogaconej kategorii C — ponownie te diagramy dotyczą morfizmów w monoidalnej kategorii M , a nie w C — czyniąc w ten sposób pojęcie asocjatywności kompozycja ma sens w ogólnym przypadku, gdy hom-obiekty $C (a, b)$ są abstrakcyjne, a sam C nie musi nawet mieć pojęcia o indywidualnym morfizmie.

Pogląd, że zwykła kategoria musi mieć morfizmy tożsamości, zostaje zastąpiony przez drugi i trzeci diagram, które wyrażają tożsamość w kategoriach lewych i prawych jednostek :

$Math-enriched category identity1.svg$

I

$Math-enriched category identity2.svg$

Wracając do przypadku, gdy M jest kategorią zbiorów z iloczynem kartezjańskim, morfizmy $id a : I \to C (a, a)$ stają się funkcjami ze zbioru jednopunktowego I i muszą wtedy dla dowolnego obiektu a identyfikować konkretny element każdego zbioru $C (a, a)$ , coś, co możemy wtedy nazwać „morfizmem tożsamości dla a w C ”. Przemienność dwóch ostatnich diagramów jest zatem stwierdzeniem, że kompozycje (określone przez funkcje °) zawierające te wyróżnione indywidualne „morfizmy tożsamości w C ” zachowują się dokładnie tak, jak według reguł tożsamości dla zwykłych kategorii.

Zauważ, że istnieje tutaj kilka odrębnych pojęć „tożsamości”:

monoidalny obiekt identyczności $I$ z M , będący tożsamością dla ⊗ tylko w sensie monoidowo -teoretycznym, a nawet wtedy tylko do izomorfizmu kanonicznego $(λ, ρ)$ .
morfizm tożsamościowy $1 C (a, b) : C (a, b) \to C (a, b)$ , który M ma dla każdego ze swoich przedmiotów na mocy tego, że jest (przynajmniej) zwykłą kategorią.
tożsamość wzbogaconej kategorii $id a : I \to C (a, a)$ dla każdego obiektu a w C , co ponownie jest morfizmem M , który nawet w przypadku, gdy uważa się, że C ma własne indywidualne morfizmy, niekoniecznie jest zidentyfikowanie konkretnego.

Przykłady kategorii wzbogaconych

Zwykłe kategorie to kategorie wzbogacone o ( Zbiór , ×, {•}), kategoria zbiorów z iloczynem kartezjańskim jako operacją monoidalną, jak wspomniano powyżej.
2-Kategorie to kategorie wzbogacone o Cat , kategorię małych kategorii , o strukturze monoidalnej nadanej przez iloczyn kartezjański. W tym przypadku 2-komórki między morfizmami a → b i odnoszącą je regułą kompozycji pionowej odpowiadają morfizmom zwykłej kategorii C ( a , b ) i jej własnej regule kompozycji.
Lokalnie małe kategorie to kategorie wzbogacone o ( SmSet , ×), kategoria małych zbiorów z iloczynem kartezjańskim jako operacją monoidalną. (Lokalnie mała kategoria to taka, której obiektami macierzystymi są małe zbiory).
Lokalnie skończone kategorie , przez analogię, to kategorie wzbogacone o ( FinSet , ×), kategoria zbiorów skończonych z iloczynem kartezjańskim jako operacją monoidalną.
Jeśli C jest zamkniętą kategorią monoidalną, to C jest wzbogacone samo w sobie.
Zbiory wstępnie uporządkowane to kategorie wzbogacone o pewną kategorię monoidalną 2 , składające się z dwóch obiektów i pojedynczej strzałki nietożsamości między nimi, którą możemy zapisać jako FAŁSZ → PRAWDA , koniunkcja jako operacja monoidalna i PRAWDA jako jej tożsamość monoidalna. Hom-obiekty 2 ( a , b ) następnie po prostu zaprzeczają lub potwierdzają określoną relację binarną na danej parze obiektów ( a , b ); ze względu na bardziej znaną notację możemy zapisać tę relację jako $a \leq b$ . Istnienie kompozycji i tożsamości wymaganych dla kategorii wzbogaconej o 2 natychmiast przekłada się odpowiednio na następujące aksjomaty

b ≤ c i a ≤ b ⇒ a ≤ c (przechodniość)

PRAWDA ⇒ a ≤ a (zwrotność)

, które są niczym innym jak aksjomatami dla ≤ bycia preorderem. A ponieważ wszystkie diagramy w 2 komutują, jest to jedyna treść aksjomatów kategorii wzbogaconej dla kategorii wzbogaconych o 2 .

Uogólnione przestrzenie metryczne Williama Lawvere'a , znane również jako przestrzenie pseudoquasimetryczne , to kategorie wzbogacone o nieujemne rozszerzone liczby rzeczywiste $R + \infty$ , gdzie tej ostatniej nadano zwykłą strukturę kategorii poprzez odwrotność jej zwykłego uporządkowania (tj. istnieje morfizm r → s iff r ≥ s ) i strukturę monoidalną poprzez dodanie (+) i zero (0). Hom-obiekty $R +\infty (a, b)$ są zasadniczo odległościami d( a , b ), a istnienie złożenia i tożsamości przekłada się na

d( b , c ) + d( a , b ) ≥ d( a , c ) (nierówność trójkąta)

0 ≥ d( a , a )

Kategorie o zerowych morfizmach to kategorie wzbogacone o ( Zbiór* , ∧), kategoria zbiorów spiczastych z iloczynem rozbicia jako operacją monoidalną; punkt specjalny obiektu hom Hom( A , B ) odpowiada morfizmowi zerowemu od A do B .
Kategoria Ab grup abelowych i kategoria R-Mod modułów nad pierścieniem przemiennym oraz kategoria Vect przestrzeni wektorowych nad danym ciałem są nad sobą wzbogacone, gdzie morfizmy dziedziczą strukturę algebraiczną „punktowo” . Mówiąc bardziej ogólnie, kategorie preaddytywne to kategorie wzbogacone o ( Ab , ⊗) iloczynem tensorowym jako operacją monoidalną (myśląc o grupach abelowych jako o modułach Z ).

Związek z funktorami monoidalnymi

Jeśli istnieje funktor monoidalny z kategorii monoidalnej M do kategorii monoidalnej N , to każda kategoria wzbogacona o M może być zreinterpretowana jako kategoria wzbogacona o N . Każda kategoria monoidalna M ma funktor monooidalny M ( I , –) do kategorii zbiorów, więc każda kategoria wzbogacona ma podstawową kategorię zwykłą. W wielu przykładach (takich jak powyższe) ten funktor jest wierny , więc kategorię wzbogaconą o M można opisać jako zwykłą kategorię z pewną dodatkową strukturą lub właściwościami.

Wzbogacone funktory

Funktor wzbogacony jest odpowiednim uogólnieniem pojęcia funktora na kategorie wzbogacone. Wzbogacone funktory są wówczas mapami między wzbogaconymi kategoriami, które respektują wzbogaconą strukturę.

Jeśli C i D są M -kategoriami (to znaczy kategoriami wzbogaconymi o kategorię monooidalną M ), funktor M -wzbogacony T : C → D jest mapą, która przypisuje każdemu obiektowi C obiekt D i każdej parze obiektów aib w C zapewnia morfizm w M Tab ₍ : C ( a , b ) → D T ( a ) , T ( b )) między obiektami hom C i D (które są obiektami w M ) , spełniające wzbogacone wersje aksjomatów funktora, czyli zachowanie tożsamości i kompozycji.

Ponieważ hom-obiekty nie muszą być ustawione w kategorii wzbogaconej, nie można mówić o konkretnym morfizmie. Nie ma już pojęcia morfizmu tożsamościowego ani szczególnego złożenia dwóch morfizmów. Zamiast tego, morfizmy z jednostki do obiektu macierzystego powinny być traktowane jako wybór tożsamości, a morfizmy z iloczynu monooidalnego powinny być traktowane jako kompozycja. Zwykłe aksjomaty funktoralne są zastępowane odpowiednimi diagramami przemiennymi obejmującymi te morfizmy.

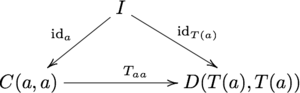
Szczegółowo, jeden ma ten schemat

dojazdów, co równa się równaniu

{\ Displaystyle T_ {aa} \ circ \ operatorname {id} _ {a} = \ operatorname {id} _ {T (a)},}

gdzie I jest obiektem jednostkowym M . Jest to analogiczne do reguły F (id _a ) = id _{F ( a )} dla zwykłych funktorów. Dodatkowo wymaga się, aby diagram

dojazd, co jest analogiczne do reguły F ( fg )= F ( f ) F ( g ) dla zwykłych funktorów.

Zobacz też

Kelly, GM (2005) [1982]. Podstawowe pojęcia rozszerzonej teorii kategorii . Przedruki w teorii i zastosowaniach kategorii. Tom. 10.
Mac Lane, Saunders (wrzesień 1998). Kategorie dla pracującego matematyka . Absolwent Teksty z matematyki . Tom. 5 (wyd. 2). Skoczek. ISBN 0-387-98403-8 .
Lawvere, FW (2002) [1973]. Przestrzenie metryczne, logika uogólniona i kategorie zamknięte . Przedruki w teorii i zastosowaniach kategorii. Tom. 1.
Wzbogacona kategoria w n Lab