Struktura krystaliczna

Struktura krystaliczna soli kuchennej (sód na fioletowo, chlor na zielono)

W krystalografii struktura krystaliczna jest opisem uporządkowanego układu atomów , jonów lub cząsteczek w materiale krystalicznym . Uporządkowane struktury wynikają z wewnętrznej natury cząstek składowych, tworząc symetryczne wzory, które powtarzają się wzdłuż głównych kierunków trójwymiarowej przestrzeni w materii.

Najmniejsza grupa cząstek w materiale, która składa się na ten powtarzający się wzór, to komórka elementarna struktury. Komórka elementarna całkowicie odzwierciedla symetrię i strukturę całego kryształu, który jest tworzony przez powtarzające się translacje komórki elementarnej wzdłuż jej głównych osi. Wektory translacji definiują węzły sieci Bravais .

Długości głównych osi lub krawędzi komórki elementarnej oraz kąty między nimi to stałe sieciowe , zwane także parametrami sieciowymi lub parametrami komórki . Właściwości symetrii kryształu są opisane przez pojęcie grup przestrzennych . Wszystkie możliwe symetryczne układy cząstek w przestrzeni trójwymiarowej można opisać za pomocą 230 grup przestrzennych.

Struktura kryształu i symetria odgrywają kluczową rolę w określaniu wielu właściwości fizycznych, takich jak rozszczepienie , struktura pasma elektronicznego i przezroczystość optyczna .

Komórka elementarna

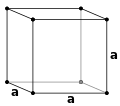
Struktura krystaliczna jest opisana w kategoriach geometrii ułożenia cząstek w komórkach elementarnych. Komórka elementarna jest definiowana jako najmniejsza powtarzalna jednostka posiadająca pełną symetrię struktury krystalicznej. Geometria komórki elementarnej jest zdefiniowana jako równoległościan , dostarczając sześć parametrów sieciowych jako długości krawędzi komórki ( a , b , c ) oraz kąty między nimi (α, β, γ). Położenia cząstek wewnątrz komórki elementarnej są opisane współrzędnymi ułamkowymi ( x i _, y i _, z i ₎ wzdłuż krawędzi komórki, mierzonymi od punktu odniesienia. Konieczne jest zatem podanie jedynie współrzędnych najmniejszego asymetrycznego podzbioru cząstek. Tę grupę cząstek można dobrać tak, aby zajmowała jak najmniejszą przestrzeń fizyczną, co oznacza, że nie wszystkie cząstki muszą fizycznie znajdować się w granicach określonych parametrami sieci. Wszystkie inne cząstki komórki elementarnej są generowane przez operacje symetrii, które charakteryzują symetrię komórki elementarnej. Zbiór operacji symetrii komórki elementarnej jest formalnie wyrażony jako grupa przestrzenna struktury krystalicznej.

Prosty sześcienny (P)
Sześcienny skoncentrowany na ciele (I)
Sześcienny centrowany na twarzy (F)

Indeksy Millera

Płaszczyzny o różnych wskaźnikach Millera w sześciennych kryształach

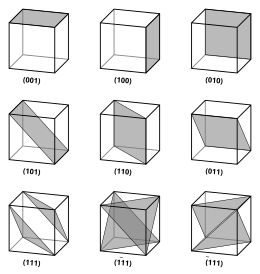
Wektory i płaszczyzny w sieci krystalicznej są opisane za pomocą trójwartościowego indeksu Millera . Ta składnia używa indeksów h , k i ℓ jako parametrów kierunkowych.

Z definicji składnia ( hkℓ ) oznacza płaszczyznę, która przecina trzy punkty a ₁ / h , a ₂ / k i a ₃ / ℓ lub ich wielokrotność. Oznacza to, że wskaźniki Millera są proporcjonalne do odwrotności punktów przecięcia płaszczyzny z komórką elementarną (na podstawie wektorów kratowych). Jeśli jeden lub więcej wskaźników wynosi zero, oznacza to, że płaszczyzny nie przecinają tej osi (tj. punkt przecięcia jest „w nieskończoności”). Płaszczyzna zawierająca oś współrzędnych jest przesuwana w taki sposób, że nie zawiera już tej osi przed określeniem jej wskaźników Millera. Indeksy Millera dla płaszczyzny są liczbami całkowitymi bez wspólnych czynników. Indeksy ujemne są oznaczone poziomymi kreskami, jak w (1 2 3). W ortogonalnym układzie współrzędnych komórki sześciennej wskaźniki Millera płaszczyzny są składowymi kartezjańskimi wektora normalnego do płaszczyzny.

Biorąc pod uwagę tylko ( hkℓ ) płaszczyzny przecinające jeden lub więcej punktów sieci (płaszczyzny sieci ), odległość d między sąsiednimi płaszczyznami sieci jest związana z (najkrótszym) odwrotnym wektorem sieci prostopadłym do płaszczyzn według wzoru

{\ Displaystyle d = {\ Frac {2 \ pi} {|\ mathbf {g} _ {hk \ ell} |}}}

Samoloty i kierunki

Kierunki krystalograficzne to geometryczne linie łączące węzły ( atomy , jony lub cząsteczki ) kryształu. Podobnie płaszczyzny krystalograficzne są płaszczyznami geometrycznymi łączącymi węzły. Niektóre kierunki i płaszczyzny mają większą gęstość węzłów. Te płaszczyzny o dużej gęstości mają następujący wpływ na zachowanie kryształu:

Właściwości optyczne : Współczynnik załamania światła jest bezpośrednio związany z gęstością (lub okresowymi fluktuacjami gęstości).
Adsorpcja i reaktywność : Fizyczna adsorpcja i reakcje chemiczne zachodzą na powierzchni atomów lub cząsteczek lub w ich pobliżu. Zjawiska te są zatem wrażliwe na gęstość węzłów.
Napięcie powierzchniowe : Kondensacja materiału oznacza, że atomy, jony lub cząsteczki są bardziej stabilne, jeśli są otoczone innymi podobnymi substancjami. Napięcie powierzchniowe interfejsu zmienia się zatem w zależności od gęstości na powierzchni.

Gęste płaszczyzny krystalograficzne

Defekty mikrostrukturalne : pory i krystality mają zwykle proste granice ziaren wzdłuż płaszczyzn o większej gęstości.
Rozszczepienie : zwykle występuje preferencyjnie równolegle do płaszczyzn o większej gęstości.
Odkształcenie plastyczne : poślizg dyslokacji występuje preferencyjnie równolegle do płaszczyzn o większej gęstości. Zaburzenie przenoszone przez dyslokację ( wektor Burgersa ) przebiega wzdłuż gęstego kierunku. Przesunięcie jednego węzła w bardziej gęstym kierunku wymaga mniejszego zniekształcenia sieci krystalicznej.

Niektóre kierunki i płaszczyzny są określone przez symetrię układu kryształów. W układach jednoskośnych, romboedrycznych, tetragonalnych i trygonalnych/sześciokątnych istnieje jedna unikalna oś (czasami nazywana osią główną ), która ma wyższą symetrię obrotową niż pozostałe dwie osie. Płaszczyzna podstawowa jest płaszczyzną prostopadłą do głównej osi w tych układach kryształów. W przypadku trójskośnych, rombowych i sześciennych układów kryształów oznaczenie osi jest dowolne i nie ma osi głównej.

Struktury sześcienne

W szczególnym przypadku prostych sześciennych kryształów wektory sieciowe są ortogonalne i równej długości (zwykle oznaczane jako ); podobnie dla kraty odwrotnej. Tak więc w tym powszechnym przypadku wskaźniki Millera ( ℓmn ) i [ ℓmn ] oznaczają po prostu normalne/kierunki we współrzędnych kartezjańskich . W przypadku sześciennych kryształów o stałej sieci a odległość d między sąsiednimi (ℓmn) płaszczyznami sieci wynosi (od góry):

{\ Displaystyle d _ {\ ell mn} = {\ Frac {a} {\ sqrt {\ ell ^ {2} + m ^ {2} + n ^ { 2}}}}}

Ze względu na symetrię sześciennych kryształów można zmieniać miejsce i znak liczb całkowitych oraz mieć równoważne kierunki i płaszczyzny:

Współrzędne w nawiasach kątowych , takie jak ⟨100⟩, oznaczają rodzinę kierunków, które są równoważne ze względu na operacje na symetrii, takie jak [100], [010], [001] lub ujemne dowolne z tych kierunków.
Współrzędne w nawiasach klamrowych lub nawiasach klamrowych , takie jak {100}, oznaczają rodzinę płaskich normalnych, które są równoważne ze względu na operacje symetrii, podobnie jak nawiasy ostrokątne oznaczają rodzinę kierunków.

W przypadku sieci sześciennych centrowanych na twarzy (fcc) i sześciennych centrowanych na ciele (bcc) prymitywne wektory sieci nie są ortogonalne. Jednak w tych przypadkach wskaźniki Millera są konwencjonalnie definiowane względem wektorów sieci sześciennej superkomórki, a zatem ponownie są po prostu kierunkami kartezjańskimi .

Odstępy międzypłaszczyznowe

Odległość d między sąsiednimi ( hkℓ ) płaszczyznami sieci jest określona wzorem:

Sześcienny:
${\ Displaystyle {\ Frac {1} {d ^ {2}}} = {\ Frac {h ^ {2} + k ^ {2} + \ell ^{2}}{a^{2}}}}$
czworokątny:
${\ Displaystyle {\ Frac {1} {d ^ {2}}} = {\ Frac {h ^ {2} + k ^ {2} }}{a^{2}}}+{\frac {\ell ^{2}}{c^{2}}}}$
Sześciokątny:
${\ Displaystyle {\ Frac {1} {d ^ {2}}} = {\ Frac {4} 3}}\left({\frac {h^{2}+hk+k^{2}}{a^{2}}}\right)+{\frac {\ell ^{2}}{c^ {2}}}}$
Romboedryczny:
${\ Displaystyle {\ Frac {1} {d ^ {2}}} = {\ Frac {(h ^ {2} + k ^ {2} + \ ell ^ {2} )\sin ^{2}\alpha +2(hk+k\ell +h\ell )(\cos ^{2}\alpha -\cos \alpha )}{a^{2}(1-3\cos ^{2}\alfa +2\cos ^{3}\alfa )}}}$
rombowy:
${\ Displaystyle {\ Frac {1} {d ^ {2}}} = {\ Frac {h ^ {2}} {a ^{2}}}+{\frac {k^{2}}{b^{2}}}+{\frac {\ell ^{2}}{c^{2}}}}$
jednoskośny:
${\ Displaystyle {\ Frac {1} {d$
trójkliniczny:
${\ Displaystyle {\ Frac {1} {d ^ {2}}} = {\ Frac {{\ Frac {h ^ {2}} {a ^ {2} }}}\sin ^{2}\alpha +{\frac {k^{2}}{b^{2}}}\sin ^{2}\beta +{\frac {\ell ^{2}} {c^{2}}}\sin ^{2}\gamma +{\frac {2k\ell }{bc}}(\cos \beta \cos \gamma -\cos \alpha )+{\frac {2h \ell }{ac}}(\cos \gamma \cos \alpha -\cos \beta )+{\frac {2hk}{ab}}(\cos \alpha \cos \beta -\cos \gamma )}{ 1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}}$

Klasyfikacja według symetrii

Cechą charakterystyczną kryształu jest jego naturalna symetria. Wykonanie pewnych operacji symetrii na sieci krystalicznej pozostawia ją niezmienioną. Wszystkie kryształy mają symetrię translacyjną w trzech kierunkach, ale niektóre mają również inne elementy symetrii. Na przykład obrócenie kryształu o 180 ° wokół określonej osi może skutkować konfiguracją atomów, która jest identyczna z pierwotną konfiguracją; kryształ ma podwójną symetrię obrotową wokół tej osi. Oprócz symetrii obrotowej kryształ może posiadać symetrię w postaci płaszczyzn lustrzanych, a także tzw. Pełną klasyfikację kryształu uzyskuje się, gdy zidentyfikowane zostaną wszystkie nieodłączne symetrie kryształu.

Systemy kratowe

Systemy kratowe to grupowanie struktur krystalicznych zgodnie z układem osiowym używanym do opisu ich sieci. Każdy układ kratownicowy składa się z zestawu trzech osi w określonym układzie geometrycznym. Wszystkie kryształy należą do jednego z siedmiu systemów kratowych. Są podobne do siedmiu systemów kryształów , ale nie do końca takie same .

Kryształowa rodzina	System kratowy	Grupa punktów ( notacja Schönfliesa )	14 krat Bravais
Kryształowa rodzina	System kratowy	Grupa punktów ( notacja Schönfliesa )	Prymitywny (P)	Wyśrodkowany na podstawie (S)	Skoncentrowany na ciele (I)	Wyśrodkowany na twarz (F)
trójklinika (a)		C _i	aP
Jednoskośny (m)		C _{2 godz}	poseł	SM
rombowy (o)		D _{2 godz}	oP	OS	o ja	z
czworokątny (t)		D _{4 godz}	tP		tI
Sześciokątny (h)	Romboedryczny	D _3d	godz
Sześciokątny (h)	Sześciokątny	D _{6 godz}	HP
Sześcienny (c)		O _godz	cP		cI	cF

Najprostszy i najbardziej symetryczny układ sześcienny lub izometryczny ma symetrię sześcianu , to znaczy posiada cztery potrójne osie obrotu zorientowane względem siebie pod kątem 109,5° ( kąt czworościenny ). Te potrójne osie leżą wzdłuż przekątnych bryły sześcianu. Pozostałe sześć systemów kratowych to heksagonalny , tetragonalny , romboedryczny (często mylony z trygonalnym układem kryształów ), rombowy , jednoskośny i trójskośny .

kraty Bravais

Sieci Bravais , zwane również sieciami przestrzennymi , opisują geometryczny układ punktów sieci, a tym samym translacyjną symetrię kryształu. Trzy wymiary przestrzeni dają 14 różnych krat Bravais opisujących symetrię translacyjną. Wszystkie znane obecnie materiały krystaliczne, z wyjątkiem kwazikryształów , pasują do jednego z tych układów. Powyżej pokazano czternaście trójwymiarowych krat, sklasyfikowanych według systemu sieci.

Struktura krystaliczna składa się z tej samej grupy atomów, podstawy , rozmieszczonych wokół każdego punktu sieci. Ta grupa atomów powtarza się zatem w nieskończoność w trzech wymiarach, zgodnie z układem jednej z sieci Bravais. Charakterystyczną symetrię rotacyjną i lustrzaną komórki elementarnej opisuje jej krystalograficzna grupa punktowa .

Układy krystaliczne

System krystaliczny to zbiór grup punktowych, w których same grupy punktowe i odpowiadające im grupy przestrzenne są przypisane do systemu kratowego. Spośród 32 grup punktowych, które istnieją w trzech wymiarach, większość jest przypisana tylko do jednego systemu sieci krystalicznej, w którym to przypadku zarówno system krystaliczny, jak i system siatkowy mają tę samą nazwę. Jednak pięć grup punktów jest przypisanych do dwóch systemów sieciowych, romboedrycznego i heksagonalnego, ponieważ oba systemy sieciowe wykazują potrójną symetrię obrotową. Te grupy punktów są przypisane do trygonalnego układu kryształów.

Kryształowa rodzina	Układ kryształów	Grupa punktowa / Klasa kryształu	Schönflies	Symetria punktowa	Zamówienie	Grupa abstrakcyjna
trójkliniczny		pedał	C ₁	polarny enancjomorfik	1	trywialny ${\ Displaystyle \ mathbb {Z} _ {1}}$
trójkliniczny		pinakoidalny	Ci ₍ S ₂ )	centrosymetryczny	2	cykliczny ${\ Displaystyle \ mathbb {Z} _ {2}}$
Jednoskośny		sferoidalny	C ₂	polarny enancjomorfik	2	cykliczny ${\ Displaystyle \ mathbb {Z} _ {2}}$
		domatyczny	C _s (C _1h )	polarny	2	cykliczny ${\ Displaystyle \ mathbb {Z} _ {2}}$
		pryzmatyczny	C _{2 godz}	centrosymetryczny	4	Klein cztery ${\ Displaystyle \ mathbb {V} = \ mathbb {Z} _ {2} \ razy \ mathbb {Z} _ {2}}$
rombowy		rombowo-disfenoidalny	re ₂ (V)	enancjomorficzny	4	Klein cztery ${\ Displaystyle \ mathbb {V} = \ mathbb {Z} _ {2} \ razy \ mathbb {Z} _ {2}}$
		rombowo- piramidalny	C _2v	polarny	4	Klein cztery ${\ Displaystyle \ mathbb {V} = \ mathbb {Z} _ {2} \ razy \ mathbb {Z} _ {2}}$
		rombowo- dwupiramidowy	re _2h (V _h )	centrosymetryczny	8	${\ Displaystyle \ mathbb {V} \ razy \ mathbb {Z} _ {2}}$
tetragonalny		czworokątno-piramidalny	C ₄	polarny enancjomorfik	4	cykliczny ${\ Displaystyle \ mathbb {Z} _ {4}}$
		tetragonalny-disfenoidalny	S ₄	niecentrosymetryczny	4	cykliczny ${\ Displaystyle \ mathbb {Z} _ {4}}$
		tetragonalno-dipiramidalny	C _{4 godz}	centrosymetryczny	8	${\ Displaystyle \ mathbb {Z} _ {4} \ razy \ mathbb {Z} _ {2}}$
		tetragonalno-trapezoedryczny	D ₄	enancjomorficzny	8	dwuścienny ${\ Displaystyle \ mathbb {D} _ {8} = \ mathbb {Z} _ {4} \ rtimes \ mathbb {Z} _ {2}}$
		dwutetragonalno-piramidalny	C _4v	polarny	8	dwuścienny ${\ Displaystyle \ mathbb {D} _ {8} = \ mathbb {Z} _ {4} \ rtimes \ mathbb {Z} _ {2}}$
		tetragonalno-skanoedryczny	re _2d (V _d )	niecentrosymetryczny	8	dwuścienny ${\ Displaystyle \ mathbb {D} _ {8} = \ mathbb {Z} _ {4} \ rtimes \ mathbb {Z} _ {2}}$
		ditetragonal-dipiramidal	D _{4 godz}	centrosymetryczny	16	${\ Displaystyle \ mathbb {D} _ {8} \ razy \ mathbb {Z} _ {2}}$
sześciokątny	trójkątny	trójkątno-piramidalny	C ₃	polarny enancjomorfik	3	cykliczny ${\ Displaystyle \ mathbb {Z} _ {3}}$
		romboedryczny	do _3i (S ₆ )	centrosymetryczny	6	cykliczny ${\ Displaystyle \ mathbb {Z} _ {6} = \ mathbb {Z} _ {3} \ razy \ mathbb {Z} _ {2}}$
		trójkątno-trapezoedryczny	D3 _{_}	enancjomorficzny	6	dwuścienny ${\ Displaystyle \ mathbb {D} _ {6} = \ mathbb {Z} _ {3} \ rtimes \ mathbb {Z} _ {2}}$
		dwutrygonalny-piramidalny	C _3v	polarny	6	dwuścienny ${\ Displaystyle \ mathbb {D} _ {6} = \ mathbb {Z} _ {3} \ rtimes \ mathbb {Z} _ {2}}$
		dwutrygonalny-skanoedryczny	D _3d	centrosymetryczny	12	dwuścienny ${\ Displaystyle \ mathbb {D} _ {12} = \ mathbb {Z} _ {6} \ rtimes \ mathbb {Z} _ {2}}$
	sześciokątny	sześciokątne-piramidalne	C ₆	polarny enancjomorfik	6	cykliczny ${\ Displaystyle \ mathbb {Z} _ {6} = \ mathbb {Z} _ {3} \ razy \ mathbb {Z} _ {2}}$
		trygonalny-dipiramidalny	C _{3 godz}	niecentrosymetryczny	6	cykliczny ${\ Displaystyle \ mathbb {Z} _ {6} = \ mathbb {Z} _ {3} \ razy \ mathbb {Z} _ {2}}$
		heksagonalny-dipiramidalny	C _{6 godz}	centrosymetryczny	12	${\ Displaystyle \ mathbb {Z} _ {6} \ razy \ mathbb {Z} _ {2}}$
		sześciokątno-trapezoedryczny	D ₆	enancjomorficzny	12	dwuścienny ${\ Displaystyle \ mathbb {D} _ {12} = \ mathbb {Z} _ {6} \ rtimes \ mathbb {Z} _ {2}}$
		dwusześciokątna piramida	C _6v	polarny	12	dwuścienny ${\ Displaystyle \ mathbb {D} _ {12} = \ mathbb {Z} _ {6} \ rtimes \ mathbb {Z} _ {2}}$
		dwutrygonalny-dipiramidalny	D _{3 godz}	niecentrosymetryczny	12	dwuścienny ${\ Displaystyle \ mathbb {D} _ {12} = \ mathbb {Z} _ {6} \ rtimes \ mathbb {Z} _ {2}}$
		diheksagonalny-dipiramidowy	D _{6 godz}	centrosymetryczny	24	${\ Displaystyle \ mathbb {D} _ {12} \ razy \ mathbb {Z} _ {2}}$
sześcienny		tetartoidalny	T	enancjomorficzny	12	na przemian ${\ Displaystyle \ mathbb {A} _ {4}}$
		diploidalny	T _godz	centrosymetryczny	24	${\ Displaystyle \ mathbb {A} _ {4} \ razy \ mathbb {Z} _ {2}}$
		żyroskopowy	O	enancjomorficzny	24	symetryczny ${\ Displaystyle \ mathbb {S} _ {4}}$
		sześciościenny	T _d	niecentrosymetryczny	24	symetryczny ${\ Displaystyle \ mathbb {S} _ {4}}$
		sześciokątny	O _godz	centrosymetryczny	48	${\ Displaystyle \ mathbb {S} _ {4} \ razy \ mathbb {Z} _ {2}}$

W sumie istnieje siedem układów kryształów: trójskośny, jednoskośny, rombowy, tetragonalny, trygonalny, sześciokątny i sześcienny.

Grupy punktowe

Grupa punktów krystalograficznych lub klasa kryształów to grupa matematyczna obejmująca operacje symetrii, które pozostawiają co najmniej jeden punkt nie poruszony i które pozostawiają niezmieniony wygląd struktury kryształu. Te operacje symetrii obejmują

Odbicie , które odzwierciedla strukturę na płaszczyźnie odbicia
Obrót , który obraca konstrukcję o określoną część okręgu wokół osi obrotu
Inwersja , która zmienia znak współrzędnych każdego punktu względem środka symetrii lub punktu inwersji
Niewłaściwy obrót , który składa się z obrotu wokół osi, po którym następuje odwrócenie.

Osie obrotu (właściwe i niewłaściwe), płaszczyzny odbicia i środki symetrii są zbiorczo nazywane elementami symetrii . Istnieją 32 możliwe klasy kryształów. Każdy z nich można zaklasyfikować do jednego z siedmiu systemów kryształów.

Grupy kosmiczne

Oprócz operacji grupy punktowej grupa przestrzenna struktury krystalicznej zawiera translacyjne operacje symetrii. Obejmują one:

Czyste translacje , które przesuwają punkt wzdłuż wektora
Śrubowe osie , które obracają punkt wokół osi, jednocześnie przesuwając się równolegle do osi.
Płaszczyzny schodzenia , które odbijają punkt przez płaszczyznę, przesuwając go równolegle do płaszczyzny.

Istnieje 230 różnych grup przestrzennych.

Koordynacja atomowa

Rozważając ułożenie atomów względem siebie, ich liczby koordynacyjne, odległości międzyatomowe, rodzaje wiązań itp., można stworzyć ogólny pogląd na struktury i alternatywne sposoby ich wizualizacji.

Zamknij pakowanie

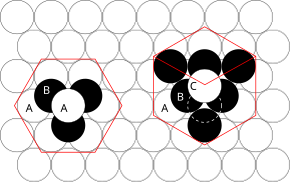
Krata hcp (po lewej) i krata fcc (po prawej)

Związane z tym zasady można zrozumieć, rozważając najskuteczniejszy sposób upakowania razem równych rozmiarów kul i ułożenia ciasno upakowanych płaszczyzn atomowych w trzech wymiarach. Na przykład, jeśli płaszczyzna A leży pod płaszczyzną B, istnieją dwa możliwe sposoby umieszczenia dodatkowego atomu na wierzchu warstwy B. Gdyby dodatkowa warstwa została umieszczona bezpośrednio nad płaszczyzną A, dałoby to następującą serię:

... ABABABAB ...

Ten układ atomów w strukturze krystalicznej jest znany jako heksagonalne ścisłe upakowanie (hcp) .

Jeśli jednak wszystkie trzy płaszczyzny są przesunięte względem siebie i sekwencja jest powtarzana dopiero po umieszczeniu czwartej warstwy bezpośrednio nad płaszczyzną A, powstaje następująca sekwencja:

... ABCABCABC ...

Ten typ układu strukturalnego jest znany jako sześcienne ścisłe upakowanie (ccp) .

Komórką elementarną układu atomów ccp jest sześcienna komórka elementarna skupiona na twarzy (fcc). Nie jest to od razu oczywiste, ponieważ ściśle upakowane warstwy są równoległe do płaszczyzn {111} komórki elementarnej fcc. Istnieją cztery różne orientacje ściśle upakowanych warstw.

APF i CN

Jedną z ważnych cech struktury krystalicznej jest jej współczynnik upakowania atomowego (APF). Oblicza się to przy założeniu, że wszystkie atomy są identycznymi kulami, których promień jest wystarczająco duży, aby każda kula stykała się z następną. Atomowy współczynnik upakowania to proporcja przestrzeni zajmowanej przez te kulki, którą można obliczyć, obliczając całkowitą objętość kul i dzieląc ją przez objętość komórki w następujący sposób:

{\ Displaystyle \ operatorname {APF} = {\ Frac {N_ {\ operatorname {cząstka}} V_ {\ operatorname {\

Inną ważną cechą struktury krystalicznej jest jej liczba koordynacyjna (CN). Jest to liczba najbliższych sąsiadów centralnego atomu w strukturze.

Poniżej przedstawiono APF i CN najpowszechniejszych struktur krystalicznych:

Struktura krystaliczna	Atomowy współczynnik upakowania	Numer koordynacyjny ( Geometria )
Diament sześcienny	0,34	4 ( czworościan )
Prosty sześcienny	0,52	6 ( ośmiościan )
Sześcienny skoncentrowany na ciele (BCC)	0,68	8 ( Kostka )
Sześcienny centrowany na twarzy (FCC)	0,74	12 ( sześcienny ośmiościan )
Sześciokątne zwarte (HCP)	0,74	12 ( Trójkątna ortobicupola )

74% wydajność upakowania FCC i HCP to maksymalna możliwa gęstość w komórkach elementarnych zbudowanych z kul tylko jednego rozmiaru.

Witryny pełnoekranowe

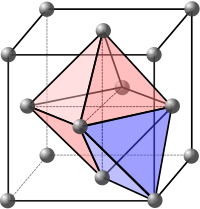
Oktaedryczne (czerwone) i czworościenne (niebieskie) miejsca śródmiąższowe w sieci sześciennej skupionej na twarzy .

Miejsca śródmiąższowe odnoszą się do pustych przestrzeni między atomami w sieci krystalicznej. Przestrzenie te mogą być wypełnione przeciwnie naładowanymi jonami, tworząc wieloelementowe struktury. Mogą być również wypełnione atomami zanieczyszczeń lub samoistnymi elementami śródmiąższowymi, tworząc defekty śródmiąższowe .

Wady i zanieczyszczenia

Prawdziwe kryształy mają defekty lub nieregularności w idealnych układach opisanych powyżej i to właśnie te defekty w decydujący sposób determinują wiele właściwości elektrycznych i mechanicznych rzeczywistych materiałów.

Zanieczyszczenia

Kiedy jeden atom zastępuje jeden z głównych składników atomowych w strukturze kryształu, może nastąpić zmiana właściwości elektrycznych i termicznych materiału. Zanieczyszczenia mogą również objawiać się jako związane ze spinem elektronów w niektórych materiałach. Badania nad zanieczyszczeniami magnetycznymi pokazują, że niewielkie stężenia zanieczyszczeń mogą wpływać na znaczną zmianę niektórych właściwości, takich jak ciepło właściwe, jak na przykład zanieczyszczenia w półprzewodnikowych stopach ferromagnetycznych mogą prowadzić do różnych właściwości, jak przewidywano po raz pierwszy pod koniec lat sześćdziesiątych.

Dyslokacje

Dyslokacje w sieci krystalicznej to defekty liniowe związane z lokalnymi polami naprężeń. Dyslokacje umożliwiają ścinanie przy niższym naprężeniu niż to potrzebne do uzyskania doskonałej struktury krystalicznej. Lokalne pola naprężeń skutkują interakcjami między dyslokacjami, które następnie skutkują umocnieniem odkształceniowym lub obróbką plastyczną na zimno .

Granice ziarna

Granice ziaren to interfejsy, na których spotykają się kryształy o różnych orientacjach. Granica ziaren to interfejs jednofazowy, w którym kryształy po obu stronach granicy są identyczne, z wyjątkiem orientacji. Termin „granica krystaliczna” jest czasami, choć rzadko, używany. Obszary graniczne ziaren zawierają te atomy, które zostały zakłócone z ich pierwotnych miejsc sieciowych, dyslokacji i zanieczyszczeń, które migrowały do granicy ziaren o niższej energii.

Traktując granicę ziaren geometrycznie jako interfejs pojedynczego kryształu podzielonego na dwie części, z których jedna jest obrócona, widzimy, że istnieje pięć zmiennych wymaganych do zdefiniowania granicy ziaren. Pierwsze dwie liczby pochodzą z wektora jednostkowego, który określa oś obrotu. Trzecia liczba oznacza kąt obrotu ziarna. Ostatnie dwie liczby określają płaszczyznę granicy ziaren (lub wektor jednostkowy normalny do tej płaszczyzny).

Granice ziaren zakłócają ruch dyslokacji w materiale, więc zmniejszenie rozmiaru krystalitów jest powszechnym sposobem poprawy wytrzymałości, jak opisuje zależność Halla-Petcha . Ponieważ granice ziaren są defektami w strukturze kryształu, mają tendencję do zmniejszania elektrycznej i cieplnej materiału. Wysoka energia międzyfazowa i stosunkowo słabe wiązanie w większości granic ziaren często czyni je preferowanymi miejscami początku korozji i wytrącania nowych faz z ciała stałego. Są również ważne dla wielu mechanizmów pełzania .

Granice ziaren mają na ogół szerokość zaledwie kilku nanometrów. W typowych materiałach krystality są na tyle duże, że granice ziaren stanowią niewielką część materiału. Jednak osiągalne są bardzo małe rozmiary ziaren. W nanokrystalicznych ciałach stałych granice ziaren stają się znaczącym ułamkiem objętościowym materiału, co ma ogromny wpływ na takie właściwości, jak dyfuzja i plastyczność . W granicy małych krystalitów, gdy udział objętościowy granic ziaren zbliża się do 100%, materiał przestaje mieć jakikolwiek charakter krystaliczny, a tym samym staje się amorficznym ciałem stałym .

Przewidywanie struktury

Trudność przewidywania stabilnych struktur krystalicznych na podstawie znajomości jedynie składu chemicznego od dawna stanowi przeszkodę na drodze do w pełni obliczeniowego projektowania materiałów. Teraz, dzięki potężniejszym algorytmom i wysokowydajnym obliczeniom, struktury o średniej złożoności można przewidywać za pomocą takich podejść, jak algorytmy ewolucyjne , losowe próbkowanie lub metadynamika.

Struktury krystaliczne prostych ciał stałych jonowych (np. NaCl lub sól kuchenna) od dawna są racjonalizowane w kategoriach reguł Paulinga , po raz pierwszy przedstawionych w 1929 roku przez Linusa Paulinga , przez wielu określanego jako „ojciec wiązania chemicznego”. Pauling rozważał również naturę sił międzyatomowych w metalach i doszedł do wniosku, że około połowa z pięciu orbitali d w metalach przejściowych bierze udział w wiązaniu, a pozostałe niewiążące orbitale d są odpowiedzialne za właściwości magnetyczne. Pauling był zatem w stanie skorelować liczbę orbitali d w tworzeniu wiązań z długością wiązań, a także z wieloma fizycznymi właściwościami substancji. Następnie wprowadził metaliczny orbital, dodatkowy orbital niezbędny do umożliwienia nieskrępowanego rezonansu wiązań walencyjnych między różnymi strukturami elektronicznymi.

W teorii rezonansowych wiązań walencyjnych czynniki decydujące o wyborze jednej spośród alternatywnych struktur krystalicznych metalu lub związku międzymetalicznego krążą wokół energii rezonansu wiązań pomiędzy pozycjami międzyatomowymi. Oczywiste jest, że niektóre mody rezonansu miałyby większy wkład (byłyby bardziej stabilne mechanicznie niż inne), aw szczególności prosty stosunek liczby wiązań do liczby pozycji byłby wyjątkowy. Wynikająca z tego zasada polega na tym, że szczególna stabilność jest związana z najprostszymi stosunkami lub „liczbami wiązań”: 1 ⁄ 2 , 1 ⁄ 3 , 2 ⁄ 3 , 1 ⁄ 4 , 3 ⁄ 4 itd. Wybór struktury i wartości stosunek osiowy (który określa względne długości wiązań) jest zatem wynikiem wysiłku atomu, aby wykorzystać swoją wartościowość do tworzenia stabilnych wiązań z prostymi ułamkowymi liczbami wiązań.

Po postulowaniu bezpośredniej korelacji między stężeniem elektronów a strukturą krystaliczną stopów fazy beta, Hume-Rothery przeanalizował trendy temperatur topnienia, ściśliwości i długości wiązań w funkcji numeru grupy w układzie okresowym pierwiastków w celu ustalenia systemu wartościowości pierwiastki przejściowe w stanie metalicznym. Zabieg ten podkreślał zatem rosnącą siłę wiązania w funkcji liczby grup. Działanie sił kierunkowych zostało podkreślone w jednym artykule na temat relacji między hybrydami wiążącymi a strukturami metalicznymi. Wynikająca z tego korelacja między strukturami elektronowymi i krystalicznymi jest podsumowana przez pojedynczy parametr, masę d-elektronów na zhybrydyzowany metaliczny orbital. Wartość „d-waga” wynosi odpowiednio 0,5, 0,7 i 0,9 dla struktur fcc, hcp i bcc. W ten sposób staje się oczywisty związek między d-elektronami a strukturą kryształu.

W przewidywaniach / symulacjach struktury krystalicznej zwykle stosuje się okresowość, ponieważ system jest wyobrażany jako nieograniczony we wszystkich kierunkach. Rozpoczynając od struktury trójskośnej bez założonej dalszej właściwości symetrii, system można zmusić do wykazania pewnych dodatkowych właściwości symetrii, stosując drugie prawo Newtona dotyczące cząstek w komórce elementarnej i niedawno opracowane równanie dynamiczne dla wektorów okresu układu (parametry sieci, w tym kąty ), nawet jeśli system podlega naprężeniom zewnętrznym.

Wielopostaciowość

Kwarc jest jedną z kilku krystalicznych form krzemionki , SiO ₂ . Do najważniejszych form krzemionki należą: α-kwarc , β-kwarc , trydymit , krystobalit , koezyt i stiszowit .

Polimorfizm to występowanie wielu form krystalicznych materiału. Występuje w wielu materiałach krystalicznych, w tym w polimerach , minerałach i metalach . Zgodnie z regułami równowag fazowych Gibbsa, te unikalne fazy krystaliczne zależą od intensywnych zmiennych, takich jak ciśnienie i temperatura. Polimorfizm jest powiązany z alotropią , która odnosi się do brył elementarnych . Pełna morfologia materiału jest opisana przez polimorfizm i inne zmienne, takie jak pokrój kryształu , frakcja amorficzna lub defekty krystalograficzne . Polimorfy mają różną stabilność i mogą spontanicznie i nieodwracalnie przekształcić się z postaci metastabilnej (lub postaci niestabilnej termodynamicznie) w postać stabilną w określonej temperaturze. Wykazują również różne temperatury topnienia , rozpuszczalności i dyfrakcji rentgenowskiej .

Dobrym tego przykładem jest kwarcowa forma dwutlenku krzemu lub SiO ₂ . W zdecydowanej większości krzemianów atom Si wykazuje tetraedryczną koordynację przy 4 atomach tlenu. Wszystkie formy krystaliczne z wyjątkiem jednej obejmują tetraedryczne jednostki {SiO ₄ } połączone ze sobą wspólnymi wierzchołkami w różnych układach. W różnych minerałach czworościany wykazują różne stopnie usieciowania i polimeryzacji. Na przykład występują pojedynczo, połączone ze sobą parami, w większych skończonych klastrach, w tym pierścieniach, w łańcuchach, podwójnych łańcuchach, arkuszach i trójwymiarowych ramach. Minerały są podzielone na grupy w oparciu o te struktury. W każdej z 7 stabilnych termodynamicznie form krystalicznych lub odmian polimorficznych krystalicznego kwarcu tylko 2 z 4 krawędzi czworościanów {SiO ₄ } są wspólne z innymi, co daje wzór chemiczny netto krzemionki: SiO ₂ .

cyna elementarna (Sn), która jest plastyczna w temperaturze zbliżonej do temperatury otoczenia, ale po schłodzeniu staje się krucha . Ta zmiana właściwości mechanicznych wynika z istnienia dwóch głównych alotropów , α- i β-cyny. Dwa alotropy , które występują przy normalnym ciśnieniu i temperaturze, α-cyna i β-cyna, są bardziej powszechnie znane odpowiednio jako cyna szara i cyna biała . Dwa kolejne alotropy, γ i σ, istnieją w temperaturach powyżej 161 ° C i ciśnieniach powyżej kilku GPa. Biała cyna jest metaliczna i jest stabilną postacią krystaliczną w temperaturze pokojowej lub wyższej. Poniżej 13,2 ° C cyna występuje w postaci szarej, która ma sześcienną strukturę krystaliczną diamentu , podobną do diamentu , krzemu lub germanu . Szara cyna nie ma żadnych właściwości metalicznych, jest matowoszarym proszkowym materiałem i ma niewiele zastosowań poza kilkoma specjalistycznymi w półprzewodnikach . Chociaż temperatura przemiany α–β cyny wynosi nominalnie 13,2°C, zanieczyszczenia (np. Al, Zn itp.) obniżają temperaturę przemiany znacznie poniżej 0°C, a po dodaniu Sb lub Bi przemiana może w ogóle nie nastąpić.

Właściwości fizyczne

Dwadzieścia z 32 klas kryształów to piezoelektryki , a kryształy należące do jednej z tych klas (grup punktowych) wykazują piezoelektryczność . Wszystkie klasy piezoelektryczne nie mają symetrii inwersji . Każdy materiał rozwija dielektryczną po przyłożeniu pola elektrycznego, ale substancja, która ma taką naturalną separację ładunków nawet przy braku pola, nazywana jest materiałem polarnym. To, czy materiał jest polarny, zależy wyłącznie od jego struktury krystalicznej. Tylko 10 z 32 grup punktów jest biegunowych . Wszystkie kryształy polarne są piroelektryczne , więc 10 klas kryształów polarnych jest czasami określanych jako klasy piroelektryczne.

Istnieje kilka struktur krystalicznych, zwłaszcza struktura perowskitu , które wykazują właściwości ferroelektryczne . Jest to analogiczne do ferromagnetyzmu , ponieważ przy braku pola elektrycznego podczas produkcji kryształ ferroelektryczny nie wykazuje polaryzacji. Po przyłożeniu pola elektrycznego o wystarczającej wielkości kryształ zostaje trwale spolaryzowany. Polaryzację tę można odwrócić za pomocą wystarczająco dużego ładunku przeciwnego, w taki sam sposób, w jaki można odwrócić ferromagnes. Jednak chociaż nazywane są ferroelektrykami, efekt wynika ze struktury krystalicznej (a nie z obecności metalu żelaznego).

Zobacz też

Strefa Brillouina - prymitywna komórka w odwrotnej sieci przestrzennej kryształów
Inżynieria kryształów
Wzrost kryształów – główny etap procesu krystalizacji
Krystalograficzna baza danych
Współrzędne ułamkowe
Fazy Franka-Kaspera
Notacja Hermanna – Mauguina - Notacja reprezentująca symetrię w grupach punktów, grupach płaszczyzn i grupach przestrzennych
Ogrzewany laserowo wzrost cokołu - technika wzrostu kryształów
Ciekły kryształ – Stan materii o właściwościach zarówno konwencjonalnych cieczy, jak i kryształów
Funkcja Pattersona - krystalografia rentgenowska
Układ okresowy (struktura krystaliczna) - (dla pierwiastków, które są stałe w standardowej temperaturze i ciśnieniu) daje strukturę krystaliczną najbardziej stabilnej termodynamicznie formy (postaci) w tych warunkach. We wszystkich innych przypadkach podana struktura dotyczy pierwiastka w jego temperaturze topnienia
Komórka prymitywna - powtarzająca się jednostka utworzona przez wektory obejmujące punkty sieci
Kryształ zaszczepiający - Mały kawałek pojedynczego kryształu używany do zainicjowania wzrostu większego kryształu
Ogniwo Wignera – Seitza - prymitywna komórka sieci krystalicznych z zastosowanym rozkładem Woronoja

Linki zewnętrzne

Media związane ze strukturami kryształów w Wikimedia Commons

Podstawowe aspekty inżynierii materiałowej
Inżynieria materiałowa	Struktura Nieruchomości Przetwarzanie Wydajność
Klasy materiałów	Ceramika Szkło Półprzewodniki Kompozyty Stopy metali polimery
Metody analizy	Analiza charakterystyki Diagram fazowy
Charakterystyka materiału	Struktura krystaliczna Struktura elektroniczna Mikrostruktura

Układy krystaliczne
krata Bravais Grupa punktów krystalograficznych
Siedem systemów 3D	trójskośny (anortyczny) Jednoskośny rombowy tetragonalny trygonalne i sześciokątne sześcienny (izometryczny)
Cztery systemy 2D	skośny prostokątny kwadrat sześciokątny